Abstract
The wind drag coefficient, , has a great influence on the numerical results obtained from shallow lakes. To analyze the modeling impacts of on wind-driven currents, a series of numerical simulations of Lake Taihu were conducted at three grid resolutions (800 m × 800 m, 400 m × 400 m, and 100 m × 100 m) using the empirical formulae of Flather (F76), Large and Pond (LP81), Large and Yeager (LY04), Andreas (A12), and Gao (G20). The G20 formula produced the optimum results of all the formulae for both the water level and velocity simulations; however, the grid resolution was found to have a significant influence on simulation in G20 cases. Thus, the G20 formula is only recommended when using a high-resolution grid to meet the accuracy requirements of analyzing wind-driven currents in the numerical modeling of Lake Taihu. A combination of the A12 formula and a coarse grid is preferred when taking computational efficiency into consideration.
1. Introduction
Lake Taihu, the third largest freshwater lake in China with a surface area of 2388 and an average water depth of 1.9 m, is a typical fetch-limited shallow lake with wind-driven currents (Tsanis 1989 [1], Wu 2006 [2], Li 2011 [3]). Its basin accounts for 7.0% of China’s water resources and supports 18.8% of the national GDP; therefore, it is vital that the water quality of Lake Taihu is maintained. Eutrophication has been the most serious environmental issue of the around-Taihu area over the past two decades. As nutrients are released into the lake’s water body from both intenal and extenal resources and varying both spatially and temporally, one of the accepted research methods is to construct high resolution numerical models of Lake Taihu, taking into account the effects of sediment release and the external loads from the tributaries (Mao 2008 [4]). The movement of wind-driven currents is considered to be the main factor affecting the water quality of large shallow lakes due to sediment redistribution, contaminant transport, and nutrient resuspension (Li 2017 [5], Chu 2019 [6]). In numerical models, the influence of wind-driven current is traditionally imposed through the wind stress term, expressed as , where is the wind stress; is the air density; ; is the wind speed at 10 m height measured over the free surface, m/s; is the wind stress drag coefficient, representing the momentum flux (Kranenburg 2010 [7], Li 2012 [8], Wróbel-Niedźwiecka 2019 [9], Zhang 2023 [10]). is invariably the most important physical parameter for determining the accuracy of wind-driven models.
As the collection of observed data has increased over the past hundred years, many empirical parameterization methods used to obtain the value of have been formulated, and they can be divided into several groups as follows:
- Ignore changes in the roughness of free surfaces and assume that the value of is constant in both time and space (Morales-Marin 2017 [11], Xu 2019 [12], Oliveira 2019 [13]);
- Assess a variety of observed data to establish a linear relationship between and the wind speed (Sheppard 1972 [14], Flather 1976 [15], Large and Pond 1981 [16], Geernaert 1987 [17], Ataktürk and Katsaros 1999 [18]). These kinds of parameterization methods can be written in the general form given by Guan and Xie (2004) [19];
- Consider the effects of surface tension and swell at low wind speeds to obtain the nonlinear relationship between the value and the wind speed (Yelland and Taylor 1996 [20], Large and Yeager 2004 [21], Andreas 2012 [22]);
- Take both wind speed and sea state parameters into consideration. Based on the theory of Janssen (1991) [23], some parameterizations have been conducted using an ocean wave model (Tolman and Chalikov 1996 [24]). These mathematical expressions of are often used in numerical simulations of storm surges. Multiple nonlinear parameterization methods of are indicated, and they are related not only to wind speed but also to wind blowing fetch and water depth (Mueller and Veron 2008 [25], Gao 2020 [26]).
In the first three parameterization methods, the value of is either constant or is only related to wind speed. However, many studies have suggested that wind stress in ocean conditions is related not only to the wind speed, but also to the sea state (Mastenbroek 1993 [27], Smith 1992 [28]). Smith (1992) [28] analyzed data measured in the North Sea and found that the value was strongly related to the wave age. By analyzing the observed data, Ebuchi (1990) [29] demonstrated that the value is negatively correlated with wave age; wave-induced stress in mature wind waves is larger than that of young wind waves. When determining the wind-induced current in fetch-limited shallow lakes, it was found that the state variables affecting the value are different from those in the ocean (Gao 2019 [30]). Elfouhail (1997) [31] studied the influence of water state parameters on wind stress and found that the effect of wind blowing fetch on wind stress value should not be ignored. It was found that when the wind speed is constant, the value has a positive correlation with wind blowing fetch and a negative correlation with water depth. Most of the parameterization methods used to calculate are based on a marine environment; previous studies have concentrated more on the effects that these parameterization methods have on wind-induced currents in this context (Chu 2019 [6], Fang 2018 [32], Moon 2004 [33]). As such, the different parameterization methods lack applicability in the context of wind-induced currents in fetch-limited shallow lakes. This study aims to investigate the influence of various parameterization methods on wind-induced current modeling in a typical fetch-limited shallow lake—Taihu Lake. For this purpose, a high-resolution unstructured model is developed based on the TELEMAC3D module and evaluated against the data obtained from Taihu Lake. Five parameterization methods are chosen for their importance in the field for testing in Taihu Lake:
- The linear relationship developed by Flather (1976) [15];
- The linear relationship developed by Large and Pond (1981) [16];
- The nonlinear relationship developed by Large and Yeager (2004) [21];
- The nonlinear relationship developed by Andreas (2012) [22];
- The nonlinear relationship considering the influence of wind blowing fetch and water depth developed by Gao (2020) [26].
The details of the five parameterization methods are described in Section 2.2. The parameterization method developed by Gao (2020) [26] requires the spatial distribution of wind blowing fetch and water depth to be known, and the grid resolution may have a great influence on the numerical results; therefore, additional cases with different grid resolutions (800 m × 800 m, 400 m × 400 m, and 100 m × 100 m) were set to study the effect of each resolution on the numerical results for the five parameterization methods. Descriptions of the methodology of this study are given in Section 2. Section 3 introduces the numerical setting and model configuration. Section 4 describes the results of the model in response to the different parameterization methods and grid resolutions. A summary and our conclusions are given in Section 5.
2. Methodology
2.1. Description of 3D Numerical Model
We chose to build our numerical model of wind-induced current and waves based on the OPEN TELEMAC-MASCARET system https://www.opentelemac.org (accessed on 5 December 2022), which was developed by the Company Electricité de France (EDF), Paris, France. The TELEMAC3D module is a three-dimensional hydrodynamic model which solves the Navier–Stokes equations using finite element techniques and uses the sigma coordinate for vertical discretization. The unstructured mesh used by the Telemac3D module is especially suitable for numerical simulations of shallow lakes possessing a complex geometry and dynamic physical processes (Costi 2018 [34], Kopmann and Markofsky 2000 [35]). The non-hydrostatic Navier–Stokes equations used in TELEMAC3D can be written as follows:
where t is time; u represents velocity; and are the water density and air density, respectively; p and are the total pressure and dynamic pressure, respectively; G is the gravity vector; g is the acceleration due to gravity; is the dynamic molecular viscosity; F is the source terms denoting the bottom friction and wind force; p is the atmospheric pressure; and z are free surface elevation and depth per layer, respectively. Equations are spatially discretized using the finite element technique. In case the influence of wind is taken into account, wind forcing appears in the equations through the condition at the surface:
where is the horizontal velocity at the free surface; is the wind drag coefficients; is the wind velocity measured 10 m above the free surface. The k- model is employed to compute the horizontal and vertical turbulence; the turbulent kinetic energy k and the dissipation of turbulent kinetic energy at the free surface consider the influence of wind and are computed as follows:
where is the Prandtl–Kolmogorov constant, , h is the local water depth.
2.2. Choice of Parameterization Methods
This study investigates the influence of parameterization methods on modeling wind-induced current. The five methods used in this study are described below.
- Flather (1976)-F76 [15]:Flather (1976) [15] parameterized based on the observed data during a storm surge in the northwest European continental shelf. This parameterization was incorporated into the default TELEMAC2D and TELEMAC3D model and is recommended by the Institute of Oceanographic Sciences (Surrey, UK).
- Large and Pond (1981)-LP81 [16]:The parameterization method developed by Large and Pond (1981) [16] is the default option in the FVCOM model. It showed good performance when measuring ocean circulation and wind-induced current in Okeechobee Lake (Ji 2008) [36] and Michigan Lake (Chen 2004) [37].
- Large and Yeager (2004)-LY04 [21]:Large and Yeager (2004) [21] used a nonlinear formula to describe the relationship between the value and wind speed. Later, this equation was chosen by the Community Climate System Model to represent the momentum transfer rate between the atmosphere and the free surface.
- Andreas (2012)-A12 [22]:Andreas (2012) [22] used the friction velocity coefficient versus the neutral-stability wind speed of 10 m and sea roughness to test the approach given by Foreman and Emeis (1993) [38]. This method has been widely used in the study of ocean circulation and lake modeling (Vieira 2020 [39], Worsnop 2017 [40]).
- Gao (2020)-G20 [26]:Gao (2020) [26] parameterized by fitting the experimental data from a wind tunnel and the observed data from shallow lakes considering the influence of wind blowing fetch and water depth. The purpose of this parameterization method is to study wind-induced currents in shallow lakes. However, it has not been used in numerical simulations yet, and therefore analyzing its applicability in this context is necessary.
Figure 1 shows the value as a function of wind speed with different parameterization methods. It was found that at low wind speeds ( 5 m/s), the differences between the values are greater than at wind speeds larger than 5 m/s. The lower the wind speed, the higher the uncertainties. When the wind speed was constant, the value calculated by the G20 method showed a positive correlation with the wind blowing fetch and a negative correlation with the water depth. The specific form of the G20 parameterization method was determined by the wind blowing fetch and water depth of each grid point.
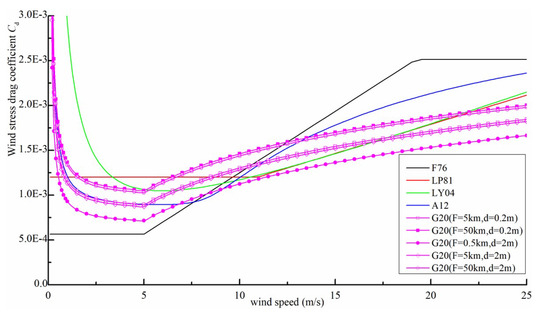
Figure 1.
Wind stress drag coefficients as a function of wind speed with different parameterizations. F76 (Equation (7), black), LP81 (Equation (8), red), LY04 (Equation (9), green), A12 (Equation (10), blue) and magenta lines with different forms of symbols represent G20 formula under different wind blowing fetches and water depths (Equation (11)).
3. Numerical Simulation
3.1. Study Area
Lake Taihu (30°55′40″~31°32′58″ N, 119°52′32′~120°36′10″ E), located in the core area of the Yangtze River Delta, is a typical limited-fetch shallow lake. The wind-induced hydrodynamic process plays an important role in its environment and ecosystem. However, the complex topography and shoreline of the lake present great challenges to the simulation of wind-induced current modeling (Hu 2006) [41]. Lake Taihu covers an area of 2338 and supplies the drinking water for the surrounding cities; it also has key roles for fisheries, aquaculture, and tourism. The average length of the lake is 68.5 in the south–north direction and 34.0 in the east–west direction. The lake shore is smooth in the southwest and tortuous in the northeast. The prevailing wind directions of Lake Taihu are southeast in summer and north in winter. A total of 172 tributaries connect to the lake. Most rivers with small discharges have no obvious impact on the flow field. For convenience, only Wangyu River, Tiaoxi River, and Taipu River were considered in this numerical simulation (Li 2011) [3].
3.2. Model Setup
The domain of our model encompasses Taihu Lake, including Wangyu River, Tiaoxi River, and Taipu River. Tributary inflow/outflow was treated in terms of source and sink. Numerical simulations were carried out from 1 to 31 August 2019. As shown in Figure 2, the model results were evaluated against the water elevations measured at the Wulou (WL), Jiapu (JP), Dapukou (DPK), Wangting (WT), Xukou (XK), and Dongtingxishan (DTXS) stations, and the velocity was measured at the V1 and V2 stations. The surface velocity was measured using two Acoustic Doppler Current Profilers (ADCPs). The initial conditions for the numerical model were a constant lake surface height of 3.55 m (the average value for the whole region) and zero velocity fields. The main driving forces for the numerical model were surface wind stress and atmospheric forcing. The wind data used to compute wind stress were acquired from 10 automatic weather stations (Taihu Basin Hydrological Information Service System) and 4 observation stations possessing sensors for detecting wind speed and direction (W1 to W4). The wind field was computed using the inverse distance weighting method with the observed data. The precipitation data were acquired by averaging the data from the Dushan and Dongtingxishan stations. Three sets of unstructured grids were set for the model (800 m × 800 m, 400 m × 400 m, and 100 m × 100 m) to analyze the effect of grid resolution sensitivity on the numerical results for the five parameterization methods. The grids used 20 layers in vertically stretched terrain following the sigma coordinate to more accurately simulate the vertical structure and changes of water bodies, as well as the variations of water flow and sediment at different depths, thereby improving the accuracy and reliability of the simulation. The specific grid parameters are shown in Table 1. The average maximum slopes of water depth for both grids were less than 0.33, avoiding pressure gradient errors from the sigma transformation (Mellor 1994) [42]. The global time step was set to 1 s in order to satisfy the Courant–Friedrichs–Lewy stability criterion (Mao 2008) [4]. The advection and diffusion of the three-dimensional variables were computed using the multidimensional upwind residual distribution scheme (MURD scheme). A calibration with respect to the Manning coefficients was carried out against the observed data (as shown in Section 4.1).
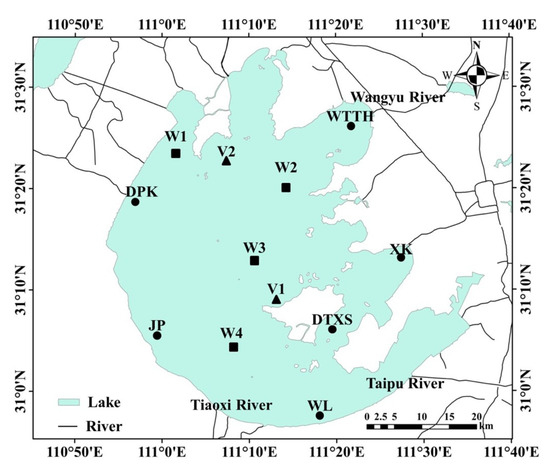
Figure 2.
The location of the study area, surrounding rivers, observational stations in and around Lake Taihu. Black circles represent the location of water level stations (WL, Wulou station; JP, Jiapu station; DPK, Dapukou station; WTTH, Wangting station; XK, Xukou station; DTXS, Dongtingxishan station). Black triangles represent the location of velocity stations (V1, ADCP1 station; V2, ADCP2 station). Black squares represent the location of wind observed stations (from W1 to W4).

Table 1.
Grid parameters with different grid resolutions.
The effectiveness of the numerical result is evaluated using the coefficient (Murphy 1992) [43] given by
where are the numerical results; are the observed values; are the mean of observed values. The performance can be classified as excellent ( > 0.65), very good (0.5 < < 0.65), good (0.2 < < 0.5), and poor ( < 0.2), respectively.
4. Results
4.1. Model Calibration
For calibration, the numerical model underwent a 4-day sequence (from 5 August to 9 August 2019) of atmospheric forcing and surface wind stress. Winds were predominantly southeasterly. The calibration of the Manning coefficients was performed with respect to the performance computed from the numerical model’s results and the data observed at the V1 station (Chen and Liu 2015) [44]. The results are shown in Figure 3. The Manning coefficients are assumed to follow a uniform distribution between 0.012 and 0.048, with values sampled randomly using the Monte Carlo method. The calibration analysis shows that when is 0.024, the coefficient of surface velocity reaches the maximum value of 0.7412; therefore, the Manning coefficient used in the numerical simulation was 0.024 for all calculated regions.
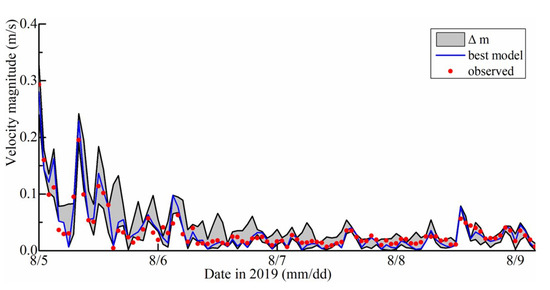
Figure 3.
Calibration of manning coefficients based on comparison of the numerical model results and observed data at V1 station. The shaded area represents the envelope of results for manning coefficients from = 0.012 (upper line) to = 0.048 (lower line); best model result ( = 0.024, the maximum value of 0.7412) is plotted as blue line, the red dot represents the observed data measured with a one-hour interval.
The results of the current structure calibration are shown in Figure 4. The observed data are given by Wu (2018) [45]. The development of wind-driven currents can cause two current structures when transporting water from the southeast portions of the lake to the northwest. Although the model current structures do not agree with the observed directions in some stations, the trend shows good agreement with the observed data. The numerical model can replicate the main feature of wind-induced circulation well.
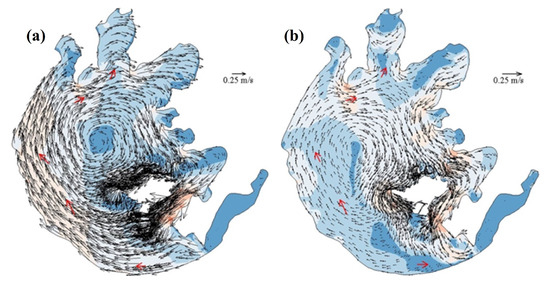
Figure 4.
(a) Surface layer current and (b) bottom layer current structures colored with velocity distribution and observed data (Wu 2018 [45]) in Lake Taihu, where black arrow denotes the modeled current structure, red arrow denotes the observed flow field.
4.2. Effects of Parameterization Methods
Figure 5 and Figure 6 show the numerical model results of the time series of water levels and velocity magnitudes produced from the five wind drag coefficient parameterization methods compared with the observed values at six water level stations and two velocity stations. The effect of the wind stress parameterization methods on the wind-induced current model is evident. The G20 shows a better performance than other four parameterization methods with the JP, DTXS, WL, and XK stations. The F76 parameterization method shows the worst performance among the six stations. For the simulation of velocity magnitude, the results of the G20 parameterization method are the closest to the observed data of the V1 and V2 velocity magnitude stations. The results of the LP81, LY04, and A12 methods are similar, while the results of the F76 parameterization method are worse at two stations. In the case of low wind speeds (<5 m/s), the velocity calculated by the LY04 parameterization method is obviously higher than the observed data due to its unrealistically high value.
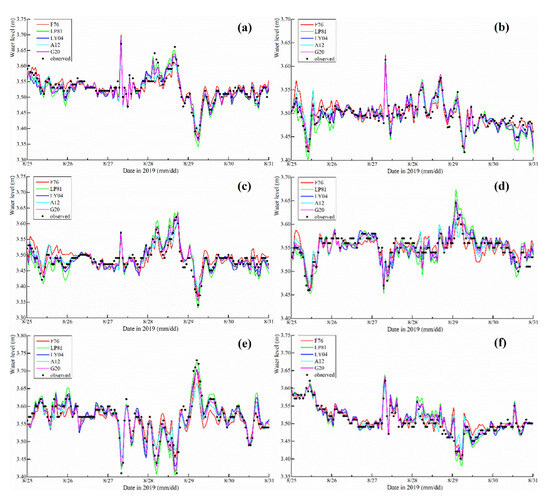
Figure 5.
Numerical model results of time series of water levels produced from F76, LP81, LY04, A12, and G20 parameterization at (a) JP, (b) DTXS, (c) WL, (d) XK, (e) WTTH, (f) DPK measurement station.
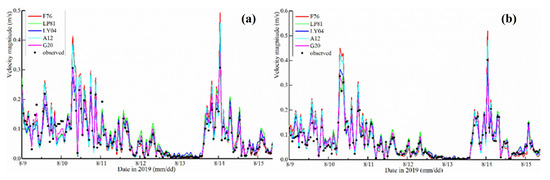
Figure 6.
Numerical model results of time series of surface velocity magnitude produced from F76, LP81, LY04, A12, and G20 parameterization at (a) V1 and (b) V2 different stations.
Table 2 and Table 3 show the coefficients of different cases between the numerical simulations and observed data. The data of the six water level stations and two velocity stations are averaged. When the wind speed is less than about 5 m/s, the LY04, A12, and G20 values are negatively correlated with wind speed; therefore, the velocity and water level data are divided into two different classes. For the water level simulation, when the wind speed is less than 5 m/s, the coefficients for the five parameterization methods are 0.6339, 0.7072, 0.7121, 0.7373, and 0.7908. The closest coefficient to 1 is obtained by the G20 parameterization method, while the farthest is obtained by the F76 method. The results are similar when the wind speed is larger than 5 m/s. For the velocity simulation, the results are similar to those of the water level simulation; the closest coefficient is produced by G20 parameterization ( = 0.7940) and the farthest is produced by F76 parameterization ( = 0.6894). From the coefficient analysis, it can be found that the G20 parameterization method shows the most satisfactory performance in both the water level and velocity simulations while the F76 parameterization method shows worse performance, and the other three parameterization methods produce similar simulation results; the A12 parameterization method shows the second best performance. Taken together, G20 parameterization is more suitable for wind-induced current simulation in shallow lakes compared to the other methods.

Table 2.
coefficients between numerical simulations and observed data. SS coefficients are obtained by averaging the results from 6 water level measurement stations (XMK, DTXS, WL, XK, WTTH, and JP).

Table 3.
The numerical model results of time series of velocity magnitude produced from different wind drag coefficients formulae compared with observed data at 2 velocity stations.
Figure 7a shows the wind stress calculated using the F76, LP81, LY04, A12, and G20 parameterization methods. It can be seen from the figure that the surface velocity at the V1 point is positively correlated with local wind speed and wind stress. A higher wind speed leads to higher wind stress and higher surface velocity. As is shown in Figure 7b, the wind stress growth rate calculated by LY04 is much higher than the other formulas with a decrease in wind speed in the low wind speed range. LY04 also shows a much higher surface velocity than that calculated by the other methods. The wind stress calculated by the F76 parameterization method is the lowest under low-wind-speed conditions, and the results of the G20, A12, and LP81 methods are similar. According to the calculation results of the two velocity stations (see Table 3), LY04 parameterization overestimates wind stress in the low wind speed range, while F76 parameterization underestimates it. A12 and G20 can simulate wind stress more effectively, and G20 parameterization has the highest accuracy.
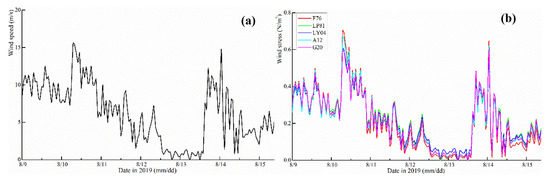
Figure 7.
(a) Wind speed and (b) wind stress produced from F76, LP81, LY04, A12, and G20 parameterization at V1 station during simulated periods from 9–15 August 2019.
4.3. Effects of Grid Resolution
Several experiments were conducted to analyze the influence of the grid resolution on wind-induced current in shallow lakes. Here, all calculation settings were kept the same except for the grid resolution. The wind stresses were calculated using the F76, LP81, LY04, A12, and G20 parameterization methods. Figure 8 compares the velocity magnitude computed using the 800 m, 400 m, and 100 m grid resolutions. Figure 8a shows the simulated velocity magnitudes under different grid resolutions at the V1 measurement station using the LP81 parameterization method. The grid resolution has a great influence on the velocity magnitude at high wind speeds, but not obviously at low wind speeds. Figure 8b shows the simulated velocity magnitudes under different grid resolutions at the V1 measurement station using the G20 parameterization, With an increase in grid resolution, the velocity magnitude gradually decreases, and the decreasing amplitude at high wind speeds is significantly higher than that at low wind speeds.
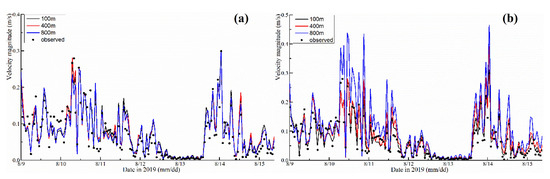
Figure 8.
Comparisons of velocity magnitude computed using the 800 m, 400 m, and 100 m grid resolution and different parameterizations of (a) LP81 and (b) G20, respectively.
Table 4 shows the average values of the five parameterization methods. From the analysis, it can be found that with an increase in grid resolution, the SS coefficients calculated by F76 and LP81 gradually decrease and the SS coefficients calculated by LY04 and A12 gradually increase. For the above four parameterization methods, the coefficients do not evidently change with a change in grid resolution. When the grid resolution increases from 800 m to 100 m, the SS coefficient of G20 rises from 0.5138 to 0.7934. For the coarse grid (800 m), the G20 parameterization method shows an undesired performance ( = 0.5138), while the SS coefficients calculated by the other four parameterization methods are all above 0.67, with A12 showing the best performance. For the medium grid (400 m), although the accuracy of the G20 is still worse than that other parameterization methods, the difference in the SS coefficients between G20 and the other four parameterization methods is very small. For the fine grid (100 m), the results are the opposite, with G20 parameterization showing the optimum result. It was found that an increase in grid resolution can improve the accuracy of the numerical simulation, and the change in grid resolution has little effect on the accuracy of the other four parameterization methods.

Table 4.
coefficients between numerical simulations and observations. Five parameterizations and different grid resolutions are compared. SS coefficients are obtained by averaging the results from 2 velocity stations (V1 and V2).
In the numerical model, the velocity magnitude is computed as the mean of the grid boxes. In a grid with high resolution, the box is small, which means that the velocity magnitude is averaged over a small area. In particular, in complex shallow lakes like Lake Taihu, the grid resolution effect can be important because high-resolution grids can better resolve the bathymetry, geography, and topography of the lake. The higher the grid resolution, the closer the bathymetry, geography, and topography obtained from the numerical simulation are to the real values, and the more accurate the flow field results. For the G20 parameterization method, the resolution effect is more important; the obtained from this method is not only related to the wind speed, but also to the wind blowing fetch and water depth at each grid node. Therefore, when the grid resolution is low, the spatial distribution of wind blowing fetch and local water depth is quite different from the real situation, which leads to a significant decrease in the accuracy of the numerical simulation’s results. It was found that the combination of a high-resolution grid and the G20 parameterization method can greatly improve the prediction of wind-induced currents in shallow lakes, while the F76, LP81, LY04, and A12 parameterization methods are not sensitive to changes in grid resolution.
4.4. Computational Efficiency
In addition, Table 5 shows the computing time taken for the different parameterization methods and grid resolutions. It is found that the computing time for the F76, LP81, LY04, and A12 calculations is similar, which is much lower than that of the G20 calculation. Table 5 shows that the higher the grid resolution, the higher the computational accuracy of G20. The calculated water depth and fetch length are closer to the real situation of Lake Taihu in a higher resolution, the value of G20 is thereby more reasonable compared to the values calculated by other four parameterization methods. When G20 parameterization is used, the wind blowing fetch on each grid node must be obtained using the wind direction before each iteration starts. As the local wind stress is calculated by combining water depth and wind speed, the G20 parameterization method takes much longer to use than the other four parameterization methods. According to Table 4 and Figure 8, when the grid is coarse, the A12 calculation time is short and its accuracy is the highest among the five parameterization methods. When the grid resolution is high, the calculation time of the G20 parameterization method is much higher than the other four parameterization methods, but its accuracy is the highest. In terms of computational efficiency, the combination of the A12 formula and a coarse grid can meet the requirements of achieving accurate simulations wind-induced current in fetch-limited shallow lakes. However, when the calculation conditions permit, the combination of the G20 formula and a high-resolution grid can significantly improve the calculation accuracy.

Table 5.
Comparisons of computing time using different parameterizations and different grid resolutions.
5. Conclusions
Wind stress is the main driving force that determines the performance of wind-induced current modeling in fetch-limited shallow lakes. parameterization, as a physical parameter used to characterize wind stress over a free surface, has a great influence on the results of numerical simulations. This study aims to analyze the influence of wind stress drag coefficient parameterization methods and grid resolutions on wind-induced currents in Lake Taihu.
A series of numerical simulations were conducted for three grid resolutions (800 m × 800 m, 400 m × 400 m, and 100 m × 100 m) using five parameterization methods. The result showed that the choice of different parameterization methods can lead to significant differences in both water level and velocity values. G20 showed a better performance in both water level and velocity simulations, while F76 showed a worse performance than other parameterization methods. In the experiments using different grid resolutions, it was found that when the grid was coarse (800 m × 800 m), the accuracy of the G20 parameterization method was at the bottom of the five methods. The combination of a high-resolution grid and the G20 parameterization method can greatly improve the prediction of wind-induced currents in shallow lakes, while the F76, LP81, LY04, and A12 parameterization methods are not sensitive to changes in grid resolution.
Apart from G20, other four parameterization methods ignore the influence of blowing wind fetch length and water depth on the wind drag coefficient, . Distinguished from that in the marine environment, is incompletely developed in shallow lakes. G20 fully considers the impacts of limited-fetch on undeveloped and thus has a higher computation accuracy than other formulas in Lake Taihu. However, we found that in the case of G20 formula, the fetch of each grid point in Lake Taihu needs to be computed before calculating at each time step, which significantly increases the amount of calculation. Therefore, for each grid resolution, the calculation time of G20 was the longest. Considering the accuracy and efficiency of calculation, the combination of the A12 formula and a coarse grid can meet the requirements for accurately simulating wind-induced currents in fetch-limited shallow lakes. We recommend the A12 parameterization method when computing resources are limited and grid resolution is low. However, when the calculation conditions permit, the combination of the G20 formula and a high-resolution grid can significantly improve the calculation accuracy.
Author Contributions
Conceptualization, C.Z. and C.W.; methodology, A.G.; validation, C.Z.; formal analysis, C.Z.; investigation, C.Z.; resources, Y.D. and G.Y.; data curation, Y.D. and J.Y.; writing—original draft preparation, C.W.; writing—review and editing, C.Z. and J.L.; visualization, C.Z.; supervision, Z.Z.; project administration, C.Z.; funding acquisition, C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Young Scientists Fund of the National Natural Science Foundation of China (No. 42401136); Open Fund of Key Laboratory of Integrated Regulation and Resources Development of Shallow Lakes of Ministry of Education (No. 2024006); Water Science and Technology Plan Project of Zhejiang Province (No. RC2455); Scientific and Technological Plan Project of Huzhou (No. 2023GZ78); Scientific research foundation of Zhejiang University of Water Resources and Electric Power (No. xky2023008); National Natural Science Foundation of China (No. 52209096).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Author Jiaqing Liao was employed by the company Hangzhou Dingchuan Information Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Tsanis, I.K. Simulation of wind-induced water currents. J. Hydraul. Eng. 1989, 115, 1113–1134. [Google Scholar] [CrossRef]
- Wu, J. Wind-induced drift currents. J. Fluid Mech. 2006, 68, 49–70. [Google Scholar] [CrossRef]
- Li, Y.; Acharya, K.; Yu, Z. Modeling impacts of Yangtze River water transfer on water ages in Lake Taihu, China. Ecol. Eng. 2011, 37, 325–334. [Google Scholar] [CrossRef]
- Jingqiao, M.A.O.; Chen, Q.; Chen, Y. Three-dimensional eutrophication model and application to Taihu Lake, China. J. Environ. Sci. 2008, 20, 278–284. [Google Scholar]
- Li, Y.; Jalil, A.; Du, W.; Gao, X.; Wang, J.; Luo, L.; Li, H.; Dai, S.; Hashim, S.; Yu, Z.; et al. Wind induced reverse flow and vertical profile characteristics in a semi-enclosed bay of large shallow Lake Taihu, China. Ecol. Eng. 2017, 102, 224–233. [Google Scholar] [CrossRef]
- Chu, D.; Zhang, J.; Wu, Y.; Jiao, X.; Qian, S. Sensitivities of modelling storm surge to bottom friction, wind drag coefficient, and meteorological product in the East China Sea. Estuar. Coast. Shelf Sci. 2019, 231, 106460. [Google Scholar] [CrossRef]
- Kranenburg, C. Wind-driven chaotic advection in a shallow model lake. J. Hydraul. Res. 2010, 30, 29–46. [Google Scholar] [CrossRef]
- Li, Y.P.; Tang, C.Y.; Yu, Z.B.; Acharya, K. Uncertainty and sensitivity analysis of large shallow lake hydrodynamic models. Adv. Water Sci. 2012, 33, 271–277. [Google Scholar]
- Wróbel-Niedźwiecka, I.; Drozdowska, V.; Piskozub, J. Effect of drag coefficient formula choice on wind stress climatology in the North Atlantic and the European Arctic. Oceanologia 2019, 61, 291–299. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, L. A review of wind-driven hydrodynamics in large shallow lakes: Importance, process-based modeling and perspectives. Camb. Prism. Water 2023, 1, e16. [Google Scholar] [CrossRef]
- Morales-Marín, L.A.; French, J.R.; Burningham, H. Implementation of a 3D ocean model to understand upland lake wind-driven circulation. Environ. Fluid Mech. 2017, 17, 1255–1278. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Zhang, M.; Jiang, H.; Jiang, H.; Tang, J.; Zhang, H.; Qiao, H. Numerical investigation of the effects of aquatic plants on wind-induced currents in Taihu Lake in China. J. Hydrodyn. 2019, 31, 778–787. [Google Scholar] [CrossRef]
- Oliveira, H.; Fernandes, E.; Möller, O., Jr.; García-Rodríguez, F. Relationships between Wind Effect, Hydrodynamics and Water Level in the World’s Largest Coastal Lagoonal System. Water 2019, 11, 2209. [Google Scholar] [CrossRef]
- Sheppard, P.A.; Tribble, D.T.; Garratt, J.R. Studies of turbulence in the surface layer over water (Lough Neagh). Part I. Instrumentation, programme, profiles. Q. J. R. Meteorol. Soc. 1972, 98, 627–641. [Google Scholar]
- Flather, R.A. Results from a Storm Surge Prediction Model of the North-West European Continental Shelf for April, November and December 1973; Report No.24; Institute of Oceanographics Sciences: Surrey, UK, 1976. [Google Scholar]
- Large, W.G.; Pond, S. Open Ocean Momentum Flux Measurements in moderate to strong winds. J. Phys. Oceanogr. 1981, 11, 324–336. [Google Scholar] [CrossRef]
- Geernaert, G.L.; Larsen, S.E.; Hansen, F. Measurements of the wind stress, heat flux, and turbulence intensity during storm conditions over the North Sea. J. Geophys. Res. Oceans 1987, 92, 13127–13139. [Google Scholar] [CrossRef]
- Ataktürk, S.S.; Katsaros, K.B. Wind Stress and Surface Waves Observed on Lake Washington. J. Phys. Oceanogr. 1999, 29, 633–650. [Google Scholar] [CrossRef]
- Guan, C.; Xie, L. On the Linear Parameterization of Drag Coefficient over Sea Surface. J. Phys. Oceanogr. 2004, 34, 2847–2851. [Google Scholar] [CrossRef]
- Yelland, M.J.; Taylor, P.K. Wind Stress Measurements from the Open Ocean. J. Phys. Oceanogr. 1996, 26, 541–558. [Google Scholar] [CrossRef]
- Large, W.G.; Yeager, S.G. Diurnal to Decadal Global Forcing For Ocean and Sea-Ice Models: The Data Sets and Flux Climatologies; National Center for Atmospheric Research: Boulder, CO, USA, 2004. [Google Scholar]
- Andreas, E.L.; Mahrt, L.; Vickers, D. A New Drag Relation for Aerodynamically Rough Flow over the Ocean. J. Atmos. Sci. 2012, 69, 2520–2537. [Google Scholar] [CrossRef]
- Janssen, P.A.; Peter, A.E.M. Quasi-Linear Theory of Wind-Wave Generation Applied to Wave Forecasting. J. Phys. Oceanogr. 1991, 21, 1631–1642. [Google Scholar] [CrossRef]
- Tolman, H.L.; Chalikov, D. Source Terms in a Third-Generation Wind Wave Model. J. Phys. Oceanogr. 1996, 26, 2497–2518. [Google Scholar] [CrossRef]
- Mueller, J.A.; Veron, F. Nonlinear Formulation of the Bulk Surface Stress over Breaking Waves: Feedback Mechanisms from Air-flow Separation. Bound.-Layer Meteorol. 2008, 130, 117–134. [Google Scholar] [CrossRef]
- Gao, A. Study on the wind drag coefficient of shallow lakes considering wind-wave-flow characteristics. Ph.D. Thesis, Nanjing Hydraulic Research Institute, Nanjing, China, 2020. [Google Scholar]
- Mastenbroek, C.; Burgers, G.; Janssen, P.A.E.M. The Dynamical Coupling of a Wave Model and a Storm Surge Model through the Atmospheric Boundary Layer. J. Phys. Oceanogr. 1993, 23, 1856–1866. [Google Scholar] [CrossRef]
- Smith, S.D.; Anderson, R.J.; Oost, W.A.; Kraan, C.; Maat, N.; De Cosmo, J.; Katsaros, K.B.; Davidson, K.L.; Bumke, K.; Hasse, L.; et al. Sea surface wind stress and drag coefficients: The hexos results. Bound.-Layer Meteorol. 1992, 60, 109–142. [Google Scholar] [CrossRef]
- Ebuchi, N.; Toba, Y.; Kawamura, H. On the wave dependence of sea-surface wind stress. J. Oceanogr. Soc. Jpn. 1990, 46, 177–183. [Google Scholar] [CrossRef]
- Gao, A.; Wu, S.; Chen, L.; Liu, S.; Xu, Z.; Zhao, Y.; Wang, F.; Zhu, S. Experiemental study on the wave height distribution of wind-induced waves in the growth stage under finite water depth. Water Supply 2019, 19, 2079–2270. [Google Scholar] [CrossRef]
- Elfouhaily, T.; Chapron, B.; Katsaros, K.; Vandemark, D. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res. Ocean. 1997, 102, 15781–15796. [Google Scholar] [CrossRef]
- Fang, P.; Zhao, B.; Zeng, Z.; Yu, H.; Lei, X.; Tan, J. Effects of Wind Direction on Variations in Friction Velocity with Wind Speed Under Conditions of Strong Onshore Wind. J. Geophys.-Res. 2018, 123, 7340–7353. [Google Scholar] [CrossRef]
- Moon, I.J.; Hara, T.; Ginis, I.; Belcher, S.E.; Tolman, H.L. Effect of Surface Waves on Air–Sea Momentum Exchange. Part I: Effect of Mature and Growing Seas. J. Atmos. Sci. 2004, 61, 2321–2333. [Google Scholar] [CrossRef]
- Costi, J.; Marques, W.C.; de Paula Kirinus, E.; de Freitas Duarte, R.; Arigony-Neto, J. Water level variability of the Mirim—São Gonçalo system, a large, subtropical, semi-enclosed coastal complex. Adv. Water Resour. 2018, 117, 75–86. [Google Scholar] [CrossRef]
- Kopmann, R.; Markofsky, M. Three-dimensional water quality modelling with TELEMAC-3D. Hydrol. Process. 2000, 14, 2279–2292. [Google Scholar] [CrossRef]
- Ji, Z.-G. Hydrodynamics and Water Quality: Modeling Rivers, Lakes, and Estuaries; John Wiley: Hoboken, NJ, USA, 2008; Volume 89, p. 676. [Google Scholar]
- Chen, C.; Wang, L.; Ji, R.; Budd, J.W.; Schwab, D.J.; Beletsky, D.; Fahnenstiel, G.L.; Verploeg, H.; Eadie, B.; Cotner, J. Impacts of suspended sediment on the ecosystem in Lake Michigan: A comparison between the 1998 and 1999 plume events. J. Geophys. Res. 2004, 109, 1–18. [Google Scholar] [CrossRef]
- Foreman, R.J.; Emeis, S. Revisiting the Definition of the Drag Coefficient in the Marine Atmospheric Boundary Layer. J. Phys. Oceanogr. 1993, 40, 2325–2332. [Google Scholar] [CrossRef]
- Vieira, V.M.; Mateus, M.; Canelas, R.; Leitão, F. The FuGas 2.5 Updated for the Effects of Surface Turbulence on the Transfer Velocity of Gases at the Atmosphere–Ocean Interface. J. Mar. Sci. Eng. 1989, 8, 435. [Google Scholar] [CrossRef]
- Worsnop, R.P.; Bryan, G.H.; Lundquist, J.K.; Zhang, J.A. Using Large-Eddy Simulations to Define Spectral and Coherence Characteristics of the Hurricane Boundary Layer for Wind-Energy Applications. Bound.-Layer Meteorol. 2017, 165, 55–86. [Google Scholar] [CrossRef]
- Hu, W.; Jørgensen, S.E.; Zhang, F. A vertical-compressed three-dimensional ecological model in Lake Taihu, China. Ecol. Model. 2006, 190, 367–398. [Google Scholar] [CrossRef]
- Mellor, G.L.; Ezer, T.; Oey, L.Y. The Pressure Gradient Conundrum of Sigma Coordinate Ocean Models. J. Atmos. Ocean. Technol. 1994, 11, 1126–1134. [Google Scholar] [CrossRef]
- Murphy, A.H. Climatology, Persistence, and Their Linear Combination as Standards of Reference in Skill Scores. Weather. Forecast. 1992, 7, 692–698. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Q. Numerical study of hydrodynamic process in Chaohu Lake. J. Hydrodyn. Ser. B 2015, 27, 720–729. [Google Scholar] [CrossRef]
- Wu, T.; Qin, B.; Ding, W.; Zhu, G.; Zhang, Y.; Gao, G.; Xu, H.; Li, W.; Dong, B.; Luo, L. Field Observation of Different Wind-Induced Basin-Scale Current Field Dynamics in a Large, Polymictic, Eutrophic Lake. J. Geophys. Res. Ocean. 2018, 123, 6945–6961. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).