Echo State Network and Sparrow Search: Echo State Network for Modeling the Monthly River Discharge of the Biggest River in Buzău County, Romania
Abstract
1. Introduction
2. Data Series and Methodology
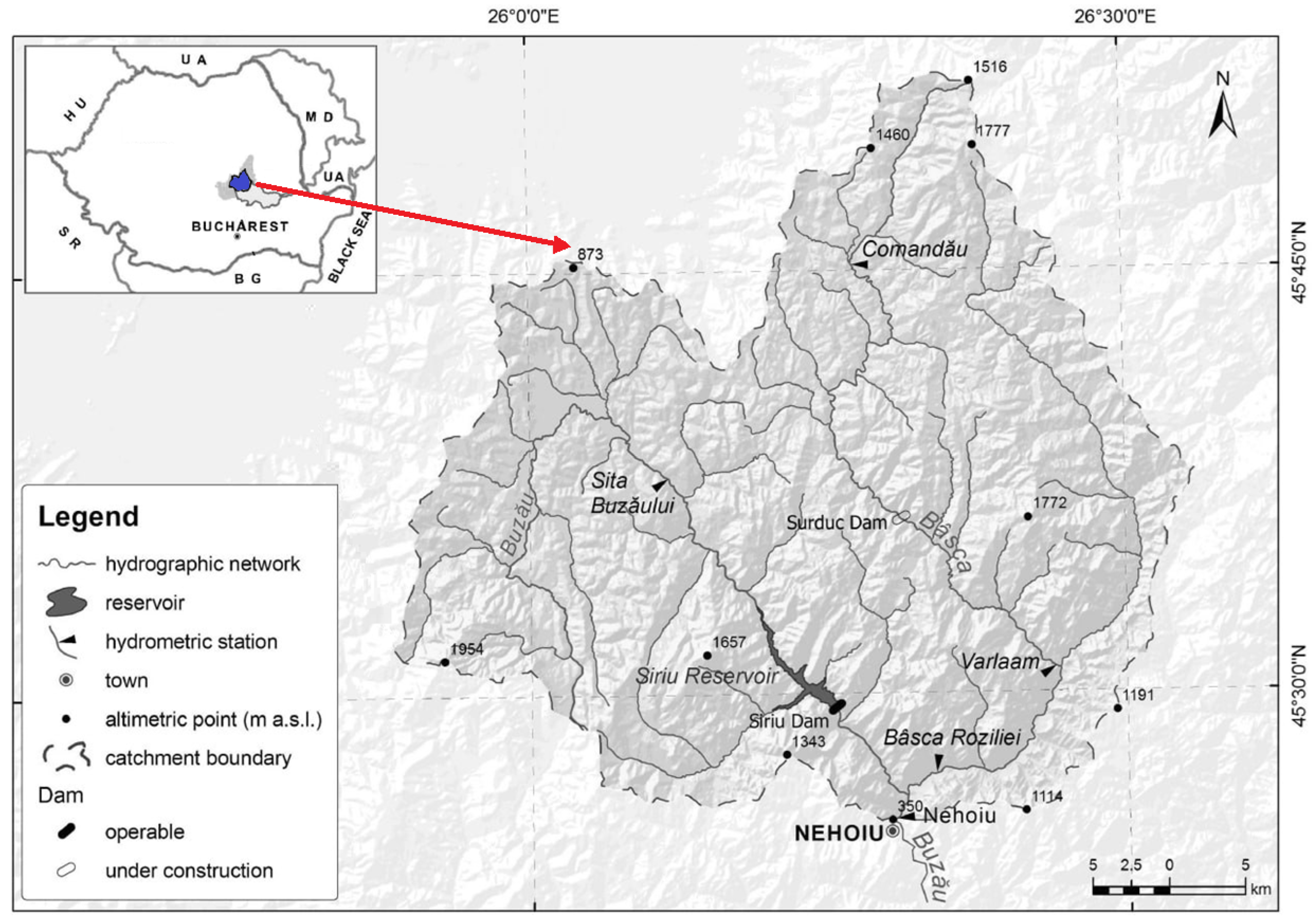
2.1. Study Area and Data Series
2.2. Methodology
- (a)
- (b)
- Compute the median of the given series.
- (c)
- Compute the residual by subtracting St and the median from the data series.
- (d)
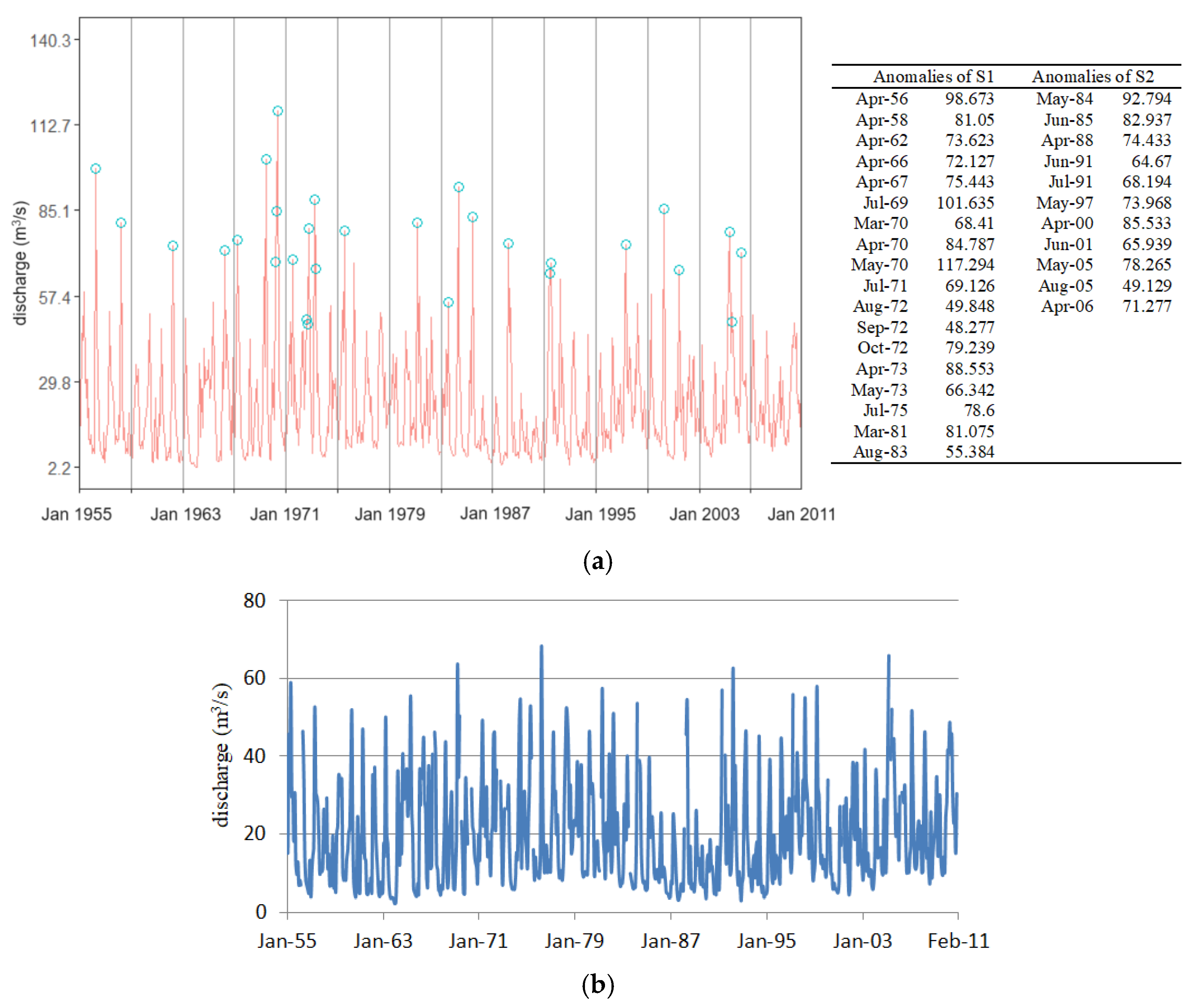
- Detect the anomalies using ESD as follows.
- Computefor the extreme value detected, where = average and s = standard deviation.
- Compare Cj with the critical value:where is the value of the Student statistics at the significance level p and degrees of freedom.
- If xj is an anomaly, discard it and compute the critical values using the new data series.
- Repeat the previous steps j times, considering that the number of anomalies is equal to the highest j for which Cj > λj.
- (e)
- List the anomalies and the corresponding timestamp.
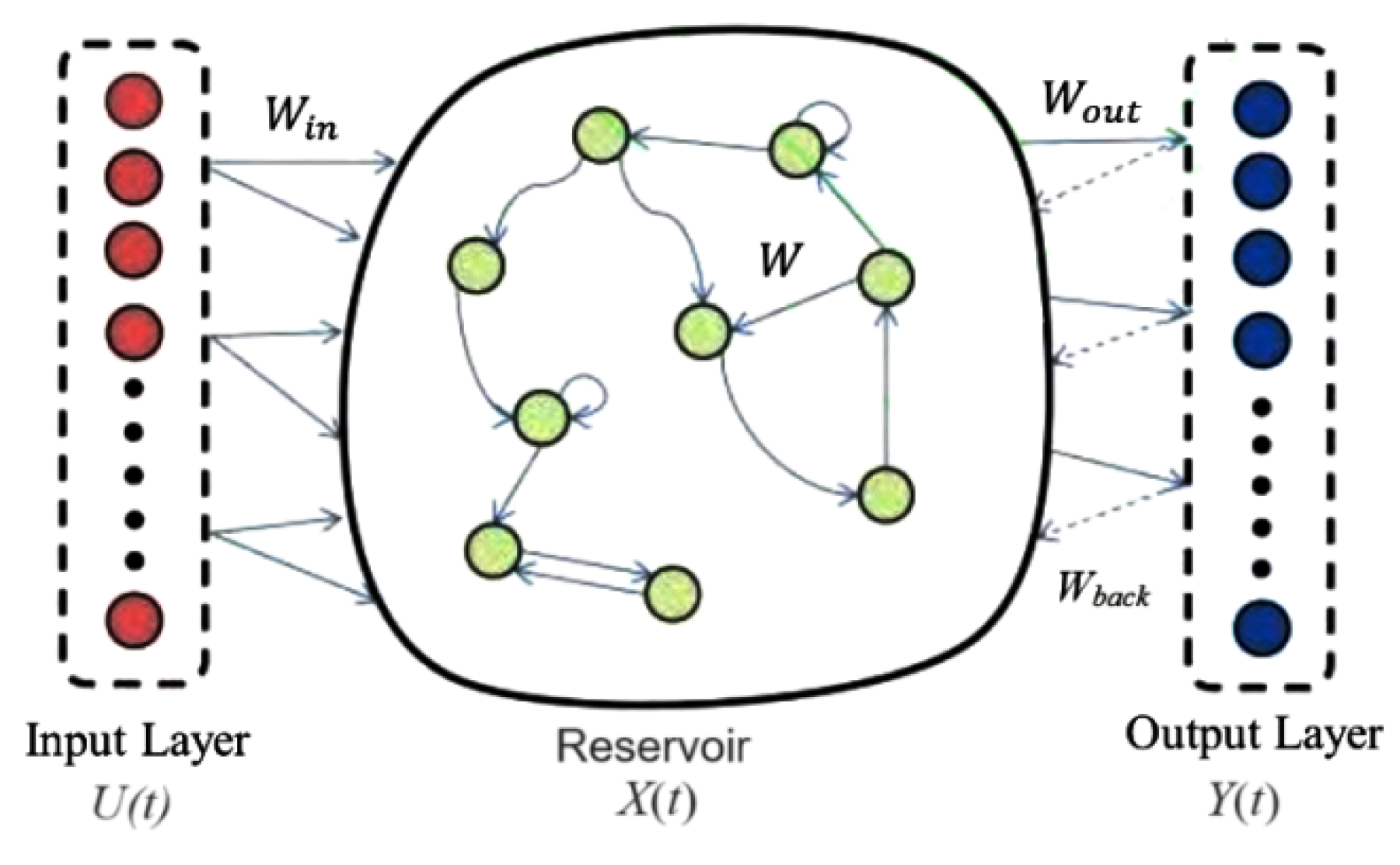
2.2.1. ESN
- Number of samples 30;
- Number of neurons in the reservoir 1000;
- Learning rate 0.1;
- Regularization parameter 0.1 [21].
2.2.2. SSA-ESN
- (1)
- Data preprocessing: Normalize the input time-series data to eliminate scale differences, enhance model convergence speed, and improve prediction accuracy.
- (2)
- Parameter initialization: Set the SSA’s key parameters—the size of the sparrow population, scouting and warning rate, flight distance (R2)—and the ESN’s basic parameter ranges (such as reservoir size, initial state, spectral radius, input weight).
- (3)
- ESN parameter optimization: Based on SSA’s randomly generated positions, calculate the population fitness according to the update formula and obtain the current global optimum and individual best values.
- (4)
- Iteration termination: If the criteria for stopping the iterations are satisfied, the iteration is stopped and the optimal result is listed. Otherwise, the algorithm is performed again from the third step for further iteration.
- (5)
- ESN network prediction: Select the best individual from SSA as the optimization solution for reservoir parameters. Utilize these optimal parameters for ESN model prediction.
- Number of parameters to be optimized = 3—learning rate, reservoir size, regularization coefficient.
- Lower bounds for the parameters—0.1, 100, and 0.1, respectively.
- Lower bounds for the parameters—2000, 1500, and 0.2, respectively.
- Sparrow population—10.
- Maximum number of iterations—50.
- Initial size of the reservoir—30.
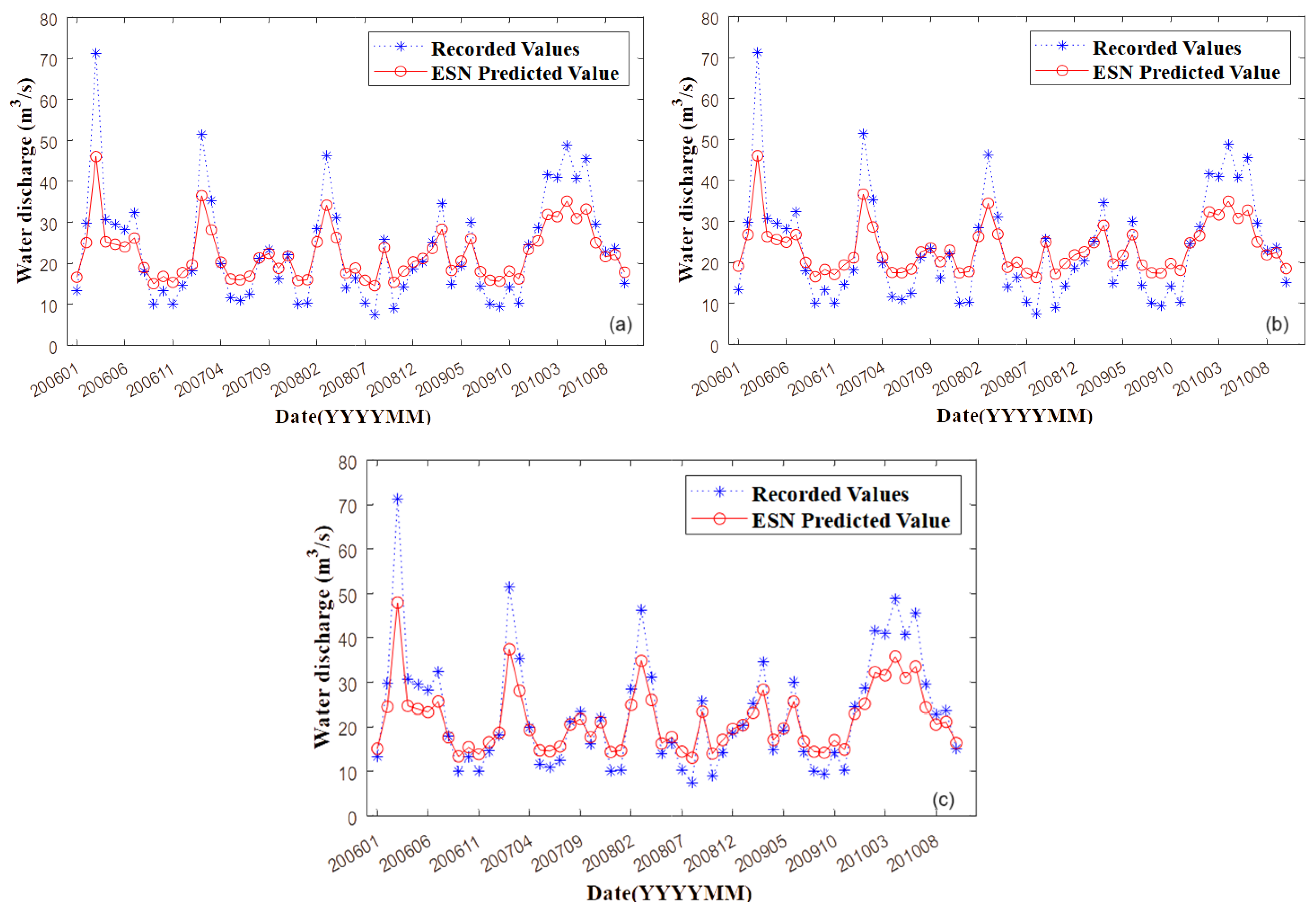
3. Results and Discussion
- Since MAE from the hybrid algorithm belongs to the interval [4.47, 4.86] for the test and [4.16, 4.42] for the training set, compared to the intervals [4.98, 5.1] and [4.40, 4.87], respectively, it results that SSA-ESN performs better in terms of MAE.
- Considering R2, ESN is the best on all series after discarding the aberrant values compared to SSA-ESN.
- The lowest run time was that of ESN on S2.
- The lowest MAEs were recorded for SSA-ESN on S2, with values of 4.16 on the training set and 4.47 on the test set.
- The lowest MSEs were obtained by running ESN on S2_a: 39.33 on the training set and 32.21 on the test set.
- The highest R2 (over 99.99%) corresponds to ESN on S2_a.
- The removal of aberrant values significantly enhanced the performance of the ESN algorithm, demonstrating its adaptability.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gharehchopogh, F.S.; Namazi, M.; Ebrahimi, L.; Abdollahzadeh, B. Advances in Sparrow Search Algorithm: A Comprehensive Survey. Arch. Computat. Methods Eng. 2023, 30, 427–455. [Google Scholar] [CrossRef]
- Isfan, M.C.; Caramete, L.-I.; Caramete, A.; Basceanu, V.-A.; Popescu, T. Data analysis for gravitational waves using neural networks on quantum computers. Rom. Rep. Phys. 2023, 75, 113. [Google Scholar]
- Dai, Z.; Zhang, M.; Nedjah, N.; Xu, D.; Ye, F. A Hydrological Data Prediction Model Based on LSTM with Attention Mechanism. Water 2023, 15, 670. [Google Scholar] [CrossRef]
- Li, S.; Yang, J. Modelling of suspended sediment load by Bayesian optimized machine learning methods with seasonal adjustment. Eng. Appl. Comput. Fluid Mech. 2022, 16, 1883–1901. [Google Scholar] [CrossRef]
- Hayder, G.; Solihin, M.I.; Mustafa, H.M. Modelling of River Flow Using Particle Swarm Optimized Cascade-Forward Neural Networks: A Case Study of Kelantan River in Malaysia. Appl. Sci. 2020, 10, 8670. [Google Scholar] [CrossRef]
- Khan, M.Y.A.; Hasan, F.; Panwar, S.; Chakrapani, G.J. Neural network model for discharge and water-level prediction for Ramganga River catchment of Ganga Basin, India. Hydrol. Sci. J. 2016, 61, 2084–2095. [Google Scholar] [CrossRef]
- Samadi, M.; Sarkardeh, H.; Jabbari, E. Prediction of the dynamic pressure distribution in hydraulic structures using soft computing methods. Soft Comput. 2021, 25, 3873–3888. [Google Scholar] [CrossRef]
- Haghiabi, A.H.; Parsaie, A.; Ememgholizadeh, S. Prediction of discharge coefficient of triangular labyrinth weirs using adaptive neuro fuzzy inference system. Alex. Eng. J. 2018, 57, 1773–1782. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Dumitriu, C.S. About the long-range dependence of cavitation effect on a copper alloy. Rom. J. Phys. 2024, 69, 904. [Google Scholar]
- Bărbulescu, A.; Dumitriu, C.S. Modeling the Voltage Produced by Ultrasound in Seawater by Stochastic and Artificial Intelligence Methods. Sensors 2022, 22, 1089. [Google Scholar] [CrossRef]
- Dumitriu, C.S.; Bărbulescu, A. Artificial intelligence models for the mass loss of copper-based alloys under the cavitation. Materials 2022, 15, 6695. [Google Scholar] [CrossRef] [PubMed]
- Dumitriu, C.Ş.; Dragomir, F.-L. Modeling the Signals Collected in Cavitation Field by Stochastic and Artificial Intelligence Methods. In Proceedings of the 2021 13th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Pitesti, Romania, 1–3 July 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Adnan, R.M.; Jaafari, A.; Mohanavelu, A.; Kisi, O.; Elbeltagi, A. Novel Ensemble Forecasting of Streamflow Using Locally Weighted Learning Algorithm. Sustainability 2021, 13, 5877. [Google Scholar] [CrossRef]
- Van Thieu, N.; Nguyen, N.H.; Sherif, M.; El-Shafie, A.; Ahmed, A.N. Integrated metaheuristic algorithms with extreme learning machine models for river streamflow prediction. Sci. Rep. 2024, 14, 13597. [Google Scholar] [CrossRef]
- Alquraish, M.M.; Khadr, M. Remote-Sensing-Based Streamflow Forecasting Using Artificial Neural Network and Support Vector Machine Models. Remote Sens. 2021, 13, 4147. [Google Scholar] [CrossRef]
- Crăciun, A.; Costache, R.; Bărbulescu, A.; Chandra Pal, S.; Costache, I.; Dumitriu, C.S. Modern techniques for flood susceptibility estimation across the Deltaic Region (Danube Delta) from the Black Sea’s Romanian Sector. J. Marine Sci. Eng. 2022, 10, 1149. [Google Scholar] [CrossRef]
- Ferreira, R.G.; da Silva, D.D.; Elesbon, A.A.A.; Fernandes-Filho, E.I.; Veloso, G.V.; Fraga, M.D.S.; Ferreira, L.B. Machine learning models for streamflow regionalization in a tropical watershed. J. Environ. Manag. 2021, 280, 111713. [Google Scholar] [CrossRef]
- Piazzi, G.; Thirel, G.; Perrin, C.; Delaigue, O. Sequential Data Assimilation for Streamflow Forecasting: Assessing the Sensitivity to Uncertainties and Updated Variables of a Conceptual Hydrological Model at Basin Scale. Water Resour. Res. 2021, 57, 57. [Google Scholar] [CrossRef]
- Popescu, C.; Bărbulescu, A. On the Flash Flood Susceptibility and Accessibility in the Vărbilău Catchment (Romania). Rom. J. Phys. 2022, 67, 811. [Google Scholar]
- Saraiva, S.V.; Carvalho, F.D.O.; Santos, C.A.G.; Barreto, L.C.; Freire, P.K.D.M.M. Daily streamflow forecasting in Sobradinho Reservoir using machine learning models coupled with wavelet transform and bootstrapping. Appl. Soft Comput. 2021, 102, 107081. [Google Scholar] [CrossRef]
- Tanty, R.; Desmukh, T.S. Application of Artificial Neural Network in Hydrology—A Review. Int. J. Eng. Res. Techn. (IJERT) 2015, 4, 184–188. [Google Scholar]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. Super ensemble learning for daily streamflow forecasting: Large-scale demonstration and comparison with multiple machine learning algorithms. Neural Comput. Appl. 2021, 33, 3053–3068. [Google Scholar] [CrossRef]
- Uca; Toriman, E.; Jaafar, O.; Maru, R.; Arfan, A.; Ahmar, A.S. Daily Suspended Sediment Discharge Prediction Using Multiple Linear Regression and Artificial Neural Network. J. Phys. Conf. Ser. 2018, 954, 012030. [Google Scholar] [CrossRef]
- Jaeger, H. Echo State Network. Available online: http://www.scholarpedia.org/article/Echo_state_network#Variants (accessed on 11 July 2024).
- Lark. Available online: https://www.larksuite.com/en_us/topics/ai-glossary/echo-state-network (accessed on 11 July 2024).
- Lukoševičius, M. A Practical Guide to Applying Echo State Networks. In Neural Networks: Tricks of the Trade. Lecture Notes in Computer Science; Montavon, G., Orr, G.B., Müller, K.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7700, pp. 659–686. [Google Scholar]
- Ma, Q.; Zhuang, W.; Shen, L.; Cottrell, G.W. Time series classification with Echo Memory Networks. Neural Netw. 2019, 117, 225–239. [Google Scholar] [CrossRef]
- Sohan, S.; Ozturk, M.C.; Principe, J.C. Signal Processing with Echo State Networks in the Complex Domain. In Proceedings of the 2007 IEEE Workshop on Machine Learning for Signal Processing, Thessaloniki, Greece, 27–29 August 2007; pp. 408–412. [Google Scholar]
- Skowronski, M.D.; Harris, J.G. Noise-Robust Automatic Speech Recognition Using a Predictive Echo State Network. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 1724–1730. [Google Scholar] [CrossRef]
- Ibrahim, H.; Loo, C.K.; Alnajjar, F. Bidirectional parallel echo state network for speech emotion recognition. Neural Comput. Appl. 2022, 34, 17581–17599. [Google Scholar] [CrossRef]
- Daneshfar, F.; Jamshidi, M.B. A Pattern Recognition Framework for Signal Processing in Metaverse. In Proceedings of the 2022 8th Iranian Conference on Signal Processing and Intelligent Systems (ICSPIS), Behshahr, Iran, 28–29 December 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Verstraeten, D.; Schrauwen, B.; D’Haene, M.; Stroobandt, D.D. An experimental unification of reservoir computing methods. Neural Netw. 2007, 2093, 391–403. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, Z.; Outbib, R. Adaptive prognostic of fuel cells by implementing ensemble echo state networks in time-varying model space. IEEE Trans. Ind. Electron. 2019, 67, 379–389. [Google Scholar] [CrossRef]
- Morando, S.; Jemei, S.; Hissel, D.; Gouriveau, R.; Zerhouni, N. ANOVA method applied to proton exchange membrane fuel cell ageing forecasting using an echo network. Math. Comput. Simul. 2017, 131, 283–294. [Google Scholar] [CrossRef]
- Mezzi, R.; Yousfi-Steiner, N.; Péra, M.C.; Hissel, D.; Larger, L. An echo state network for fuel cell lifetime prediction under a dynamic micro-cogeneration load profile. Appl. Energ. 2021, 283, 116–297. [Google Scholar] [CrossRef]
- Jin, J.; Chen, Y.; Xie, C. Remaining useful life prediction of PEMFC based on cycle reservoir with jump model. Int. J. Hydrogen Energy 2021, 46, 40001–40013. [Google Scholar] [CrossRef]
- Morando, S.; Jemei, S.; Hissel, D.; Gouriveau, R.; Zerhouni, N. Show more Proton exchange membrane fuel cell ageing forecasting algorithm based on Echo State Network. Int. J. Hydrogen Energy 2017, 42, 1472–1480. [Google Scholar] [CrossRef]
- Jaeger, H.; Haas, H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science 2004, 304, 78–80. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, C.; Tang, F.; Zhu, D.; Qiu, Y.; Liu, Y. Application of improved sparrow search algorithm in concrete. J. Phys. Conf. Ser. 2021, 2082, 012014. [Google Scholar] [CrossRef]
- Fathy, A.; Alanazi, T.; Rezk, H.; Yousri, D. Optimal energy management of micro-grid using sparrow search algorithm. Energy Rep. 2022, 8, 758–773. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, B. An ensemble neural network based on variational mode decomposition and an improved sparrow search algorithm for wind and solar power forecasting. IEEE Access 2021, 9, 166709–166719. [Google Scholar] [CrossRef]
- Song, J.; Jin, L.; Xie, Y.; Wei, C. Optimized XGBoost based sparrow search algorithm for short-term load forecasting. In Proceedings of the 2021 IEEE International Conference on Computer Science, Artificial Intelligence and Electronic Engineering (CSAIEE), Virtual Event, 20–22 August 2021; IEEE: New York, NY, USA, 2021; pp. 213–217. [Google Scholar]
- Lv, J.; Sun, W.; Wang, H.; Zhang, F. Coordinated approach fusing RCMDE and sparrow search algorithm-based SVM for fault diagnosis of rolling bearings. Sensors 2021, 21, 5297. [Google Scholar] [CrossRef]
- Xiong, Q.; Zhang, X.; He, S.; Shen, J. A fractional-order chaotic sparrow search algorithm for enhancement of long distance IRIS image. Mathematics 2021, 9, 2790. [Google Scholar] [CrossRef]
- Li, L.L.; Xiong, J.L.; Tseng, M.L.; Yan, Z.; Lim, M. Using multi-objective sparrow search algorithm to establish active distribution network dynamic reconfiguration integrated optimization. Expert Syst. Appl. 2022, 193, 116445. [Google Scholar] [CrossRef]
- Thenmozhi, R.; Nasir, A.; Sonthi, V.; Avudaiappan, T.; Kadry, S.; Pin, K.; Nam, Y. An improved sparrow search algorithm for node localization in WSN. Comput. Mater. Contin. 2022, 71, 2037–2051. [Google Scholar]
- Jiang, F.; Han, X.; Zhang, W.; Chen, G. Atmospheric PM2.5 prediction using Deepar optimized by sparrow search algorithm with opposition-based and fitness-based learning. Atmosphere 2021, 12, 894. [Google Scholar] [CrossRef]
- An, G.; Jiang, Z.; Chen, L.; Cao, X.; Li, Z.; Zhao, Y.; Sun, H. Ultra short-term wind power forecasting based on sparrow search algorithm optimization deep extreme learning machine. Sustainability 2021, 13, 10453. [Google Scholar] [CrossRef]
- Awadallah, M.A.; Al-Betar, M.A.; Doush, I.A.; Makhadmeh, S.N.; Al-Naymat, G. Recent Versions and Applications of Sparrow Search Algorithm. Arch. Computat. Methods Eng. 2023, 30, 2831–2858. [Google Scholar] [CrossRef]
- Mocanu-Vargancsik, C.A.; Bărbulescu, A. Analysis on Variability of Buzau River Monthly Discharges. Ovidius Univ. Ann. Ser. Civil Eng. 2018, 20, 51–55. [Google Scholar] [CrossRef]
- Mocanu-Vargancsik, C.A.; Bărbulescu, A. On the variability of a river water flow, under seasonal conditions. Case study. IOP Conf. Ser. Earth Environ. Sci. 2019, 344, 012028. [Google Scholar] [CrossRef]
- Mocanu-Vargancsik, C.; Tudor, G. On the linear trends of a water discharge data under temporal variation. Case study: The upper sector of the Buzău river (Romania). Forum Geogr. 2020, XIX, 37–44. [Google Scholar] [CrossRef]
- Minea, G.; Bărbulescu, A. Statistical assessing of hydrological alteration of Buzău River induced by Siriu dam (Romania). Forum Geogr. 2014, 13, 50–58. [Google Scholar] [CrossRef]
- Bărbulescu, Statistical Assessment and Model for a River Flow under Variable Conditions. Available online: https://cest2017.gnest.org/sites/default/files/presentation_file_list/cest2017_00715_poster_paper.pdf (accessed on 7 September 2024).
- Bărbulescu, A.; Mohammed, N. Study of the river discharge alteration. Water 2024, 16, 808. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Zhen, L. Forecasting the River Water Discharge by Artificial Intelligence Methods. Water 2024, 16, 1248. [Google Scholar] [CrossRef]
- Zhen, L.; Bărbulescu, A. Comparative Analysis of Convolutional Neural Network-Long Short-Term Memory, Sparrow Search Algorithm-Backpropagation Neural Network, and Particle Swarm Optimization-Extreme Learning Machine for the Water Discharge of the Buzău River, Romania. Water 2024, 16, 289. [Google Scholar] [CrossRef]
- Chendeş, V. Water Resources in Curvature Subcarpathians. Geospatial Assessments; Editura Academiei Române: Bucureşti, Romania, 2011; (In Romanian with English Abstract). [Google Scholar]
- Updated Management Plan of the Buzau-Ialomita Hydrographic Area. Available online: http://buzau-ialomita.rowater.ro/wp-content/uploads/2021/02/PMB_ABABI_Text_actualizat.pdf (accessed on 17 October 2023). (In Romanian).
- Chai, Y.; Zhu, B.; Yue, Y.; Yang, Y.; Li, S.; Ren, J.; Xiong, H.; Cui, X.; Yan, X.; Li, Y. Reasons for the homogenization of the seasonal discharges in the Yangtze River. Hydrol. Res. 2020, 51, 470–483. [Google Scholar] [CrossRef]
- Chai, Y.; Yue, Y.; Zhang, L.; Miao, C.; Borthwick, A.G.L.; Zhu, B.; Li, Y.; Dolman, A.J. Homogenization and polarization of the seasonal water discharge of global rivers in response to climatic and anthropogenic effects. Sci. Total Environ. 2020, 709, 136062. [Google Scholar] [CrossRef] [PubMed]
- McManamay, R.A.; Orth, D.J.; Dolloff, C.A. Revisiting the homogenization of dammed rivers in the southeastern US. J. Hydrol. 2012, 424–425, 217–237. [Google Scholar] [CrossRef]
- Poff, N.L.; Olden, J.D.; Merritt, D.M.; Pepin, D.M. Homogenization of regional river dynamics by dams and global biodiversity implications. Proc. Nat. Acad. Sci. USA 2007, 104, 5732–5737. [Google Scholar] [CrossRef] [PubMed]
- Golyandina, N.; Korobeynikov, A. Basic Singular Spectrum Analysis and forecasting with R. Comp. Stat. Data An. 2014, 71, 934–954. [Google Scholar] [CrossRef]
- Golyandina, N.; Korobeynikov, A.; Zhigljavsky, A. Singular Spectrum Analysis with R; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Nguyen, A.D.; Le Nguyen, P.; Vu, V.H.; Pham, Q.V.; Nguyen, V.H.; Nguyen, M.H. Accurate discharge and water level forecasting using ensemble learning with genetic algorithm and singular spectrum analysis-based denoising. Sci. Rep. 2022, 12, 19870. [Google Scholar] [CrossRef]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Proc. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Chu, T.-Y.; Huang, W.-C. Application of Empirical Mode Decomposition Method to Synthesize Flow Data: A Case Study of Hushan Reservoir in Taiwan. Water 2020, 12, 927. [Google Scholar] [CrossRef]
- Liu, F.; Li, J.; Liu, L.; Huang, L.; Fang, G. Application of the EEMD method for distinction and suppression of motion-induced noise in grounded electrical source airborne TEM system. J. Appl. Geophys. 2017, 139, 109–116. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.B.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? J. Econ. 1992, 54, 159–178. [Google Scholar]
- Conover, W.J.; Johnson, M.E.; Johnson, M.M. A comparative study of tests for homogeneity of variances, with applications to the outer continental shelf bidding data. Technometrics 1981, 23, 351–361. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change point problem. J. Royal Stat. Soc. Ser. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Fox, A.J. Outliers in Time Series. J. Royal Stat. Soc. Ser. B 1972, 34, 350–363. [Google Scholar] [CrossRef]
- Blázquez-García, A.; Conde, A.; Mori, U.; Lozano, J.A. A Review on Outlier/Anomaly Detection in Time Series Data”. ACM Comput. Surv. 2021, 54, 1–33. [Google Scholar] [CrossRef]
- AnomalyDetection R Package. Available online: https://github.com/twitter/AnomalyDetection/tree/master (accessed on 17 July 2024).
- Rosner, B. Percentage Points for a Generalized ESD Many-Outlier Procedure. Technometrics 1983, 25, 165–172. [Google Scholar] [CrossRef]
- Hochenbaum, J.; Vallis, O.S.; Kejariwal, A. Automatic Anomaly Detection in the Cloud Via Statistical Learning. 2017. Available online: https://arxiv.org/pdf/1704.07706 (accessed on 17 July 2024).
- Cleveland, W.S. Robust locally weighted regression and smoothing scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I.J. STL: A seasonal-trend decomposition procedure based on loess. J. Official Stat. 1990, 6, 3–33. [Google Scholar]
- He, K.; Mao, L.; Yu, J.; Huang, W.; He, Q.; Jackson, L. Long-term performance prediction of PEMFC based on LASSO-ESN. IEEE Trans. Instrum. Meas. 2021, 70, 3511611. [Google Scholar] [CrossRef]
- Jin, C.; Jiashu, J.; Yuepeng, C.; Changjun, X.; Bojun, L. PEMFC Performance Degradation Prediction Based on Bayesian Optimized ESN (In Chinese). Available online: https://www.researchgate.net/publication/380696856_jiyubeiyesiyouhuaESNdePEMFCxingnengtuihuayuce#fullTextFileContent (accessed on 11 July 2024).
- Sun, C.; Song, M.; Hong, S.; Li, H. A Review of Designs and Applications of Echo State Networks. Available online: https://arxiv.org/pdf/2012.02974 (accessed on 11 July 2024).
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Ding, D.; Zhang, M.; Pan, X.; Yang, M.; He, X. Modeling Extreme Events in Time Series Prediction. Available online: http://staff.ustc.edu.cn/~hexn/papers/kdd19-timeseries.pdf (accessed on 8 September 2024).
- Zhang, M.; Ding, D.; Pan, X.; Yang, M. Enhancing Time Series Predictors With Generalized Extreme Value Loss. IEEE Trans. Knowl. Data Eng. 2023, 35, 1473–1487. [Google Scholar] [CrossRef]
- Yen, M.H.; Liu, D.W.; Hsin, Y.C.; Lin, C.E.; Chen, C.C. Application of the deep learning for the prediction of rainfall in Southern Taiwan. Sci. Rep. 2019, 9, 12774. [Google Scholar] [CrossRef] [PubMed]


| Series | Training Set | Test Set | |||||
|---|---|---|---|---|---|---|---|
| Run Time (s) | MAE | MSE | R2 (%) | MAE | MSE | R2 (%) | |
| S | 0.99927 | 6.69 | 80.58 | 99.76 | 5.00 | 42.71 | 99.69 |
| S1 | 0.89032 | 7.60 | 102.95 | 98.91 | 5.56 | 48.74 | 99.16 |
| S2 | 0.86929 | 5.74 | 57.35 | 99.48 | 4.48 | 36.61 | 99.52 |
| Series | Training Set | Test Set | |||||
|---|---|---|---|---|---|---|---|
| Run Time (s) | MAE | MSE | R2 (%) | MAE | MSE | R2 (%) | |
| S | 0.96 | 6.69 | 80.58 | 99.75 | 5.00 | 42.72 | 99.68 |
| S1 | 0.86 | 7.60 | 102.94 | 98.93 | 5.56 | 48.73 | 99.17 |
| S2 | 0.79 | 5.74 | 57.34 | 99.48 | 4.48 | 36.60 | 99.53 |
| Series | Training Set | Test Set | |||||
|---|---|---|---|---|---|---|---|
| Run Time (s) | MAE | MSE | R2 (%) | MAE | MSE | R2 (%) | |
| S_a | 2.27 | 5.10 | 40.33 | 99.68 | 4.40 | 33.28 | 99.72 |
| S1_a | 1.06 | 6.06 | 54.87 | 94.69 | 4.87 | 37.95 | 96.34 |
| S2_a | 0.94 | 4.98 | 39.33 | 99.99 | 4.47 | 32.21 | 99.99 |
| Series | Training Set | Test Set | |||||
|---|---|---|---|---|---|---|---|
| Run Time (s) | MAE | MSE | R2 (%) | MAE | MSE | R2 (%) | |
| S_a | 155.59 | 4.86 | 44.49 | 91.91 | 4.42 | 37.41 | 91.32 |
| S1_a | 62.99 | 5.48 | 54.64 | 92.84 | 4.69 | 37.97 | 93.83 |
| S2_a | 110.31 | 4.47 | 39.73 | 90.95 | 4.16 | 35.46 | 90.59 |
| MLP | BPNN | ELM | ESN | LSTM | CNN-LSTM | PSO-ELM | SSA-BP | SSA-ESN | |
|---|---|---|---|---|---|---|---|---|---|
| S | 5.11 | 1.32 | 0.70 | 1.00 | 4.33 | 10.18 | 84.35 | 475.43 | 0.96 |
| S1 | 3.87 | 1.23 | 0.75 | 0.89 | 3.57 | 6.35 | 57.37 | 399.83 | 0.86 |
| S2 | 2.11 | 1.16 | 0.65 | 0.87 | 3.59 | 5.86 | 51.52 | 435.16 | 0.79 |
| Method | Series | Training Set | Test Set | ||||
|---|---|---|---|---|---|---|---|
| MAE | MSE | R2 (%) | MAE | MSE | R2 (%) | ||
| S | 12.04 | 221.17 | 34.13 | 10.90 | 234.79 | 26.80 | |
| ARIMA | S1 | 13.92 | 239.56 | 45.23 | 11.49 | 260.64 | 25.01 |
| S2 | 10.22 | 192.18 | 34.18 | 12.36 | 299.09 | 48.82 | |
| S | 10.16 | 206.05 | 35.76 | 9.75 | 146.23 | 9.69 | |
| MLP | S1 | 11.41 | 252.19 | 27.44 | 8.85 | 135.73 | 16.18 |
| S2 | 9.26 | 181.70 | 36.93 | 10.10 | 158.14 | 2.33 | |
| ESN | S | 6.69 | 80.58 | 99.76 | 5.00 | 42.72 | 99.69 |
| S1 | 7.60 | 102.95 | 98.91 | 5.56 | 48.74 | 99.16 | |
| S2 | 5.74 | 57.35 | 99.48 | 4.48 | 36.61 | 99.52 | |
| ELM | S | 6.01 | 98.12 | 83.05 | 4.60 | 41.29 | 88.70 |
| S1 | 6.79 | 126.33 | 76.14 | 5.21 | 54.54 | 81.84 | |
| S2 | 5.03 | 78.63 | 79.71 | 4.01 | 32.21 | 89.71 | |
| LSTM | S | 6.79 | 87.69 | 99.39 | 4.92 | 41.48 | 99.83 |
| S1 | 10.51 | 213.22 | 98.99 | 7.64 | 98.74 | 99.74 | |
| S2 | 5.72 | 60.07 | 99.92 | 4.49 | 35.65 | 99.97 | |
| BPNN | S | 6.96 | 152.44 | 52.89 | 5.52 | 125.06 | 31.07 |
| S1 | 11.00 | 326.62 | 18.30 | 7.94 | 116.36 | 40.80 | |
| S2 | 8.14 | 145.38 | 50.21 | 8.29 | 158.55 | 42.17 | |
| SSA-ESN | S | 6.69 | 80.58 | 99.75 | 5.00 | 42.72 | 99.68 |
| S1 | 7.60 | 102.94 | 98.93 | 5.56 | 48.73 | 99.17 | |
| S2 | 5.74 | 57.34 | 99.48 | 4.48 | 36.60 | 99.53 | |
| SSA-BP | S | 5.73 | 91.26 | 83.97 | 4.29 | 32.50 | 92.97 |
| S1 | 7.00 | 105.40 | 92.76 | 5.20 | 44.62 | 96.12 | |
| S2 | 7.71 | 132.45 | 53.11 | 8.09 | 168.60 | 19.76 | |
| CNN-LSTM | S | 6.03 | 93.81 | 89.45 | 4.24 | 36.00 | 94.58 |
| S1 | 6.52 | 115.09 | 88.39 | 4.48 | 39.98 | 94.26 | |
| S2 | 4.74 | 62.00 | 93.01 | 3.52 | 29.83 | 95.04 | |
| PSO-ELM | S | 6.01 | 98.13 | 83.05 | 4.60 | 41.28 | 88.68 |
| S1 | 6.78 | 126.55 | 75.96 | 5.13 | 52.18 | 83.35 | |
| S2 | 5.04 | 70.70 | 79.66 | 3.99 | 30.968 | 89.94 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhen, L.; Bărbulescu, A. Echo State Network and Sparrow Search: Echo State Network for Modeling the Monthly River Discharge of the Biggest River in Buzău County, Romania. Water 2024, 16, 2916. https://doi.org/10.3390/w16202916
Zhen L, Bărbulescu A. Echo State Network and Sparrow Search: Echo State Network for Modeling the Monthly River Discharge of the Biggest River in Buzău County, Romania. Water. 2024; 16(20):2916. https://doi.org/10.3390/w16202916
Chicago/Turabian StyleZhen, Liu, and Alina Bărbulescu. 2024. "Echo State Network and Sparrow Search: Echo State Network for Modeling the Monthly River Discharge of the Biggest River in Buzău County, Romania" Water 16, no. 20: 2916. https://doi.org/10.3390/w16202916
APA StyleZhen, L., & Bărbulescu, A. (2024). Echo State Network and Sparrow Search: Echo State Network for Modeling the Monthly River Discharge of the Biggest River in Buzău County, Romania. Water, 16(20), 2916. https://doi.org/10.3390/w16202916








