A Water Level Forecasting Method Based on an Improved Jellyfish Search Algorithm Optimized with an Inverse-Free Extreme Learning Machine and Error Correction
Abstract
1. Introduction
2. Methodology
2.1. Time-Varying Filter-Based Empirical Mode Decomposition
2.2. Jellyfish Search Algorithm
2.2.1. Standard Jellyfish Search Algorithm
2.2.2. Optimized Jellyfish Search Algorithm Based on Tent Map
2.3. The Extreme Learning Machine and Its Improved Versions
2.3.1. Extreme Learning Machine
2.3.2. Inverse-Free Extreme Learning Machine
2.3.3. Online Sequential Extreme Learning Machine
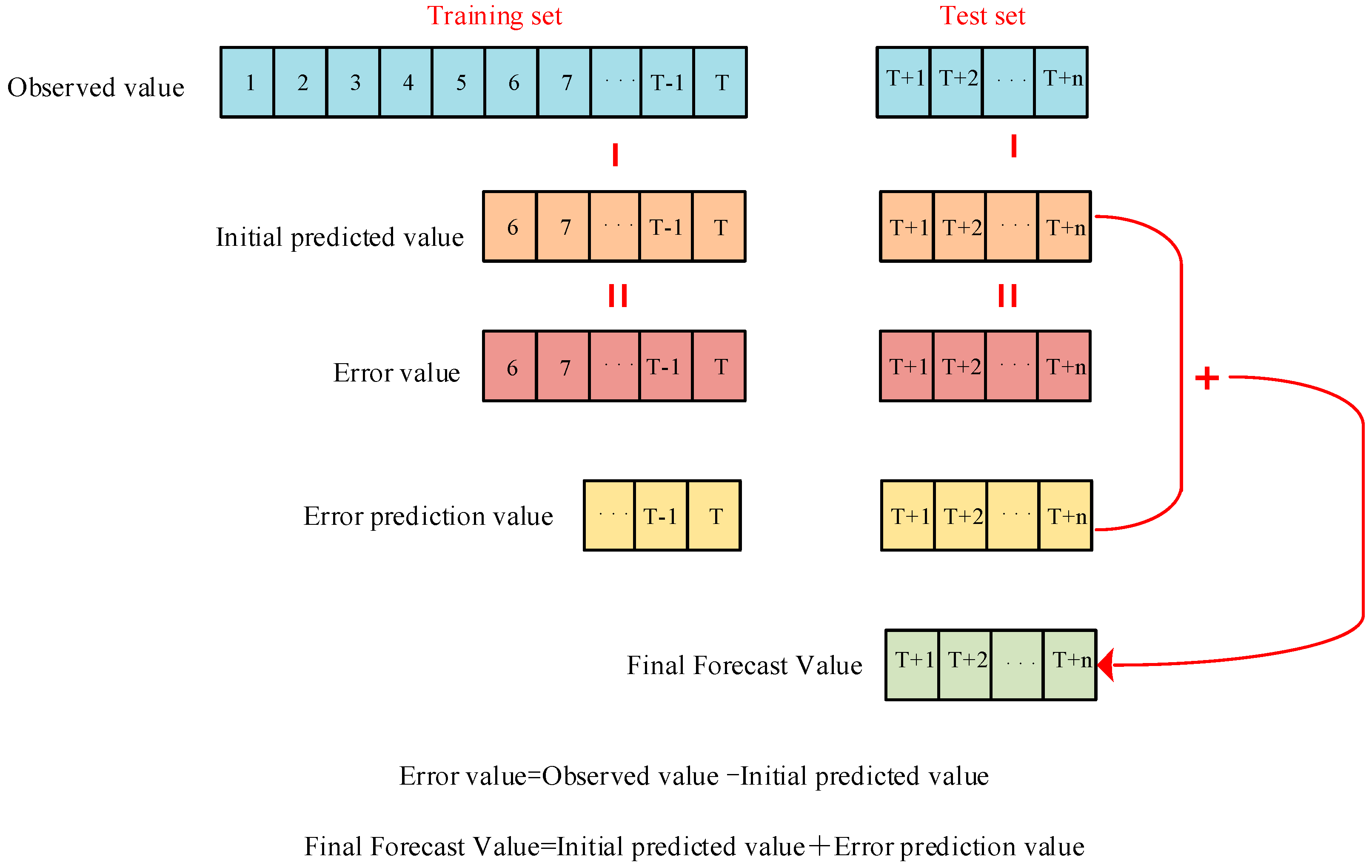
2.4. Error Correction
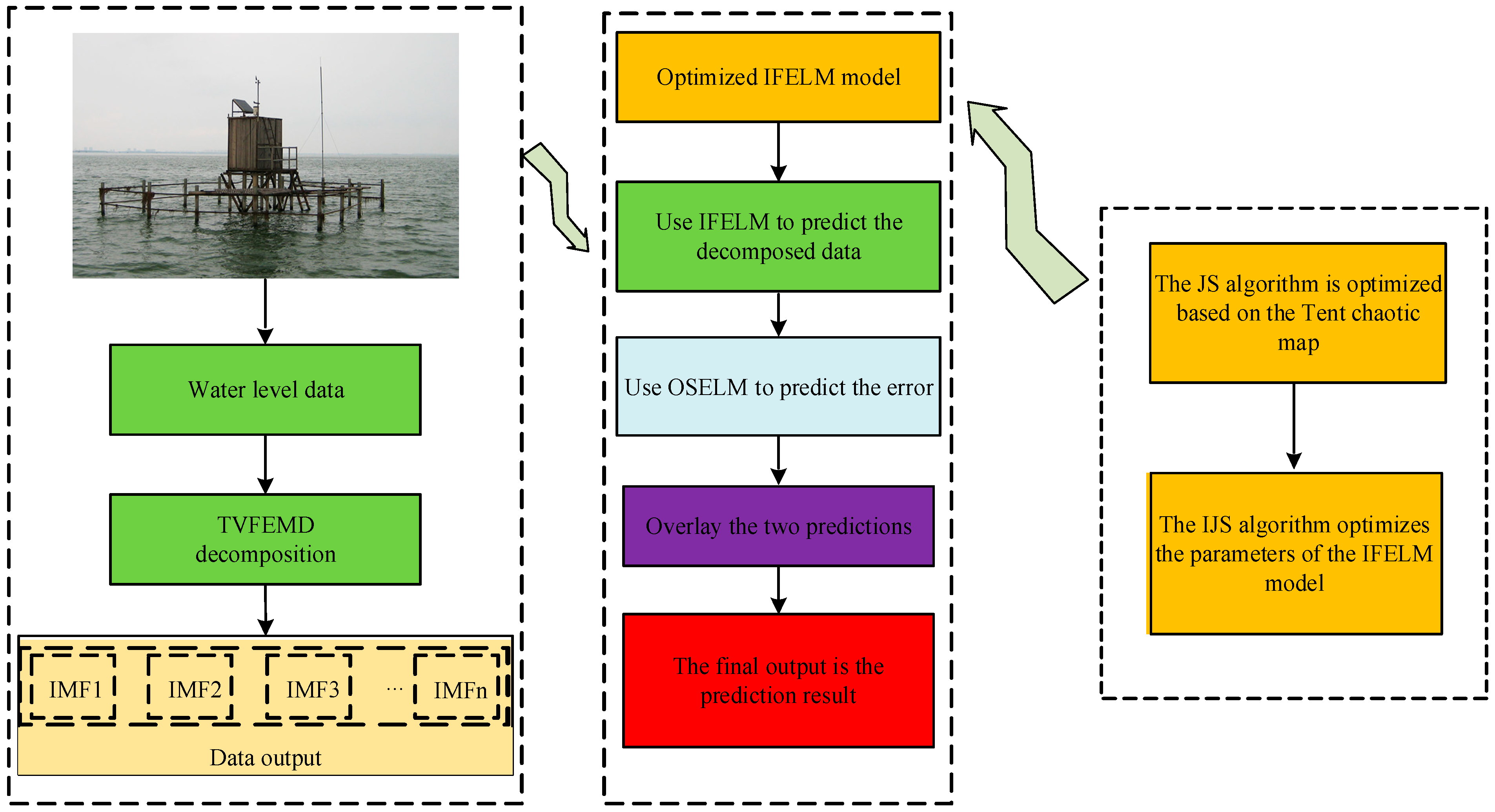
2.5. Construction of Water Level Forecasting Model
- (1)
- First, the historical water level data are selected from the Taihu and the TVFEMD method is used. The vector obtained from the decomposition of the historical water level single-variable data is denoted as X1, and its specific representation is as follows:In the formula, n represents the number of components obtained after TVFEMD.
- (2)
- The first 80% of the steady-state components are set as the training set. Taking the historical water level data of 13 years, totaling 4557 days, as the overall observed values, the water level data of the previous 10 days are used to predict the water level value of the 11th day to achieve a 1-day water level forecast. Taking the i-th (i = 1, 2, …, t) component after decomposition as an example, the input model dataset and the corresponding output are
- (3)
- Utilizing the IJS algorithm to optimize the IFELM model, the input and output data obtained from Step (2) are divided into training and testing datasets, which then serve as inputs for the optimized IFELM model. The model is trained and used to predict the testing data, yielding water level forecast values. Subsequently, the OSELM model is employed to correct the errors in the original water level data, resulting in corrected forecast values. Finally, the water level predictions and the error-corrected values are superimposed to obtain the final forecast values, as shown in Figure 2.
- (4)
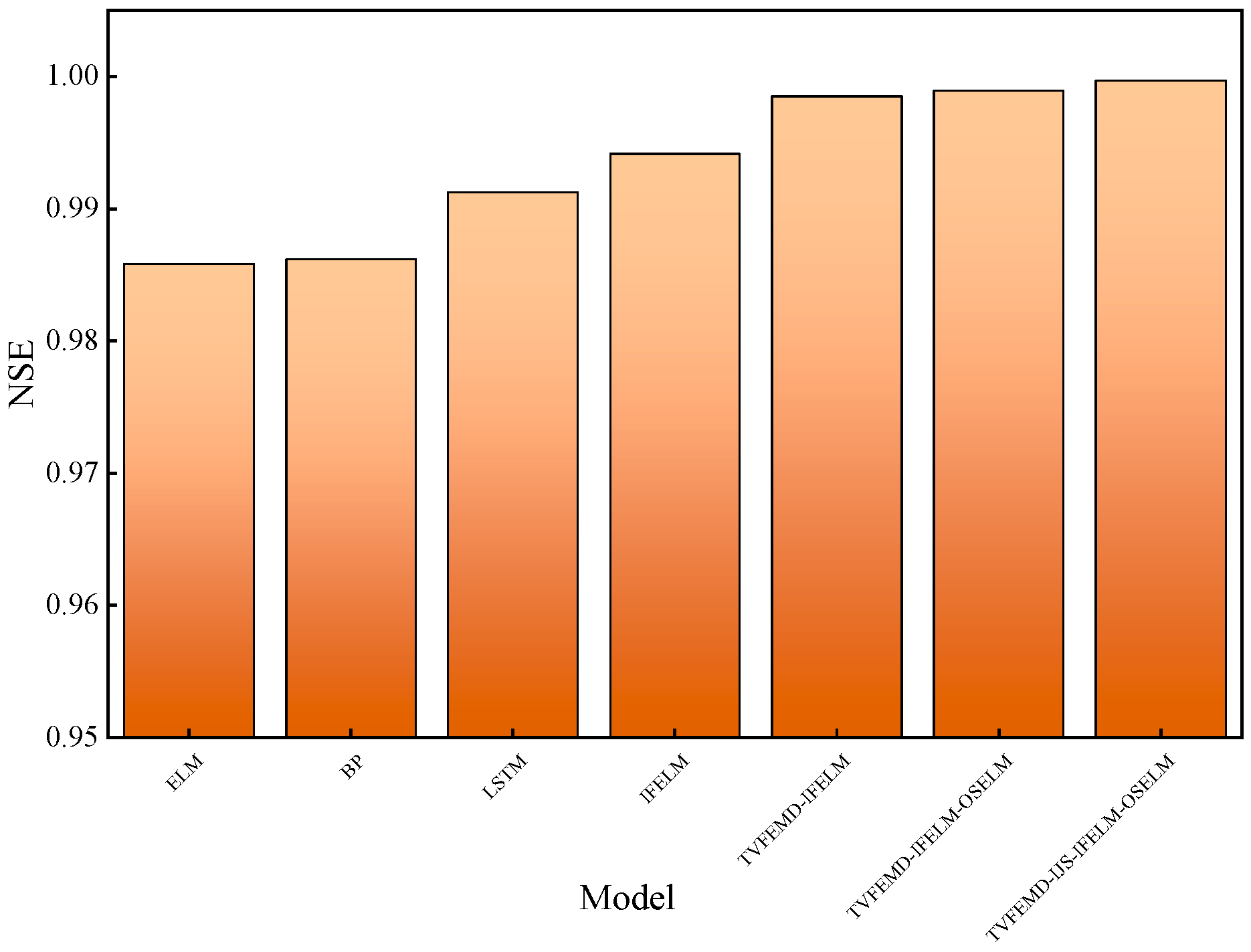
- To verify the performance of the model, ELM (Extreme Learning Machine), BP (Backpropagation), LSTM (Long Short-Term Memory), IFELM (Inverse-Free Extreme Learning Machine), TVFEMD-IFELM, and TVFEMD-IFELM-OSELM are set as comparative models. The model’s credibility is assessed using the Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and Nash Efficiency Coefficient/Coefficient of Determination (NSE) as the evaluation criteria for model performance.
3. Watershed Introduction and Evaluation Indicators
3.1. Watershed Introduction
3.2. Evaluation Metrics
4. Experimental Results and Case Studies
4.1. Data Preprocessing
4.2. Comparative Experimental Design and Result Analysis
5. Conclusions
- (1)
- The original water level data exhibit low regularity. By introducing the TVFEMD algorithm to decompose the original sequence, the complex original sequence is broken down into simpler sub-sequences, which improves the computational efficiency and, at the same time, enhances the accuracy of prediction.
- (2)
- By employing the TVFEMD technique, the original water level data are decomposed into more regular sub-sequences, which are then divided into datasets for use as inputs for the TVFEMD-IJS-IFELM-OSELM model. Initially, the Tent map is used to enhance the Jellyfish Search (JS) algorithm, optimizing the parameters of the IFELM to boost the model’s predictive accuracy and efficiency. Subsequently, the sub-sequences derived from TVFEMD are fed into the model for water level forecasting. Then, the Online Sequential Extreme Learning Machine (OSELM) is used to predict the error series of the original data. Finally, the predictive outcomes of the IFELM model and the error predictions from the OSELM are combined to yield the final forecast.
- (3)
- This paper introduces the TVFEMD-IJS-IFELM-OSELM model, which employs the methods of feature decomposition and reorganization followed by prediction and error correction. This approach achieved an NSE (Nash–Sutcliffe Efficiency) of 0.9997 on the testing set for one-day-ahead water level forecasting, signifying an exceptional performance. This suggests that the TVFEMD-IJS-IFELM-OSELM model offers very effective predictive capabilities for water level data.
6. Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peng, T.; Zhang, C.; Zhou, J. Intra- and Inter-Annual Variability of Hydrometeorological Variables in the Jinsha River Basin, Southwest China. Sustainability 2019, 11, 5142. [Google Scholar] [CrossRef]
- Li, G.; Shu, Z.; Lin, M.; Zhang, J.; Yan, X.; Liu, Z. Comparison of strategies for multistep-ahead lake water level forecasting using deep learning models. J. Clean. Prod. 2024, 444, 141228. [Google Scholar] [CrossRef]
- Boo, K.B.W.; El-Shafie, A.; Othman, F.; Khan, M.H.; Birima, A.H.; Ahmed, A.N. Groundwater level forecasting with machine learning models: A review. Water Res. 2024, 252, 121249. [Google Scholar] [CrossRef]
- Dai, R.; Wang, W.; Zhang, R.; Yu, L. Multimodal deep learning water level forecasting model for multiscale drought alert in Feiyun River basin. Expert Syst. Appl. 2024, 244, 122951. [Google Scholar] [CrossRef]
- Mohammed, K.S.; Shabanlou, S.; Rajabi, A.; Yosefvand, F.; Izadbakhsh, M.A. Prediction of groundwater level fluctuations using artificial intelligence-based models and GMS. Appl. Water Sci. 2023, 13, 54. [Google Scholar] [CrossRef]
- Li, H.; Zhang, L.; Zhang, Y.; Yao, Y.; Wang, R.; Dai, Y. Water-Level Prediction Analysis for the Three Gorges Reservoir Area Based on a Hybrid Model of LSTM and Its Variants. Water 2024, 16, 1227. [Google Scholar] [CrossRef]
- Wang, C.; Tang, W. Temporal Fusion Transformer-Gaussian Process for Multi-Horizon River Level Prediction and Uncertainty Quantification. J. Circuits Syst. Comput. 2023, 32, 18. [Google Scholar] [CrossRef]
- Wang, H.; Song, L. Water Level Prediction of Rainwater Pipe Network Using an SVM-Based Machine Learning Method. Int. J. Pattern Recognit. Artif. Intell. 2020, 34, 2051002. [Google Scholar] [CrossRef]
- Pan, M.; Zhou, H.; Cao, J.; Liu, Y.; Hao, J.; Li, S.; Chen, C.H. Water Level Prediction Model Based on GRU and CNN. IEEE Access 2020, 8, 60090–60100. [Google Scholar] [CrossRef]
- Yan, P.; Zhang, Z.; Hou, Q.; Lei, X.; Liu, Y.; Wang, H. A Novel IBAS-ELM Model for Prediction of Water Levels in Front of Pumping Stations. J. Hydrol. 2023, 616, 128810. [Google Scholar] [CrossRef]
- Zhu, H.; Wu, Y. Inverse-Free Incremental Learning Algorithms with Reduced Complexity for Regularized Extreme Learning Machine. IEEE Access 2020, 8, 177318–177328. [Google Scholar] [CrossRef]
- Guo, F.; Li, S.; Zhao, G.; Hu, H.; Zhang, Z.; Yue, S.; Zhang, H.; Xu, Y. A SOM-LSTM Combined Model for Groundwater Level Prediction in Karst Critical Zone Aquifers Considering Connectivity Characteristics. Environ. Earth Sci. 2024, 83, 267. [Google Scholar] [CrossRef]
- Hou, M.; Chen, S.; Chen, X.; He, L.; He, Z. A Hybrid Coupled Model for Groundwater-Level Simulation and Prediction: A Case Study of Yancheng City in Eastern China. Water 2023, 15, 1085. [Google Scholar] [CrossRef]
- Li, Y.; Shi, H.; Liu, H. A Hybrid Model for River Water Level Forecasting: Cases of Xiangjiang River and Yuanjiang River, China. J. Hydrol. 2020, 587, 124934. [Google Scholar] [CrossRef]
- Hu, J.; Li, X.; Wang, C. Displacement prediction of deep excavated expansive soil slopes with high groundwater level based on VDM-LSSVM. Bull. Eng. Geol. Environ. 2023, 82, 320. [Google Scholar] [CrossRef]
- Peng, T.; Zhou, J.; Zhang, C.; Fu, W. Streamflow Forecasting Using Empirical Wavelet Transform and Artificial Neural Networks. Water 2017, 9, 406. [Google Scholar] [CrossRef]
- Cui, X.; Wang, Z.; Xu, N.; Wu, J.; Yao, Z. A Secondary Modal Decomposition Ensemble Deep Learning Model for Groundwater Level Prediction Using Multi-Data. Environ. Model. Softw. 2024, 175, 105969. [Google Scholar] [CrossRef]
- Huan, S. A novel interval decomposition correlation particle swarm optimization-extreme learning machine model for short-term and long-term water quality prediction. J. Hydrol. 2023, 625, 130034. [Google Scholar] [CrossRef]
- Bai, Y.; Xing, W.; Ding, L.; Yu, Q.; Song, W.; Zhu, Y. Application of a Hybrid Model Based on Secondary Decomposition and ELM Neural Network in Water Level Prediction. J. Hydrol. Eng. 2024, 29, 04024002. [Google Scholar] [CrossRef]
- Yao, Z.; Wang, Z.; Wu, T.; Lu, W. A Hybrid Data-Driven Deep Learning Prediction Framework for Lake Water Level Based on Fusion of Meteorological and Hydrological Multi-source Data. Nat. Resour. Res. 2023, 33, 163–190. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P.; Goncalves, P. On Empirical Mode Decomposition and Its Algorithms. In Proceedings of the IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing IEEE, Grado, Italy, 8–11 June 2003. [Google Scholar]
- Zhang, Z.; Deng, A.; Wang, Z.; Li, J.; Zhao, H.; Yang, X. Wind Power Prediction Based on EMD-KPCA-BiLSTM-ATT Model. Energies 2024, 17, 2568. [Google Scholar] [CrossRef]
- Li, H.; Li, Z.; Mo, W. A Time Varying Filter Approach for Empirical Mode Decomposition. Signal Process. 2017, 138, 146–158. [Google Scholar] [CrossRef]
- Suo, L.; Peng, T.; Song, S.; Zhang, C.; Wang, Y.; Fu, Y.; Nazir, M.S. Wind Speed Prediction by a Swarm Intelligence Based Deep Learning Model via Signal Decomposition and Parameter Optimization Using Improved Chimp Optimization Algorithm. Energy 2023, 276, 127526. [Google Scholar] [CrossRef]
- Chou, J.-S.; Truong, D.-N. A Novel Metaheuristic Optimizer Inspired by Behavior of Jellyfish in Ocean. Appl. Math. Comput. 2021, 389, 125535. [Google Scholar] [CrossRef]
- Ha, P.T.; Dinh, B.H.; Phan, T.M.; Nguyen, T.T. Jellyfish Search Algorithm for Optimization Operation of Hybrid Pumped Storage-Wind-Thermal-Solar Photovoltaic Systems. Heliyon 2024, 10, e29339. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme Learning Machine: Theory and Applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Ge, D.; Jin, G.; Wang, J.; Zhang, Z. A Novel Data-Driven IBA-ELM Model for SOH/SOC Estimation of Lithium-Ion Batteries. Energy 2024, 305, 132395. [Google Scholar] [CrossRef]
- Li, S.; You, Z.H.; Guo, H.; Luo, X.; Zhao, Z.Q. Inverse-Free Extreme Learning Machine with Optimal Information Updating. IEEE Trans. Cybern. 2015, 46, 1229–1241. [Google Scholar] [CrossRef]
- Lan, Y.; Soh, Y.C.; Huang, G.-B. Ensemble of Online Sequential Extreme Learning Machine. Neurocomputing 2009, 72, 3391–3395. [Google Scholar] [CrossRef]
- Thamizharasu, P.; Shanmugan, S.; Sivakumar, S.; Pruncu, C.I.; Kabeel, A.E.; Nagaraj, J.; Videla, L.S.; Anand, K.V.; Lamberti, L.; Laad, M. Revealing an OSELM Based on Traversal Tree for Higher Energy Adaptive Control Using an Efficient Solar Box Cooker. Sol. Energy 2021, 218, 320–336. [Google Scholar] [CrossRef]




| Evaluation Indicators | Formula |
|---|---|
| Root mean square error (RMSE) | |
| Mean absolute error (MAE) | |
| Mean absolute percentage error (MAPE) | |
| Nash–Sutcliffe efficiency (NSE) |
| Model | RMSE | MAE | NSE | MAPE (%) |
|---|---|---|---|---|
| ELM | 0.035705 | 0.016863 | 0.9858 | 0.4931 |
| BP | 0.037793 | 0.018175 | 0.9862 | 0.4665 |
| LSTM | 0.030096 | 0.017741 | 0.9912 | 0.4998 |
| IFELM | 0.024579 | 0.015147 | 0.9941 | 0.4301 |
| TVFEMD-IFELM | 0.012359 | 0.004262 | 0.9985 | 0.1084 |
| TVFEMD-IFELM-OSELM | 0.010474 | 0.004195 | 0.9989 | 0.1101 |
| TVFEMD-IJS-IFELM-OSELM | 0.005562 | 0.002995 | 0.9997 | 0.0824 |
| Year | 2016 | 2017 | 2018 | Average Error (%) | |
|---|---|---|---|---|---|
| Model | Measured Peak Water Level (cm) | 4.860 | 3.600 | 3.700 | |
| ELM | Predicted Value (cm) | 4.592 | 3.589 | 3.685 | 2.075 |
| Predicted Absolute Error (%) | 5.514 | 0.306 | 0.405 | ||
| BP | Predicted Value (cm) | 4.631 | 3.595 | 3.681 | 1.803 |
| Predicted Absolute Error (%) | 4.772 | 0.139 | 0.514 | ||
| LSTM | Predicted Value(cm) | 4.743 | 3.585 | 3.704 | 0.997 |
| Predicted Absolute Error (%) | 2.407 | 0.417 | 0.108 | ||
| IFELM | Predicted Value (cm) | 4.775 | 3.588 | 3.691 | 0.775 |
| Predicted Absolute Error (%) | 1.749 | 0.333 | 0.243 | ||
| TFVEMD-IFELM | Predicted Value (cm) | 4.784 | 3.589 | 3.698 | 0.641 |
| Predicted Absolute Error (%) | 1.564 | 0.306 | 0.054 | ||
| TFVEMD-IFELM -OSELM | Predicted Value (cm) | 4.796 | 3.596 | 3.696 | 0.512 |
| Predicted Absolute Error (%) | 1.317 | 0.111 | 0.108 | ||
| TFVEMD-IJS -IFELM-OSELM | Predicted Value (cm) | 4.901 | 3.603 | 3.699 | 0.316 |
| Predicted Absolute Error (%) | 0.837 | 0.084 | 0.027 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Shou, W.; Wang, X.; Zhao, R.; He, R.; Zhang, C. A Water Level Forecasting Method Based on an Improved Jellyfish Search Algorithm Optimized with an Inverse-Free Extreme Learning Machine and Error Correction. Water 2024, 16, 2871. https://doi.org/10.3390/w16202871
Zhang Q, Shou W, Wang X, Zhao R, He R, Zhang C. A Water Level Forecasting Method Based on an Improved Jellyfish Search Algorithm Optimized with an Inverse-Free Extreme Learning Machine and Error Correction. Water. 2024; 16(20):2871. https://doi.org/10.3390/w16202871
Chicago/Turabian StyleZhang, Qiwei, Weiwei Shou, Xuefeng Wang, Rongkai Zhao, Rui He, and Chu Zhang. 2024. "A Water Level Forecasting Method Based on an Improved Jellyfish Search Algorithm Optimized with an Inverse-Free Extreme Learning Machine and Error Correction" Water 16, no. 20: 2871. https://doi.org/10.3390/w16202871
APA StyleZhang, Q., Shou, W., Wang, X., Zhao, R., He, R., & Zhang, C. (2024). A Water Level Forecasting Method Based on an Improved Jellyfish Search Algorithm Optimized with an Inverse-Free Extreme Learning Machine and Error Correction. Water, 16(20), 2871. https://doi.org/10.3390/w16202871





