3D Numerical Model Validation Using Experimental Test Data for Patrind Hydropower Project

Abstract

Whilst numerical modelling is commonly used for simulation to check the design of water conveyance, sluicing and spillway structure design, the numerical modelling has rarely been compared with the physical model tests. The objective of this research presented in this paper was to examine the validity and suitability of the numerical computational fluid dynamics (CFD) modeling method within an ANSYS Fluent/CFD R 18.2 software and compare its results with a fully instrumented and well-run physical model test at the 1:45 scale, carried out for Patrind Hydropower Project located in Pakistan. The physical model test was conducted for confirmation and optimization of a natural de-sanding basin, and diversion of suspended sediment-rich flood waters using a bypass tunnel. The numerical simulation was able to reproduce physical model test results and data gathered over a 7-year project operation to an acceptable level of accuracy. A detailed explanation of the approach used in numerical modelling together with analysis of simulation diagrams of ANSYS Fluent/CFD is also presented. The research shows that a 3D numerical model with accurate boundary conditions and mesh size can replace the need for physical model tests.

1. Introduction

Inflow and deposition of sediments in hydropower reservoirs reduce useable reservoir storage and block inlet conduits and sand-size suspended sediments from causing damage to turbines. The effective sediment management of reservoirs is one of the most crucial factors in prolonging the life, and trouble-free operation, of hydropower projects. Different site-specific strategies are globally used for sediment control and evacuation. Traditionally, surface and underground de-sanding structures are used for enabling conveyance of sand-free decanted water into turbines. Most of the conventional de-sanders are inefficient and require suitable site conditions for their economic and safe construction.

Owing to multiple technical, scheduling, and financial issues at Patrind HPP, a relatively novel solution of using a natural de-sander was proposed and subsequently its feasibility design was tested using a 1:45 scaled physical model, considered the minimum modeling scale recommended by the International Commission of Large Dams [1]. The physical model test was aimed at the optimization of the proposed natural de-sanding basin and effectiveness of the bypass tunnel in diverting flood waters that were high in suspended sediment ensuring the sustainability of the upper reservoir capacity.

Construction of a good physical model, equipped with miniature sensors, requires a large model bed and hydraulic laboratories supervised by experienced staff. Such facilities exist only in a few countries and some of these have an excellent reputation. Physical model testing provides several features to determine appropriate hydraulic design plus understanding of hydrodynamics [2]. Selecting appropriate scale factors allows for the representation of the complexity of prototype flows. Physical model construction and operation, however, is time consuming and expensive. Additionally, flow visualization can be challenging, and accurate non-intrusive variable measurement calls for caution, proper techniques, and the right equipment.

On the other hand, over recent decades, numerical simulation of three-dimensional flow patterns has improved, and among other applications, has become a useful tool for realistically representing hydrodynamics and flow regimes in complex environment such as headworks of hydropower project. ANSYS Fluent/CFD numerical modelling has been used for power intakes, spillways, river flows, and dam break simulations [3,4,5,6].

Evaluating the numerical model performance and its comparison with a good physical model test provides an incredibly good opportunity for validation of numerical modelling techniques and optimization. While Lemos et al. (2009), Gerritsen et al. (2009), and Gerritsen et al. (2011) [7,8,9] attempted something similar with wave propagation and cross-shore sediment transport, Sanchez-Arcilla et al. (2009) used wave flume tests of beach erosion and accretion at three different scales [10]. The research presented in this article used Ansys Fluent/CFD R 18.2 simulation software for a comprehensive numerical analysis and compared results with the physical model test experimental test data performed at Patrind HPP. This project was chosen as a case study because two authors of this paper worked on it.

The research validated 3D numerical simulation and its use is proposed instead of physical model tests provided that appropriate simulation procedures, governing equations and boundary conditions are applied. This article provides details of methods followed and also makes further recommendations regarding the use of numerical modelling to replace the need for physical model testing.

2. Natural Desander at Patrind Hydropower Project

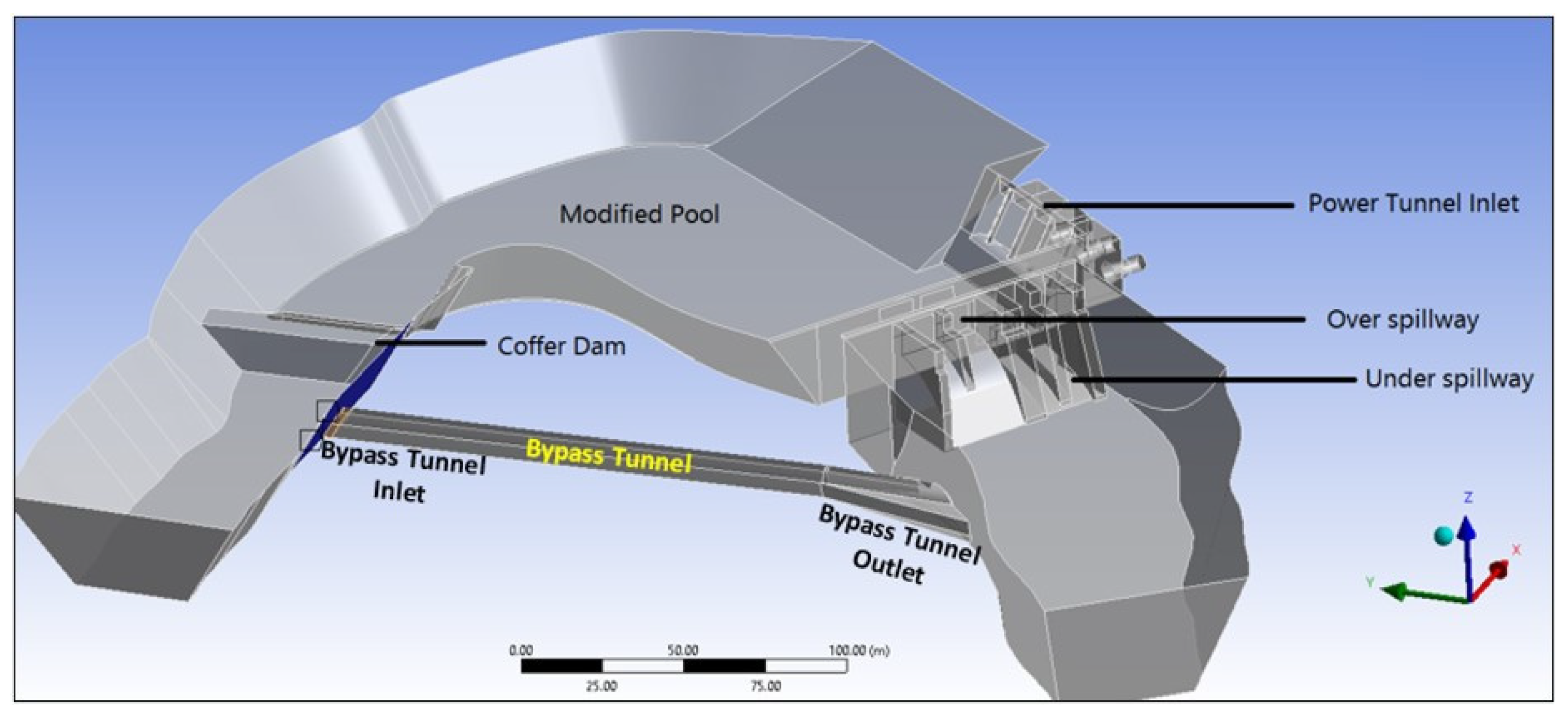
The 150 MW Patrind Hydropower Plant (HPP) in Pakistan is located on the Kunhar River is the subject of the case study Figure 1. Star Hydro Power Ltd., owned by the Korean independent power producer (K-Water) developed the project and Daewoo E&C was engaged as an EPC contractor. This run-of-the-river project headwork structures are comprised of a gravity dam with two underflow spillway (US) and two overflow spillway (OS) sections and power intake structure, a bypass tunnel for discharging of high floods, as well as a top-able upstream concrete cofferdam. A 2.5 km long headrace provides a 90 m head for power generation. In this seismically active region, the valley slopes are generally deteriorated and have had several historic landslides.

A 300 m long, three-bay sand trap was envisioned as part of the feasibility study concept for the headrace tunnel. It had sluicing channels and de-sanding chambers. This necessitated a significant underground excavation. For this reason, the EPC contractor decided for a shorter surface de-sanding concrete structure which proved inefficient [11,12,13].

Figure 1. Kunhar River Catchment and completed Patrind headworks [12].

Figure 1. Kunhar River Catchment and completed Patrind headworks [12].

The concept of de-sanders is based on the principle first described by Hjulstrøm, F. (1935 and 1939) [14,15]. He discovered that a certain flow velocity is required to bring a sediment of a particular size into floatation. Once in floatation, the suspended particle remains in floatation until the flow velocity is sufficiently decreased (about half of the required floatation velocity) before the suspended particle is deposited.

In Figure 2, the Hjulstrøm diagram [14,15] shows the relationship between the flow velocity ranges causing erosion, transport and suspension as well as threshold velocities required for deposition of various grain sizes and transport of lose grains as shown. It is feasible to determine from the below the range of flow velocities that will mobilize sediment of various sizes as well as cause their deposition.

Following the determination that the surface de-sander proposed by the EPC contractor was inefficient, its design was changed again using a relatively recent and novel concept [12] that involves diversion of high flows from within the upper reservoir allowing only design flow through the lower reservoir and power intakes. This limits the flow velocity and encourages sedimentation of sand sized quartz particles thus preventing erosion damage to turbines. In order to control flow amount and velocity, a bypass tunnel was added for diversion of floods larger than the design flow (153.6 m³/s) capacity. The region known as the modified pool (MP) serves as a natural sand trap area located between a cofferdam and a weir structure. The implemented design is given in Figure 3 [16].

Once the surface flow velocity reaches the required threshold (0.2 m/s), and considering that vertical velocity of sediment laden water, at any given location in the MP, significantly decreases with depth due to increasing density and shear stress close to stream bed of MP, coarse sand grains settle in the modified pool (MP) during the Normal Plant Operation (NPO).

Physical models have long been used in hydraulic studies because they accurately and dynamically represent flow phenomena; however, the results are influenced by the scale effects. The Laboratory of Hydraulics, Hydrology, and Glaciology (VAW) of the Swiss Federal Institute of Technology Zurich (ETH Zurich) was commissioned to investigate hydraulics and sediment management of the Patrind HPP using a physical model at a 1:45 minimum scale recommended by the ICOLD. The physical model used is shown in Figure 4 below.

The model represented a 300 m long reservoir reach upstream of the cofferdam, the cofferdam itself, the bypass tunnel, the 300 m long modified pool ending at a gravity dam with spillway sluices and power intake structures, as well as a 330 m stretch of downstream river was also modelled. The model’s results helped in optimization of the layout which also included a 7.5 m wide by an 8.5 m high bypass tunnel. As a result of initial model runs, relocation of the bypass tunnel inlet and reshaping of intake and outlet chute was performed. Some shape optimization was also needed and implemented in sluicing and overflow structures.

The modelled and simulated flow conditions were found to be satisfactory within the physical model perimeter [13]. The spillway and bypass tunnel capacities were confirmed to be sufficient in handling of high floods including the PMF (probable maximum flood) exceeding 10,000 years return period. The natural sand trap system works as intended, and the redesigned de-sanding basin (i.e., MP) low flow velocities facilitate the settling and temporary storage of fine sediments ensuring largely sediment free water reaches the power intake. For the crucial sand grain of >0.2 mm size, the trap efficiency in the reservoir is 100% with sustainable sediment management.

Findings from a 1-D numerical model of the upper reservoir corroborated the long-term sustainability of active storage capacity as confirmed by the past 7 years of reservoir operation.

3. Numerical Model Construction and Simulation

3.1. Model Construction

As computing power has greatly improved recently, the numerical simulations of hydrodynamic processes, such as flow through tunnels, reservoirs, and spillways, have become attractive and are increasingly in use. In order to carryout numerical simulation, a 3D computer model of the Patrind HPP headworks was developed in three key processes that resulted in the effective construction and running of the final model.

Initially, 3D AutoCAD was used to construct model geometry Figure 5. After the geometry was completed, the model was transferred to the 3D ANSYS Fluent/CFD software, where mesh generation was performed (Figure 6) and assignment of the parameters took place (Figure 7). The flow discharge rate was the only variable that was altered throughout the four numerical model runs. The main construction steps are further elaborated below.

As a 1st step for the creation of CFD computation domain, as-built drawings of the project headworks were used in construction of a 3D AutoCAD model (Figure 5). Once complete, these files were converted to Standard Triangle Language (.stl) format files and uploaded to ANSYS Fluent/CFD.

In the 2nd step, the CFD computational domain was meshed. A mesh in a 3D domain can be tetrahedral, pyramidal, prismatic, or hexagonal depending on the geometry of the cell [17]. For this research tetrahedral mesh was used because tetrahedral elements are well suited for complicated and irregular geometry. In contrast to hexahedral meshes, which are effective at filling spaces with block-like structures, tetrahedrons can fill practically any shaped space with minimal distortion. Tetrahedral meshes are more effective in accurately representing curved surfaces and asymmetrical shaped structures, essential for capturing the fluid dynamics around these areas.

Verification for sufficiency of selected mesh size and density was performed by refinement and optimization until the model details were generally comparable to those of the physical model. It is important to improve the accuracy of analysis by assessing these metrics, to make sure the mesh is appropriate for CFD simulations. Before finalizing the mesh, mesh metrics were checked and found that most important metrics like aspect ratio, skewness, Jacobian ratio, and orthogonal quality were in the accepted range as given in

Table 1. Mesh metrics comparison between selected mesh for the model and accepted ranges according to the ANSYS software manual.

Metric	Accepted Range	Software Assessment of Applied Mesh Characteristics
		Min	Max	Average	Std Dev
Skewness	<0.5 (Ideal), <0.9 (Acceptable)	0.001174	0.89981	0.2362	0.17296
Aspect Ratio	<5 (Ideal for Fluent)	1.176	5.21	1.8133	0.41512
Orthogonal Quality	>0.1 (Poor), >0.6 (Good), ~1 (Ideal)	1.0	1.0	0.70442	0.1311
Jacobian Ratio	Close to 1 (Ideal)	1	1	1	0

and compared favorably with the metrics’ ideal values.

In computational fluid dynamics simulations, the turbulent flow close to the wall borders must be precisely captured for the accuracy of wall boundary treatments and this requires focused mesh refinement. The number of elements in the mesh in ANSYS is directly influenced by the mesh size as well as other parameters, such as element type (tetrahedrons, hexahedrons, etc.). ANSYS Fluent automatically discretizes the geometry in accordance with the specified parameters after finalization of the mesh size settings and calculates the number of elements and nodes.

For the computational analysis to be precise, adhering to the appropriate y+ range is essential. The typical application of wall functions in the RNG k − ε turbulence model is most effective within a y+ range of 30 to 300. This range is particularly advantageous for large-scale basin and channel models that experience significant water gradients. In these scenarios, the wall functions adeptly capture the turbulent flow and effectively account for the impacts of wall roughness. This is accomplished without the necessity for an excessively fine mesh to resolve the viscous sub-layer, which essentially becomes redundant. For both laminar and turbulence flows’ velocity close to a river’s bed and sides drops rapidly near these surfaces due to friction and roughness height (non-slip condition).

Furthermore, for this research, wall functions were employed as the primary flow is more important than the flow near the surfaces. By using this method, the cumbersome fine grid was not necessary. By allowing intricate interaction between the flow velocity and the roughness elements, this approach ensured a more accurate representation of real-world flow conditions in large models [18].

In this study, the initial mesh metrics, and y+ values in the complicated wall sections were notably high in the simulation using the RNG k − ε model. By decreasing the mesh size in these specific areas, mesh metrics and the y+ values were successfully brought within an acceptable range. The y+ values used in the current study for a variety of structures (walls) are within the ideal allowable range (

Table 2. Comparison of measured y+ values with the ideal RNG k − ε model allowable ranges.

Section/Wall	y+ Value of the Model Walls	Ideal y+ Range for RNG k − ε
Spillway chute	95.4	30–300
Weir dam-wall	103.9	30–300
Modified pool upstream of the dam	70.8	30–300
Modified pool left bank wall	68.3	30–300
Power inlet	145.8	30–300
Spillway and bypass tunnel stilling basin	69.6	30–300
Bypass tunnel section above spring line (arch)	37.5	30–300
Cofferdam	145.2	30–300
Bypass tunnel invert	67.2	30–300
Bypass tunnel chute	67.8	30–300
Riverbed upstream of cofferdam	65.6	30–300
River channel left and right bank upstream of cofferdam	68.3	30–300

) specified for the RNG k − ε model. This adherence validates the employed mesh capacity to effectively represent the turbulent boundary flow layer in the numerical simulation.

Local mesh refinement was used in locations that needed a finer mesh, including those close to walls or in complex regions. This affects the total element count by raising the element density in the designated regions.

In the model, the mesh element size was finally determined at 0.5 m in the complex areas like bypass tunnel, power inlet and spillways, and the rest of the area such as modified pond (MP), was kept at 4 m. The total number of nodes and elements in the solid model was 115,710 and 578,590, respectively, and these were consecutively connected with tetrahedral mesh. The fully meshed model is given in Figure 6.

The 3rd step involved selection of specifying the conditions and boundaries. Since air is at the top of the domain, it has historically been described as having a set pressure and a fluid percentage of zero (free surface). Fresh water density was given as 1000 kg/m³ and relevant discharge was selected according to each specified case reflecting the relevant discharge rate. The momentum value was derived from the initial velocity and density of the fresh water. Turbulent viscosity is derived by the turbulence model RNG k − ε. For the boundary conditions, the outflow in the current study depicts the amount of water leaving the geometry’s downstream end and through and over various outlets (bypass tunnel, over spillway, under spillway and power intake) without re-entering the domain. For all four modelled scenarios, the upstream boundary condition was chosen for the mass inflow (based on water head and inflow rate) and a free flow condition established for each outlet unless regulated. A non-slip surface for all concrete and shotcrete surfaces for the model assumed a roughness constant of 0.5 and a suitably set roughness height of 0.6 mm.

In the final 4th step, methods and equations were selected which are given in Section 3.2. Figure 7 shows all the given boundary conditions except in those cases when over and under spillways, bypass tunnel inlets/outlets and power intake are closed or regulated.

3.2. Computational and Modelling Modules of ANSYS Fluent/CFD R 18.2

Recent years have seen the emergence of numerical modelling as a method for resolving complex issues that are expensive or difficult to accomplish in the lab [19,20,21,22]. For this research ANSYS Fluent/CFD R 18.2 software was used. It is a sophisticated numerical software capable of complex hydrodynamic simulations. In addition, it interfaces with numerical modeling tool called CFD (computational fluid dynamics), simulating water flows in rivers, over and around hydraulic structures, or where fluids and solid structures interact [23,24,25]. CFD is widely used to simulate fluid flow for better understanding of engineering, industrial and environmental issues.

The Finite Volume Method (FVM) is the foundation of ANSYS Fluent/CFD. It deals with a numerical method for resolving partial differential equations that come up in the context of heat transfer, fluid flow, and related processes. In the present research, it was primarily used to solve the Navier–Stokes equations, which describes the motion of fluid substances.

Appropriate methods and equations were selected from the software and used to run the research model; details are explained hereafter. The SIMPLE algorithm stands for Semi-Implicit Pressure-Linked Equations method, and it is used for resolving the Navier–Stokes equations in computational fluid dynamics (CFD). In order to satisfy the momentum equations and the continuity equation (mass conservation) in fluid flow simulations, this approach iteratively corrects the pressure and velocity fields. When managing the pressure-velocity coupling in incompressible flow models, it is especially helpful.

The second-order upwind scheme is used, the spatial discretization technique known as second-order upwind methods is used to approximate the flow variables at the cell faces. Using data from the upstream side, the second-order upwind approach uses the direction of the flow to compute a more precise value of a variable at a cell face. Because it reduces numerical diffusion and more accurately depicts the gradients in the flow field, which are crucial in turbulent flows, this approach is more accurate than first-order systems.

The Pressure Staggering Option (PRESTO!) scheme, built in the software, uses a discrete continuity balance similar to the staggard grid schemes and it is available for all meshes. Strong vortices and recirculation’s are two scenarios in which PRESTO becomes useful and especially good at managing steep pressure gradients. Pressure and velocity variables are staggered ensuring a more accurate depiction of the pressure field. For transient formulation, the first-order implicit technique first-order was applied. In an implicit scheme, the present and future time step values are used to calculate the system’s state at an upcoming time step. Explicit techniques, on the other hand, compute the future state just from the current state (time step being calculated at any given point in the simulation process). According to software, the solution at the current time step is calculated using the solution from the previous time step in the first-order implicit approach, which is a time discretization technique. It requires less computing and is more stable. The combined use of the above methods helps accomplish a balance among accuracy and computational efficiency. Particularly in situations when the flow field has steep gradients, such as in turbulence, second-order upwind techniques tend to yield more accurate answers than first-order methods. In both steady-state and transient simulations, the SIMPLE technique is commonly utilized to couple velocity and pressure fields [23,25].

The modelling domain is discretized using the FVM into a grid of control volumes, and the flows of mass, momentum, and energy are conservatively balanced over the faces of these control volumes. The flexibility of this software in simulating alternative geometries and performing sensitivity analyses, its visualization capabilities, its ability to model large structures or areas, and its low cost in comparison to physical modeling makes it particularly appealing from an engineering standpoint for hydraulic design [26].

To deal with the turbulent flow, RNG k − ε, and k − ε are the most recent advanced turbulence models that are being employed extensively in hydraulic engineering [27]. Numerical models are highly capable of displaying the flow pattern within and over hydraulic structures, which is occasionally just as significant as flow attributes, in addition to defining hydraulic features [28,29]. Macián-Pérez et al. (2020a & 2020b) examined the turbulence models, in relation to the flow behavior in the USBR-II stilling basins. The results of the investigation showed that the RNG k − ε model had superior accuracy for the free surface, roller lengths, and hydraulic jump efficiency; additionally, velocity profiles were also examined using the RNG k − ε model [30,31]. The RNG k − ε model has been used for validation by various authors [32,33]. ANSYS Fluent/CFD Software uses the following Navier–Stokes governing equations used for the simulations that are for flow.

The continuity Equation (1), which expresses mass conservation, is given by:

$$\nabla ·\left(\rho u\right)=0$$

(1)

where u is the vector of velocity and $\rho$ is the fluid density.

The momentum equation accounts for forces acting on fluid elements, Equation (2) is written as:

$$\partial \left(\rho u\right)/\partial t+\nabla ·\left(\rho \overrightarrow{u}\overrightarrow{u}\right)=\nabla p+\nabla ·\left(\mu \left(\nabla u+{\left(\nabla u\right)}^T\right)\right)$$

(2)

here, the time rate of change in momentum is denoted by ∂($\rho u$)/∂t, the convective acceleration is denoted by ∇·($\rho \overrightarrow{u}\overrightarrow{u}$), the pressure gradient is denoted by −∇p, and the viscous forces are denoted by ∇·(μ(∇u + (∇u)^T)) and finally μ is the fluid’s dynamic viscosity in this equation.

The turbulence model, RNG k − ε is used [17] in order to simulate turbulent flow, which closely resembles the Navier–Stokes equation. The re-normalization group (RNG) model is an effective turbulence model that performs well in simulating vortex; as a result, this model is incredibly helpful in simulating flow patterns. There are two main equations which are utilized in the RNG model, Equations (3) and (4) [23,25,34,35].

The turbulent kinetic energy (k) equation:

$$\frac{\partial }{\partial t }\left(\rho k\right)+\frac{\partial }{\partial x}\left(\rho u_{i}k\right)=\frac{\partial }{{\partial x}_i}\left({\alpha }_k{\mu }_{eff}\frac{\partial k}{{\partial x}_i}\right)+G_k+G_b-\rho \mathsf{ϵ}+S_K$$

(3)

The turbulent dissipation rate $\left(\mathsf{ϵ}\right)$ equation:

$$\frac{\partial }{\partial t}\left(\rho \mathsf{ϵ}\right)+\frac{\partial }{\partial x}\left(\rho u_i\mathsf{ϵ}\right)=\frac{\partial }{{\partial x}_i}\left({\alpha }_{\mathsf{ϵ}}{u}_{eff}\frac{\partial \mathsf{ϵ}}{{\partial x}_i}\right)+C_{1\mathsf{ϵ}}\frac{\mathsf{ϵ}}{k}\left(G_k+C_{3\mathsf{ϵ}}{G}_b\right)-C_{2\mathsf{ϵ}}\rho \frac{{\mathsf{ϵ}}^2}{k}+S_{ϵ}$$

(4)

In the above equations, G_k stands to produce kinetic energy from turbulence caused by mean velocity gradients, G_b is the buoyancy-induced creation of kinetic energy in turbulence. The value ${\alpha }_k$ is the inverse effective Prandtl numbers for $k$ and ϵ. The default values for the model variables $C_{1\mathsf{ϵ}}$, $C_{2\mathsf{ϵ}}$, $C_{\mu }$, ${\alpha }_k$, and $\alpha \mathsf{ϵ}$ are as follows:

$$C_{1\mathsf{ϵ}}=1.42, C_{2\mathsf{ϵ}}=1.68, C_{\mu }=0.0845, {\alpha }_k=1.39 \mathrm{and} {\alpha }_{\mathsf{ϵ}}=1.39$$

Equation (5) calculates the turbulent viscosity $\left({\mu }_t\right)$

$${\mu }_t=\rho C_{\mu }\frac{k^2}{\mathsf{ϵ}}$$

(5)

${\mu }_t$ symbolizes the turbulent viscosity, which is an effective viscosity that takes into consideration the extra momentum transfer brought on by turbulence. $\rho$ is the fluid density and based on the flow conditions, the software automatically calculates the coefficient $C_{\mu }$ whereas turbulent kinetic energy is denoted by $k$ and the rate at which turbulent kinetic energy dissipates is expressed as ϵ.

In the end, the roughness height was maintained at 0.6 mm for each of the four numerical casers, and the wall roughness constant in the numerical model was set at 0.5 mm to maintain uniform surface roughness throughout the model perimeter.

4. Numerical Simulation versus Physical Model Testing

This study focused on using ANSYS Fluent/CFD R 18.2 to simulate water flow at Patrind HPP headworks comprised weir, spillways, bypass tunnel, modified pond, cofferdam and power tunnel intake. The simulation results were compared with the physical model tests carried out Institute of Technology Zurich (ETH, Zurich, Switzerland).

Four operational scenarios, detailed in

Table 3. The operation rules for Patrind Hydropower Project for physical and numerical models.

Inflow [m3/s]	ANSYS Fluent [m3/s]	Flood Return Period	Operation	Turbine Water Discharge QTW [m3/s]	Flap Gate Discharge QFG [m3/s]	Underflow Spillway Discharge QUS [m3/s]	Overflow Spillway Discharge QOS [m3/s]	Bypass Tunnel Discharge QBT [m3/s]	Water Level Hmp HR [m a.s.l.]
155.9–200	155.9	-	Normal operation	153.7	2.2–46.1	-	-	-	765
200–800	800	Up to HQ5	Regulated Flood control	153.7	-	-	-	fully open	765
2029–2799	2799	Up to HQ350	Unregulated/Drawdown	-	-	fully open	fully open	fully open	765
4061	4.061	PMF	Unregulated/Drawdown	-	-	fully open	fully open	fully open	767.5

and previously tested in a physical model, were simulated in the numerical modeling. It should be noted that only maximum discharge values were used for HQ₃₅₀ and for the PMF to curtail research model runs and for comparison purposes. However, intermediate floods could have been simulated due to the inherent advantage and flexibility of 3D numerical modelling techniques.

In accordance with the above reservoir operation rules, the bypass tunnel is used to divert excessive flow during high floods thus preventing high flow velocities and turbulence in the MP. The flushing of fine sediments out of the modified pool through the underflow spillway (US) once a year under a free flow regime is implemented. Also, once a year, in free flow conditions, the bypass tunnel is utilized to remove bedload sediments from the upper reservoir and wash away into the downstream river reach.

To examine the variations between the physical model and the 3D ANSYS Fluent/CFD model, the flow pattern and velocities over the spillway crest, modified pool, bypass tunnel and cofferdam were established. During HQ₃₅₀ and larger floods, power generation is shut down and the outflow structures, such as the BT (bypass tunnel), the US (under spillway), and the OS (over spillway) are fully opened to discharge sediment laden flood water and to remove suspended and deposited sediments from the modified pond (MP) and lower the reservoir as a part of optimizing reservoir and sediment management. An advantage of this reservoir management strategy is that it makes use of significant drag and erosive forces during large floods to remove previously deposited sediments from the reservoir.

Two reservoir levels (760 m.a.s.l and 750 m.a.s.l) were tested for Normal Plant Operation (NPO). These demonstrated that a decrease in velocity to 0.2 m/s was required for the removal of particles up to 0.2 mm. This layout’s efficiency worked well between flows as high as 750 m³/s and within the intended flow range (154 m³/s). However, when the flow is greater than 750 m³/s, the situation changes. The power plant’s design discharge is 153.6 m³/s. The lowest plant operation discharge is 25 m³/s. The minimum operation level (MOL) at Patrind HPP is at 760 m.a.s.l, while the full supply level (FSL) is at 765 m.a.s.l. The active storage volume between these two levels is therefore of particular relevance as it ensures long-term sustainability of the economic plant operation.

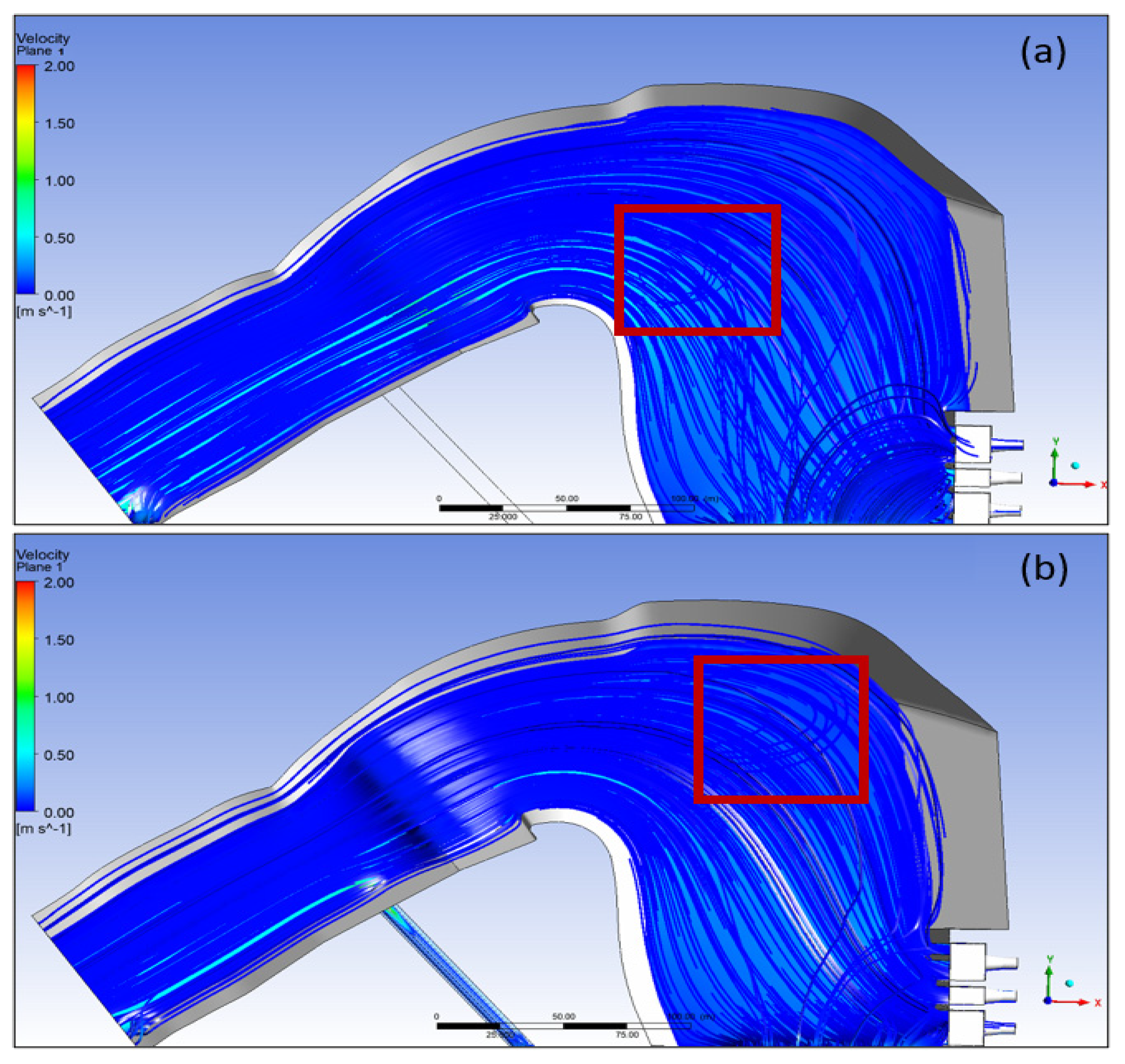
Both the physical model and the numerical model measure the flow velocities at 760 m.a.s.l. upstream of the cofferdam and in the MP, respectively. In the MP area close to the power intake during NPO, flow velocities drop to the crucial value of 0.2 m/s.

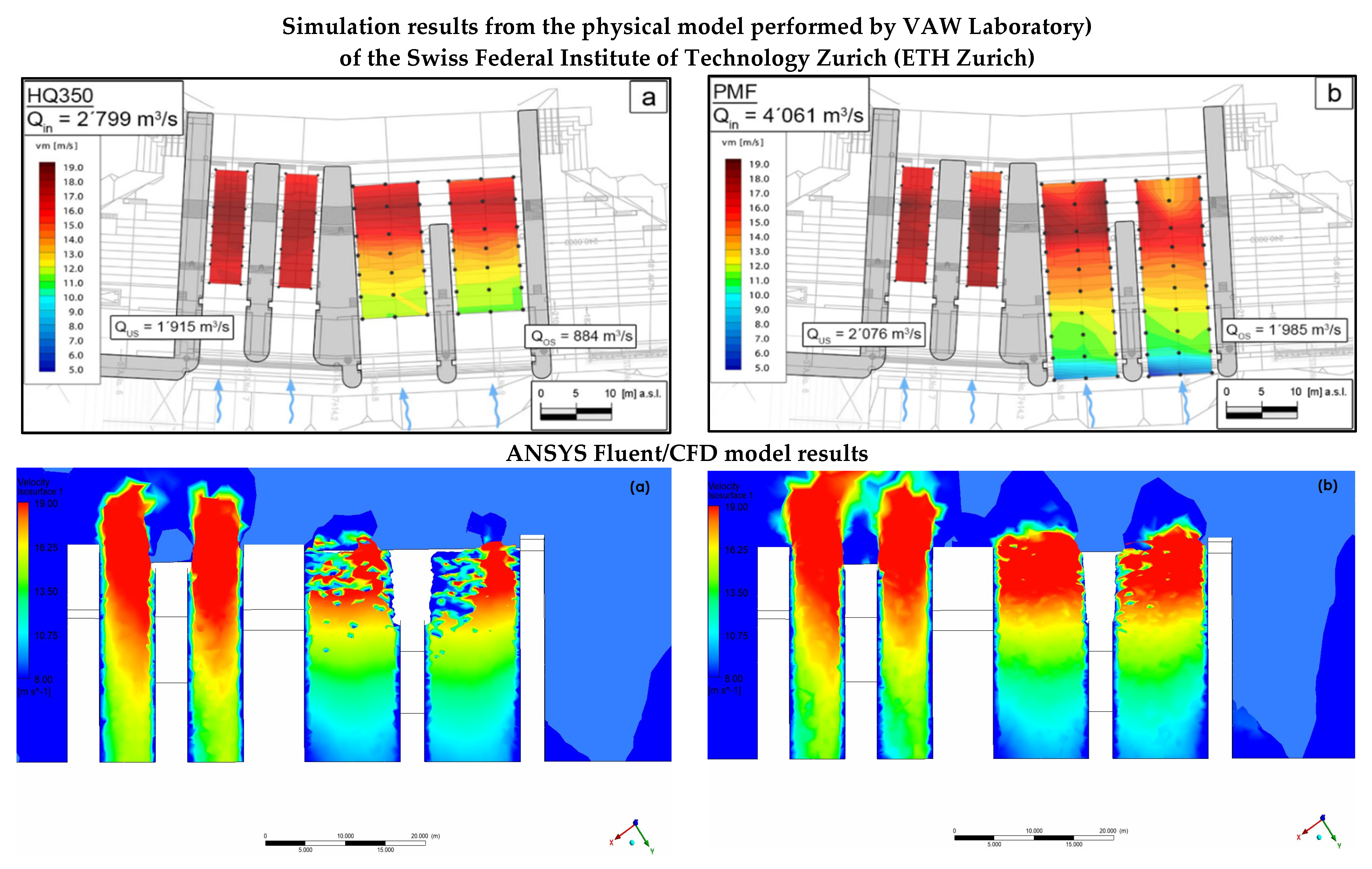
Figure 8 shows the results of both the physical model and ANSYS Fluent/CFD display a similar pattern.

The physical model test shows that in the upstream section of the MP, the flow in concentrated towards the right bank in case of HQ₅ and further towards on the left bank and the center of the MP in case of NPO (as seen in Figure 8a,b).

Figure 9b shows turbulent flow immediately downstream of the cofferdam thus setting a pronounced vortex flow with flow lines in the velocity plots as highlighted in the numerical modeling simulation in Figure 8. The sediment grains are anticipated to settle in the rotation center. In the case of HQ₅, fine sediments spread out throughout the entire area of the MP. The deposition level above the earlier deposits up to 1.1 m were observed at similar locations in the physical model test.

Downstream of the cofferdam, the flow travels toward the right embankment, is reflected, and then moves toward the left embankment and the MP’s outer curve. This effect can be seen to be stronger during HQ₅ (5-year flood). Additionally, because of the larger flow circulations during the HQ₅ (5-year flood), the MP’s overall flow velocities are a little bit higher than they are during NPO. Backwater and vortex flow are further advanced during HQ₅ (5-year flood), according to the streamline patterns. Up to 9 m/s of flow velocity crosses the cofferdam during the HQ₃₅₀ (350-year flood) and a PMF (probable maximum flood peak).

There were slight variations in flow pattern and velocity vectors between the physical model and numerical simulation as can be seen in Figure 8. This may be due to the fact that the numerical model geometry and boundary conditions did not exactly replicate the physical model test which was based on intermediate topographic situation at site before the final construction design. The numerical model morphology was based on the as-built design drawings based on the final topographic conditions. In the case of the numerical simulation, the right bank in the middle section of the MP is not as curved as constructed and used at a physical model (1:45) scale. A google earth image Figure 10, of the MP confirms the numerical model geometry. In view of the above, the numerical model test in fact provides a correct and favorable flow regime for simulated floods than the physical model test.

Results of the 3D numerical modeling of normal operations (NOP) showed the same pattern similar to the physical modeling—that flow velocity in the modified pool (MP) progressively decreases towards the power intake. It eventually drops to or below the critical threshold of 0.2 m/s, thereby facilitating retention of 0.2 mm sand particles in the MP, enabling relatively clean water to reach the power intake.

Flow velocities over the cofferdam reach as high as 8.0 m/s during the HQ₃₅₀ and as high as 8.8 m/s during the PMF in the physical model. Whereas slightly higher velocities of up to 8.3 m/s and 9 m/s respectively, were recorded in the numerical model. The scale effect could be a reason, and also may be due to turbulent flow and friction losses in the physical model test. The numerical model operating as a full-scale model using effective application of RNG k − ε in normalization of Navier–Stokes equations is generally free of such impediments.

Figure 11 shows that flow velocities measured over the OS (over spillway) and US (under spillway) chutes during the HQ₃₅₀-A (350-year flood) simulation and the PMF-A (probable maximum flood peak) results for the physical model simulation and the ANSYS Fluent/CFD model, respectively.

On the US chute, where there is high turbulence and flow velocities of up to 19 m/s, the velocity distribution is uneven, in case of HQ₃₅₀ (350-year flood) the flow on the OS is more turbulent than the PMF (probable maximum flood peak) case in numerical simulation results. Before being absorbed by the water flow in the stilling basin, flow rates on the OS chute reach a maximum of 18 m/s near the toe of the chute in case of numerical simulation whereas physical model simulation shows that it ranges from 12 to 17 m/s, there is a slight difference in velocities for the spillway flow.

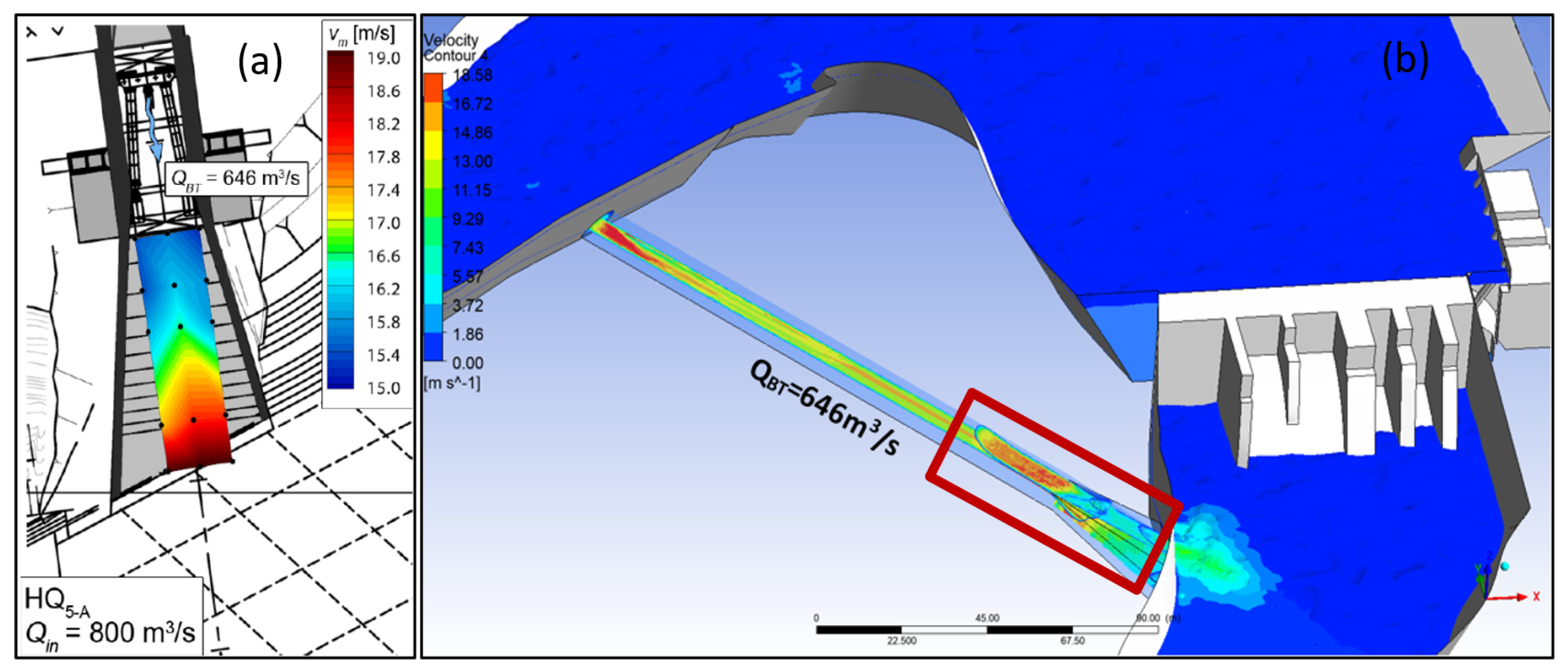
For the HQ₅ (5-year flood) case, with Q_BT = 646 m³/s, the flow conditions over the BT outlet chute are analyzed. On the BT spillway chute toe during HQ₅ (5-year flood), mean flow velocities up to 19.2 m/s are noted in the measuring points shown in Figure 12a. The software in this instance may have underestimated the flow velocities due to geometry difference, as the bypass outlet chute in the numerical model is closed while it is open in the physical model. Friction losses and scale effect also may have contributed to the numerical model’s lower velocity than the physical model, approximately 17 m/s; however, the ANSYS Fluent/CFD model showed a maximum velocity of up to 18.58 m/s slightly before within the bypass tunnel outlet chute Figure 12b.

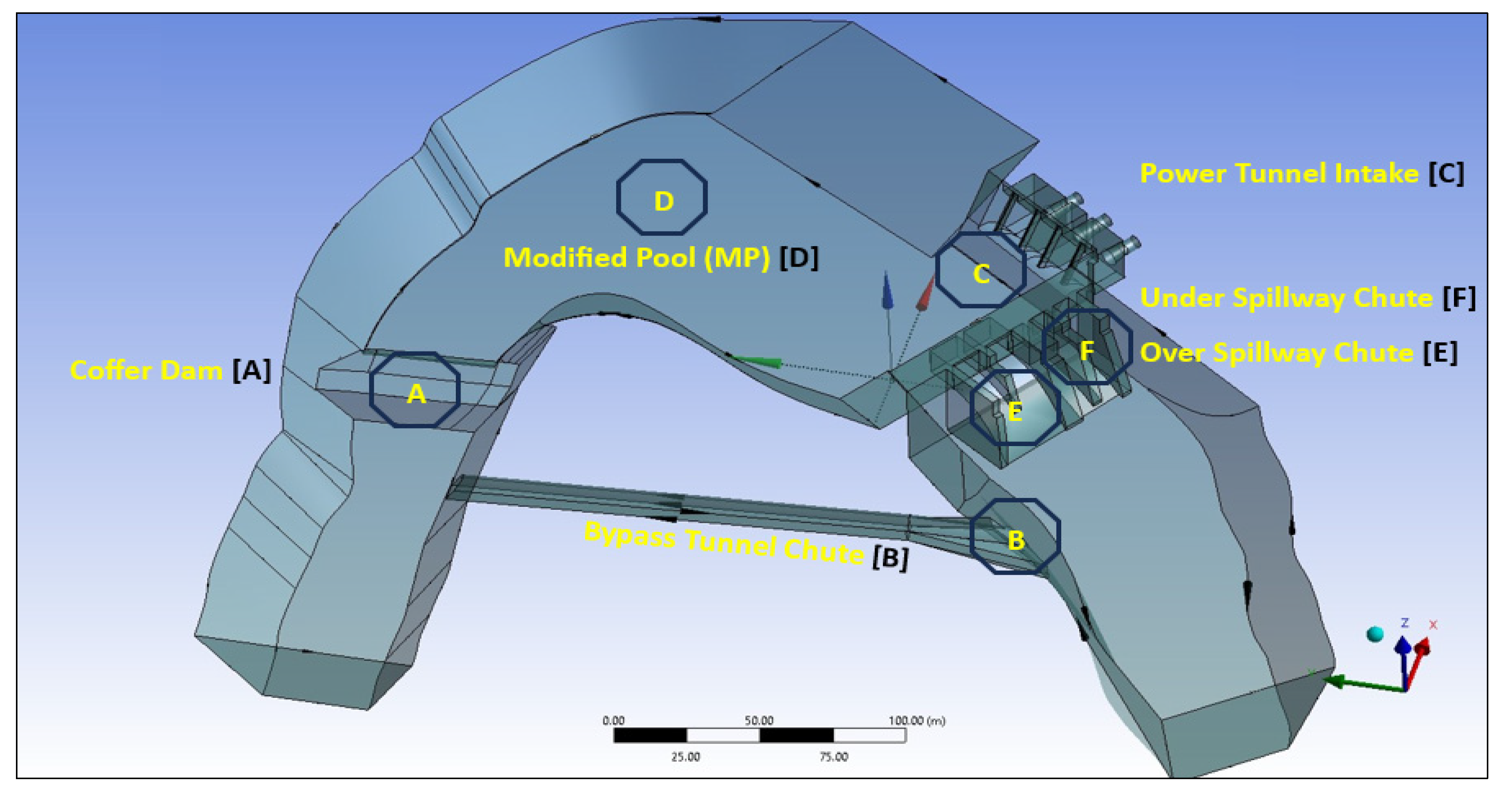
Figure 13 shows points A to F, where the flow velocity results were compared between the physical and ANSYS Fluent/CFD model simulation.

Between the physical model and the numerical model, the flow velocities are similar for 50% of the results. The remaining results are approximately within 2–6%, with one result showing 8% variation. The main variation between flow velocities in the physical and numerical simulation and measurement taken in the physical model test is in vicinity of the cofferdam. This is because of the turbulent flow in the model test due to the scale effect and effective application of RNG k − ε in normalization of Navier–Stokes equations.

Table 4. Percentage difference in the velocities of the numerical and physical models.

Location		Flow Discharge Period	Flow Discharge Q (m3/s)	Physical Model Range Max (m/s)	Fluent Model Range Max (m/s)	% Difference
A	Cofferdam	NPO	156	0.42	0.4	5
		HQ5	800	1.3	1.5	8
		HQ350	2799	8	8.2	2
		PMF	4061	8.8	9	2
B	Bypass tunnel chute	HQ5	800	19.2	18.58	3
C	Power intake	NPO	156	0.4	0.42	5
		HQ5	800	0.4	0.42	5
		HQ350	2799	3.5	3.5	0
		PMF	4061	3.5	3.5	0
D	Modified pool	NPO	156	0.15	0.15	0
		HQ5	800	0.2	0.21	5
		HQ350	2799	3.6	3.8	6
		PMF	4061	4.5	4.6	2
E	Under spillway chute	HQ350	2799	19	19.5	3
		PMF	4061	19	19.5	3
F	Over spillway chute	HQ350	2799	17	18	6
		PMF	4061	17	18	6

shows the relevant data at these locations for different discharges.

To verify results, post-convergence graphs were checked to assess the accuracy of the simulation. A high residual denotes a significant discrepancy and a far-out convergence of the simulation toward a solution. A smaller difference and a tighter search for a convergent solution in the simulation are indicated by a lower residual. Reducing these residuals to a small enough number indicates that the solution is approaching the true physical behavior well within the user-specified bounds in iterative numerical simulations. The precise cutoff point for an acceptable residual is determined by the application of the simulation and the level of precision needed [35].

A residual value of 1e−03 is considered appropriate for many engineering applications similar to this research. The solution flow time and time step varied case to case as simulation results were recorded after all the variables and equations converged below 1e−03 threshold, after which the model runs reached a steady state with further improvement and variations. This validated the post-processing results and the suitable mesh grid size. The convergence graphs are given for the studied cases (as per the operation rules in Table 3) are given in Figure 14.

5. Advantages and Disadvantages of Numerical and Physical Modelling

Physical models have been successfully used as a design verification tool for various hydrodynamic situations. These also allow understanding of flow patterns and sedimentation processes. However, the disadvantages include the scale effect, need for large modelling space, and time-consuming expensive construction. The model runs and the number of simulations is generally pre-determined under contract and agreed with model testing laboratories. It is also expensive to retain a model in the extended time should there be a need for further testing for any required design or operational optimization.

The 3D numerical modelling in its current refined state, and use of widely available powerful computational capability of computers and cloud computing is rapidly replacing the need for physical modelling. Available commercial software such as ANSYS Fluent/CFD with the capability of several user-friendly interface software is fully capable of complex simulations. It is possible that further refinement of governing hydrodynamic equations, including built-in default software functions and constants, may become necessary in future for better accuracy. Finally, both physical model tests and numerical simulations require sound engineering judgement based on extensive practical experience.

The unique aspect of this research is not only in its use of ANSYS Fluent but it is about how thoroughly and comprehensively ANSYS Fluent is used to model an entire run-of-the-river hydropower scheme. The thorough simulation of the complete system, including complex structures like the bypass tunnel, modified pool, power inlet, and spillways, makes this strategy very novel. This study presents a comprehensive perspective, capturing the flow regimes through and over all the hydropower project structures, in contrast to earlier research that addressed numerical simulation of individual components of hydropower projects and river system. The novelty of this work is further highlighted by the application of particular modeling techniques and boundary conditions in ANSYS Fluent to fit the particular dynamics of run-of-the-river schemes. This degree of precision in 3D modeling, along with the possibility of useful applications in design optimization and the early stages of developing hydropower technology and sustainability, make it an impressive combination.

6. Conclusions and Recommendations

There was a negligible divergence with the physical model simulation. The difference may have resulted from scale effects as well as variation in the geometry between the physical and numerical models. The currently accepted minimum scale of 1:45 for physical modelling and used for Patrind HPP appears to slightly underestimate flow velocities in the modified pond (MP). The discharge rates of the physical model at the 1:45 scale is consistently lower than the results of the full-scale numerical model. It is possible that the discharge flow velocities at the actual site substantially resemble the numerical model result. What sets these two models apart may be brought on by the scaling effect.

The ANSYS Fluent/CFD RNG k − ε model results for free surface and for depth-averaged velocity generally fit the physical model data. Instead of using a physical model, one may simulate a numerical model with engineering judgement and perhaps further refinement based on real data collection from the implemented projects. Further optimization and use of numerical modelling in resolving engineering design issues can reduce both design time and subsequent detailed design and construction costs. In view of the foregoing, the following main points are concluded, and recommendations made:

• The research results achieved and described in this paper confirmed that numerical simulation carried out using ANSYS Fluent/CFD RNG k − ε model and compared with the physical model at the 1:45 scale gave remarkably similar and accurate results. The slight variations in the two models’ outcomes show the scale effect of the physical model.
• A minimum model size of 1:45 is mostly accepted as appropriate; however, it gives lower flow velocities, albeit within an acceptable range. This research results, subject to further limited verification, make the need for a physical model test largely redundant. However, a slightly larger model at the 1:40 scale, if desired, is expected to replicate closely the 3D numerical simulation and the project performance.
• The development and availability of sophisticated commercial 3D numerical modeling software, with simulation capabilities independent of the scale factor constraints, are practical alternatives to physical model testing.
• Further research is recommended to numerically simulate the physical model conditions using reliable case histories, and compare results of the physical model test, project performance data, and the results of ANSYS Fluent/CFD numerical model to confirm the applicability of the numerical modelling simulation for validation of the project final layout and design of hydraulic structures. This will reduce the time and cost required to complete multiple simulations to minimize or eliminate potential design issues.