The Effect of Different Swell and Wind-Sea Proportions on the Transformation of Bimodal Spectral Waves over Slopes
Abstract
1. Introduction
2. Experimental Setup
2.1. Wave Flume and Instrumentation Setup
2.2. Wave Conditions
3. Experimental Results
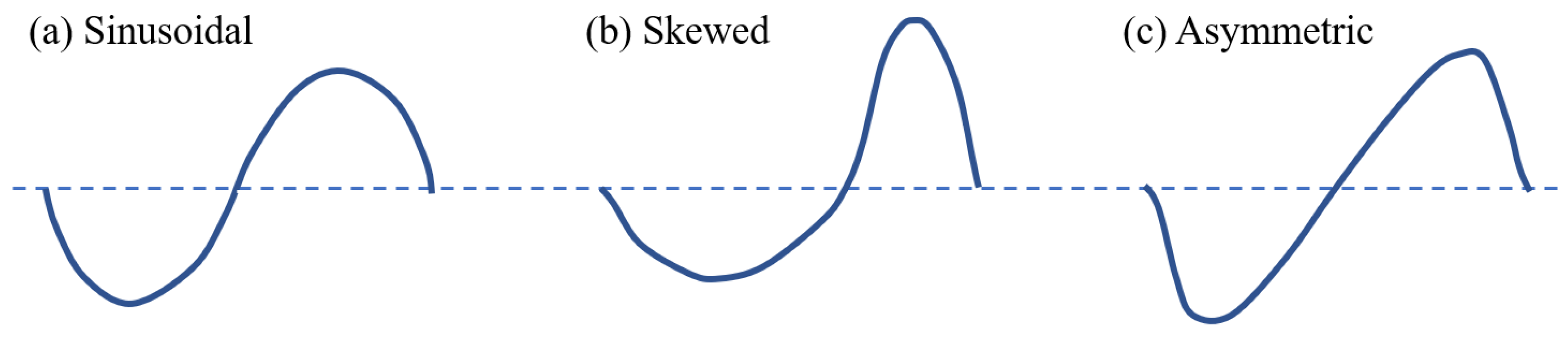
3.1. Variation in Water Surface Elevations
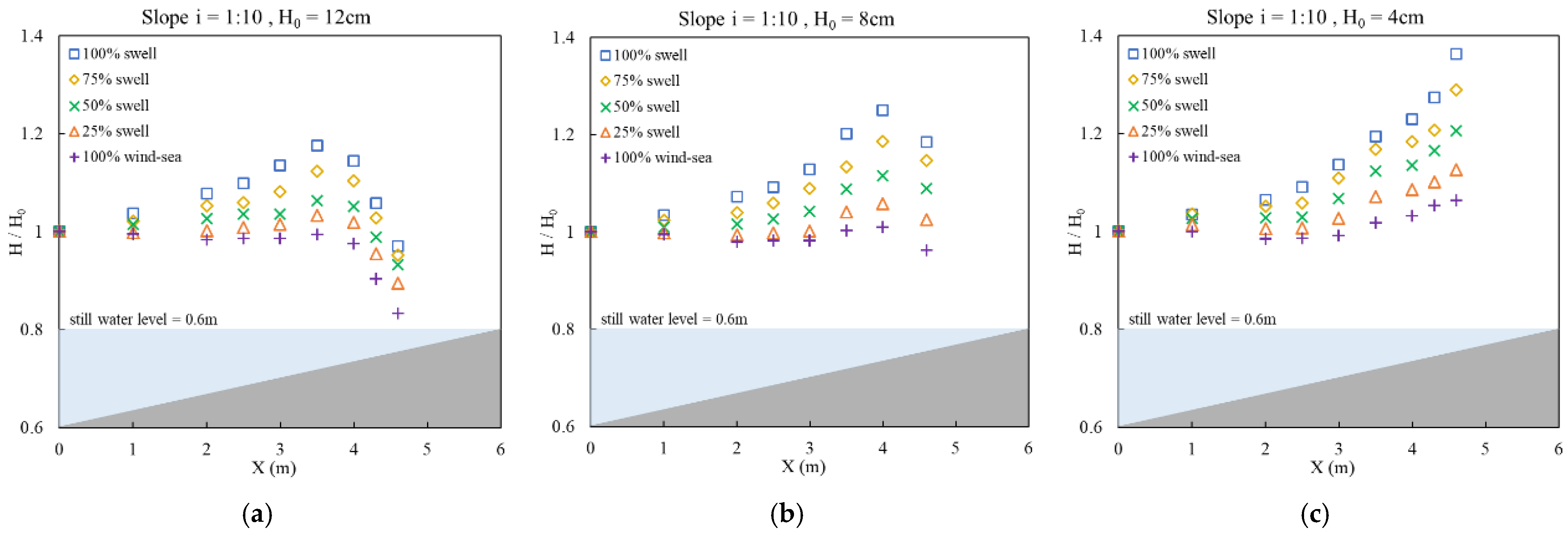
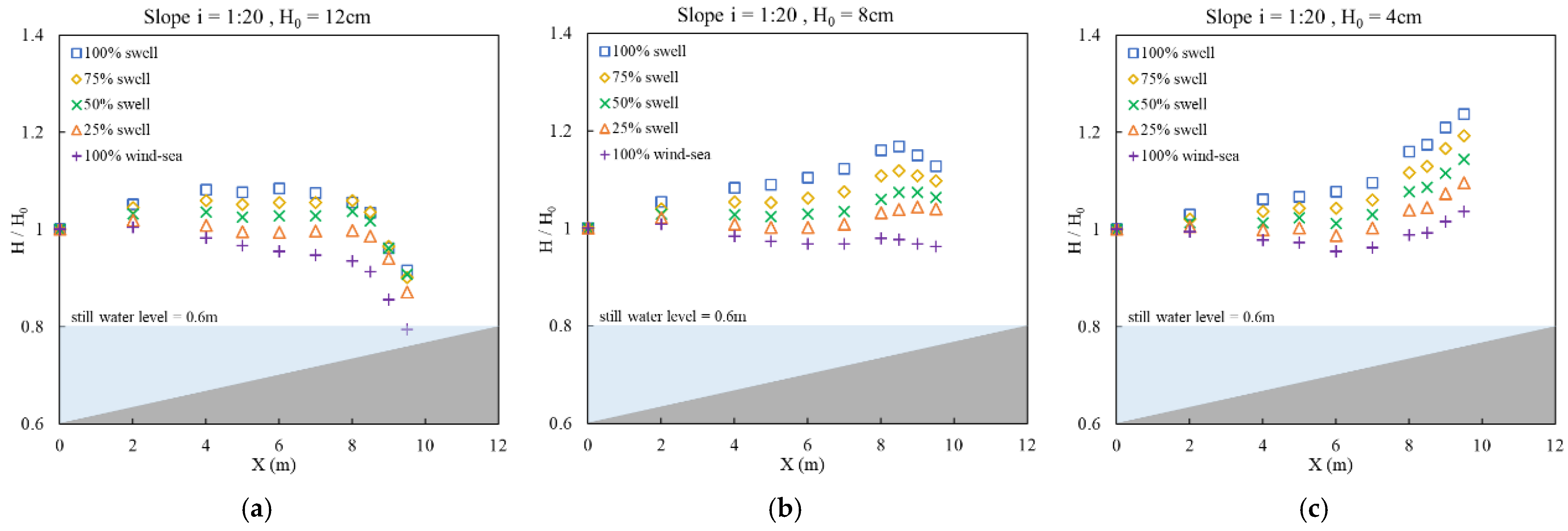
3.2. Wave Height Distribution on Slopes
- 1:10 slope: 117.5% (12 cm), 125.0% (8 cm), 136.2% (4 cm);
- 1:20 slope: 108.4% (12 cm), 116.8% (8 cm), 123.8% (4 cm).
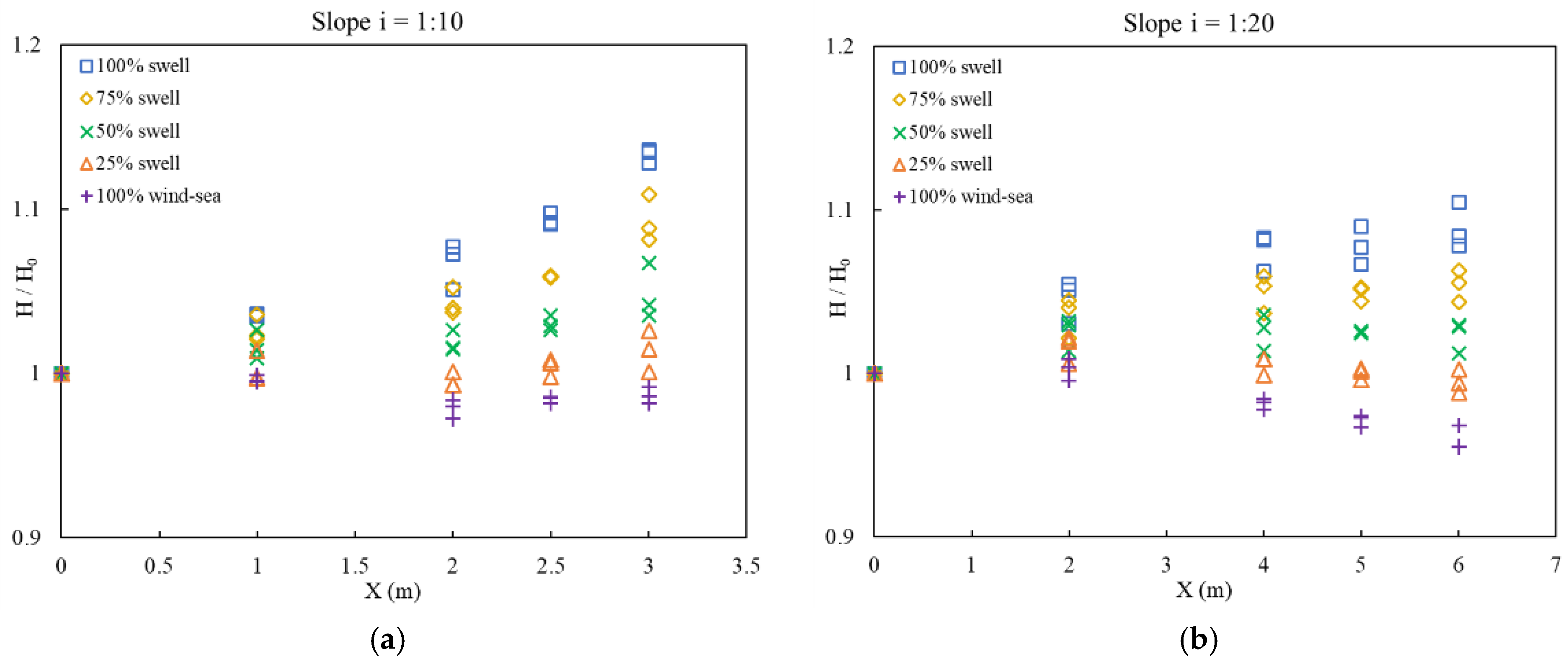
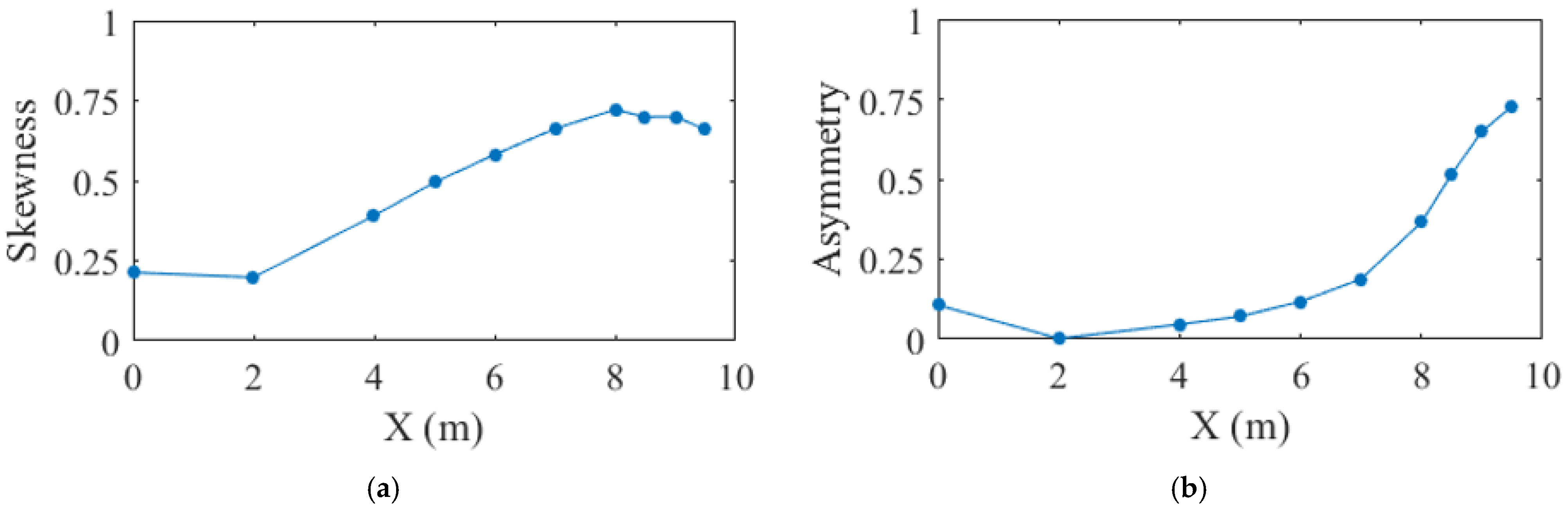
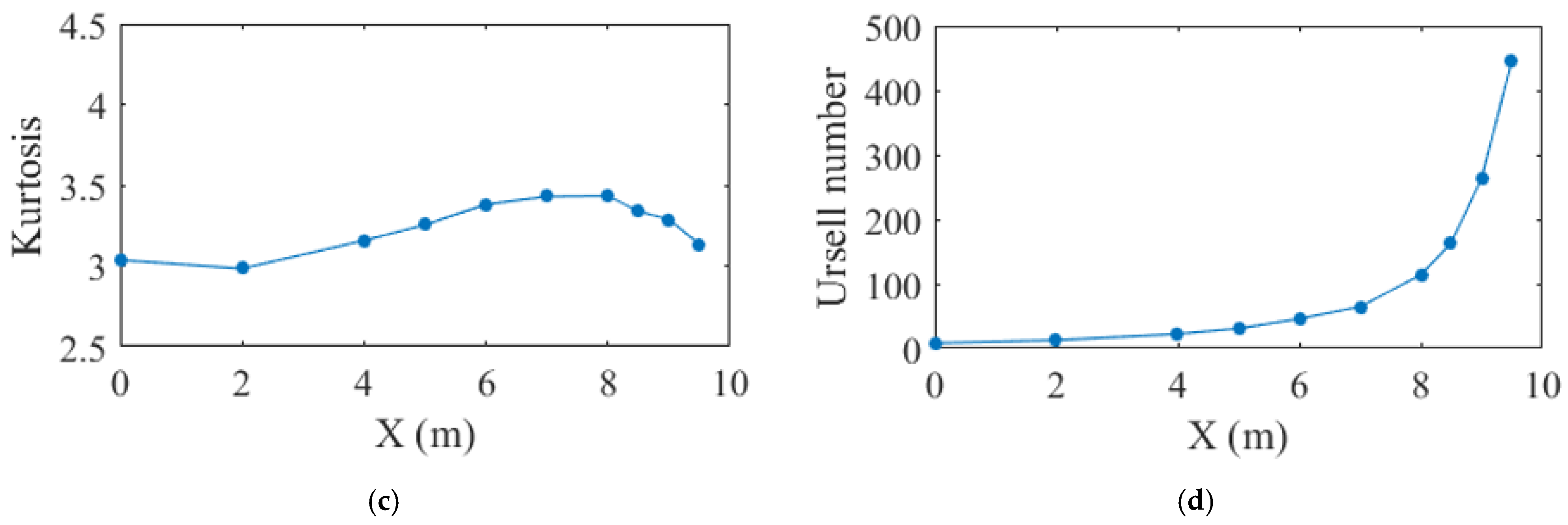
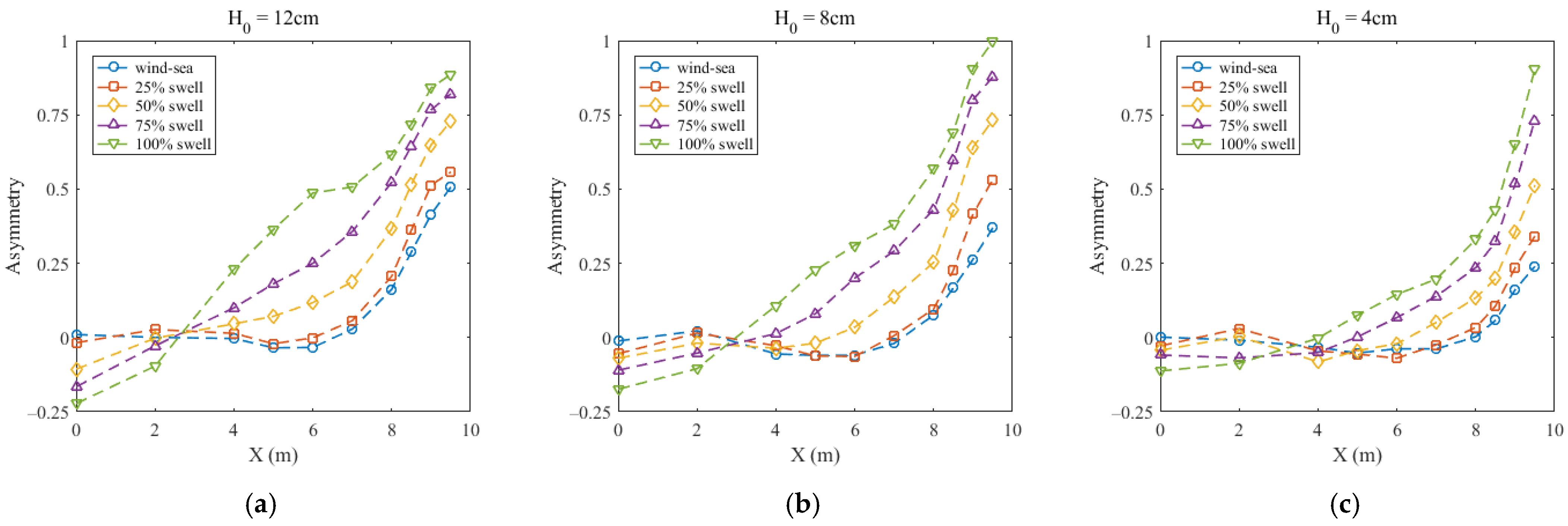
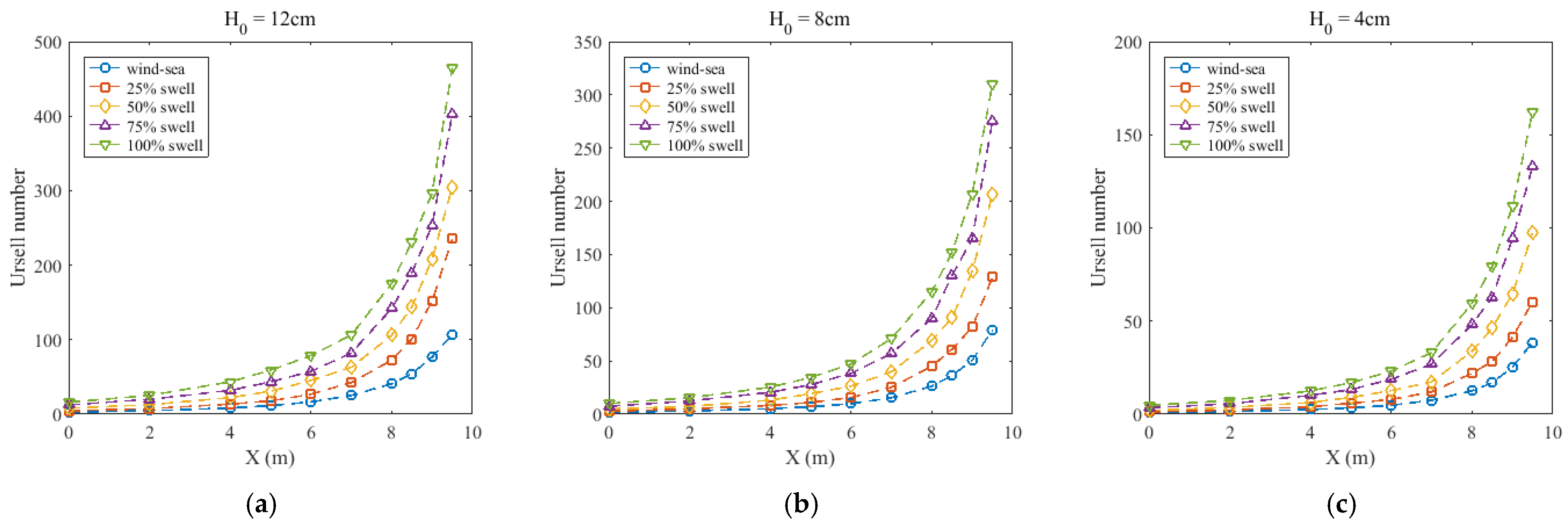
3.3. Nonlinear Indicators of Waves
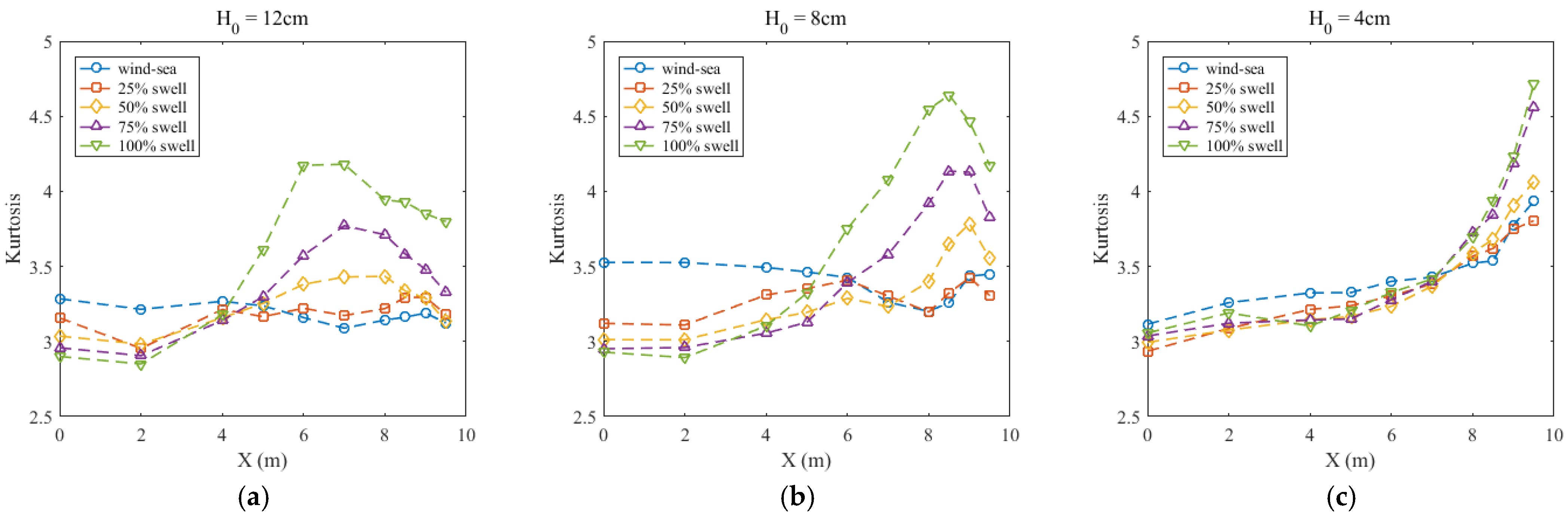
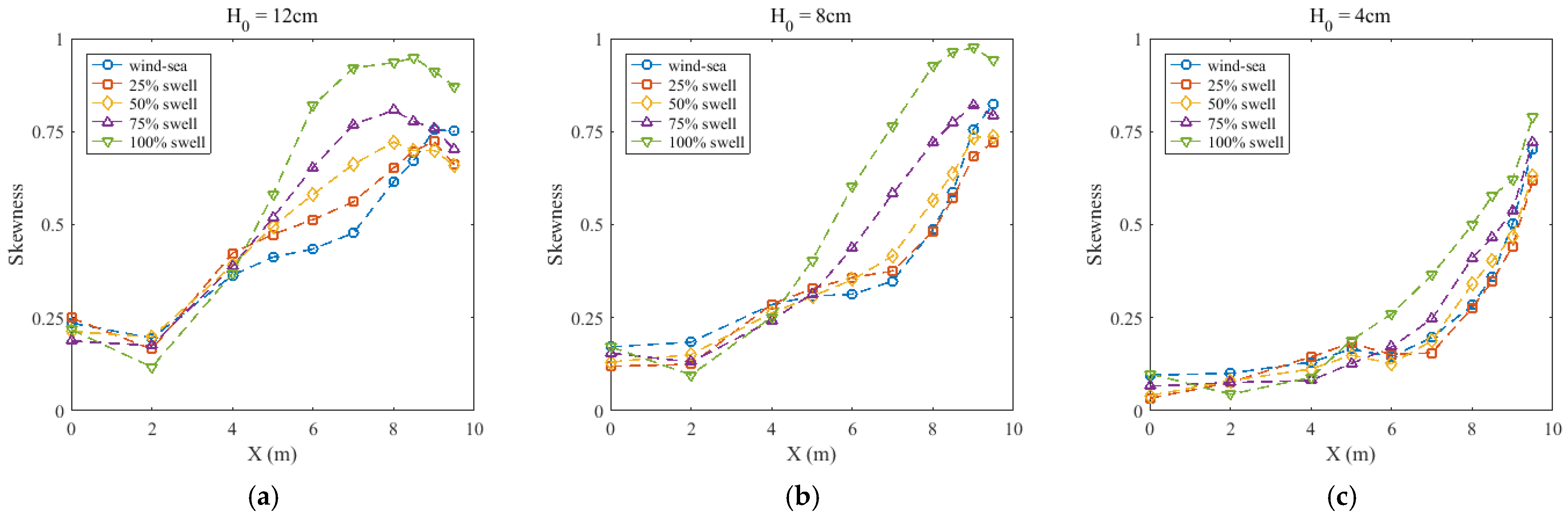
3.4. Variation in Wave Nonlinearity over Slopes
4. Discussion and Conclusions
- For bimodal spectral waves, two main factors influence the maximum wave height. One is the swell proportion, and the other is the slope. An increase in these two factors causes a higher maximum wave height. The swell proportion also influences the effect of wave shoaling. Swell has a larger increase in significant wave height. The relationship between different swell proportions in the bimodal spectrum and the unimodal spectrum is approximately linear in wave height.
- Wave nonlinearity is determined by the water depth and swell proportion. The water depth, wavelength, and wave height control the stages of nonlinear changes. The swelling proportion of the bimodal spectrum influences the trend of nonlinear change in shallow water. The kurtosis, skewness, and asymmetry of swells are larger than wind-sea. The trend of large swell proportions is similar to the unimodal swell. The relationship seems not to be linear.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Almar, R.; Kestenare, E.; Reyns, J.; Jouanno, J.; Anthony, E.J.; Laibi, R.; Hemer, M.; Du Penhoat, Y.; Ranasinghe, R. Response of the Bight of Benin (Gulf of Guinea, West Africa) coastline to anthropogenic and natural forcing, Part1: Wave climate variability and impacts on the longshore sediment transport. Cont. Shelf Res. 2015, 110, 48–59. [Google Scholar] [CrossRef]
- Goda, Y. A Comparative Review on the Functional Forms of Directional Wave Spectrum. Coast. Eng. J. 1999, 41, 1–20. [Google Scholar] [CrossRef]
- Toffoli, A.; Onorato, M.; Monbaliu, J. Wave statistics in unimodal and bimodal seas from a second-order model. Eur. J. Mech.-B/Fluids 2006, 25, 649–661. [Google Scholar] [CrossRef]
- Hanson, J.L.; Phillips, O.M. Wind Sea Growth and Dissipation in the Open Ocean. J. Phys. Oceanogr. 1999, 29, 1633–1648. [Google Scholar] [CrossRef]
- Alford, M.H. Internal Swell Generation: The Spatial Distribution of Energy Flux from the Wind to Mixed Layer Near-Inertial Motions. J. Phys. Oceanogr. 2001, 31, 2359–2368. [Google Scholar] [CrossRef]
- Semedo, A.; Vettor, R.; Breivik, Ø.; Sterl, A.; Reistad, M.; Soares, C.G.; Lima, D. The wind sea and swell waves climate in the Nordic seas. Ocean Dyn. 2015, 65, 223–240. [Google Scholar] [CrossRef]
- Vettor, R.; Guedes Soares, C. A global view on bimodal wave spectra and crossing seas from ERA-interim. Ocean Eng. 2020, 210, 107439. [Google Scholar] [CrossRef]
- Arena, F.; Soares, C.G. Nonlinear High Wave Groups in Bimodal Sea States. J. Waterw. Port Coast. Ocean Eng. 2009, 135, 69–79. [Google Scholar] [CrossRef]
- Hasselmann, D.E.; Dunckel, M.; Ewing, J.A. Directional Wave Spectra Observed during JONSWAP 1973. J. Phys. Oceanogr. 1980, 10, 1264–1280. [Google Scholar] [CrossRef]
- Clauss, G.F. Dramas of the sea: Episodic waves and their impact on offshore structures. Appl. Ocean Res. 2002, 24, 147–161. [Google Scholar] [CrossRef]
- Guachamin-Acero, W.; Portilla-Yandún, J. A study on vessel fatigue damage as a criterion for heading selection by application of 2D actual bimodal and JONSWAP wave spectra. Ocean Eng. 2021, 226, 108822. [Google Scholar] [CrossRef]
- Liu, P.L.F.; Losada, I.J. Wave propagation modeling in coastal engineering. J. Hydraul. Res. 2002, 40, 229–240. [Google Scholar] [CrossRef]
- Barthélemy, E. Nonlinear Shallow Water Theories for Coastal Waves. Surv. Geophys. 2004, 25, 315–337. [Google Scholar] [CrossRef]
- Wu, G.X.; Taylor, R.E. The coupled finite element and boundary element analysis of nonlinear interactions between waves and bodies. Ocean Eng. 2003, 30, 387–400. [Google Scholar] [CrossRef]
- Hur, D.-S.; Kim, C.-H.; Yoon, J.-S. Numerical study on the interaction among a nonlinear wave, composite breakwater and sandy seabed. Coast. Eng. 2010, 57, 917–930. [Google Scholar] [CrossRef]
- Shi, J.; Feng, X.; Toumi, R.; Zhang, C.; Hodges, K.I.; Tao, A.; Zhang, W.; Zheng, J. Global increase in tropical cyclone ocean surface waves. Nat. Commun. 2024, 15, 174. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Gabin, W. Wave bimodal spectrum based on swell and wind-sea components. IFAC-PapersOnLine 2015, 48, 223–228. [Google Scholar] [CrossRef]
- Liu, X.; Chen, W.; Sun, Z.; Cai, Z.; Hou, Y. Investigation on the reconstruction of wave bimodal spectrum in the lagoon near islands and reefs. Ocean Eng. 2022, 265, 112615. [Google Scholar] [CrossRef]
- Abessolo Ondoa, G.; Bonou, F.; Tomety, F.S.; Du Penhoat, Y.; Perret, C.; Degbe, C.G.E.; Almar, R. Beach Response to Wave Forcing from Event to Inter-Annual Time Scales at Grand Popo, Benin (Gulf of Guinea). Water 2017, 9, 447. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.; Gienapp, A.; Hasselmann, D.; Kruseman, P. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Ergaenzungsheft Zur Dtsch. Hydrogr. Z. Reihe A 1973, 12, 1–95. [Google Scholar]
- Hwang, P.A.; Teague, W.J.; Jacobs, G.A.; Wang, D.W. A statistical comparison of wind speed, wave height, and wave period derived from satellite altimeters and ocean buoys in the Gulf of Mexico region. J. Geophys. Res. Ocean. 1998, 103, 10451–10468. [Google Scholar] [CrossRef]
- Ruessink, B.v.; Van Den Berg, T.; Van Rijn, L. Modeling sediment transport beneath skewed asymmetric waves above a plane bed. J. Geophys. Res. Ocean. 2009, 114, C11021. [Google Scholar] [CrossRef]
- Grasso, F.; Michallet, H.; Barthélemy, E. Sediment transport associated with morphological beach changes forced by irregular asymmetric, skewed waves. J. Geophys. Res. Ocean. 2011, 116, C03020. [Google Scholar] [CrossRef]
- Yao, A.; Wu, C.H. Spatial and temporal characteristics of transient extreme wave profiles on depth-varying currents. J. Eng. Mech. 2006, 132, 1015–1025. [Google Scholar] [CrossRef]
- Kjeldsen, S.; Myrhaug, D. Breaking waves in deep water and resulting wave forces. In Proceedings of the Offshore technology conference, Houston, TX, USA, 30 April–3 May 1979. [Google Scholar]
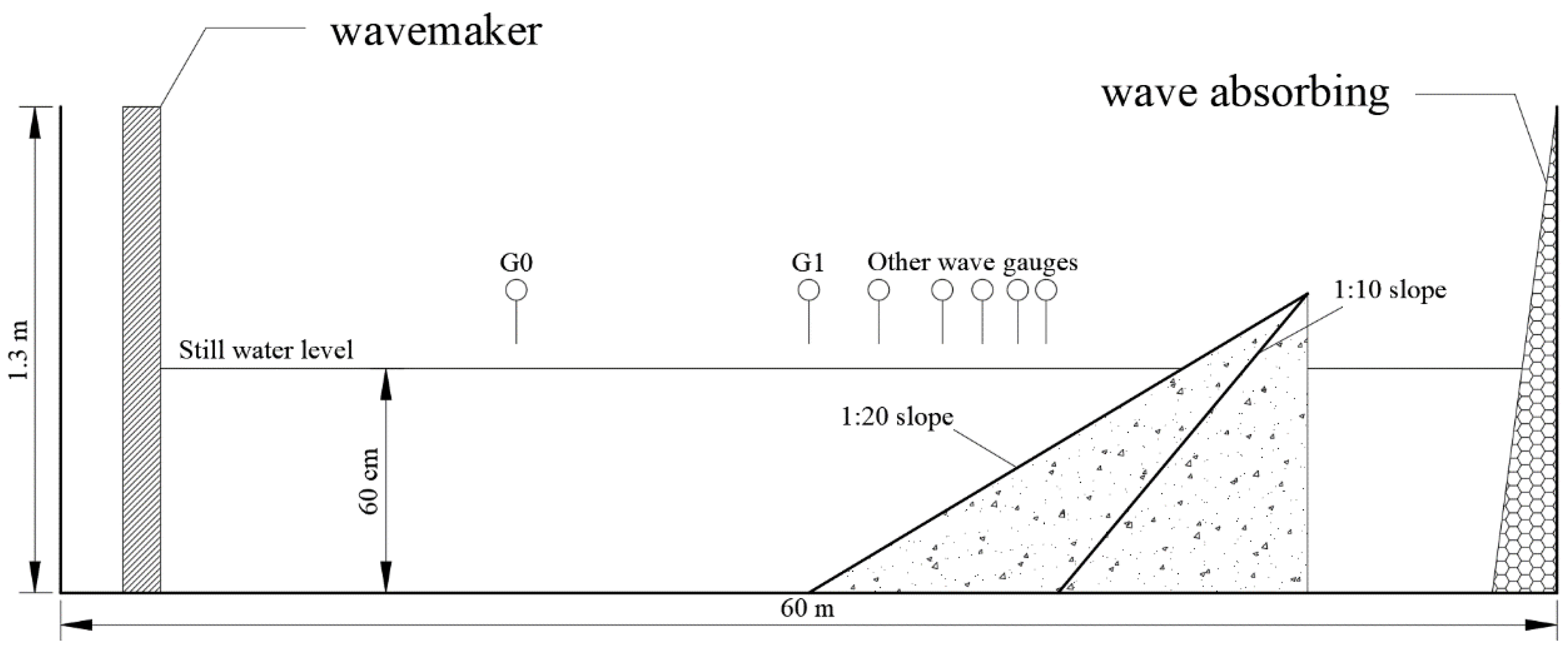
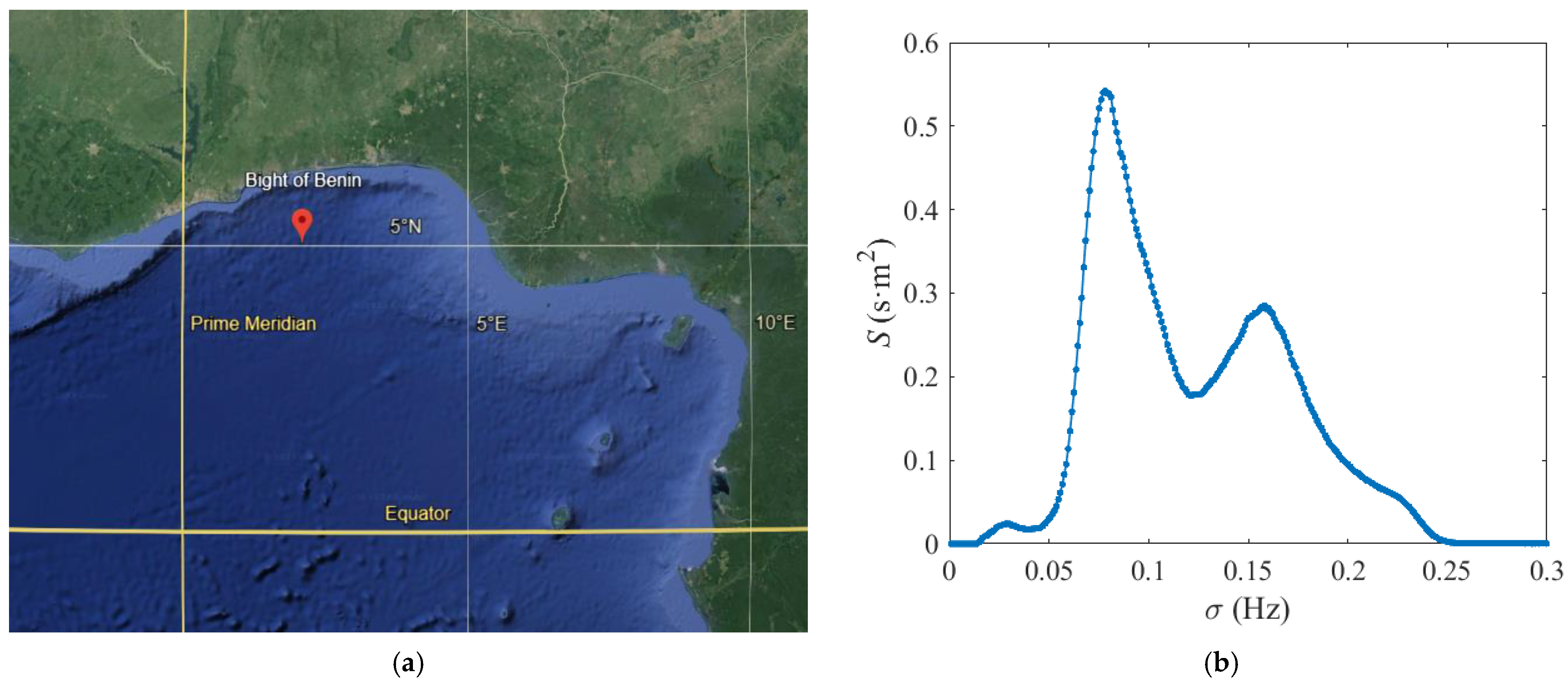
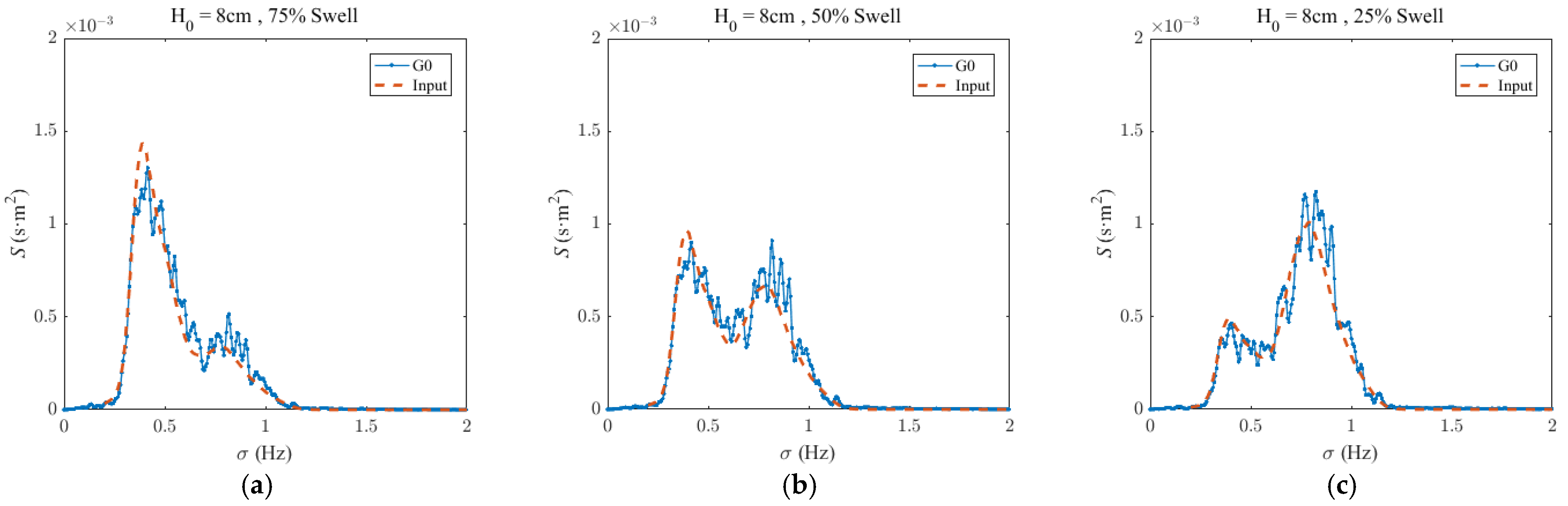
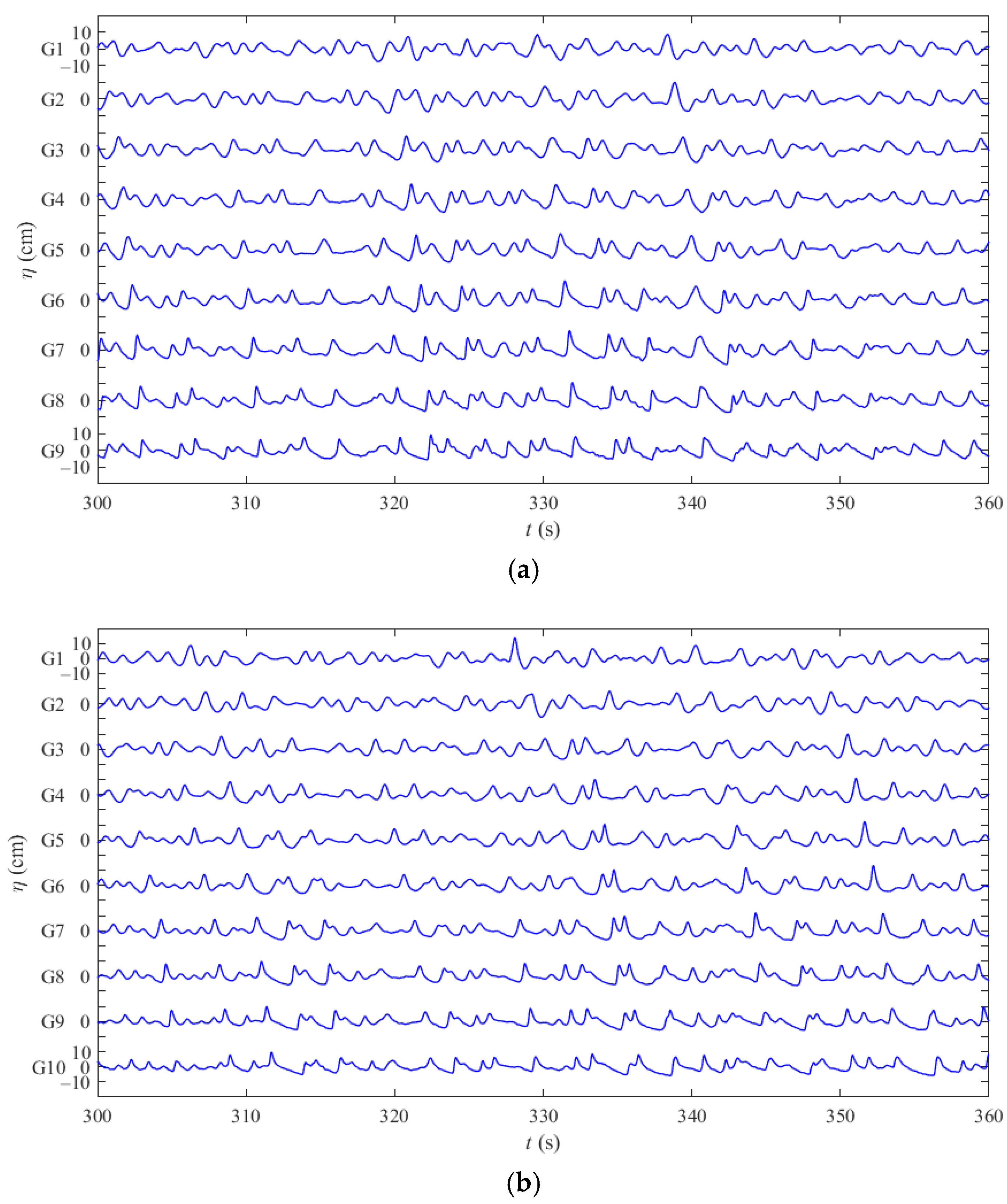
| Slope | Wave Gauges | Distance from G1 X (m) | Water Depth h (cm) |
|---|---|---|---|
| 1:10 | G1 | 0.0 | 60 |
| G2 | 1.0 | 50 | |
| G3 | 2.0 | 40 | |
| G4 | 2.5 | 35 | |
| G5 | 3.0 | 30 | |
| G6 | 3.5 | 25 | |
| G7 | 4.0 | 20 | |
| G8 | 4.3 | 17 | |
| G9 | 4.6 | 14 | |
| 1:20 | G1 | 0.0 | 60 |
| G2 | 2.0 | 50 | |
| G3 | 4.0 | 40 | |
| G4 | 5.0 | 35 | |
| G5 | 6.0 | 30 | |
| G6 | 7.0 | 25 | |
| G7 | 8.0 | 20 | |
| G8 | 8.5 | 17.5 | |
| G9 | 9.0 | 15 | |
| G10 | 9.5 | 12.5 |
| Wave Spectrum | Case | Significant Wave Height H0 (cm) | Swell Proportion | Wind-Sea Proportion |
|---|---|---|---|---|
| Unimodal | 1 | 12 | 100% | 0% |
| 2 | 8 | 100% | 0% | |
| 3 | 4 | 100% | 0% | |
| Bimodal | 4 | 12 | 75% | 25% |
| 5 | 8 | 75% | 25% | |
| 6 | 4 | 75% | 25% | |
| 7 | 12 | 50% | 50% | |
| 8 | 8 | 50% | 50% | |
| 9 | 4 | 50% | 50% | |
| 10 | 12 | 25% | 75% | |
| 11 | 8 | 25% | 75% | |
| 12 | 4 | 25% | 75% | |
| Unimodal | 13 | 12 | 0% | 100% |
| 14 | 8 | 0% | 100% | |
| 15 | 4 | 0% | 100% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Zhang, K.; Shi, J. The Effect of Different Swell and Wind-Sea Proportions on the Transformation of Bimodal Spectral Waves over Slopes. Water 2024, 16, 296. https://doi.org/10.3390/w16020296
Wang G, Zhang K, Shi J. The Effect of Different Swell and Wind-Sea Proportions on the Transformation of Bimodal Spectral Waves over Slopes. Water. 2024; 16(2):296. https://doi.org/10.3390/w16020296
Chicago/Turabian StyleWang, Guangsheng, Kai Zhang, and Jian Shi. 2024. "The Effect of Different Swell and Wind-Sea Proportions on the Transformation of Bimodal Spectral Waves over Slopes" Water 16, no. 2: 296. https://doi.org/10.3390/w16020296
APA StyleWang, G., Zhang, K., & Shi, J. (2024). The Effect of Different Swell and Wind-Sea Proportions on the Transformation of Bimodal Spectral Waves over Slopes. Water, 16(2), 296. https://doi.org/10.3390/w16020296






