Performance of Ergun’s Equation in Simulations of Heterogeneous Porous Medium Flow with Smoothed-Particle Hydrodynamics
Abstract
1. Introduction
2. Basic Equations and SPH Solver
2.1. Governing Fluid Flow Equations
2.2. The Ergun Equation
2.3. LES Filtering and SPH Solver
2.4. Variable Timestep Calculation
3. Test Model
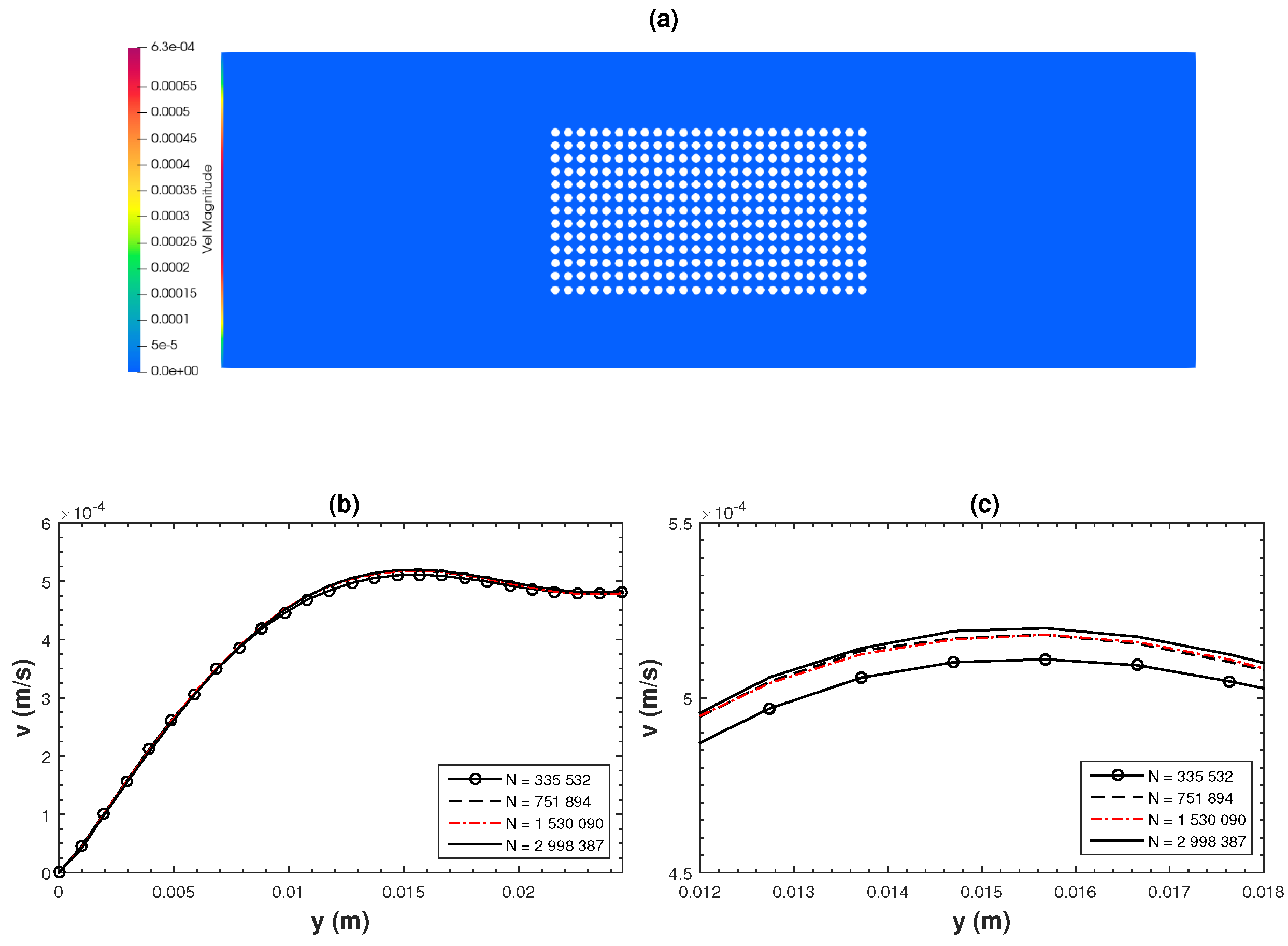
4. Validation and Convergence Study
5. Results
5.1. Flow Structure and Outlet Velocity Profiles
5.2. Pressure Losses
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Warren, J.E.; Price, H.S. Flow in heterogeneous porous media. Soc. Pet. Eng. J. 1961, 1, 153–169. [Google Scholar] [CrossRef]
- Li, T.; Li, M.; Jing, X.; Xiao, W.; Cui, Q. Influence mechanism of pore-scale anisotropy and pore distribution heterogeneity on permeability of porous media. Pet. Explor. Dev. 2019, 46, 594–604. [Google Scholar] [CrossRef]
- Kueper, B.H.; Abbott, W.; Farquhar, G. Experimental observations of multiphase flow in heterogeneous porous media. J. Contam. Hydrol. 1989, 5, 83–95. [Google Scholar] [CrossRef]
- Ko, D.D.; Ji, H.; Ju, Y.S. Prediction of pore-scale flow in heterogeneous porous media from periodic structures using deep learning. AIP Adv. 2023, 13, 045324. [Google Scholar] [CrossRef]
- Kamrava, S.; Sahimi, M.; Tahmasebi, P. Simulating fluid flow in complex porous materials by integrating the governing equations with deep-layered machines. npj Comput. Mater. 2021, 7, 127. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; American Elesevier: New York, NY, USA, 1972. [Google Scholar]
- Koekemoer, A.; Luckos, A. Effect of material type and particle size distribution on pressure drop in packed beds of large particles: Extending the Ergun equation. Fuel 2015, 158, 232–238. [Google Scholar] [CrossRef]
- Mathias, S.A. Hydraulics, Hydrology and Environmental Engineering; Springer: Berlin, Germany, 2023. [Google Scholar]
- Seta, T.; Takegoshi, E.; Kitano, K.; Okui, K. Thermal lattice Boltzmann model for incompressible flows through porous media. J. Therm. Sci. Technol. 2006, 1, 90–100. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Prog. 1952, 48, 89–94. [Google Scholar]
- Alvarado-Rodríguez, C.E.; Díaz-Damacillo, L.; Plaza, E.; Sigalotti, L.D.G. Smoothed particle hydrodynamics simulations of porous medium flow using Ergun’s fixed-bed equation. Water 2023, 15, 2358. [Google Scholar] [CrossRef]
- Lai, T.; Liu, X.; Xue, S.; Xu, J.; He, M.; Zhang, Y. Extension of Ergun equation for the calculation of the flow resistance in porous media with higher porosity and open celled-structure. Appl. Therm. Eng. 2020, 173, 115262. [Google Scholar] [CrossRef]
- Bazmi, M.; Hashemabadi, S.H.; Bayat, M. Modification of Ergun equation for application in trickle bed reactors randomly packed with trilobe particles using computational fluid dynamics techniques. Korean J. Chem. Eng. 2011, 28, 1340–1346. [Google Scholar] [CrossRef]
- Li, Q.; Tang, R.; Wang, S.; Zou, Z. A coupled LES-LBM-IMB-DEM modeling for evaluating pressure drop of a heterogeneous alternating-layer packed bed. Chem. Eng. J. 2022, 433, 133529. [Google Scholar] [CrossRef]
- Li, Q.; Guo, S.; Wang, S.; Zou, Z. CFD-DEM investigation on pressure drops of heterogeneous alternative-layer particle beds for low-carbon operating blast furnaces. Metals 2022, 12, 1507. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M.; Siddiqui, A.A. The instability onset of generalized isoflux mean flow using Brinkman-Darcy-Bénard model in a fluid saturated porous channel. Int. J. Therm. Sci. 2023, 188, 108249. [Google Scholar] [CrossRef]
- Jiang, F.; Oliveira, M.S.A.; Sousa, A.C.M. Mesoscale SPH modeling of fluid flow in isotropic porous media. Comput. Phys. Commun. 2007, 176, 471–480. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Ward, A.L.; Meakin, P. Pore-scale simulations of drainage of heterogeneous and anisotropic porous media. Phys. Fluids 2007, 19, 103301. [Google Scholar] [CrossRef]
- Kunz, P.; Zarikos, I.M.; Karadimitriou, N.K.; Huber, M.; Nieken, U.; Hassanizadeh, S.M. Study of multi-phase flow in porous media: Comparison of SPH simulations with micro-model experiments. Transp. Porous Media 2016, 114, 581–600. [Google Scholar] [CrossRef]
- Peng, C.; Xu, G.; Wu, W.; Yu, H.; Wang, C. Multiphase SPH modeling of free surface flow in porous media with variable porosity. Comput. Geotech. 2017, 81, 239–248. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Trask, N.; Pan, K.; Jones, B.; Pan, W.; Williams, J.R. Smoothed particle hydrodynamics and its applications for multiphase flow and reactive transport in porous media. Comput. Geosci. 2016, 20, 807–834. [Google Scholar] [CrossRef]
- Bui, H.H.; Nguyen, G.D. A coupled fluid-solid SPH approach to modelling flow through deformable porous media. Int. J. Solids Struct. 2017, 125, 244–264. [Google Scholar] [CrossRef]
- Lenaerts, T.; Adams, B.; Dutré, P. Porous flow in particle-based fluid simulations. ACM Trans. Graph. 2008, 27, 1–8. [Google Scholar] [CrossRef]
- Shigorina, E.; Rüdiger, F.; Tartakovsky, A.M.; Sauter, M.; Kordilla, J. Multiscale smoothed particle hydrodynamics model development for simulating preferential flow dynamics in fractured porous media. Water Resour. Res. 2021, 57, e2020WR027323. [Google Scholar] [CrossRef]
- Bui, H.H.; Nguyen, G.D. Smoothed particle hydrodynamics (SPH) and its applications in geomechanics: From solid fracture to granular behaviour and multiphase flows in porous media. Comput. Geotech. 2021, 138, 104315. [Google Scholar] [CrossRef]
- Nithiarasu, P.; Seetharamu, K.N.; Sundararajan, T. Natural convective heat transfer in a fluid saturated variable porosity medium. Int. J. Heat Mass Transf. 1997, 40, 3955–3967. [Google Scholar] [CrossRef]
- Nithiarasu, P.; Seetharamu, K.N.; Sundararajan, T. Effect of porosity on natural convective heat transfer in a fluid saturated porous medium. Int. J. Heat Fluid Flow 1998, 19, 56–58. [Google Scholar] [CrossRef]
- Becker, M.; Teschner, M. Weakly compressible SPH for free surfaces. In Proceedings of the 2007 ACM SIGGRAPH/Europhysics Symposium on Computer Animation, San Diego, CA, USA, 2–4 August 2007; Metaxas, D., Popoovic, J., Eds.; pp. 32–58. [Google Scholar]
- McCabe, W.L. Unit Operations of Chemical Engineering. Chemical Engineering Series; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Dukhan, N. Forced convection of nanofluids in metal foam: An essential review. Int. J. Therm. Sci. 2023, 187, 108156. [Google Scholar] [CrossRef]
- Rabbani, A.; Jamshidi, S.; Salehi, S. Determination of specific surface of rock grains by 2D imaging. J. Geophys. Res. 2014, 2014, 945387. [Google Scholar] [CrossRef]
- Montillet, A. Flow through a finite packed bed of spheres: A note on the limit of applicability of the Forchheimer-type equation. J. Fluids Eng. 2004, 126, 139–143. [Google Scholar] [CrossRef]
- Venkataraman, P.; Rao, P.R.M. Validation of Forchheimer’s law for flow through porous media with converging boundaries. J. Hydraul. Eng. 2000, 126, 63–71. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Fourtakas, G.; Altomare, C.; Canelas, R.B.; Tafuni, A.; García-Feal, O.; Martínez-Estévez, I.; Mokos, A.; Vacondio, R.; Crespo, A.J.C.; et al. DualSPHysics: From fluid dynamics to multiphysics problems. Comput. Part. Mech. 2022, 9, 867–895. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Bonet, J.; Lok, T.S.L. Variational and momentum preservation aspects of smoothed particle hydrodynamics formulations. Comput. Appl. Mech. Eng. 1999, 180, 97–115. [Google Scholar] [CrossRef]
- Lo, E.Y.M.; Shao, S. Simulation of near-shore solitary wave mechanics by an incompressible SPH method. Appl. Ocean Res. 2002, 24, 275–286. [Google Scholar] [CrossRef]
- Dehnen, W.; Aly, H. Improving convergence in smoothed particle hydrodynamics simulations without pairing instability. Mon. R. Astron. Soc. 2012, 425, 1068–1082. [Google Scholar] [CrossRef]
- Alvarado-Rodríguez, C.E.; Klapp, J.; Sigalotti, L.D.G.; Domínguez, J.M.; de la Cruz Sánchez, E. Non-reflective outlet boundary conditions for incompressible flows using SPH. Comput. Fluids 2017, 159, 177–188. [Google Scholar] [CrossRef]
- Zhao, C.Y. Review on thermal transport in high porosity cellular metal foams with open cells. Int. J. Heat Mass Transf. 2012, 55, 3618–3632. [Google Scholar] [CrossRef]





| Density of Water | Inlet Velocity | Reynolds Number | Porosities | |||
|---|---|---|---|---|---|---|
| Re | ||||||
| (kg m−3) | (m s−1) | |||||
| 1000 | 46.875 | 0.77 | 0.55 | 0.44 | 0.30 |
| Number of Particles | Inter-Particle Distance | Smoothing Length |
|---|---|---|
| (m) | (m) | |
| 335,532 | 0.00015 | 0.00030 |
| 751,894 | 0.00010 | 0.00020 |
| 1,530,090 | 0.00007 | 0.00014 |
| 2,998,387 | 0.00005 | 0.00010 |
| Geometry of Grains | Position along Channel | RMSE |
|---|---|---|
| ReNoSt | Bottom | |
| ReNoSt | Center | |
| ReNoSt | Top | |
| ReSt | Bottom | |
| ReSt | Center | |
| ReSt | Top | |
| Ran | Bottom | |
| Ran | Center | |
| Ran | Top |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz-Damacillo, L.; Alvarado-Rodríguez, C.E.; Sigalotti, L.D.G.; Vargas, C.A. Performance of Ergun’s Equation in Simulations of Heterogeneous Porous Medium Flow with Smoothed-Particle Hydrodynamics. Water 2024, 16, 2801. https://doi.org/10.3390/w16192801
Díaz-Damacillo L, Alvarado-Rodríguez CE, Sigalotti LDG, Vargas CA. Performance of Ergun’s Equation in Simulations of Heterogeneous Porous Medium Flow with Smoothed-Particle Hydrodynamics. Water. 2024; 16(19):2801. https://doi.org/10.3390/w16192801
Chicago/Turabian StyleDíaz-Damacillo, Lamberto, Carlos E. Alvarado-Rodríguez, Leonardo Di G. Sigalotti, and Carlos A. Vargas. 2024. "Performance of Ergun’s Equation in Simulations of Heterogeneous Porous Medium Flow with Smoothed-Particle Hydrodynamics" Water 16, no. 19: 2801. https://doi.org/10.3390/w16192801
APA StyleDíaz-Damacillo, L., Alvarado-Rodríguez, C. E., Sigalotti, L. D. G., & Vargas, C. A. (2024). Performance of Ergun’s Equation in Simulations of Heterogeneous Porous Medium Flow with Smoothed-Particle Hydrodynamics. Water, 16(19), 2801. https://doi.org/10.3390/w16192801







