Groundwater Level Prediction Using Machine Learning and Geostatistical Interpolation Models
Abstract
1. Introduction
2. Materials and Methods
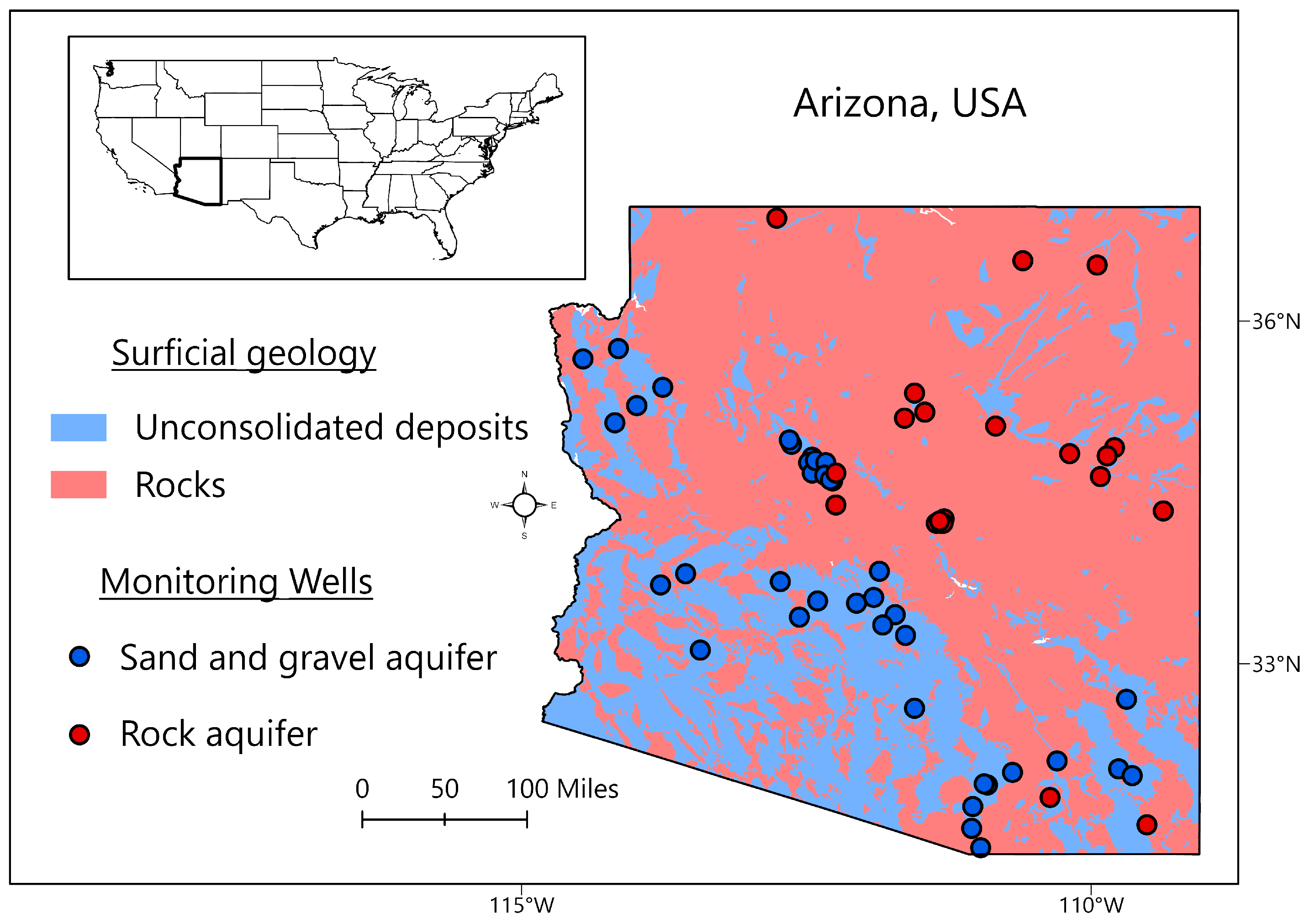
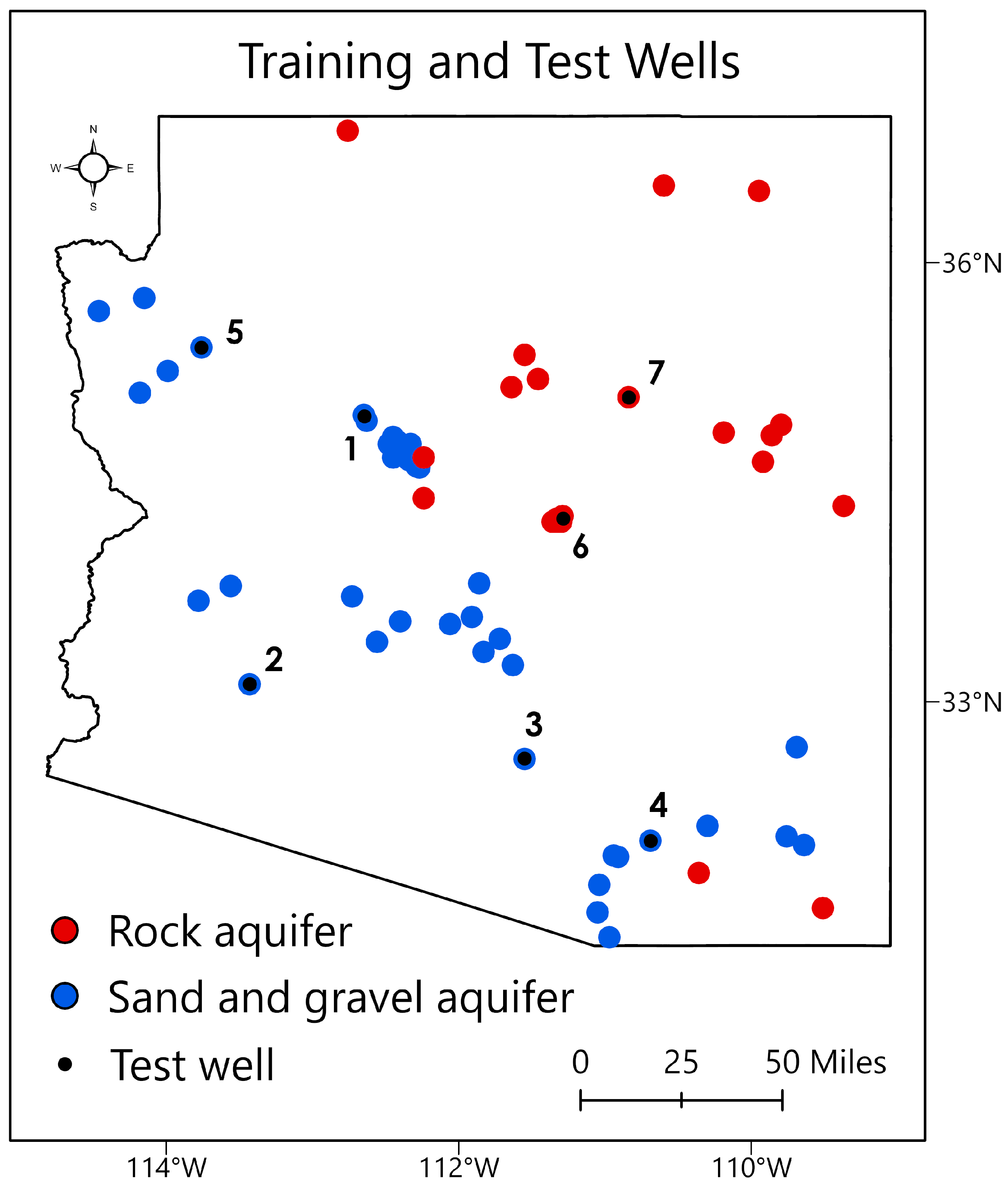
2.1. The Study Area and Target Variable
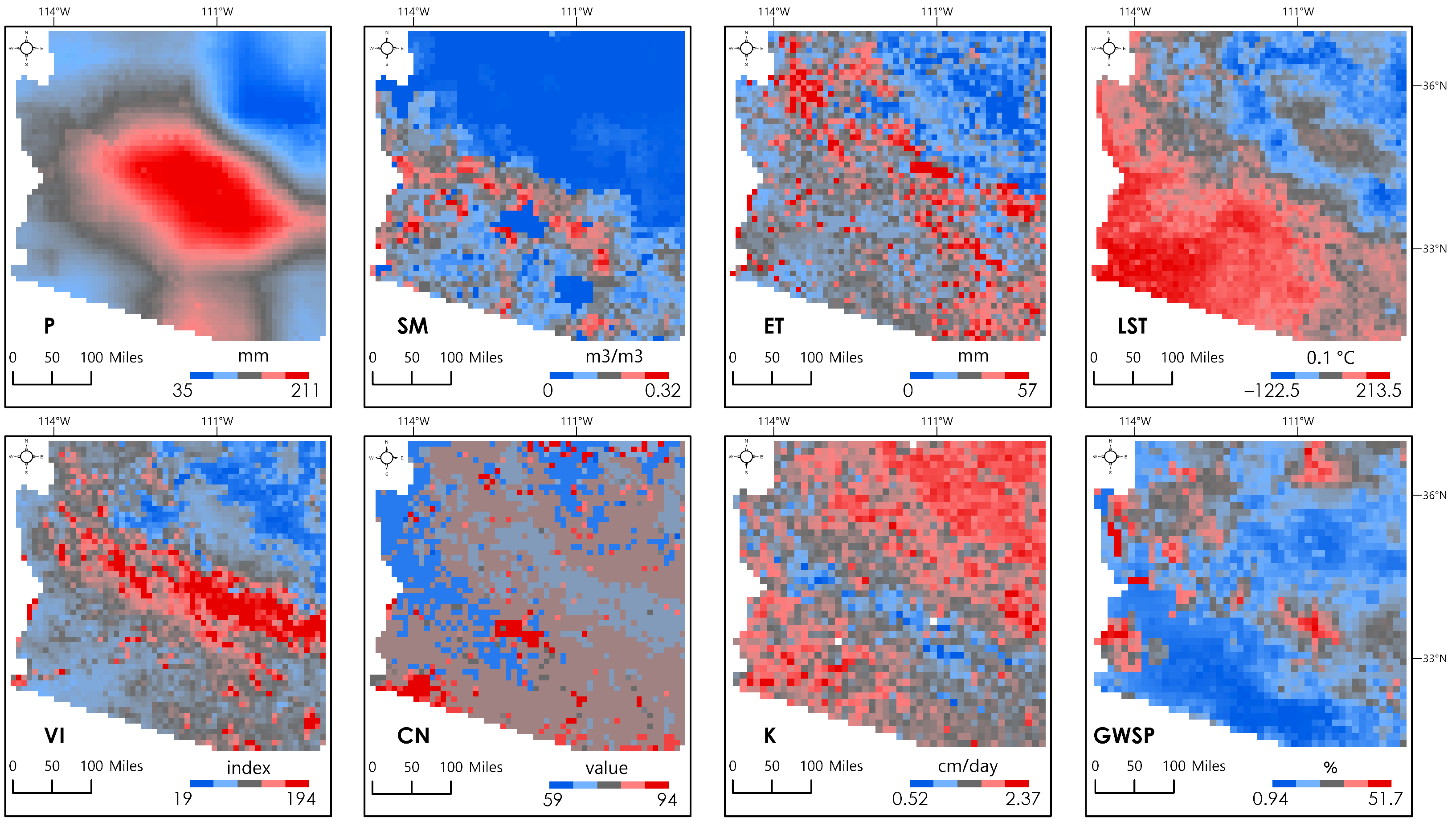
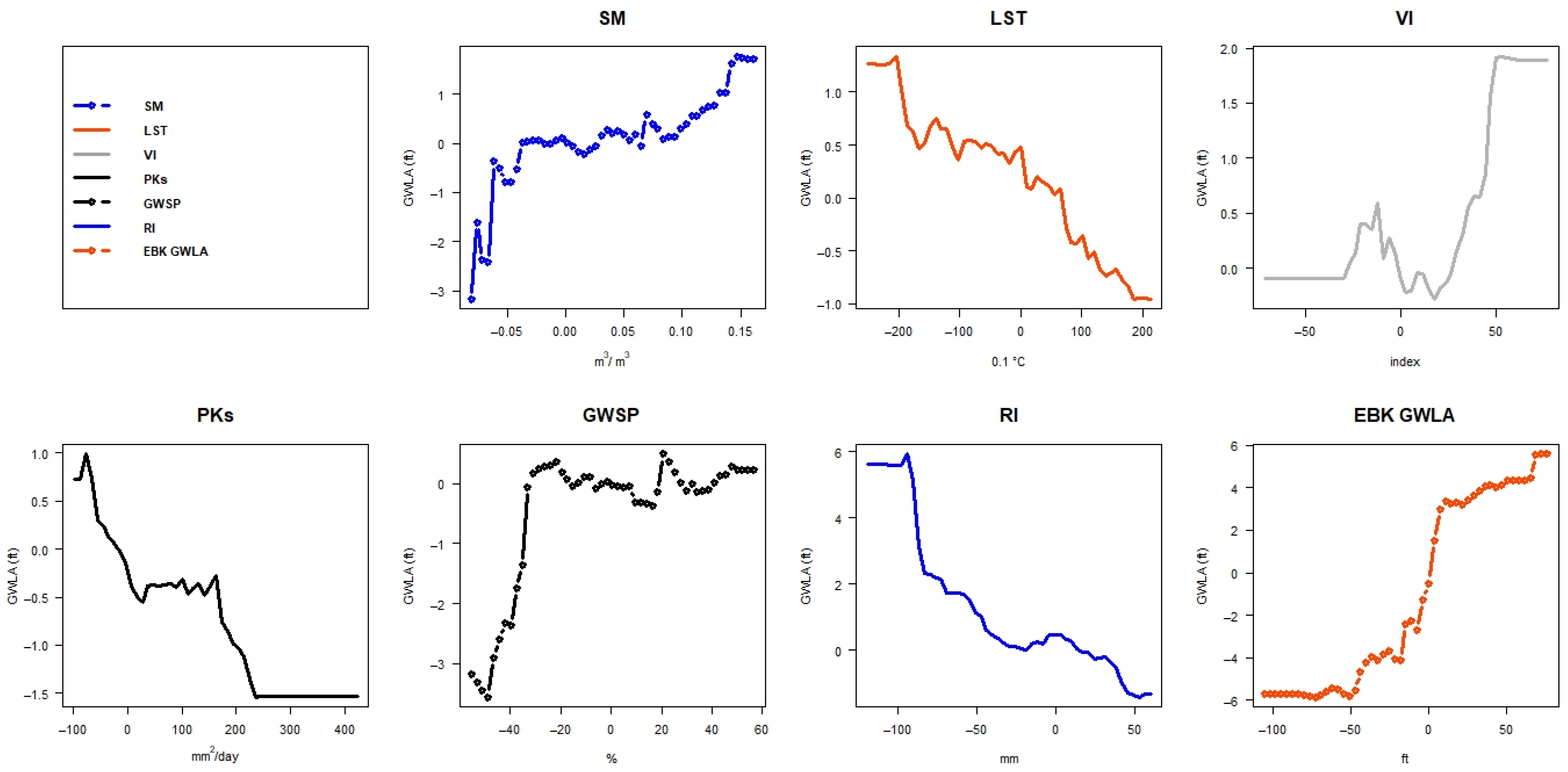
2.2. Predictor Variables
2.2.1. Precipitation (P)
2.2.2. Soil Moisture (SM)
2.2.3. Evapotranspiration (ET)
2.2.4. Land Surface Temperature (LST)
2.2.5. Vegetation Index (VI)
2.2.6. Curve Number (CN) and Runoff Depth (R)
2.2.7. Soil Saturated Hydraulic Conductivity (Ks and PKs)
2.2.8. Groundwater Storage Percentile (GWSP)
2.3. Model Algorithms
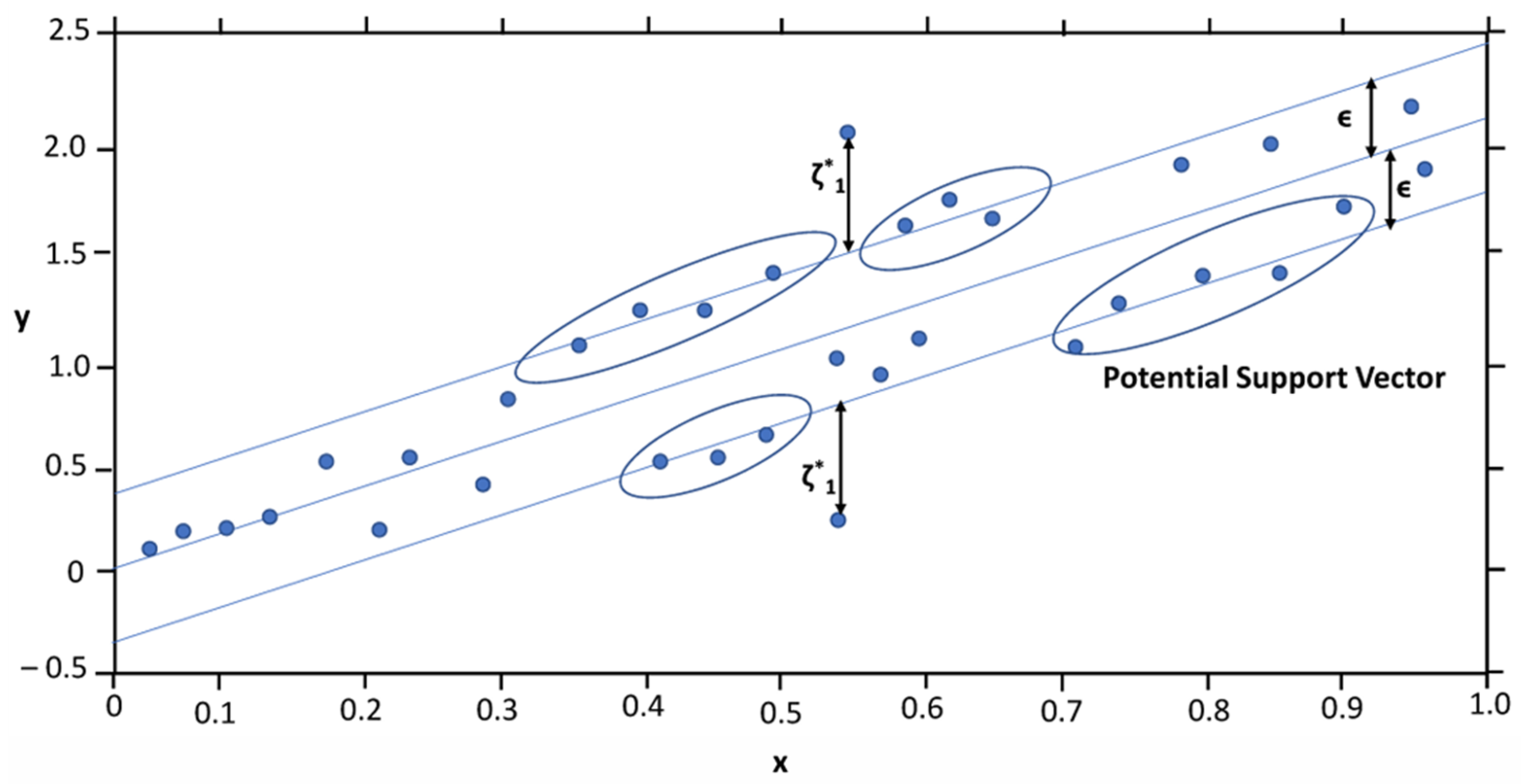
2.3.1. The SVM and SVR
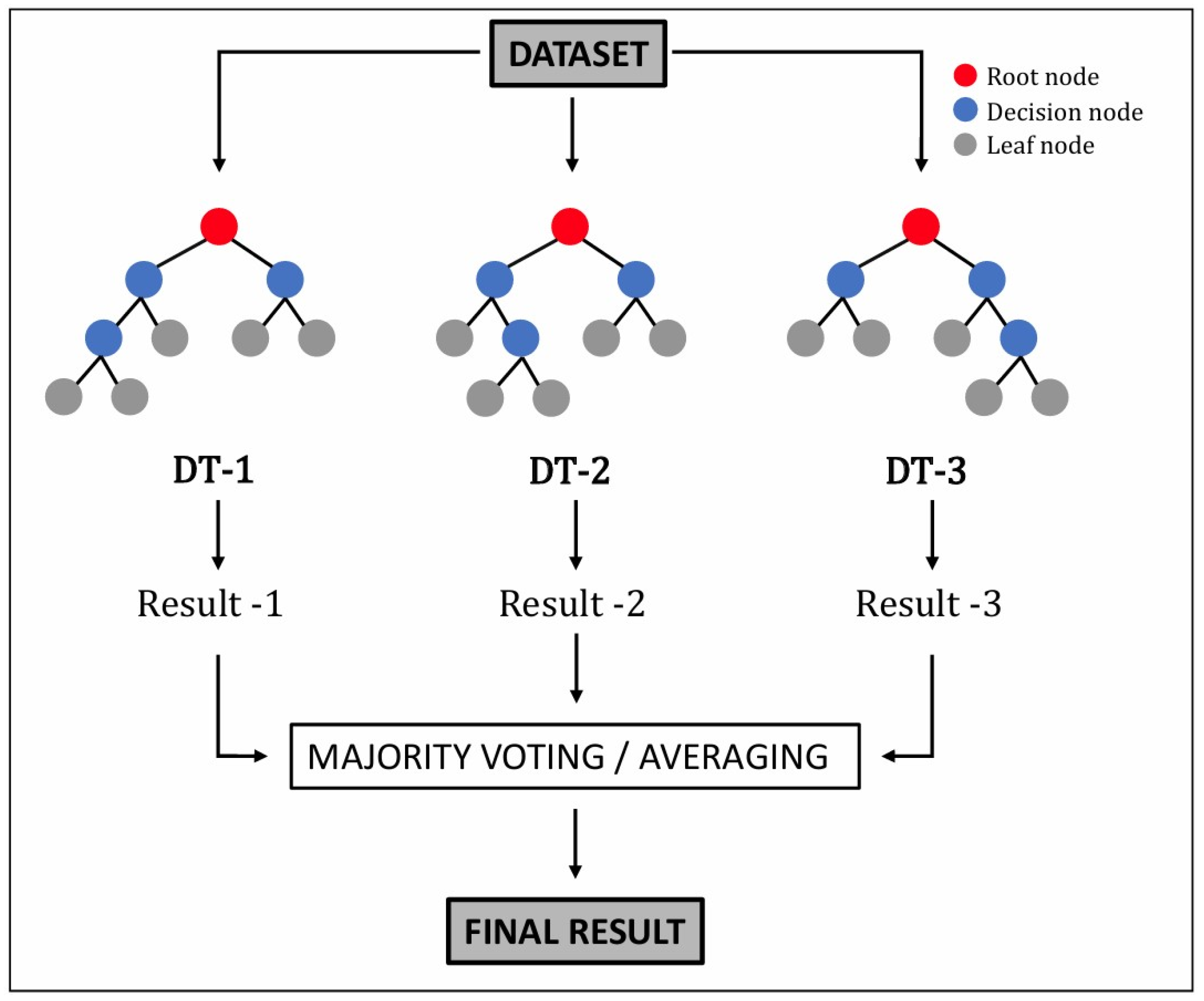
2.3.2. RF
2.3.3. EBK
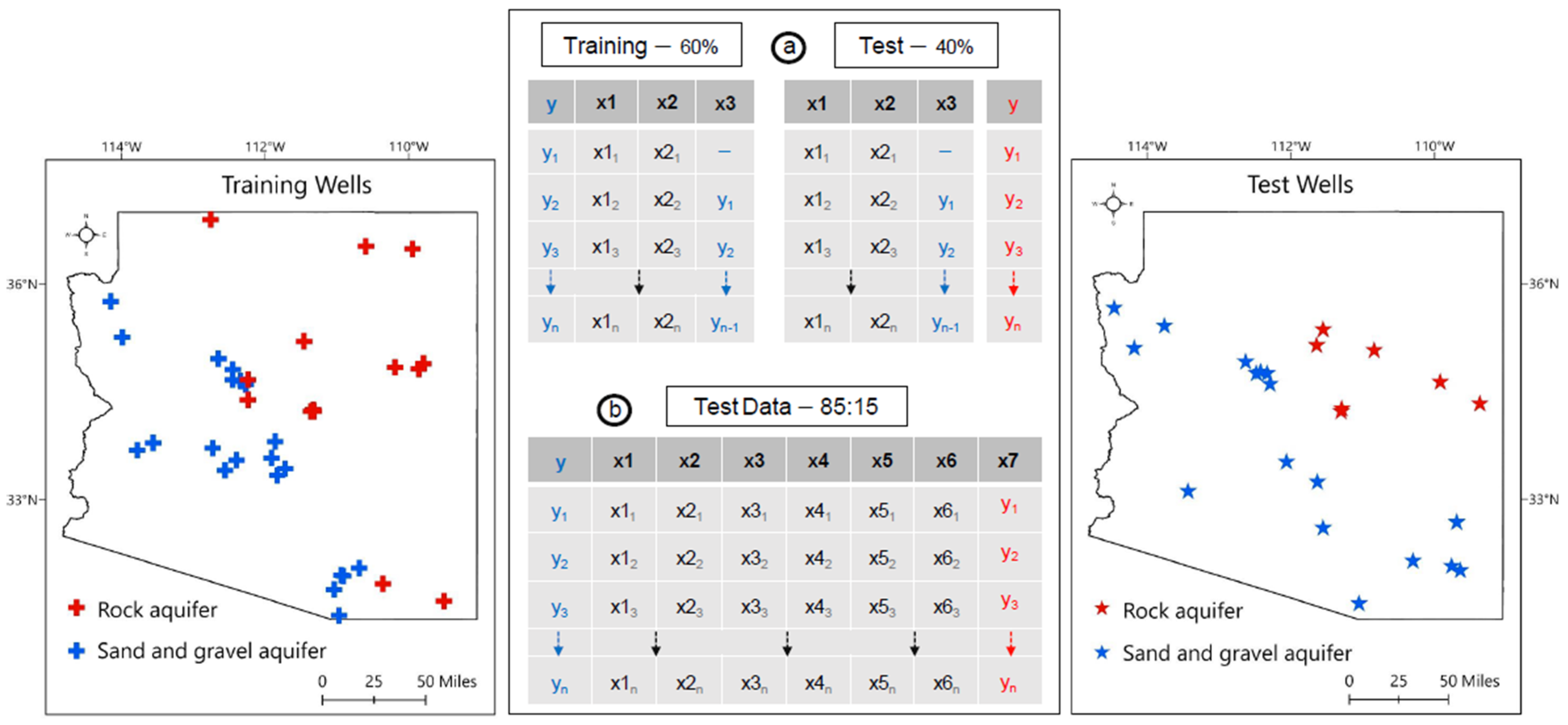
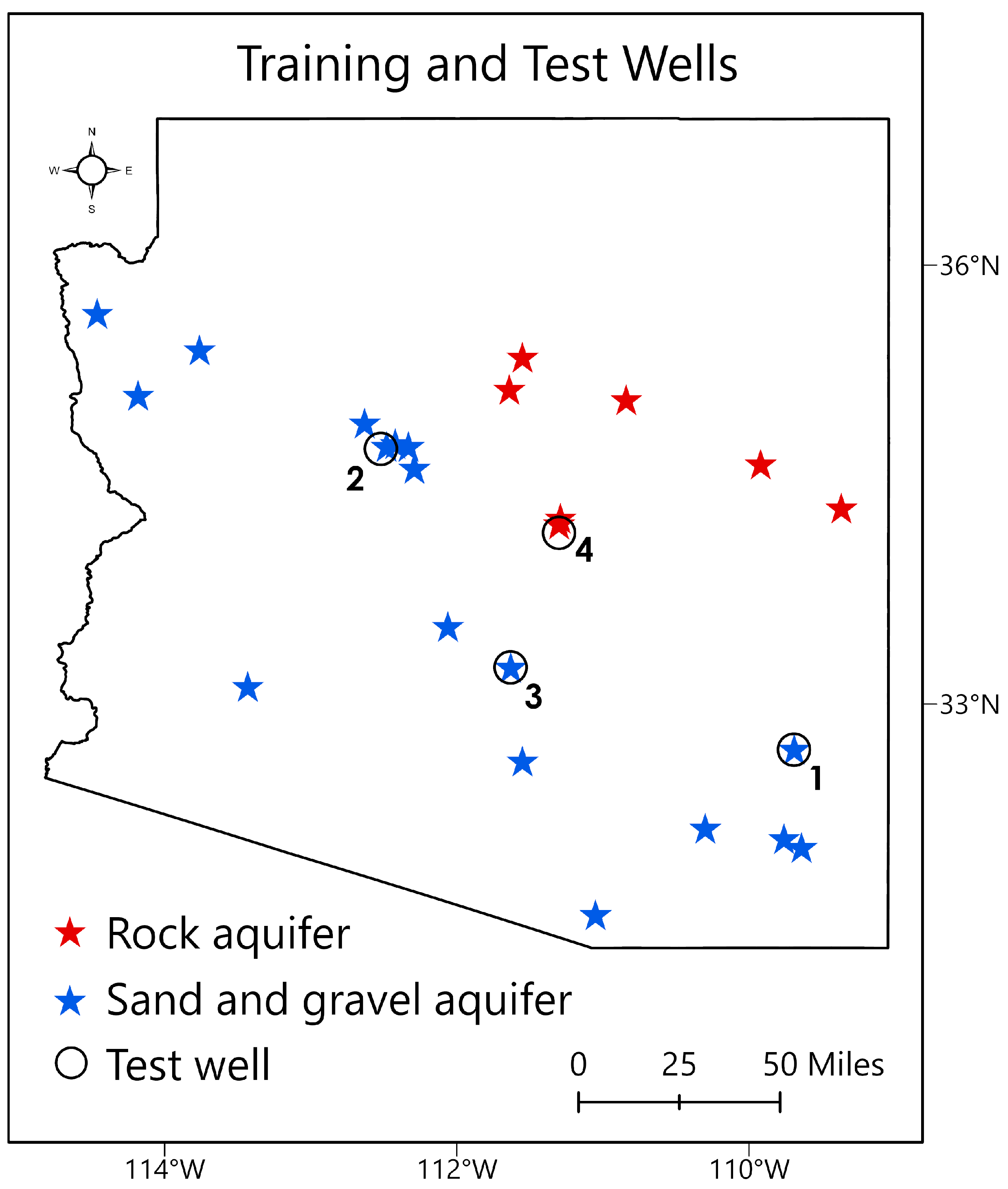
2.4. Model Design
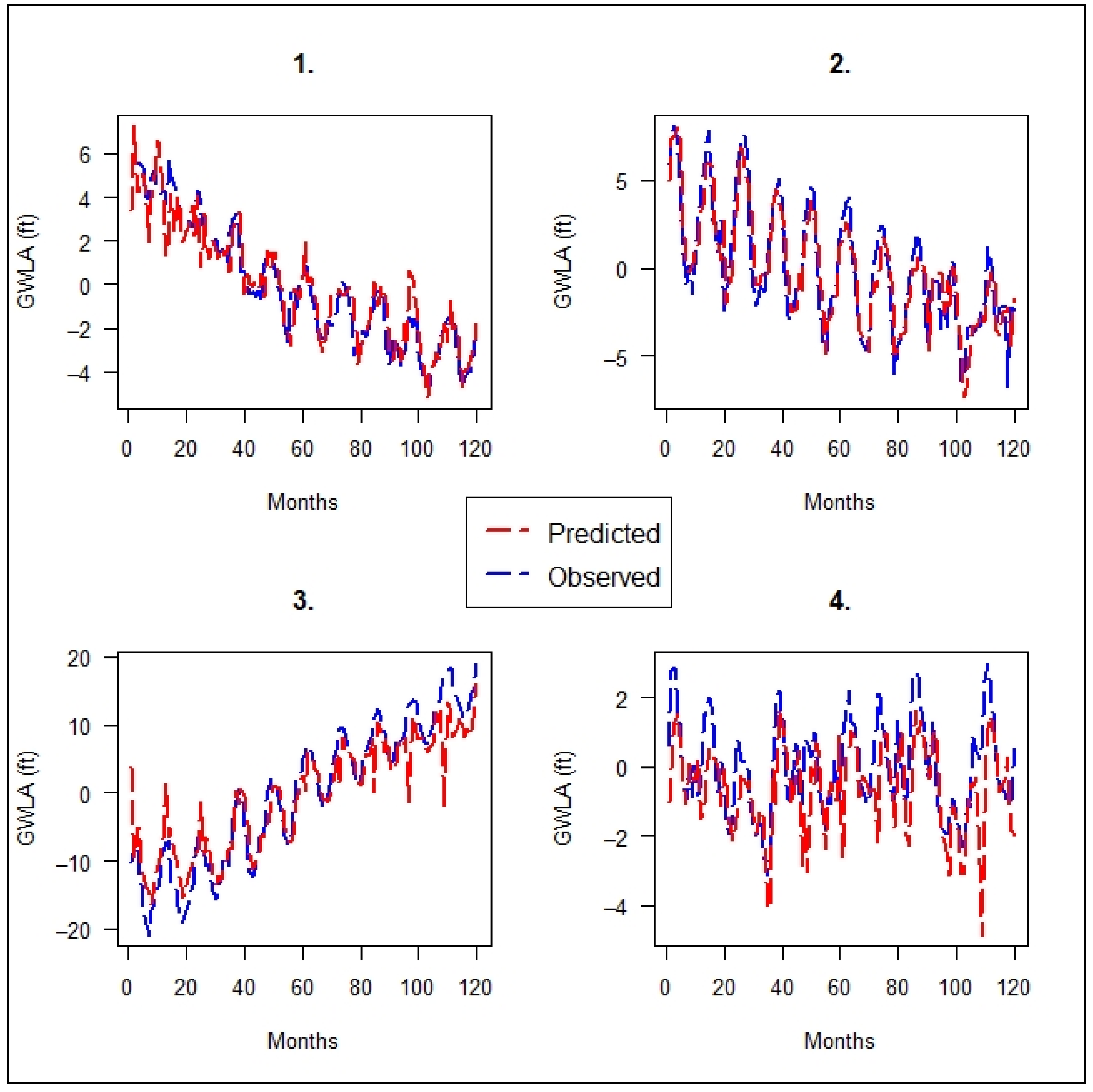
3. Results
3.1. Initial Assessment of ML Capabilities
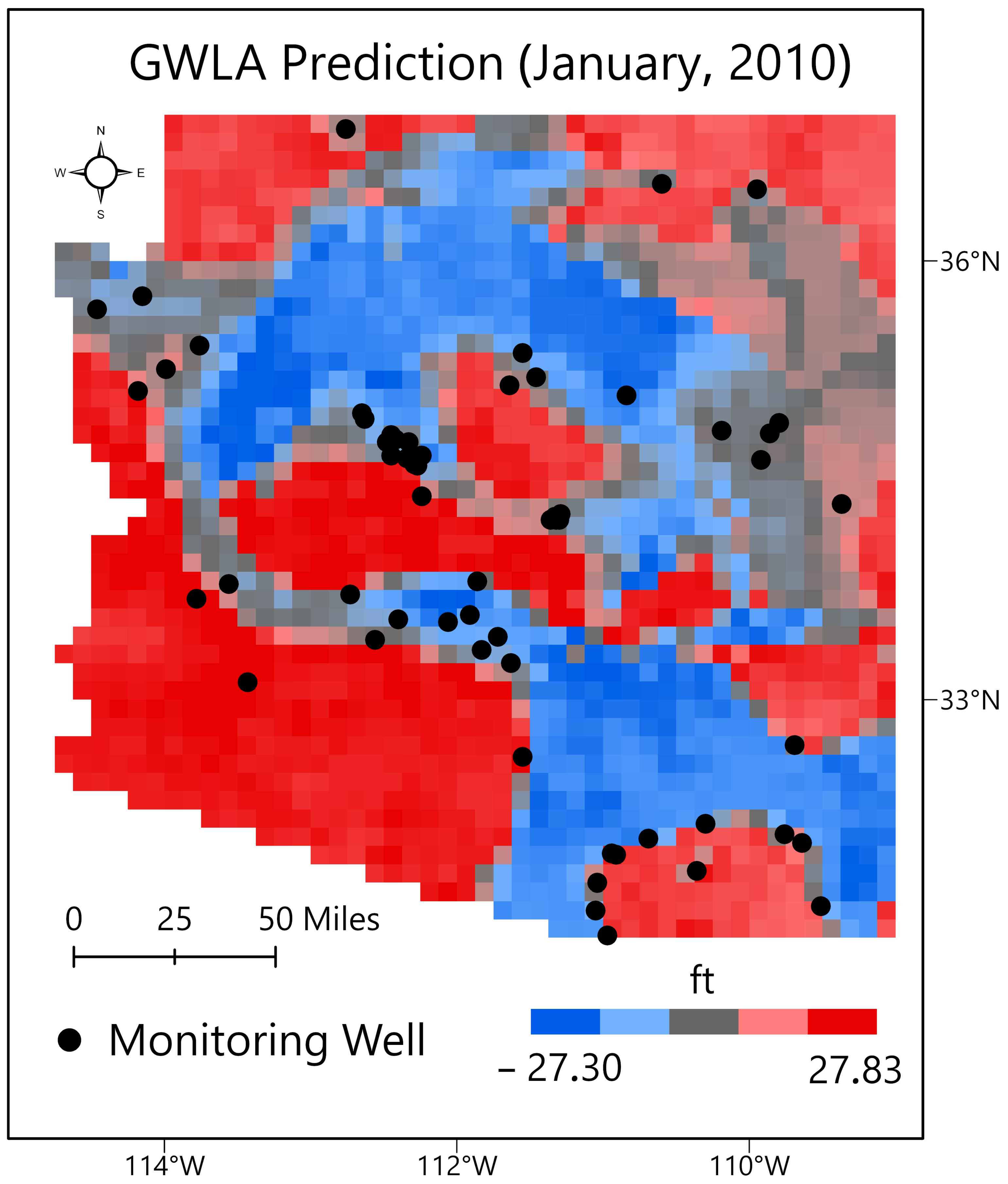
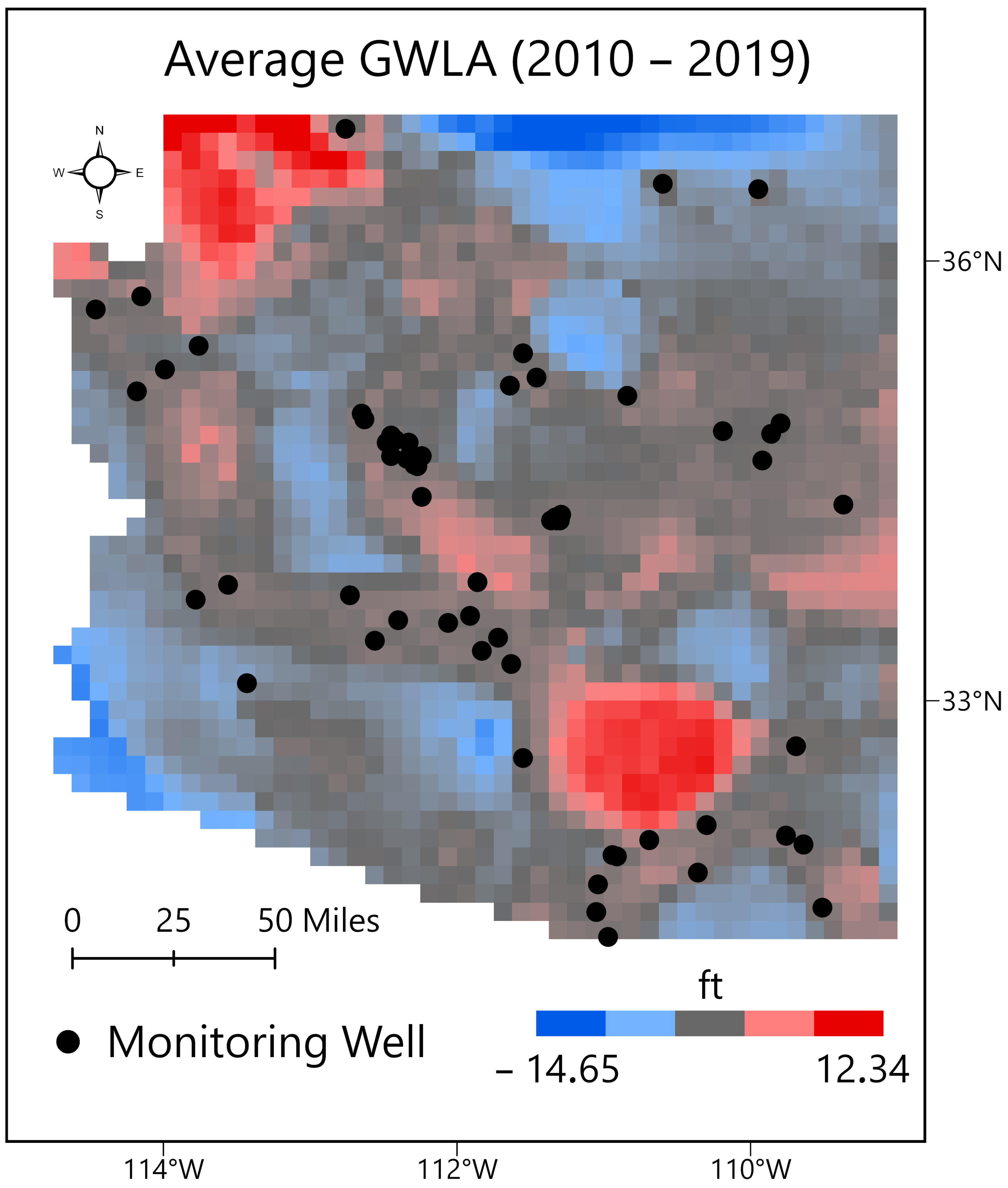
3.2. Integrating EBK GWL Predictions
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADWR | Arizona Department of Water Resources |
| AMA | Active Management Area |
| ANN | Artificial neural network |
| ARIMA | Autoregressive integrated moving average |
| CONUS | Contiguous United States |
| CK | Classical kriging |
| CN | Curve number |
| CV | Coefficient of variation |
| DL | Deep learning |
| DT | Decision tree |
| EBK | Empirical Bayesian kriging |
| ET | Evapotranspiration |
| GBM | Gradient boosting mechanism |
| GI | Geostatistical interpolation |
| GRACE | Gravity Recovery and Climate Experiment |
| GWL | Groundwater level |
| GWLA | Groundwater level anomaly |
| GWSP | Groundwater storage percentile |
| KNN | K-nearest neighbors |
| Ks | Soil saturated hydraulic conductivity |
| LST | Land surface temperature |
| MAE | Mean absolute error |
| MI | Mean imputation |
| ML | Machine learning |
| MLR | Multilinear regression |
| MSE | Mean squared error |
| NGWMN | National Groundwater Monitoring Network |
| P | Precipitation |
| PDP | Partial dependence plot |
| PKs | Precipitation x soil saturated hydraulic conductivity |
| R | Runoff depth |
| RBF | Radial basis function |
| RBF-NN | Radial basis function neural network |
| RBF-SVR | Radial basis function support vector regression |
| RF | Random forest |
| RI | Recharge index |
| RMSE | Root mean square error |
| SM | Soil moisture |
| SVM | Support vector machine |
| SVR | Support vector machine for regression |
| USGS | U.S. Geological Survey |
| VI | Vegetation index |
| WCI | Water cycle intensity |
References
- Scanlon, B.R.; Keese, K.E.; Flint, A.L.; Flint, L.E.; Gaye, C.B.; Edmunds, W.M.; Simmers, I. Global synthesis of groundwater recharge in semiarid and arid regions. Hydrol. Process. 2006, 20, 3335–3370. [Google Scholar] [CrossRef]
- Dawoud, M.A. Groundwater economics in arid regions: Abu Dhabi Emirate case study. In Recent Advances in Environmental Science from the Euro-Mediterranean and Surrounding Regions, Proceedings of Euro-Mediterranean Conference for Environmental Integration (EMCEI-1), Sousse, Tunisia, 20–25 November 2017; Springer: Cham, Switzerland, 2017; pp. 611–613. [Google Scholar]
- Liu, Q.; Gui, D.; Zhang, L.; Niu, J.; Dai, H.; Wei, G.; Hu, B.X. Simulation of regional groundwater levels in arid regions using interpretable machine learning models. Sci. Total Environ. 2022, 831, 154902. [Google Scholar] [CrossRef] [PubMed]
- Haider, A.; Lee, G.; Jafri, T.H.; Yoon, P.; Piao, J.; Jhang, K. Enhancing Accuracy of Groundwater Level Forecasting with Minimal Computational Complexity Using Temporal Convolutional Network. Water 2023, 15, 4041. [Google Scholar] [CrossRef]
- Tao, H.; Hameed, M.M.; Marhoon, H.A.; Zounemat-Kermani, M.; Heddam, S.; Kim, S.; Sulaiman, S.O.; Tan, M.L.; Sa’adi, Z.; Mehr, A.D.; et al. Groundwater level prediction using machine learning models: A comprehensive review. Neurocomputing 2022, 489, 271–308. [Google Scholar] [CrossRef]
- Ardana, P.D.H.; Redana, I.W.; Yekti, M.I.; Simpen, I.N. Groundwater Level Forecasting Using Multiple Linear Regression and Artificial Neural Network Approaches. Civ. Eng. Archit. 2022, 10, 784–799. [Google Scholar] [CrossRef]
- Najafabadipour, A.; Kamali, G.; Nezamabadi-Pour, H. Application of Artificial Intelligence Techniques for the Determination of Groundwater Level Using Spatio–Temporal Parameters. ACS Omega 2022, 7, 10751–10764. [Google Scholar] [CrossRef]
- Sahoo, M.; Kasot, A.; Dhar, A.; Kar, A. On predictability of groundwater level in shallow wells using satellite observations. Water Resour. Manag. 2018, 32, 1225–1244. [Google Scholar] [CrossRef]
- Li, B.; Yang, G.; Wan, R.; Dai, X.; Zhang, Y. Comparison of random forests and other statistical methods for the prediction of lake water level: A case study of the Poyang Lake in China. Hydrol. Res. 2016, 47 (Suppl. S1), 69–83. [Google Scholar] [CrossRef]
- Afrifa, S.; Zhang, T.; Appiahene, P.; Varadarajan, V. Mathematical and machine learning models for groundwater level changes: A systematic review and bibliographic analysis. Future Internet 2022, 14, 259. [Google Scholar] [CrossRef]
- Gonzalez, R.Q.; Arsanjani, J.J. Prediction of groundwater level variations in a changing climate: A Danish case study. ISPRS Int. J. Geo-Inf. 2021, 10, 792. [Google Scholar] [CrossRef]
- Guzman, S.M.; Paz, J.O.; Tagert, M.L.M.; Mercer, A.E. Evaluation of seasonally classified inputs for the prediction of daily groundwater levels: NARX networks vs support vector machines. Environ. Model. Assess. 2019, 24, 223–234. [Google Scholar] [CrossRef]
- Yoon, H.; Hyun, Y.; Ha, K.; Lee, K.K.; Kim, G.B. A method to improve the stability and accuracy of ANN-and SVM-based time series models for long-term groundwater level predictions. Comput. Geosci. 2016, 90, 144–155. [Google Scholar] [CrossRef]
- Behzad, M.; Asghari, K.; Coppola, E.A., Jr. Comparative study of SVMs and ANNs in aquifer water level prediction. J. Comput. Civ. Eng. 2010, 24, 408–413. [Google Scholar] [CrossRef]
- Nie, S.; Bian, J.; Wan, H.; Sun, X.; Zhang, B. Simulation and uncertainty analysis for groundwater levels using radial basis function neural network and support vector machine models. Res. Technol.—AQUA 2017, 66, 15–24. [Google Scholar] [CrossRef]
- Tapak, L.; Rahmani, A.R.; Moghimbeigi, A. Prediction the groundwater level of Hamadan-Bahar plain, west of Iran using support vector machines. J. Res. Health Sci. 2013, 14, 82–87. [Google Scholar]
- Tiwari, V.; Verma, M. Prediction of Groundwater Level Using Advance Machine Learning Techniques. In Proceedings of the 3rd IEEE International Conference on Intelligent Technologies (CONIT), Hubli, India, 23–25 June 2023; pp. 1–6. [Google Scholar]
- Hikouei, I.S.; Eshleman, K.N.; Saharjo, B.H.; Graham, L.L.; Applegate, G.; Cochrane, M.A. Using machine learning algorithms to predict groundwater levels in Indonesian tropical peatlands. Sci. Total Environ. 2023, 857, 159701. [Google Scholar] [CrossRef]
- Kanyama, Y.; Ajoodha, R.; Seyler, H.; Makondo, N.; Tutu, H. Application of machine learning techniques in forecasting groundwater levels in the grootfontein aquifer. In Proceedings of the 2nd IEEE International Multidisciplinary Information Technology and Engineering Conference (IMITEC), Kimberley, South Africa, 25–27 November 2020; pp. 1–8. [Google Scholar]
- Alam, M.J.; Kar, S.; Zaman, S.; Ahamed, S.; Samiya, K. Forecasting Underground Water Levels: LSTM Based Model Outperforms GRU and Decision Tree Based Models. In Proceedings of the IEEE International Women in Engineering (WIE) Conference on Electrical and Computer Engineering (WIECON-ECE), Naya Raipur, India, 30–31 December 2022; pp. 280–283. [Google Scholar]
- Biernacik, P.; Kazimierski, W.; Włodarczyk-Sielicka, M. Comparative Analysis of Selected Geostatistical Methods for Bottom Surface Modeling. Sensors 2023, 23, 3941. [Google Scholar] [CrossRef]
- Manda, S.; Patil, A. Analysis of groundwater level differences in Ganges basin using geostatistical modeling. Int. J. Agric. Eng. 2018, 11, 392–396. [Google Scholar] [CrossRef]
- Krivoruchko, K. Empirical bayesian kriging. ArcUser Fall 2012, 6, 1145. [Google Scholar]
- Bouhout, S.; Haboubi, K.; Zian, A.; Elyoubi, M.S.; Elabdouni, A. Evaluation of two linear kriging methods for piezometric levels interpolation and a framework for upgrading groundwater level monitoring network in Ghiss-Nekor plain, north-eastern Morocco. Arab. J. Geosci. 2022, 15, 1016. [Google Scholar] [CrossRef]
- Hussain, M.M.; Bari, S.H.; Tarif, M.E.; Rahman, M.T.U.; Hoque, M.A. Temporal and spatial variation of groundwater level in Mymensingh district, Bangladesh. Int. J. Hydrol. Sci. Technol. 2016, 6, 188–197. [Google Scholar] [CrossRef]
- Deshmukh, M.M.; Elbeltagi, A.; Kouadri, S. Climate Change Impact on Groundwater Resources in Semi-arid Regions. In Climate Change Impact on Groundwater Resources: Human Health Risk Assessment in Arid and Semi-Arid Regions; Panneerselvam, B., Pande, C.B., Muniraj, K., Balasubramanian, A., Ravichandran, N., Eds.; Springer: Cham, Switzerland, 2022; pp. 9–23. [Google Scholar]
- Zowam, F.J.; Milewski, A.M.; Richards IV, D.F. A Satellite-Based Approach for Quantifying Terrestrial Water Cycle Intensity. Remote Sens. 2023, 15, 3632. [Google Scholar] [CrossRef]
- McCafferty, A.E.; San Juan, C.A.; Lawley, C.J.M.; Graham, G.E.; Gadd, M.G.; Huston, D.L.; Kelley, K.D.; Paradis, S.; Peter, J.M.; Czarnota, K. National-Scale Geophysical, Geologic, and Mineral Resource Data and Grids for the United States, Canada, and Australia: Data in Support of the Tri-National Critical Minerals Mapping Initiative: US Geological Survey Data Release. Available online: https://www.sciencebase.gov/catalog/item/623a013ed34e915b67cddcfa (accessed on 22 February 2024).
- Bedinger, M.S.; Anderson, T.W.; Langer, W.H. Groundwater Units and Withdrawal, Basin and Range Province, Arizona. Water-Resources Investigations Report (No. 83-4114-A); U.S. Geological Survey: Reston, VA, USA, 1984. [Google Scholar] [CrossRef]
- Tillman, F.D.; Flynn, M.E. Arizona Groundwater Explorer: Interactive maps for evaluating the historical and current groundwater conditions in wells in Arizona, USA. Hydrogeol. J. 2024, 32, 645–661. [Google Scholar] [CrossRef]
- Bertsimas, D.; Pawlowski, C.; Zhuo, Y.D. From predictive methods to missing data imputation: An optimization approach. J. Mach. Learn. Res. 2018, 18, 1–39. [Google Scholar]
- Petrazzini, B.O.; Naya, H.; Lopez-Bello, F.; Vazquez, G.; Spangenberg, L. Evaluation of different approaches for missing data imputation on features associated to genomic data. BioData Min. 2021, 14, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Muharemi, F.; Logofătu, D.; Leon, F. Review on general techniques and packages for data imputation in R on a real world dataset. In Computational Collective Intelligence, Proceedings of the 10th International Conference, Bristol, UK, 5–7 September 2018; Part II 10; Springer International Publishing: Cham, Switzerland, 2018; pp. 386–395. [Google Scholar]
- Lande, R. On comparing coefficients of variation. Syst. Zool. 1977, 26, 214–217. [Google Scholar] [CrossRef]
- Seyoum, W.M.; Kwon, D.; Milewski, A.M. Downscaling GRACE TWSA data into high-resolution groundwater level anomaly using machine learning-based models in a glacial aquifer system. Remote Sens. 2019, 11, 824. [Google Scholar] [CrossRef]
- Moeck, C.; Grech-Cumbo, N.; Podgorski, J.; Bretzler, A.; Gurdak, J.J.; Berg, M.; Schirmer, M. A global-scale dataset of direct natural groundwater recharge rates: A review of variables, processes and relationships. Sci. Total Environ. 2020, 717, 137042. [Google Scholar] [CrossRef]
- Pradhan, R.K.; Markonis, Y.; Godoy, M.R.V.; Villalba-Pradas, A.; Andreadis, K.M.; Nikolopoulos, E.I.; Papalexiou, S.M.; Rahim, A.; Tapiador, F.J.; Hanel, M. Review of GPM IMERG performance: A global perspective. Remote Sens. Environ. 2022, 268, 112754. [Google Scholar] [CrossRef]
- Milewski, A.; Elkadiri, R.; Durham, M. Assessment and comparison of TMPA satellite precipitation products in varying climatic and topographic regimes in Morocco. Remote Sens. 2015, 7, 5697–5717. [Google Scholar] [CrossRef]
- Mohammed, S.A.; Hamouda, M.A.; Mahmoud, M.T.; Mohamed, M.M. Performance of GPM-IMERG precipitation products under diverse topographical features and multiple-intensity rainfall in an arid region. Hydrol. Earth Syst. Sci. 2020, 2020, 1–27. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.H. NASA global precipitation measurement (GPM) integrated multi-satellite retrievals for GPM (IMERG). Algorithm Theor. Basis Doc. (ATBD) 2015, 4, 30. [Google Scholar]
- Malik, M.S.; Shukla, J.P.; Mishra, S. Effect of groundwater level on soil moisture, soil temperature and surface temperature. J. Indian Soc. Remote Sens. 2021, 49, 2143–2161. [Google Scholar] [CrossRef]
- Maihemuti, B.; Simayi, Z.; Alifujiang, Y.; Aishan, T.; Abliz, A.; Aierken, G. Development and evaluation of the soil water balance model in an inland arid delta oasis: Implications for sustainable groundwater resource management. Glob. Ecol. Conserv. 2021, 25, e01408. [Google Scholar] [CrossRef]
- Otoko, G.R. Mathematical Relationship between Soil Moisture and Groundwater Level in A Loamy Sand Soil in The Niger Delta Region of Nigeria. Int. J. Adv. Res. Sci. Eng. Technol. 2014, 5, 1–8. [Google Scholar]
- Hongtao, J.; Huanfeng, S.; Xinghua, L.; Lili, L. The 43-Year (1978–2020) Global 9 km Remotely Sensed Soil Moisture Product: PANGAEA. Available online: https://doi.org/10.1594/PANGAEA.940409 (accessed on 12 February 2023).
- Elnashar, A.; Wang, L.; Wu, B.; Zhu, W.; Zeng, H. Synthesis of global actual evapotranspiration from 1982 to 2019. Earth Syst. Sci. Data 2021, 13, 447–480. [Google Scholar] [CrossRef]
- Zhang, T.; Zhou, Y.; Zhu, Z.; Li, X.; Asrar, G.R. A global seamless 1 km resolution daily land surface temperature dataset (2003–2020). Earth Syst. Sci. Data 2021, 2021, 651–664. [Google Scholar] [CrossRef]
- Grove, M.; Harbor, J.; Engel, B. composite vs. distributed curve numbers: Effects on estimates of storm runoff depths. J. Am. Water Resour. Assoc. 1998, 34, 1015–1023. [Google Scholar] [CrossRef]
- Arisanty, D.; Rahmawati, N.; Rosadi, D. Soil Physical Characteristics and Saturated Hydraulic Conductivity in the Landform of Barito Delta, Kalimantan, Indonesia. Appl. Environ. Soil Sci. 2022, 2022, 9118461. [Google Scholar] [CrossRef]
- Gupta, S.; Lehmann, P.; Bonetti, S.; Papritz, A.; Or, D. Global prediction of soil saturated hydraulic conductivity using random forest in a covariate-based geoTransfer function (CoGTF) framework. J. Adv. Model. Earth Syst. 2021, 13, e2020MS002242. [Google Scholar] [CrossRef]
- Beaudoing, H.; Rodell, M.; Getirana, A.; Li, B. Groundwater and Soil Moisture Conditions from GRACE and GRACE-FO Data Assimilation L4 7-Days 0.125 × 0.125 Degree U.S. V4.0; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2021. Available online: https://disc.gsfc.nasa.gov/datasets/GRACEDADM_CLSM0125US_7D_4.0/summary (accessed on 30 October 2023).
- Dhungel, R.; Fiedler, F. Water balance to recharge calculation: Implications for watershed management using systems dynamics approach. Hydrology 2016, 3, 13. [Google Scholar] [CrossRef]
- Ahmadi, A.; Olyaei, M.; Heydari, Z.; Emami, M.; Zeynolabedin, A.; Ghomlaghi, A.; Daccache, A.; Fogg, G.E.; Sadegh, M. Groundwater level modeling with machine learning: A systematic review and meta-analysis. Water 2022, 14, 949. [Google Scholar] [CrossRef]
- Ding, J.; Tarokh, V.; Yang, Y. Model selection techniques: An overview. IEEE Signal Process. Mag. 2018, 35, 16–34. [Google Scholar] [CrossRef]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Awad, M.; Khanna, R. Support Vector Machines for Classification. In Efficient Learning Machines; Apress: Berkeley, CA, USA, 2015; p. 268. [Google Scholar]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, A. Support vector regression machines. Adv. Neural. Inf. Process Syst. 1996, 9, 161–226. [Google Scholar]
- Amirkhalili, Y.S.; Aghsami, A.; Jolai, F. Comparison of Time Series ARIMA Model and Support Vector Regression. Int. J. Hybrid Inf. Technol. 2020, 13, 7–18. [Google Scholar] [CrossRef]
- Ranković, V.; Grujović, N.; Divac, D.; Milivojević, N. Development of support vector regression identification model for prediction of dam structural behaviour. Struct. Saf. 2014, 48, 33–39. [Google Scholar] [CrossRef]
- Ayodeji, A.; Liu, Y.K. SVR optimization with soft computing algorithms for incipient SGTR diagnosis. Ann. Nucl. Energy 2018, 121, 89–100. [Google Scholar] [CrossRef]
- Açıkkar, M.; Altunkol, Y. A novel hybrid PSO-and GS-based hyperparameter optimization algorithm for support vector regression. Neural Comput. 2023, 35, 19961–19977. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013. [Google Scholar]
- Al-Anazi, A.F.; Gates, I.D. Support vector regression for porosity prediction in a heterogeneous reservoir: A comparative study. Comput. Geosci. 2010, 36, 1494–1503. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Samet, H.; Marzbani, F. A new hybrid modified firefly algorithm and support vector regression model for accurate short term load forecasting. Expert Syst. Appl. 2014, 41, 6047–6056. [Google Scholar] [CrossRef]
- Karatzoglou, A.; Meyer, D.; Hornik, K. Support vector machines in R. J. Stat. Softw. 2006, 15, 1–28. [Google Scholar] [CrossRef]
- Kaneko, H.; Funatsu, K. Fast optimization of hyperparameters for support vector regression models with highly predictive ability. Chemom. Intell. Lab. Syst. 2015, 142, 64–69. [Google Scholar] [CrossRef]
- Tsirikoglou, P.; Abraham, S.; Contino, F.; Lacor, C.; Ghorbaniasl, G. A hyperparameters selection technique for support vector regression models. Appl. Soft Comput. 2017, 61, 139–148. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wu, D.J.; Feng, T.; Naehrig, M.; Lauter, K. Privately evaluating decision trees and random forests. Proc. Priv. Enh. Technol. 2015, 2016, 335–355. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Rigatti, S.J. Random forest. J. Insur. Med. 2017, 47, 31–39. [Google Scholar] [CrossRef]
- Maliva, R.G. Geostatistical methods and applications. In Aquifer Characterization Techniques; Springer: Cham, Switzerland, 2016; No. 4; pp. 595–617. [Google Scholar]
- Li, Y.; Hernandez, J.H.; Aviles, M.; Knappett, P.S.; Giardino, J.R.; Miranda, R.; Puy, M.J.; Padilla, F. Morales, J. Empirical Bayesian Kriging method to evaluate inter-annual water-table evolution in the Cuenca Alta del Río Laja aquifer, Guanajuato, México. J. Hydrol. 2020, 582, 124517. [Google Scholar] [CrossRef]
- Kanyama, Y. Application of Machine Learning Techniques in Predicting Groundwater Levels and Discharge Rates in the Northwest Aquifers. Master’s Thesis, The University of the Witwatersrand, Johannesburg, South Africa, 22 April 2021. [Google Scholar]
- Yin, W.; Fan, Z.; Tangdamrongsub, N.; Hu, L.; Zhang, M. Comparison of physical and data-driven models to forecast groundwater level changes with the inclusion of GRACE–A case study over the state of Victoria, Australia. J. Hydrol. 2021, 602, 126735. [Google Scholar] [CrossRef]
- Janiesch, C.; Zschech, P.; Heinrich, K. Machine learning and deep learning. Electron. Mark. 2021, 31, 685–695. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, Y.; Sekula, P.; Ding, L. Machine learning in construction: From shallow to deep learning. Dev. Built Environ. 2021, 6, 100045. [Google Scholar] [CrossRef]
- Sk, M.; Ramanujam, N.; Champoil, V.; Biswas, S.K.; Rasool, Q.A.; Ojha, C. Identification of groundwater in hard rock terrain using 2D electrical resistivity tomography imaging technique: Securing water scarcity at the time of seasonal rainfall failure, South Andaman. Int. J. Geosci. 2018, 9, 59. [Google Scholar] [CrossRef]
- Arizona Department of Water Resources. Overview of the Arizona Groundwater Management Code. Available online: https://www.azwater.gov/sites/default/files/media/Arizona%20Groundwater_Code_1.pdf (accessed on 14 June 2024).
- Hirt, P.; Snyder, R.; Hester, C.; Larson, K. Water consumption and sustainability in Arizona: A tale of two desert cities. J. Southwest 2017, 59, 264–301. [Google Scholar] [CrossRef]
- Megdal, S.B. Arizona groundwater management. Water Rep. 2012, 104, 9–15. [Google Scholar]




| ID | Variable | Processing | Unit |
|---|---|---|---|
| 1 | Soil moisture (SM) | × ○ | m3/m3 |
| 2 | Land surface temperature (LST) | × ∆ ○ | °C |
| 3 | Vegetation index (VI) | ○ | |
| 4 | Saturated hydraulic conductivity (PKs) * | ○ ∆ □ | mm2/day |
| 5 | Groundwater storage percentile (GWSP) | % | |
| 6 | Recharge index (RI) * | ○ | ○ | □ | mm |
| Model | NSE | R2 | |
|---|---|---|---|
| 1 | January | – | – |
| 2 | February | 0.88 | 0.88 |
| 3 | March | 0.71 | 0.71 |
| 4 | April | 0.51 | 0.51 |
| 5 | May | 0.87 | 0.89 |
| 6 | June | 0.90 | 0.93 |
| 7 | July | 0.96 | 0.97 |
| 8 | August | 0.87 | 0.87 |
| 9 | September | 0.80 | 0.81 |
| 10 | October | 0.77 | 0.78 |
| 11 | November | 0.83 | 0.83 |
| 12 | December | 0.91 | 0.92 |
| ID | Test Well | Aquifer Type | NSE | R2 |
|---|---|---|---|---|
| 1 | Artesia School [D-08-26 33CDC1] | Sand and gravel | 0.87 | 0.87 |
| 2 | Geiler [B-16-02 21BAA2] | Sand and gravel | 0.80 | 0.80 |
| 3 | Queen Creek [D-02-07 22BBC] | Sand and gravel | 0.84 | 0.87 |
| 4 | PE–11 [A-10-10 11ACB] | Rock | −0.13 | 0.28 |
| ID | Validation Well | Aquifer Type | NSE | R2 |
|---|---|---|---|---|
| 1 | Antelope Wash [B-18-04 25AAA2] | Sand and gravel | 0.81 | 0.83 |
| 2 | Turtleback [C-03-11 31DBB] | Sand and gravel | 0.63 | 0.65 |
| 3 | Rumsey Park [A-10-10 04ABB] | Rock | 0.41 | 0.41 |
| ID | Test Well | Aquifer Type | NSE | R2 |
|---|---|---|---|---|
| 1 | Antelope Wash [B-18-04 25AAA2] * | Sand and gravel | 0.98 | 0.99 |
| 2 | Turtleback [C-03-11 31DBB] * | Sand and gravel | 0.86 | 0.88 |
| 3 | Friendly Corners [D-09-08 29BCC] | Sand and gravel | 0.82 | 0.87 |
| 4 | Pantano Wash North [D-16-16 15ABD] | Sand and gravel | 0.88 | 0.94 |
| 5 | Truxton South [B-24-14 33ADA] | Sand and gravel | 0.84 | 0.90 |
| 6 | GC–3 [A-11-10 26DAB] | Rock | 0.44 | 0.46 |
| 7 | [A-19-14 03AAC1] | Rock | 0.20 | 0.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zowam, F.J.; Milewski, A.M. Groundwater Level Prediction Using Machine Learning and Geostatistical Interpolation Models. Water 2024, 16, 2771. https://doi.org/10.3390/w16192771
Zowam FJ, Milewski AM. Groundwater Level Prediction Using Machine Learning and Geostatistical Interpolation Models. Water. 2024; 16(19):2771. https://doi.org/10.3390/w16192771
Chicago/Turabian StyleZowam, Fabian J., and Adam M. Milewski. 2024. "Groundwater Level Prediction Using Machine Learning and Geostatistical Interpolation Models" Water 16, no. 19: 2771. https://doi.org/10.3390/w16192771
APA StyleZowam, F. J., & Milewski, A. M. (2024). Groundwater Level Prediction Using Machine Learning and Geostatistical Interpolation Models. Water, 16(19), 2771. https://doi.org/10.3390/w16192771







