1. Introduction
Artificial intelligence (AI) is the effort to automate intellectual tasks normally performed by humans, and it includes machine learning (ML) and deep learning (DL) [
1]. AI–ML performs statistical learning and seeks to discover rules that are data-based or statistics-based, rather than physics-based, for implementing tasks like data analysis and data comparison using inputs, or features, and corresponding outputs, or outcomes [
2]. Inputs, features, independent variables, and predictors are synonyms. Likewise, outputs, responses, and dependent variables are all descriptions of learned or calculated outcomes. Statistical, or machine, learning needs: (1) input data, (2) observed responses attributable to the inputs, and (3) a prediction skill metric that describes skill using the goodness-of-fit between predicted and observed outcomes [
1,
2].
Observed outcomes, or measurements, can be quantitative, i.e., represented with real-valued numbers, or qualitative, i.e., categorized or represented with discrete labels [
2]. Two top-level functionalities are available for supervised learning with AI–ML: (1) classification and (2) regression [
3]. Classification implements the outcome of labeling images or complex collections of features to predict categorical outcomes. Regression-style AI–ML provides a real-valued estimate for a collection of features. Regression-style AI–ML performs analogous estimation to ordinary least squares (OLS) statistical regression. This paper focuses on regression-style AI–ML in water resources.
The goal of model creation and development is generalization ability, which is the prediction capability in terms of matching observed to predicted outcomes for an independent data set [
2]. Independent denotes information that was not part of “learning”, training, and calibration. Ideally, the development of a model, or predictor, involves a data set split into three components: (1) training, (2) testing, and (3) validation. Each component includes inputs and corresponding observed outcomes.
The training component is used for model fitting, which is optimizing the internal “weight” values to produce the best match between predicted and observed outcomes. The testing set is used to estimate prediction error, the difference between model-predicted and observed outcomes, for “final” model selection, which is selection of the “optimal” combination of internal weight values and the internal algorithm structure. The validation component should be set aside until training, testing, and model selection are complete. It provides for an estimation of the generalization error of the “final” model on an independent data set and the assessment of the model-predictive skill and generalization ability [
1,
2]. Note that the training and testing components are used repeatedly as part of selecting the “final” model; consequently, the prediction error for the “final” model will underestimate the true generalization error, sometimes substantially [
2]. This underestimation of generalization error is caused by overfitting.
Overfitting is the difference between training and testing accuracy, represented by prediction error, and generalization accuracy, represented by generalization error. It occurs because the optimization of internal weights and structure seeks the best performance on the training and testing components. AI–ML model complexity can be increased during development and optimization using various hyper-parameter-related approaches, like tuning a complexity or smoothing parameter, and by increasing the degrees of freedom through the addition of “weights”. Testing and prediction errors consistently decrease with increases in model complexity and will typically drop to zero if complexity is increased sufficiently. This consistent bias decrease with increased complexity occurs as the model learns to reproduce the measurement error and noise in the training data set by increasing the degrees of freedom in the representation. Zero training error means that the model is overfit to the training data set and will typically generalize poorly [
1,
2,
4,
5].
Statistical learning algorithms provide a tradeoff between prediction bias and variance during model training that is moderated by model complexity.
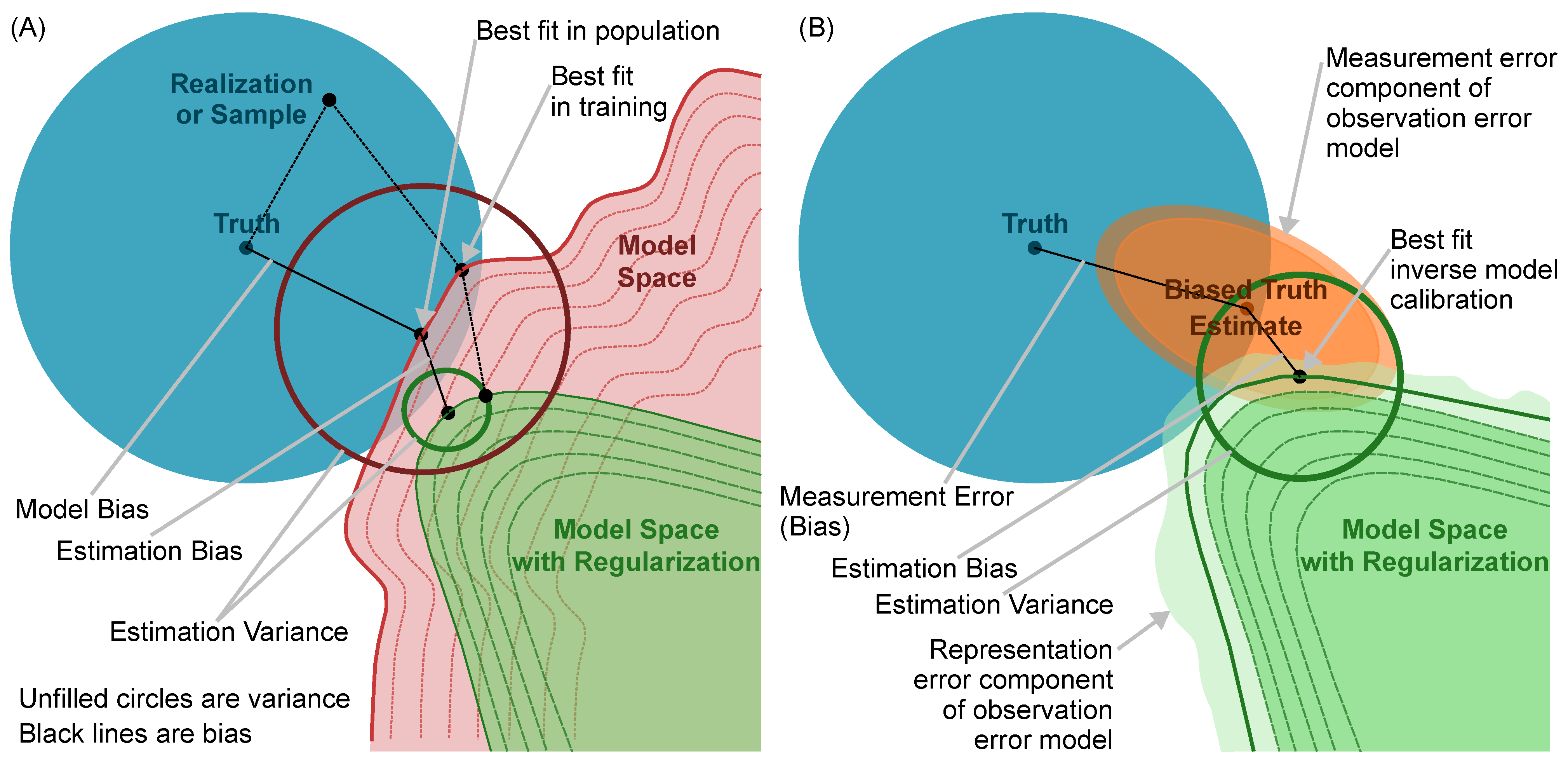
Figure 1A explains this tradeoff graphically. Assuming that errors are represented by the mean squared error of residuals, which are the differences between observed outcomes and predicted outcomes, prediction bias is the systematic error represented with the squared difference between the observed mean and the predicted mean. The prediction variance,
, is the expected squared deviation for predictions from the predicted mean. The bias–variance tradeoff is that variance generally increases and bias decreases with increased model complexity and that the opposite occurs as complexity decreases. In
Figure 1, regularization denotes techniques to limit complexity and reduce degrees of freedom and thus reduce the dimensionality of the model. Ideally, model complexity would be selected to trade bias against variance in order to minimize generalization error. However, prediction error is not a good estimate of generalization error because of overfitting, and this trade is typically impossible to optimize for a real system with real data [
2].
A key assumption of statistical learning, and thus AI–ML, is that training and testing data sets have the information content necessary to “learn” unique and certain relationships and correlations between independent variables, i.e., inputs, and dependent variables, i.e., outcomes [
6]. The collection of internal weights and other modifiable parameters provides the relationship between inputs and outputs and is optimized during training to produce “intelligence” and “learning”. Data sets that enable learning are ‘‘clean’’, i.e., certain or precise and accurate, and relatively homogeneous, i.e., with no extreme events or other rare features [
1]. In other words, we seek samples that reproduce the descriptive statistics of the underlying population and that represent the “Truth” shown in
Figure 1A. Because AI–ML is completely data-driven and only learns from available data sets, AI–ML model complexity can only be increased, without overfitting, through the collection of more and better data [
1].
Unfortunately, important water resource data sets concerning, for example, river discharge and evaporation rate are typically composed of estimated, rather than observed, values. These calculated and uncertain data sets often comprise noisy observed values, for which the statistical structure of the noise is uncertain and likely highly correlated across space and time. Noisy estimated values will most likely provide a poor representation of the underlying population, i.e., the difference between “Truth” and “Biased Truth Estimate” in
Figure 1B.
Data uncertainty is a long-standing and important problem in water resources. Since the 1980s, our best physics-based numerical models have provided more accurate and certain predictions than are available in key, derived, rather than measured, data sets. Analyses are not limited by AI–ML and physics-based model capabilities but by our abilities to appropriately describe complex environments to models, to accurately observe or measure history matching targets, and to specify boundary forcing for the models. In other words, analyses are limited by our data sets, and there is not currently an easy or immediate route to significant data-set improvement [
6].
Although the collection of more and better data is the direct approach to the improvement of models, feature engineering and other data augmentation and processing approaches are used to counteract data scarcity and quality issues. Feature engineering is the use of non-learned transformations on, or augmentations to, feature data sets [
1]. The goal of feature engineering, and other synthetic data augmentation approaches, is to bring out the structure of the training and testing data in order to enhance the ability of the AI–ML algorithm to learn important relationships and correlations. It provides a way to “externally” improve data sets used in the learning process in order to address noise and extreme event issues.
In physics-informed machine learning (PIML), physics information is incorporated into the learning process as additionally “engineered” features to provide a constraint on the resulting learned relations in order to enforce more plausible outcomes in response to a given set of inputs. According to PIML terminology, a bias describes how physics information is enforced to ML, rather than a systematic error. PIML “observational bias” may be implemented using data sets derived from the inputs and information from a physics- or process-based numerical model that incorporates relevant relationships based on an understanding of the underlying physics [
3,
7].
PIML involves extracting solutions to problems, which lack a sufficient quantity and veracity of data, using learning informed by physically relevant prior information. In PIML taxonomy, physics information is communicated to AI–ML learning through “observational bias”, “inductive bias”, and “learning bias”. “Inductive bias” is implemented via AI–ML algorithm architecture-level decisions that influence modeling choices with physical principles. “Learning bias” uses loss functions, which are often generated via the calculation of residuals from underlying physics equations, to provide physics-informed constraints to AI–ML learning [
3,
7]. A PIML “bias” functions to limit complexity in the AI–ML model to a physically plausible representation and provides a type of regularization like that identified as the “Model Space with Regularization” in
Figure 1A. Note that regularization works to increase model bias and decrease variability in the traditional bias–variance tradeoff.
“Differentiable Modeling” has been proposed as a means to unify ML and physics-based models. “Differentiable” means accurately and efficiently calculating gradients with respect to model variables or parameters. “Differentiable Modeling” relies on “Differentiable Programming”, which efficiently computes accurate derivatives of model outputs with respect to inputs and intermediate variables. “Differentiable Modeling” extends PIML because it requires that the entire learning workflow be differentiable, while PIML might solely provide physics-based constraints via custom loss functions or physically derived feature data sets [
8]. “Differentiable Modeling” as a concept does not explicitly address or reduce data and model uncertainty or model complexity and is an approach that falls under the
Figure 1A representation.
The PEST [
4,
9] and PEST++ [
5,
10] toolsets provide calibration-constrained uncertainty analyses that utilize gradients between model inputs and outputs, in a similar fashion to the “Differentiable Modeling” and “Differentiable Programming” concepts. In PEST toolsets, the calculation of the Jacobian matrix of partial derivatives of model outputs with respect to model parameters provides “Differentiable Programming” functionality. PEST and PEST++ are data assimilation (DA) algorithms. DA is more general, and therefore, it is more efficient than “Differentiable Modeling” because it can be applied to many forward model formulations.
DA is an umbrella concept that includes a variety of methods that seek to produce an optimal combination of “forward” model simulations with observed outcomes. It is generally used to (1) compute the best possible estimate of a model state at a given point in time and (2) implement the inverse-style estimation of model parameters or the deduction of optimal model forcing, given all historic observations [
11]. DA approaches can be utilized with any numerical model but are generally used with physics- and process-based models to obtain a combined physics- and data-based prediction tool. It explicitly addresses model, input, parameter, and observation imperfections and uncertainties. DA algorithms have been used in water resource studies for projecting the optimal estimate of a model state (e.g., [
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27]) and for parameter estimation and uncertainty analysis (e.g., [
28,
29,
30,
31,
32,
33]) within “calibration-constrained uncertainty analyses” like those provided using the
PEST (accessed on 27 February 2023) and
PEST++ (accessed on 12 October 2022) toolsets.
Figure 1B is a schematic description of the bias-variance tradeoff for DA. The observation error model, which is part of many DA approaches, provides an explicit representation and description of observation error and model representation error and allows for increasing “Estimation Variance” in the presence of regularization. Increased “Estimation Bias” is a necessary outcome of regularization in
Figure 1A,B. However, regularization acts to reduce possibilities for overfitting. Increased “Estimation Variance” with regularization is a DA feature that is only present in
Figure 1B and that further reduces the likelihood of overfitting when DA is used. Model solution variability is increased in accordance with, or correlated to, the uncertainty description in the observation error model for data and model representation uncertainty. In other words, DA assumes that data sets and forward models are imperfect, and it provides for explicit description and characterization of data- and model-related uncertainty.
In this paper, we examine the following research questions. What are the potential decision support implications and risks from purely data-driven AI–ML implementations trained on uncertain data? Are there ways to avoid the overfitting of AI–ML models when training uses these derived and uncertain data? Can AI–ML models be included within data assimilation (DA) frameworks to leverage the skill of physics-based models and the efficiency of AI–ML models with the valuable and reliable components of uncertain data sets? We compare select results from an AI–ML study [
6] and a DA [
34] study, which examined similar water resources questions in the same region and were completed and published in 2023, to compare AI–ML and DA implementations in general, to seek approaches to handling data uncertainty as part of model application, and to outline mitigation measures for dealing with data uncertainty risk. Although these studies were published in 2023, the comparison presented here, examining relative AI–ML data uncertainty risk and mitigation using DA, constitutes a new analysis.
2. Methods and Data
The Southwest Research Institute
® (SwRI
®) Internal Research and Development Project “Integration of Process-Driven and Data-Driven Hydrologic Models in an Environment of Process Uncertainty” provided the umbrella project that included the AI–ML [
6] and DA [
34] example implementations as sub-components. The AI–ML model is a data-driven model, and
Figure 1A applies to Ref. [
6]. In contrast, the DA forward model is a process-driven model, and
Figure 1B applies to Ref. [
34]. The comparison of these sub-components to examine data uncertainty risk and DA-based mitigation provides model integration findings and results.
Examples of uncertain water resource data sets are provided in
Section 2.1, along with plausible ranges of expected error and bias in these data sets. Bias, except when applied to PIML enforcement of physical principles, is systematic errors that occur during data gathering and statistical calculations that engender inaccurate, skewed, or erroneous depictions of reality. The specific AI–ML and DA algorithms employed to predict stream discharge are discussed in
Section 2.2 and
Section 2.3, respectively. Goodness-of-fit metrics provide for the quantification of prediction and generalization accuracy and error for AI–ML and DA. The specific metric used to compare accuracy and error between the two sub-component studies is presented in
Section 2.4.
A custom observation error model for stream discharge was developed as part of the umbrella study and is documented in Ref. [
34]. Observation-error models are part of a DA and are not directly applicable to AI–ML; however, they provide an explicit description and quantification of uncertainty in outcome data sets.
Section 2.5 summarizes the development of the discharge observation error model that was used to ameliorate overfitting in the DA and AI–ML models.
2.1. Uncertain Water Resource Data Sets
Increased uncertainty for water resource data sets results when the physical quantity of interest cannot be directly observed or measured. If the specific quantity is unobservable, then it is calculated or simulated using approximate or truncated physical process descriptions and leveraging assumptions based on professional judgment. When calculation and simulation are responsible for estimating quantities of interest, the resulting data may inherit errors from approximations and inaccuracies accrued through the data processing and transformation steps. These biases are compounded with any existing observation error related to measurement precision.
Accuracy considerations are a type of bias, and they include the degree of approximation or fidelity of physical process representation within the calculation of the complete mechanics known to control the physical process from first principles and truncation, which is the order of accuracy expected for a discrete representation of theoretically continuous physics (i.e., Taylor-series expansion truncation analysis). When the physical quantity of interest can be directly observed or measured, there are only error considerations from stochastic precision, or white noise, assuming that the measurement instruments are maintained in a calibrated and validated state, an assumption that is commonly violated in practice.
Three common examples of uncertain water resource data sets, in which the physical quantity of interest is unobservable and in which most data set uncertainty is generated from bias engendered by approximate calculation methods, are those concerning (1) aquifer storage volumes when estimated from water levels observed in wells, (2) evapotranspiration rates when calculated from weather parameters and vegetation type, and (3) river discharge when derived from measurements of stage using a rating curve.
Water levels observed in wells provide point observations of the height dimension for aquifer storage volume calculation. The areal extent of the aquifer geometry is rarely known with much precision. Even if the spatial coverage of the aquifer is known, the total amount of interconnected pore spaces and the spatial distribution of interconnected pore spaces within the aquifer are unobservable and unknown. Consequently, aquifer storage volume is normally a speculative quantity based on the point observation of water levels and assumptions concerning the volume of interconnected pore space across large areas and vertical thicknesses [
27].
The accuracy of evapotranspiration rates calculated from observed weather parameters and the characterization of existing vegetation are highly dependent on the (1) number and type of weather parameters employed and (2) spatial resolution of weather parameter and existing vegetation characterization. The preferred calculation approach is often to use a Penman–Monteith-style equation, which employs four to five weather parameters and which could provide expected errors on the order of five to seven percent [
35]. When temperature is the only observed weather parameter value available for estimating evapotranspiration, then calculated evapotranspiration rates have expected errors on the order of 25% [
6,
36]. Note that the correlation structure of these errors is unknown and may be an important consideration when applying the derived evapotranspiration quantities.
A common way to estimate river discharge is to use a water stage recorder with a derived rating curve in order to transform observed water depth into a discharge estimate. Ref. [
37] provides flow regime-dependent, expected error estimates of ±50–100% for low flows, ±10–20% for medium to high flows, and ±40% for out-of-bank high flows for discharge calculated using a stage measurement combined with a rating curve. River discharge is the uncertain water resources data set used for results comparison in
Section 3.
In terms of
Figure 1B, the three examples of unobservable, estimated, and uncertain water resource data sets provide “Biased Truth Estimate” samples. The “Truth” population is not observable and is uncertain. Consequently, the “Measurement Error”, or observation bias, is unknown.
Stationarity
Time stationarity requires that the statistical properties, and statistical moments, of a series be invariant with time. No change with time in statistical properties is generally too restrictive a condition. Consequently, a relaxed form of stationarity, called weak stationarity, is often used for the analysis of water resource observations. It requires a constant mean and an autocovariance function that depends only on the time difference, or lag, and is independent of the points in time that are differenced [
38,
39], and thus, it only affects the first two statistical moments.
Water resource data are influenced by hydrometeorology and climate, are expected to have trends in time and space, and are rarely stationary. Weak stationarity may be assumed for climate-related observations to facilitate statistical description, and a common duration for assuming weak stationarity is the 30-year Climate Normals [
40]. In many decision-support settings, modeling is used to forecast system behavior under previously unseen future forcings, meaning that the assumed stationarity between the training data set and the predictive outcomes of the model is highly questionable.
Weak stationarity is a common assumption required to calculate Climate Normals and other statistics. Purely data-driven AI–ML models, however, can only learn from training data and are only expected to predict values with reasonable accuracy, which are represented in training data. This is in direct contrast to physics- and process-based models, which contain descriptions of how physical processes work and are designed to work seamlessly with unseen forcings, which fall within the stability and accuracy constraints of the numerical representations. Consequently, non-stationarity poses issues and risks for AI–ML model implementations, especially when training feature sets include weather data and the training weather features are non-stationary in time with the prediction or projection of weather features. Prediction, or projection, features are not used in training but only in prediction or validation. An example of this consideration is training an AI–ML model using features derived from historical weather data and then predicting outcomes with the trained AI–ML model using features derived from future projected weather. We know that future projected weather is highly non-stationary with historical weather [
41]. A workaround for this issue is to devise a scheme to generate future outcomes corresponding to future projected weather and retraining the AI–ML model using future features and future outcomes [
6].
2.2. Machine Learning (ML) and Deep Learning (DL)
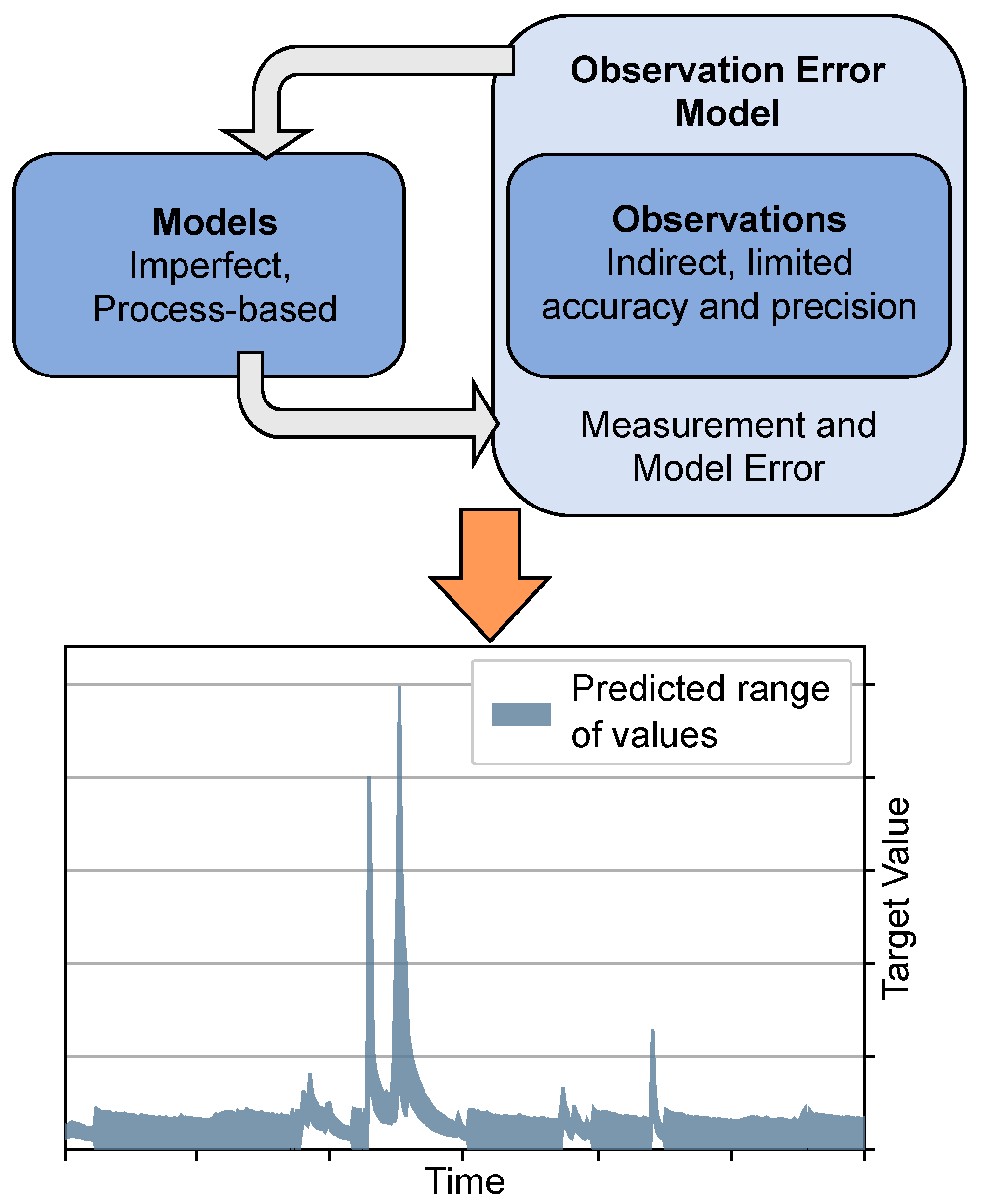
Figure 2 provides a schematic of the workflow for AI–ML from feature engineering, through learning, and then finally prediction. The goal of AI–ML approaches is generalization ability, which is skill in predicting outcomes from unseen feature data sets.
The complete data set, including features and outcomes, is divided into training, testing, and validation components. The training set is used to optimize the internal weight values, and it is where the model learns to predict outcomes. The test set, which is not part of the learning process, provides an initial evaluation of generalization ability and is used to select the “final” model configuration. This approach allows the training of different model iterations on different portions of the data set using techniques like Kfold cross-validation [
42]. The training and testing process is analogous to model calibration for a process-based model. The validation set, which is not part of training and testing implementations, is an independent data set that has never been “seen” by the trained model. It provides an assessment of generalization ability [
1]. Ref. [
2] suggests that the validation component should be 25% of the full data set in data-rich environments. When data scarcity is a consideration, Ref. [
6] suggests that the validation component should be about 15% of the complete data set. There is not a strict rule for the relative validation data set size; however, the purpose of the validation data set is to demonstrate generalization ability, and the validation data set must be large enough to “generally” describe the complete data set.
A common-sense baseline should be used for DL models to evaluate the generalization skill because of the risk of overfitting and the inherent assumption of “perfect” data in
Figure 1A. The baseline provides a simple means to identify whether data sets are sufficient in information content to learn correlations between features and outcomes. If the trained DL model cannot improve on the pre-determined baseline, then the data are imperfect; the model cannot be trained to effectively learn the patterns among features and outcomes, and it cannot produce generalized predictions. The optimal method to improve generalization ability is training on more, or on improved, data so that the trained model can improve relative to the independent baseline. Noisy or inaccurate data impair generalization ability and thus the ability of a model to improve on the baseline [
1].
2.2.1. Long Short-Term Memory (LSTM) Networks
Long short-term memory (LSTM) networks are one of the AI–ML algorithms used in the Ref. [
6] sub-component study, and they are the DL method used here for the comparison of stream discharge predictions. LSTM networks are a DL implementation because they can have multiple layers, which denotes a deep structure. LSTM networks have memory cells that allow them to learn to forget and retain state information [
43,
44]. The ability to use time series, or sequences, as inputs and to predict corresponding time series outputs differentiates LSTM from other AI–ML algorithms. The explicit incorporation of time series provides for a representation and learning of system dynamics. The most common time sequence- and LSTM-related task is forecasting, predicting what will happen at the next interval in the time series [
1].
Here, LSTM implementation follows Refs. [
45,
46] and is an example of the Entity-Aware-LSTM (EA-LSTM) approach of Ref. [
46]. The reader is referred to these sources for details of this LSTM algorithm. The reader is also referred to Ref. [
6] for details of the application of AI–ML algorithms to the example scenario presented in
Section 3.1. Dynamic inputs to LSTM models are time series with a defined sequence length or number of time intervals into the past.
Note that LSTM networks, and all purely data-driven approaches, have the bias–variance tradeoff presented in
Figure 1A. LSTM network complexity can be increased by adding cells to an existing layer or by increasing the number of layers. Both additions function to increase the number of weights, or degrees of freedom, that are optimized during training to produce learning.
2.2.2. Standardization
The statistical learning process, which is the foundation for AI–ML methods, needs a meaningful transformation of data to assist in correlating transformed outcomes with transformed features [
1]. Learning-based algorithms will perform poorly if the training, testing, and validation data sets are not transformed to be like standard, normally distributed data, i.e., with zero mean (
) and unit variance (
where
is the standard deviation) [
1,
2,
47]. This transformation is called standardization, and standardization is a form of regularization. Standardization implicitly enforces weak stationarity requirements when time series, or sequence, values are used in the AI–ML implementation as features and outcomes [
6].
Power transforms are an advanced standardization approach that attempt to map data from any input distribution shape to close to a Gaussian shape [
47]. A more complex distribution shape may require the representation of more than the mean and variance and thus may require the assumption of strict stationarity, rather than only weak stationarity. Ref. [
6] found that power transform performed better for precipitation and stream discharge data sets because these quantities are generally represented with non-Gaussian distributions like extreme value distributions. Additionally, Ref. [
6] suggests creating a synthetic future data set of outcomes using physics- or process-based model simulation results using synthetic future forcing data sets and re-training (and re-validating) AI–ML models using the synthetic future data sets for the prediction of future outcomes influenced by climate. Future climate is expected to be non-stationary relative to historical climate, and re-training and re-validating AI–ML models using synthetic future data sets provides a means to robustly address non-stationarity between historical and future climatic conditions.
Additional details of standardization approaches used for the AI–ML sub-component study are available in Ref. [
6].
2.3. Data Assimilation (DA)
DA seeks an optimal combination of numerical model simulations and noisy observations. Note that the correctness or otherwise of the model is not assumed. It uses a “forward” model to project, or simulate, forward in time for unobserved quantities. Measurements are combined with simulation predictions to derive updated system states that assimilate the “best” components of observations and model results while accounting for uncertainties and bias in both models and observations. The history matching of simulated values to observations, i.e., calibration or training, provides a constraint on the optimal predictions for unobserved values.
Figure 3 displays a conceptual schematic of the DA workflow and results.
Conceptually, DA employs Bayes’s theorem, Equation (
1), to provide assimilation conditional upon the history matching skill, and it identifies how to rigorously update prior information, i.e., model projections, as new observations become available [
11]. Equation (
1) provides a framework for the quantification of model-parameter uncertainty, where
k represents model parameters,
h are observations or targets, and
() denotes a probability distribution. Consequently,
is the prior parameter probability distribution,
is the likelihood function, and
is the posterior parameter probability distribution. The posterior parameter probability distribution
is the focus for DA approaches seeking calibration, and it is the probability distribution of model parameters updated via conditioning to observations [
5].
2.3.1. Ensemble Methods
The DA algorithm used in the Ref. [
34] sub-component study is the iterative ensemble smoother (iES) algorithm, which is an ensemble method [
48,
49]. The specific iES algorithm is the iES toolset in PEST++, PESTPP-IES [
5,
10,
49]. PESTPP-IES provides inverse-style approaches to the estimation of uncertain model inputs and the deduction of optimal model forcing, and it provides “calibration constrained uncertainty analysis”.
The advantages of the iES approach are that it can cope with non-linearity in the relation between model inputs (i.e., parameters) and outputs while seeking samples of the posterior parameter probability distribution (
in Equation (
1)). Additionally, it is relatively computationally efficient in very high-dimensional settings, where the computational cost of evaluating the forward model can be high [
49].
PESTPP-IES simultaneously adjusts an ensemble of parameter realizations and uses an ensemble of innovations to approximate the posterior parameter ensemble. Innovations are the differences between observations, or targets, and simulated values. iES algorithms provide the explicit incorporation of a wide range of observation error models into the assimilation process, or model calibration. The available observation error model types include standard error specification, spatially and temporally correlated errors, and the use of inequality-type/uniform noise models.
2.3.2. Observation Error Models
Observation error models can be included in assimilation to account for the uncertainty inherent to observations, uncertain forward model inputs, and limitations in the fidelity of the numerical model representation with reality [
11]. The observation error model is part of the
term in Equation (
1). Observation uncertainty includes a consideration of expected measurement errors. The model representation error accounts for different forward model representations of reality from what is actually observed during measurement. For numerical weather prediction and oceanographic forward models, numerical representation errors are often due to scales and physical processes that are unresolved by either the numerical model or the measurement [
11,
50].
Figure 1B schematically depicts the function and impacts of observation error models in DA. They add variability, representing uncertainty, to data and model results. The extra variability and uncertainty are represented with “halos” in
Figure 1B, and they serve to increase the “Estimation Variance”, which reduces the likelihood of overfitting. Consequently,
Figure 1B provides a slightly different optimization of the bias–variance tradeoff from
Figure 1A because we are accepting an ideally small increase in estimation bias for “Model Space with Regularization” relative to “Model Space” and adding in additional variance, the relatively larger “Estimation Variance” in
Figure 1B, to account for model and data uncertainty. In this way, DA with observation error models seeks to limit bias in and minimize the variance of the posterior parameter distribution,
in Equation (
1), while still explicitly addressing knowledge limitations, i.e., the “Biased Truth Estimate” sample in
Figure 1B, is not an accurate description of the “Truth” population. As with AI–ML models, bias is generated through overfitting in the presence of unaccounted-for and unrepresented uncertainty.
Implementation of observation error model functionality in PESTPP-IES is the inclusion of realizations of additive observation uncertainty (i.e., added to observed values) with prior parameter realizations in the forward model. Note that a different observation error model with an independent uncertainty model can be used for each datum or observation type and location. The purpose of adding some variability to observations is to explore posterior parameter uncertainty and assist in describing the predictive uncertainty of the model. Additive observation uncertainty involves the inclusion of a slightly different “target data set” in each adjustment of each parameter realization during the parameter adjustment process [
5].
These slightly altered noisy observation realizations allow PESTPP-IES to analyze prior-data conflict [
51,
52,
53]. Prior-data conflict is simulated history matching target values that do not statistically agree with observed values plus additive observation uncertainty. Statistical disagreement indicates the presence of additional and unaccounted-for sources of uncertainty and bias such as model error. It implies that unlikely parameter values or extreme parameter combinations are needed to reproduce “conflicted” observations. Extreme parameter estimates are assumed to be “biased” estimates and continuing the training or calibration, i.e., parameter adjustment, process when prior-data conflicts are present will generate parameter bias and forecast bias. The removal of prior-data conflicts prevents the propagation of representation error into posterior parameter uncertainty [
5].
The range of expected, or acceptable, variance allowed by an observation error model without generating a prior-data conflict is important. If the range is too large, parameter values have minimal constraint or conditioning on assimilation, which results in high posterior parameter uncertainties and high variance in the posterior parameter distribution. If the variance, or range of values, is too small, too much accuracy and precision are allocated to observations, i.e., the data set, and overfitting will occur where the posterior parameter distribution is too narrow and is biased. Prior-data conflicts provide an automated means to optimize the bias–variance tradeoff for observation error models and DA.
2.4. Goodness-of-Fit Metric
DA provides the optimal combination of forward model results and observed values. Optimality is determined using a goodness-of-fit metric. Similarly, in AI–ML analyses, models are trained to best reproduce data using a score value representing the goodness-of-fit between estimated values and testing data sets. To compare results between DA and AI–ML implementations,
from Equation (
2) is used as a goodness-of-fit metric.
ranges from
to 2.0 with 2.0, representing “perfect” fit.
is the sum of (1) Nash–Sutcliffe efficiency (
) [
54] and (2) Kling–Gupta efficiency (
) [
55]. Refs. [
6,
34] provide additional details and equations related to
.
2.5. Discharge Uncertainty Envelope
Ref. [
34] developed an advanced observation error model, which is also a discharge uncertainty envelope, designed specifically for discharge data sets that are estimated from depth observations using a rating curve. This uncertainty envelope accounts for the flow regime-dependent expected error, and it accounts for larger relative error expectations for low flows (i.e., expected errors are ±50–100% for low flows, ±10–20% for medium to high flows, and ±40% for out of bank high flows from Ref. [
37]). It provides a rating curve representation error component in addition to the typically expected measurement error and forward model representation error components in observation error models. Note that the discharge uncertainty envelope is an observation error model and not an estimator of measurement error or accuracy for gauging stations. The purpose of an observation error model, see
Figure 1B, is to facilitate the optimal combination of forward models and observations and to avoid bias in and minimize the variance of the posterior parameter distribution.
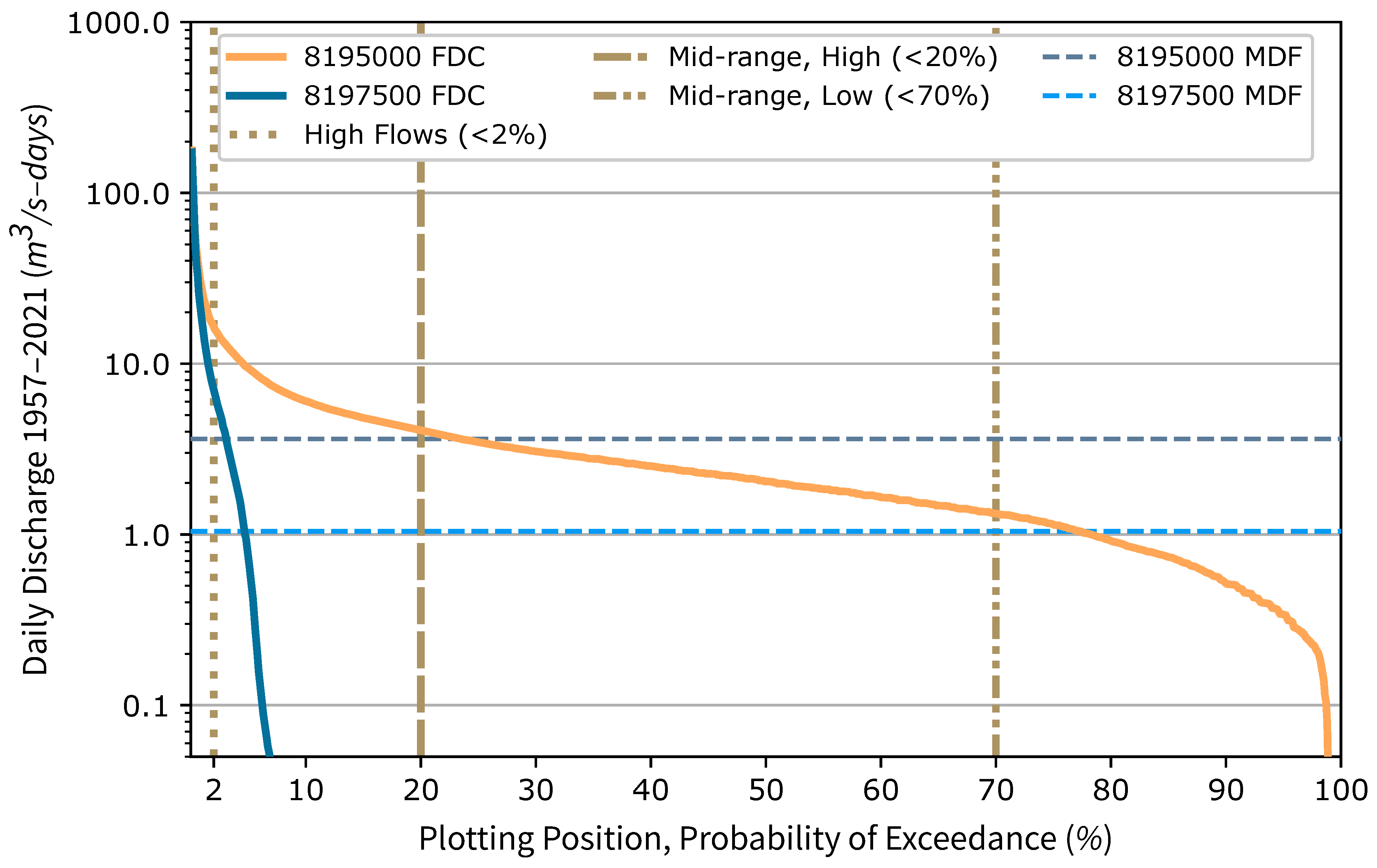
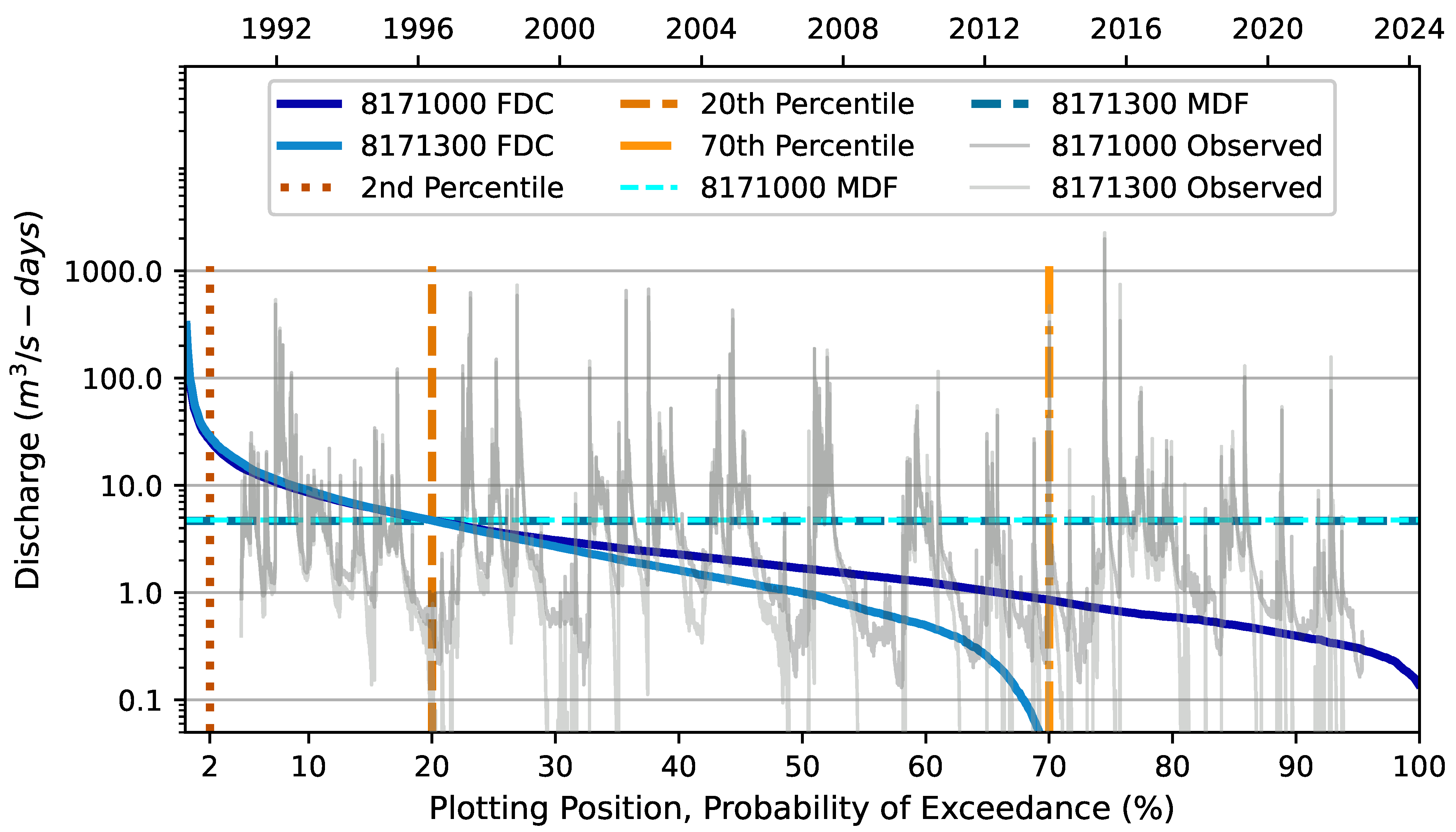
To create the discharge uncertainty envelope, an off-line Monte Carlo model generates realizations of synthetic discharge from the gauging station time series. For each time interval in the series, the synthetic discharge is determined by (1) classifying the flow regime for the gauging station discharge and (2) applying a stochastic error term determined using a random variate multiplied by the largest relative error expected for that flow regime. Flow duration curves (FDCs) [
56] provide flow regime classification. For example, if the gauging station discharge at that time interval is in the low flow regime, then the error value to which the random variate is applied, would be 100% of the low flow threshold discharge.
Ref. [
34] used 1000 synthetic discharge realizations and calculated the root mean square error (RMSE) from the 1000 synthetic discharge realizations and the gauging station discharge for each time series interval. The RMSE for each time series interval provides the observation error model for use in PESTPP-IES, which is the specification of the range of the additive observation uncertainty magnitude for each time series interval observed discharge. Ref. [
34] examined unbiased and biased random variates. Unbiased variate values were obtained from sampling from the standard normal distribution (
= 0.0 and
= 1.0). Biased variate values were derived by sampling from a shifted normal distribution (
= 1.0 and
= 1.0).
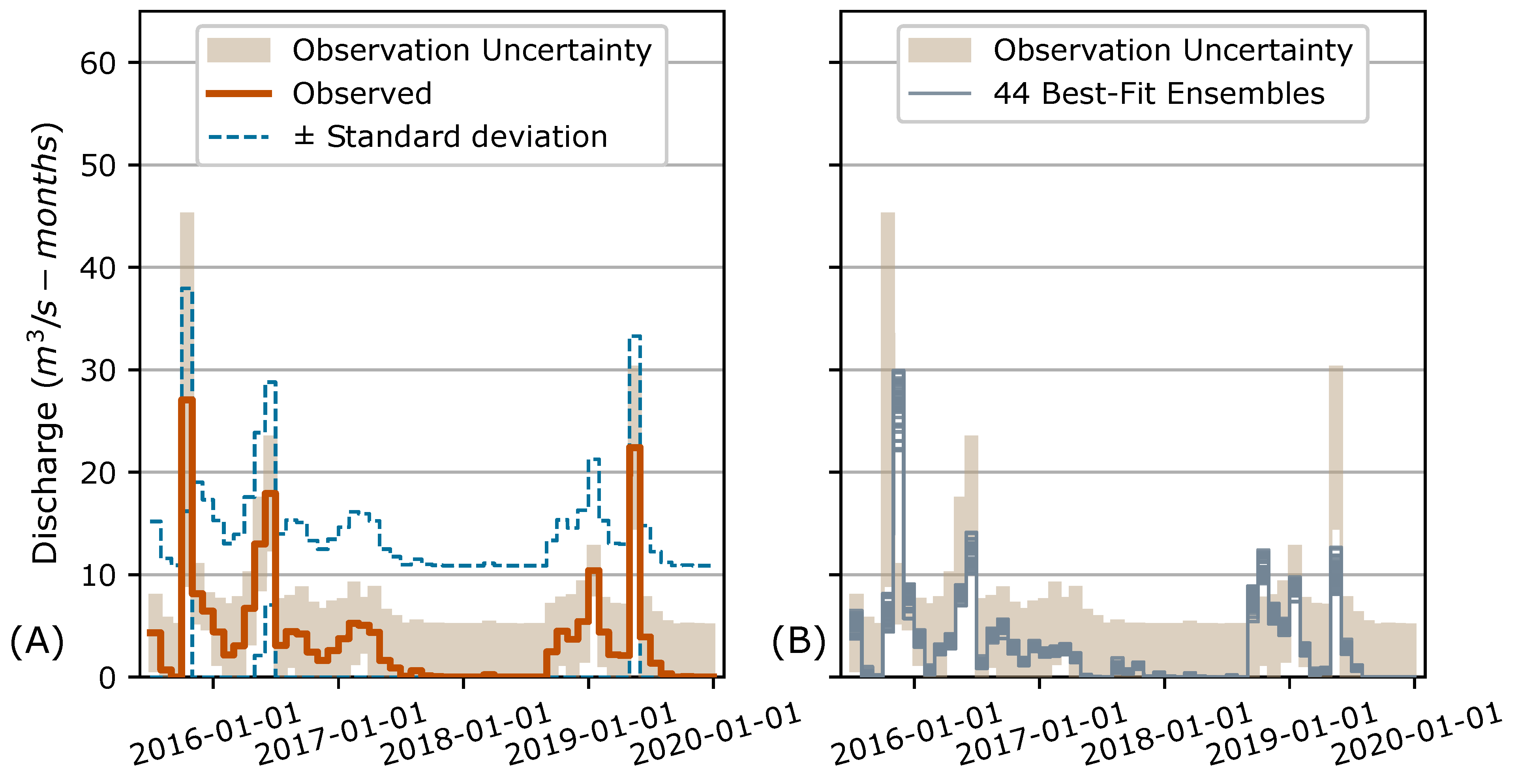
The
goodness-of-fit metric is also calculated for each synthetic discharge realization compared to the gauging station discharge time series. Maximum and minimum
values are used as thresholds for estimating the information content in the discharge record factoring of the uncertainty description with the observation error model. If calibrated model results produce a
value that exceeds the maximum threshold, that is good, but it is possible that the model is overfitting if an inverse-style calibration enforces parameter selection to achieve history matching beyond the maximum threshold. The minimum
value provides a threshold that can be used to constrain the selection of best-fit parameter ensembles and thus the ensemble of best-fit models. An ensemble of models generates the range of values shown in
Figure 3.
Ref. [
6] employed the discharge uncertainty envelope to develop a common-sense baseline for an AI–ML implementation. This common-sense baseline is an acceptable range of
values obtained from discharge uncertainty envelope analysis. The baseline range has an upper threshold and a lower threshold. Conceptually, the lower threshold represents the “worst” fit between synthetic and observed discharge that can be obtained by factoring in the amount of expected error present in observed river discharge by flow regime. A DL model can demonstrate skill by producing validation set
values that equal or exceed the lower threshold. The upper threshold represents the “best” fit between synthetic discharge and observed discharge.
values above the upper threshold suggest the possibility of overfitting. All models that provide
greater than or equal to the upper threshold should be considered equally skilled [
6].
4. Discussion
Select results from two studies completed and published in 2023 were compared and contrasted to examine research questions pertaining to AI–ML risk from uncertain data, ways to mitigate these risks and avoid overfitting models during training, and approaches to incorporating AI–ML to DA frameworks in order to explicitly address data uncertainty concerns. The AI–ML results were generated via an EA-LSTM model that predicts daily Frio River discharge at station 8197500. The DA results came from the ensemble-based DA of a process-based model to project Blanco River discharge at station 8171300. Both gauging stations are located just downstream of the BFZ Edwards Aquifer Recharge Zone, which means both stations have low flow discharges from 80 to 90% of the time. Observations of low flows were expected to have the greatest relative uncertainty, ±100%, at both stations. Consequently, the example results are estimates for river discharge observations at sites with an expected high degree of uncertainty.
What are the potential risks from AI–ML implementations trained on uncertain data? One risk from uncertain input and outcome data sets is that the information content in training data sets is insufficient to learn reliable and robust correlations among inputs and outcomes. The negative consequence that is likely to occur from poor data quality is assuming that the trained model provides predictive ability and generalization skill and using model predictions to guide decision making.
The best way to improve an AI–ML model is to train and validate it on more and better data [
1]. Data sets should always be cleaned to remove obvious errors and corruptions and then extensively analyzed prior to use in AI–ML model training, or physics-based model calibration, to produce “better” data. Cleaning and filtering does necessarily result in “less”, rather than “more”, data. Uncertainty means a lack of knowledge, which is not equivalent to specious information. Specious data will produce phantom correlations, rather than learning, and all data sets should be cleaned to remove errors before they are analyzed for uncertainty. In short, all models adhere to the “garbage in, garbage out” principle, and uncertainty is not equal to “garbage”.
It is fairly easy to generate “more” data using sampling approaches. With uncertain and un-observable data sets that provide a “Biased Truth Sample”, see
Figure 1B, sampling-based approaches will only reinforce the biases and uncertainties present in the “Biased Truth Sample”. “Better” data in this context are independent samples that provide descriptive statistics that are similar to the underlying population statistics; “better” data adequately represent “Truth” in
Figure 1. For uncertain and un-observable data sets, like stream discharge and others discussed in
Section 2.1, there is not a foreseeable means to immediately collect “better” data. Consequently, the explicit description and treatment of inherent uncertainty for these data sets needs to be used in and propagated through model implementations.
A common way to validate AI–ML generalization skill is a comparison to an independent common-sense baseline [
1]. If the trained model demonstrates improved prediction skill using independent data sets, relative to the common-sense baseline, then the model has demonstrated generalization ability. This type of comparison is used in
Section 3.1 to demonstrate generalization skill for the AI–ML example model implementation. The common-sense baseline was derived from discharge uncertainty envelope analysis of station 8197500 data sets as the lower
threshold. Demonstrating generalization ability proves that the model has learned reliable and robust correlations and can be used, cautiously, for decision support.
The primary risk from uncertain data is overfitting during the training of AI–ML estimators. Overfitting occurs when the model is over-optimized to produce the “best” goodness-of-fit metrics on training and testing data and subsequently demonstrates limited generalization skill when applied to an independent validation set because it has learned biases unique to the training and testing data set. The negative consequence of overfitting is erroneous confidence in AI–ML predictions that were trained to reproduce measurement error and calculation uncertainty in addition to the estimate of the physical quantity of interest. This type of erroneous confidence in model predictions leads to sub-optimal, and in some cases inappropriate, water resource management.
AI–ML algorithms are especially prone to overfitting because it is typically easy to increase model complexity using hyperparameters, increased cells or neurons per layer, and by increasing the number of layers. The complexity of the EA-LSTM model in the
Section 3.1 example can be increased during training by increasing the number of cells per layer, i.e., by modifying a hyperparameter. Increased model complexity generally works to reduce “Model Bias” and increase “Estimation Variance” in
Figure 1A, and it functions to encourage overfitting. Regularization, on the other hand, is a reduction in model complexity, which works to increase “Model Bias”, decrease “Estimation Variance”, and discourage overfitting.
Ease in increasing model complexity is, however, one of the fundamental strengths of AI–ML algorithms. For physics-based models that implement calculations on a three-dimensional mesh, increasing model complexity requires re-meshing, which can take weeks or even months. This time requirement for implementing increased complexity in physics-based models is one part of the “complexity penalty” [
6]. The other part of the complexity penalty is that an increased number of parameters in a physics-based model typically increases the size of the matrices involved in the iterative, matrix inversion-based solution for each time step. This can generate a non-linear increase in the computational burden for physics-based model predictions. AI–ML algorithms, in contrast, only use gradient descent methods as part of training and typically have a relatively smaller increase in the computational burden with increased model complexity for trained model predictions. Note that increased model complexity for AI–ML and physics-based approaches requires an increase in the number of computations and, thus, in the computational burden for the training and testing of AI–ML and for the inverse-style calibration of physics-based models. An increase in the computational burden for training and calibration is directly proportional to the increase in the number of adjustable weights for AI–ML and in the number of adjustable parameters for physics-based models.
Are there ways to avoid the overfitting of AI–ML models when training uses uncertain data? Regularization techniques and an independent validation data set, which has been pre-analyzed for uncertainty and information content, are two ways to avoid overfitting when working in the traditional data-centric environment of
Figure 1A. The independent validation set should be an approximately 15%, or greater, proportion of the complete data set [
6]. The AI–ML example in
Section 3.1 provides a worked example employing the data set regularization technique of standardization and an independent validation set.
The training, testing, and validation of the EA-LSTM model was implemented sequentially within Kfold cross-validation [
42] with an approach that calculated the independent validation set goodness-of-fit for the best-fit, trained model for every iteration within each fold. This approach allowed for the selection of a final trained model with a validation goodness-of-fit between the
thresholds, i.e., ≥0.71
1.33, to avoid overfitting. These thresholds were derived from a discharge uncertainty envelope analysis of station 8197500 data sets, and the upper threshold demarcates the region where the model is likely learning to overfit to the uncertain discharge data set.
PIML is a regularization technique, and regularization provides avenues for counter-acting overfitting to imprecise and noisy training data. Results from physics-based numerical models can be used to provide cleaner, more certain, and improved data sets that embody physics-based principles (i.e., PIML “observational bias” can be enforced to training and testing data sets). PIML “inductive bias” can be used to enforce AI–ML algorithms to structurally produce predictions that are physically justified and physics-informed constraints on loss functions and score evaluation (i.e., the enforcement of “learning bias”) can also reduce the capacity of training to promote overfitting at the expense of generalization ability. Note that PIML will still produce a predicted value for each outcome projection interval, as shown in
Figure 2, and is a
Figure 1A approach.
Can AI–ML models be included within DA frameworks to leverage the skill of physics-based models and AI–ML models with the valuable and reliable components of uncertain data sets? AI–ML can be included within DA frameworks in three ways: (1) as additional observations because AI–ML learns to mimic existing outcome observations, (2) as a forward model after training, testing, and validation are complete, and (3) as the forward model in a training and testing framework that mimics inverse-style model calibration with observation error models.
It should be noted that the inclusion of an AI–ML model within DA is a separate consideration from hybrid forecasting using both physics-based and data-driven models for forecasting precipitation and other climate parameters. Hybrid AI–ML approaches combine data-driven, i.e., AI–ML, and physics-based models to overcome data-driven model limitations and to improve the accuracy and reliability of forecasts. Ref. [
60] identifies how data-driven models can be used to derive augmented forecasts from simulation results from an ensemble of physics-based models. The goal for hybrid AI–ML approaches is to capture diverse patterns in data by leveraging the unique capabilities of the two types of models [
61]. This goal and approach is distinct from DA with uncertain data, which seeks to include enough variability in calibrated, or trained, model projections to account for data uncertainty and model representation error in order to support decision making.
AI–ML seeks to replicate the patterns in the training data set [
8]. Consequently, it is a natural candidate to provide additional “observations”, especially for stationary conditions and for missing values within an existing series. Ref. [
27] provides an example of incorporating a AI–ML model, which provides projected values for missing observations, into a DA framework. Ref. [
62] presents an implementation of hybrid ML techniques to overcome incomplete stream discharge data sets for discharge simulation in under-monitored river basins. Although the Ref. [
62] implementation provides for additional “observations” for incomplete stream discharge data, it is not a DA implementation.
DA algorithms need a forward model. It can be a physics-based, empirical, statistical, or AI–ML model. Consequently, a trained and validated AI–ML model can provide a forward model for DA that seeks to compute the best possible estimate of a model state at a given point in time. An advantage of AI–ML approaches is that they have no “complexity penalty” and can perform well for complex problems with the same amount of model set-up as needed for a relatively simple problem. For physics-based models, the amount of effort required to create the model typically increases with complexity [
6,
7,
8]. Kernel-based regression methods, like Gaussian processes, provide an AI–ML approach to embed physics in ML and to provide “simple” implementations for complex problems [
7]. Ref. [
25] provides a stream discharge forecasting implementation that uses an AI–ML algorithm as the forward model within a DA; however, the observation error model concept is not used in this DA to increase the variance of future state predictions to account for model and data uncertainty.
It could also be possible to train an AI–ML model using a DA framework that implements ensemble methods for the inverse-style estimation of weights, including an observation error model. Kfold cross-validation algorithms could be modified to provide the iterations, i.e., folds, and realizations, i.e., Kfold iterations, needed for ensemble methods. Stochastic additive uncertainty could be added to outcomes for each realization to implement observation error models. The primary departures from Kfold training would be that an ensemble of best-fit models would need to be produced to provide the range of values shown in
Figure 3, and the number of realizations would need to be set so that the additive uncertainty from the observation error model produces “Estimation Variance”, rather than “Estimation Bias” in
Figure 1B.
From the perspective of applying science in the real world, rather than in theoretical or completely controlled laboratory-like settings, the advantage of DA is the optimization of the bias–variance tradeoff for training, or calibration, and prediction through an explicit description of expected data- and forward model-related uncertainty, i.e., see the uncertainty “halos” in
Figure 1B. Science is typically applied to support decision making in the presence of uncertainty. A single deterministic, discrete, and definite projection or prediction provides insufficient decision support because knowledge is limited. Additionally, forward models developed with limited budgets and observations made in dynamic field settings will be imperfect. These limitations and imperfections mean that predicted outcomes should be presented as a range of values, as shown in
Figure 3, to support decision making. The main advantages of bringing AI–ML into a DA framework are the explicit incorporation and description of model representation error and observation error in consideration of the bias–variance tradeoff for the posterior parameter, or weight value, distribution.
Future Work
Future work will focus on the incorporation of AI–ML models as the forward model in DA implementations. Two specific areas of interest are (1) the development of the representation error components of observation error models for AI–ML models that are applicable to future conditions and (2) the replacement of complex physics-based forward models with AI–ML approaches. The observation error model used in this paper was developed from observations [
34]. For future conditions, observations are unavailable, and the expected representation error needs to account for non-stationarity. Currently, our working hypothesis is that the process- and physics-based simulation of expected future conditions, combined with the analysis of changes between historical and future simulations, can be used to develop representation-error components of observation-error models for future conditions. This, however, requires that future model forcing be projected with sufficient accuracy to provide for a meaningful process- and physics-based simulation of unknown future conditions.
The replacement of complex physics-based forward models with statistical learning approaches, generally, is an active and apparently successful area of research, as evidenced by PIML [
3,
7] and hybrid AI–ML climate and precipitation forecasting approaches [
60,
61]. The development of the representation error component of the observation error model is the condition limiting replacement when the incorporation of uncertainty is important for decision support.
5. Conclusions
The primary risk from AI–ML implementations trained on uncertain data is that AI–ML models, without a demonstrated and relevant generalization ability, will be used to support decision making. The likely negative consequence is that unsupported confidence in model predictions will generate inappropriate and misguided water resource management.
Overfitting occurs when a model, either AI–ML or physics-based, is trained or calibrated to over-optimize prediction skill on training and testing data sets at the expense of generalization skill for independent data sets. A strength of AI–ML approaches is that it is trivially easy to increase and decrease model complexity. Regularization approaches function to decrease model complexity. As shown in
Figure 1, increased model complexity decreases “Model Bias”, increases “Estimation Variance”, and tends to promote overfitting. Regularization increases “Model Bias”, decreases “Estimation Variance”, and tends to counteract overfitting.
Within the data-centric learning framework of
Figure 1A, a common-sense baseline can be used for the confirmation of generalization ability, and regularization approaches can reduce the likelihood of overfitting. However, the way to improve an AI–ML model is to use a larger data set that provides a representative sample of “Truth” in
Figure 1A; in other words, AI–ML model improvement comes from more and better data.
Inherently uncertain and un-observed water resource data sets, like stream discharge estimated from stages with a rating curve, provide a unique challenge to regression-style AI–ML because these data sets provide a “Biased Truth Sample”, shown in
Figure 1B. We know that significant “Measurement Error” exists that separates the “Biased Truth Sample” from “Truth”, but we cannot quantify “Measurement Error” without better data. In the near term, we are stuck with the “Biased Truth Sample” because there is not an immediate route to more and better data.
DA algorithms and techniques provide for explicit description of data- and model-related uncertainty and the propagation of uncertainty in simulation results. The observation error model conceptualization in DA is a description of the expected measurement error from data uncertainty and model representation error from inherent model limitations. The discharge uncertainty envelope, discussed in
Section 2.5, is an observation error model for stream discharge target observations. It is used in the purely data-driven AI–ML implementation, presented in
Section 3.1, to provide a common-sense baseline for a demonstration of generalization ability and to estimate the information content in discharge target observations in order to prevent overfitting.
AI–ML models can also be directly incorporated into DA frameworks to provide additional “observations” for assimilation or as a forward model. DA combines forward model results with observations for the purposes of prediction of a future system state and the inverse-style estimation of model parameters. For prediction, a trained and validated AI–ML model would provide a forward model that would make predictions that would be subsequently updated via assimilation with observations. For calibration or training, AI–ML internal weight values could be optimized using Kfold cross-validation modified to implement ensemble methods.
DA methods provide mitigation for AI–ML risks by explicitly characterizing and subsequently propagating uncertainty to predictions. Purely data-driven AI–ML has to assume that training and testing data sets adequately represent “Truth” in
Figure 1. In contrast, DA provides a modified bias–variance tradeoff, as shown schematically in
Figure 1B, where regularization increases “Estimation Bias”, but the additional uncertainty introduced via the observation error model, see “halos” in
Figure 1B, increases “Estimation Variance”. The goal of this tradeoff is to increase solution variability in accordance with data- and model-related uncertainty and to propagate this uncertainty through training or calibration in order to produce an ensemble of best-fit models, which provide a range of predicted values, as shown in
Figure 3.