Research on Failure Pressure Prediction of Water Supply Pipe Based on GA-BP Neural Network
Abstract
1. Introduction
2. Methodology
2.1. BP Neural Network
- (1)
- Forward propagation process
- (2)
- Back propagation of error
2.2. Principles of Genetic Algorithms
- (1)
- It starts from the solution set of a class of problems, covers a wide range, and facilitates global optimization.
- (2)
- Multiple schemes can be evaluated, and the algorithm itself is easy to parallel.
- (3)
- Only the adaptive function is used to evaluate the individual, and the application range is wide.
- (4)
- The probability transfer rule (probabilistic transfer rules are a way of describing the probability of state transfer for stochastic processes) is used to guide the search direction.
- (5)
- It has the ability to self-organize, self-adapt, and self-learn.
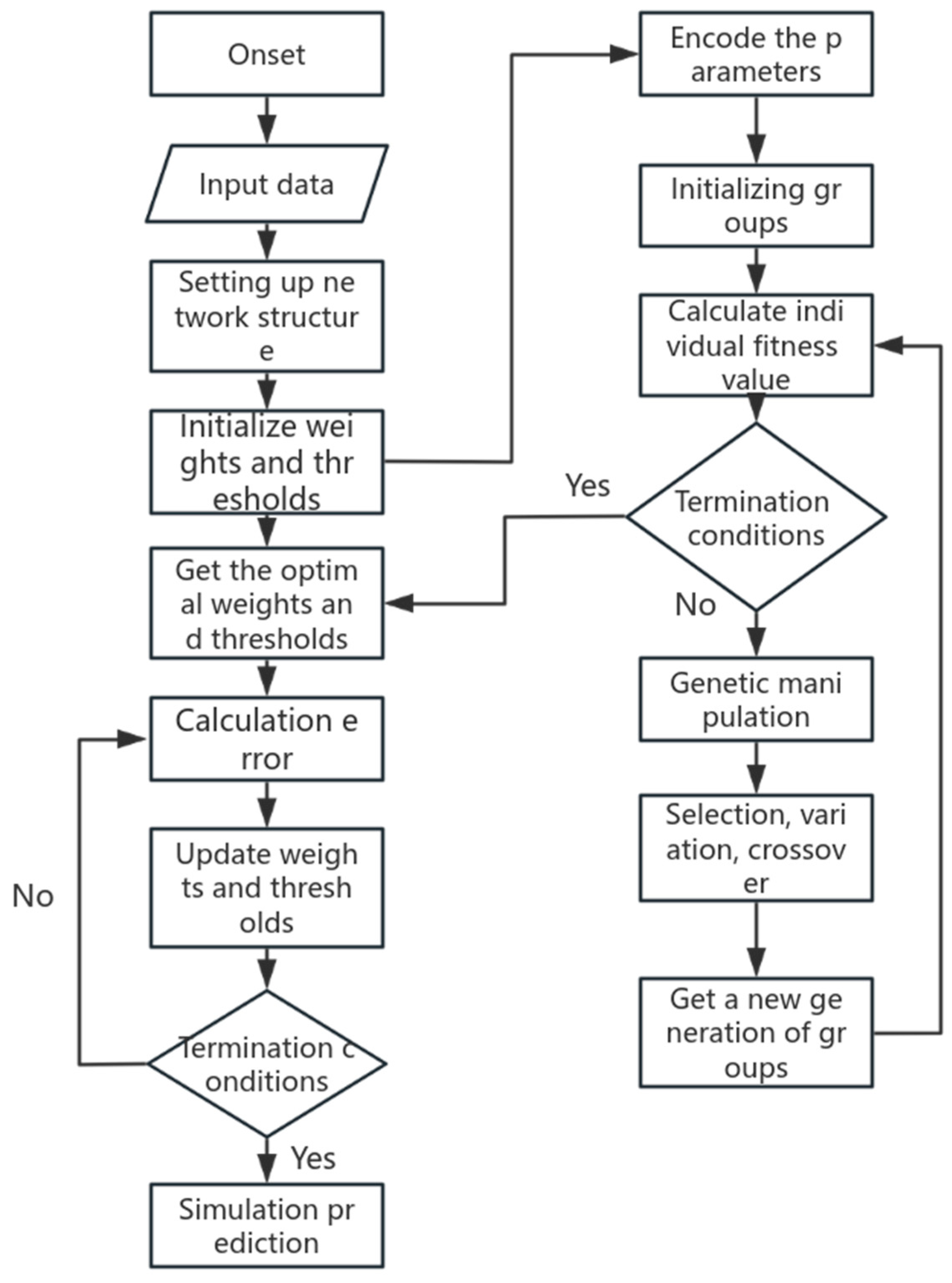
2.3. Establishment of GA-BP Neural Network Model
3. Case Analysis
3.1. Data Selecting
3.2. Model Construction
3.2.1. Construction of BP Neural Network Model
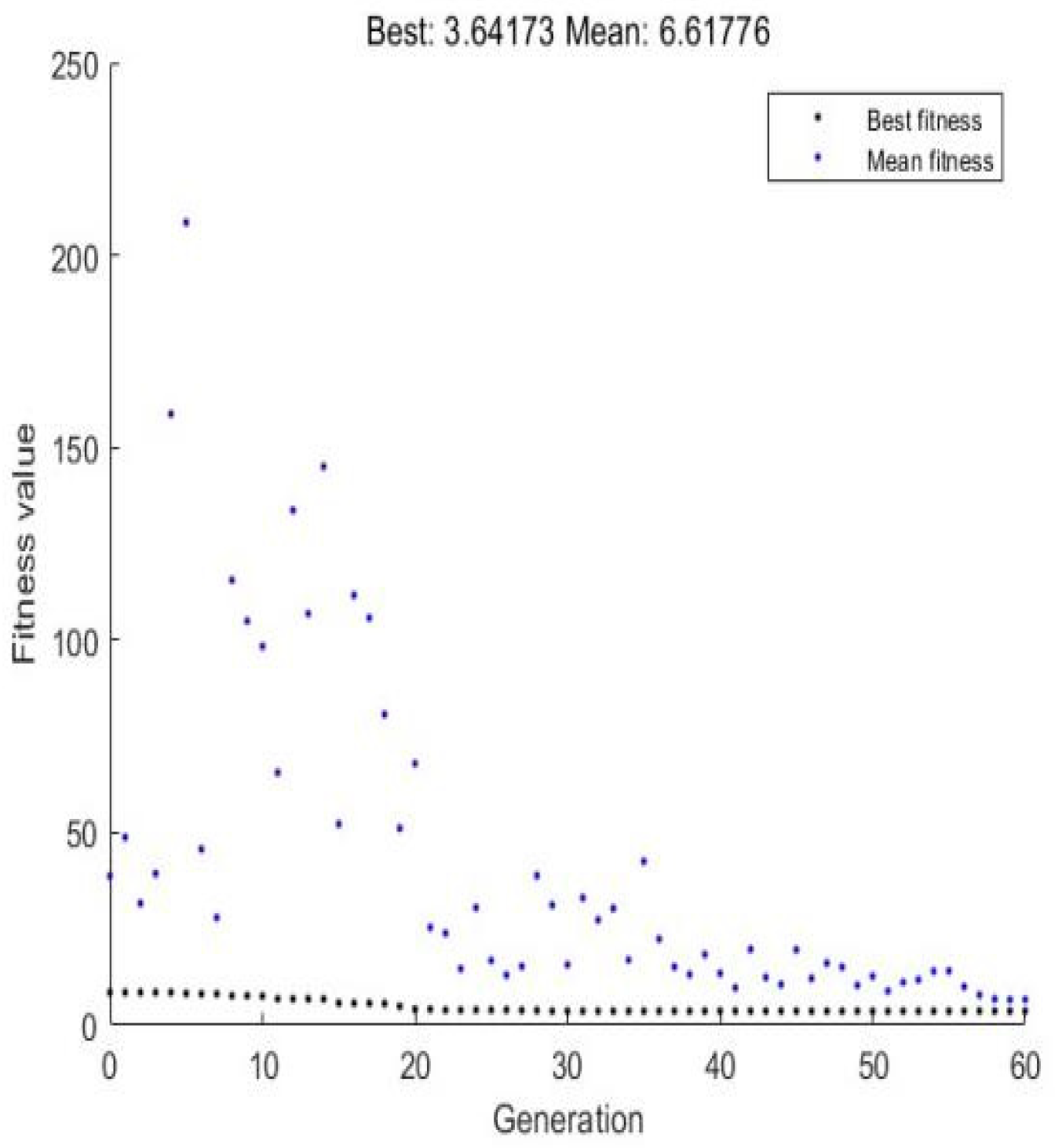
3.2.2. Parameter Selection of GA Algorithm
4. Results
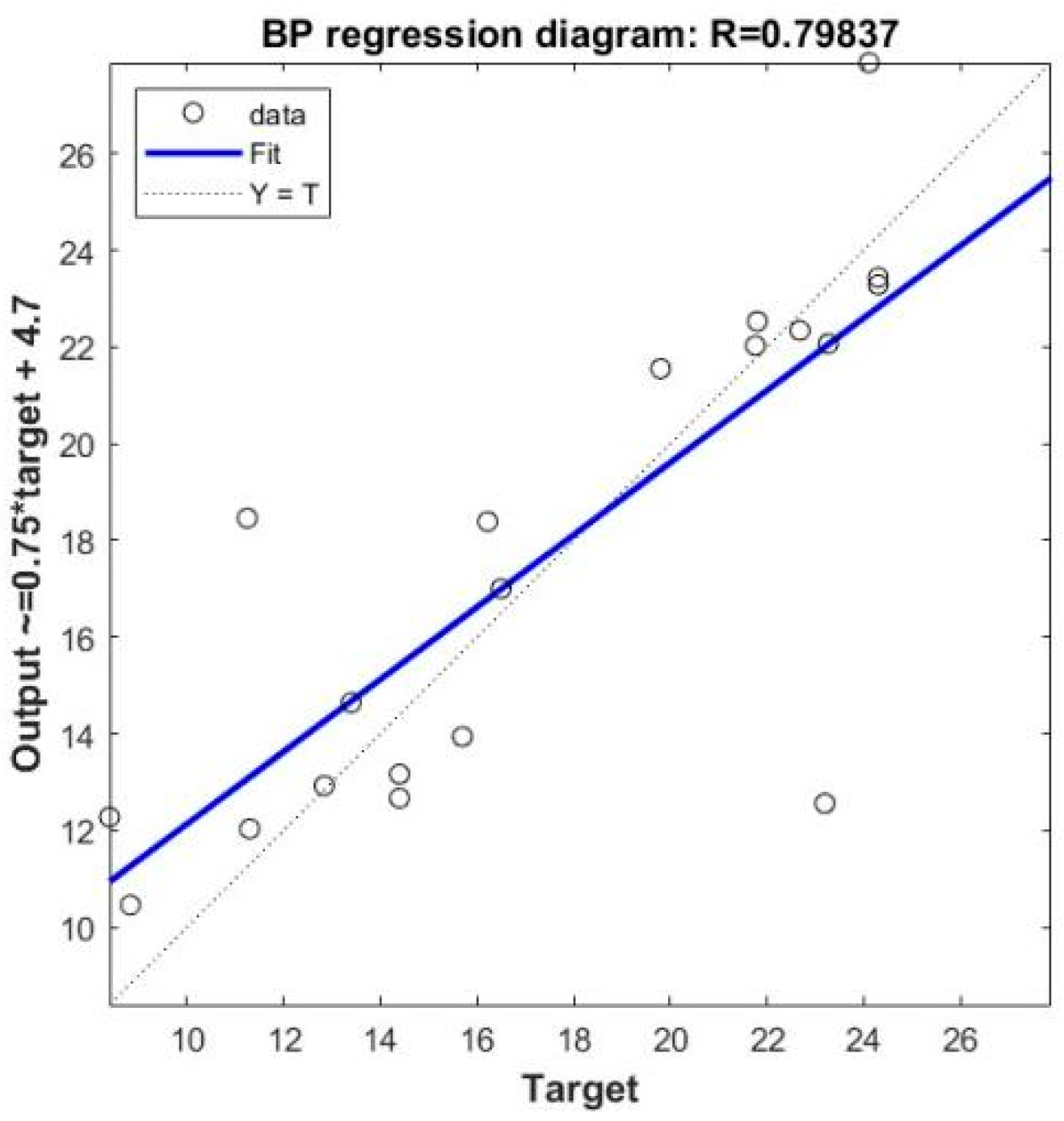
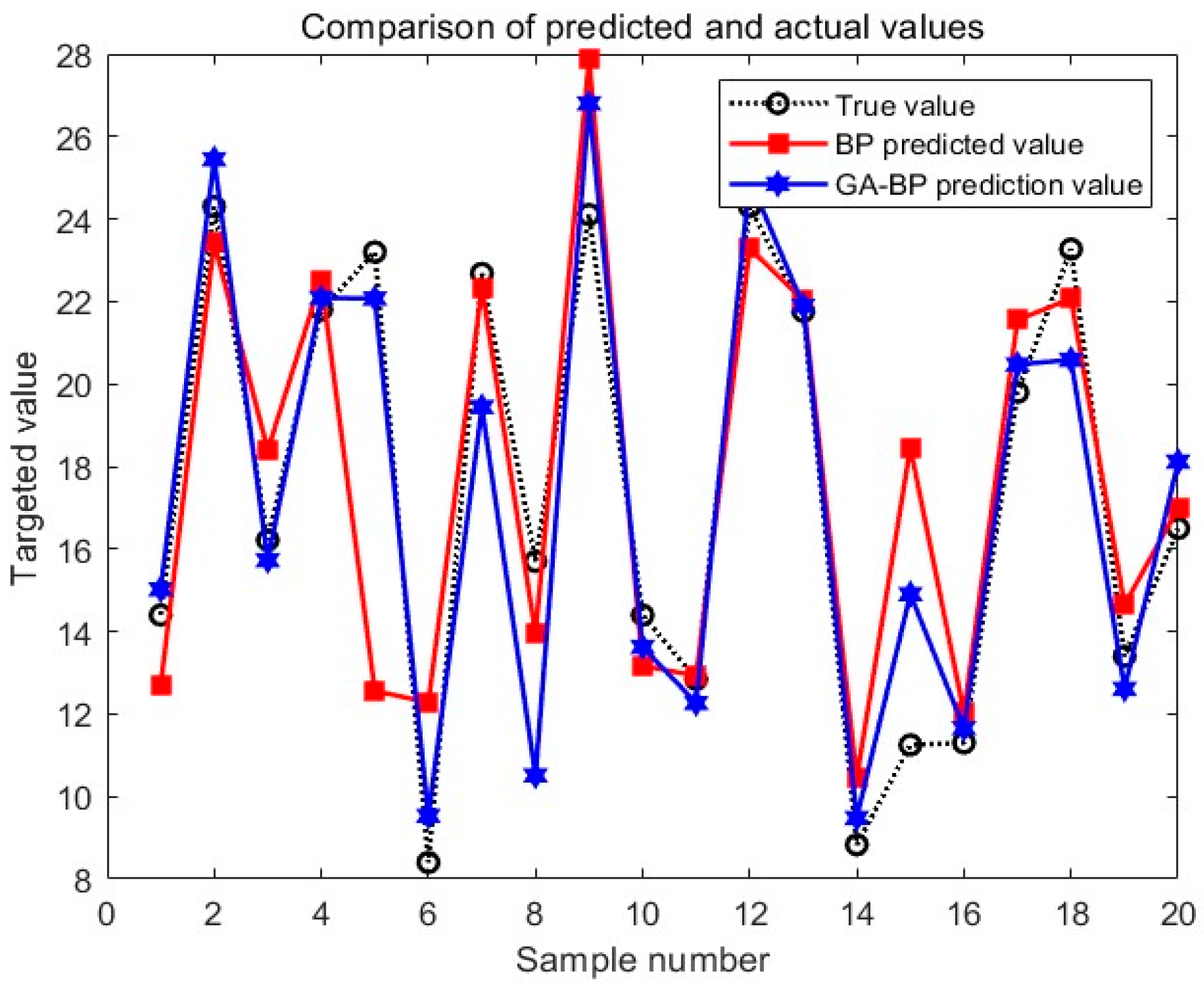
5. Model Performance Analysis
6. Conclusions
- When setting parameters for the BP neural network, since the initial weights and thresholds of the BP neural network are randomly set, resulting in certain prediction errors, introducing the GA algorithm to optimize the weights and thresholds of the BP neural network can effectively reduce errors and improve the prediction accuracy of the model.
- This paper uses seven factors including the pipe diameter, wall thickness, tensile strength, yield strength, defect length, depth, and width as the failure factors of the pipeline. The prediction accuracy of the model is 91.15%. Therefore, the GA-BP neural network optimization algorithm proposed in this paper can be used for pipeline failure prediction research.
- Since training the network requires a large amount of data support, the accuracy of the data has a significant impact on the prediction accuracy of the model. The method proposed in this paper is only a preliminary study based on the available data. To improve the prediction accuracy of the model, further research is still needed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, T. Research on Pipe Burst Risk Prediction Model of Water Supply Pipe Network Based on BP Neural Network. Master’s Thesis, Chongqing University, Chongqing, China, 2019. [Google Scholar]
- Zhang, H. Research and Application of Pipeline Risk Evaluation in Urban Water Supply Networks. Master’s Thesis, Changán University, Xi’an, China, 2020. [Google Scholar]
- Jing, Y. Optimal Scheduling of Urban Water Supply Network Systems Considering Failure Risk Assessment Factors. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2021. [Google Scholar]
- Wang, C. Research on Risk Evaluation of Water Supply Pipelines Based on Bayesian Theory. Ph.D. Thesis, Tianjin University, Tianjin, China, 2010. [Google Scholar]
- Qing, X.; Zhao, X.; Zhang, H.; Tian, Y. Pipe burst prediction model for water supply network. China Water Supply Drain. 2012, 28, 68–71. [Google Scholar]
- Yang, Y.; He, K.; Ji, J.; Tan, Y.; Xu, S.; Zhang, K. Gray cast pipe failure prediction model in water distribution system based on Zero-inflated Poisson model. J. Cent. South Univ. Sci. Technol. 2022, 53, 560–568. [Google Scholar]
- Demissie, G.; Tesfamariam, S.; Sadiq, R. Prediction of Pipe Failure by Considering Time-Dependent Factors: Dynamic Bayesian Belief Network Model. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A-Civ. Eng. 2017, 3, 04017017. [Google Scholar] [CrossRef]
- Thi Minh Lanh, P.; Hai Ha, P.; Nguyen Anh Thu, D.; Dinh Hong, L. Proposed probabilistic models of pipe failure in water distribution system. MATEC Web Conf. 2018, 193, 02002. [Google Scholar] [CrossRef][Green Version]
- Burn, S.; Davis, P.; Gould, S. Risk Analysis for Pipeline Assets-The Use of Models for Failure Prediction in Plastics Pipelines. In Proceedings of the 4th International Symposium on Service Life Prediction, Key Largo, FL, USA, 3–8 December 2009; pp. 183–204. [Google Scholar]
- Hajali, M.; Shdid, C.A. Using numerical modeling for asset management of buried prestressed concrete cylinder pipes. Struct. Concr. 2020, 22, 1487–1499. [Google Scholar] [CrossRef]
- Xu, W.-Z.; Li, C.B.; Choung, J.; Lee, J.-M. Corroded pipeline failure analysis using artificial neural network scheme. Adv. Eng. Softw. 2017, 112, 255–266. [Google Scholar] [CrossRef]
- Peng, S.; Cheng, R.; Wu, Q.; Cheng, J.; Meng, T. Research on pipe burst identification in water supply network based on extreme learning machine algorithm. China Water Supply Drain. 2022, 38, 56–62. [Google Scholar] [CrossRef]
- Qi, F.; Kam, B.; Cheng, T.; Ma, W.; Yao, T.; Wang, K. Failure prediction and sensitivity analysis of pipe girth welds based on neural network. J. Southwest Univ. (Nat. Sci. Ed.) 2024, 46, 159–167. [Google Scholar] [CrossRef]
- Asnaashari, A.; McBean, E.A.; Gharabaghi, B.; Tutt, D. Forecasting watermain failure using artificial neural network modelling. Can. Water Resour. J. 2013, 38, 24–33. [Google Scholar] [CrossRef]
- Hoseingholi, P.; Moeini, R. Pipe failure prediction of wastewater network using genetic programming: Proposing three approaches. Ain Shams Eng. J. 2023, 14, 101958. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Z.; Liu, Z.; Xiong, S.; Zhang, S. Random Forest and Whale Optimization Algorithm to Predict the Invalidation Risk of Backfilling Pipeline. Mathematics 2023, 11, 1636. [Google Scholar] [CrossRef]
- Li, X.; Jing, H.; Liu, X.; Chen, G.; Han, L. The prediction analysis of failure pressure of pipelines with axial double corrosion defects in cold regions based on the BP neural network. Int. J. Press. Vessel. Pip. 2023, 202, 104907. [Google Scholar] [CrossRef]
- Zali, R.B.; Latifi, M.; Javadi, A.A.; Farmani, R. Semisupervised Clustering Approach for Pipe Failure Prediction with Imbalanced Data Set. J. Water Resour. Plan. Manag. 2024, 150, 04023078. [Google Scholar] [CrossRef]
- Zhang, T.; Shuai, J.; Shuai, Y.; Hua, L.; Xu, K.; Xie, D.; Mei, Y. Efficient prediction method of triple failure pressure for corroded pipelines under complex loads based on a backpropagation neural network. Reliab. Eng. Syst. Saf. 2023, 231, 108990. [Google Scholar] [CrossRef]
- Geem, Z.W.; Tseng, C.L.; Kim, J.; Bae, C. Trenchless Water Pipe Condition Assessment Using Artificial Neural Network. In Pipelines 2007: Advances and Experiences with Trenchless Pipeline Projects—Proceedings of the ASCE International Conference on Pipeline Engineering and Construction; American Society of Civil Engineers (ASCE): Charleston, SC, USA, 2012. [Google Scholar]
- Cho, Y.T.; Lee, G.H.; Hong, J.-H.; Woo, G.Z. Prediction of Photovoltaic Generation Using Machine Learning Models with Various Weight Optimization Techniques. J. Korean Inst. Intell. Syst. 2022, 32, 1–6. [Google Scholar]
- Shirzad, A.; Safari, M.J.S. Pipe failure rate prediction in water distribution networks using multivariate adaptive regression splines and random forest techniques. Urban Water J. 2019, 16, 653–661. [Google Scholar] [CrossRef]
- Verheugd, J.; da Costa, P.R.D.; Afshar, R.R.; Zhang, Y.Q.; Boersma, S. Predicting Water Pipe Failures with a Recurrent Neural Hawkes Process Model. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), Electr Network, Toronto, ON, Canada, 11–14 October 2020; pp. 2628–2633. [Google Scholar]
- Wen, Z.; Sun, H.K. MATLAB Intelligent Algorithms; Tsinghua University Press: Beijing, China, 2017. [Google Scholar]
- Yue, S.; He, S.; Wang, G.; Liu, W.; Chen, C. Research on Optimal Deployment Problem of Weapon System Based on Improved Genetic Bee Colony Algorithm. J. Weapons Equip. Eng. 2022, 43, 80–86. [Google Scholar]
- Zhao, Y.; Ru, T. Comparative Analysis of Implementation and Performance of Genetic Algorithm for Small Habitat with Shared Adaptation Value. J. Tonghua Norm. Coll. 2014, 35, 48–50. [Google Scholar] [CrossRef]
- Zhang, X.S.; Zhang, Y. Prediction of failure pressure of corroded pipeline based on Lasso-PSO-BP neural network. Mater. Prot. 2020, 53, 46–52. [Google Scholar] [CrossRef]
- Shen, X. Prediction of Girth Weld Defect Failure of Long Distance Pipeline. Master’s Thesis, Xi’an Shiyou University, Xi’an, China, 2022. [Google Scholar]




| Model | Author | Method |
|---|---|---|
| Statistical modeling | Zhang Haoyang [2] | Risk assessment method |
| Jing Yidan [3] | Logistic regression | |
| Wang Chenwan [4] | Bayesian theory | |
| Qing Xiaofei [5] | Generalized linear model | |
| Yang [6] | Poisson model | |
| Demissie [7] | Dynamic Bayes | |
| Pham [8] | Logistics regression model and decision tree mode | |
| Physical model | Burn [9] | Theory of fracture mechanics |
| Masood [10] | Nonlinear finite element method | |
| Xu [11] | Finite element method, artificial neural network | |
| Intelligent algorithm model | Penson [12] | Extreme learning machine algorithms |
| Qi Feng [13] | Neural network model | |
| Ahmad Asnaashari [14] | Artificial neural network model | |
| Pegah Hoseingholi [15] | Genetic programming prediction | |
| Liu [16] | Random forest and whale optimization algorithms | |
| Li [17] | BP neural network | |
| Zali [18] | XGBoost, random forests, and logistic regression | |
| Zhang [19] | Back propagation neural networks | |
| Zong [20] | Artificial neural networks | |
| Shirzad [22] | MARS and RF | |
| Verheugd [23] | Recursive neural Hawkes process model |
| Numbering | Pipe Outer Diameter/mm | Wall Thickness/mm | Defect Length/mm | Defect Depth/mm | Corrosion Width/mm | Yield Strength/MPa | Tensile Strength/MPa | Failure Pressure/MPa |
|---|---|---|---|---|---|---|---|---|
| 1 | 458.8 | 8.1 | 39.6 | 5.39 | 31.9 | 601 | 684 | 22.68 |
| 2 | 323.9 | 9.8 | 255.6 | 7.08 | 95.3 | 452 | 542 | 14.4 |
| 3 | 323.9 | 9.66 | 305.6 | 6.76 | 95.3 | 452 | 542 | 14.07 |
| 4 | 323.9 | 9.71 | 394.5 | 6.91 | 95.3 | 452 | 542 | 12.84 |
| 5 | 323.9 | 9.91 | 433.4 | 7.31 | 95.3 | 452 | 542 | 12.13 |
| 6 | 323.9 | 9.74 | 466.7 | 7.02 | 95.3 | 452 | 542 | 11.92 |
| 7 | 323.9 | 9.79 | 488.7 | 6.99 | 95.3 | 452 | 542 | 11.91 |
| 8 | 323.9 | 9.79 | 500 | 6.99 | 95.3 | 452 | 542 | 11.99 |
| 9 | 323.9 | 9.74 | 527.8 | 7.14 | 95.3 | 452 | 542 | 11.3 |
| 10 | 508 | 14.3 | 500 | 10.3 | 97 | 478 | 600 | 13.4 |
| The Number of Hidden Layer Nodes | 5 | 6 | 7 | 8 |
| The mean square error value (MSE)/Mpa | 0.13744 | 0.070572 | 0.12722 | 0.19304 |
| The number of hidden layer nodes | 9 | 10 | 11 | 12 |
| The mean square error value (MSE)/Mpa | 0.070124 | 0.040284 | 0.16152 | 0.049901 |
| Index | GA-BP | BP | Differentials |
|---|---|---|---|
| MSE/Mpa | 3.7734 | 10.937 | 7.1636 |
| RMSE/Mpa | 1.9425 | 3.3071 | 1.3646 |
| MAPE/Mpa | 8.8512% | 14.135% | 5.2838% |
| MAE/Mpa | 1.4253 | 2.1376 | 0.7123 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Li, Z. Research on Failure Pressure Prediction of Water Supply Pipe Based on GA-BP Neural Network. Water 2024, 16, 2659. https://doi.org/10.3390/w16182659
Li Q, Li Z. Research on Failure Pressure Prediction of Water Supply Pipe Based on GA-BP Neural Network. Water. 2024; 16(18):2659. https://doi.org/10.3390/w16182659
Chicago/Turabian StyleLi, Qingfu, and Zeyi Li. 2024. "Research on Failure Pressure Prediction of Water Supply Pipe Based on GA-BP Neural Network" Water 16, no. 18: 2659. https://doi.org/10.3390/w16182659
APA StyleLi, Q., & Li, Z. (2024). Research on Failure Pressure Prediction of Water Supply Pipe Based on GA-BP Neural Network. Water, 16(18), 2659. https://doi.org/10.3390/w16182659






