LSTM-Autoencoder Based Detection of Time-Series Noise Signals for Water Supply and Sewer Pipe Leakages
Abstract
1. Introduction
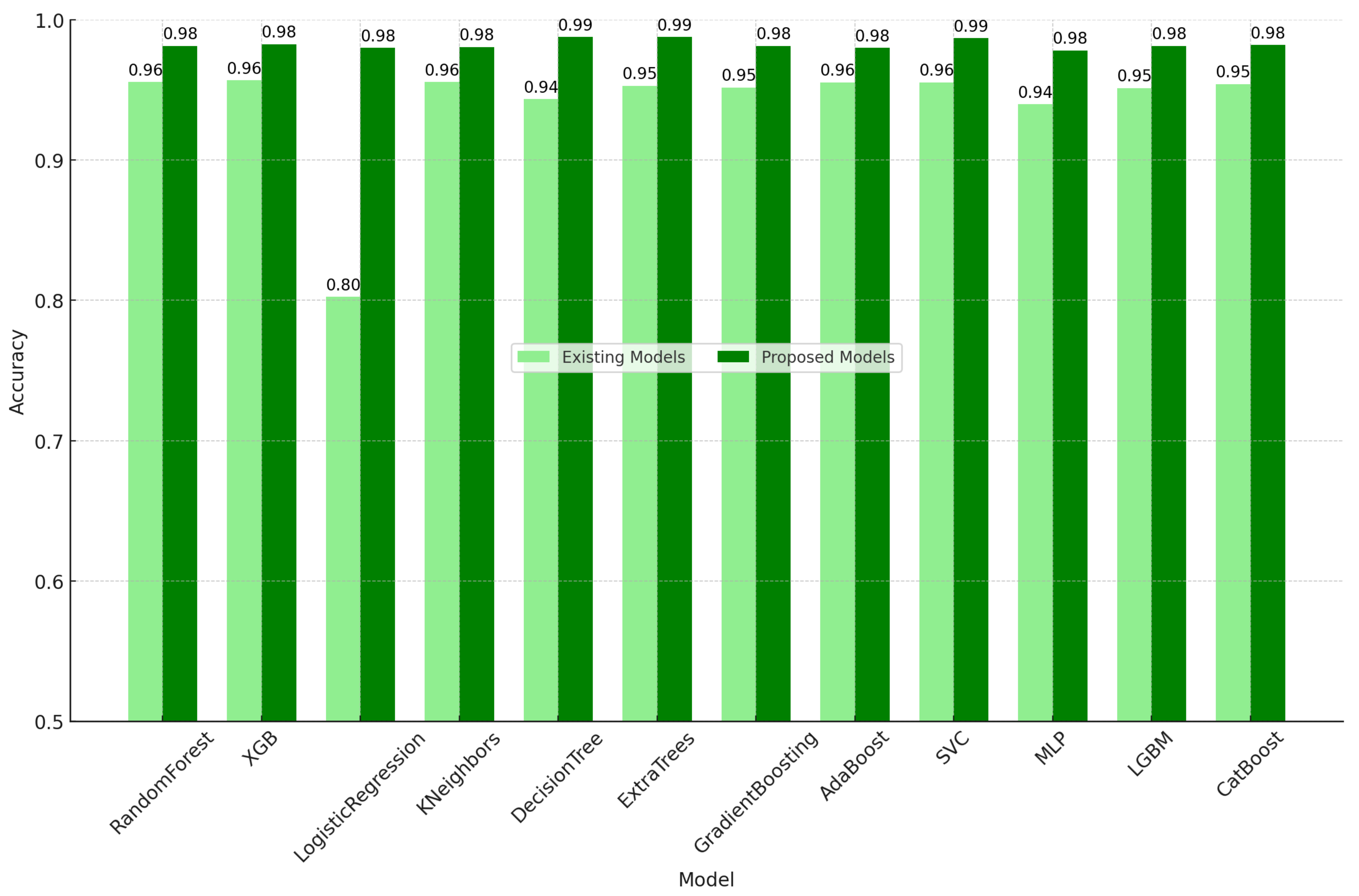
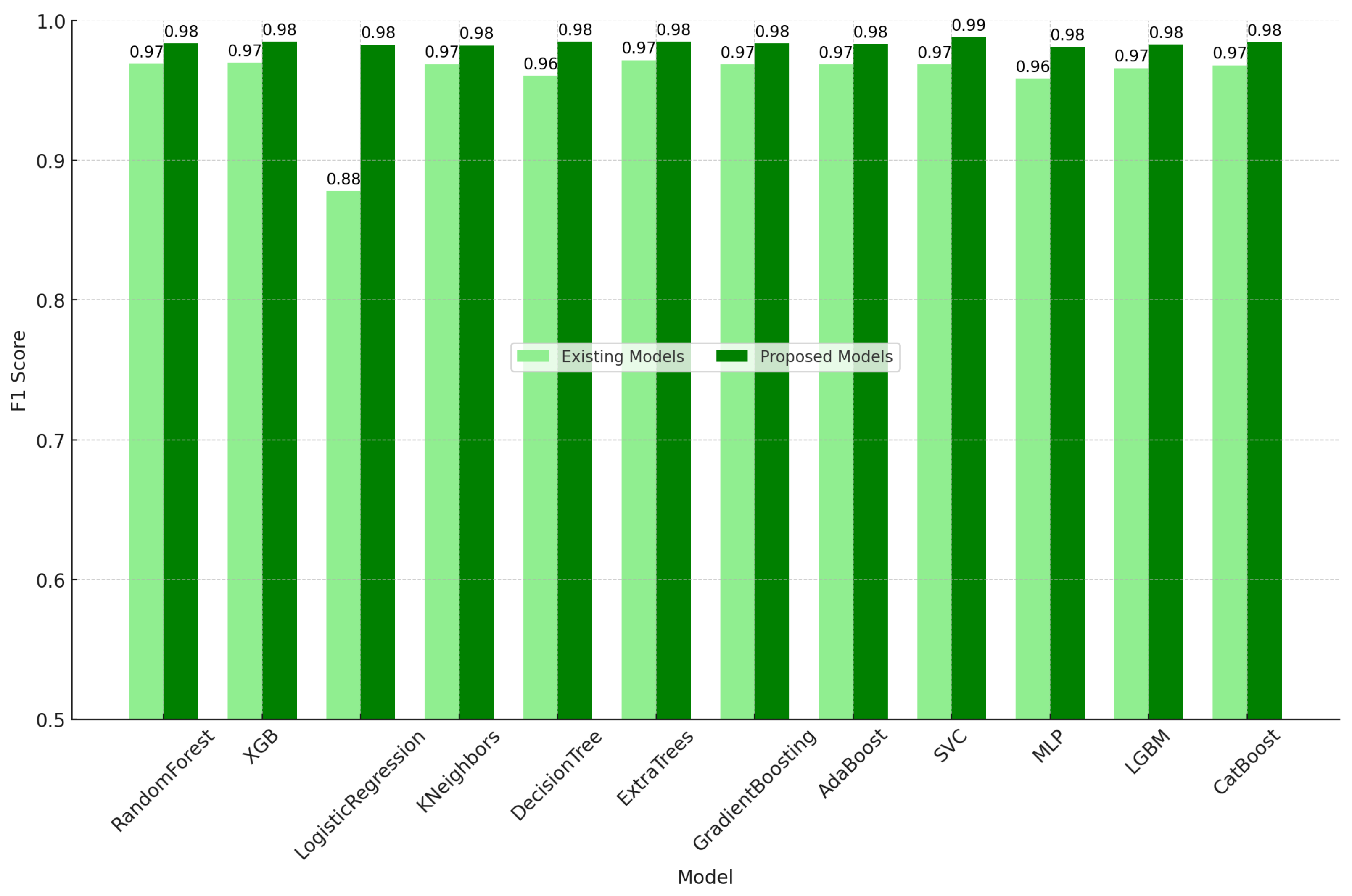
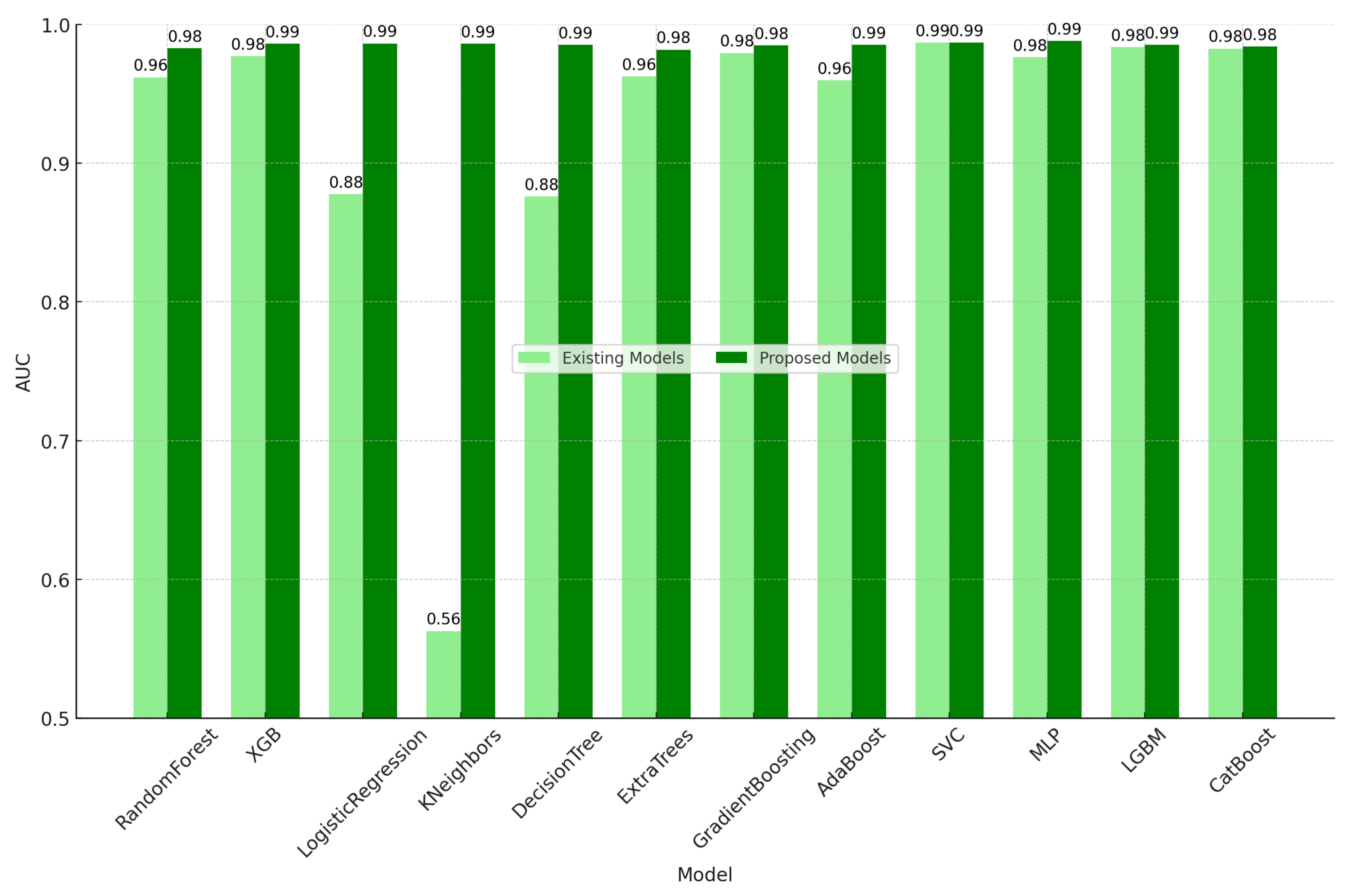
- Improvement in accuracy: The accuracy of the random forest classifier increased from 0.9558 to 0.9814, and the F1 score of the CatBoost classifier improved from 0.968 to 0.9844. These results represent substantial progress in addressing critical infrastructure problems using machine learning technologies.
- Potential of combined models: This advancement highlights the potential of combining LSTM and ensemble models, providing a scalable and robust solution for global water management systems.
2. Related Work
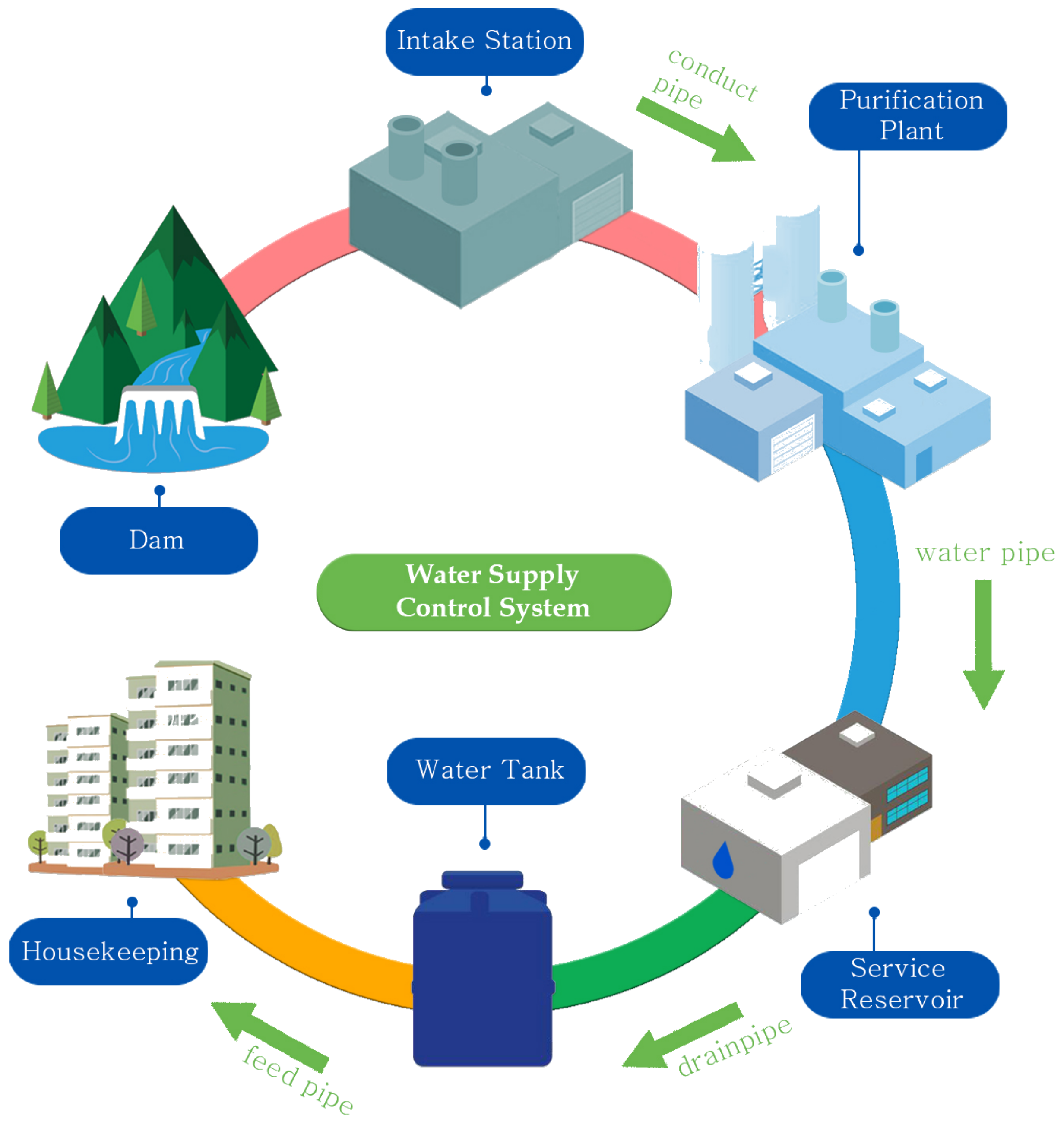
2.1. Water Supply and Sewage System
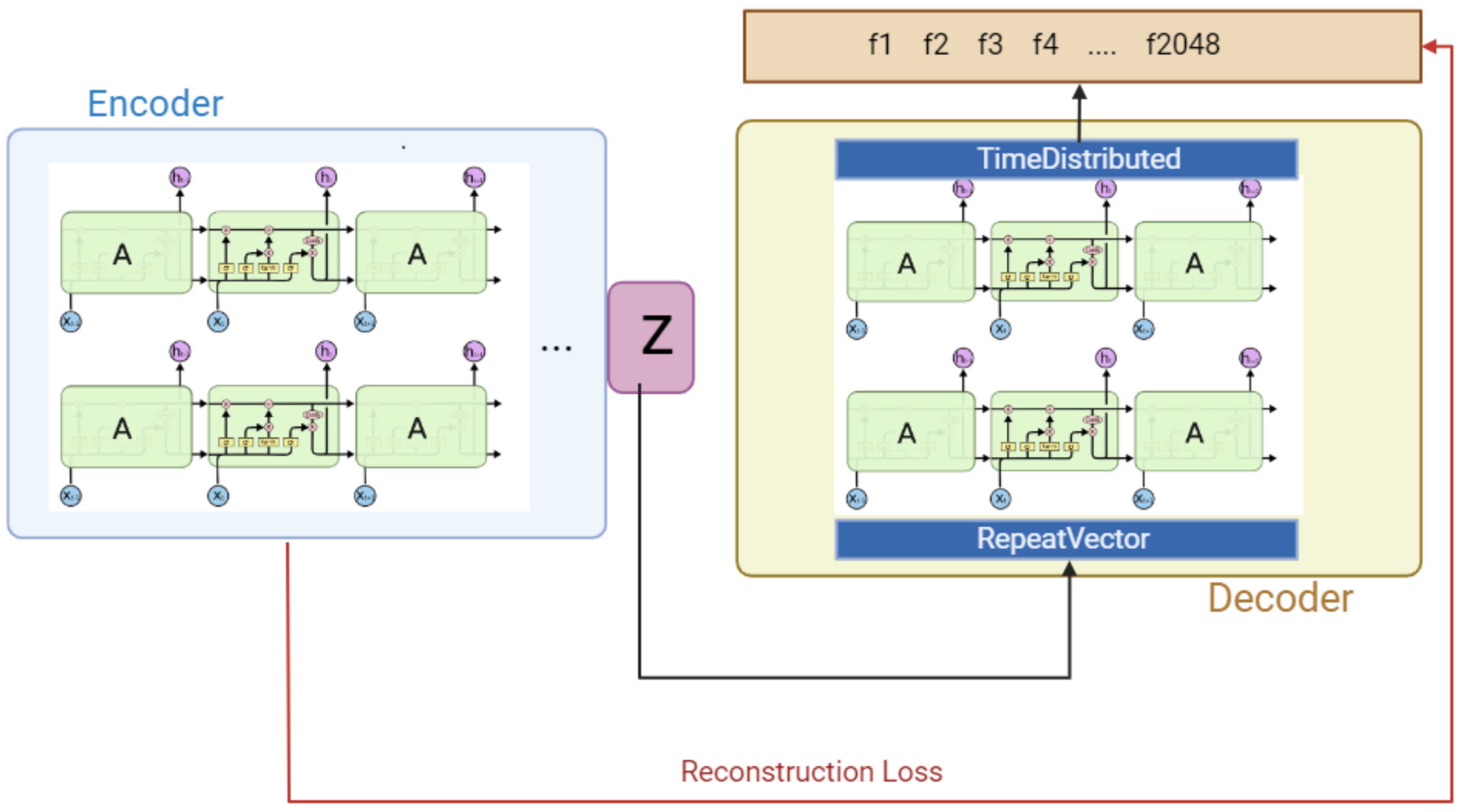
2.2. LSTM-Autoencoder
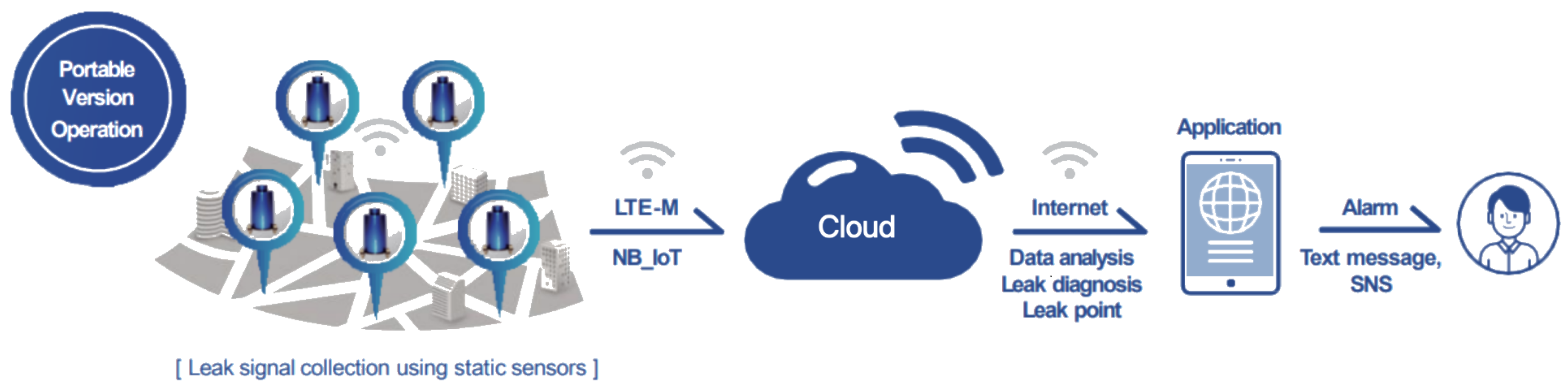
2.3. Signal Detection
2.4. Ensemble Model
- RandomForestClassifier: Combines multiple decision trees trained on random subsets of data. The final output is determined by averaging the predictions of these trees, offering high accuracy and resistance to overfitting.
- XGBClassifier: An enhanced gradient-boosting model that corrects the errors of previous models sequentially. It is known for its fast speed and high performance, especially in data science competitions.
- LogisticRegression: A probabilistic model for binary classification, predicting the probability of a specific class by limiting results to values between 0 and 1.
- KNeighborsClassifier: An instance-based learning algorithm that classifies data points by finding the k nearest neighbors in the dataset.
- DecisionTreeClassifier: A tree-structured model where nodes represent decisions based on data features, and leaf nodes indicate final classification outcomes.
- ExtraTreesClassifier: An ensemble learning technique that is similar to RandomForest but uses more trees and introduces additional randomness in the decision splits.
- GradientBoostingClassifier: Sequentially improves weak predictive models by focusing on reducing errors and minimizing the loss function during training.
- AdaBoostClassifier: Combines weak learners into a strong learner by sequentially improving models, giving higher weights to misclassified instances.
- SVC (Support Vector Classifier): A support vector machine-based classifier that identifies the decision boundary with the maximum margin between classes.
- MLPClassifier (Multi-Layer Perceptron Classifier): A neural network-based classifier with one or more hidden layers, which is capable of learning complex patterns in data.
- LGBMClassifier (LightGBM Classifier): A lightweight gradient boosting machine known for its efficiency in handling large-scale data and fast learning speeds.
- CatBoostClassifier: A gradient boosting classifier that excels in handling and converting categorical variables automatically.
3. LSTM-Autoencoder-Based Noise Signal Detection
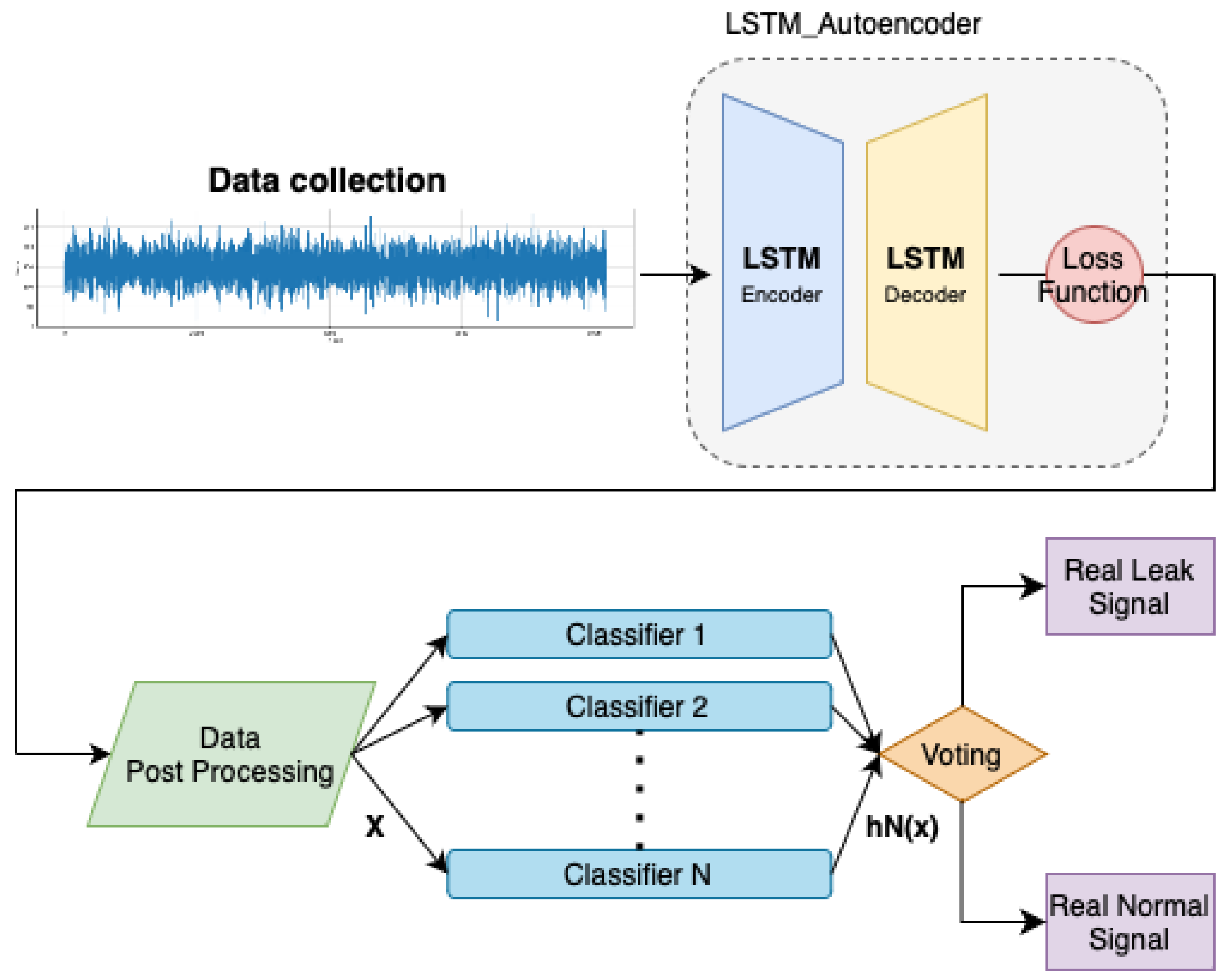
3.1. System Framework
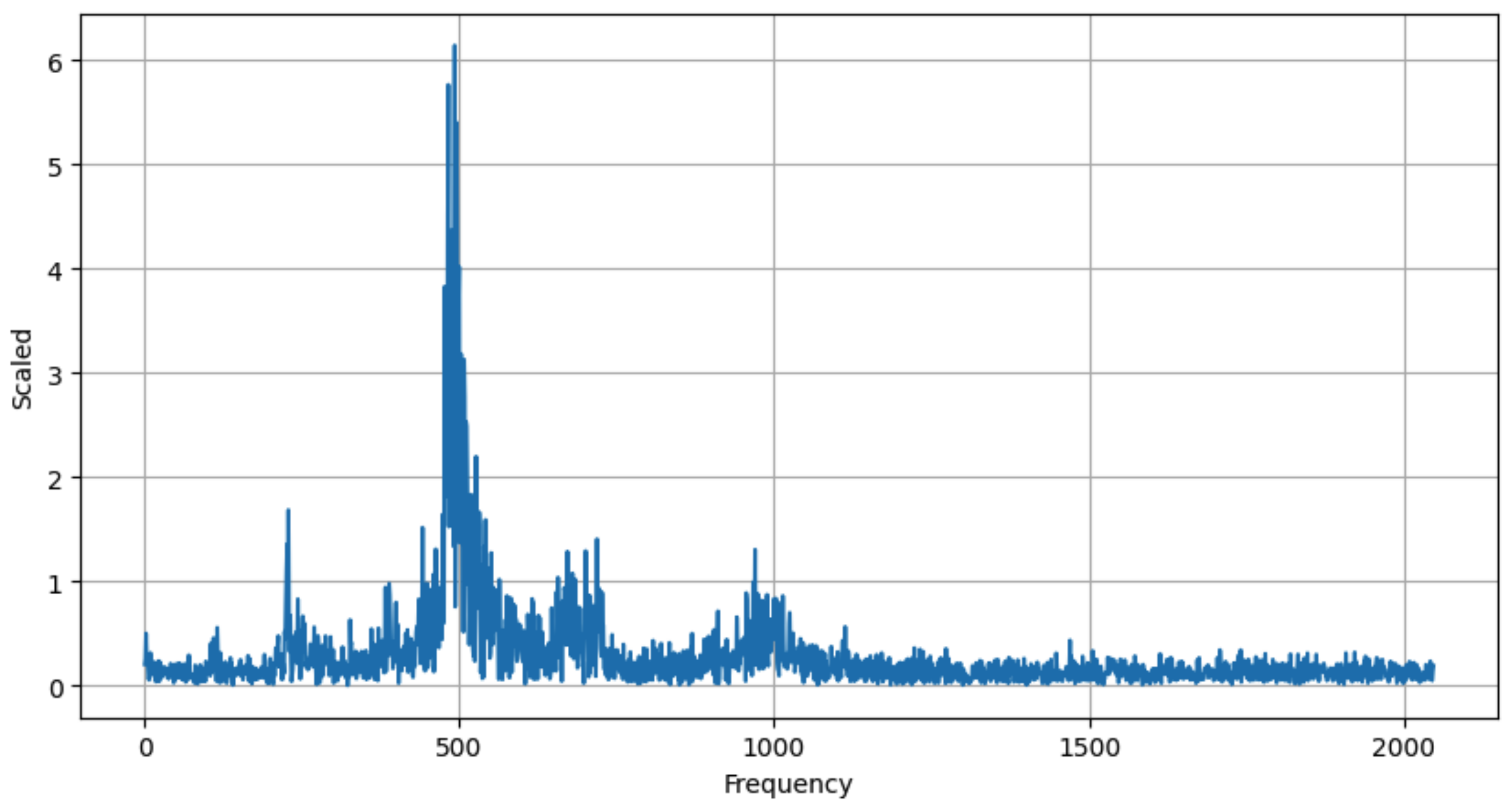
- Noise Signal Estimation: This process is the initial process after collecting time-series data. In the LSTM-autoencoder, the key features of the time-series data are learned and condensed into a low-dimensional representation, denoted as Z. Noise is detected by comparing this compressed representation with the original time-series data; significant discrepancies indicate the presence of noise. This process allows for the identification of anomaly causes in the data and minimizes the impact of noise.
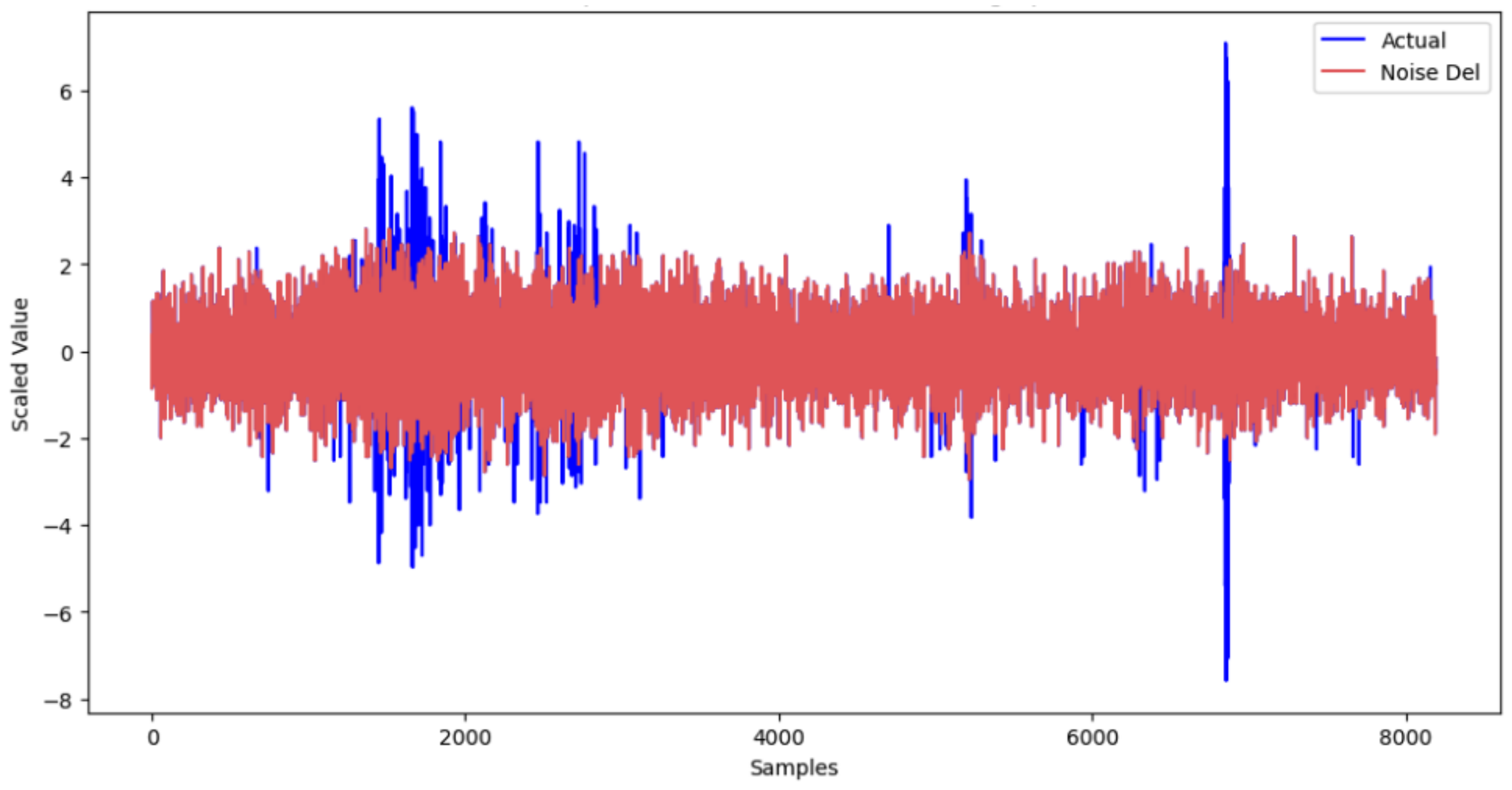
- Noise Signal Attenuation: This process removes the noise identified in the noise signal estimation process. It detects parts with significant deviations compared to the actual data and focuses on noise reduction in areas with a high proportion of anomalies. This includes reducing outliers while optimizing the overall data’s loss value. After processing, the noise-reduced data are passed to the next process, the ensemble model.
- Normal and Leak Data Classification: In the final process, the ensemble model, which combines multiple classifiers (Classifier 1 to Classifier N), performs a final prediction. Each classifier learns different aspects of the data, and their results are reflected in the final decision through voting. The combined ensemble model provides a more robust and accurate classification performance than a single model. As a result, the noise-reduced data are accurately classified into ’Real Leak Signal’ and ’Real Normal Signal’.
3.2. Loss Function
3.3. Voting
4. Experimental Application
4.1. Experimental Environment
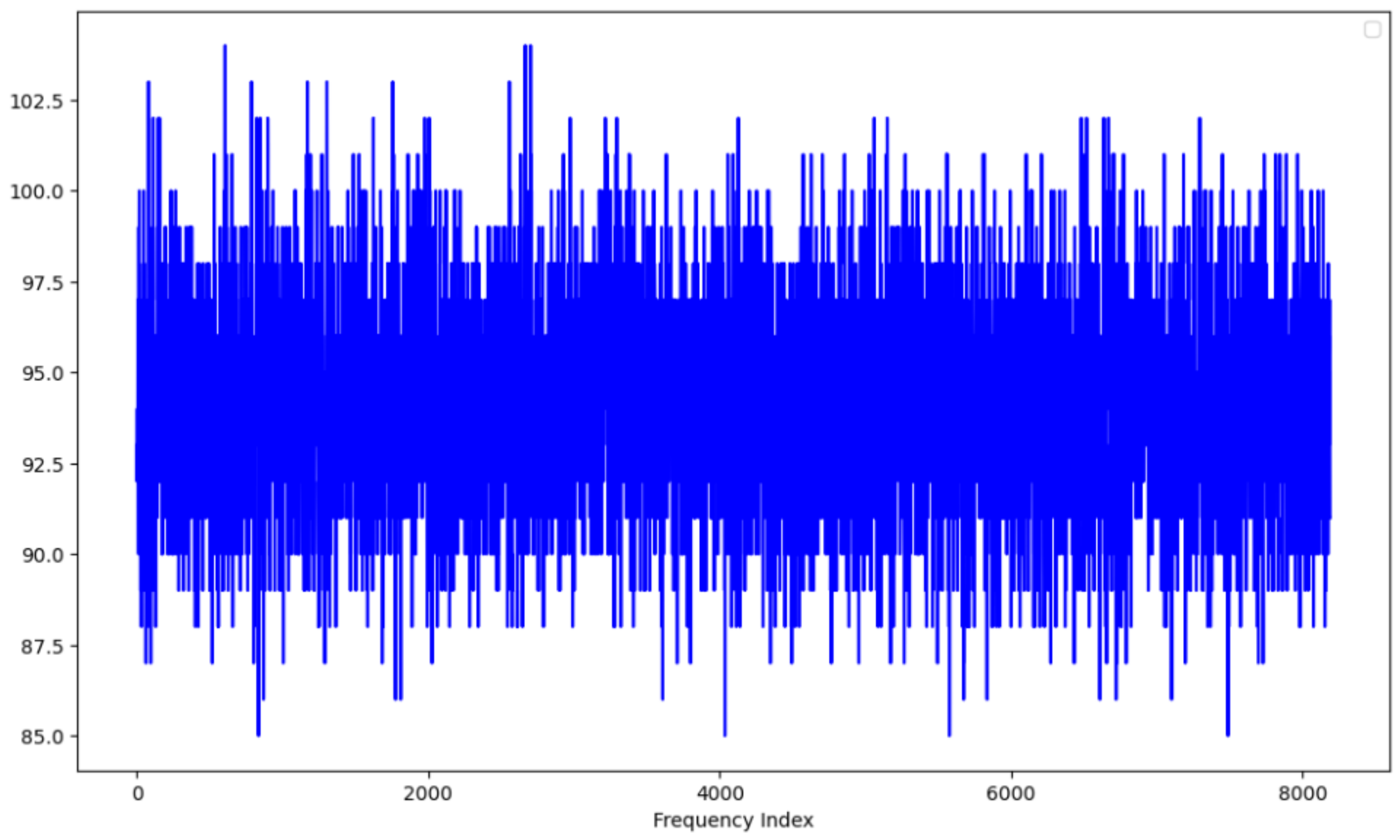
4.2. Dataset and Data Preprocessing
4.3. Evaluation Metrics
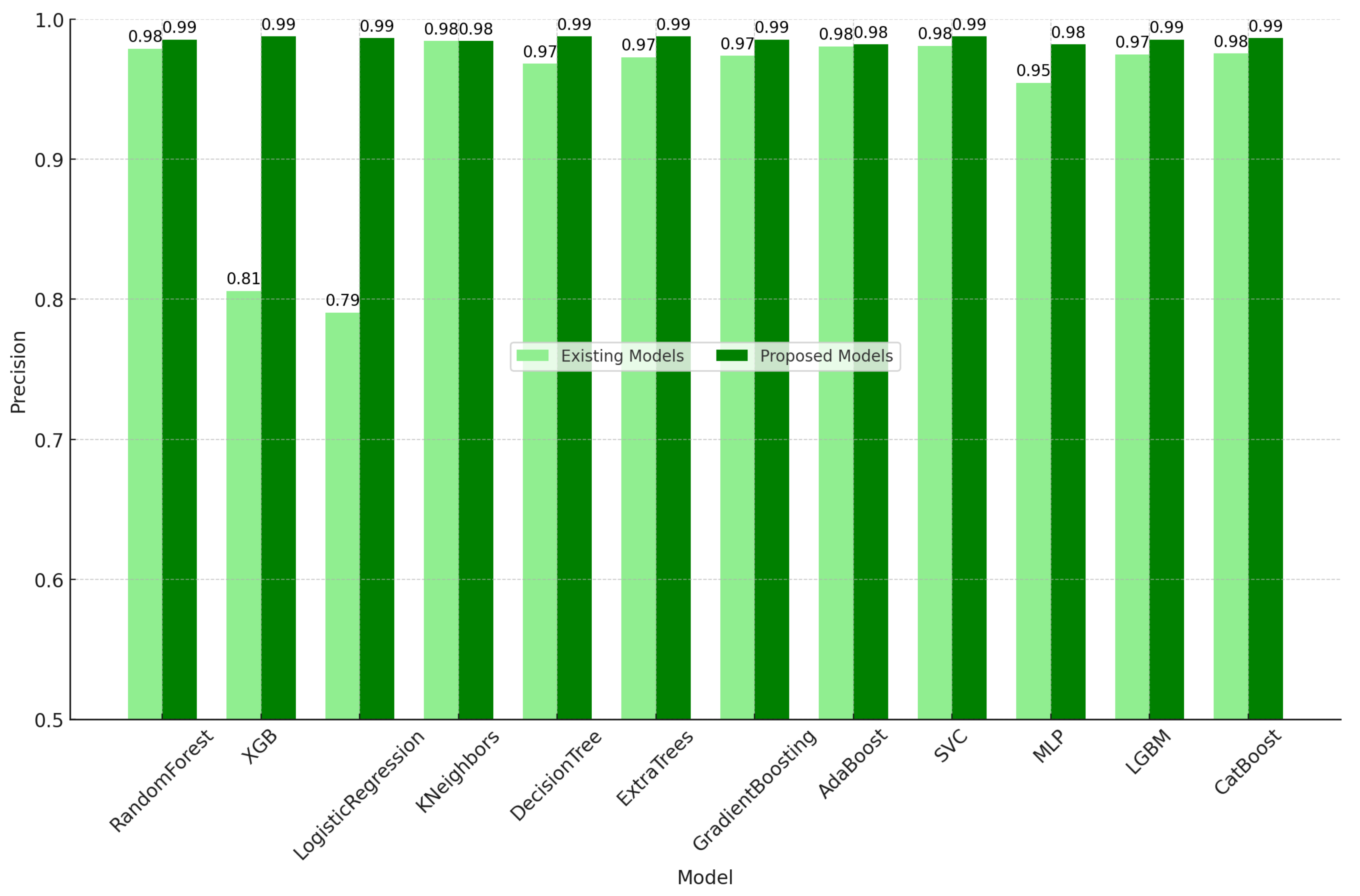
5. Results and Discussion
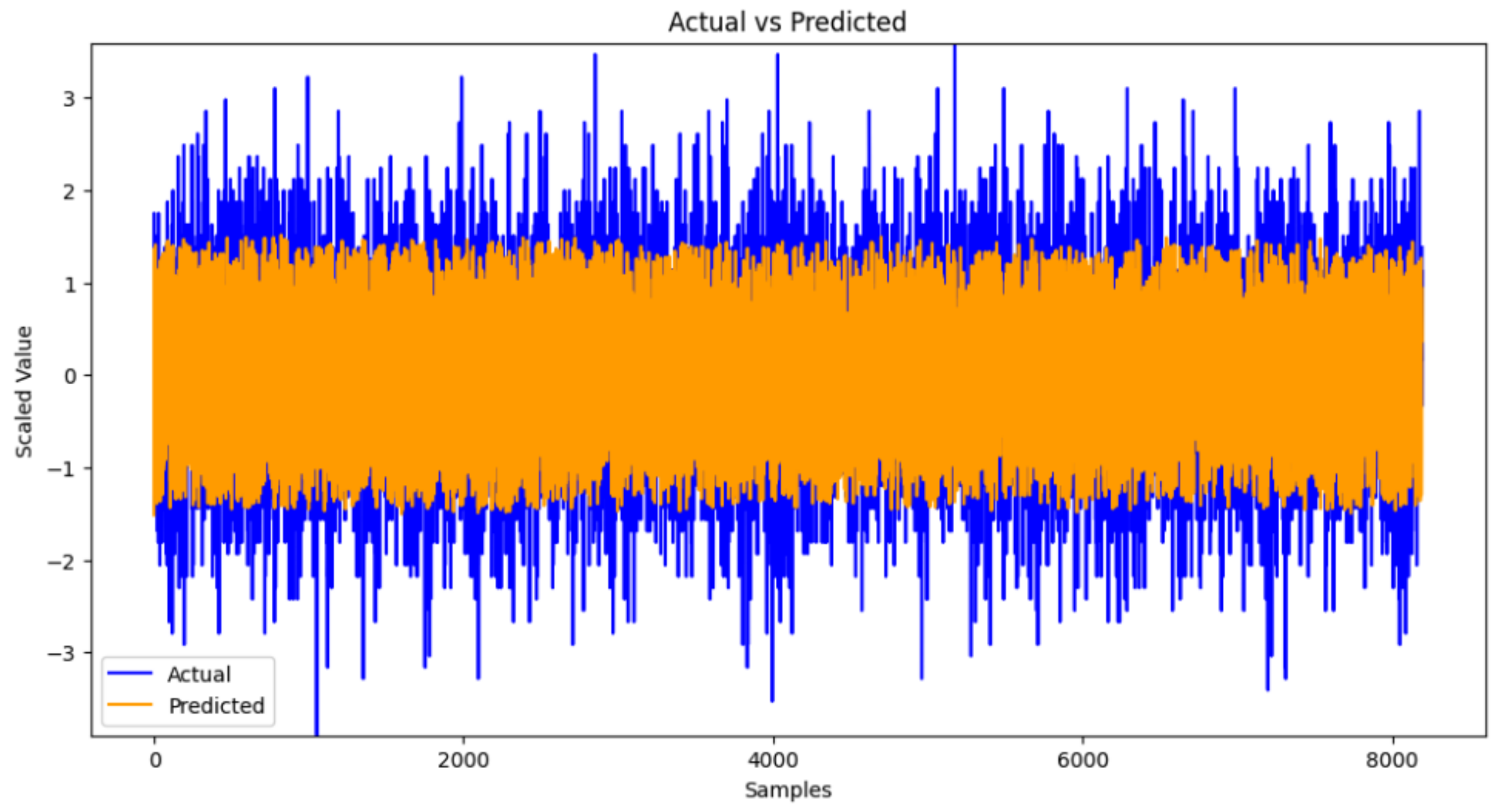
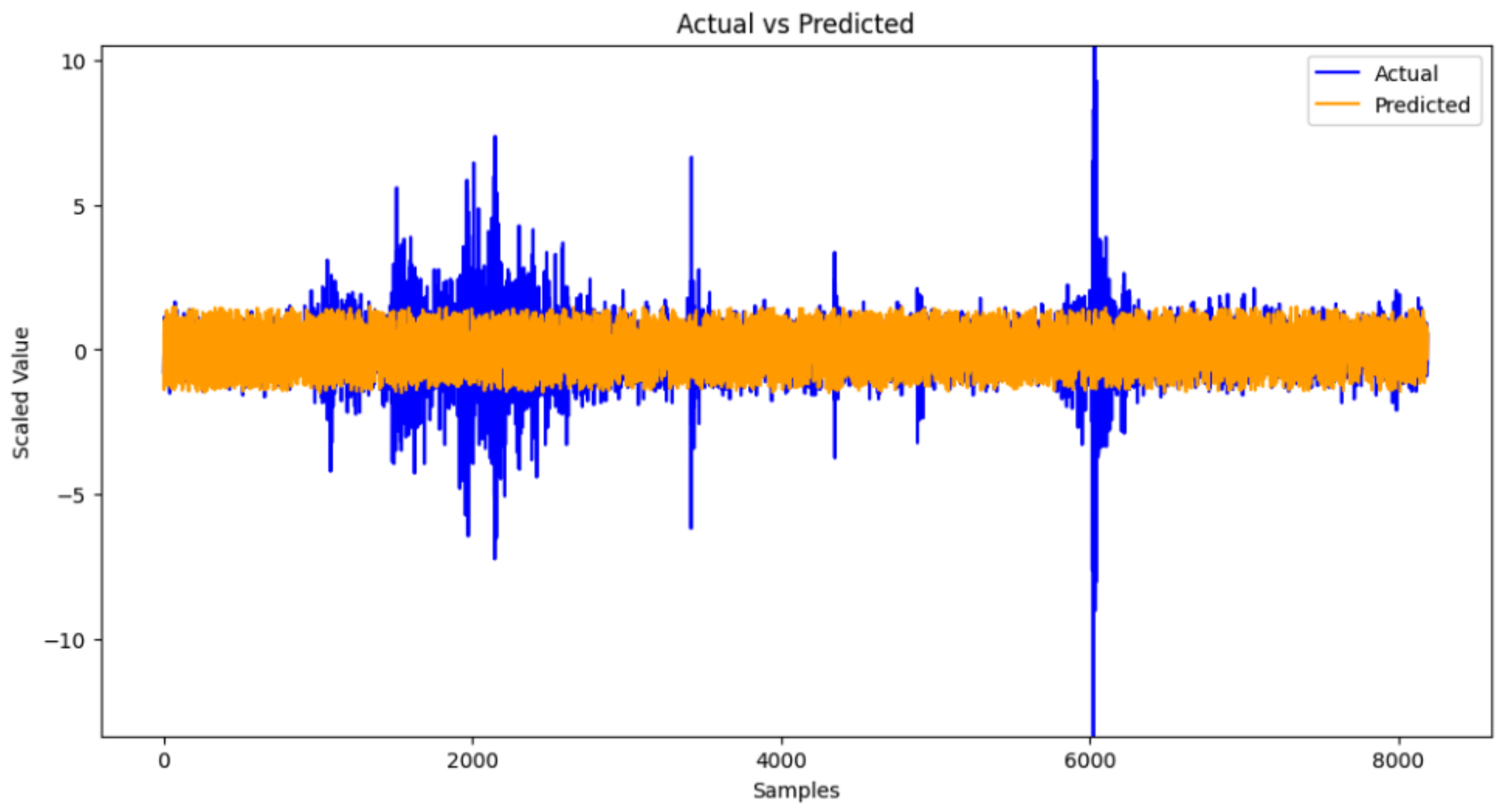
5.1. Results
5.2. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Islam, M.R.; Azam, S.; Shanmugam, B.; Mathur, D. A Review on Current Technologies and Future Direction of Water Leakage Detection in Water Distribution Network. IEEE Access 2022, 10, 107177. [Google Scholar] [CrossRef]
- Olatinwo, S.O.; Joubert, T.-H. Energy-Efficient Solutions in Wireless Sensor Systems for Water Quality Monitoring: A Review. IEEE Sens. J. 2019, 19, 1596–1602. [Google Scholar] [CrossRef]
- Aivazidou, E.; Banias, G.; Lampridi, M.; Vasileiadis, G.; Anagnostis, A.; Papageorgiou, E.; Bochtis, D. Smart Technologies for Sustainable Water Management: An Urban Analysis. Sustainability 2021, 13, 13940. [Google Scholar] [CrossRef]
- Sousa, D.P.; Du, R.; Silva, J.M.B., Jr.; Cavalcante, C.C.; Fischione, C. Leakage Detection in Water Distribution Networks Using Machine-Learning Strategies. Water Supply 2023, 23, 1115. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Kim, N.; Ahn, J.; Jeong, J. CNN-BiLSTM Based Federated Learning for Field Worker Safety. In Proceedings of the 2023 IEEE/ACIS 8th International Conference on Big Data, Cloud Computing, and Data Science (BCD), Ho Chi Minh City, Vietnam,, 14–16 December 2023; pp. 92–97. [Google Scholar]
- Ahn, J.; Lee, Y.; Kim, N.; Park, C.; Jeong, J. Federated Learning for Predictive Maintenance and Anomaly Detection Using Time Series Data Distribution Shifts in Manufacturing Processes. Sensors 2023, 23, 7331. [Google Scholar] [CrossRef]
- Elhalwagy, A.; Kalganova, T. Multi-Channel LSTM-Capsule Autoencoder Network for Anomaly Detection on Multivariate Data. Appl. Sci. 2022, 12, 11393. [Google Scholar] [CrossRef]
- Lee, D.; Choo, H.; Jeong, J. Anomaly Detection Based on 1D-CNN-LSTM Auto-Encoder for Bearing Data. WSEAS Trans. Inf. Sci. Appl. 2023, 20, 1–6. [Google Scholar] [CrossRef]
- Gonçalves, R.; Soares, J.J.M.; Lima, R.M.F. An IoT-Based Framework for Smart Water Supply Systems Management. Future Internet 2020, 12, 42. [Google Scholar] [CrossRef]
- Beach, B. Water Infrastructure and Health in U.S. Cities. Reg. Sci. Urban Econ. 2022, 94, 103674. [Google Scholar] [CrossRef]
- Xiao, R.; Joseph, P.F.; Muggleton, J.M.; Li, J. Limits for Leak Noise Detection in Gas Pipes Using Cross Correlation. J. Sound Vib. 2022, 520, 116639. [Google Scholar] [CrossRef]
- Xiang, S.; Fei, X.; Long, X.; Jidong, C. Research on Transformer Voiceprint Feature Extraction Oriented to Complex Noise Environment. Int. J. Acoust. Vib. 2023, 28, 193–199. [Google Scholar] [CrossRef]
- Wei, Y.; Jang-Jaccard, J.; Xu, W.; Sabrina, F.; Camtepe, S.; Boulic, M. LSTM-autoencoder-based Anomaly Detection for Indoor Air Quality Time-Series Data. IEEE Sens. J. 2023, 23, 3787–3800. [Google Scholar] [CrossRef]
- AI-Tekreeti, W.; Kashyzadeh, K.R.; Ghorbani, S. Fault Detection in the Gas Turbine of the Kirkuk Power Plant: An Anomaly Detection Approach Using DLSTM-Autoencoder. Eng. Fail. Anal. 2024, 160, 108213. [Google Scholar]
- Elsayed, M.S.; Le-Khac, N.A.; Dev, S.; Jurcut, A.D. Network Anomaly Detection Using LSTM Based Autoencoder. In Proceedings of the 16th ACM Symposium on QoS and Security for Wireless and Mobile Networks, Alicante, Spain, 16–20 November 2020; pp. 37–45. [Google Scholar]
- Mallak, A.; Fathi, M. Sensor and Component Fault Detection and Diagnosis for Hydraulic Machinery Integrating LSTM Autoencoder Detector and Diagnostic Classifiers. Sensors 2021, 21, 433. [Google Scholar] [CrossRef]
- Kim, J.; Chae, M.; Han, J.; Park, S.; Lee, Y. The Development of Leak Detection Model in Subsea Gas Pipeline Using Machine Learning. J. Nat. Gas Sci. Eng. 2021, 94, 104134. [Google Scholar] [CrossRef]
- Joo, J.; Jung, J. Ensemble Underwater Shapelet Transformation with Reference to Feature Extraction of Time Series Data. In Proceedings of the Korea Communications Society Conference, Seoul, Republic of Korea, 14–17 May 2019; p. 192. [Google Scholar]
- Rincy, T.N.; Gupta, R. Ensemble Learning Techniques and Its Efficiency in Machine Learning: A Survey. In Proceedings of the 2nd International Conference on Data, Engineering and Applications (IDEA), Bhopal, India, 28–29 February 2020; pp. 1–6. [Google Scholar]
- Mohammed, A.; Kora, R. A Comprehensive Review on Ensemble Deep Learning: Opportunities and Challenges. J. King Saud-Univ.-Comput. Inf. Sci. 2023, 35, 757–774. [Google Scholar] [CrossRef]
- Liu, P.; Sun, X.; Han, Y.; He, Z.; Zhang, W.; Wu, C. Arrhythmia Classification of LSTM Autoencoder Based on Time Series Anomaly Detection. Biomed. Signal Process. Control 2022, 71, 103228. [Google Scholar] [CrossRef]
- Lee, D.; Choo, H.; Jeong, J. Leak Detection and Classification of Water Pipeline Data Using LSTM Auto-Encoder with Xavier Initialization. In Proceedings of the 2023 IEEE/ACIS 8th International Conference on Big Data, Cloud Computing and Data Science (BCD), Ho Chi Minh City, Vietnam, 14–16 December 2023; pp. 69–74. [Google Scholar]
- Batool, A.; Byun, Y.C. Towards Improving Breast Cancer Classification Using an Adaptive Voting Ensemble Learning Algorithm. IEEE Access 2024, 12, 12869–12882. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble Learning for Data Mining. Data Min. Knowl. Discov. 2002, 6, 5–28. [Google Scholar]
- Dietterich, T.G. Ensemble Methods in Machine Learning. In Proceedings of the First International Workshop on Multiple Classifier Systems, Cagliari, Italy, 21–23 June 2000; pp. 1–15. [Google Scholar]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Narula, S.C. The Minimum Sum of Absolute Errors Regression. J. Qual. Technol. 1987, 19, 37–45. [Google Scholar] [CrossRef]
- Dubot, T. Predicting Sector Configuration Transitions with Autoencoder-Based Anomaly Detection. In Proceedings of the International Conference for Research in Air Transportation, Catalonia, Spain, 25–29 June 2018; pp. 26–29. [Google Scholar]
- Yu, K.; Jones, M. Local Linear Quantile Regression. J. Am. Stat. Assoc. 1998, 93, 228–237. [Google Scholar] [CrossRef]
- Taghikhah, M.; Kumar, N.; Šegvić, S.; Eslami, A.; Gumhold, S. Quantile-Based Maximum Likelihood Training for Outlier Detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Stanford, CA, USA, 25–27 March 2024; Volume 38, pp. 21610–21618. [Google Scholar]
- Cochran, W.T.; Cooley, J.W.; Favin, D.L.; Helms, H.D.; Kaenel, R.A.; Lang, W.W.; Welch, P.D. What is the Fast Fourier Transform? Proc. IEEE 1967, 55, 1664–1674. [Google Scholar] [CrossRef]
- Bloomfield, P. Fourier Analysis of Time Series: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Chi, L.; Jiang, B.; Mu, Y. Fast Fourier Convolution. Adv. Neural Inf. Process. Syst. 2020, 33, 4479–4488. [Google Scholar]
- Jalayer, M.; Orsenigo, C.; Vercellis, C. Fault Detection and Diagnosis for Rotating Machinery: A Model Based on Convolutional LSTM, Fast Fourier and Continuous Wavelet Transforms. Comput. Ind. 2021, 125, 103378. [Google Scholar] [CrossRef]
- Gao, X.; Shan, C.; Hu, C.; Niu, Z.; Liu, Z. An Adaptive Ensemble Machine Learning Model for Intrusion Detection. IEEE Access 2019, 7, 82512–82521. [Google Scholar] [CrossRef]
- Gunturi, S.K.; Sarkar, D. Ensemble Machine Learning Models for the Detection of Energy Theft. Electr. Power Syst. Res. 2021, 192, 106904. [Google Scholar] [CrossRef]
- Phyo, P.P.; Byun, Y.C.; Park, N. Short-Term Energy Forecasting Using Machine-Learning-Based Ensemble Voting Regression. Symmetry 2022, 14, 160. [Google Scholar] [CrossRef]
- Park, J.-H.; Kim, Y.-J.; Kim, J.-W.; Na, K.-Y.; Shin, Y.-K. Machine Learning Based Automatic Leakage Detection System for Smart Management of Water Distribution Networks. Korean Soc. Next-Gener. Comput. 2023, 19, 58–72. [Google Scholar]
- Lee, J.; Kim, T.Y.; Baek, S.; Moon, Y.; Jeong, J. Real-Time Pose Estimation Based on ResNet-50 for Rapid Safety Prevention and Accident Detection for Field Workers. Electronics 2023, 12, 3513. [Google Scholar] [CrossRef]
- Streiner, D.L.; Norman, G.R. Precision and Accuracy: Two Terms that are Neither. J. Clin. Epidemiol. 2006, 59, 327–330. [Google Scholar] [CrossRef]




| Section | Description |
|---|---|
| Encoder Architecture | Input size: Size of input dimension |
| Hidden size: Size of hidden state in LSTM layer | |
| Layers: Single LSTM layer | |
| Decoder Architecture | Hidden size: Size of hidden state (same as encoder’s hidden size) |
| Output size: Size of output dimension (same as encoder’s input size) | |
| Layers: Single LSTM layer | |
| Autoencoder Architecture | Model structure composed of encoder and decoder combination |
| Loss Function | Mean squared error (MSE) |
| Optimizer | Adam optimizer |
| Learning rate: Value of learning rate (lr) | |
| Training Method | Epochs: Total number of training epochs (num_epochs) |
| Early stopping: Early stopping with patience of 3 days | |
| Batch size: Batch size for train_loader and val_loader | |
| Model Evaluation | Model evaluation using test loader |
| Measure model performance by returning average loss |
| Hardware Environment | Software Environment |
|---|---|
| CPU: Intel Xeon Silver 4216 CPU @ 2.10 GHz | |
| GPU: 4 x NVIDIA RTX A5000 | |
| Memory: 256GB DDR4 | |
| Storage: 2TB SSD | OS: Ubuntu 18.04.6 LTS |
| Framework: TensorFlow 2.11.0 | |
| Programming Language: Python 3.10.9 |
| Model | Existing Models | Proposed Models | ||||||
|---|---|---|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1 Score | Accuracy | Precision | Recall | F1 Score | |
| RandomForest | 0.9558 | 0.979 | 0.9593 | 0.969 | 0.9814 | 0.9855 | 0.9822 | 0.9838 |
| XGB | 0.957 | 0.9806 | 0.9593 | 0.9699 | 0.9827 | 0.9877 | 0.9822 | 0.9849 |
| LogisticRegression | 0.8025 | 0.7906 | 0.9872 | 0.878 | 0.9801 | 0.9865 | 0.9789 | 0.9827 |
| KNeighbors | 0.9558 | 0.9845 | 0.9537 | 0.9689 | 0.9807 | 0.9844 | 0.9822 | 0.9833 |
| DecisionTree | 0.9434 | 0.9683 | 0.9526 | 0.9604 | 0.9827 | 0.9877 | 0.9822 | 0.9849 |
| ExtraTrees | 0.953 | 0.9729 | 0.9615 | 0.9672 | 0.982 | 0.9855 | 0.9833 | 0.9844 |
| GradientBoosting | 0.9518 | 0.974 | 0.9588 | 0.9663 | 0.9814 | 0.9855 | 0.9822 | 0.9838 |
| AdaBoost | 0.9554 | 0.9806 | 0.9571 | 0.9687 | 0.9801 | 0.9822 | 0.9833 | 0.9828 |
| SVC | 0.9554 | 0.9811 | 0.9565 | 0.9687 | 0.982 | 0.9877 | 0.9811 | 0.9844 |
| MLP | 0.9398 | 0.9546 | 0.9621 | 0.9584 | 0.9782 | 0.9822 | 0.98 | 0.9811 |
| LGBM | 0.9514 | 0.975 | 0.9571 | 0.966 | 0.9814 | 0.9855 | 0.9822 | 0.9838 |
| CatBoost | 0.9542 | 0.9757 | 0.9604 | 0.968 | 0.982 | 0.9866 | 0.9822 | 0.9844 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, Y.; Na, K.Y.; Kim, S.E.; Kyung, E.J.; Choi, H.G.; Jeong, J. LSTM-Autoencoder Based Detection of Time-Series Noise Signals for Water Supply and Sewer Pipe Leakages. Water 2024, 16, 2631. https://doi.org/10.3390/w16182631
Shin Y, Na KY, Kim SE, Kyung EJ, Choi HG, Jeong J. LSTM-Autoencoder Based Detection of Time-Series Noise Signals for Water Supply and Sewer Pipe Leakages. Water. 2024; 16(18):2631. https://doi.org/10.3390/w16182631
Chicago/Turabian StyleShin, Yungyeong, Kwang Yoon Na, Si Eun Kim, Eun Ji Kyung, Hyun Gyu Choi, and Jongpil Jeong. 2024. "LSTM-Autoencoder Based Detection of Time-Series Noise Signals for Water Supply and Sewer Pipe Leakages" Water 16, no. 18: 2631. https://doi.org/10.3390/w16182631
APA StyleShin, Y., Na, K. Y., Kim, S. E., Kyung, E. J., Choi, H. G., & Jeong, J. (2024). LSTM-Autoencoder Based Detection of Time-Series Noise Signals for Water Supply and Sewer Pipe Leakages. Water, 16(18), 2631. https://doi.org/10.3390/w16182631








