Comprehensive Resilience Assessment Framework for Water Distribution Networks
Abstract
1. Introduction
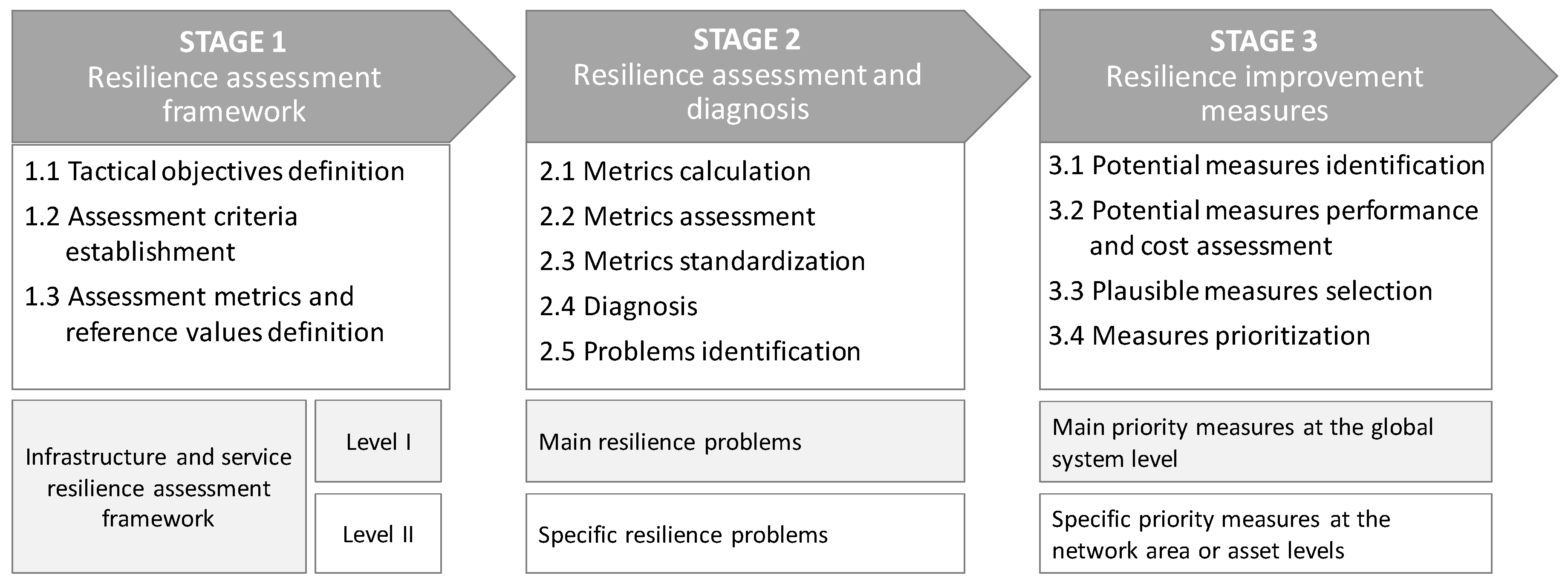
2. Methodology
2.1. Resilience Assessment Approach
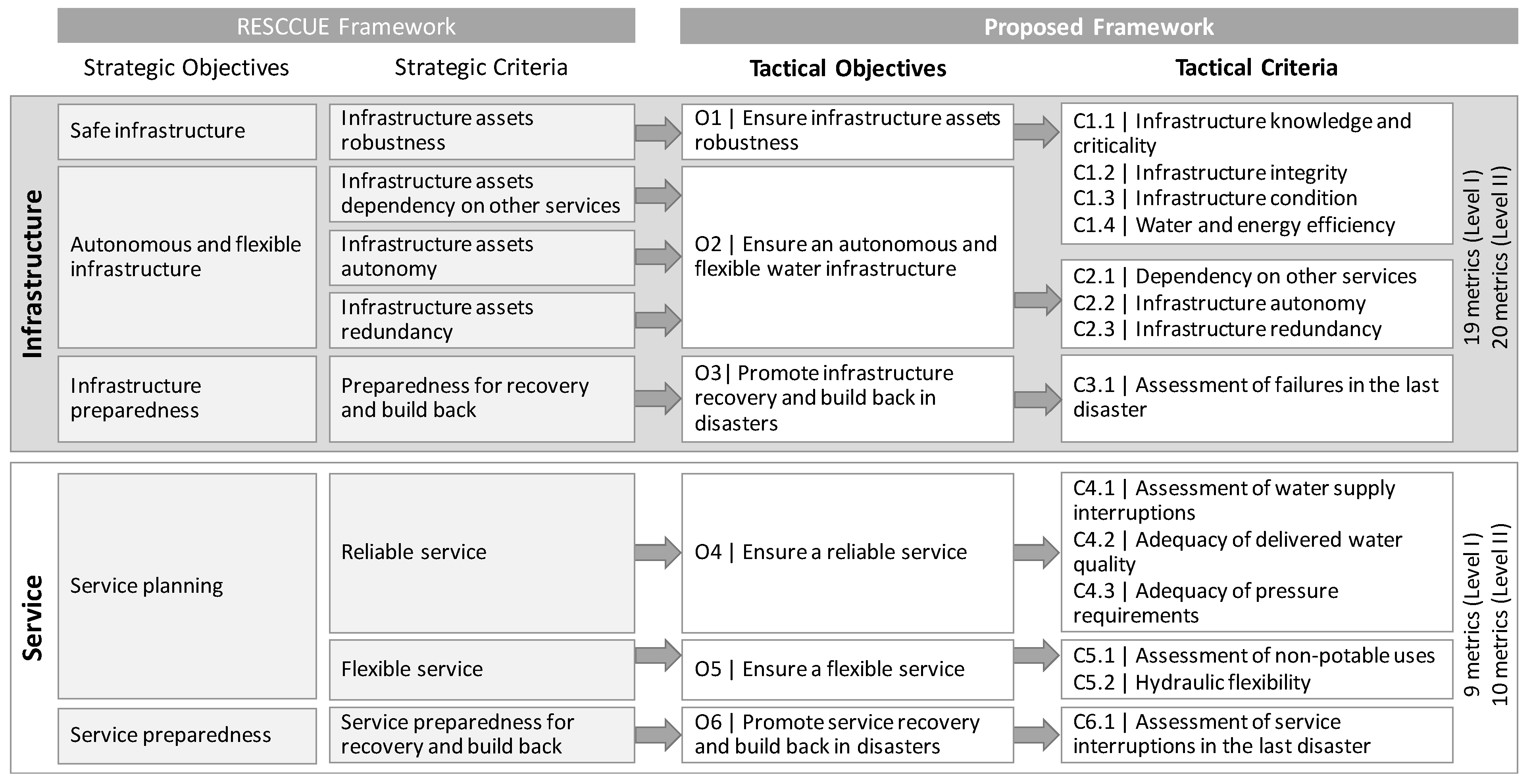
2.2. Resilience Assessment Framework
2.3. Resilience Assessment and Diagnosis
2.4. Improvement Measures
3. Results
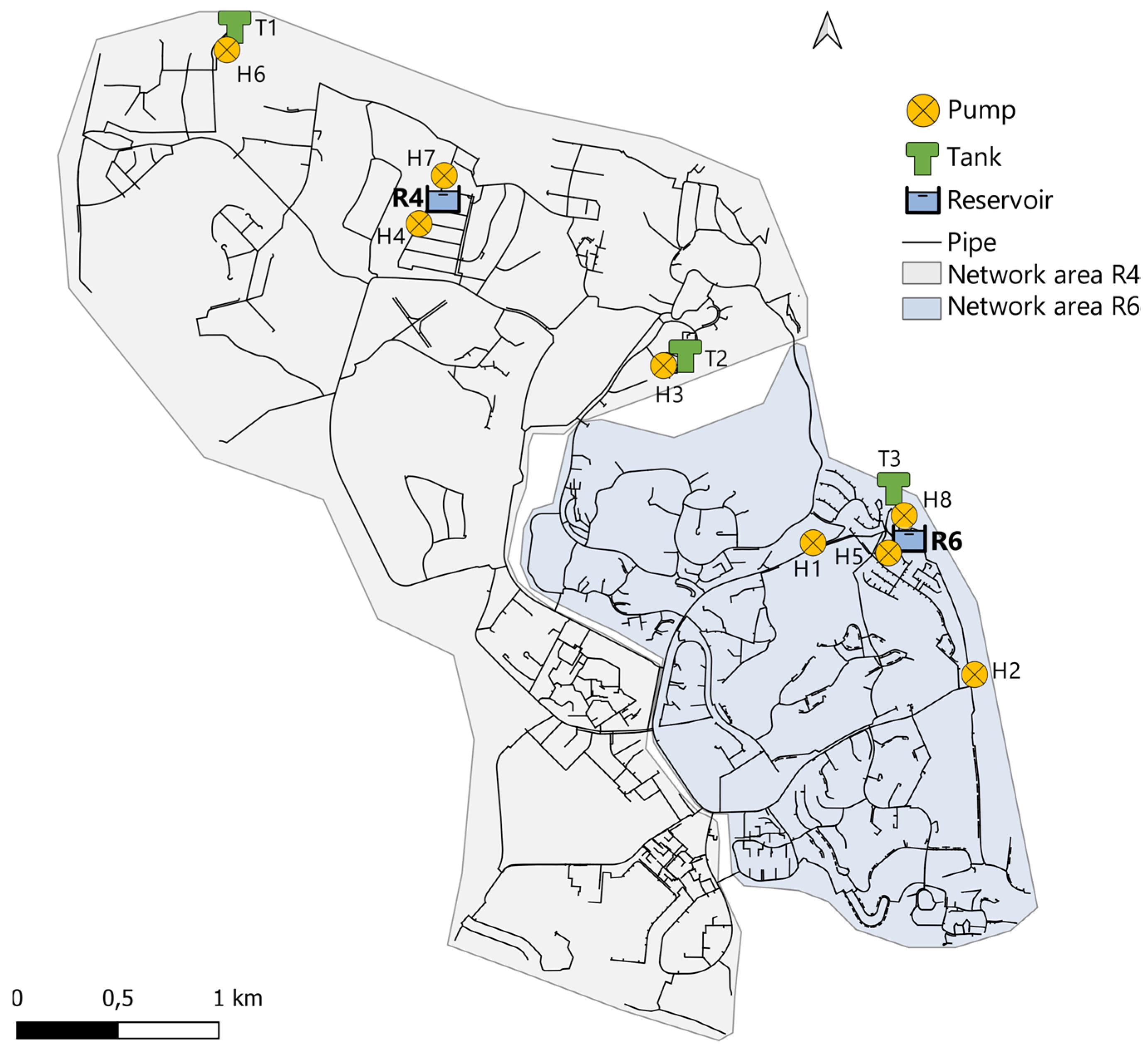
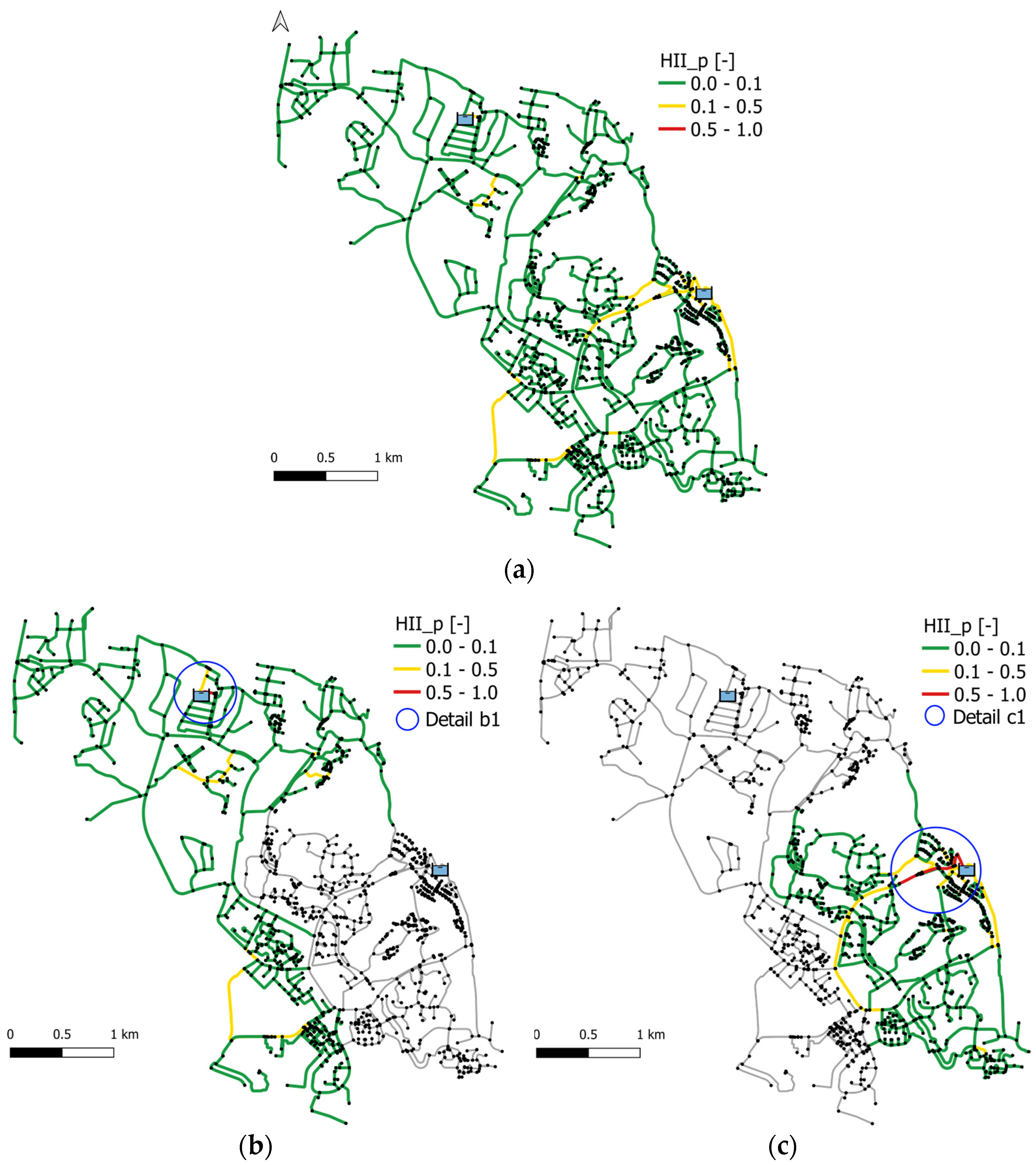
3.1. Case Study
3.2. Results of Metrics Assessment
3.3. Resilience Assessment Framework Application
3.3.1. Application of Resilience Assessment Framework for System Diagnosis
3.3.2. Network Area Prioritization
3.3.3. Detailed Diagnosis of Priority Network Area
3.4. Improvement Measures Recommendations
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| M1.1.1 | Infrastructural knowledge index | [-] | Level I | |||||||||||||||||||||||||||||
Assesses the water utility knowledge over its infrastructure, evaluating the following classes:
| ||||||||||||||||||||||||||||||||
| Calculation Sum of each analysis class, which are composed by a set of questions, with a predefined number of points for each question. See LNEC and ERSAR (2017) for more information. In case of not applicable classes or subclasses to the system, a conversion factor proportional to the score of the applicable classes or subclasses is considered. The index varies between 0 and 200. | ||||||||||||||||||||||||||||||||
| Data source: Water utility survey. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed in this study, considering that minimum knowledge for fair performance corresponds to having the information needed in paper (87 points), and a minimum knowledge for good performance corresponds to having the information needed in computer-readable form (142 points). | ||||||||||||||||||||||||||||||||
| M1.1.2 | Knowledge and protection of critical assets index | [-] | Level I | |||||||||||||||||||||||||||||
Assesses the water utility knowledge and protection of critical assets, evaluating the following questions:
| ||||||||||||||||||||||||||||||||
| Calculation If critical infrastructure assets are not identified (Q1 = 0), then Q2 and Q3 are not assessed, and final score is 0. If critical infrastructure assets are totally or partially identified (Q1 = 1 or 0.5), knowledge and protection of critical assets index () is calculated as: | ||||||||||||||||||||||||||||||||
| (A1) | ||||||||||||||||||||||||||||||||
| where (-) is the score of question Q2, (-) is the score of question Q3 and (-) is the score of question Q1. The index varies between 0 and 3. | ||||||||||||||||||||||||||||||||
| Data source: Water utility survey. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed in this study. Considering the index varies between 0 and 3, the minimum KPCAI for fair performance corresponds to a score of 1, and a minimum KPCAI for good performance to a score of 2. | ||||||||||||||||||||||||||||||||
| M1.1.3 | Assets criticality index | [-] | Level I | |||||||||||||||||||||||||||||
| Assesses the assets (pipes, pumps and storage tanks) criticality by evaluating the drop in consumption due to the deactivation or failure of each asset. Adapted from [36,37]. | ||||||||||||||||||||||||||||||||
| Calculation Assets criticality index () corresponds to the weighted average of the assets hydraulic importance index () by the flowrate, defined as follows: | ||||||||||||||||||||||||||||||||
| (A2) | ||||||||||||||||||||||||||||||||
| where is the total number of assets (No.), is the flowrate relative to asset (m3/h), assesses the consumption that is not supplied due the deactivation or failure of asset (-), calculated as: | ||||||||||||||||||||||||||||||||
| (A3) | ||||||||||||||||||||||||||||||||
| where is the total number of nodes (No.), is the required consumption at node (m3/h) and is the effective demand at node when asset is deactivated (m3/h). In order to simulate nodal consumption after the failure, pressure driven analysis is preferred to simulate nodal consumption after the deactivation or failure of the assets. If a demand driven analysis is made, it is suggested that nodes with pressure lower than the minimum required are considered with null demand. and varies between 0 and 1. Higher values indicate greater criticality. | ||||||||||||||||||||||||||||||||
| Data source: System hydraulic model. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed in this study, in Section 3.2. Considering varies between 0 and 1, bellow 0.1 correspond to good performance, between 0.1 and 0.5 correspond to fair performance, and above 0.5 correspond to poor performance. | ||||||||||||||||||||||||||||||||
| M1.1.3a | Pipes criticality index | [-] | Level II | |||||||||||||||||||||||||||||
| Assesses the pipes criticality by evaluating the drop in consumption due to the deactivation or failure of each pipe. Adapted from [36,37]. | ||||||||||||||||||||||||||||||||
| Calculation Similar to M1.1.3, considering only pipes as assets. | ||||||||||||||||||||||||||||||||
| Data source: System hydraulic model. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed herein to be equal to M1.1.3. | ||||||||||||||||||||||||||||||||
| M1.1.3b | Pumps criticality index | [-] | Level II | |||||||||||||||||||||||||||||
| Assesses the pumps criticality by evaluating the drop in consumption due to the deactivation or failure of each pump. Adapted from [36,37]. | ||||||||||||||||||||||||||||||||
| Calculation Similar to M1.1.3, considering only pumps as assets. | ||||||||||||||||||||||||||||||||
| Data source: System hydraulic model. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed herein to be equal to M1.1.3. | ||||||||||||||||||||||||||||||||
| M1.1.3c | Storage tanks criticality index | [-] | Level II | |||||||||||||||||||||||||||||
| Assesses the storage tanks criticality by evaluating the drop in consumption due to the deactivation or failure of each tank. Adapted from [36,37]. | ||||||||||||||||||||||||||||||||
| Calculation Similar to M1.1.3, considering only storage tanks as assets. | ||||||||||||||||||||||||||||||||
| Data source: System hydraulic model. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed herein to be equal to M1.1.3. | ||||||||||||||||||||||||||||||||
| M1.2.1 | Number of failures | [No./(100 km·year)] | Level I | |||||||||||||||||||||||||||||
| Addresses failures frequency in the system. It is defined as the total number of failures (all assets) per 100 km of network length. Adapted from [33], identified as Op31. | ||||||||||||||||||||||||||||||||
| Calculation Performance indicator number of failures, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A4) | ||||||||||||||||||||||||||||||||
| where is the total number of failures in all assets (No.) and is the total length of the network (km). | ||||||||||||||||||||||||||||||||
| Data source: Water utility work orders. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed in this study to be the same as indicator AA10b of [28], herein corresponding to M1.2.1a, as the main contributor are the network pipes. | ||||||||||||||||||||||||||||||||
| M1.2.1a | Pipes failures | [No./(100 km·year)] | Level II | |||||||||||||||||||||||||||||
| Addresses pipe failures frequency in the system. It is defined as the total number of pipe failures per 100 km of network length. Source: [28], identified as AA10b. | ||||||||||||||||||||||||||||||||
| Calculation Performance indicator pipes failures, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A5) | ||||||||||||||||||||||||||||||||
| where is the total number of failures in pipes (No.) and is the total length of the network (km). | ||||||||||||||||||||||||||||||||
| Data source: Water utility work orders. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [28] for indicator AA10b. | ||||||||||||||||||||||||||||||||
| M1.2.1b | Pump failures | [days/pump] | Level II | |||||||||||||||||||||||||||||
| Addresses pump failures frequency in the system. It is defined as the sum, for all pumps, of the number of days when the pump is out of order by the total number of pumps. Source: [33], identified as Op30. | ||||||||||||||||||||||||||||||||
| Calculation Performance indicator pump failures, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A6) | ||||||||||||||||||||||||||||||||
| where is the total pump failures duration (days) and is the total number of pumps (No.). | ||||||||||||||||||||||||||||||||
| Data source: Water utility work orders. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [7] for indicator PWts08, which corresponds to Op30 from [33]. Reference values were not proposed in [33]. | ||||||||||||||||||||||||||||||||
| M1.2.1c | Service connection failures | [No./(1000 connections·year)] | Level II | |||||||||||||||||||||||||||||
| Addresses service connection failures frequency in the system. It is defined as the number of service connection failures per 1000 connections. Source: [33], identified as Op32. | ||||||||||||||||||||||||||||||||
| Calculation Performance indicator service connection failures is calculated as: | ||||||||||||||||||||||||||||||||
| (A7) | ||||||||||||||||||||||||||||||||
| where is the total number of failures in service connection (No.) and is the total number of service connections (No.). | ||||||||||||||||||||||||||||||||
| Data source: Water utility work orders. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [7] for indicator PWts10, which corresponds to Op32 from [33]. Reference values were not proposed in [33]. | ||||||||||||||||||||||||||||||||
| M1.2.2 | Total duration of failures | [Days/No. failure] | Level I | |||||||||||||||||||||||||||||
| Addresses failures duration in the system. It is defined as the total inoperative period for all failures (including recovery time) per number of failures. Adapted from [7], identified as PWts16. | ||||||||||||||||||||||||||||||||
| Calculation Performance indicator number of failures, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A8) | ||||||||||||||||||||||||||||||||
| where is the sum of inoperative period for all failures (days) and is the total number of failures (No.). | ||||||||||||||||||||||||||||||||
| Data source: Water utility work orders. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed in this study to be the same as indicator PWts16 of [7]. | ||||||||||||||||||||||||||||||||
| M1.3.1 | Pipes rehabilitation | [%/year] | Level I | |||||||||||||||||||||||||||||
| Addresses the continuous rehabilitation practice. It is defined as the annual average percentage of pipes with age over 10 years rehabilitated in the last 5 years. Source: [28], identified as AA09. | ||||||||||||||||||||||||||||||||
| Calculation Pipes rehabilitation, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A9) | ||||||||||||||||||||||||||||||||
| where is the length of pipes rehabilitated in the last 5 years (km) and is the length of pipes with age over 10 years (km). | ||||||||||||||||||||||||||||||||
| Data source: Water utility infrastructure data. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [28], for indicator AA09. | ||||||||||||||||||||||||||||||||
| M1.3.2 | Infrastructure value index | [-] | Level I | |||||||||||||||||||||||||||||
| Defined as the ratio between the current value of the infrastructure and its replacement cost. Source: [28], identified as PAA04. | ||||||||||||||||||||||||||||||||
| Calculation The infrastructure value index, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A10) | ||||||||||||||||||||||||||||||||
| in which is the replacement cost of asset (€), is the residual service life of asset (years), is the expected service life of asset (years) and is the total number of assets (No.). | ||||||||||||||||||||||||||||||||
| Data source: Water utility infrastructural data. | ||||||||||||||||||||||||||||||||
| Reference values: Adapted from [34], since reference values were not proposed in [28]. | ||||||||||||||||||||||||||||||||
| M1.3.2a | Pipes value index | [-] | Level II | |||||||||||||||||||||||||||||
| Defined as the ratio between the current pipes value and its replacement cost. Adapted from [28], identified as PAA04. | ||||||||||||||||||||||||||||||||
| Calculation Similar to M1.3.2. | ||||||||||||||||||||||||||||||||
| Data source: Water utility infrastructural data. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed herein to be equal to M1.3.2. | ||||||||||||||||||||||||||||||||
| M1.3.2b | Pumps value index | [-] | Level II | |||||||||||||||||||||||||||||
| Defined as the ratio between the current pumps value and its replacement cost. Adapted from [28], identified as PAA04. | ||||||||||||||||||||||||||||||||
| Calculation Similar to M1.3.2. | ||||||||||||||||||||||||||||||||
| Data source: Water utility infrastructural data. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed herein to be equal to M1.3.2. | ||||||||||||||||||||||||||||||||
| M1.3.2c | Tanks value index | [-] | Level II | |||||||||||||||||||||||||||||
| Defined as the ratio between the current storage tanks value and its replacement cost. Adapted from [28], identified as PAA04. | ||||||||||||||||||||||||||||||||
| Calculation Similar to M1.3.2. | ||||||||||||||||||||||||||||||||
| Data source: Water utility infrastructural data. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed herein to be equal to M1.3.2. | ||||||||||||||||||||||||||||||||
| M1.4.1 | System supplied energy index | [-] | Level I | |||||||||||||||||||||||||||||
| Addresses energy efficiency. It is defined as the energy supplied to the system per the minimum energy necessary. Source: [30], identified as dE3. | ||||||||||||||||||||||||||||||||
| Calculation System supplied energy index, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A11) | ||||||||||||||||||||||||||||||||
| where is the energy supplied to the system (kWh) and is the minimum energy necessary (kWh). | ||||||||||||||||||||||||||||||||
| Data source: Simplified energy balance. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [30], for indicator dE3. | ||||||||||||||||||||||||||||||||
| M1.4.1a | Energy efficiency in pumping stations | [kWh/(m3·100m)] | Level II | |||||||||||||||||||||||||||||
| Addresses energy efficiency, particularly regarding pumping inefficiencies. It is defined as the normalised average energy consumption of pumping stations. Source: [28], identified as AA16. | ||||||||||||||||||||||||||||||||
| Calculation Energy efficiency in pumping stations, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A12) | ||||||||||||||||||||||||||||||||
| where is he total energy consumption for pumping and is the uniformization factor, calculates as: | ||||||||||||||||||||||||||||||||
| (A13) | ||||||||||||||||||||||||||||||||
| where is the total number of pumping stations (No.), the water volume of pumping station (m3/h) and the manometric pressure head of pumping station (m). | ||||||||||||||||||||||||||||||||
| Data source: Pumping data. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [28], for indicator AA16. | ||||||||||||||||||||||||||||||||
| M1.4.1b | Surplus energy index | [-] | Level II | |||||||||||||||||||||||||||||
| Addresses energy efficiency, particularly regarding surplus energy. It is defined as the surplus energy of the system per the minimum energy necessary. Proposed in this study. | ||||||||||||||||||||||||||||||||
| Calculation Surplus energy index, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A14) | ||||||||||||||||||||||||||||||||
| where is the surplus energy of the system (kWh), is the minimum energy (kWh), γ is the specific weight of water (9800 N/m3), is the conversion factor from Ws to kWh, is the total number of demand nodes (No.), is the total number of timesteps (No.), is the demand associated with authorised consumption in node (m3/s) for time , is the hydraulic head in node (m) at time , is the reference elevation (m) and is the timestep (s). | ||||||||||||||||||||||||||||||||
| Data source: Complete energy balance and system hydraulic model. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed in this study, see Section 3.2, as such: if is equal to 0, the supplied energy equals the minimum required energy and there is no additional energy available to be used in case of a demand increase. If surplus energy index equals 1, the supplied energy is the double of the minimum required energy, indicating that the system may be overdesigned. A threshold of 0.75 of the minimum energy is proposed to alert the approximation of high surplus energy. | ||||||||||||||||||||||||||||||||
| M1.4.1c | Average unit head loss | [m/km] | Level II | |||||||||||||||||||||||||||||
| Addresses energy efficiency, particularly regarding unit head loss. It is defined as the average head loss weighted with flow and length for the entire pipe network. Source: [38]. | ||||||||||||||||||||||||||||||||
| Calculation Average unit head loss, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A15) | ||||||||||||||||||||||||||||||||
| where is the total number of pipes (No.), is the head loss in pipe (m/km), is the flowrate relative to pipe (m3/s) and is the length of pipe (m). | ||||||||||||||||||||||||||||||||
| Data source: System hydraulic model. | ||||||||||||||||||||||||||||||||
| Reference values: Suggested herein based on threshold values from [41], since reference values were not proposed in [38]. | ||||||||||||||||||||||||||||||||
| M1.4.2 | Water losses | [L/(connection·day)] | Level I | |||||||||||||||||||||||||||||
| Addresses water efficiency. It is defined as the total water losses (real and apparent water losses) per service connections. Adapted from [28], identified as AA15. | ||||||||||||||||||||||||||||||||
| Calculation Water losses, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A16) | ||||||||||||||||||||||||||||||||
| where is the volume of water losses (l), is the volume of real water losses (l), is the volume of apparent water losses (l) and is the total number of service connection (No.). | ||||||||||||||||||||||||||||||||
| Data source: Water balance. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed in this study, see Section 3.2. Water losses are a sum of real and apparent water losses. A comparison between the reported real water losses and apparent water losses, demonstrated that water losses are mainly due to real water losses, without a relationship with the number of apparent water losses. As such, water losses reference values are considered similar to the real water losses (see M1.4.2a) added 50 L/[connection.day]. | ||||||||||||||||||||||||||||||||
| M1.4.2a | Real water losses | [L/(connection·day)] | Level II | |||||||||||||||||||||||||||||
| Addresses water efficiency, particularly regarding real water losses. It is defined as the real water losses per service connections. Source: [28], identified as AA15. | ||||||||||||||||||||||||||||||||
| Calculation Real water losses, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A17) | ||||||||||||||||||||||||||||||||
| where is the volume of real water losses (l) and is the total number of service connection (No.). | ||||||||||||||||||||||||||||||||
| Data source: Water balance. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [28], for indicator AA15. | ||||||||||||||||||||||||||||||||
| M1.4.2b | Apparent water losses | [% volume] | Level II | |||||||||||||||||||||||||||||
| Addresses water efficiency, particularly regarding apparent water losses. It is defined as the percentage of the water provided to the system that corresponds to apparent losses. Source: [33], identified as Op25. | ||||||||||||||||||||||||||||||||
| Calculation Apparent water losses, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A18) | ||||||||||||||||||||||||||||||||
| where is the volume of apparent water losses (l) and is the water provided to the system (l). Note: in water distribution systems, refers to the system input volume minus exported water. | ||||||||||||||||||||||||||||||||
| Data source: Water balance. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [35], since reference values were not proposed in [33]. | ||||||||||||||||||||||||||||||||
| M2.1.1 | Level of dependency to bulk water utility | [% input volume] | Level I | |||||||||||||||||||||||||||||
| Assesses the system’s level of dependency on the bulk water utility. It is defined as the percentage of the system input volume that is provided by the bulk water utility. Adapted from [7], identified as PWts23. | ||||||||||||||||||||||||||||||||
| Calculation Level of dependency on the bulk water utility, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A19) | ||||||||||||||||||||||||||||||||
| where is the volume is provided by the bulk water utility (m3) and is the system input volume (m3). | ||||||||||||||||||||||||||||||||
| Data source: Water utility volumes data. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [7], for indicator PWts23. | ||||||||||||||||||||||||||||||||
| M2.1.2 | Level of dependency on pumping | [% input volume] | Level I | |||||||||||||||||||||||||||||
| Assesses the system’s level of dependency on pumping. It is defined as the percentage of the system input volume that is pumped. Adapted from [7], identified as PWts23. | ||||||||||||||||||||||||||||||||
| Calculation Level of dependency on pumping, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A20) | ||||||||||||||||||||||||||||||||
| where is the system input volume (m3) and is the volume that is (once) pumped (m3), that is, water that is pumped twice or more times must only be accounted once. | ||||||||||||||||||||||||||||||||
| Data source: Water utility volumes data. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from, for indicator PWts23. | ||||||||||||||||||||||||||||||||
| M2.2.1 | Treated water storage capacity | [days] | Level I | |||||||||||||||||||||||||||||
| Assesses the treated water supply autonomy through storage tanks. It is defined as the total capacity of treated water storage over the system input volume. Source: [33], identified as Ph3. | ||||||||||||||||||||||||||||||||
| Calculation The treated water storage capacity, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A21) | ||||||||||||||||||||||||||||||||
| where is the volume of reservoir (m3), is the system input volume (m3/year) and is the number of reservoirs (No.). | ||||||||||||||||||||||||||||||||
| Data source: Infrastructure and volumes data. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [7], for indicator PWts23, which corresponds to Ph3 from [33]. Reference values were not proposed in [33]. | ||||||||||||||||||||||||||||||||
| M2.2.2 | Level of autonomy to electric grid from alternative infrastructures | [% dependent volume] | Level I | |||||||||||||||||||||||||||||
| Assesses the system capacity to keep providing water in case of an electric grid failure, through alternative infrastructures. treated water supply autonomy through storage tanks. It is defined as the percentage of pumping dependent volume, that benefit from alternative infrastructures (e.g., bypass to pumping station). Adapted from [7], identified as PWts25. | ||||||||||||||||||||||||||||||||
| Calculation Level of autonomy to electric grid from alternative infrastructures, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A22) | ||||||||||||||||||||||||||||||||
| where is the pumping dependent volume that benefit from alternative infrastructures (m3) and is the pumped volume (m3). | ||||||||||||||||||||||||||||||||
| Data source: Water utility volumes data. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [7], for indicator PWts25. | ||||||||||||||||||||||||||||||||
| M2.2.3 | Energy self-production | [% pumped energy] | Level I | |||||||||||||||||||||||||||||
| Assesses the water utility energy self-production. It is defined as the percentage of the consumed energy that came from self-production. Source: [28], identified as AA18. | ||||||||||||||||||||||||||||||||
| Calculation The energy self-production index, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A23) | ||||||||||||||||||||||||||||||||
| where is the energy from self-production (kWh) and is the total consumed energy (kWh). | ||||||||||||||||||||||||||||||||
| Data source: Energy data. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [28], for indicator AA18. | ||||||||||||||||||||||||||||||||
| M2.2.3a | Wind energy self-production | [% pumped energy] | Level II | |||||||||||||||||||||||||||||
| Assesses the water utility wind energy self-production. It is defined as the percentage of the consumed energy that came from wind self-production. Adapted from [28], identified as AA18. | ||||||||||||||||||||||||||||||||
| Calculation Similar to M2.2.3. | ||||||||||||||||||||||||||||||||
| Data source: Energy data. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed herein to be equal to M2.2.3. | ||||||||||||||||||||||||||||||||
| M2.2.3b | Solar energy self-production | [% pumped energy] | Level II | |||||||||||||||||||||||||||||
| Assesses the water utility solar energy self-production. It is defined as the percentage of the consumed energy that came from solar self-production. Adapted from [28], identified as AA18. | ||||||||||||||||||||||||||||||||
| Calculation Similar to M2.2.3. | ||||||||||||||||||||||||||||||||
| Data source: Energy data. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed herein to be equal to M2.2.3. | ||||||||||||||||||||||||||||||||
| M2.2.3c | Hydropower energy self-production | [% pumped energy] | Level II | |||||||||||||||||||||||||||||
| Assesses the water utility hydropower energy self-production. It is defined as the percentage of the consumed energy that came from Hydropower self-production. Adapted from [28], identified as AA18. | ||||||||||||||||||||||||||||||||
| Calculation Similar to M2.2.3. | ||||||||||||||||||||||||||||||||
| Data source: Energy data. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed herein to be equal to M2.2.3. | ||||||||||||||||||||||||||||||||
| M2.3.1 | Potential alternative water sources | [% volume] | Level I | |||||||||||||||||||||||||||||
| Assesses the potential alternative water sources from the water utility, active and inactive. It is defined as the percentage of yield capacity of alternative sources per system input volume. Adapted from [33], identified as WR3. | ||||||||||||||||||||||||||||||||
| Calculation The potential alternative water sources index, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A24) | ||||||||||||||||||||||||||||||||
| where is the yield capacity of alternative sources (m3) and is the system input volume (m3). | ||||||||||||||||||||||||||||||||
| Data source: Water utility data. | ||||||||||||||||||||||||||||||||
| Reference values: Suggested herein, considering that a yield capacity of alternative sources lower than 50% of the total input volume has poor performance, between 50% and 75% it has fair performance, and above 75% has good performance. | ||||||||||||||||||||||||||||||||
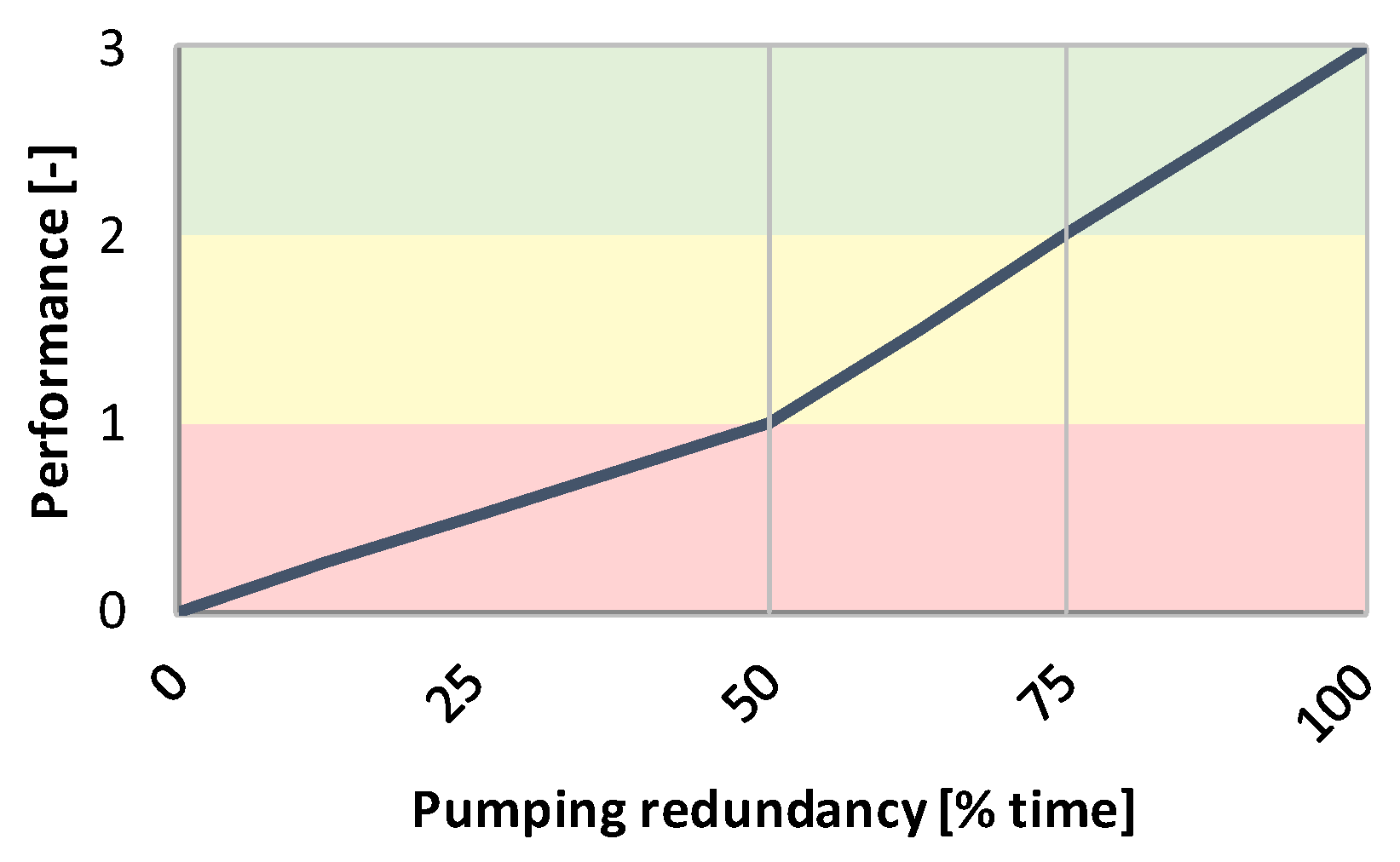
| M2.3.2 | Pumping redundancy | [% time] | Level I | |||||||||||||||||||||||||||||
| Assesses the redundancy of pumping stations. It is defined as the percentage of time pumping groups are not working simultaneously (including the reserve pump) by the total pumping station functioning time. Proposed in this study. | ||||||||||||||||||||||||||||||||
| Calculation The redundancy of pumping stations, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A25) | ||||||||||||||||||||||||||||||||
| where is the time pumping groups are working simultaneously (h) and is the total pumping station functioning time (h). | ||||||||||||||||||||||||||||||||
| Data source: Water utility. | ||||||||||||||||||||||||||||||||
| Reference values: Suggested herein, considering that the time pumping groups have, at least, one pump not working lower than 50% of the total pumping station functioning time has poor performance, between 50% and 75% it has fair performance, and above 75% has good performance. | ||||||||||||||||||||||||||||||||
| M2.3.3 | Pipes topological redundancy | [-] | Level I | |||||||||||||||||||||||||||||
| Assessed by the meshedness coefficient, defined as fraction between the total and the maximum number of independent loops in planar graphs. Source: [18]. | ||||||||||||||||||||||||||||||||
| Calculation The meshedness coefficient, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A26) | ||||||||||||||||||||||||||||||||
| where is the number of edges, is the number of nodes of the mathematical graph. | ||||||||||||||||||||||||||||||||
| Data source: System hydraulic model. | ||||||||||||||||||||||||||||||||
| Reference values: Suggested herein, where bellow 0.01 corresponds to poor performance, between 0.01 and 0.1 corresponds to fair performance and values higher than 0.1 corresponds to good performance. | ||||||||||||||||||||||||||||||||
| M3.1.1 | Number of failures in the last disaster | [No./100 km] | Level I | |||||||||||||||||||||||||||||
| Addresses failures in the last disaster. It is defined as the total number of failures (all assets) in the last disaster per 100 km of network length. Adapted from [7], identified as PWts42. | ||||||||||||||||||||||||||||||||
| Calculation Equal to Equation (A4), with being the total number of failures in the last disaster (No.). | ||||||||||||||||||||||||||||||||
| Data source: Water utility data. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed in this study to be the same as indicator PWts42 of [7], herein corresponding to M3.1.1a, as the main contributor are the network pipes. | ||||||||||||||||||||||||||||||||
| M3.1.1a | Pipes failures in the last disaster | [No./(100 km·year)] | Level II | |||||||||||||||||||||||||||||
| Addresses pipe failures frequency in the last disaster. It is defined as the total number of pipe failures in the last disaster per 100 km of network length. Source: [7], identified as PWts42. | ||||||||||||||||||||||||||||||||
| Calculation Equal to Equation (A5), with being the total number of pipe failures in the last disaster (No.). | ||||||||||||||||||||||||||||||||
| Data source: Water utility data. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [7], for indicator PWts42. | ||||||||||||||||||||||||||||||||
| M3.1.1b | Pump failures in the last disaster | [days/(pump)] | Level II | |||||||||||||||||||||||||||||
| Addresses pump failures frequency in the system. It is defined as the number of days that pumps are out of order, due to the last disaster, by the total number of pumps. Source: [7], identified as PWts41. | ||||||||||||||||||||||||||||||||
| Calculation Equal to Equation (A6), with being the total pump failures duration in the last disaster (days). | ||||||||||||||||||||||||||||||||
| Data source: Water utility data. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [7], for indicator PWts41. | ||||||||||||||||||||||||||||||||
| M3.1.1c | Service connection failures in the last disaster | [No./(1000 connections)] | Level II | |||||||||||||||||||||||||||||
| Addresses service connection failures frequency in the last disaster. It is defined as the number of service connection failures in the last disaster per 1000 connections. Source: [7], identified as PWts43. | ||||||||||||||||||||||||||||||||
| Calculation Equal to Equation (A7), with being the number of service connection failures in the last disaster (No.). | ||||||||||||||||||||||||||||||||
| Data source: Water utility data. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [7], for indicator PWts43. | ||||||||||||||||||||||||||||||||
| M3.1.2 | Duration of failure till restoration in the last disaster | [Days] | Level I | |||||||||||||||||||||||||||||
| Addresses failures duration in the last disaster. It is defined as the maximum out-of-service period for all failures (including recovery time) in the last disaster. Source: [7], identified as PWts49. | ||||||||||||||||||||||||||||||||
| Calculation Duration of failure (days) till restoration in the last disaster is calculated as the maximum out-of-service period for all failures (including recovery time) in the last disaster. | ||||||||||||||||||||||||||||||||
| Data source: Water utility data. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [7], for indicator PWts49. | ||||||||||||||||||||||||||||||||
| M4.1.1 | Number of service interruptions | [No./(1000 connections·year)] | Level I | |||||||||||||||||||||||||||||
| Addresses frequency of service interruptions. It is defined as the number of service interruptions pondered by 1000 connection. Source: [32], identified as AA03b. | ||||||||||||||||||||||||||||||||
| Calculation Performance indicator number of service interruptions is calculated as: | ||||||||||||||||||||||||||||||||
| (A27) | ||||||||||||||||||||||||||||||||
| where is the total number of failures in service connection (No.) and is the total number of service connections (No.). | ||||||||||||||||||||||||||||||||
| Data source: Water utility data. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [32], identified as AA03b. | ||||||||||||||||||||||||||||||||
| M4.1.1a | Number of interruptions due to pipe and equipment failures | [No./(1000 connections·year)] | Level II | |||||||||||||||||||||||||||||
| Addresses frequency of service interruptions due to pipe and equipment (pumps, valves, hydrants) failures. It is defined as the number of service interruptions due to pipe and equipment failures pondered by 1000 connection. Adapted from [32], identified as AA03b. | ||||||||||||||||||||||||||||||||
| Calculation Similar to M4.1.1, considering only service interruptions due to pipe and equipment failures. | ||||||||||||||||||||||||||||||||
| Data source: Water utility data. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed herein to be equal to M4.1.1. | ||||||||||||||||||||||||||||||||
| M4.1.1b | Number of interruptions due to rehabilitation or new constructions | [No./(1000 connections·year)] | Level II | |||||||||||||||||||||||||||||
| Addresses frequency of service interruptions due to rehabilitation or new constructions. It is defined as the number of service interruptions due to rehabilitation or new constructions pondered by 1000 connection. Adapted from [32], identified as AA03b. | ||||||||||||||||||||||||||||||||
| Calculation Similar to M4.1.1, considering only service interruptions due to rehabilitation or new constructions. | ||||||||||||||||||||||||||||||||
| Data source: Water utility data. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed herein to be equal to M4.1.1. | ||||||||||||||||||||||||||||||||
| M4.1.1c | Number of interruptions due to water quality inadequacy | [No./(1000 connections·year)] | Level II | |||||||||||||||||||||||||||||
| Addresses frequency of service interruptions due to water quality inadequacy. It is defined as the number of service interruptions due to water quality inadequacy pondered by 1000 connection. Adapted from [32], identified as AA03b. | ||||||||||||||||||||||||||||||||
| Calculation Similar to M4.1.1, considering only service interruptions due water quality inadequacy. | ||||||||||||||||||||||||||||||||
| Data source: Water utility data. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed herein to be equal to M4.1.1. | ||||||||||||||||||||||||||||||||
| M4.1.1d | Number of interruptions due to external issues | [No./(1000 connections·year)] | Level II | |||||||||||||||||||||||||||||
| Addresses frequency of service interruptions due to external issues. It is defined as the number of service interruptions due to external issues pondered by 1000 connection. Adapted from [32], identified as AA03b. | ||||||||||||||||||||||||||||||||
| Calculation Similar to M4.1.1, considering only service interruptions due external issues. | ||||||||||||||||||||||||||||||||
| Data source: Water utility data. | ||||||||||||||||||||||||||||||||
| Reference values: Proposed herein to be equal to M4.1.1. | ||||||||||||||||||||||||||||||||
| M4.1.2 | Average duration of service interruptions | [h] | Level I | |||||||||||||||||||||||||||||
| Addresses duration of service interruptions. It is defined as the average duration of all service interruptions. Suggested herein. | ||||||||||||||||||||||||||||||||
| Calculation Performance indicator number of service interruptions is calculated as: | ||||||||||||||||||||||||||||||||
| (A28) | ||||||||||||||||||||||||||||||||
| where is the duration (h) of interruption and is the total number of service interruptions (No.). | ||||||||||||||||||||||||||||||||
| Data source: Water utility data. | ||||||||||||||||||||||||||||||||
| Reference values: Suggested herein, based on the technical guides from the Portuguese regulatory entity for the water sector. It is considered that an average duration below 4 h correspond to good performance, between 4 and 6 h it corresponds to air performance, and service interruptions above 6 h is has poor performance. | ||||||||||||||||||||||||||||||||
| M4.2.1 | Quality of supplied water | [% tests] | Level I | |||||||||||||||||||||||||||||
| Addresses water quality delivered to the consumers. It is defined as the percentage of total number of treated water tests complying with the applicable standards or legislation per total number of tests of treated water carried out. Source: [33], identified as QS18 | ||||||||||||||||||||||||||||||||
| Calculation Performance indicator quality of supplied water, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A29) | ||||||||||||||||||||||||||||||||
| where is the of total number of treated water tests complying with the applicable standards or legislation (No.) and is the total number of tests of treated water carried out (No.). | ||||||||||||||||||||||||||||||||
| Data source: Water quality data. | ||||||||||||||||||||||||||||||||
| Reference values: Suggested herein, considering that over 90% of complying tests corresponds to good performance, between 70% and 90% corresponds to fair performance and below 70% the system has poor performance. | ||||||||||||||||||||||||||||||||
| M4.2.1a | Minimum velocity performance index | [-] | Level II | |||||||||||||||||||||||||||||
| Addresses the performance of minimum velocity in the network pipes. Source: [39,40]. | ||||||||||||||||||||||||||||||||
| Calculation Relates pipes velocity (m/s) with a performance function for each pipe. Herein, the performance function is as follows: | ||||||||||||||||||||||||||||||||
| Excellent [3] | Good [2–3] | Fair [1–2] | Poor [0–1] | Null [0] | ||||||||||||||||||||||||||||
| ≥0.5 | ≥ and <0.5 | ≥ and < | ≥0 and < | 0 | ||||||||||||||||||||||||||||
| where , with the pipe’s diameter (mm), and . The network minimum velocity performance () is obtained through the weighted average by the pipes flowrate. | ||||||||||||||||||||||||||||||||
| (A30) | ||||||||||||||||||||||||||||||||
| where is the total number of pipes (No.), is the minimum velocity performance of pipe (-) and is the flowrate relative to pipe (m3/s). | ||||||||||||||||||||||||||||||||
| Data source: System hydraulic model. | ||||||||||||||||||||||||||||||||
| Reference values: Considering the performance index varies between 0 and 3, the reference values correspond to the same intervals. | ||||||||||||||||||||||||||||||||
| M4.2.1b | Water age performance index | [-] | Level II | |||||||||||||||||||||||||||||
| Addresses the performance of water age at the network nodes. Source: [39,40]. | ||||||||||||||||||||||||||||||||
| Calculation Relates water age (h) with a performance function for each node. Herein, the performance function is as follows: | ||||||||||||||||||||||||||||||||
| Excellent [3] | Good [2–3] | Fair [1–2] | Poor [0–1] | Null [0] | ||||||||||||||||||||||||||||
| 0 | >0 and ≤ | > and ≤ | > and ≤1.5 | >1.5 | ||||||||||||||||||||||||||||
| where h, and h. The network water age performance () is obtained through the weighted average by the node demand. | ||||||||||||||||||||||||||||||||
| (A31) | ||||||||||||||||||||||||||||||||
| where is the total number of demand nodes (No.), is the minimum velocity performance of node (-) and is the demand in node (m3/s). | ||||||||||||||||||||||||||||||||
| Data source: System hydraulic model. | ||||||||||||||||||||||||||||||||
| Reference values: Considering the performance index varies between 0 and 3, the reference values correspond to the same intervals. | ||||||||||||||||||||||||||||||||
| M4.2.1c | Network travel time index | [-] | Level II | |||||||||||||||||||||||||||||
| Addresses the performance of network travel time at the network nodes. Adapted from [39,40]. | ||||||||||||||||||||||||||||||||
| Calculation Relates network travel time (h) with a performance function for each node. Herein, the performance function is as follows: | ||||||||||||||||||||||||||||||||
| Excellent [3] | Good [2–3] | Fair [1–2] | Poor [0–1] | Null [0] | ||||||||||||||||||||||||||||
| ≤ | > and ≤ | > and ≤ | > and ≤1.5 | ≥1.5 | ||||||||||||||||||||||||||||
| where h, and h. The network travel time performance is obtained through the weighted average by the node demand, similar to Equation (A31). | ||||||||||||||||||||||||||||||||
| Data source: System hydraulic model. | ||||||||||||||||||||||||||||||||
| Reference values: Considering the performance index varies between 0 and 3, the reference values correspond to the same intervals. | ||||||||||||||||||||||||||||||||
| M4.3.1 | Service complaints due to lack of pressure | [No. complaints/(1000 connections)] | Level I | |||||||||||||||||||||||||||||
| Addresses lack of pressure in the system through service complaints. It is defined as the number of service complaints due to lack of pressure per 1000 connections. Adapted from [33], identified as AA05. | ||||||||||||||||||||||||||||||||
| Calculation Performance indicator quality of service complaints due to lack of pressure, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A32) | ||||||||||||||||||||||||||||||||
| where is the number of service complaints due to lack of pressure and is the total number of service connections. | ||||||||||||||||||||||||||||||||
| Data source: Water utility | ||||||||||||||||||||||||||||||||
| Reference values: Suggested herein based on the results of Portuguese water utilities, considering that bellow 0.15 corresponds to good performance, between 0.15 and 1.5 corresponds to fair performance and over 1.5 corresponds to poor performance. | ||||||||||||||||||||||||||||||||
| M4.3.1a | Minimum pressure performance index | [-] | Level II | |||||||||||||||||||||||||||||
| Addresses the performance of minimum pressure at the network nodes. Source: [39,40]. | ||||||||||||||||||||||||||||||||
| Calculation Relates pressure (m) with a performance function for each node. Herein, the performance function is as follows: | ||||||||||||||||||||||||||||||||
| Excellent [3] | Good [2–3] | Fair [1–2] | Poor [0–1] | Null [0] | ||||||||||||||||||||||||||||
| ≥ | ≥ and < | ≥ and < | ≥ and < | 10 m | ||||||||||||||||||||||||||||
| where m, corresponding to maximum regulatory pressure, and m, corresponding to the minimum required pressure established by the water utility. The network minimum pressure performance is obtained through the weighted average by the node demand, similar to Equation (A31). | ||||||||||||||||||||||||||||||||
| Data source: System hydraulic model. | ||||||||||||||||||||||||||||||||
| Reference values: Considering the performance index varies between 0 and 3, the reference values correspond to the same intervals. | ||||||||||||||||||||||||||||||||
| M4.3.1b | Maximum pressure performance index | [-] | Level II | |||||||||||||||||||||||||||||
| Addresses the performance of maximum pressure at the network nodes. Source: [39,40]. | ||||||||||||||||||||||||||||||||
| Calculation Relates pressure (m) with a performance function for each node. Herein, the performance function is as follows: | ||||||||||||||||||||||||||||||||
| Excellent [3] | Good [2–3] | Fair [1–2] | Poor [0–1] | Null [0] | ||||||||||||||||||||||||||||
| ≤ | > and ≤ | > and ≤ | > and ≤1.5 | ≥1.5 | ||||||||||||||||||||||||||||
| where m, corresponding to maximum regulatory pressure. The network maximum pressure performance is obtained through the weighted average by the node demand, similar to Equation (A31). | ||||||||||||||||||||||||||||||||
| Data source: System hydraulic model. | ||||||||||||||||||||||||||||||||
| Reference values: Considering the performance index varies between 0 and 3, the reference values correspond to the same intervals. | ||||||||||||||||||||||||||||||||
| M4.3.1c | Pressure fluctuation performance index | [-] | Level II | |||||||||||||||||||||||||||||
| Addresses the performance of pressure fluctuation at the network nodes. Source: [39,40]. | ||||||||||||||||||||||||||||||||
| Calculation Relates pressure fluctuation (m) with a performance function for each node. Herein, the performance function is as follows: | ||||||||||||||||||||||||||||||||
| Excellent [3] | Good [2–3] | Fair [1–2] | Poor [0–1] | Null [0] | ||||||||||||||||||||||||||||
| 0 m | >0 and ≤ | > and ≤ | > and ≤1.5 | >1.5 | ||||||||||||||||||||||||||||
| where m. The network pressure fluctuation performance is obtained through the weighted average by the node demand, similar to Equation (A31). | ||||||||||||||||||||||||||||||||
| Data source: System hydraulic model. | ||||||||||||||||||||||||||||||||
| Reference values: Considering the performance index varies between 0 and 3, the reference values correspond to the same intervals. | ||||||||||||||||||||||||||||||||
| M5.1.1 | Drinking water supplied for non-potable uses | [% drinking water] | Level I | |||||||||||||||||||||||||||||
| Addresses non-potable uses. It is defined as the percentage of drinking water used for non-potable uses per total input volume. Source: [7], identified as FWts35. | ||||||||||||||||||||||||||||||||
| Calculation The drinking water supplied for non-potable uses index, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A33) | ||||||||||||||||||||||||||||||||
| where is the drinking water supplied for non-potable uses (m3) and is the system input volume (m3). | ||||||||||||||||||||||||||||||||
| Data source: Water utility volumes data. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [7], identified as FWts35. | ||||||||||||||||||||||||||||||||
| M5.1.2 | Recycled water supplied for non-potable uses | [% total volume] | Level I | |||||||||||||||||||||||||||||
| Addresses recycled water. It is defined as the percentage of recycled water supplied for non-potable uses per total input volume. Adapted from [33], identified as WR4. | ||||||||||||||||||||||||||||||||
| Calculation The recycled water supplied for non-potable uses index, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A34) | ||||||||||||||||||||||||||||||||
| where is the recycled water supplied (m3) and is the potable system input volume (m3). | ||||||||||||||||||||||||||||||||
| Data source: Water utility volumes data. | ||||||||||||||||||||||||||||||||
| Reference values: Suggested herein, considering that below 10% of recycled water corresponds to poor performance, between 10% and 25% corresponds to fair performance and above 25% the system has good performance. | ||||||||||||||||||||||||||||||||
| M5.2.1 | Network resilience index | [-] | Level I | |||||||||||||||||||||||||||||
| Addresses the hydraulic capacity to overcome eventual increasing demands. It is defined as the ratio of surplus energy per energy in excess, providing the energy available at the consumption nodes above the minimum required to supply the consumers, incorporating a uniformity coefficient rewarding the uniformity of the pipes’ diameter. Source: [11]. | ||||||||||||||||||||||||||||||||
| Calculation The network resilience index, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A35) | ||||||||||||||||||||||||||||||||
| (A36) | ||||||||||||||||||||||||||||||||
| where is the specific weight of water (9800 N/m3), is the total number of demand nodes (No.), is the total number of reservoirs, is the total number of pumps (No.), is the demand in node (m3/s), is the flow input from reservoir (m3/s), is the power of pump (kW), is the head in node (m), is the required head in node (m), is the uniformity coefficient of node for the network resilience index (-), is the number of pipes entering into node (No.), is the diameter (mm) of pipe that is connected to node . | ||||||||||||||||||||||||||||||||
| Data source: System hydraulic model. | ||||||||||||||||||||||||||||||||
| Reference values: Suggested herein, considering that NRI below 0.5 correspond to poor performance, between 0.5 and 0.75 corresponds to fair performance and above 0.75 correspond to good performance. | ||||||||||||||||||||||||||||||||
| M6.1.1 | Water supply interruptions for consumers in the last disaster | [% connections] | Level I | |||||||||||||||||||||||||||||
| Addresses water supply interruptions in the last disaster. It is defined as the percentage of connections affected by water supply interruptions in the last disaster. Adapted from [7], identified as FWts58. | ||||||||||||||||||||||||||||||||
| Calculation Performance indicator number of service interruptions, , is calculated as: | ||||||||||||||||||||||||||||||||
| (A37) | ||||||||||||||||||||||||||||||||
| where is the number of connections (No.) affected by water supply interruptions in the last disaster and is the total number of service connections (No.). | ||||||||||||||||||||||||||||||||
| Data source: Water utility data. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [7], identified as FWts58. | ||||||||||||||||||||||||||||||||
| M6.1.2 | Total duration of water supply interruption in the last disaster | [days] | Level I | |||||||||||||||||||||||||||||
| Addresses water supply interruptions in the last disaster. It is defined as the days of water supply interruptions in the last disaster. Adapted from [7], identified as FWts66. | ||||||||||||||||||||||||||||||||
| Calculation Number of days that supply was interrupted in the last disaster. | ||||||||||||||||||||||||||||||||
| Data source: Water utility data. | ||||||||||||||||||||||||||||||||
| Reference values: Retrieved from [7], identified as FWts66. | ||||||||||||||||||||||||||||||||
Appendix B
| C1.1 Infrastructure Knowledge | System | R4 | R6 | |
| M1.1.1 | Infrastructural knowledge index [-] | 196 ⏺ | 196 ⏺ | 196 ⏺ |
| M1.1.2 | Knowledge and protection of critical assets index [-] | 0.0 ⏺ | 0.0 ⏺ | 0.0 ⏺ |
| M1.1.3 | Assets criticality index [-] | 0.53 ⏺ | 0.99 ⏺ | 0.97 ⏺ |
| M1.1.3a | Pipes criticality index [-] | 0.14 ⏺ | 0.13 ⏺ | 0.31 ⏺ |
| M1.1.3b | Pumps criticality index [-] | 0.35 ⏺ | 0.09 ⏺ | 0.71 ⏺ |
| M1.1.3c | Storage tanks criticality index [-] | 0.53 ⏺ | 0.99 ⏺ | 0.97 ⏺ |
| C1.2 Infrastructure integrity | System | R4 | R6 | |
| M1.2.1 | Number of failures [No./(100 km·year)] | 13.6 ⏺ | 6.0 ⏺ | 23.9 ⏺ |
| M1.2.1a | Pipes failures [No./(100 km·year)] | 12.8 ⏺ | 6.0 ⏺ | 21.9 ⏺ |
| M1.2.1b | Pump failures [days/(pump·year)] | 6.1 ⏺ | 0.0 ⏺ | 9.3 ⏺ |
| M1.2.1c | Service connection failures [No./(1000 connections·year)] | NA | NA | NA |
| M1.2.2 | Total duration of failures [Days/No. failure] | 8.8 ⏺ | 0.0 ⏺ | 11.7 ⏺ |
| C1.3 Infrastructure sustainability | System | R4 | R6 | |
| M1.3.1 | Pipes rehabilitation [%/year] | 0.2 ⏺ | 0.2 ⏺ | 0.2 ⏺ |
| M1.3.2 | Infrastructure value index [-] | 0.4 ⏺ | 0.4 ⏺ | 0.2 ⏺ |
| M1.3.2a | Pipes infrastructure value index [-] | 0.18 ⏺ | 0.26 ⏺ | 0.05 ⏺ |
| M1.3.2b | Pumps infrastructure value index [-] | 0.16 ⏺ | 0.49 ⏺ | 0.00 ⏺ |
| M1.3.2c | Storage tanks infrastructure value index [-] | 0.43 ⏺ | 0.43 ⏺ | 0.36 ⏺ |
| C1.4 Water and energy efficiency | System | R4 | R6 | |
| M1.4.1 | System supplied energy index [-] | 2.24 ⏺ | 2.32 ⏺ | 2.15 ⏺ |
| M1.4.1a | Energy efficiency in pumping stations [kWh/(m3 · 100 m)] | 0.57 ⏺ | 0.51 ⏺ | 0.58 ⏺ |
| M1.4.1b | Surplus energy index [-] | 0.73 ⏺ | 1.00 ⏺ | 0.43 ⏺ |
| M1.4.1c | Average unit head loss [m/km] | 2.98 ⏺ | 2.97 ⏺ | 2.99 ⏺ |
| M1.4.2 | Water losses [L/(connection·day)] | 157 ⏺ | 147 ⏺ | 166 ⏺ |
| M1.4.2a | Real water losses [L/(connection·day)] | 120 ⏺ | 98 ⏺ | 140 ⏺ |
| M1.4.2b | Apparent water losses [%volume] | 2% ⏺ | 2% ⏺ | 1% ⏺ |
| C2.1 Dependency on other services | System | R4 | R6 | |
| M2.1.1 | Level of dependency on bulk water utility [%volume] | 100% ⏺ | 100% ⏺ | 100% ⏺ |
| M2.1.2 | Level of dependency on pumping [% input volume] | 60% ⏺ | 16% ⏺ | 100% ⏺ |
| C2.2 Autonomy | System | R4 | R6 | |
| M2.2.1 | Treated water storage capacity [Days] | 1.1 ⏺ | 0.2 ⏺ | 1.9 ⏺ |
| M2.2.2 | Level of autonomy to electric grid from alternative infrastructures [% dependent volume] | 0% ⏺ | 0% ⏺ | 0% ⏺ |
| M2.2.3 | Energy self-production [% pumped energy] | 0% ⏺ | 0% ⏺ | 0% ⏺ |
| M2.2.3a | Wind energy self-production [% pumped energy] | 0% ⏺ | 0% ⏺ | 0% ⏺ |
| M2.2.3b | Solar energy self-production [% pumped energy] | 0% ⏺ | 0% ⏺ | 0% ⏺ |
| M2.2.3c | Hydropower energy self-production [% pumped energy] | 0% ⏺ | 0% ⏺ | 0% ⏺ |
| C2.3 Redundancy | System | R4 | R6 | |
| M2.3.1 | Potential alternative sources [%volume] | 3% ⏺ | 5% ⏺ | 0% ⏺ |
| M2.3.2 | Pumping redundancy [%time] | 88% ⏺ | 75% ⏺ | 100% ⏺ |
| M2.3.3 | Pipes topological redundancy [-] | 0.02 ⏺ | 0.03 ⏺ | 0.02 ⏺ |
| C3.1 Assessment of failures in the last disaster | System | R4 | R6 | |
| M3.1.1 | Number of failures in the last disaster [No./100 km] | NA | NA | NA |
| M3.1.1a | Pipes failures in the last disaster [No./(100 km)] | NA | NA | NA |
| M3.1.1b | Pump failures in the last disaster [days/(pump)] | NA | NA | NA |
| M3.1.1c | Service connection failures in the last disaster [No./(1000 connections)] | NA | NA | NA |
| M3.1.2c | Duration of failure till restoration in the last disaster [Days] | NA | NA | NA |
| C4.1 Water supply interruptions | System | R4 | R6 | |
| M4.1.1 | Number of service interruptions [No./(1000 connections·year)] | 2.5 ⏺ | 2.5 ⏺ | 2.5 ⏺ |
| M4.1.1a | Number of interruptions due to pipe and equipment failures [No./(1000 connections·year)] | NA | NA | NA |
| M4.1.1b | Number of interruptions due to rehabilitation or new constructions [No./(1000 connections·year)] | NA | NA | NA |
| M4.1.1c | Number of interruptions due to water quality inadequacy [No./(1000 connections·year)] | NA | NA | NA |
| M4.1.1d | Number of interruptions due to external issues [No./(1000 connections·year)] | NA | NA | NA |
| M4.1.2 | Average duration of service interruptions [h] | 5.7 ⏺ | 5.7 ⏺ | 5.7 ⏺ |
| C4.2 Adequacy of delivered water quality | System | R4 | R6 | |
| M4.2.1 | Quality of supplied water [%tests] | 100 ⏺ | 100 ⏺ | 100 ⏺ |
| M4.2.1a | Minimum velocity performance in network links [-] | 0.75 ⏺ | 0.62 ⏺ | 0.94 ⏺ |
| M4.2.1b | Water age performance [-] | 2.85 ⏺ | 2.79 ⏺ | 2.91 ⏺ |
| M4.2.1c | Network travel time performance [-] | 2.75 ⏺ | 2.50 ⏺ | 3.00 ⏺ |
| C4.3 Adequacy of pressure requirements | System | R4 | R6 | |
| M4.3.1 | Service complaints due to lack of pressure [No. complaints/(1000 connections·year)] | 0.0 ⏺ | 0.0 ⏺ | 0.0 ⏺ |
| M4.3.1a | Minimum pressure performance index [-] | 2.11 ⏺ | 2.34 ⏺ | 1.83 ⏺ |
| M4.3.1b | Maximum pressure performance index [-] | 2.55 ⏺ | 2.23 ⏺ | 2.86 ⏺ |
| M4.3.1c | Pressure fluctuation performance index [-] | 2.74 ⏺ | 2.74 ⏺ | 2.76 ⏺ |
| C5.1 Assessment of non-potable uses | System | R4 | R6 | |
| M5.1.1 | Drinking water supplied for non-potable uses [% drinking volume] | 58% ⏺ | 58% ⏺ | 58% ⏺ |
| M5.1.2 | Recycled water for non-potable uses [% total volume] | 0% ⏺ | 0% ⏺ | 0% ⏺ |
| C5.2 Hydraulic flexibility | System | R4 | R6 | |
| M5.2.1 | Network resilience index [-] | 1.91 ⏺ | 1.70 ⏺ | 2.31 ⏺ |
| C6.1 Assessment of service interruptions in the last disaster | System | R4 | R6 | |
| M6.1.1 | Water supply interruptions for consumers in the last disaster [% connections] | NA | NA | NA |
| M6.1.2 | Total duration of water supply interruption in the last disaster [days] | NA | NA | NA |
References
- ISO/TR 22370:2020; Security and Resilience—Urban Resilience. International Organization for Standardization: Geneva, Switzerland, 2020. Available online: https://www.iso.org/standard/50273.html (accessed on 8 August 2024).
- ISO 22300:2021; Security and Resilience—Vocabulary. International Organization for Standardization: Geneva, Switzerland, 2021. Available online: https://www.iso.org/standard/77008.html (accessed on 8 August 2024).
- OECD. Guidelines for Resilience Systems Analysis: How to Analyse Risk and Build a Roadmap to Resilience; OECD Publishing: Paris, France, 2014. [Google Scholar] [CrossRef]
- Shuang, Q.; Liu, H.J.; Porse, E. Review of the quantitative resilience methods in water distribution networks. Water 2019, 11, 1189. [Google Scholar] [CrossRef]
- Alegre, H.; Coelho, S.T. Infrastructure Asset Management of Urban Water Systems. In Water Supply System Analysis—Selected Topics; Ostfeld, A., Ed.; InTech: Houston, TX, USA, 2012. [Google Scholar] [CrossRef]
- Beceiro, P.; Galvão, A.; Brito, R.S. Resilience assessment framework for nature based solutions in stormwater management and control: Application to cities with different resilience maturity. Sustainability 2020, 12, 10040. [Google Scholar] [CrossRef]
- Cardoso, M.A.; Brito, R.S.; Pereira, C.; Gonzalez, A.; Stevens, J.; Telhado, M.J. RAF Resilience Assessment Framework—A Tool to Support Cities’ Action Planning. Sustainability 2020, 12, 2349. [Google Scholar] [CrossRef]
- UNDRR. Disaster resilience scorecard for cities. Preliminary level assessment. In United Nations International Strategy for Disaster Reduction United; Nations Office for Disaster Reduction: Geneva, Switzerland, 2017. [Google Scholar]
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in Optimisation of Water Distribution Systems? A Literature Review of System Design. Water 2018, 10, 307. [Google Scholar] [CrossRef]
- Todini, E. Looped water distribution networks design using a resilience index based heuristic approach. Urban Water 2000, 2, 115–122. [Google Scholar] [CrossRef]
- Prasad, T.D.; Park, N.-S. Multiobjective genetic algorithms for design of water distribution networks. J. Water Resour. Plan. Manag. 2004, 130, 73–82. [Google Scholar] [CrossRef]
- Jayaram, N.; Srinivasan, K. Performance-based optimal design and rehabilitation of water distribution networks using life cycle costing. Water Resour. Res. 2008, 44, 1–15. [Google Scholar] [CrossRef]
- Creaco, E.; Franchini, M.; Todini, E. The combined use of resilience and loop diameter uniformity as a good indirect measure of network reliability. Urban Water 2016, 13, 167–181. [Google Scholar] [CrossRef]
- Sousa, J.; Muranho, J.; Bonora, M.A.; Maiolo, M. Why aren’t surrogate reliability indices so reliable? Can they be improved? In Proceedings of the 2nd International Joint Conference on Water Distribution Systems Analysis & Computing and Control in the Water Industry—WDSA/CCWI, Valencia, Spain, 18–22 July 2022.
- Awumah, K.; Goulter, I.C.; Bhatt, S.K. Assessment of reliability in water distribution networks using entropy based measures. Stoch. Hydrol. Hydraul. 1990, 4, 309–320. [Google Scholar] [CrossRef]
- Tanyimboh, T.T.; Templeman, A.B. Maximum entropy flows for single-source networks. Eng. Optim. 1993, 22, 49–63. [Google Scholar] [CrossRef]
- Liu, H.; Savić, D.; Kapelan, Z.; Zhao, M.; Yuan, Y.; Zhao, H. A diameter-sensitive flow entropy method for reliability consideration in water distribution system design. Water Resour. Res. 2014, 50, 5597–5610. [Google Scholar] [CrossRef]
- Yazdani, A.; Otoo, R.A.; Jeffrey, P. Resilience enhancing expansion strategies for water distribution systems: A network theory approach. Environ. Model. Softw. 2011, 26, 1574–1582. [Google Scholar] [CrossRef]
- Pandit, A.; Crittenden, J.C. Index of network resilience for urban water distribution systems. Int. J. Crit. Infrastruct. 2016, 12, 120–142. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Tinebra, A.; Renschler, C.; Fragiadakis, M. New Resilience Index for Urban Water Distribution Networks. J. Struct. Eng. 2016, 142, 1–13. [Google Scholar] [CrossRef]
- Cassottana, B.; Balakrishnan, S.; Aydin, N.Y.; Sansavini, G. Designing resilient and economically viable water distribution systems: A Multi-dimensional approach. Resilient Cities Struct. 2023, 2, 19–29. [Google Scholar] [CrossRef]
- Rasoulkhani, K.; Mostafavi, A.; Cole, J.; Sharvelle, S. Resilience-based infrastructure planning and asset management: Study of dual and singular water distribution infrastructure performance using a simulation approach. Sustain. Cities Soc. 2019, 48, 101577. [Google Scholar] [CrossRef]
- Makropoulos, C.; Nikolopoulos, D.; Palmen, L.; Kools, S.; Segrave, A.; Vries, D.; Koop, S.; van Alphen, H.J.; Vonk, E.; van Thienen, P.; et al. A resilience assessment method for urban water systems. Urban Water 2018, 15, 316–328. [Google Scholar] [CrossRef]
- Hosseini, S.; Barker, K.; Ramirez-Marquez, J.E. A review of definitions and measures of system resilience. Reliab. Eng. Syst. Saf. 2016, 145, 47–61. [Google Scholar] [CrossRef]
- ISO 24510:2024; Activities Relating to Drinking Water and Wastewater Services—Guidelines for the Assessment and for the Improvement of the Service to Users. International Organization for Standardization: Geneva, Switzerland, 2024. Available online: https://www.iso.org/standard/81484.html (accessed on 8 August 2024).
- ISO 24512:2024; Activities Relating to Drinking Water and Wastewater Services—Guidelines for the Management of Drinking Water Utilities and for the Assessment of Drinking Water Services. International Organization for Standardization: Geneva, Switzerland, 2024. Available online: https://www.iso.org/standard/82490.html (accessed on 8 August 2024).
- ISO 24513:2019; Service Activities Relating to Drinking Water Supply, Wastewater and Stormwater Systems—Vocabulary. International Organization for Standardization: Geneva, Switzerland, 2019. Available online: https://www.iso.org/standard/72607.html (accessed on 8 August 2024).
- Cardoso, M.A.; Rosa, M.J.; Brito, R.S.; Silva, C.; Beceiro, P.; Jorge, C.; Alegre, H.; Martinho, G.; Pina, J.; Silveira, A.; et al. Guide for the Assessment of the Quality of Service in Water and Waste Services; 4th Generation assessment system. Technical Guide series, n.27; ERSAR, LNEC; NOVA: Lisboa, Portugal, 2024; ISBN 978-989-8360-44-1. (In Portuguese) [Google Scholar]
- Cardoso, M.A.; Poças, A.; Silva, M.S.; Ribeiro, R.; Almeida, M.C.; Brito, R.S.; Coelho, S.T.; Alegre, H. Innovation results of IAM planning in urban water services. Water Sci. Technol. 2016, 74, 1518–1526. [Google Scholar] [CrossRef][Green Version]
- Loureiro, D.; Silva, C.; Cardoso, M.A.; Mamade, A.; Alegre, H.; Rosa, M.J. The Development of a Framework for Assessing the Energy Efficiency in Urban Water Systems and Its Demonstration in the Portuguese Water Sector. Water 2020, 12, 134. [Google Scholar] [CrossRef]
- ERSAR. Annual Report on Water and Waste Services in Portugal (RASARP); ERSAR: Lisbon, Portugal, 2024; Volume 1, ISBN 978-989-8360-46-5. (In Portuguese) [Google Scholar]
- LNEC; ERSAR. Guide for the Assessment of the Quality of Service in Water and Waste Services; 3rd generation assessment system. Technical Guide series, n.21; Water and Waste Services Regulation Authority (ERSAR): Lisboa, Portugal, 2022. (In Portuguese) [Google Scholar]
- Alegre, H.; Baptista, J.M.; Cabrera, E.; Cubillo, F.; Duarte, P.; Hirner, W.; Merkel, W.; Parena, R. Performance Indicators for Water Supply Services: Third Edition; IWA Manual of Best Practice; IWA Publishing: London, UK, 2017. [Google Scholar] [CrossRef]
- Alegre, H.; Vitorino, D.; Coelho, S. Infrastructure Value Index: A Powerful Modelling Tool for Combined Long-term Planning of Linear and Vertical Assets. Procedia Eng. 2014, 89, 1428–1436. [Google Scholar] [CrossRef]
- Loureiro, D.; Mamade, A.; Silva, M.A.; Arregui, F.; Alegre, H. Análise de sensibilidade às componentes do balanço hídrico para suporte a uma melhor gestão de perdas em sistemas de abastecimento de água. Águas Resíduos 2020, 8, 27 (In Portuguese). [Google Scholar] [CrossRef]
- Almeida, M.C.; Leitão, J.P.; Coelho, S.T. Risk management in urban water infrastructures. Application to water and wastewater systems. In Water Management. Uncertainties and Risks; Almeida, A.B., Ed.; Esfera do Caos: Lisbon, Portugal, 2011; ISBN 9789896800444. (In Portuguese) [Google Scholar]
- Izadi, A.; Yazdandoost, F.; Ranjbar, R. Asset-Based Assessment of Resiliency in Water Distribution Networks. Water Resour. Manag. 2020, 34, 1407–1422. [Google Scholar] [CrossRef]
- Cabrera, E.; Gómez, E.; Cabrera, E., Jr.; Soriano, J. Calculating the Economic Level of Friction in Pressurized Water Systems. Water 2018, 10, 763. [Google Scholar] [CrossRef]
- Coelho, S.T. Performance in Water Distribution—A Systems Approach; Series Water Engineering and management systems; Research Studies Press; John Wiley and Sons: Lisbon, Portugal, 1997. [Google Scholar]
- Silva, C.; Quadros, S.; Ramalho, P.; Rosa, M.J. A tool for a comprehensive assessment of treated wastewater quality. J. Environ. Manag. 2014, 146, 400–406. [Google Scholar] [CrossRef]
- American Water Works Association (AWWA). Computer Modeling of Water Distribution Systems. In Manual of Water Supply Practices M32, 4th ed.; Velantine, M., Ed.; AWWA: Denver, CO, USA, 2018. [Google Scholar]
- Carneiro, J.; Loureiro, D.; Covas, D. Exploratory Analysis of Surrogate Metrics to Assess the Resilience of Water Distribution Networks. Water Resour. Res. 2023, 59, e2022WR034289. [Google Scholar] [CrossRef]
- Carneiro, J.; Loureiro, D.; Cabral, M.; Covas, D. Integrating Uncertainty in Performance Assessment of Water Distribution Networks by Scenario Building. Water 2024, 16, 977. [Google Scholar] [CrossRef]
| Criteria | Metrics | Reference Values | Source | |||
|---|---|---|---|---|---|---|
| Good ⏺ | Fair ⏺ | Poor ⏺ | ||||
| C1.1 Infrastructure knowledge and criticality | M1.1.1 | Infrastructural knowledge index [-] | [142; 200] | [87; 142[ | [0; 87[ | [28] ** |
| M1.1.2 | Knowledge and protection of critical assets index [-] | [2; 3] | [1; 2[ | [0; 1[ | [7] *,** | |
| M1.1.3 | Assets criticality index [-] | [0; 0.1] | ]0.1; 0.5] | ]0.5; 1] | [36,37] *,** | |
| M1.1.3a | Pipes criticality index [-] | [0; 0.1] | ]0.1; 0.5] | ]0.5; 1] | [36,37] *,** | |
| M1.1.3b | Pumps criticality index [-] | [0; 0.1] | ]0.1; 0.5] | ]0.5; 1] | [36,37] *,** | |
| M1.1.3c | Storage tanks criticality index [-] | [0; 0.1] | ]0.1; 0.5] | ]0.5; 1] | [36,37] *,** | |
| C1.2 Infrastructure integrity | M1.2.1 | Number of failures [No./(100 km·year)] | [0; 30] | ]30; 60] | ]60; +∞[ | [33] *,** |
| M1.2.1a | Pipes failures [No./(100 km·year)] | [0; 30] | ]30; 60] | ]60; +∞[ | [28] | |
| M1.2.1b | Pump failures [days/(pump·year)] | [0; 1] | ]1; 3] | ]3; +∞[ | [7,33] | |
| M1.2.1c | Service connection failures [No./(1000 connections·year)] | [0; 1] | ]1; 2.5[ | [2.5; +∞] | [7,33] | |
| M1.2.2 | Total duration of failures [Days/No. failure] | [0; 1] | ]1; 3] | ]3; +∞[ | [7] *,** | |
| C1.3 Infrastructure condition | M1.3.1 | Pipes rehabilitation [%/year] | [1.5; 4] | [0.8; 1.5[ or ]4;20] | [0; 0.8[ | [28] |
| M1.3.2 | Infrastructure value index [-] | [0.6; 1] | [0.4; 0.6[ | [0; 0.4[ | [28,34] | |
| M1.3.2a | Pipes value index [-] | [0.6; 1] | [0.4; 0.6[ | [0; 0.4[ | [28,34] *,** | |
| M1.3.2b | Pumps value index [-] | [0.6; 1] | [0.4; 0.6[ | [0; 0.4[ | [28,34] *,** | |
| M1.3.2c | Tanks value index [-] | [0.6; 1] | [0.4; 0.6[ | [0; 0.4[ | [28,34] *,** | |
| C1.4 Water and energy efficiency | M1.4.1 | System supplied energy index [-] | [1; 2] | ]2; 3] | ]3; +∞[ | [30] |
| M1.4.1a | Energy efficiency in pumping stations [kWh/(m3 · 100 m)] | [0.27; 0.43] | ]0.43; 0.6] | ]0.6; +∞[ | [28] | |
| M1.4.1b | Surplus energy index [-] | [0; 0.75] | ]0.75; 1] | ]1; +∞[ | ||
| M1.4.1c | Average unit head loss [m/km] | [0; 2] | ]2; 5] | ]5; +∞[ | [38,41] ** | |
| M1.4.2 | Water losses [L/(connection·day)] | [0; 120] | ]120; 170] | ]170; +∞[ | [28] *,** | |
| M1.4.2a | Real water losses [L/(connection·day)] | [0; 100] | ]100; 150] | ]150; +∞[ | [28] | |
| M1.4.2b | Apparent water losses [%volume] | [0; 3] | ]3; 6] | ]6; 100[ | [33,35] | |
| C2.1 Dependency on other services | M2.1.1 | Level of dependency to bulk water utility [% input volume] | [0; 10] | ]10; 20] | ]20; 100] | [7] * |
| M2.1.2 | Level of dependency on pumping [% input volume] | [0; 10] | ]10; 20] | ]20; 100] | [7] * | |
| C2.2 Infrastructure autonomy | M2.2.1 | Treated water storage capacity [Days] | [2; +∞[ | [1; 2[ | [0; 1[ | [7,33] |
| M2.2.2 | Level of autonomy to electric grid from alternative infrastructures [% dependent volume] | [80; 100] | [70; 80[ | [0; 70[ | [7] | |
| M2.2.3 | Energy self-production [% pumped energy] | [10; 100[ | [5; 10[ | [0; 5[ | [28] | |
| M2.2.3a | Wind energy self-production [% pumped energy] | [10; 100[ | [5; 10[ | [0; 5[ | [28] * | |
| M2.2.3b | Solar energy self-production [% pumped energy] | [10; 100[ | [5; 10[ | [0; 5[ | [28] * | |
| M2.2.3c | Hydropower energy self-production [% pumped energy] | [10; 100[ | [5; 10[ | [0; 5[ | [28] * | |
| C2.3 Infrastructure redundancy | M2.3.1 | Potential alternative water sources [% volume] | [75; 100] | [50; 75[ | [0; 50[ | [33] * |
| M2.3.2 | Pumping redundancy [% time] | [75; 100] | [50; 75[ | [0; 50[ | ||
| M2.3.3 | Pipes topological redundancy index [-] | [0.1; 1] | [0.01; 0.1[ | [0; 0.01[ | [18] ** | |
| C3.1 Assessment of failures in the last disaster | M3.1.1 | Number of failures in the last disaster [No./100 km] | [0; 30] | ]30; 60] | ]60; +∞[ | [7]* |
| M3.1.1a | Pipes failures in the last disaster [No./(100 km)] | [0; 30] | ]30; 60] | ]60; +∞[ | [7] | |
| M3.1.1b | Pump failures in the last disaster [days/(pump)] | [0; 1] | ]1; 3] | ]3; +∞[ | [7] | |
| M3.1.1c | Service connection failures in the last disaster [No./(1000 connections)] | [0; 1] | ]1; 2.5] | ]2.5; +∞[ | [7] | |
| M3.1.2 | Duration of failure till restoration in the last disaster [Days] | [0; 1] | ]1; 3] | ]3; +∞[ | [7] | |
| Criteria | Metrics | Reference Values | Source | |||
|---|---|---|---|---|---|---|
| Good ⏺ | Fair ⏺ | Poor ⏺ | ||||
| C4.1 Assessment of water supply interruptions | M4.1.1 | Number of service interruptions [No./(1000 connections·year)] | [0;1] | ]1;2.5] | ]2.5; +∞[ | [32] |
| M4.1.1a | Number of interruptions due to pipe and equipment failures [No./(1000 connections·year)] | [0;1] | ]1;2.5] | ]2.5; +∞[ | [32] * | |
| M4.1.1b | Number of interruptions due to rehabilitation or new constructions [No./(1000 connections·year)] | [0;1] | ]1;2.5] | ]2.5; +∞[ | [32] * | |
| M4.1.1c | Number of interruptions due to water quality inadequacy [No./(1000 connections·year)] | [0;1] | ]1;2.5] | ]2.5; +∞[ | [32] * | |
| M4.1.1d | Number of interruptions due to external issues [No./(1000 connections·year)] | [0;1] | ]1;2.5] | ]2.5; +∞[ | [32] * | |
| M4.1.2 | Average duration of service interruptions [h] | [0;4] | ]4;6] | ]6; +∞[ | ||
| C4.2 Adequacy of delivered water quality | M4.2.1 | Quality of supplied water [% tests] | [100;90] | ]90;70] | ]70; 0[ | [33] ** |
| M4.2.1a | Minimum velocity performance index [-] | [2; 3] | [1; 2[ | [0; 1[ | [39,40] | |
| M4.2.1b | Water age performance index [-] | [2; 3] | [1; 2[ | [0; 1[ | [39,40] * | |
| M4.2.1c | Network travel time performance index [-] | [2; 3] | [1; 2[ | [0; 1[ | [39,40] * | |
| C4.3 Adequacy of pressure requirements | M4.3.1 | Service complaints due to lack of pressure [No. complaints/(1000 connections·year)] | [0; 0.15] | [0.15; 1.5[ | [1.5; +∞[ | [33] *,** |
| M4.3.1a | Minimum pressure performance index [-] | [2; 3] | [1; 2[ | [0; 1[ | [39,40] | |
| M4.3.1b | Maximum pressure performance index [-] | [2; 3] | [1; 2[ | [0; 1[ | [39,40] | |
| M4.3.1c | Pressure fluctuation performance index [-] | [2; 3] | [1; 2[ | [0; 1[ | [39,40] | |
| C5.1 Assessment of non-potable uses | M5.1.1 | Drinking water supplied for non-potable uses [% drinking volume] | [0; 25] | ]25; 50] | ]50; 100] | [7] |
| M5.1.2 | Recycled water for non-potable uses [% total volume] | [25; 100] | [10; 25[ | [0; 10[ | [33] *,** | |
| C5.2 Hydraulic flexibility | M5.2.1 | Network resilience index [-] | [0.75; 1] | [0.5; 0.75[ | [0; 0.5[ | [11] ** |
| C6.1 Assessment of service interruptions in the last disaster | M6.1.1 | Water supply interruptions for consumers in the last disaster [% connections] | ]0; 2.5] | ]2.5; 7.5] | [7.5; 100] | [7] * |
| M6.1.2 | Total duration of water supply interruption in the last disaster [days] | [0; 1] | ]1; 3] | ]3; +∞[ | [7] | |
| Dimension | Identified Problem/Weakness | Potential Improvement Measures |
|---|---|---|
| Infrastructure | Low infrastructure knowledge Low critical assets knowledge |
|
| Aged infrastructure |
| |
| High water losses |
| |
| High dependency on other services |
| |
| Reduced autonomy |
| |
| Service | Excessive use of drinking water for non-potable uses |
|
| High burst rate |
| |
| Low water quality |
| |
| High surplus energy |
|
| Dimension | Objective | Criteria | Metric with Worst Performance | ||
|---|---|---|---|---|---|
|
Infrastructure 0.99 ⏺ | O1 Ensure infrastructure assets robustness 1.32 ⏺ | C1.1 Infrastructure knowledge and criticality | 1.28 ⏺ | M1.1.2 Knowledge and protection of critical assets index [-] | 0.0 ⏺ |
| C1.2 Infrastructure integrity | 1.53 ⏺ | M1.2.2 Total duration of failures [Days/No. failure] | 10.3 ⏺ | ||
| C1.3 Infrastructure condition | 0.67 ⏺ | M1.3.1 Pipe rehabilitation [%/year] | 0.2 ⏺ | ||
| C1.4 Water and energy efficiency | 1.81 ⏺ | M1.4.1 System supplied energy index [-] | 2.24 ⏺ | ||
|
O2 Ensure an autonomous water infrastructure 0.59 ⏺ | C2.1 Dependency on other services | 0.25 ⏺ | M2.1.1 Level of dependency on bulk water utility [%volume] | 100% ⏺ | |
| C2.2 Infrastructure autonomy | 0.35 ⏺ | M2.2.3 Energy self-production [% pumped energy] | 0% ⏺ | ||
| C2.3 Infrastructure redundancy | 1.28 ⏺ | M2.3.1 Potential alternative water sources [%volume] | 3% ⏺ | ||
| O3 Promote infrastructure recovery and build back in disasters NA | C3.1 Assessment of failures in the last disaster | NA | NA | ||
| Dimension | Objective | Criteria | Metric with Worst Performance | ||
|---|---|---|---|---|---|
| Service 1.63 ⏺ | O4 Ensure a reliable service 2.20 ⏺ | C4.1 Assessment of water supply interruptions | 1.41 ⏺ | M4.1.1 Number of service interruptions [No./(1000 connections·year)] | 2.5 ⏺ |
| C4.2 Adequacy of delivered water quality | 3.0 ⏺ | M4.2.1 Quality of supplied water [%tests] | 100 ⏺ | ||
| C4.3 Adequacy of pressure requirements | 3.0 ⏺ | M4.3.1 Service complaints due to lack of pressure [No. complaints/(1000 connections·year)] | 0.0 ⏺ | ||
|
O5 Ensure a flexible service 0.86 ⏺ | C5.1 Assessment of non-potable uses | 0.34 ⏺ | M5.1.2 Recycled water for non-potable uses [% total volume] | 0% ⏺ | |
| C5.2 Hydraulic flexibility | 1.91 ⏺ | M5.2.1 Network resilience index | 0.73 ⏺ | ||
| O6 Promote service recovery and build back in disasters NA | C6.1 Assessment of service interruptions in the last disaster | NA | NA | ||
| Dimension | Objective | Criteria | ||||||
|---|---|---|---|---|---|---|---|---|
| R4 | R6 | R4 | R6 | R4 | R6 | |||
| Infrastructure | 1.10 ⏺ | 0.91 ⏺ | O1 Ensure infrastructure assets robustness | 1.54 ⏺ | 1.07 ⏺ | C1.1 Infrastructure knowledge | 0.98 ⏺ | 0.99 ⏺ |
| C1.2 Infrastructure integrity | 2.90 ⏺ | 1.24 ⏺ | ||||||
| C1.3 Infrastructure condition | 0.69 ⏺ | 0.33 ⏺ | ||||||
| C1.4 Water and energy efficiency | 1.85 ⏺ | 1.76 ⏺ | ||||||
| O2 Ensure an autonomous water infrastructure | 0.53 ⏺ | 0.69 ⏺ | C2.1 Dependency on other services | 0.72 ⏺ | 0.00 ⏺ | |||
| C2.2 Infrastructure autonomy | 0.06 ⏺ | 0.62 ⏺ | ||||||
| C2.3 Infrastructure redundancy | 1.05 ⏺ | 1.50 ⏺ | ||||||
| O3 Promote infrastructure recovery and build back in disasters | NA | NA | C3.1 Assessment of failures in the last disaster | NA | NA | |||
| Service | 1.60 ⏺ | 1.68 ⏺ | O4 Ensure a reliable service | 2.20 ⏺ | 2.20 ⏺ | C4.1 Assessment of water supply interruptions | 1.41 ⏺ | 1.41 ⏺ |
| C4.2 Adequacy of delivered water quality | 3.0 ⏺ | 3.0 ⏺ | ||||||
| C4.3 Adequacy of pressure requirements | 3.0 ⏺ | 3.0 ⏺ | ||||||
| O5 Ensure a flexible service | 0.79 ⏺ | 0.99 ⏺ | C5.1 Assessment of non-potable uses | 0.34 ⏺ | 0.34 ⏺ | |||
| C5.2 Hydraulic flexibility | 1.70 ⏺ | 2.31 ⏺ | ||||||
| O6 Promote service recovery and build back in disasters | NA | NA | C6.1 Assessment of service interruptions in the last disaster | NA | NA | |||
| C1.2 Infrastructure integrity | 1.24⏺ | |
| M1.2.1 | Number of failures [No./(100 km·year)] | 23.9 ⏺ |
| M1.2.1a | Pipes failures [No./(100 km·year)] | 21.9 ⏺ |
| M1.2.1b | Pump failures [days/(pump·year)] | 9.3 ⏺ |
| M1.2.2 | Total duration of failures [Days/No. failure] | 13.7 ⏺ |
| C1.3 Infrastructure condition | 0.33⏺ | |
| M1.3.1 | Pipes rehabilitation [%/year] | 0.20 ⏺ |
| M1.3.2 | Infrastructure value index [-] | 0.20 ⏺ |
| M1.3.2a | Pipes infrastructure value index [-] | 0.05 ⏺ |
| M1.3.2b | Pumps infrastructure value index [-] | 0.00 ⏺ |
| M1.3.2c | Storage tanks infrastructure value index [-] | 0.36 ⏺ |
| C2.1 Dependency on other services | 0.0⏺ | |
| M2.1.1 | Level of dependency on bulk water utility [%volume] | 100% ⏺ |
| M2.1.2 | Level of dependency on pumping [% input volume] | 100% ⏺ |
| C2.2 Autonomy | 0.62⏺ | |
| M2.2.1 | Treated water storage capacity [Days] | 1.9 ⏺ |
| M2.2.2 | Level of autonomy to electric grid from alternative infrastructures [% dependent volume] | 0% ⏺ |
| M2.2.3 | Energy self-production [% pumped energy] | 0% ⏺ |
| M2.2.3a | Wind energy self-production [% pumped energy] | 0% ⏺ |
| M2.2.3b | Solar energy self-production [% pumped energy] | 0% ⏺ |
| M2.2.3c | Hydropower energy self-production [% pumped energy] | 0% ⏺ |
| C5.1 Non-potable uses | ||
| M5.1.1 | Drinking water supplied for non-potable uses [% drinking volume] | 58% ⏺ |
| M5.1.2 | Recycled water supplied for non-potable uses [% total volume] | 0% ⏺ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carneiro, J.; Loureiro, D.; Cabral, M.; Covas, D. Comprehensive Resilience Assessment Framework for Water Distribution Networks. Water 2024, 16, 2611. https://doi.org/10.3390/w16182611
Carneiro J, Loureiro D, Cabral M, Covas D. Comprehensive Resilience Assessment Framework for Water Distribution Networks. Water. 2024; 16(18):2611. https://doi.org/10.3390/w16182611
Chicago/Turabian StyleCarneiro, Joana, Dália Loureiro, Marta Cabral, and Dídia Covas. 2024. "Comprehensive Resilience Assessment Framework for Water Distribution Networks" Water 16, no. 18: 2611. https://doi.org/10.3390/w16182611
APA StyleCarneiro, J., Loureiro, D., Cabral, M., & Covas, D. (2024). Comprehensive Resilience Assessment Framework for Water Distribution Networks. Water, 16(18), 2611. https://doi.org/10.3390/w16182611







