Application of GIS Spatial Analysis for the Assessment of Storm Surge Inundation Risks in the Guangdong–Macao–Hong Kong Great Bay Area
Abstract
1. Introduction
2. Storm Surge Calculation Method
2.1. Storm Surge Model
- t—time (s);
- —horizontal cartesian coordinate system (m);
- —longitude and latitude;
- —latitude and longitude of the central point of the area calculated on a grid;
- —total water depth of the water column (m);
- —free surface height from mean sea level (m);
- —undisturbed ocean depth, i.e., the distance from mean sea level to the seabed (m);
- —the radius of the Earth (m), taking 6,378,135 m;
- —depth-averaged seawater horizontal velocity (ms−1);
- —Coriolis parameter (s−1), which is the angular velocity of the Earth’s rotation;
- —gravity acceleration (ms−2);
- —seawater density, the default is 1025 kg m−3;
- —atmospheric pressure on the free surface of seawater (Nm−2);
- —Newton tidal potential (m);
- — and components (N) of sea surface stress, which may include wind stress and wave radiation stress;
- — and components of sea bed friction force (N);
- —horizontal diffusion term of momentum equation.
2.2. Typhoon Model
- is the radius of maximum wind speed;
- is the distance from the calculation point to the typhoon center;
- is the typhoon moving speed;
- is the maximum wind speed of the typhoon;
- and (, ) represent the coordinates of the calculation points and the typhoon center respectively.
- is the center pressure of the typhoon, and is the atmospheric pressure at infinity.
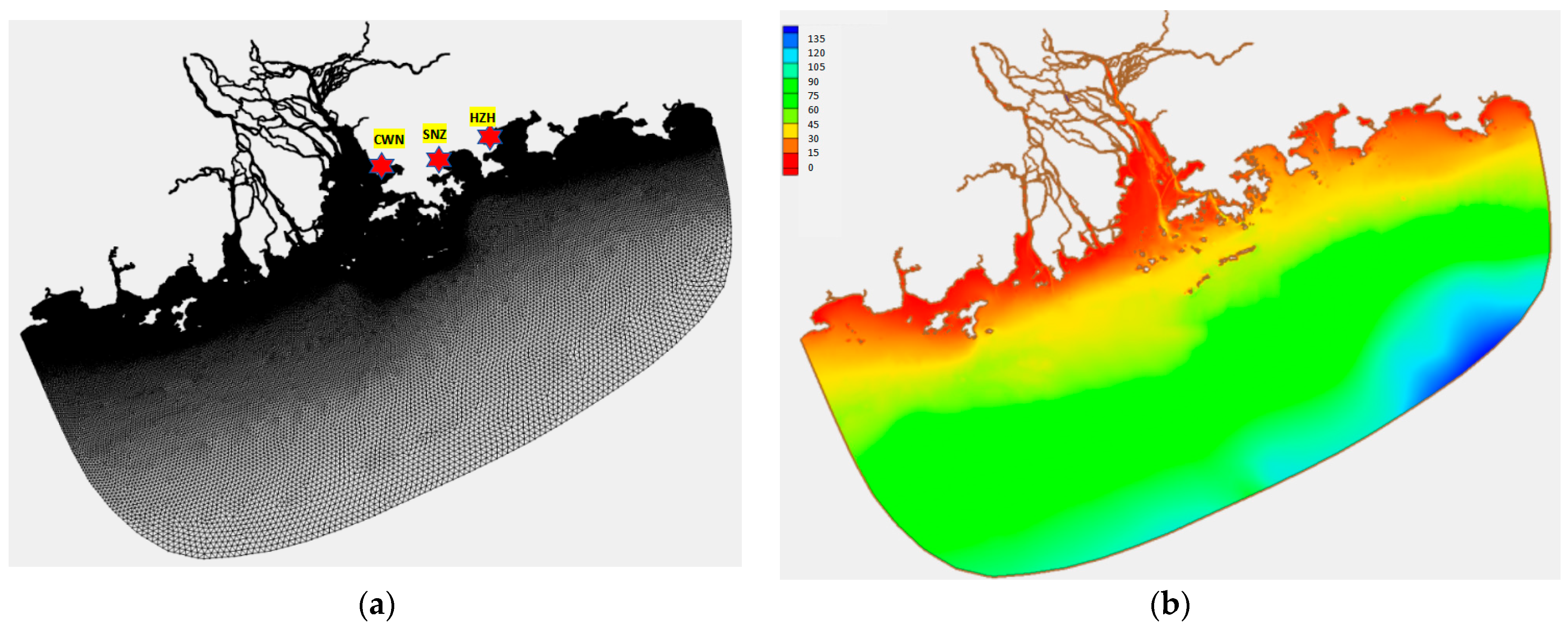
2.3. Model Domain and Mesh Generation
2.4. Water Levels at the Open Boundary
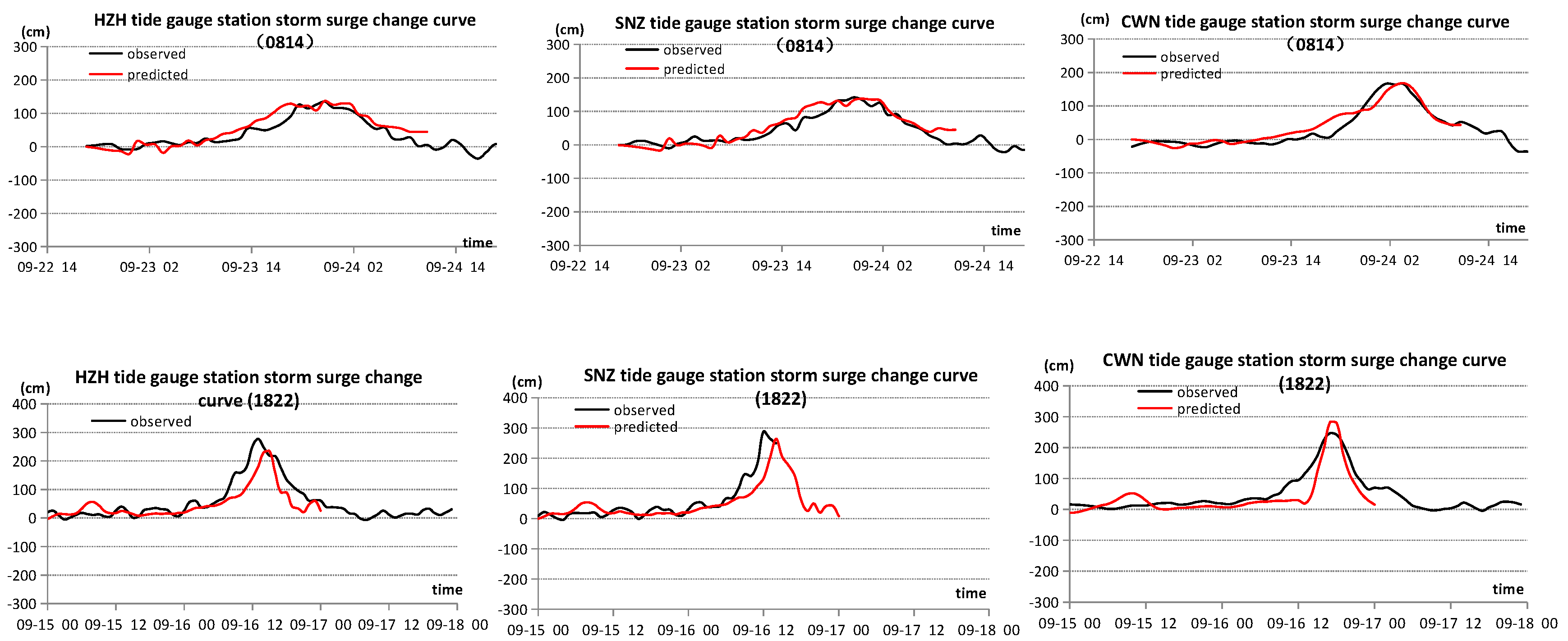
2.5. Model Validation
3. Risk Analysis of Different Levels of Storm Surges
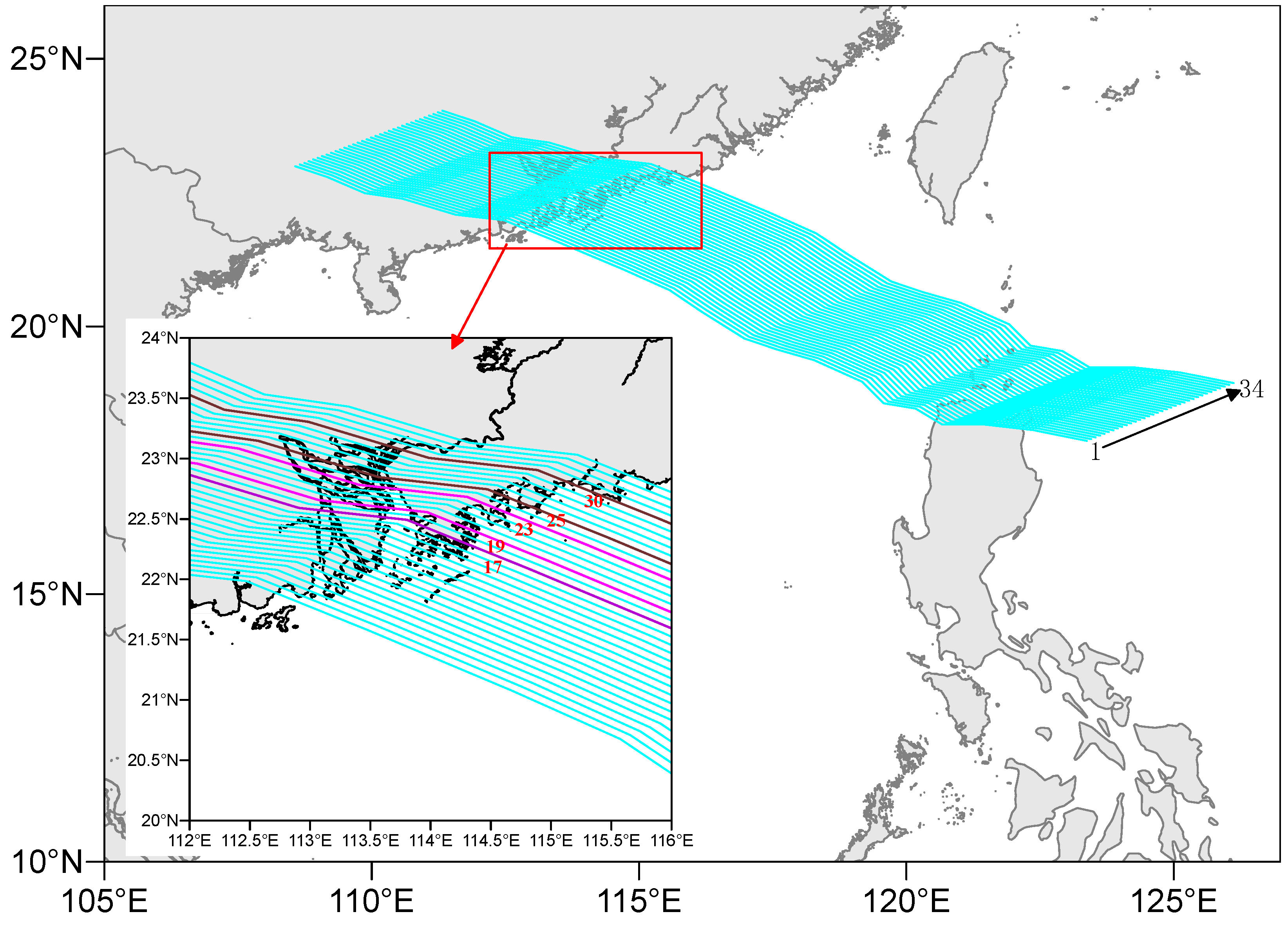
3.1. Selection of the Least Favorable Path for Typhoons
- (1)
- To assess the potential impact of the maximum possible typhoon, as per the guidelines, the extreme value I distribution is employed to determine the P0 value (P0 = 876 hPa), which represents the central pressure of such a typhoon occurring once every 1000 years.
- (2)
- To evaluate the general influence of typhoons, the guidelines dictate using the P0 value (P0 = 900 hPa) derived from the extreme value I distribution for an event occurring once every 200 years as a baseline. From this, the minimum pressure at the typhoon’s center is incrementally increased, thereby constructing four typhoons with progressively weaker intensities.
3.2. Assessment of Storm Surge Inundation Risk Based on High-Precision DEM Data
3.2.1. DEM Data Preprocessing
3.2.2. The Method for Calculating Storm Surge Includes the Determination of Range and Water Depth
- (1)
- According to the model, the tidal level H under the influence of storm surge across six grades (876 hPa, 910 hPa, 920 hPa, 930 hPa, 940 hPa, and 950 hPa) along the coast was calculated.
- (2)
- According to the tidal level H, the modified DEM raster data were reclassified into two categories: ‘>H’ and ‘≤H’.
- (3)
- Among them, ‘≤H’ represents the ‘passive’ submerged area, and the grid file was converted into Polygon factor data. By applying condition judgment and selection, the corresponding Polygon factor data connected to the sea area was outputted, thereby converting the ‘passive’ submerged area into an ‘active’ submerged area and obtaining the range of submergence under each level of storm surge.
- (4)
- The Polygon element data of the ‘active’ submerged area was converted into Raster format, and as a judgment condition, the tidal level H and DEM data were algebraically subtracted to obtain the depth D of submerged water.
- (5)
- Referring to the relevant methods of “risk level determination” in the “Technical Guidelines for Risk Assessment and Zoning of Storm Surge Disasters,” an area with ‘D < 0.15 m’ is considered nondangerous and was excluded. By following steps (2) to (5), we finally obtain the submerged area with water depth ‘0.15 ≤ D < H’ and its corresponding water depth raster data.
- (6)
- For a small amount of edge burr data that does not conform to the actual situation due to the pixel resolution problem in the algebraic operation process, the modified water depth raster data can be obtained by filtering through the conditional selection tool. The water depth raster data was suitable for partially submerged areas of land, but for original land-water system areas such as rivers and pond surfaces, it was necessary to obtain presubmergence water depth data in order to determine storm surge depths under various grades.
4. Results
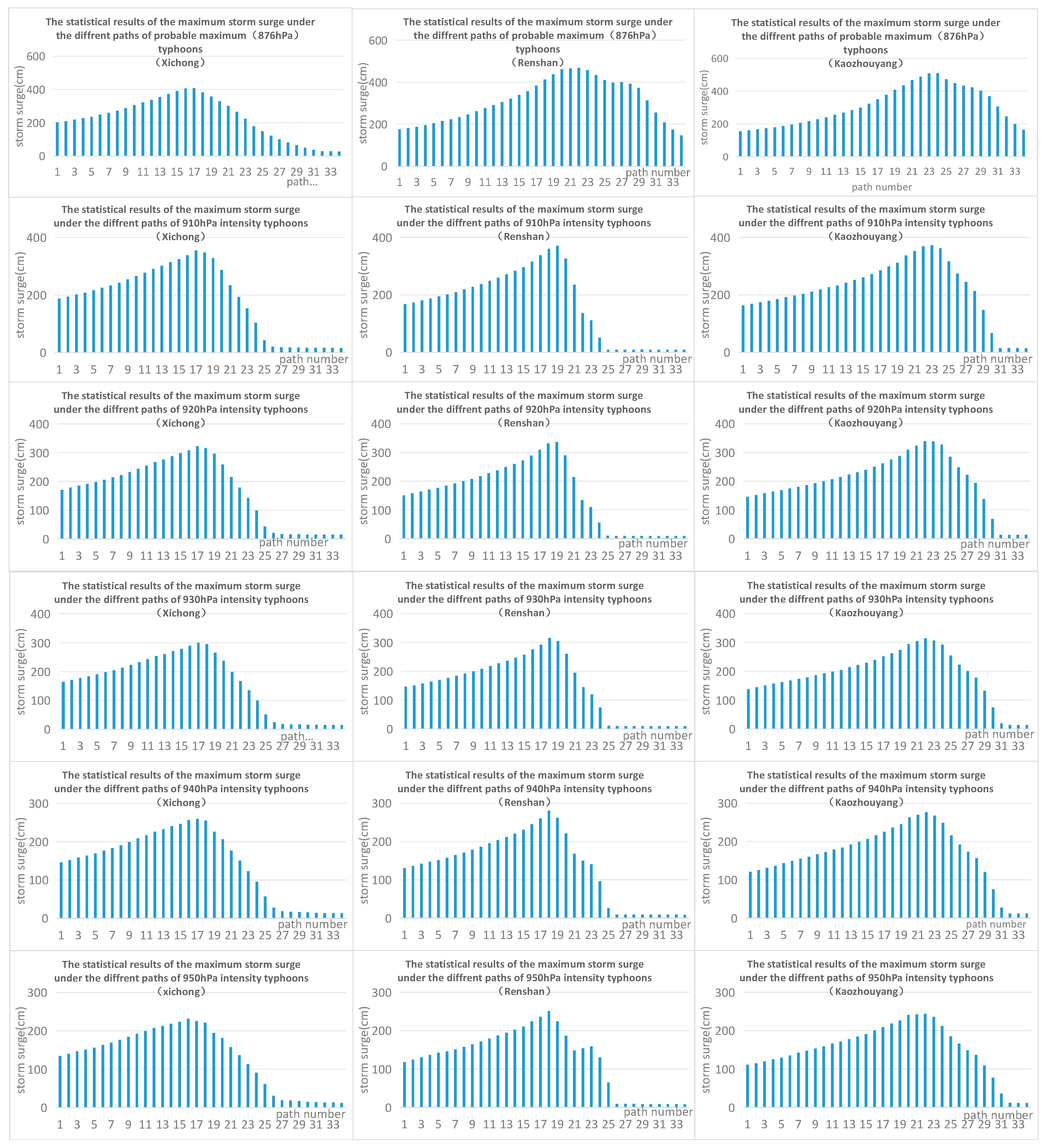
4.1. Storm Surges Induced by Different Typhoon Intensities
4.2. Influences of Typhoon Paths
4.3. Analysis of Different Levels of Storm Surge Inundation
5. Discussion
5.1. Effect of Coastline Shapes on Storm Surges
5.2. Effect of Terrain Topography under Human Activities
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dana, M. Real-time, sketch-based GIS database. In Proceedings of the GeoDesign Summit, Redlands, CA, USA, 6–8 January 2010; pp. 230–236. [Google Scholar]
- Goodchild, M. Spatial by design. In Proceedings of the GeoDesign Summit, Redlands, CA, USA, 6–8 January 2010; pp. 419–423. [Google Scholar]
- Wu, W.; Sun, W.-X. The calculation of storm surge inundations some coasts of time bohai sea. J. Ocean. Univ. Qingdao 1995, 25, 146–152. [Google Scholar]
- Sha, R.-N.; Yin, B.-S.; Yang, D.-Z. A numerical study on storm surge and inundation induced by hurricanes in the nearshore of Tianjin. Mar. Sci. 2007, 31, 63–67. [Google Scholar]
- Zhu, J.-Z.; Yu, P.-B. Numerical method for the storm tide overflow model in Hangzhou bay and Qiantangjiang estuary. Adv. Water Sci. 2009, 20, 269–274. [Google Scholar]
- Wu, W.; Fu, C.-F.; Yu, F.-J.; Liu, Q.-X. Numerical simulation of the influence of Wenzhou coastal dike on storm surge inundation. J. Mar. Sci. 2012, 30, 36. [Google Scholar]
- Cao, C.H.; Bau, T.; Gao, S.; Xu, J.; Cao, Y.; Wu, L.; Zhao, P. High resolution 3D storm surge and inundation numerical model used in the Jiaozhou Bay. Mar. Sci. 2013, 37, 118–125. [Google Scholar]
- Li, Y.; Fang, W.-H.; Lin, W.; Ye, Y.-T. Parameterization of synthetic tropical cyclones at various scales for probable maximum storm surge risk modeling. Mar. Sci. 2014, 38, 71–80. [Google Scholar]
- Zhang, X.-J.; Deng, Y.-F.; Qiu, J.-F.; Bei, Z.Y.; Chen, B.R.; Wang, J.; Qian, Y.C.; Huang, W.T. Preliminary Exploration and Application of Integrated Method of Storm Surge Disaster Risk Assessment and Zoning Results in Adjacent Areas. Ocean. Dev. Manag. 2022, 39, 43–48. [Google Scholar]
- Ding, Y.-R.; Wang, S.-B.; Liu, S.-C. Research on the risk assessment and zoning of storm surge in Huanghua City. Mar. Forecast. 2022, 39, 9–15. [Google Scholar]
- Zhang, M.; Luo, J.; Hu, J.L.; Zeng, X.Z. Inundation risk assessment of storm surge along Lei Zhou coastal areas. J. Trop. Oceanogr. 2019, 38, 1–12. [Google Scholar]
- Mu, L.; Liu, D.-R.; Wang, D.-S. A Typhoon Storm Surge Risk Assessment Method and System Based on ArcGIS Platform. Chinese Patent CN110377674A, 25 October 2019. [Google Scholar]
- Gao, Z.-C.; Yu, M.; Ding, Z.-D. Typhoon storm surge risk assessment based on GIS-A case study of Taizhou. Mar. Environ. Sci. 2012, 21, 439–447. [Google Scholar]
- Liang, H.-Y.; Zhou, X.-Q. Risk assessment on storm surge in the Haikou Bay. Acta Oceanol. Sin. 2005, 27, 22–29. [Google Scholar]
- Tang, F.-P.; Guo, J.-B.; Yu, H.-F.; Pan, X.-J. Scenario simulation method and plantform of typhoon storm surge inundation based on geographic information system. Geogr. Geo-Inf. Sci. 2019, 35, 6–19. [Google Scholar]
- Wang, X.-N.; Wang, X.-W.; Huang, H.-B.; Liu, C.X. Research on storm surge disaster risk early warning method based on GIS. China Flood Drought Manag. 2021, 31, 15–20. [Google Scholar]
- Wang, S.; Mu, L.; Qin, H.; Wang, L.Z.; Yao, Z.F.; Zhao, E.J. The utilization of physically based models and GIS techniques for comprehensive risk assessment of storm surge: A case study of Huizhou. Coast. Ocean. Process. 2022, 9, 939380. [Google Scholar] [CrossRef]
- Besset, M.; Anthony, E.J.; Bouchette, F. Multi-decadal variations in delta shorelines and their relationship to river sediment supply: An assessment and review. Earth Sci. Rev. 2019, 193, 199–219. [Google Scholar] [CrossRef]
- Deng, J.; Bao, Y. Morphologic evolution and hydrodynamic variation during the last 30 years in the LINGDING Bay, South China Sea. J. Coast. Res. SI 2011, 64, 1482–1489. [Google Scholar]
- Wei, X.; Cai, S.; Zhan, W. Impact of anthropogenic activities on morphological and deposition flux changes in the Pearl River Estuary, China. Sci. Rep. 2021, 11, 16643. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Lin, J.; Huang, H.; Deng, J.; Chen, A. Analysis on the Dynamics of Coastline and Reclamation in Pearl River Estuary in China for Nearly Last Half Century. Water 2022, 14, 1228. [Google Scholar] [CrossRef]
- Kolar, R.L.; Gray, W.G.; Westerink, J.J.; Luettich, R.A., Jr. Shallow water modeling in spherical coordinates: Equation formulation, numerical implementation and application. J. Hydraul. Res. 1994, 32, 3–24. [Google Scholar] [CrossRef]
- Jelesnianski, C.P. Numerical computations of storm surges without bottom stress. Mon. Weather Rev. 1966, 94, 379–394. [Google Scholar] [CrossRef]
- HY/T0273-2019; Technical Directives for Risk Assessment and Zoning of Marine Disasters Part 1: Storm Surge. The Ministry of Natural Resources of the People’s Republic China: Beijing, China, 2019.

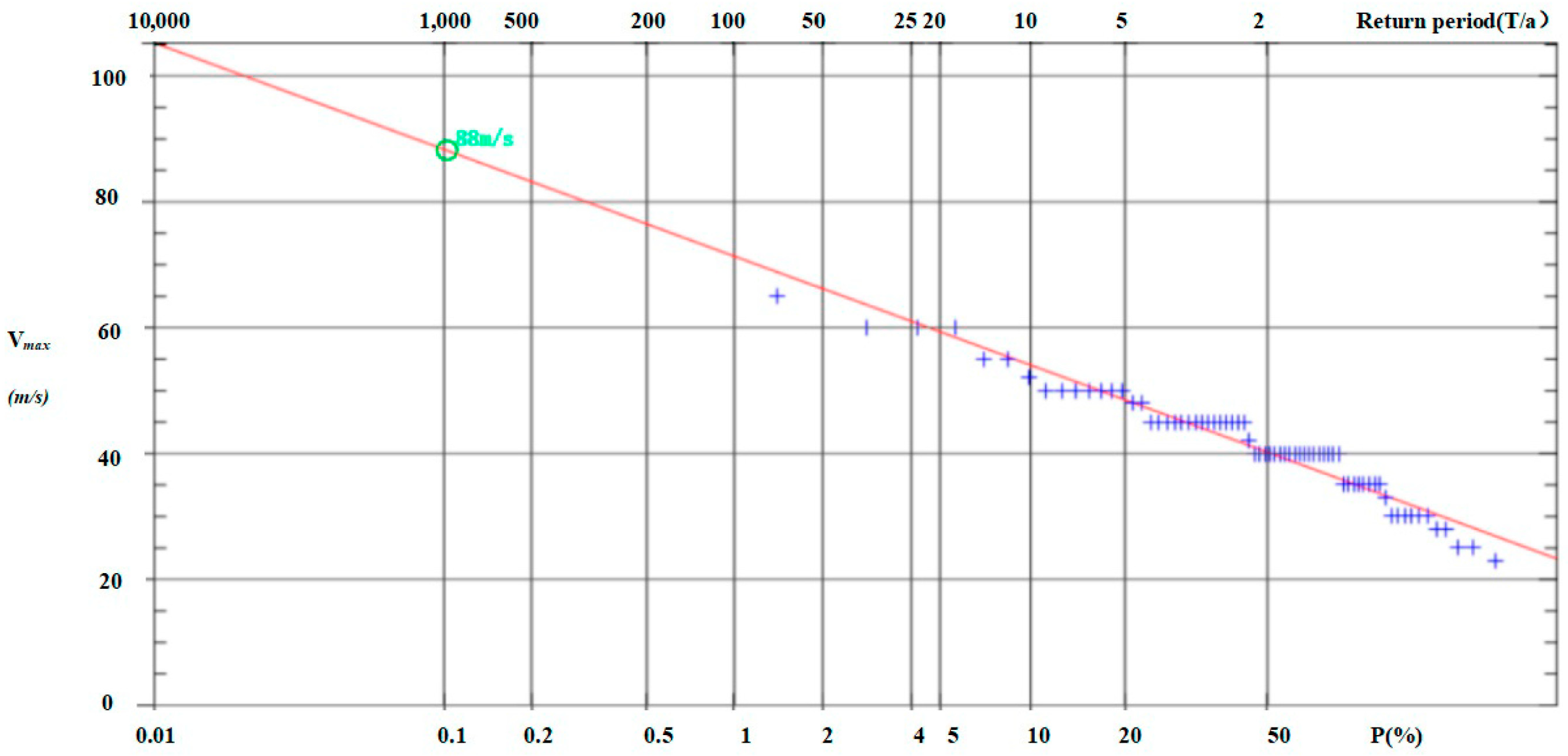
| Grade | Grade1 (Probable Maximum Typhoon) | Grade2 | Grade 3 | Grade 4 | Grade 5 | Grade 6 |
|---|---|---|---|---|---|---|
| The lowest pressure (hPa) | 876 | 910 | 920 | 930 | 940 | 950 |
| Recurrence period (years) | 1000 | 100 | 50 | 20 | 10 | 5 |
| Maximum wind speed (m/s) | 88 | 60 | 56 | 52 | 48 | 44 |
| Maximum wind speed radius (km) | 21 | 30 | 30 | 33 | 35 | 38 |
| Outer sea level pressure (hPa) | 1006 | 1006 | 1006 | 1006 | 1006 | 1006 |
| Move speed (km/h) | 15 | 15 | 15 | 15 | 15 | 15 |
| Number of paths (interval 10 km) | 34 | 34 | 34 | 34 | 34 | 34 |
| Serial Number | Typhoon Level | The Maximum Storm Surge Under Different Intensity Typhoons (cm) | ||
|---|---|---|---|---|
| Xichong | Renshan | Kaozhouyang | ||
| 1 | 876 hPa | 408 | 468 | 508 |
| 2 | 910 hPa | 355 | 370 | 372 |
| 3 | 920 hPa | 323 | 336 | 339 |
| 4 | 930 hPa | 300 | 316 | 315 |
| 5 | 940 hPa | 259 | 280 | 276 |
| 6 | 950 hPa | 231 | 251 | 244 |
| Serial Number | Typhoon Level | Under the Condition of 10% Monthly Astronomical Tide High Tide Level | Under the Condition of Average Tidal Level | ||||
|---|---|---|---|---|---|---|---|
| Xichong | Renshan | Kaozhouyang | Xichong | Renshan | Kaozhouyang | ||
| 1 | 876 hPa | 2.4 | 31.9 | 68.1 | 1.9 | 28.7 | 62.4 |
| 2 | 910 hPa | 2.2 | 29.6 | 59.8 | 1.6 | 26.0 | 31.7 |
| 3 | 920 hPa | 2.1 | 28.4 | 33.6 | 1.5 | 11.6 | 30.3 |
| 4 | 930 hPa | 2.0 | 28.0 | 32.7 | 1.4 | 2.3 | 29.2 |
| 5 | 940 hPa | 1.7 | 26.9 | 31.5 | 1.2 | 2.0 | 27.4 |
| 6 | 950 hPa | 1.6 | 26.2 | 30.3 | 1.2 | 1.9 | 22.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Xu, W.; Xu, B.; Zhao, J.; Liang, C.; Zhang, W.; Deng, J. Application of GIS Spatial Analysis for the Assessment of Storm Surge Inundation Risks in the Guangdong–Macao–Hong Kong Great Bay Area. Water 2024, 16, 2554. https://doi.org/10.3390/w16172554
Zhang J, Xu W, Xu B, Zhao J, Liang C, Zhang W, Deng J. Application of GIS Spatial Analysis for the Assessment of Storm Surge Inundation Risks in the Guangdong–Macao–Hong Kong Great Bay Area. Water. 2024; 16(17):2554. https://doi.org/10.3390/w16172554
Chicago/Turabian StyleZhang, Juan, Weiming Xu, Boliang Xu, Junpeng Zhao, Changxia Liang, Wenjing Zhang, and Junjie Deng. 2024. "Application of GIS Spatial Analysis for the Assessment of Storm Surge Inundation Risks in the Guangdong–Macao–Hong Kong Great Bay Area" Water 16, no. 17: 2554. https://doi.org/10.3390/w16172554
APA StyleZhang, J., Xu, W., Xu, B., Zhao, J., Liang, C., Zhang, W., & Deng, J. (2024). Application of GIS Spatial Analysis for the Assessment of Storm Surge Inundation Risks in the Guangdong–Macao–Hong Kong Great Bay Area. Water, 16(17), 2554. https://doi.org/10.3390/w16172554






