Interrelationship between Wall and Beach Erosion in Loc An, Vietnam: Remote Sensing and Numerical Modeling Approaches
Abstract
1. Introduction
2. Materials and Methods
2.1. Remote Sensing
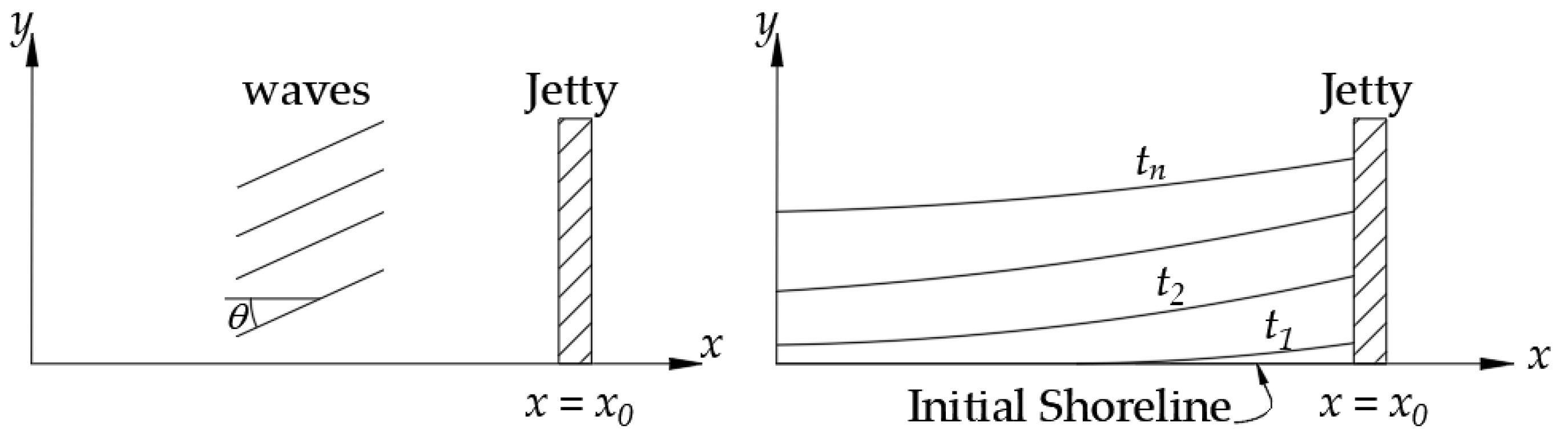
2.2. One-Line Model
3. Results of Satellite Image Analysis
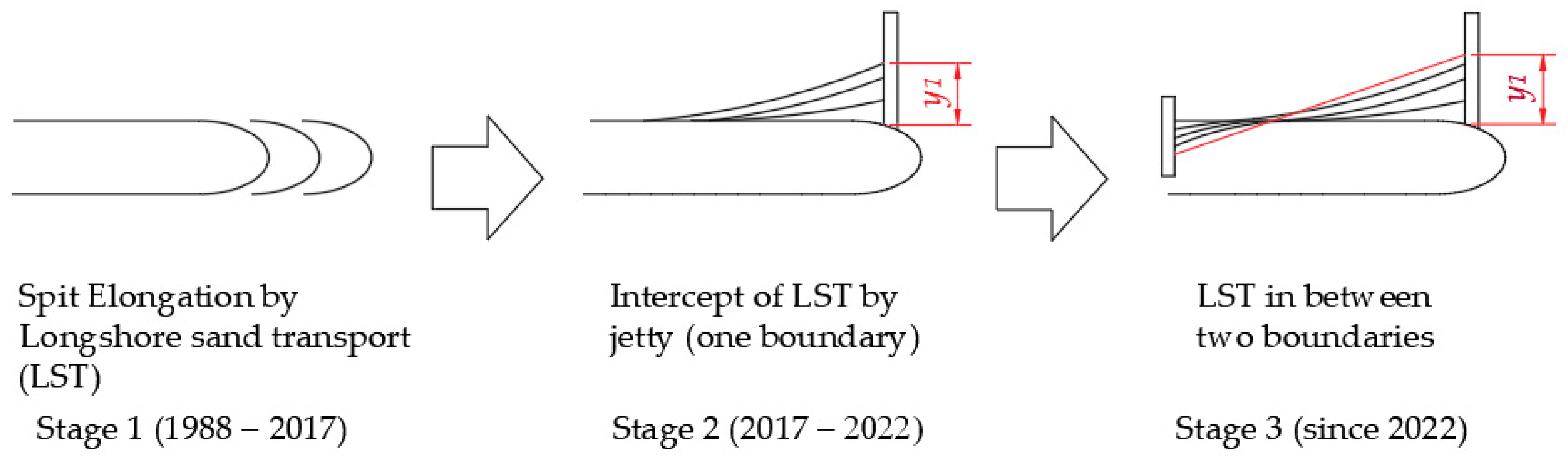
3.1. Stage 1: Elongation of the Sand Spit
3.2. Stage 2: Intercept of LST by a Jetty
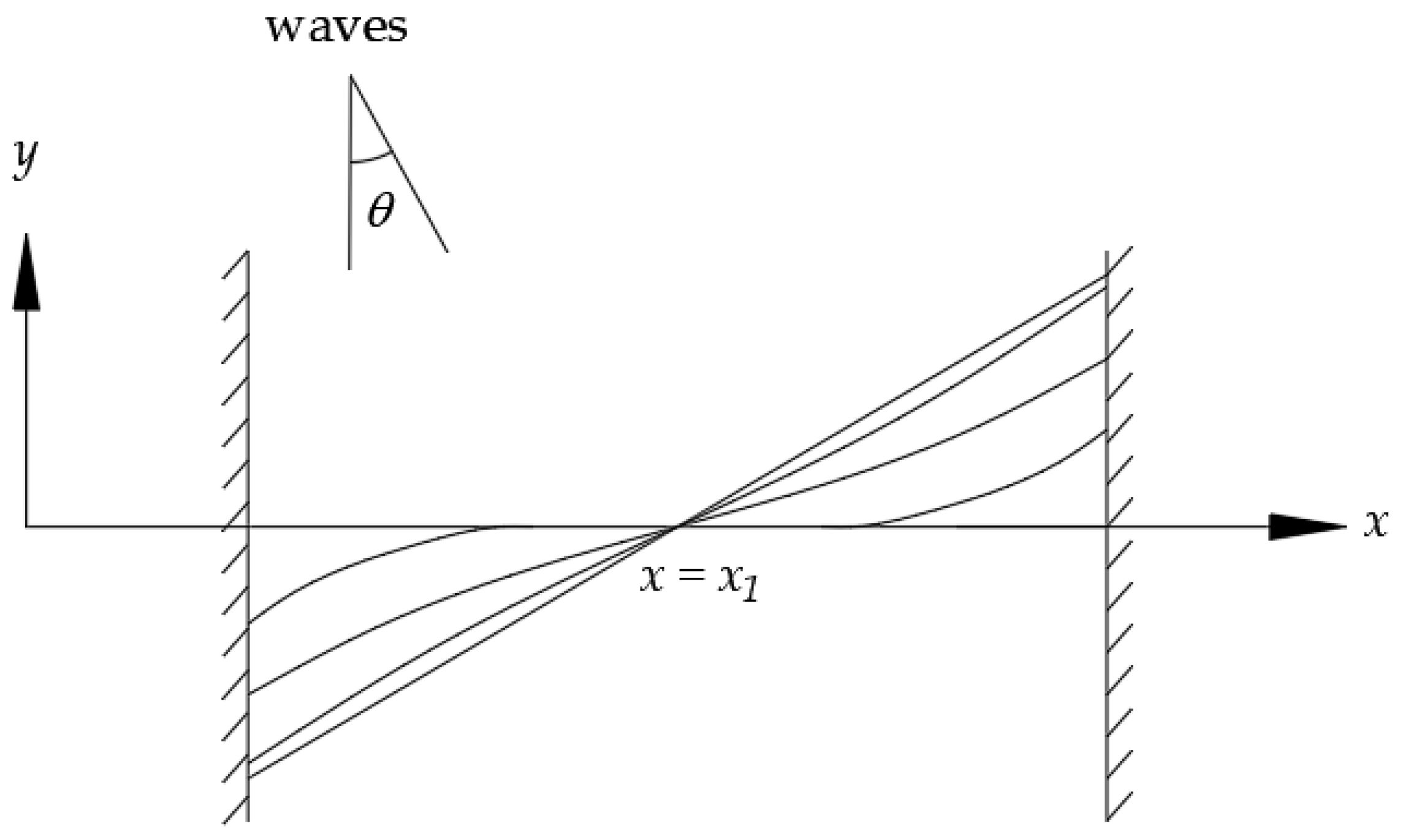
3.3. Stage 3: Construction of the Seawall and LST in between Two Boundaries
4. Application of One-Line Model
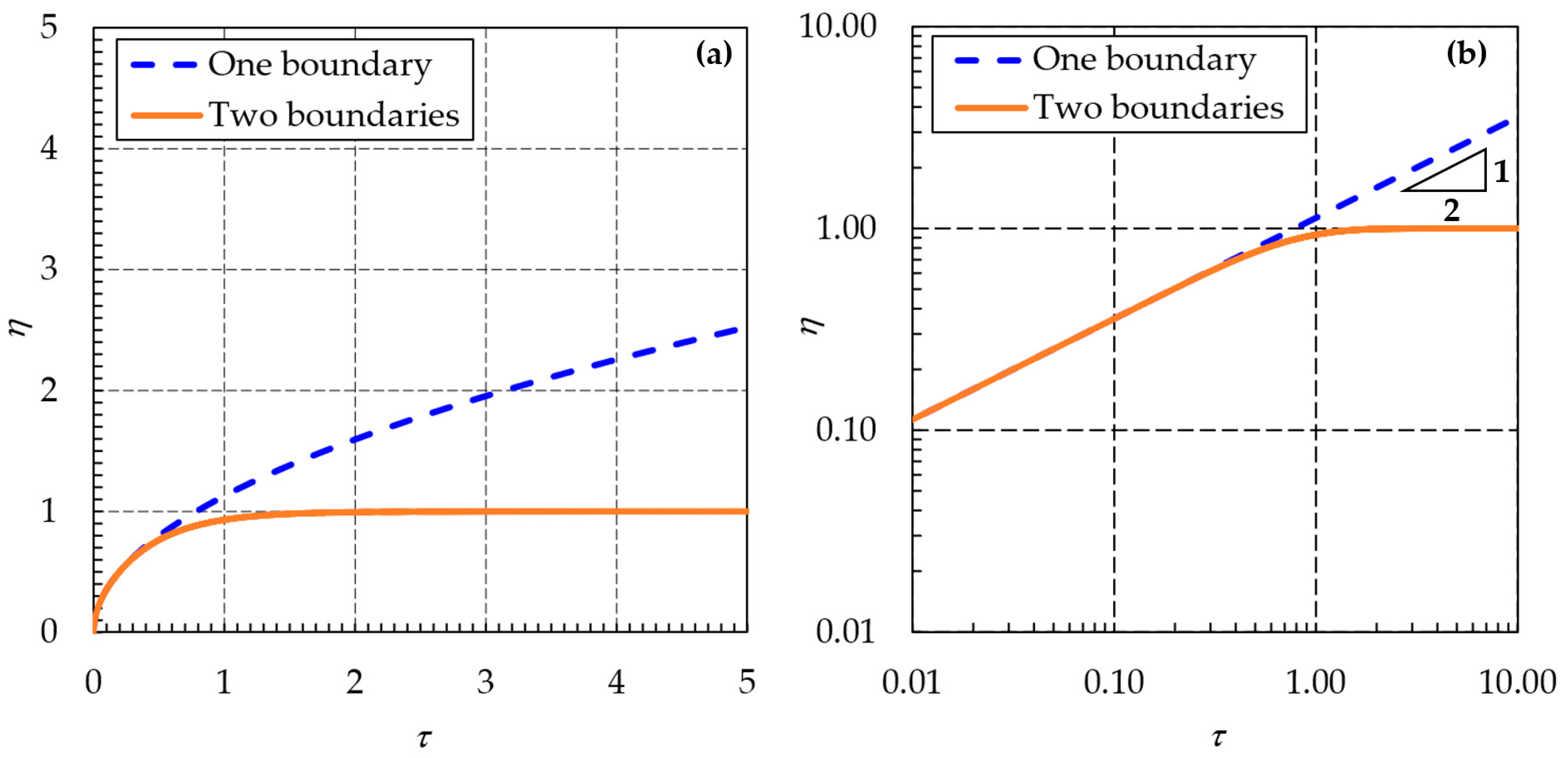
4.1. Solution for Sandy Beach with One Boundary
4.2. Solution for Sandy Beach with Two Boundaries
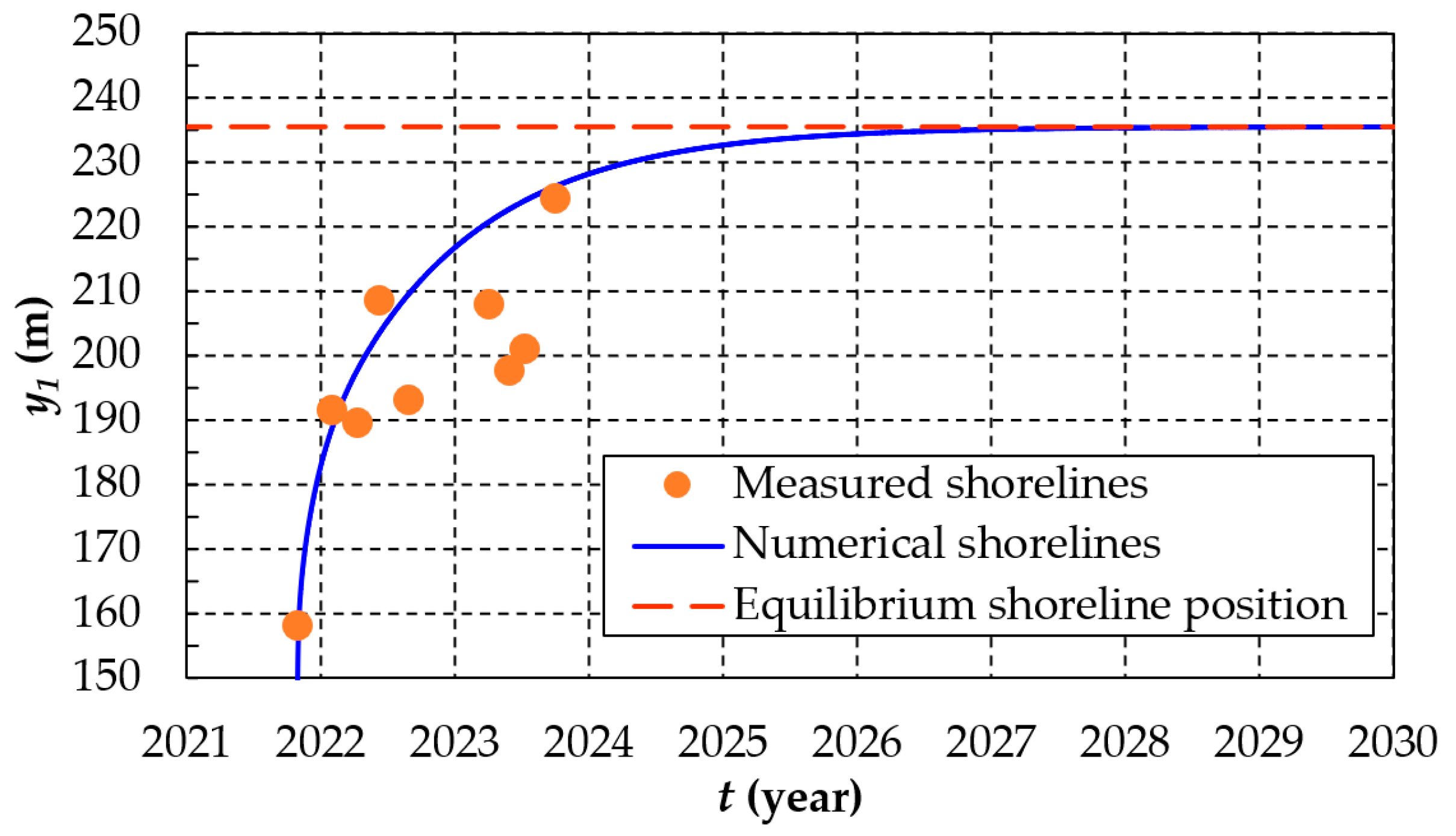
4.3. Comparison with Field Measured Data
5. Discussion
5.1. Tidal Effect to the Shoreline Positions
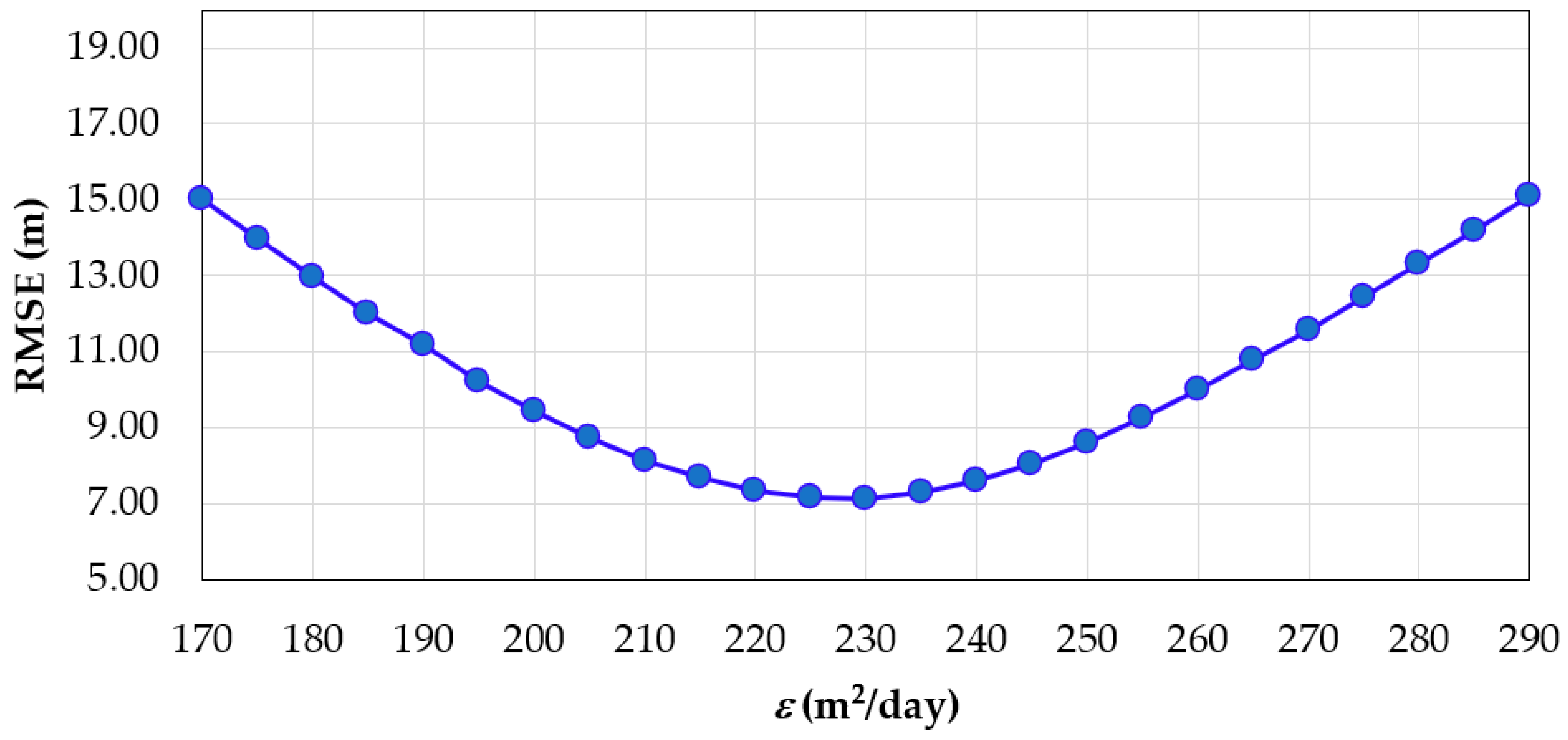
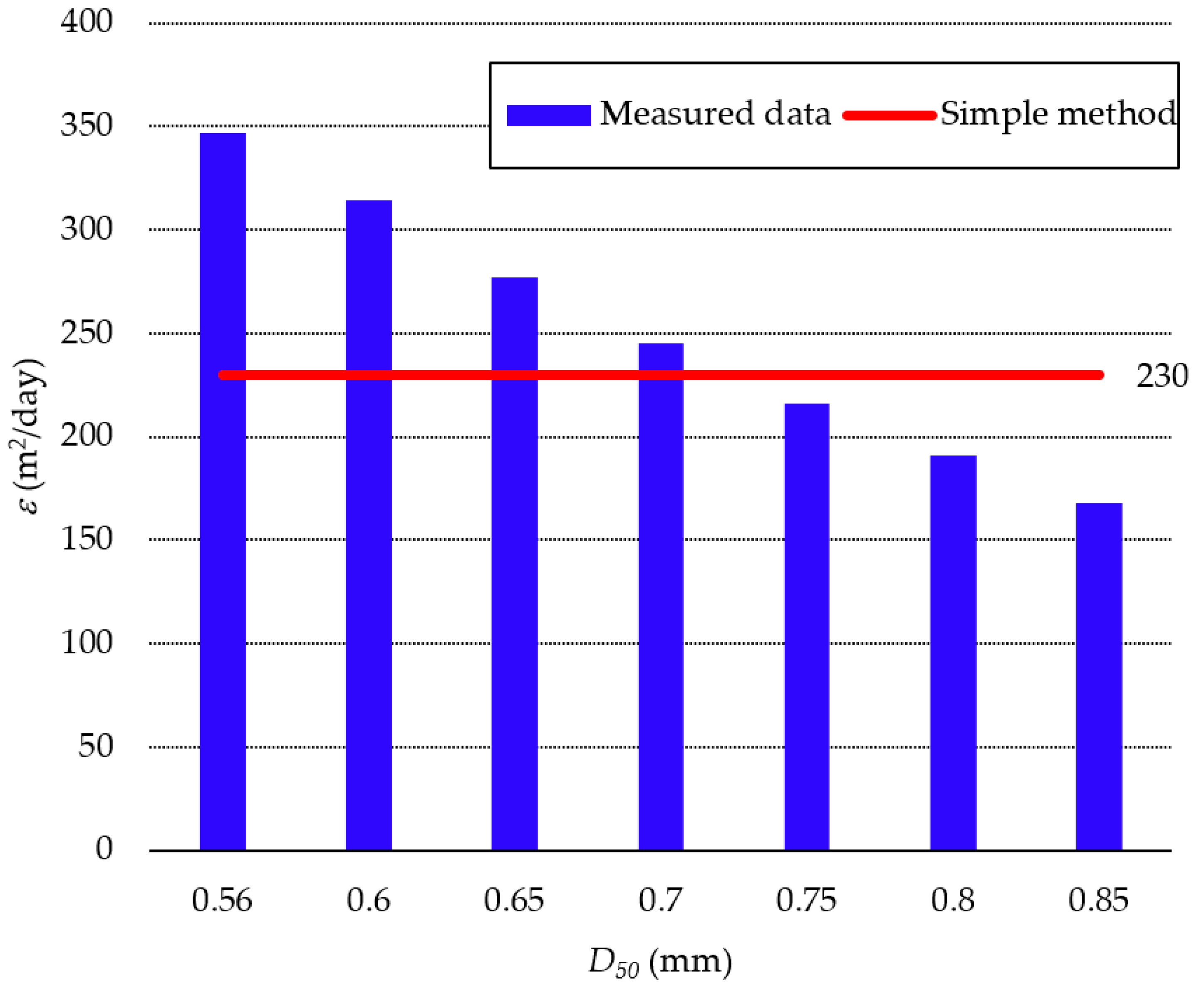
5.2. Determination of ε Value
6. Conclusions
- -
- The evolution of the Loc An sand spit was divided into three stages in which the first stage showed the elongation of the sand spit because of LST without human intervention. The second stage showed the shoreline buildup upstream of the jetties. In the third stage, the shoreline at the Loc An sand spit was affected by both the jetties and the seawall and the shoreline approached equilibrium conditions.
- -
- The value of shoreline diffusivity and the breaking wave angle at the Loc An coastline were determined as 230 m2/day and 18 degrees, respectively.
- -
- Although erosion occurred after the construction of the seawall, this erosion was limited and the shoreline still progressed towards equilibrium conditions.
- -
- A comparison between the measured and calculated data of shoreline evolution at the jetty was conducted. Although there were some fluctuations in the measured data, they generally followed the trend of the calculated shoreline evolution. This indicates the reliability of the simple shoreline model used in this study.
- -
- There is a good agreement between the simple method proposed in this study and the measured data for calculating ε. Hence, the method can determine the value of ε for data-scarce localities.
- -
- If the sand bypass at the eastern jetty and sediment transport along the seawall are neglected, the shoreline at the Loc An sand spit is expected to reach its equilibrium condition by mid-2027.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Crossland, C.; Kremer, H. Coastal zones: Ecosystems under pressure. In Proceedings of the Oceans and Coasts at RIO+ 10-Global Conference, Paris, France, 3–7 December 2001; UNESCO: Paris, France, 2001. [Google Scholar]
- Almar, R.; Marchesiello, P.; Almeida, L.P.; Thuan, D.H.; Tanaka, H.; Viet, N.T. Shoreline response to a sequence of typhoon and monsoon events. Water 2017, 9, 364. [Google Scholar] [CrossRef]
- Viet, N.T.; Tanaka, H. Study on the effect of morphology change on salinity distribution in the Dinh An estuary, lower Mekong River of Vietnam. J. Coast. Res. 2007, SI 50, 268–272. [Google Scholar] [CrossRef]
- Duy, D.V.; Ty, T.V.; Than, C.T.N.; Thang, C.N.; Hong, H.T.C.; Viet, N.T.; Tanaka, H. Coastal Erosion Caused by River Mouth Migration on a Cuspate Delta: An Example from Thanh Hoa, Vietnam. Hydrology 2023, 10, 189. [Google Scholar] [CrossRef]
- Duc Anh, N.Q. Comprehensive Study on the Sand Spit Elongation at Tidal Inlets in Vietnam. Ph.D. Dissertation, Tohoku University, Sendai, Japan, 2021; p. 184. [Google Scholar]
- Quang, D.N.; Ngan, V.H.; Tam, H.S.; Viet, N.T.; Tinh, N.X.; Tanaka, H. Long-Term Shoreline Evolution Using DSAS Technique: A Case Study of Quang Nam Province, Vietnam. J. Mar. Sci. Eng. 2021, 9, 1124. [Google Scholar] [CrossRef]
- Tinh, N.X.; Thanh, T.M.; Tanaka, H.; Viet, N.T.; Mitobe, Y.; Dien, D.C. Numerical investigation of the effect of seasonal variations of depth-of-closure on shoreline evolution. Int. J. Sediment Res. 2021, 36, 1–16. [Google Scholar]
- Thanh, T.M.; Tanaka, H.; Mitobe, Y.; Viet, N.T.; Almar, R. Seasonal variation of morphology and sediment movement on nha trang coast, vietnam. J. Coast. Res. 2018, 81, 22–31. [Google Scholar]
- Duy, D.V.; Tanaka, H.; Mitobe, Y.; Anh, N.Q.; Viet, N.T. Sand spit elongation and sediment balance at cua lo inlet in central Vietnam. J. Coast. Res. 2018, 81, 32–39. [Google Scholar]
- Duy, D.V.; Ty, T.V.; Thanh, T.N.; Minh, H.V.T.; De, C.V.; Duong, V.H.T.; Dan, T.C.; Viet, N.T.; Tanaka, H. Sand Spit Morphology at an Inlet on Phu Quoc Island, Vietnam. Water 2023, 15, 1941. [Google Scholar] [CrossRef]
- António, M.H.; Fernandes, E.H.; Muelbert, J.H. Impact of Jetty Configuration Changes on the Hydrodynamics of the Subtropical Patos Lagoon Estuary, Brazil. Water 2020, 12, 3197. [Google Scholar] [CrossRef]
- Liang, T.-Y.; Chang, C.-H.; Hsiao, S.-C.; Huang, W.-P.; Chang, T.-Y.; Guo, W.-D.; Liu, C.-H.; Ho, J.-Y.; Chen, W.-B. On-site investigations of coastal erosion and accretion for the northeast of Taiwan. J. Mar. Sci. Eng. 2022, 10, 282. [Google Scholar] [CrossRef]
- Siemes, R.W.A.; Duong, T.M.; Willemsen, P.W.J.M.; Borsje, B.W.; Hulscher, S.J.M.H. Morphological Response of a Highly Engineered Estuary to Altering Channel Depth and Restoring Wetlands. J. Mar. Sci. Eng. 2023, 11, 2150. [Google Scholar] [CrossRef]
- Tanaka, H.; Shuto, N. Field investigation at a mouth of small river. In Coastal Engineering 1992; American Society of Civil Engineers: Reston, VA, USA, 1993; pp. 2486–2499. [Google Scholar]
- Tanaka, H.; Lee, H.-S. Influence of jetty construction on morphology and wave set-up at a river mouth. Coast. Eng. J. 2003, 45, 659–683. [Google Scholar] [CrossRef]
- Lawson, S.K.; Tanaka, H.; Udo, K.; Hiep, N.T.; Tinh, N.X. Morphodynamics and Evolution of Estuarine Sandspits along the Bight of Benin Coast, West Africa. Water 2021, 13, 2977. [Google Scholar] [CrossRef]
- Tanaka, N.; Nadaoka, K. Development and Application of a Numerical Model for the Prediction of Shoreline Changes; Tech. Note 436; Port and Harbour Research Institute, Ministry of Transport: Yokosuka, Japan, 1982; p. 40. (In Japanese)
- Duc Anh, N.Q.; Duy, D.V.; Tanaka, H.; Tinh, N.X.; Viet, N.T. Elongation of sand spit at Loc An river mouth, Southern Vietnam. J. Jpn. Soc. Civ. Eng. Ser. B3 (Ocean. Eng.) 2018, 74, I_695–I_700. [Google Scholar]
- Duy, D.V.; Tanaka, H.; Larson, M.; Viet, N.T. A Theory for Estuarine Delta Formation with Finite Beach Length under Sediment Supplied from the River. J. Mar. Sci. Eng. 2022, 10, 947. [Google Scholar] [CrossRef]
- Mishra, D.R.; Gould, R.W. Preface: Remote Sensing in Coastal Environments. Remote Sens. 2016, 8, 665. [Google Scholar] [CrossRef]
- Waqas, M.; Nazeer, M.; Shahzad, M.I.; Zia, I. Spatial and temporal variability of open-ocean barrier islands along the Indus Delta region. Remote Sens. 2019, 11, 437. [Google Scholar] [CrossRef]
- Zanutta, A.; Lambertini, A.; Vittuari, L. UAV Photogrammetry and Ground Surveys as a Mapping Tool for Quickly Monitoring Shoreline and Beach Changes. J. Mar. Sci. Eng. 2020, 8, 52. [Google Scholar] [CrossRef]
- Pham, T.D.; Le, N.N.; Ha, N.T.; Nguyen, L.V.; Xia, J.; Yokoya, N.; To, T.T.; Trinh, H.X.; Kieu, L.Q.; Takeuchi, W. Estimating mangrove above-ground biomass using extreme gradient boosting decision trees algorithm with fused sentinel-2 and ALOS-2 PALSAR-2 data in can Gio biosphere reserve, Vietnam. Remote Sens. 2020, 12, 777. [Google Scholar] [CrossRef]
- Papageorgiou, D.; Topouzelis, K.; Suaria, G.; Aliani, S.; Corradi, P. Sentinel-2 Detection of Floating Marine Litter Targets with Partial Spectral Unmixing and Spectral Comparison with Other Floating Materials (Plastic Litter Project 2021). Remote Sens. 2022, 14, 5997. [Google Scholar] [CrossRef]
- Abdelhady, H.U.; Troy, C.D.; Habib, A.; Manish, R. A Simple, Fully Automated Shoreline Detection Algorithm for High-Resolution Multi-Spectral Imagery. Remote Sens. 2022, 14, 557. [Google Scholar] [CrossRef]
- Vos, K.; Splinter, K.D.; Palomar-Vázquez, J.; Pardo-Pascual, J.E.; Almonacid-Caballer, J.; Cabezas-Rabadán, C.; Kras, E.C.; Luijendijk, A.P.; Calkoen, F.; Almeida, L.P.; et al. Benchmarking satellite-derived shoreline mapping algorithms. Commun. Earth Environ. 2023, 4, 345. [Google Scholar] [CrossRef]
- Zollini, S.; Dominici, D.; Alicandro, M.; Cuevas-González, M.; Angelats, E.; Ribas, F.; Simarro, G. New Methodology for Shoreline Extraction Using Optical and Radar (SAR) Satellite Imagery. J. Mar. Sci. Eng. 2023, 11, 627. [Google Scholar] [CrossRef]
- Baba, M.W.; Thoumyre, G.; Bergsma, E.W.J.; Daly, C.J.; Almar, R. Deriving Large-Scale Coastal Bathymetry from Sentinel-2 Images Using an HIGH-Performance Cluster: A Case Study Covering North Africa’s Coastal Zone. Sensors 2021, 21, 7006. [Google Scholar] [CrossRef]
- Bergsma, E.W.; Almar, R. Coastal coverage of ESA’Sentinel 2 mission. Adv. Space Res. 2020, 65, 2636–2644. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Hoang, V.C.; Tanaka, H.; Mitobe, Y. A method for correcting tidal effect on shoreline position extracted from an image with unknown capture time. Geosciences 2017, 7, 62. [Google Scholar] [CrossRef]
- Royal_Haskoning_DHV. Coastal Erosion Protection—Ho Tram Strip. In Coastal Erosion Protection Concept Study; Ho Tram Project Company Ltd.: Ba Ria-Vung Tau, Vietnam, 2018; p. 72. [Google Scholar]
- Ciccaglione, M.C.; Buccino, M.; Calabrese, M. Beaches in a Semi-Insulated Compartment: Engineering Tools from the Diffusion Theory. Estuar. Coast. Shelf Sci. 2014, 301, 108726. [Google Scholar] [CrossRef]
- Pelnard-Considère, R. Essai de theorie de l’evolution des formes de rivage en plages de sable et de galets. Journées de L’hydraulique 1957, 4, 289–298. [Google Scholar]
- Larson, M.; Hanson, H.; Kraus, N.C. Analytical Solutions of the One-Line Model of Shoreline Change; Coastal Engineering Research Center: Vicksburg, MS, USA, 1987. [Google Scholar]
- Ashton, A.D.; Murray, A.B. High-angle wave instability and emergent shoreline shapes: 1. Modeling of sand waves, flying spits, and capes. J. Geophys. Res. Earth Surf. 2006, 111, F04011. [Google Scholar] [CrossRef]
- Ashton, A.D.; Murray, A.B. High-angle wave instability and emergent shoreline shapes: 2. Wave climate analysis and comparisons to nature. J. Geophys. Res. Earth Surf. 2006, 111, F04012. [Google Scholar] [CrossRef]
- Falqués, A. On the diffusivity in coastline dynamics. Geophys. Res. Lett. 2003, 30, 2119. [Google Scholar] [CrossRef]
- Falqués, A.; Calvete, D. Large-scale dynamics of sandy coastlines: Diffusivity and instability. J. Geophys. Res. Ocean. 2005, 110, C03007. [Google Scholar] [CrossRef]
- Walton, T.L., Jr.; Dean, R.G. Longshore sediment transport via littoral drift rose. Ocean. Eng. 2010, 37, 228–235. [Google Scholar] [CrossRef]
- Carslaw, H.; Jaeger, J. Conduction of Heat in Solids; Clarendon Press: Oxford, UK, 1959; p. 510. [Google Scholar]
- Crank, P. The Mathematics of Diffusion, 2nd ed.; Oxford University Press: Oxford, UK, 1975; p. 421. [Google Scholar]
- Rosati, J.D.; Walton, T.; Bodge, K. Longshore sediment transport. In Coastal Engineering Manual; U.S. Army Corps of Engineers: Washington, DC, USA, 2002; p. 119. [Google Scholar]
- del Valle, R.; Medina, R.; Losada, M.A. Dependence of coefficient K on grain size. J. Waterw. Port Coast. Ocean. Eng. 1993, 119, 568–574. [Google Scholar] [CrossRef]
- Sana, A. Teaching fundamental concepts of coastal engineering using excel spreadsheet. Comput. Appl. Eng. Educ. 2017, 25, 304–310. [Google Scholar] [CrossRef]
- Weggel, R.J. Maximum breaker height. J. Waterw. Harb. Coast. Eng. Div. 1972, 98, 529–548. [Google Scholar] [CrossRef]












| No. | Date | Sensor | Resolution (m) | Data Source |
|---|---|---|---|---|
| 1 | 05 December 2015 | MSI | 10 | Sentinel 2–1LC |
| 2 | 25 December 2015 | MSI | 10 | Sentinel 2–1LC |
| 3 | 14 January 2016 | MSI | 10 | Sentinel 2–1LC |
| 4 | 24 March 2016 | MSI | 10 | Sentinel 2–1LC |
| 5 | 26 March 2016 | MSI | 10 | Sentinel 2–1LC |
| 6 | 08 January 2017 | MSI | 10 | Sentinel 2–1LC |
| 7 | 18 April 2017 | MSI | 10 | Sentinel 2–1LC |
| 8 | 31 August 2017 | MSI | 10 | Sentinel 2–1LC |
| 9 | 05 September 2017 | MSI | 10 | Sentinel 2–1LC |
| 10 | 10 October 2017 | MSI | 10 | Sentinel 2–1LC |
| 11 | 06 February 2018 | MSI | 10 | Sentinel 2–1LC |
| 12 | 25 October 2018 | MSI | 10 | Sentinel 2–1LC |
| 13 | 04 November 2018 | MSI | 10 | Sentinel 2–1LC |
| 14 | 13 January 2019 | MSI | 10 | Sentinel 2–1LC |
| 15 | 27 July 2019 | MSI | 10 | Sentinel 2–1LC |
| 16 | 15 October 2019 | MSI | 10 | Sentinel 2–1LC |
| 17 | 26 July 2020 | MSI | 10 | Sentinel 2–1LC |
| 19 | 04 September 2020 | MSI | 10 | Sentinel 2–1LC |
| 20 | 29 October 2021 | MSI | 10 | Sentinel 2–1LC |
| 21 | 16 February 2022 | MSI | 10 | Sentinel 2–1LC |
| 22 | 28 November 2022 | MSI | 10 | Sentinel 2–1LC |
| 23 | 13 March 2023 | MSI | 10 | Sentinel 2–1LC |
| 24 | 27 April 2023 | MSI | 10 | Sentinel 2–1LC |
| 25 | 06 July 2023 | MSI | 10 | Sentinel 2–1LC |
| 26 | 27 January 2024 | MSI | 10 | Sentinel 2–1LC |
| Diffusion coefficient, ε (m2/day) | Unknown |
| Breaking wave angle, θ (degrees) | Unknown |
| Modeling time, t (years) | 1.9 |
| Diffusion coefficient, ε (m2/day) | 230 |
| Breaking wave angle, θ (degrees) | 18 |
| Modeling time, t (years) | 1.9 |
| D50 (mm) | K |
|---|---|
| 0.56 | 0.35 |
| 0.60 | 0.31 |
| 0.65 | 0.28 |
| 0.70 | 0.24 |
| 0.75 | 0.21 |
| 0.80 | 0.19 |
| 0.85 | 0.17 |
| D50 (mm) | K | ε (m2/day) |
|---|---|---|
| 0.56 | 0.35 | 347 |
| 0.60 | 0.31 | 314 |
| 0.65 | 0.28 | 277 |
| 0.70 | 0.24 | 245 |
| 0.75 | 0.21 | 216 |
| 0.80 | 0.19 | 191 |
| 0.85 | 0.17 | 168 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Duy, D.; Duc Anh, N.Q.; Viet, N.T.; Tanaka, H. Interrelationship between Wall and Beach Erosion in Loc An, Vietnam: Remote Sensing and Numerical Modeling Approaches. Water 2024, 16, 2553. https://doi.org/10.3390/w16172553
Van Duy D, Duc Anh NQ, Viet NT, Tanaka H. Interrelationship between Wall and Beach Erosion in Loc An, Vietnam: Remote Sensing and Numerical Modeling Approaches. Water. 2024; 16(17):2553. https://doi.org/10.3390/w16172553
Chicago/Turabian StyleVan Duy, Dinh, Nguyen Quang Duc Anh, Nguyen Trung Viet, and Hitoshi Tanaka. 2024. "Interrelationship between Wall and Beach Erosion in Loc An, Vietnam: Remote Sensing and Numerical Modeling Approaches" Water 16, no. 17: 2553. https://doi.org/10.3390/w16172553
APA StyleVan Duy, D., Duc Anh, N. Q., Viet, N. T., & Tanaka, H. (2024). Interrelationship between Wall and Beach Erosion in Loc An, Vietnam: Remote Sensing and Numerical Modeling Approaches. Water, 16(17), 2553. https://doi.org/10.3390/w16172553










