Numerical Study on the Hydraulic and Mixing Performance of Fluid Flow within a Channel with Different Numbers of Sector Bodies
Abstract
1. Introduction
2. Numerical Setup
2.1. Simulation Model
2.2. Numerical Methods
2.3. Mesh Convergence Test and Data Validation
3. Results and Discussion
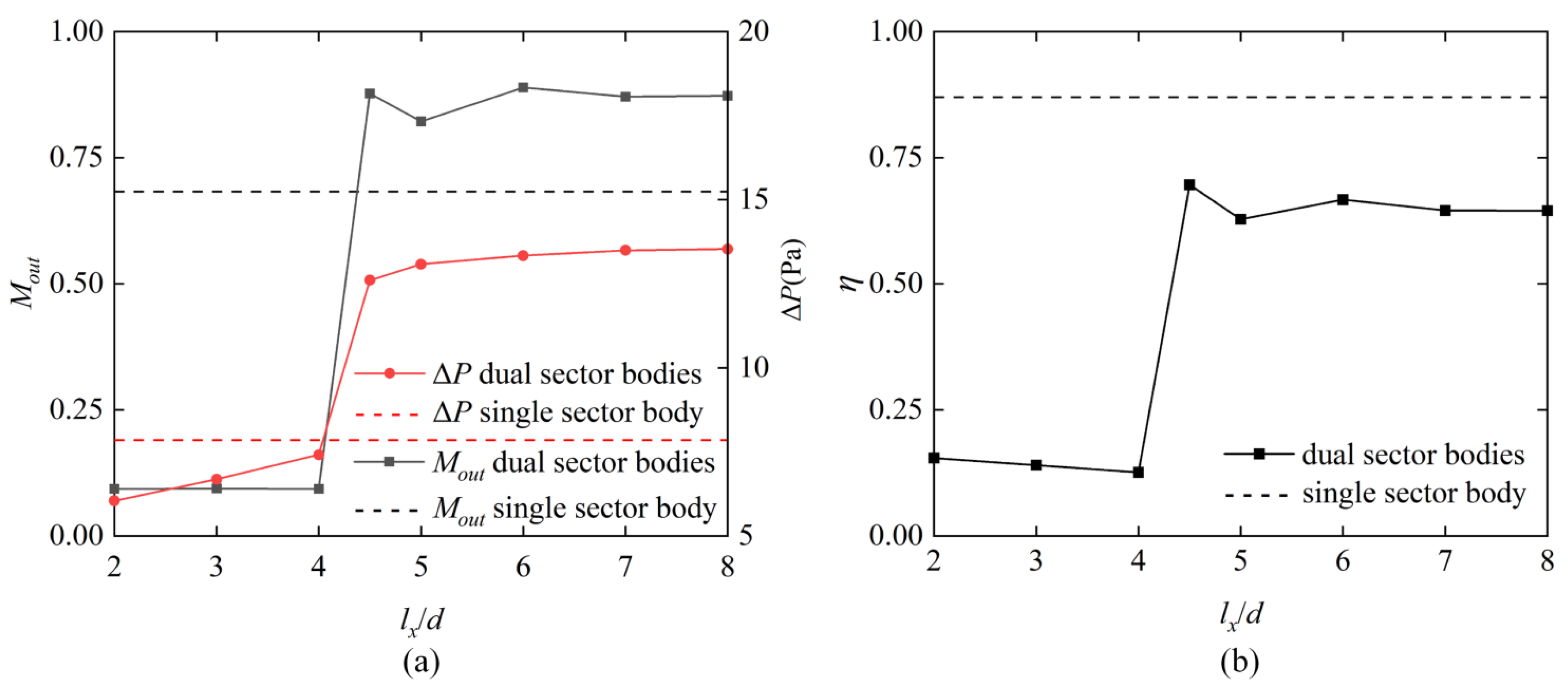
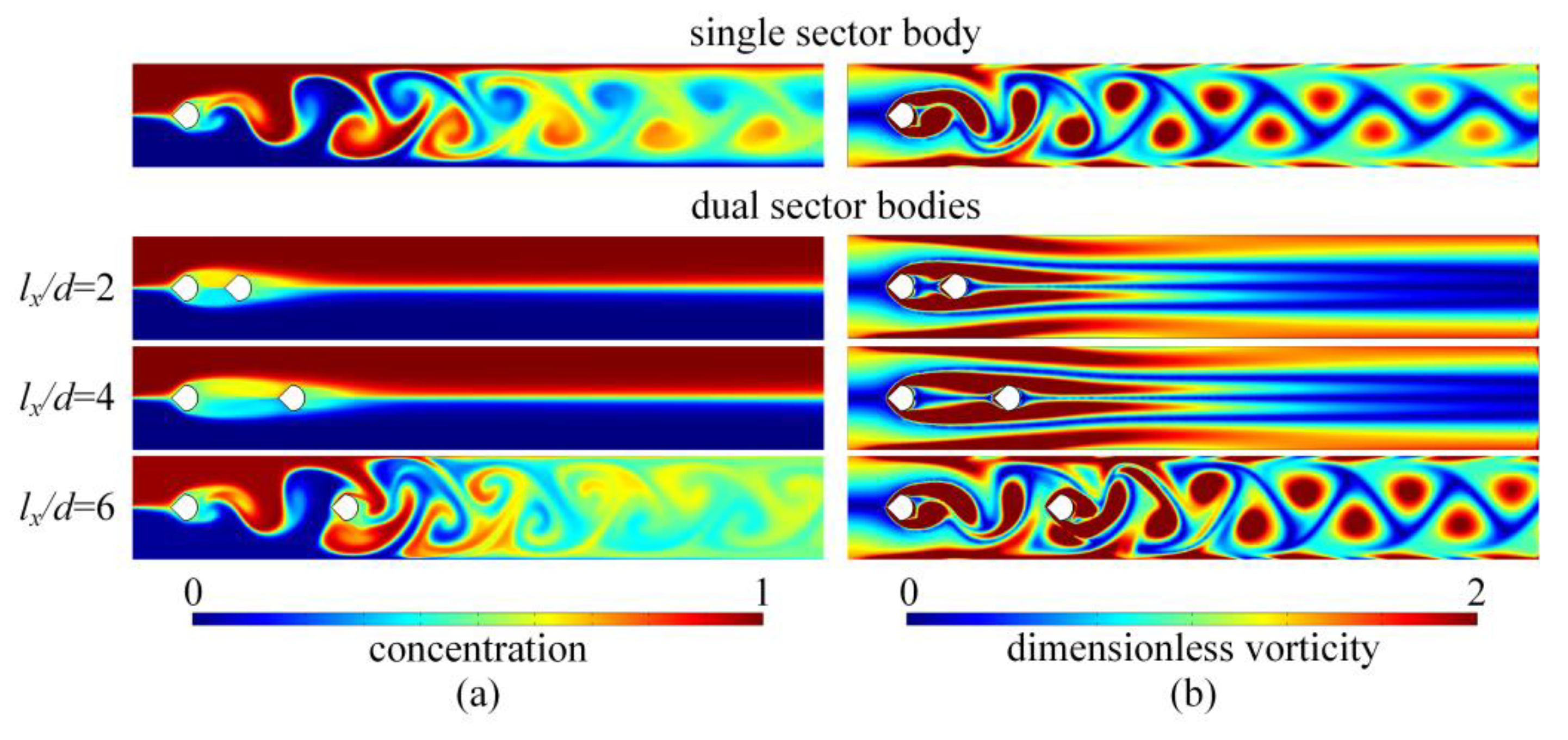
3.1. Performance of CDSB
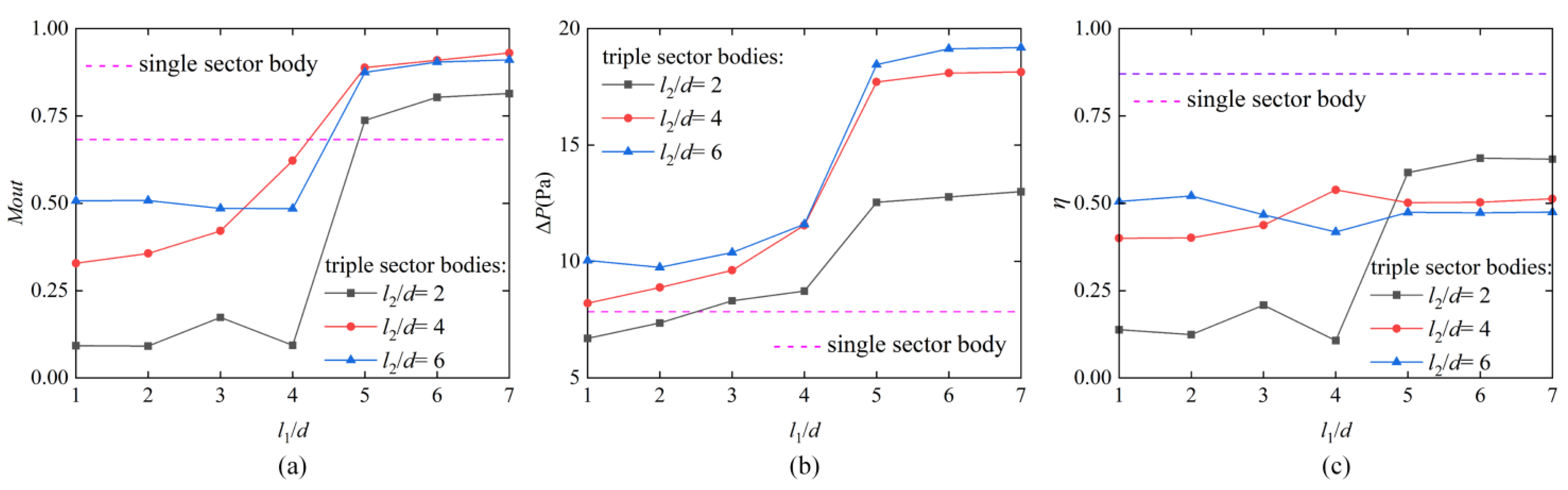
3.2. Performance of CTSB
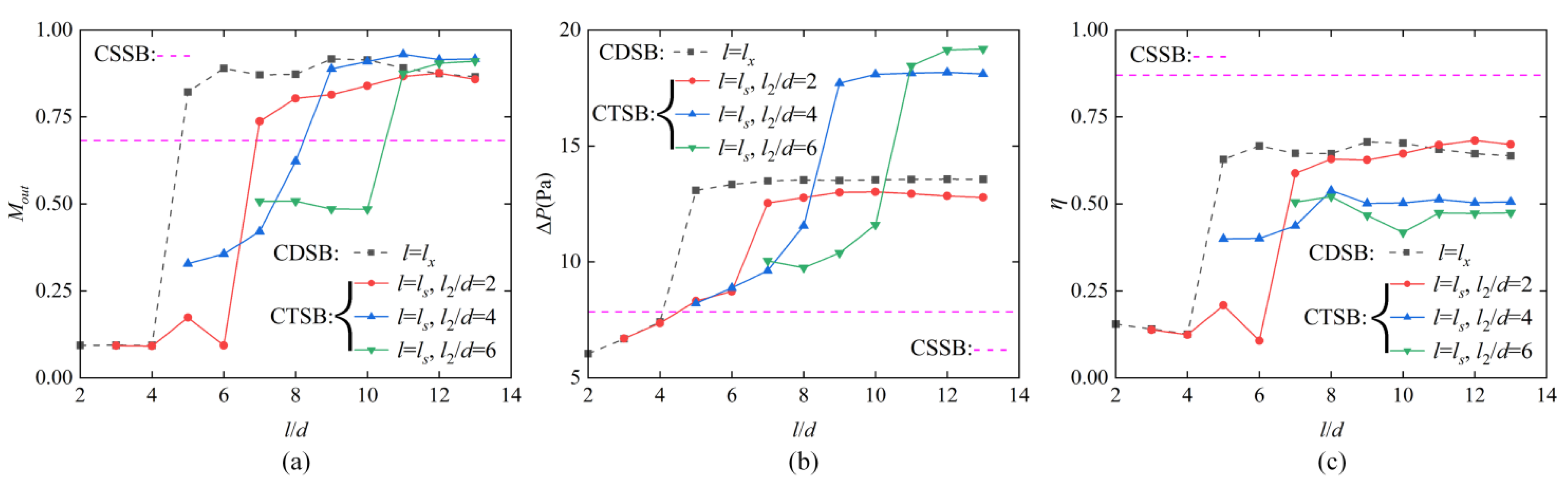
3.3. Performance Comparisons of CSSB, CDSB and CTSB
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | the distance between the center of the first sector body and the channel inlet (m) | ΔP* | dimensionless pressure loss |
| Red | Reynolds number based on the sector body dimension | ||
| c | concentration of liquid (mol/m3) | ||
| ci | concentration (mol/m3) | ReH | Reynolds number based on channel height |
| cref | reference concentration (mol/m3) | ||
| Dc | diffusion coefficient (m2/s) | T | a period of time after achieving periodic stability of the mixing inside the channel (s) |
| d | characteristic dimension of sector body (m) | ||
| H | channel height (m) | ||
| L | channel length (m) | t | time (s) |
| lx | the spacing between the two sector bodies in the channel with dual sector bodies (m) | u | fluid velocity (m/s) |
| u0 | mean inlet velocity (m/s) | ||
| l1 | the spacing between the first two sector bodies in the channel with triple sector bodies (m) | uin | inlet flow velocity (m/s) |
| ω* | dimensionless vorticity | ||
| ω | vorticity (1/s) | ||
| l2 | the spacing between the last two sector bodies in the channel with triple sector bodies (m) | ||
| Acronyms | |||
| CSSB | channel with single sector body | ||
| ls | the total length between the first and the third sector bodies in the channel with triple sector bodies (m) | CDSB | channel with dual sector bodies |
| CTSB | channel with triple sector bodies | ||
| Mout | outlet mixing efficiency (mol2/m6) | Greek letters | |
| P | pressure (Pa) | μ | fluid dynamic viscosity (Pa·s) |
| Pin | inlet pressure (Pa) | ρf | fluid density (kg/m3) |
| Pout | outlet pressure (Pa) | η | comprehensive performance parameter |
| ΔP | pressure loss (Pa) | ||
References
- Hessel, V.; Löwe, H.; Schönfeld, F. Micromixers—A review on passive and active mixing principles. Chem. Eng. Sci. 2005, 60, 2479–2501. [Google Scholar] [CrossRef]
- Lee, C.Y.; Wang, W.T.; Liu, C.C.; Fu, L.M. Passive mixers in microfluidic systems: A review. Chem. Eng. J. 2016, 288, 146–160. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Wang, B.; Cai, Y.; Song, Q. An overview on state-of-art of micromixer designs, characteristics and applications. Anal. Chim. Acta 2023, 1279, 341685. [Google Scholar] [CrossRef] [PubMed]
- Bazaz, S.R.; Sayyah, A.; Hazeri, A.H.; Salomon, R.; Mehrizi, A.A.; Warkiani, M.E. Micromixer research trend of active and passive designs. Chem. Eng. Sci. 2024, 293, 120028. [Google Scholar] [CrossRef]
- Niculescu, A.G.; Chircov, C.; Bîrcă, A.C.; Grumezescu, A.M. Fabrication and applications of microfluidic devices: A review. Int. J. Mol. Sci. 2021, 22, 2011. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Shen, J. Simulation and experimental analysis of a SAR micromixer with F-shape mixing units. Anal. Methods 2017, 9, 1885–1890. [Google Scholar] [CrossRef]
- Viktorov, V.; Nimafar, M. A novel generation of 3D SAR-based passive micromixer: Efficient mixing and low pressure drop at a low Reynolds number. J. Micromech. Microeng. 2013, 23, 055023. [Google Scholar] [CrossRef]
- Javaid, M.U.; Cheema, T.A.; Park, C.W. Analysis of passive mixing in a serpentine microchannel with sinusoidal side walls. Micromachines 2017, 9, 8. [Google Scholar] [CrossRef]
- Rhoades, T.; Kothapalli, C.R.; Fodor, P.S. Mixing optimization in grooved serpentine microchannels. Micromachines 2020, 11, 61. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Cai, Y.; Wang, B.; Luo, X. A cost-effective serpentine micromixer utilizing ellipse curve. Anal. Chim. Acta 2021, 1155, 338355. [Google Scholar] [CrossRef]
- Mondal, B.; Mehta, S.K.; Patowari, P.K.; Pati, S. Numerical study of mixing in wavy micromixers: Comparison between raccoon and serpentine mixer. Chem. Eng. Process.-Process Intensif. 2019, 136, 44–61. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Yang, Y.; Cai, Y.; Song, Q.; Wang, B. Effects of sidewall roughness on mixing performance of zigzag microchannels. Chem. Eng. Process.-Process Intensif. 2022, 179, 109057. [Google Scholar] [CrossRef]
- Hong, C.C.; Choi, J.W.; Ahn, C.H. A novel in-plane passive microfluidic mixer with modified Tesla structures. Lab Chip 2004, 4, 109–113. [Google Scholar] [CrossRef] [PubMed]
- Hossain, S.; Fuwad, A.; Kim, K.Y.; Jeon, T.J.; Kim, S.M. Investigation of mixing performance of two-dimensional micromixer using Tesla structures with different shapes of obstacles. Ind. Eng. Chem. Res. 2020, 59, 3636–3643. [Google Scholar] [CrossRef]
- Fang, Y.; Ye, Y.; Shen, R.; Zhu, P.; Guo, R.; Hu, Y.; Wu, L. Mixing enhancement by simple periodic geometric features in microchannels. Chem. Eng. J. 2012, 187, 306–310. [Google Scholar] [CrossRef]
- Alam, A.; Afzal, A.; Kim, K.Y. Mixing performance of a planar micromixer with circular obstructions in a curved microchannel. Chem. Eng. Res. Des. 2014, 92, 423–434. [Google Scholar] [CrossRef]
- Zhang, S.; Cagney, N.; Lacassagne, T.; Balabani, S.; Naveira-Cotta, C.P.; Tiwari, M.K. Mixing in flows past confined microfluidic cylinders: Effects of pin and fluid interface offsetting. Chem. Eng. J. 2020, 397, 125358. [Google Scholar] [CrossRef]
- Cao, Y.; Tamura, T. Supercritical flows past a square cylinder with rounded corners. Phys. Fluids 2017, 29, 085110. [Google Scholar] [CrossRef]
- Ortega-Casanova, J. On the onset of vortex shedding from 2D confined rectangular cylinders having different aspect ratios: Application to promote mixing fluids. Chem. Eng. Process.-Process Intensif. 2017, 120, 81–92. [Google Scholar] [CrossRef]
- Sharma, B.; Barman, R.N. Steady laminar flow past a slotted circular cylinder. Phys. Fluids 2020, 32, 073605. [Google Scholar] [CrossRef]
- Hsu, L.C. Heat transfer of flow past a cylinder with a slit. Int. J. Therm. Sci. 2021, 159, 106582. [Google Scholar] [CrossRef]
- Yu, J.J.; Jiang, L.Y.; Huang, L.; Li, G.Y.; Bake, M.; Li, Y.R. Hydrodynamic cavitation of nematic liquid crystal in Stokes flow behind bluff body with different shapes in microchannel. Phys. Fluids 2024, 36, 012006. [Google Scholar] [CrossRef]
- Tafarojnoruz, A.; Lauria, A. Large eddy simulation of the turbulent flow field around a submerged pile within a scour hole under current condition. Coast. Eng. J. 2020, 62, 489–503. [Google Scholar] [CrossRef]
- Zhang, S.; Han, Y.; Lacassagne, T.; Cagney, N.; Naveira-Cotta, C.P.; Balabani, S.; Tiwari, M.K. Flow dynamics and mixing past pairs of confined microfluidic cylinders. Chem. Eng. Sci. 2023, 267, 118349. [Google Scholar] [CrossRef]
- Xiao, J.; Jing, D. Fluid flow and mixing in a channel with dual bluff bodies. Phys. Fluids 2024, 36, 012020. [Google Scholar] [CrossRef]
- Agrawal, A.; Djenidi, L.; Antonia, R.A. Investigation of flow around a pair of side-by-side square cylinders using the lattice Boltzmann method. Comput. Fluids 2006, 35, 1093–1107. [Google Scholar] [CrossRef]
- Patil, P.P.; Tiwari, S. Numerical investigation of laminar unsteady wakes behind two inline square cylinders confined in a channel. Eng. Appl. Comput. Fluid Mech. 2009, 3, 369–385. [Google Scholar] [CrossRef]
- Chatterjee, D. Mixed convection heat transfer from tandem square cylinders in a vertical channel at low Reynolds numbers. Numer. Heat Transf. Part A Appl. 2010, 58, 740–755. [Google Scholar] [CrossRef]
- Rajpoot, R.S.; Anirudh, K.; Dhinakaran, S. Numerical investigation of unsteady flow across tandem square cylinders near a moving wall at Re = 100. Case Stud. Therm. Eng. 2021, 26, 101042. [Google Scholar] [CrossRef]
- Li, L.; Liu, J.; Pan, Z. Enhancement of heat transfer and mixing with two side-by-side freely rotatable cylinders in microchannel. Int. J. Heat Mass Transf. 2022, 189, 122717. [Google Scholar] [CrossRef]
- Bhagat, A.A.S.; Peterson, E.T.K.; Papautsky, I. A passive planar micromixer with obstructions for mixing at low Reynolds numbers. J. Micromech. Microeng. 2007, 17, 1017. [Google Scholar] [CrossRef]
- Dundi, T.M.; Raju, V.R.K.; Chandramohan, V.P. Characterization of mixing in an optimized designed T–T mixer with cylindrical elements. Chin. J. Chem. Eng. 2019, 27, 2337–2351. [Google Scholar] [CrossRef]
- Antognoli, M.; Stoecklein, D.; Galletti, C.; Brunazzi, E.; Di Carlo, D. Optimized design of obstacle sequences for microfluidic mixing in an inertial regime. Lab Chip 2021, 21, 3910–3923. [Google Scholar] [CrossRef] [PubMed]
- Shams-ul-Islam, S.I.; Nazeer, G.; Ying, Z.C. Numerical investigation of flow past 17-cylinder array of square cylinders. AIP Adv. 2018, 8, 065004. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, W.; Wang, B.; Wang, L. Numerical simulation of the flow past six-circular cylinders in rectangular configurations. J. Mar. Sci. Technol. 2020, 25, 718–742. [Google Scholar] [CrossRef]
- Hosseini, N.; Griffith, M.D.; Leontini, J.S. Flow states and transitions in flows past arrays of tandem cylinders. J. Fluid Mech. 2021, 910, A34. [Google Scholar] [CrossRef]
- Duong, V.D.; Nguyen, V.L.; Nguyen, V.T.; Palar, P.S.; Zuhal, L.R.; Ngo, T.T.; Dinh, C.T.; Wang, W.C. A numerical study on dynamic flows past three tandem inclined elliptic cylinders near moving wall. Phys. Fluids 2024, 36, 023615. [Google Scholar] [CrossRef]
- Dadvand, A.; Hosseini, S.; Aghebatandish, S.; Khoo, B.C. Enhancement of heat and mass transfer in a microchannel via passive oscillation of a flexible vortex generator. Chem. Eng. Sci. 2019, 207, 556–580. [Google Scholar] [CrossRef]
- Jing, D.; Zhan, X. Numerical studies on the hydraulic and mixing performances of fluid flow around a cylinder in microchannel with vertical flexible flag. Chem. Eng. J. 2022, 430, 133009. [Google Scholar] [CrossRef]
- Zhan, X.; Jing, D. Influence of geometric parameters on the fluidic and mixing characteristics of T-shaped micromixer. Microsyst. Technol. 2020, 26, 2989–2996. [Google Scholar] [CrossRef]

| Channel length (L) | 26d |
| Channel height (H) | 4d |
| The distance between the center of the first sector body and the inlet of channel (a) | 2d |
| Spacing distance of the sector bodies (lx, ls) | 2d–13d |
| Reynolds number based on sector body dimension (Red) | 100 |
| Reynolds number based on the channel height (ReH) | 800 |
| Test Number i | Mesh Number | Mout | (|Mout i+1 − Mout i|)/ Mout i | Time Cost |
|---|---|---|---|---|
| 1 | 8679 | 0.7038 | 1.9 h | |
| 2 | 16,803 | 0.8365 | 18.85% | 3.6 h |
| 3 | 29,297 | 0.8108 | 3.07% | 5.8 h |
| 4 | 43,832 | 0.8033 | 0.93% | 9.8 h |
| 5 | 93,872 | 0.7984 | 0.61% | 18.3 h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, J.; Jing, D. Numerical Study on the Hydraulic and Mixing Performance of Fluid Flow within a Channel with Different Numbers of Sector Bodies. Water 2024, 16, 2451. https://doi.org/10.3390/w16172451
Xiao J, Jing D. Numerical Study on the Hydraulic and Mixing Performance of Fluid Flow within a Channel with Different Numbers of Sector Bodies. Water. 2024; 16(17):2451. https://doi.org/10.3390/w16172451
Chicago/Turabian StyleXiao, Jian, and Dalei Jing. 2024. "Numerical Study on the Hydraulic and Mixing Performance of Fluid Flow within a Channel with Different Numbers of Sector Bodies" Water 16, no. 17: 2451. https://doi.org/10.3390/w16172451
APA StyleXiao, J., & Jing, D. (2024). Numerical Study on the Hydraulic and Mixing Performance of Fluid Flow within a Channel with Different Numbers of Sector Bodies. Water, 16(17), 2451. https://doi.org/10.3390/w16172451






