Identification of Groundwater Contamination Sources Based on a Deep Belief Neural Network
Abstract
1. Introduction
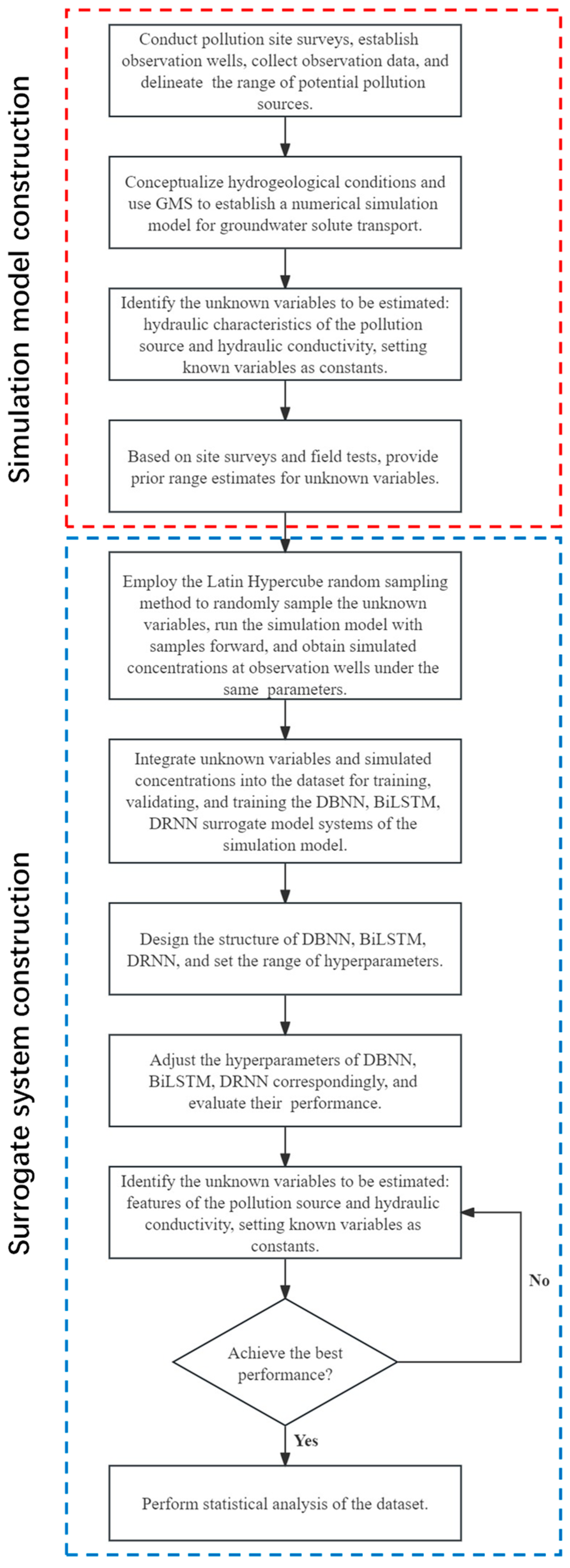
2. Methodology and Theory
2.1. Multiphase Flow Numerical Simulation Model
2.2. Surrogate Model
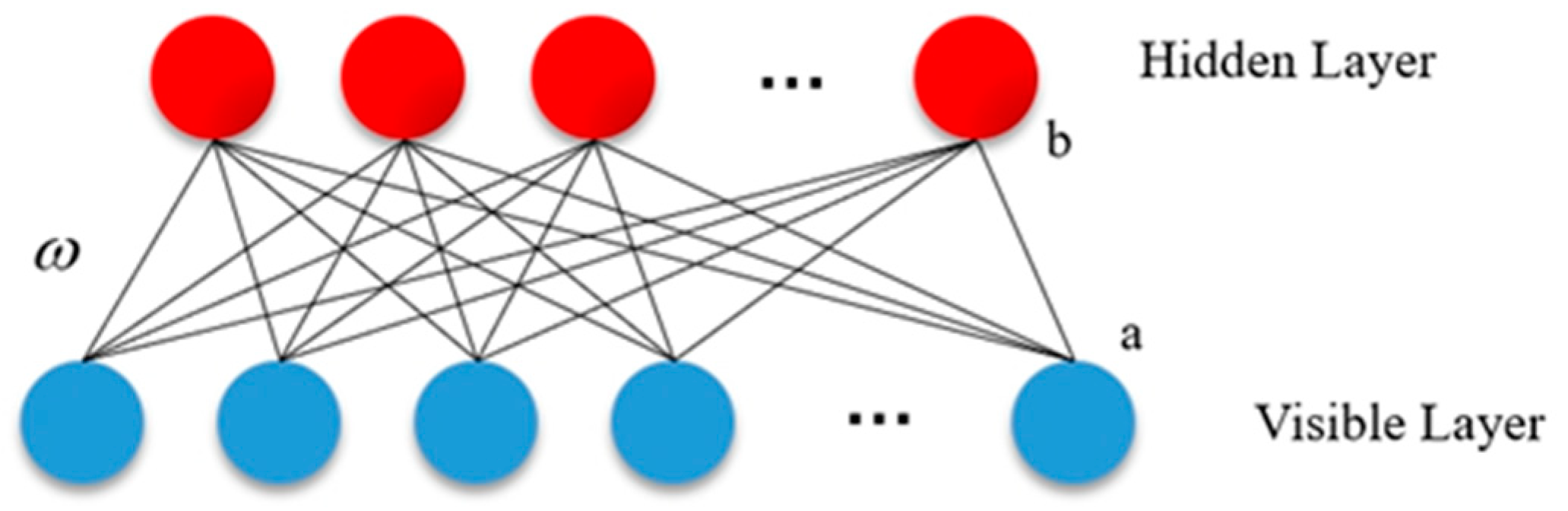
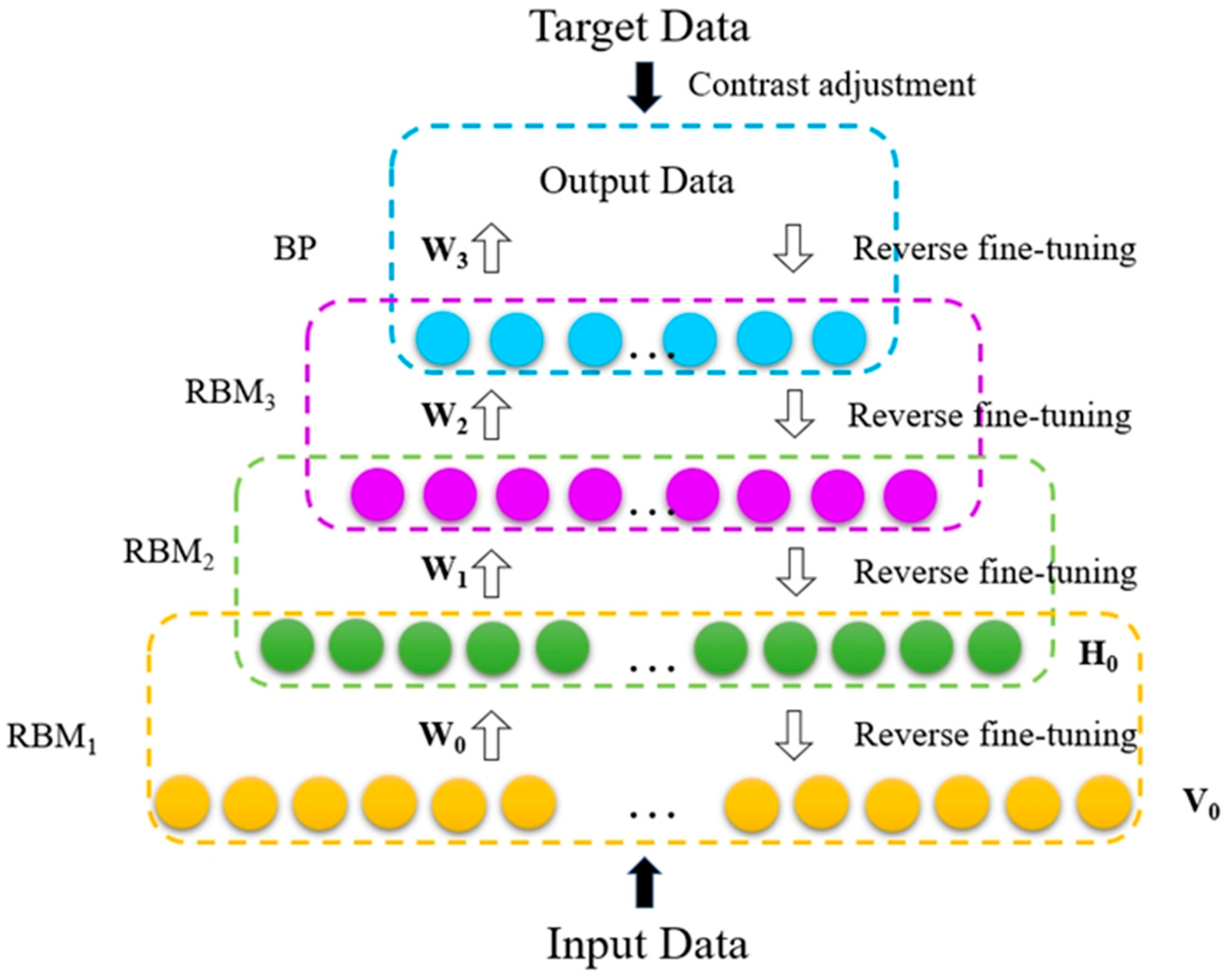
2.2.1. The DBNN Method
- The unsupervised learning training stage.
- 2.
- The supervised learning training stage.
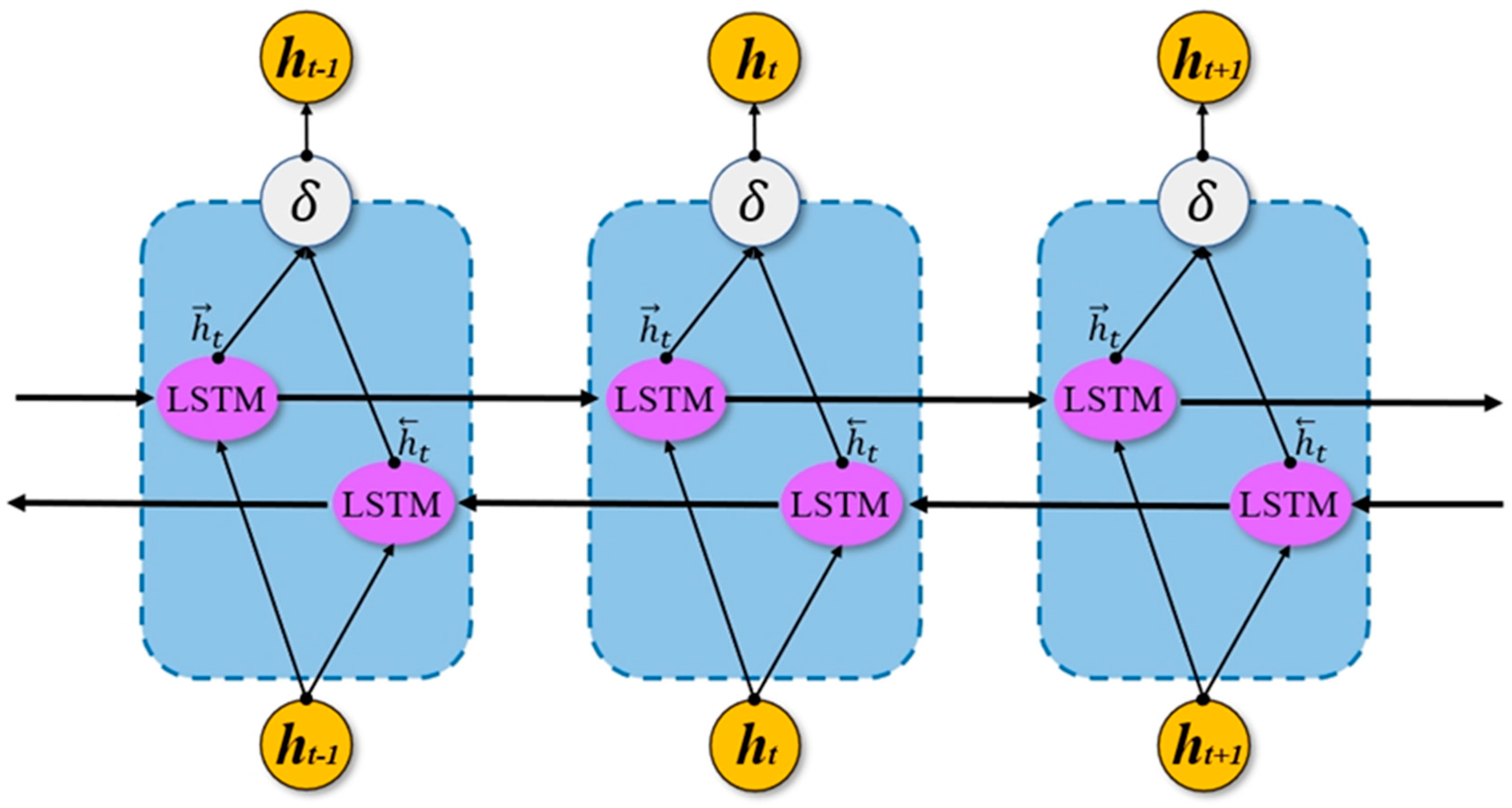
2.2.2. The BiLSTM Method
2.2.3. The DRNN Method
3. Case Description
4. Results and Discussion
4.1. Performance of Surrogate System
4.2. Inverse Characteristic Result
4.3. Ablation Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lapworth, D.J.; Boving, T.B.; Kreamer, D.K.; Kebede, S.; Smedley, P.L. Groundwater quality: Global threats, opportunities and realising the potential of groundwater. Sci. Total. Environ. 2022, 811, 152471. [Google Scholar] [CrossRef]
- Ayvaz, M.T. A linked simulation–optimization model for solving the unknown groundwater pollution source identification problems. J. Contam. Hydrol. 2010, 117, 46–59. [Google Scholar] [CrossRef] [PubMed]
- Mahar, P.S.; Datta, B. Optimal identification of ground-water pollution sources and parameter estimation. J. Water Res. Plan. Man. 2001, 127, 20–29. [Google Scholar] [CrossRef]
- Liu, X.; Zhai, Z.J. Prompt tracking of indoor airborne contaminant source location with probability-based inverse multi-zone modeling. Build. Environ. 2009, 44, 1135–1143. [Google Scholar] [CrossRef]
- van der Velde, Y.; de Rooij, G.H.; Rozemeijer, J.C.; van Geer, F.C.; Broers, H.P. Nitrate response of a lowland catchment; on the relation between stream concentration and travel time distribution dynamics. Water Resour. Res. 2010, 46, W11534. [Google Scholar] [CrossRef]
- Zhao, Y.; Qu, R.; Xing, Z.; Lu, W. Identifying groundwater contaminant sources based on a KELM surrogate model together with four heuristic optimization algorithms. Adv. Water Resour. 2020, 138, 103540. [Google Scholar] [CrossRef]
- Li, J.; Lu, W.; Wang, H.; Fan, Y.; Chang, Z. Groundwater contamination source identification based on a hybrid particle swarm optimization-extreme learning machine. J. Hydrol 2020, 584, 124657. [Google Scholar] [CrossRef]
- Guo, Q.; Dai, F.; Zhao, Z. Comparison of Two Bayesian-MCMC Inversion Methods for Laboratory Infiltration and Field Irrigation Experiments. Int. J. Environ. Res. Public Health 2020, 17, 1108. [Google Scholar] [CrossRef]
- Zhang, J.; Vrugt, J.A.; Shi, X.; Lin, G.; Wu, L.; Zeng, L. Improving Simulation Efficiency of MCMC for Inverse Modeling of Hydrologic Systems With a Kalman-Inspired Proposal Distribution. Water Resour. Res. 2020, 56, e2019WR025474. [Google Scholar] [CrossRef]
- Datta, B.; Chakrabarty, D.; Dhar, A. Identification of unknown groundwater pollution sources using classical optimization with linked simulation. J. Hydro-Environ. Res. 2011, 5, 25–36. [Google Scholar] [CrossRef]
- Seyedpour, S.M.; Kirmizakis, P.; Brennan, P.; Doherty, R.; Ricken, T. Optimal remediation design and simulation of groundwater flow coupled to contaminant transport using genetic algorithm and radial point collocation method (RPCM). Sci. Total. Environ. 2019, 669, 389–399. [Google Scholar] [CrossRef]
- Gaur, S.; Chahar, B.R.; Graillot, D. Analytic elements method and particle swarm optimization based simulation–optimization model for groundwater management. J. Hydrol. 2011, 402, 217–227. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, W. Groundwater Contamination Source Recognition Based on a Two-Stage Inversion Framework with a Deep Learning Surrogate. Water 2024, 16, 1907. [Google Scholar] [CrossRef]
- Hussain, M.S.; Javadi, A.A.; Ahangar-Asr, A.; Farmani, R. A surrogate model for simulation–optimization of aquifer systems subjected to seawater intrusion. J. Hydrol. 2015, 523, 542–554. [Google Scholar] [CrossRef]
- Neupauer, R.M.; Borchers, B.; Wilson, J.L. Comparison of inverse methods for reconstructing the release history of a groundwater contamination source. Water Resour. Res. 2000, 36, 2469–2475. [Google Scholar] [CrossRef]
- Asher, M.J.; Croke, B.F.W.; Jakeman, A.J.; Peeters, L.J.M. A review of surrogate models and their application to groundwater modeling. Water Resour. Res. 2015, 51, 5957–5973. [Google Scholar] [CrossRef]
- Secci, D.; Molino, L.; Zanini, A. Contaminant source identification in groundwater by means of artificial neural network. J. Hydrol. 2022, 611, 128003. [Google Scholar] [CrossRef]
- Knoll, L.; Breuer, L.; Bach, M. Large scale prediction of groundwater nitrate concentrations from spatial data using machine learning. Sci. Total. Environ. 2019, 668, 1317–1327. [Google Scholar] [CrossRef]
- Daliakopoulos, I.N.; Coulibaly, P.; Tsanis, I.K. Groundwater level forecasting using artificial neural networks. J. Hydrol. 2005, 309, 229–240. [Google Scholar] [CrossRef]
- Baudron, P.; Alonso-Sarría, F.; García-Aróstegui, J.L.; Cánovas-García, F.; Martínez-Vicente, D.; Moreno-Brotóns, J. Identifying the origin of groundwater samples in a multi-layer aquifer system with Random Forest classification. J. Hydrol. 2013, 499, 303–315. [Google Scholar] [CrossRef]
- Rashid, M.; Bari, B.S.; Yusup, Y.; Kamaruddin, M.A.; Khan, N. A Comprehensive Review of Crop Yield Prediction Using Machine Learning Approaches With Special Emphasis on Palm Oil Yield Prediction. IEEE Access. 2021, 9, 63406–63439. [Google Scholar] [CrossRef]
- Barzegar, R.; Moghaddam, A.A.; Deo, R.; Fijani, E.; Tziritis, E. Mapping groundwater contamination risk of multiple aquifers using multi-model ensemble of machine learning algorithms. Sci. Total. Environ. 2018, 621, 697–712. [Google Scholar] [CrossRef] [PubMed]
- Siade, A.J.; Cui, T.; Karelse, R.N.; Hampton, C. Reduced-Dimensional Gaussian Process Machine Learning for Groundwater Allocation Planning Using Swarm Theory. Water Resour. Res. 2020, 56, e2019WR026061. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Mendes, M.P.; Garcia-Soldado, M.J.; Chica-Olmo, M.; Ribeiro, L. Predictive modeling of groundwater nitrate pollution using Random Forest and multisource variables related to intrinsic and specific vulnerability: A case study in an agricultural setting (Southern Spain). Sci. Total. Environ. 2014, 476–477, 189–206. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.M.; Datta, B. Artificial neural network modeling for identification of unknown pollution sources in groundwater with partially missing concentration observation data. Water Resour. Manag. 2007, 21, 557–572. [Google Scholar] [CrossRef]
- Motevalli, A.; Naghibi, S.A.; Hashemi, H.; Berndtsson, R.; Pradhan, B.; Gholami, V. Inverse method using boosted regression tree and k-nearest neighbor to quantify effects of point and non-point source nitrate pollution in groundwater. J. Clean. Prod. 2019, 228, 1248–1263. [Google Scholar] [CrossRef]
- Kouadri, S.; Elbeltagi, A.; Islam, A.R.M.T.; Kateb, S. Performance of machine learning methods in predicting water quality index based on irregular data set: Application on Illizi region (Algerian southeast). Appl. Water Sci. 2021, 11, 190. [Google Scholar] [CrossRef]
- Sze, V.; Chen, Y.; Yang, T.; Emer, J.S. Efficient Processing of Deep Neural Networks: A Tutorial and Survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef]
- Liang, T.; Glossner, J.; Wang, L.; Shi, S.; Zhang, X. Pruning and quantization for deep neural network acceleration: A survey. Neurocomputing 2021, 461, 370–403. [Google Scholar] [CrossRef]
- Jiang, Z.; Tahmasebi, P.; Mao, Z. Deep residual U-net convolution neural networks with autoregressive strategy for fluid flow predictions in large-scale geosystems. Adv. Water Resour. 2021, 150, 103878. [Google Scholar] [CrossRef]
- Yan, L.; Feng, J.; Hang, T.; Zhu, Y. Flow interval prediction based on deep residual network and lower and upper boundary estimation method. Appl. Soft Comput. 2021, 104, 107228. [Google Scholar] [CrossRef]
- Murad, A.; Pyun, J. Deep Recurrent Neural Networks for Human Activity Recognition. Sensors 2017, 17, 2556. [Google Scholar] [CrossRef]
- Chen, Z.; Ma, M.; Li, T.; Wang, H.; Li, C. Long sequence time-series forecasting with deep learning: A survey. Inf. Fusion 2023, 97, 101819. [Google Scholar] [CrossRef]
- Vu, M.; Jardani, A.; Massei, N.; Fournier, M. Reconstruction of missing groundwater level data by using long short-term memory (LSTM) deep neural network. J. Hydrol. 2021, 597, 125776. [Google Scholar] [CrossRef]
- Vu, M.T.; Jardani, A.; Massei, N.; Deloffre, J.; Fournier, M.; Laignel, B. Long-run forecasting surface and groundwater dynamics from intermittent observation data: An evaluation for 50 years. Sci. Total Environ. 2023, 880, 163338. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.; Hu, S.; Wan, H.; Xie, Y.; Cai, Y.; Wen, J. A unified deep learning framework for water quality prediction based on time-frequency feature extraction and data feature enhancement. J. Environ. Manag. 2024, 351, 119894. [Google Scholar] [CrossRef] [PubMed]
- Sohn, I. Deep belief network based intrusion detection techniques: A survey. Expert Syst. Appl. 2021, 167, 114170. [Google Scholar] [CrossRef]
- Pan, Z.; Lu, W.; Chang, Z.; Wang, H. Simultaneous identification of groundwater pollution source spatial-temporal characteristics and hydraulic parameters based on deep regularization neural network-hybrid heuristic algorithm. J. Hydrol. 2021, 600, 126586. [Google Scholar] [CrossRef]
- Anul Haq, M.; Khadar Jilani, A.; Prabu, P. Deep Learning Based Modeling of Groundwater Storage Change. Comput. Mater. Contin. 2022, 70, 4599–4617. [Google Scholar] [CrossRef]
- Jiang, S.; Fan, J.; Xia, X.; Li, X.; Zhang, R. An Effective Kalman Filter-Based Method for Groundwater Pollution Source Identification and Plume Morphology Characterization. Water 2018, 10, 1063. [Google Scholar] [CrossRef]
- Yuan, X.; Ou, C.; Wang, Y.; Yang, C.; Gui, W. A novel semi-supervised pre-training strategy for deep networks and its application for quality variable prediction in industrial processes. Chem. Eng. Sci. 2020, 217, 115509. [Google Scholar] [CrossRef]
- Li, J.; Wu, Z.; He, H.; Lu, W. Identifying groundwater contamination sources based on the hybrid grey wolf gradient algorithm and deep belief neural network. Stoch. Environ. Res. Risk A 2023, 37, 1697–1715. [Google Scholar] [CrossRef]
- Karhunen, J.; Raiko, T.; Cho, K. Unsupervised deep learning: A short review. Adv. Indep. Compon. Anal. Learn. Mach. 2015, 125–142. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Wang, Y.; Zou, R.; Liu, F.; Zhang, L.; Liu, Q. A review of wind speed and wind power forecasting with deep neural networks. Appl. Energ. 2021, 304, 117766. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference On Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]


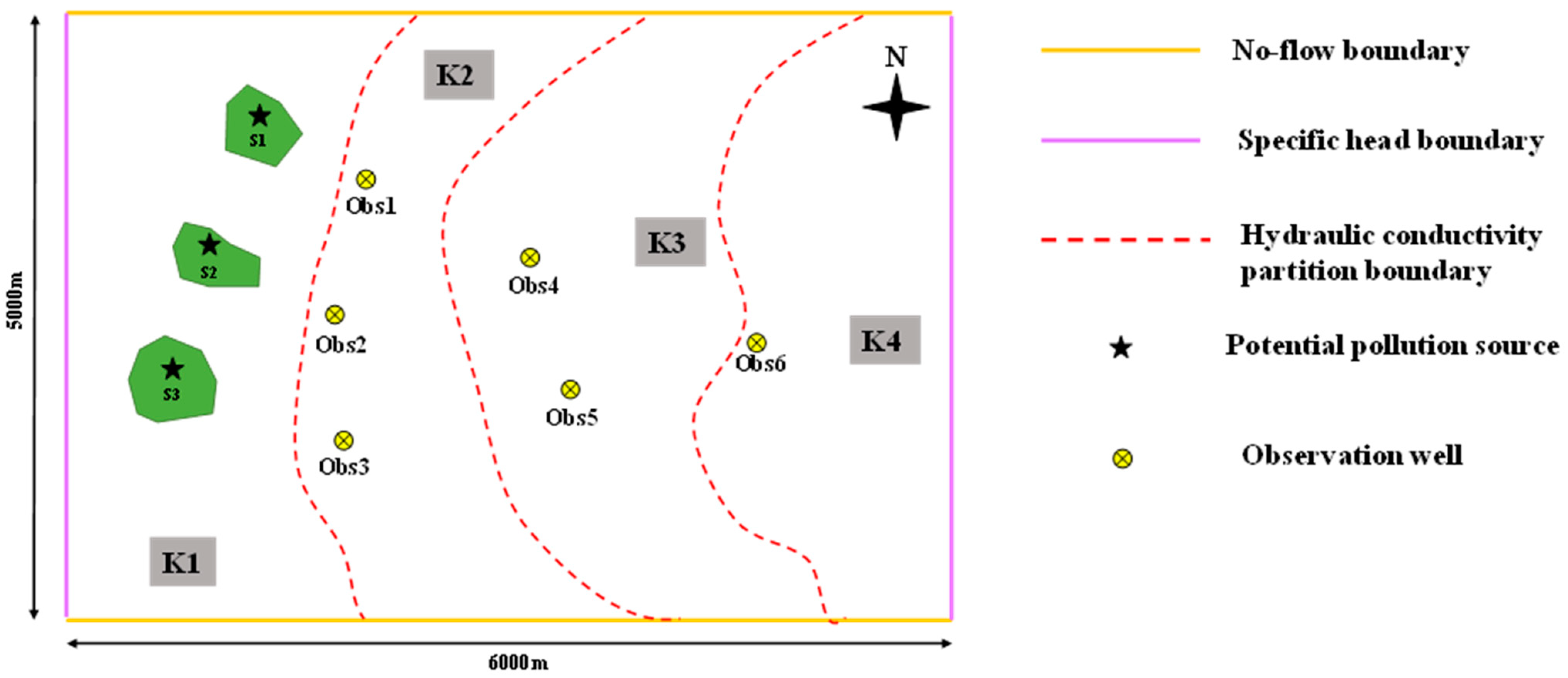

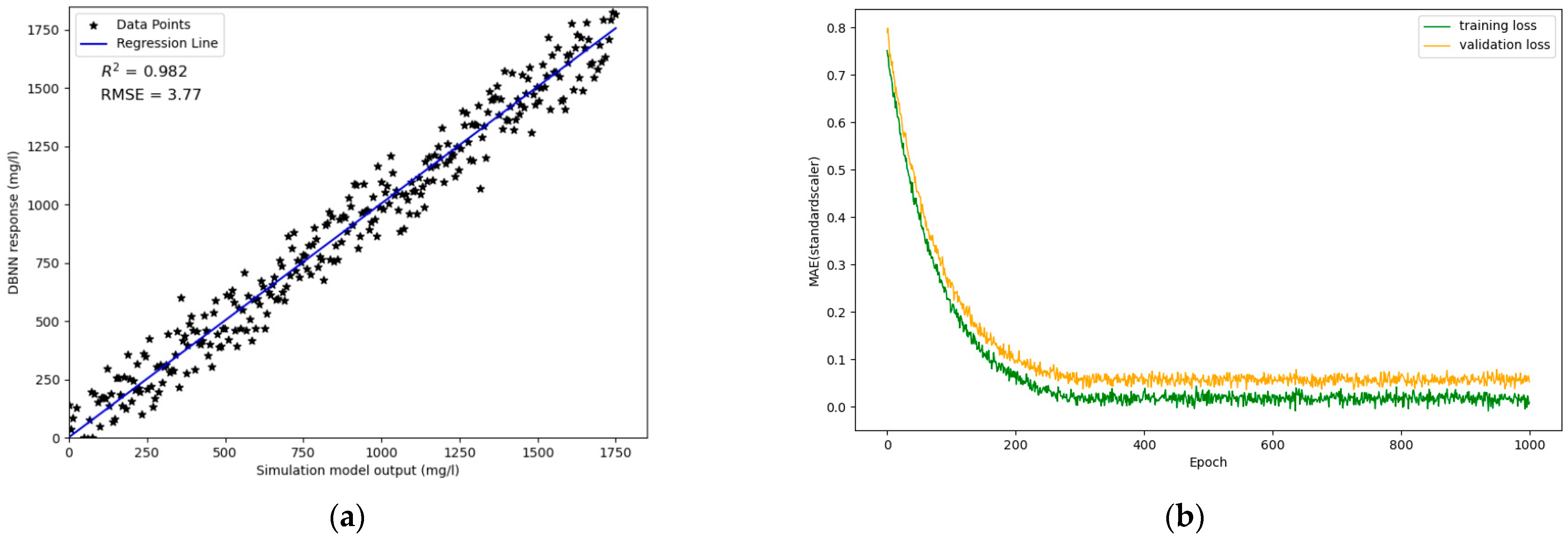

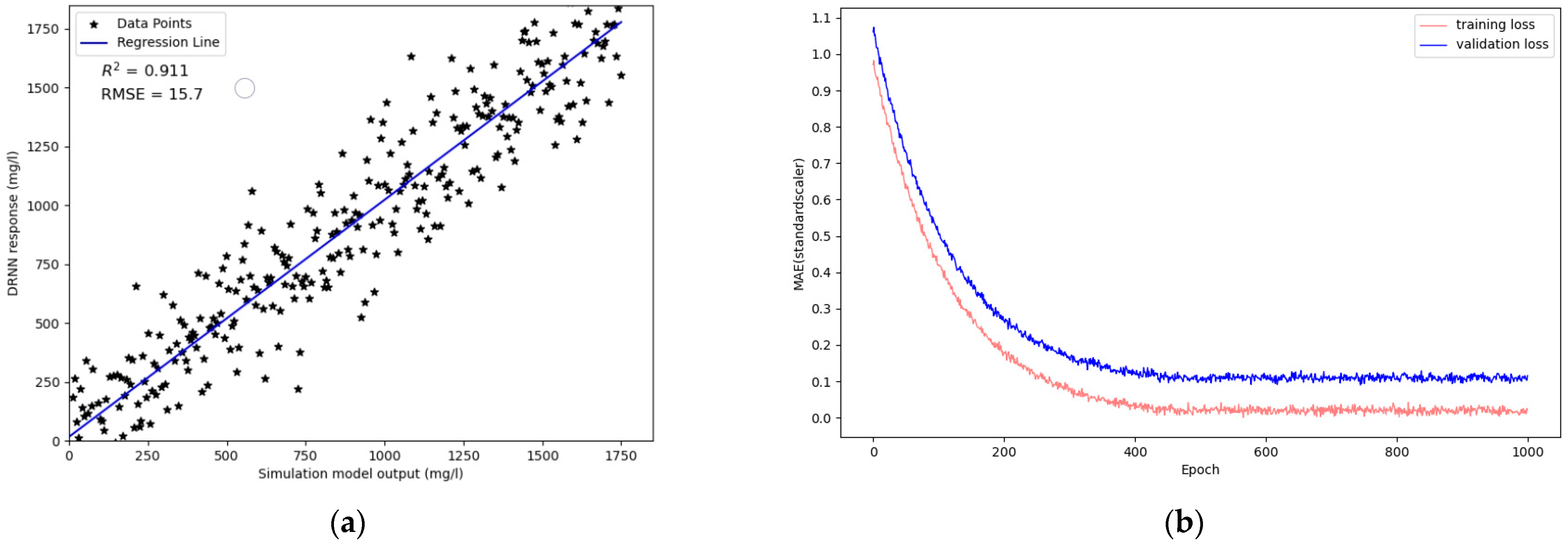


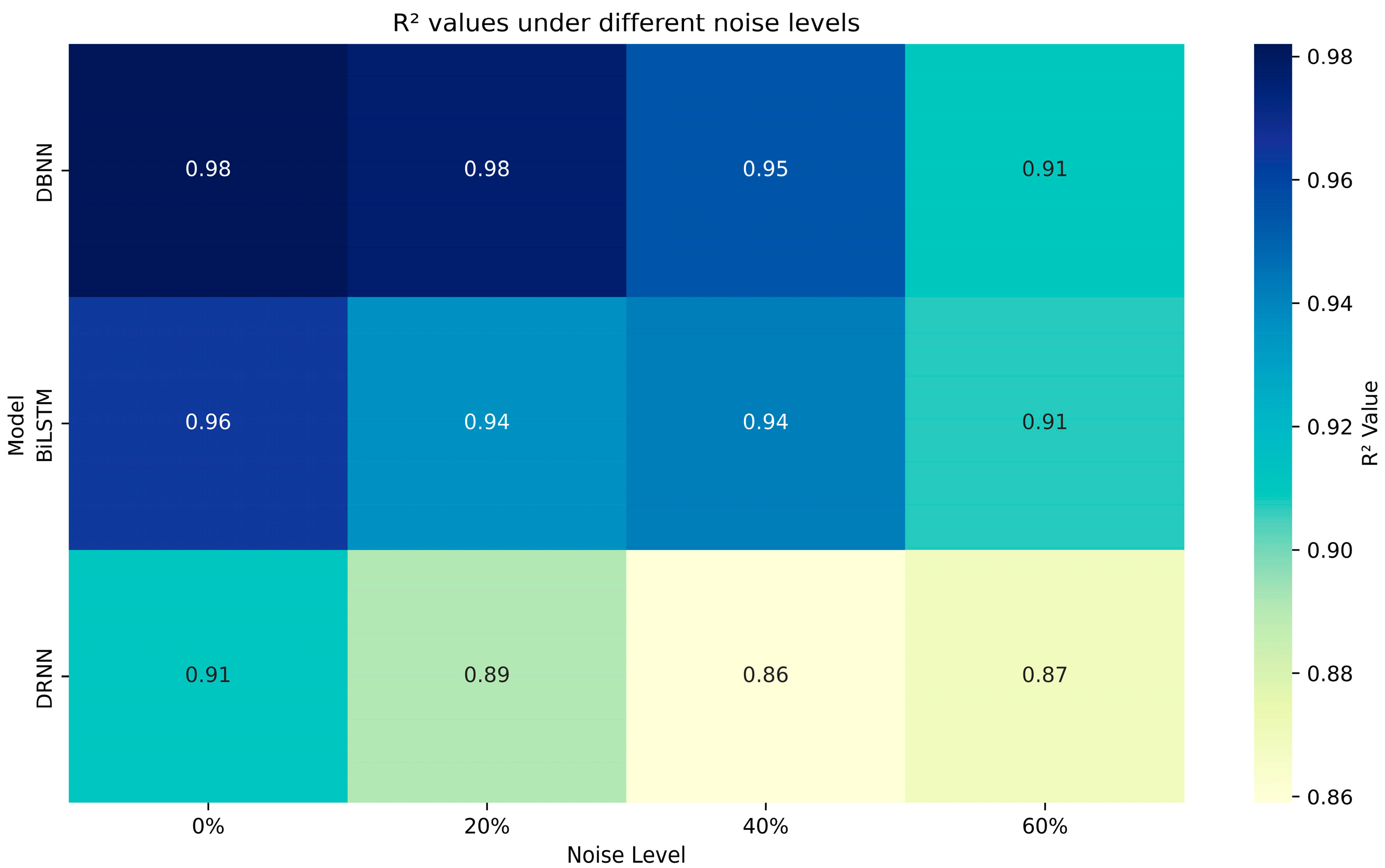
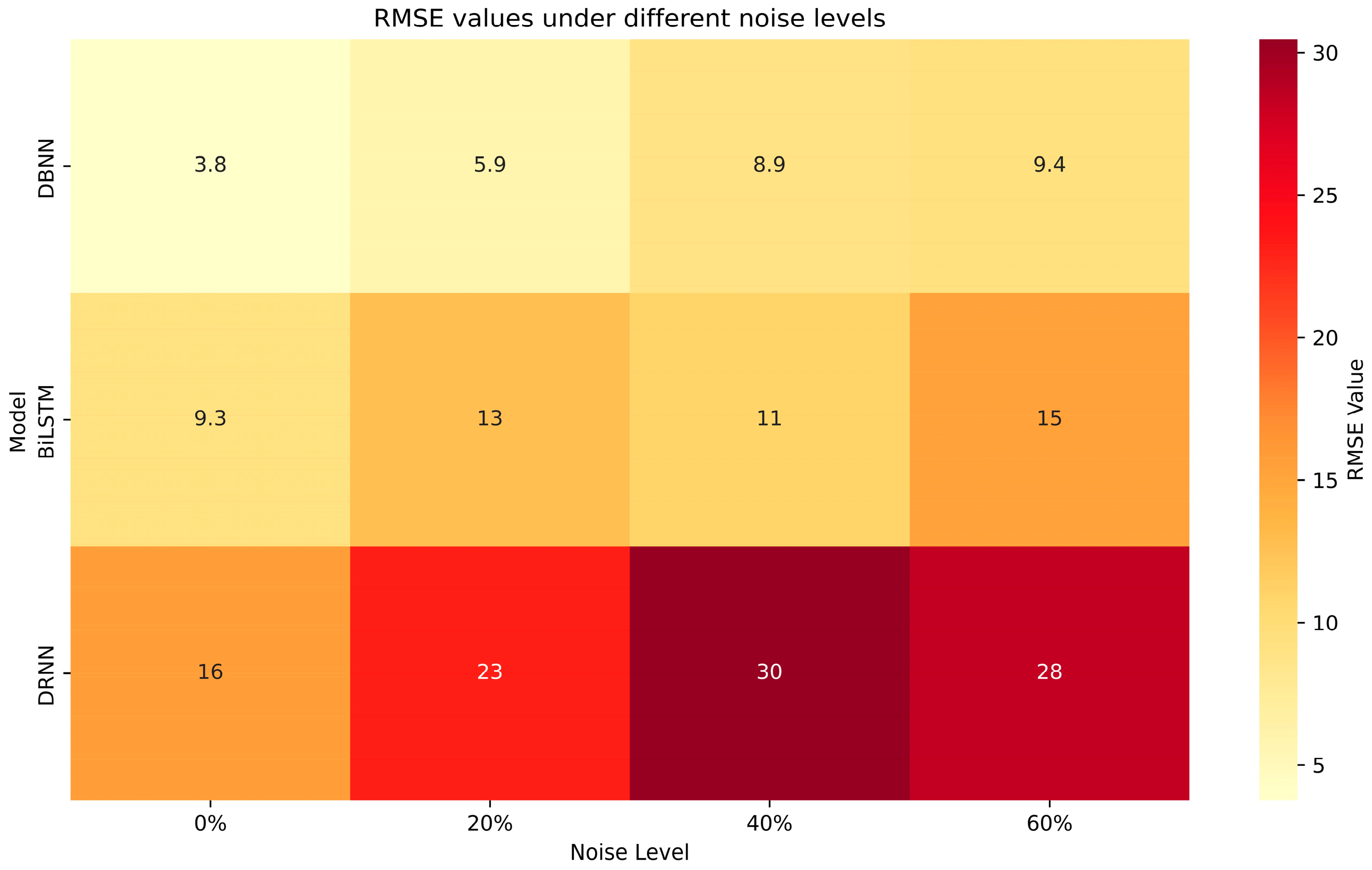
| Parameter | Value/Range |
|---|---|
| Hydraulic conductivity (m/day) | (30, 60) |
| Specific yield | 0.22 |
| Saturated thickness (m) | 50 |
| Longitudinal dispersivity | 45 |
| Transverse dispersivity | 19.6 |
| Grid spacing in x-direction (m) | 10 |
| Grid spacing in y-direction (m) | 10 |
| Stress periods (year) | 5 |
| Fluxes of contamination source during stress period (g/day) | (0, 69) |
| Unknown Variables to Identify | Reference Value |
|---|---|
| Fluxes of pollution source, S1T1 (g/d) | 36 |
| Fluxes of pollution source, S1T2 (g/d) | 41 |
| Fluxes of pollution source, S1T3 (g/d) | 55 |
| Fluxes of pollution source, S1T4 (g/d) | 60 |
| Fluxes of pollution source, S1T5 (g/d) | 59 |
| Fluxes of pollution source, S2T1 (g/d) | 28 |
| Fluxes of pollution source, S2T2 (g/d) | 30 |
| Fluxes of pollution source, S2T3 (g/d) | 34 |
| Fluxes of pollution source, S2T4 (g/d) | 36 |
| Fluxes of pollution source, S2T5 (g/d) | 35 |
| Fluxes of pollution source, S3T1 (g/d) | 46 |
| Fluxes of pollution source, S3T2 (g/d) | 51 |
| Fluxes of pollution source, S3T3 (g/d) | 58 |
| Fluxes of pollution source, S3T4 (g/d) | 56 |
| Fluxes of pollution source, S3T5 (g/d) | 62 |
| Hydraulic conductivity in partition, k1(m/d) | 41.1 |
| Hydraulic conductivity in partition, k1(m/d) | 55.7 |
| Hydraulic conductivity in partition, k1(m/d) | 50.2 |
| Hydraulic conductivity in partition, k1(m/d) | 52.9 |
| Unknown Variables to Identify | Reference Value |
|---|---|
| Fluxes of pollution source, S1T1 (g/d) | 36 |
| Fluxes of pollution source, S1T2 (g/d) | 41 |
| Fluxes of pollution source, S1T3 (g/d) | 55 |
| Fluxes of pollution source, S1T4 (g/d) | 60 |
| Fluxes of pollution source, S1T5 (g/d) | 59 |
| Fluxes of pollution source, S2T1 (g/d) | 28 |
| Fluxes of pollution source, S2T2 (g/d) | 30 |
| Fluxes of pollution source, S2T3 (g/d) | 34 |
| Fluxes of pollution source, S2T4 (g/d) | 36 |
| Fluxes of pollution source, S2T5 (g/d) | 35 |
| Fluxes of pollution source, S3T1 (g/d) | 46 |
| Fluxes of pollution source, S3T2 (g/d) | 51 |
| Fluxes of pollution source, S3T3 (g/d) | 58 |
| Fluxes of pollution source, S3T4 (g/d) | 56 |
| Fluxes of pollution source, S3T5 (g/d) | 62 |
| Unknown Variables | True Value | Inference Value Calculated by DBNN |
|---|---|---|
| S1T1 | 36 | 36.75 |
| S1T2 | 41 | 41.99 |
| S1T3 | 55 | 54.98 |
| S1T4 | 60 | 60.12 |
| S1T5 | 59 | 59.68 |
| S2T1 | 28 | 28.76 |
| S2T2 | 30 | 29.97 |
| S2T3 | 34 | 34.36 |
| S2T4 | 36 | 35.61 |
| S2T5 | 35 | 35.89 |
| S3T1 | 46 | 45.88 |
| S3T2 | 51 | 51.74 |
| S3T3 | 58 | 58.36 |
| S3T4 | 56 | 56.50 |
| S3T5 | 62 | 62.25 |
| Unknown Variable | Reference Value | Estimation under Measurement Noise Level | 0 | 0.005 | 0.010 | 0.015 |
|---|---|---|---|---|---|---|
| S1T1 | 36 | 36.04 | 36.03 | 36.39 | 35.75 | |
| S1T2 | 41 | 41 | 40.95 | 40.86 | 40.88 | |
| S1T3 | 55 | 55 | 55.02 | 53.99 | 55.10 | |
| S1T4 | 60 | 60.01 | 60.08 | 59.69 | 59.92 | |
| S1T5 | 59 | 59 | 59.09 | 58.78 | 58.66 | |
| S2T1 | 28 | 28 | 27.82 | 28.08 | 27.93 | |
| S2T2 | 30 | 30 | 30.02 | 29.65 | 31.01 | |
| S2T3 | 34 | 34 | 34.09 | 33.90 | 33.07 | |
| S2T4 | 36 | 36.02 | 36.15 | 36.28 | 33.53 | |
| S2T5 | 35 | 34.99 | 34.99 | 36.82 | 35.56 | |
| S3T1 | 46 | 46.01 | 45.80 | 46.29 | 46.05 | |
| S3T2 | 51 | 51 | 51.17 | 50.88 | 49.44 | |
| S3T3 | 58 | 58.03 | 57.78 | 57.79 | 57.27 | |
| S3T4 | 56 | 55.96 | 55.95 | 56.33 | 55.09 | |
| S3T5 | 62 | 61.98 | 62.38 | 62.07 | 62.10 |
| Unknown Variable | Reference Value | Estimation under Measurement Noise Level | 0 | 0.005 | 0.010 | 0.015 |
|---|---|---|---|---|---|---|
| S1T1 | 36 | 36 | 36.02 | 35.73 | 36.02 | |
| S1T2 | 41 | 41.01 | 41.07 | 41.16 | 41.34 | |
| S1T3 | 55 | 55 | 54.96 | 54.96 | 54.89 | |
| S1T4 | 60 | 60 | 60.18 | 60.30 | 59.75 | |
| S1T5 | 59 | 59 | 59.09 | 59.35 | 59.10 | |
| S2T1 | 28 | 27.98 | 28.05 | 28.29 | 30.00 | |
| S2T2 | 30 | 30 | 29.79 | 29.67 | 29.18 | |
| S2T3 | 34 | 34 | 33.99 | 34.25 | 33.35 | |
| S2T4 | 36 | 36 | 36.06 | 36.19 | 36.73 | |
| S2T5 | 35 | 35.02 | 35.11 | 34.61 | 35.69 | |
| S3T1 | 46 | 46.01 | 46.51 | 45.91 | 45.47 | |
| S3T2 | 51 | 50.96 | 51.03 | 53.11 | 50.61 | |
| S3T3 | 58 | 58 | 57.71 | 57.76 | 58.19 | |
| S3T4 | 56 | 56 | 56.12 | 56.39 | 55.97 | |
| S3T5 | 62 | 61.95 | 61.92 | 61.86 | 61.60 |
| Unknown Variable | Reference Value | Estimation under Measurement Noise Level | 0 | 0.005 | 0.010 | 0.015 |
|---|---|---|---|---|---|---|
| S1T1 | 36 | 36 | 35.83 | 35.59 | 34.29 | |
| S1T2 | 41 | 41 | 41.02 | 40.75 | 41.62 | |
| S1T3 | 55 | 55.02 | 55.11 | 55.33 | 54.25 | |
| S1T4 | 60 | 59.99 | 59.75 | 60.09 | 59.79 | |
| S1T5 | 59 | 59 | 58.96 | 57.74 | 59.02 | |
| S2T1 | 28 | 28.02 | 28.36 | 27.63 | 26.94 | |
| S2T2 | 30 | 30 | 29.82 | 30.15 | 30.27 | |
| S2T3 | 34 | 34 | 34.05 | 32.94 | 35.04 | |
| S2T4 | 36 | 36 | 35.99 | 35.77 | 35.19 | |
| S2T5 | 35 | 34.96 | 34.87 | 34.88 | 34.64 | |
| S3T1 | 46 | 46 | 46.18 | 46.13 | 43.93 | |
| S3T2 | 51 | 51.08 | 50.93 | 50.66 | 52.22 | |
| S3T3 | 58 | 58 | 57.77 | 58.29 | 57.59 | |
| S3T4 | 56 | 55.95 | 56.14 | 55.96 | 56.35 | |
| S3T5 | 62 | 62 | 62.22 | 60.82 | 61.76 |
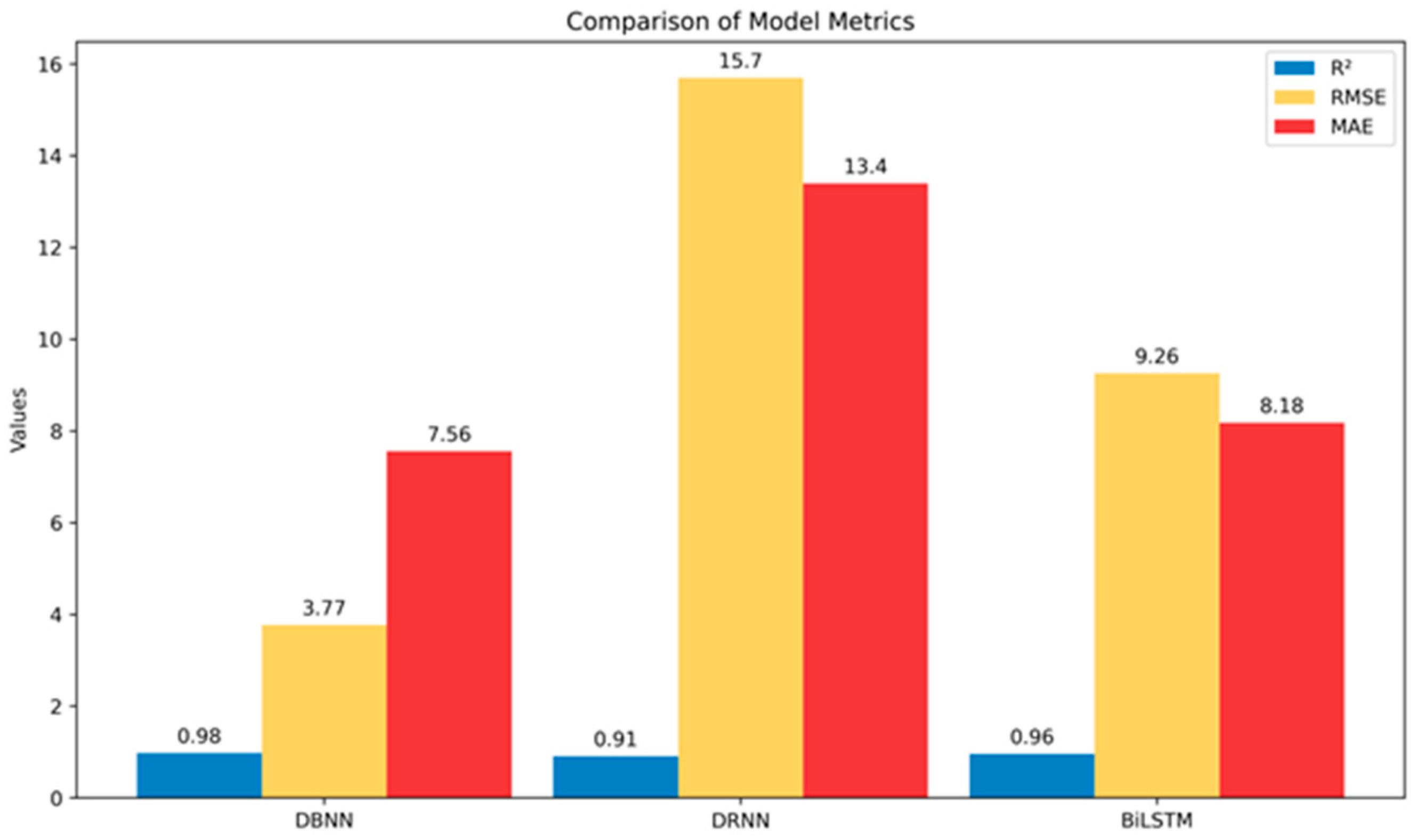
| DBNN | BiLSTM | DRNN | |
|---|---|---|---|
| average error value | 0.24 | 0.28 | 0.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Tan, Z.; Sheng, W.; Liu, Z.; Wu, X.; Ma, L.; Li, Z. Identification of Groundwater Contamination Sources Based on a Deep Belief Neural Network. Water 2024, 16, 2449. https://doi.org/10.3390/w16172449
Wang B, Tan Z, Sheng W, Liu Z, Wu X, Ma L, Li Z. Identification of Groundwater Contamination Sources Based on a Deep Belief Neural Network. Water. 2024; 16(17):2449. https://doi.org/10.3390/w16172449
Chicago/Turabian StyleWang, Borui, Zhifang Tan, Wanbao Sheng, Zihao Liu, Xiaoqi Wu, Lu Ma, and Zhijun Li. 2024. "Identification of Groundwater Contamination Sources Based on a Deep Belief Neural Network" Water 16, no. 17: 2449. https://doi.org/10.3390/w16172449
APA StyleWang, B., Tan, Z., Sheng, W., Liu, Z., Wu, X., Ma, L., & Li, Z. (2024). Identification of Groundwater Contamination Sources Based on a Deep Belief Neural Network. Water, 16(17), 2449. https://doi.org/10.3390/w16172449




