Influence of Valvular Structures on the Flow Characteristics in an Island-Type Fishway
Abstract
:1. Introduction
2. Materials and Methods
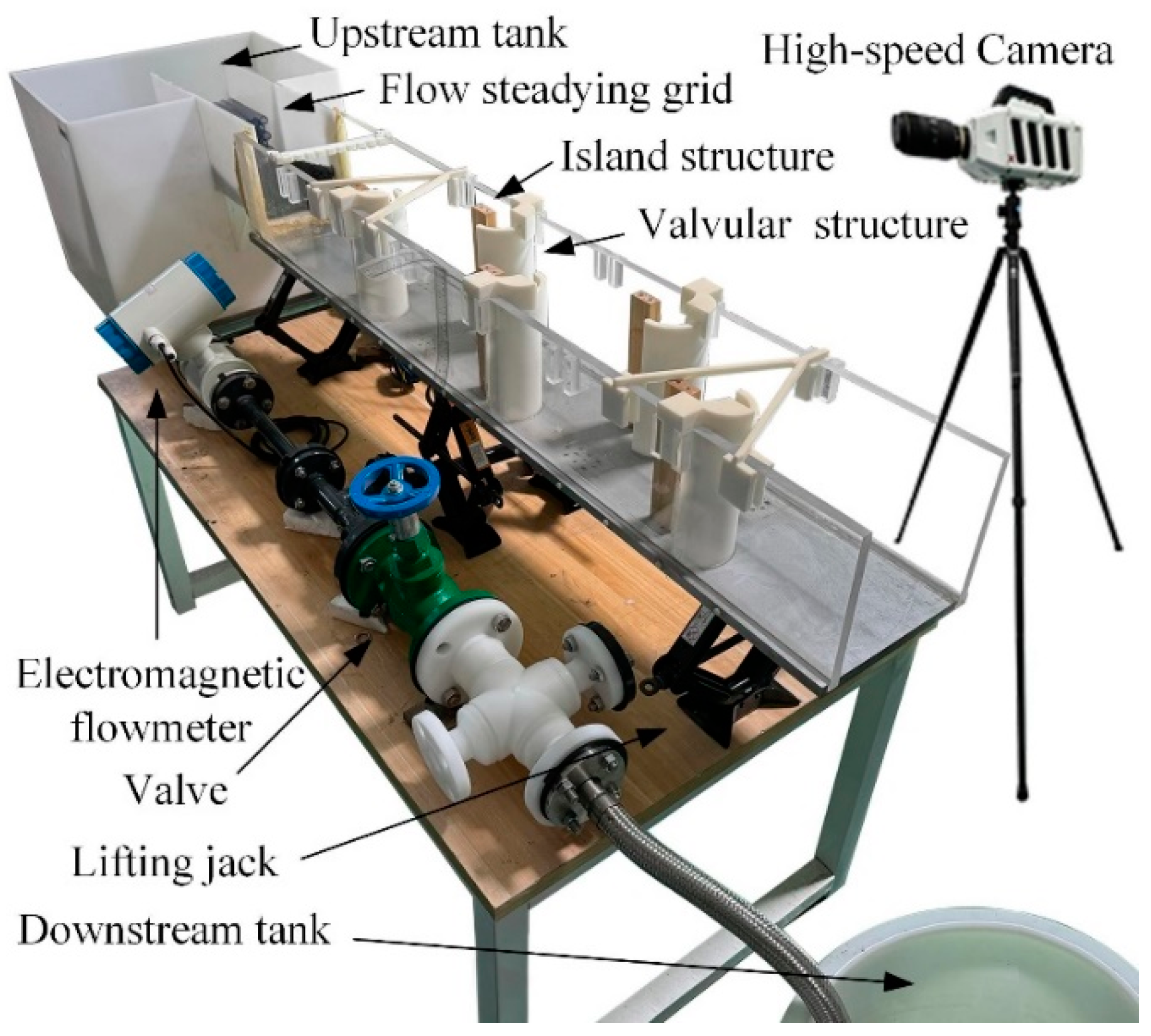
2.1. Island-Type Fishway Experimental Platform and Testing Methodology
2.2. Numerical Modeling Approach and Computational Methods
3. Results and Discussion
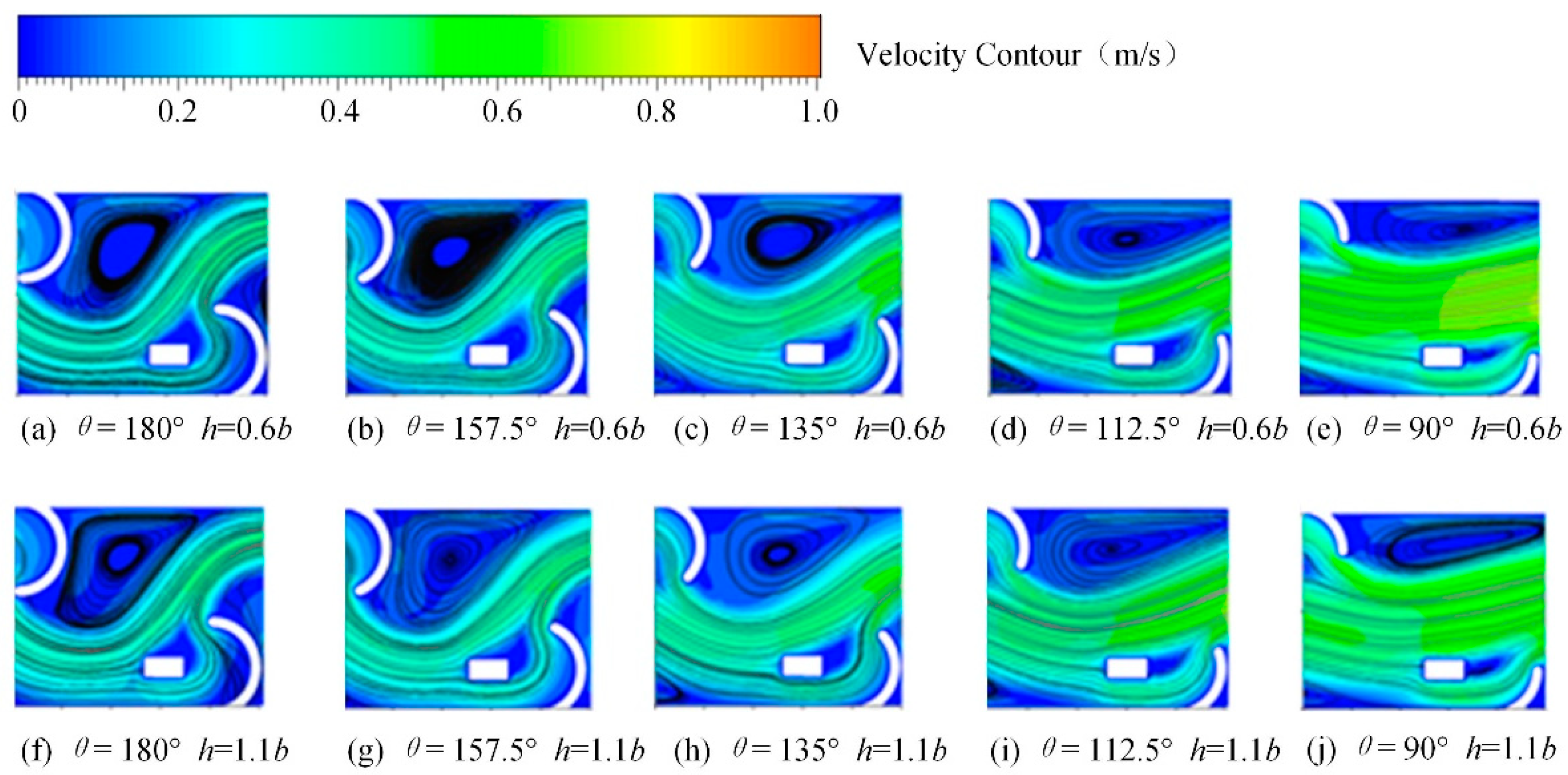
3.1. Velocity Field Distribution
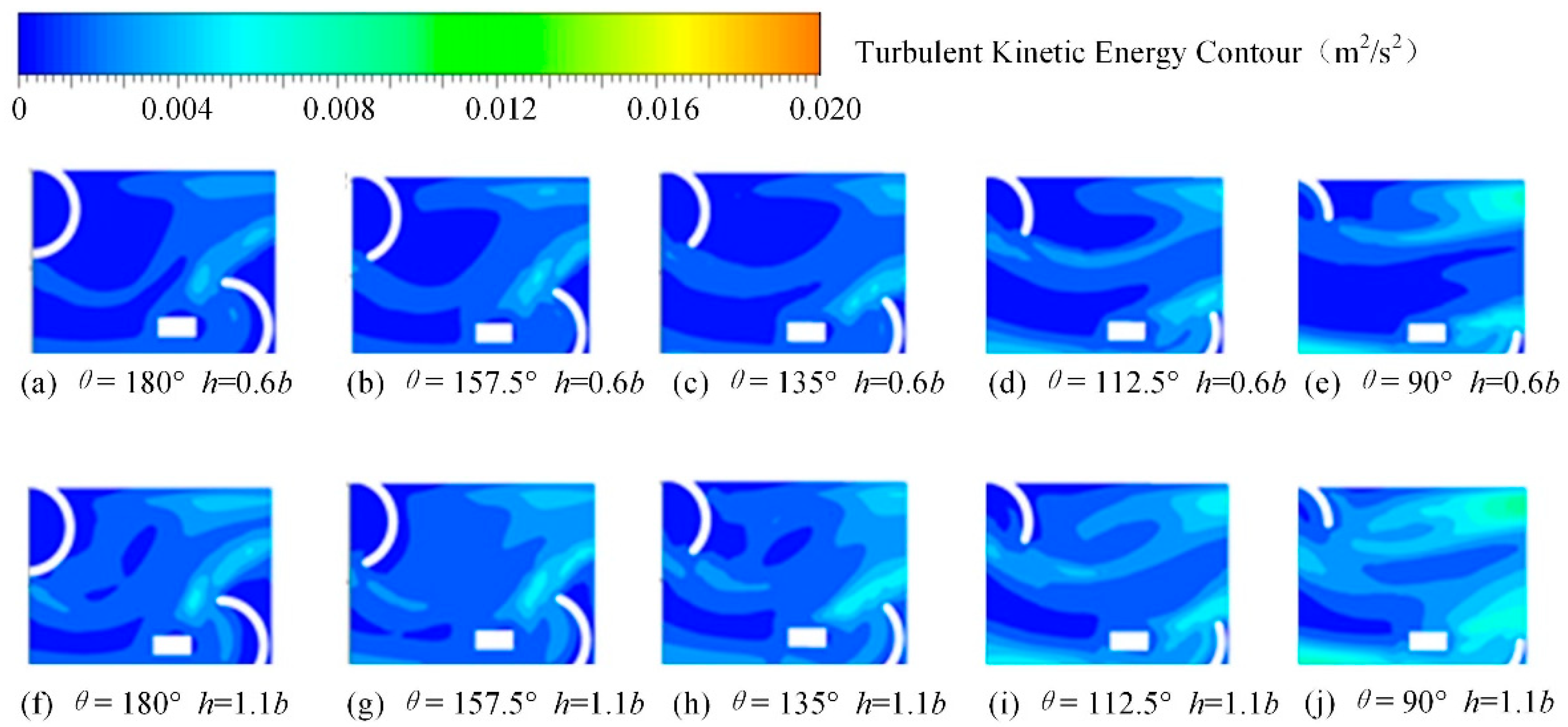
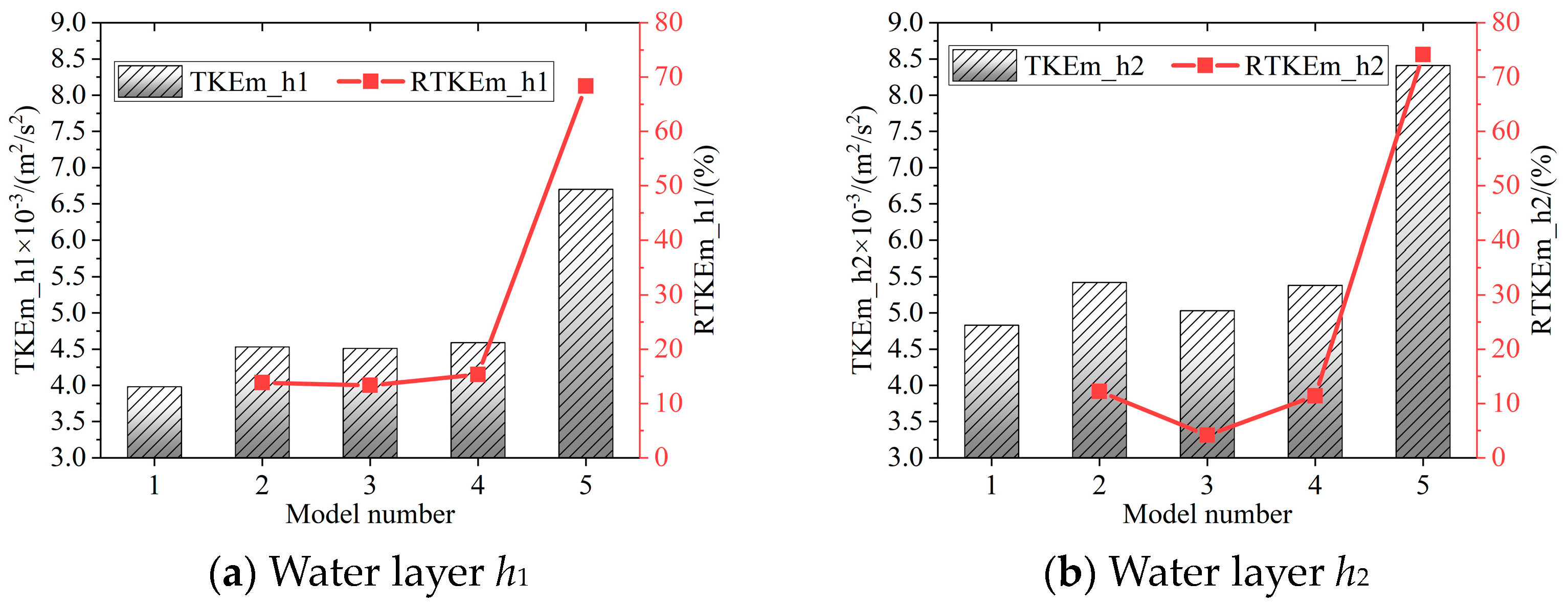
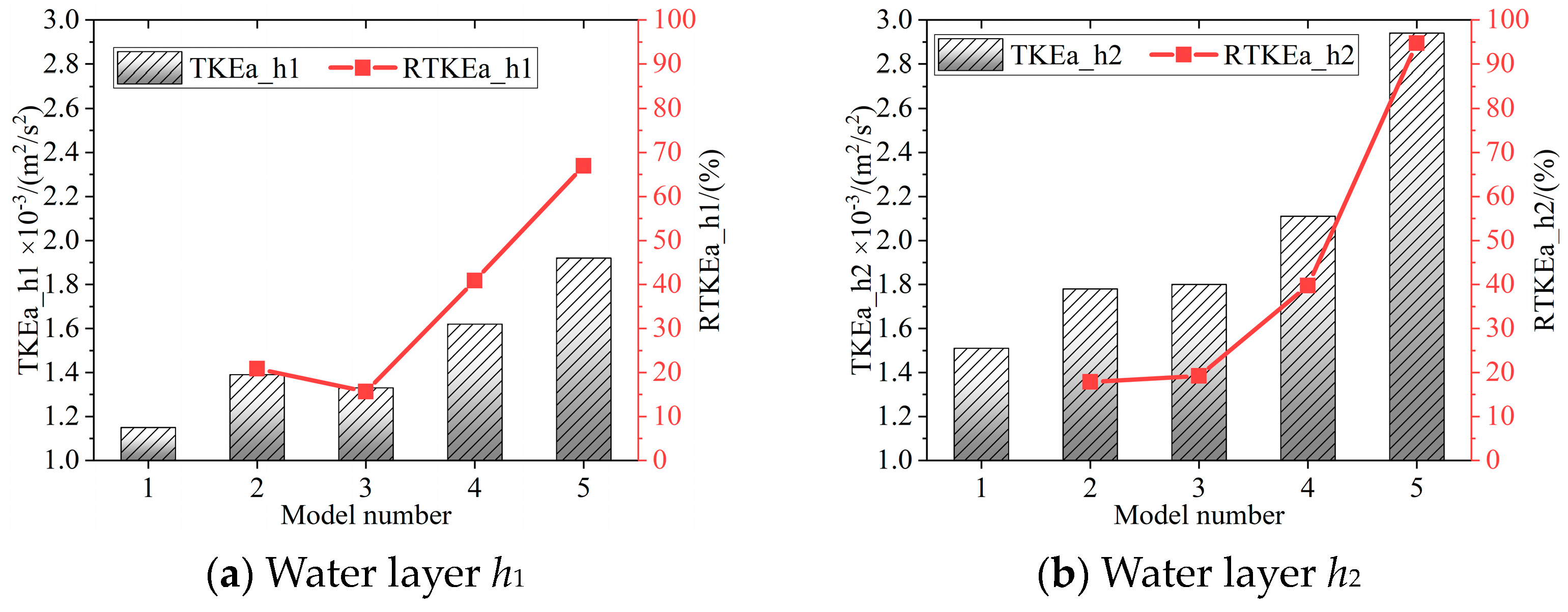
3.2. Turbulent Kinetic Energy Distribution
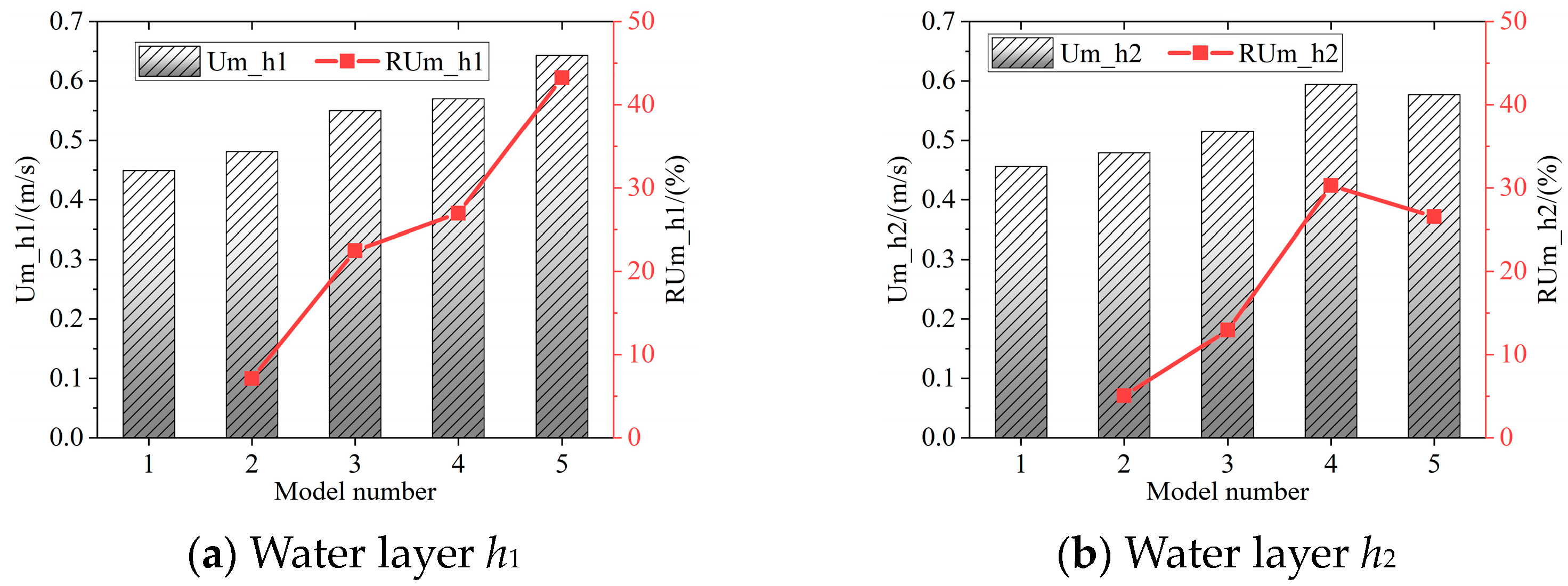
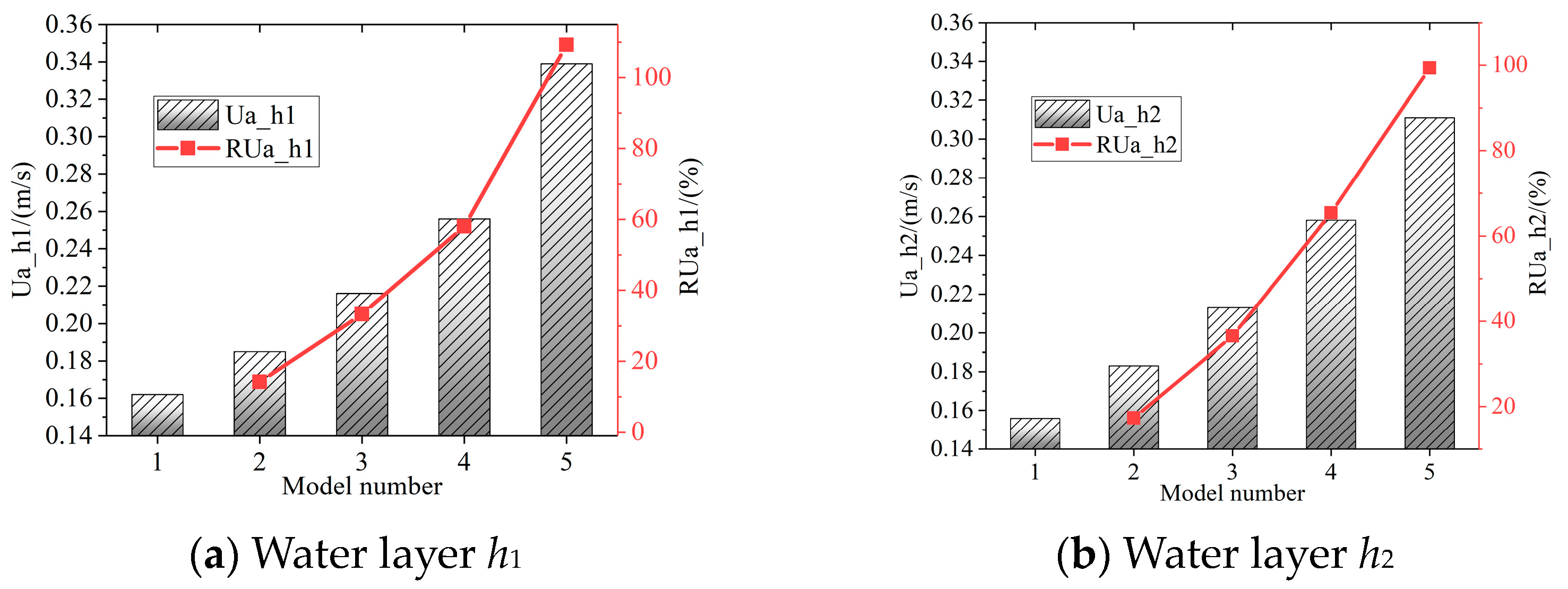
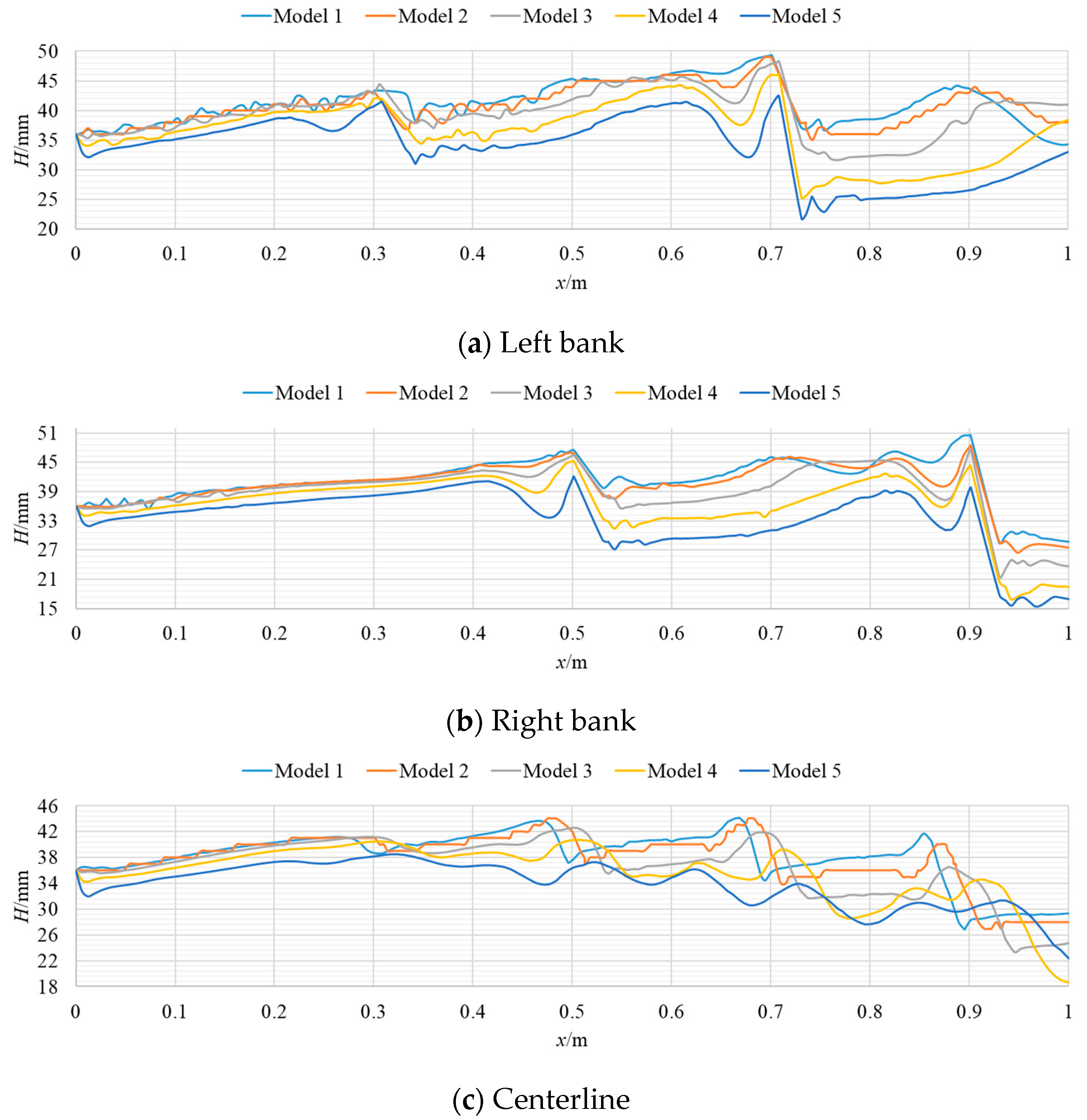
3.3. The Change in Water Level
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pavlova, A.; Beheregaray, L.B.; Coleman, R.; Gilligan, D.; Harrisson, K.A.; Ingram, B.A.; Kearns, J.; Lamb, A.M.; Lintermans, M.; Lyon, J. Severe consequences of habitat fragmentation on genetic diversity of an endangered Australian freshwater fish: A call for assisted gene flow. Evol. Appl. 2017, 10, 531–550. [Google Scholar] [CrossRef] [PubMed]
- Baharvand, S.; Lashkar-Ara, B. Hydraulic design criteria of the modified meander C-type fishway using the combined experimental and CFD models. Ecol. Eng. 2021, 164, 106207. [Google Scholar] [CrossRef]
- Birnie-Gauvin, K.; Franklin, P.; Wilkes, M.; Aarestrup, K. Moving beyond fitting fish into equations: Progressing the fish passage debate in the Anthropocene. Aquat. Conserv. 2019, 29, 1095–1105. [Google Scholar] [CrossRef]
- Katopodis, C.; Williams, J.G. The development of fish passage research in a historical context. Ecol. Eng. 2012, 48, 8–18. [Google Scholar] [CrossRef]
- Mao, X. Review of fishway research in China. Ecol. Eng. 2018, 115, 91–95. [Google Scholar] [CrossRef]
- Sanagiotto, D.G.; Rossi, J.B.; Bravo, J.M. Applications of computational fluid dynamics in the design and rehabilitation of nonstandard vertical slot fishways. Water 2019, 11, 199. [Google Scholar] [CrossRef]
- Kasischke, K.; Oertel, M. Discharge Coefficients of a Specific Vertical Slot Fishway Geometry—New Fitting Parameters. Water 2023, 15, 1193. [Google Scholar] [CrossRef]
- Puertas, J.; Pena, L.; Teijeiro, T. Experimental approach to the hydraulics of vertical slot fishways. J. Hydraul. Eng. 2004, 130, 10–23. [Google Scholar] [CrossRef]
- Wu, S.; Rajaratnam, N.; Katopodis, C. Structure of flow in vertical slot fishway. J. Hydraul. Eng. 1999, 125, 351–360. [Google Scholar] [CrossRef]
- Bermúdez, M.; Puertas, J.; Cea, L.; Pena, L.; Balairón, L. Influence of pool geometry on the biological efficiency of vertical slot fishways. Ecol. Eng. 2010, 36, 1355–1364. [Google Scholar] [CrossRef]
- Dong, Z.; Tong, J.; Huang, Z. Turbulence characteristics in a weir-orifice-slot combined fishway with an identical layout. J. Turbul. 2022, 23, 327–351. [Google Scholar] [CrossRef]
- Kim, J. Hydraulic characteristics by weir type in a pool-weir fishway. Ecol. Eng. 2001, 16, 425–433. [Google Scholar] [CrossRef]
- Foulds, W.L.; Lucas, M.C. Extreme inefficiency of two conventional, technical fishways used by European river lamprey (Lampetra fluviatilis). Ecol. Eng. 2013, 58, 423–433. [Google Scholar] [CrossRef]
- Odeh, M. Discharge rating equation and hydraulic characteristics of standard Denil fishways. J. Hydraul. Eng. 2003, 129, 341–348. [Google Scholar] [CrossRef]
- Katopodis, C.; Rajaratnam, N.; Wu, S.; Tovell, D. Denil fishways of varying geometry. J. Hydraul. Eng. 1997, 123, 624–631. [Google Scholar] [CrossRef]
- Bunt, C.; Castro-Santos, T.; Haro, A. Performance of fish passage structures at upstream barriers to migration. River Res. Appl. 2012, 28, 457–478. [Google Scholar] [CrossRef]
- Towler, B.; Mulligan, K.; Haro, A. Derivation and application of the energy dissipation factor in the design of fishways. Ecol. Eng. 2015, 83, 208–217. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Ma, X.; Li, X. Flow features in a pooled fishway with V-shaped weir formation. Eng. Appl. Comput. Fluid Mech. 2020, 14, 1337–1350. [Google Scholar] [CrossRef]
- Baki, A.B.M.; Zhu, D.Z.; Rajaratnam, N. Turbulence characteristics in a rock-ramp-type fish pass. J. Hydraul. Eng. 2015, 141, 04014075. [Google Scholar] [CrossRef]
- Baki, A.B.M.; Zhu, D.Z.; Harwood, A.; Lewis, A.; Healey, K. Hydraulic design aspects of rock-weir fishways with notch for habitat connectivity. TJoE 2020, 5, 94–109. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Ansell, A. Evaluation of pool-type fish passage with labyrinth weirs. Sustainability 2022, 14, 1098. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, C.; Shi, X.; Liu, Y.; Qu, Y. A novel H-shape fishway with excellent hydraulic characteristics. J. Hydrol. Hydromech. 2022, 71, 64–79. [Google Scholar] [CrossRef]
- Stuart, I.G.; Marsden, T.J.; Jones, M.J.; Moore, M.T.; Baumgartner, L.J. Rock fishways: Natural designs for an engineered world. Ecol. Eng. 2024, 206, 107317. [Google Scholar] [CrossRef]
- Cassan, L.; Miranda, F.C.; Laurens, P.; Courret, D. Hydraulic of rock-ramp fishway with lateral slope. Environ. Fluid Mech. 2024, 24, 1–18. [Google Scholar] [CrossRef]
- Mirkhorli, P.; Ghaderi, A.; Alizadeh Sanami, F.; Mohammadi, M.; Kuriqi, A.; Kisi, O. An investigation on hydraulic aspects of rectangular labyrinth pool and weir fishway using FLOW-3D. Arab. J. Sci. Eng. 2024, 49, 6061–6087. [Google Scholar] [CrossRef]
- Vowles, A.S.; Montali-Ashworth, D.; Karageorgopoulos, P.; Kemp, P.S. Hydraulic conditions created by a ‘large’diameter Cylindrical Bristle Cluster fish pass. Ecol. Eng. 2024, 207, 107337. [Google Scholar] [CrossRef]
- Zeng, G.; Xu, M.; Mou, J.; Hua, C.; Fan, C. Application of Tesla Valve’s Obstruction Characteristics to Reverse Fluid in Fish Migration. Water 2022, 15, 40. [Google Scholar] [CrossRef]
- Qian, J.-y.; Wu, J.-y.; Gao, Z.-x.; Wu, A.; Jin, Z.-j. Hydrogen decompression analysis by multi-stage Tesla valves for hydrogen fuel cell. Int. J. Hydrogen Energy 2019, 44, 13666–13674. [Google Scholar] [CrossRef]
- Zeng, G.; Xu, M.; Mou, J.; Wang, K.; Ren, Y. Research on the Hydraulic Characteristics of Island Fishways by Experimental and Numerical Methods. Water 2023, 15, 2592. [Google Scholar] [CrossRef]
- Feurich, R.; Boubée, J.; Olsen, N.R.B. Improvement of fish passage in culverts using CFD. Ecol. Eng. 2012, 47, 1–8. [Google Scholar] [CrossRef]
- Richmond, M.C.; Deng, Z.; Guensch, G.R.; Tritico, H.; Pearson, W.H. Mean flow and turbulence characteristics of a full-scale spiral corrugated culvert with implications for fish passage. Ecol. Eng. 2007, 30, 333–340. [Google Scholar] [CrossRef]
- Cea, L.; Pena, L.; Puertas, J.; Vázquez-Cendón, M.; Peña, E. Application of several depth-averaged turbulence models to simulate flow in vertical slot fishways. J. Hydraul. Eng. 2007, 133, 160–172. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, J.; Chen, Y.; Mo, K.; Wang, J.; Tang, L.; Lin, Y.; Chen, L.; Gao, Y.; Jiang, W. Inducing flow velocities to manage fish reproduction in regulated rivers. Engineering 2021, 7, 178–186. [Google Scholar] [CrossRef]
- Yang, Q.; Hu, P.; Yang, Z.; Chu, L.; Yang, J. Suitable flow rate and adaptive threshold for grass carp (Ctenopharyngodon idellus) migration. J. Hydroecology 2019, 40, 93–100. [Google Scholar]




| Grid Scheme | Average Mesh Size (mm) | Number of Mesh (Thousand) | e (%) |
|---|---|---|---|
| M1 | 10 | 59 | 7.01 |
| M2 | 8 | 112 | 6.08 |
| M3 | 6 | 257 | 5.95 |
| M4 | 5 | 461 | 5.98 |
| Measurement Point Number | Velocity Measured by Experiment (m/s) | Velocity Calculated by CFD with M3 Mesh (m/s) |
|---|---|---|
| 1 | 0.065 | 0.068 |
| 2 | 0.057 | 0.063 |
| 3 | 0.036 | 0.039 |
| 4 | 0.078 | 0.081 |
| 5 | 0.143 | 0.147 |
| 6 | 0.248 | 0.265 |
| 7 | 0.381 | 0.389 |
| 8 | 0.253 | 0.273 |
| 9 | 0.081 | 0.087 |
| 10 | 0.055 | 0.061 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, M.; Zeng, G.; Xu, M.; Mou, J.; Gu, Y. Influence of Valvular Structures on the Flow Characteristics in an Island-Type Fishway. Water 2024, 16, 2336. https://doi.org/10.3390/w16162336
Dong M, Zeng G, Xu M, Mou J, Gu Y. Influence of Valvular Structures on the Flow Characteristics in an Island-Type Fishway. Water. 2024; 16(16):2336. https://doi.org/10.3390/w16162336
Chicago/Turabian StyleDong, Mengxue, Guorui Zeng, Maosen Xu, Jiegang Mou, and Yunqing Gu. 2024. "Influence of Valvular Structures on the Flow Characteristics in an Island-Type Fishway" Water 16, no. 16: 2336. https://doi.org/10.3390/w16162336
APA StyleDong, M., Zeng, G., Xu, M., Mou, J., & Gu, Y. (2024). Influence of Valvular Structures on the Flow Characteristics in an Island-Type Fishway. Water, 16(16), 2336. https://doi.org/10.3390/w16162336











