Interpretation of Soil Characteristics and Preferential Water Flow in Different Forest Covers of Karst Areas of China
Abstract
1. Introduction
2. Materials and Methods
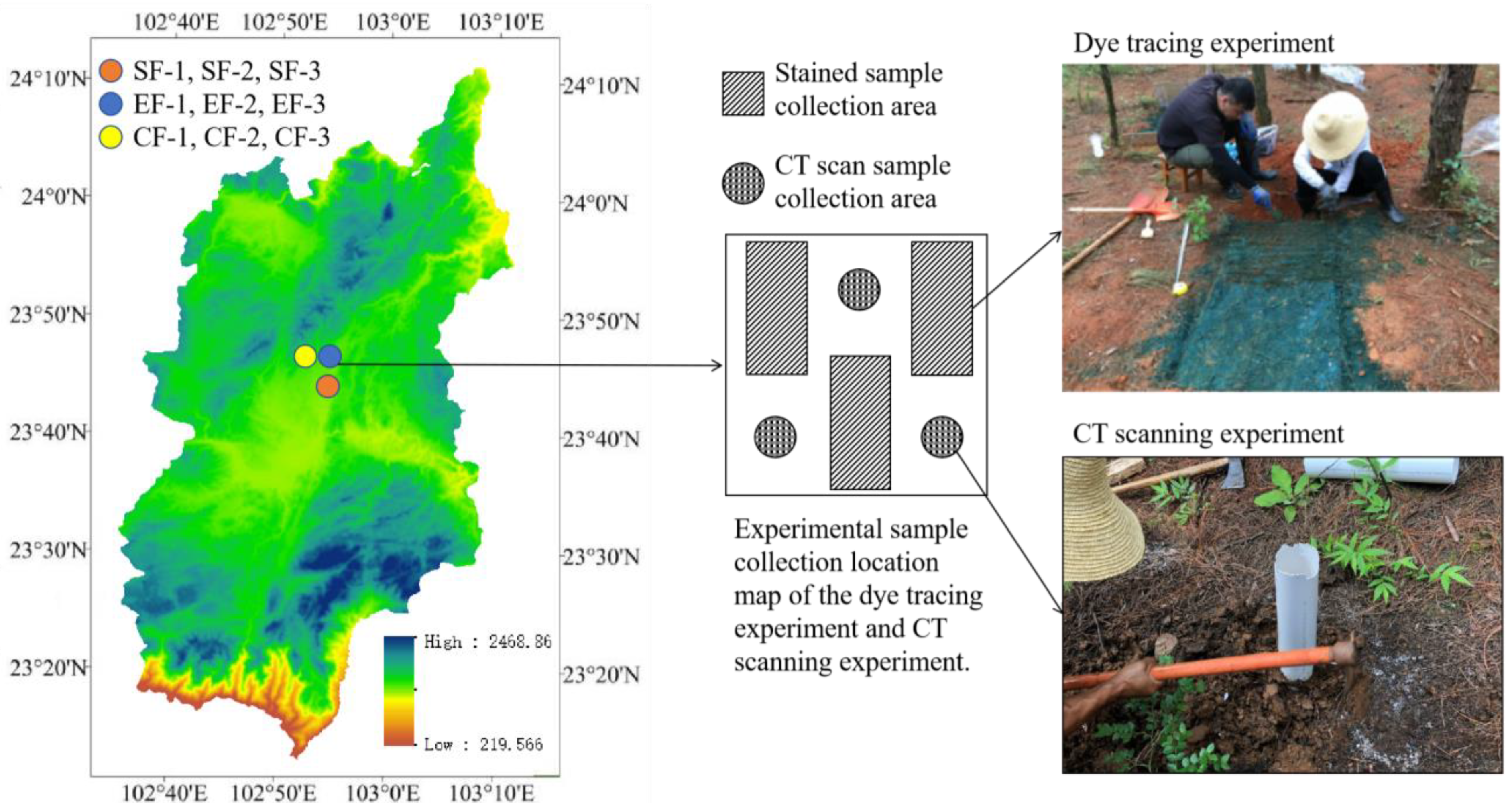
2.1. Environmental Characteristics of the Experimental Sites
2.2. Measurement of Soil Physical Properties
2.3. Industrial CT Scan
2.4. Dyeing Experiment
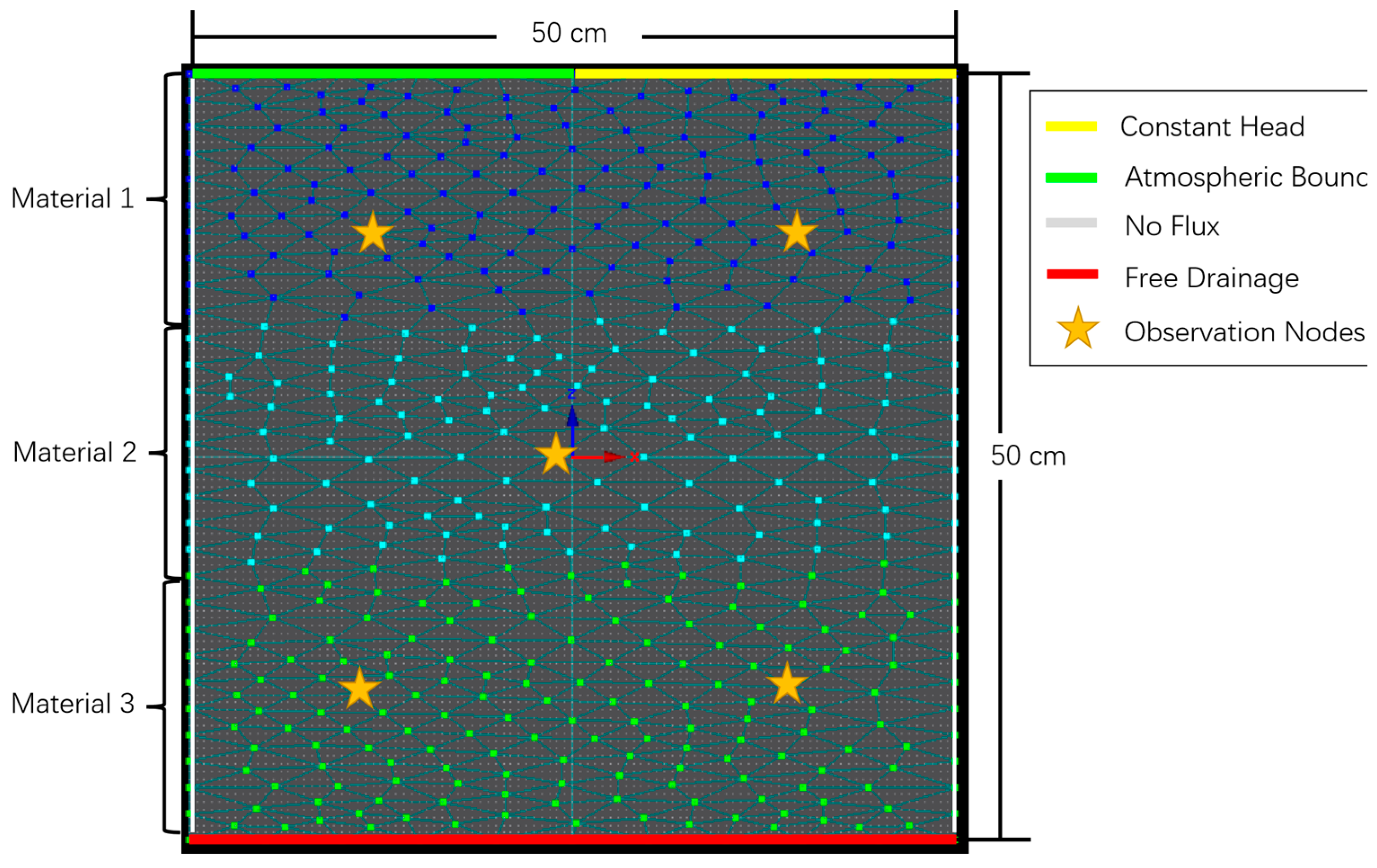
2.5. HYDRUS-2D Modelling
2.6. Statistical Analysis
3. Results
3.1. Physical Properties of Soil
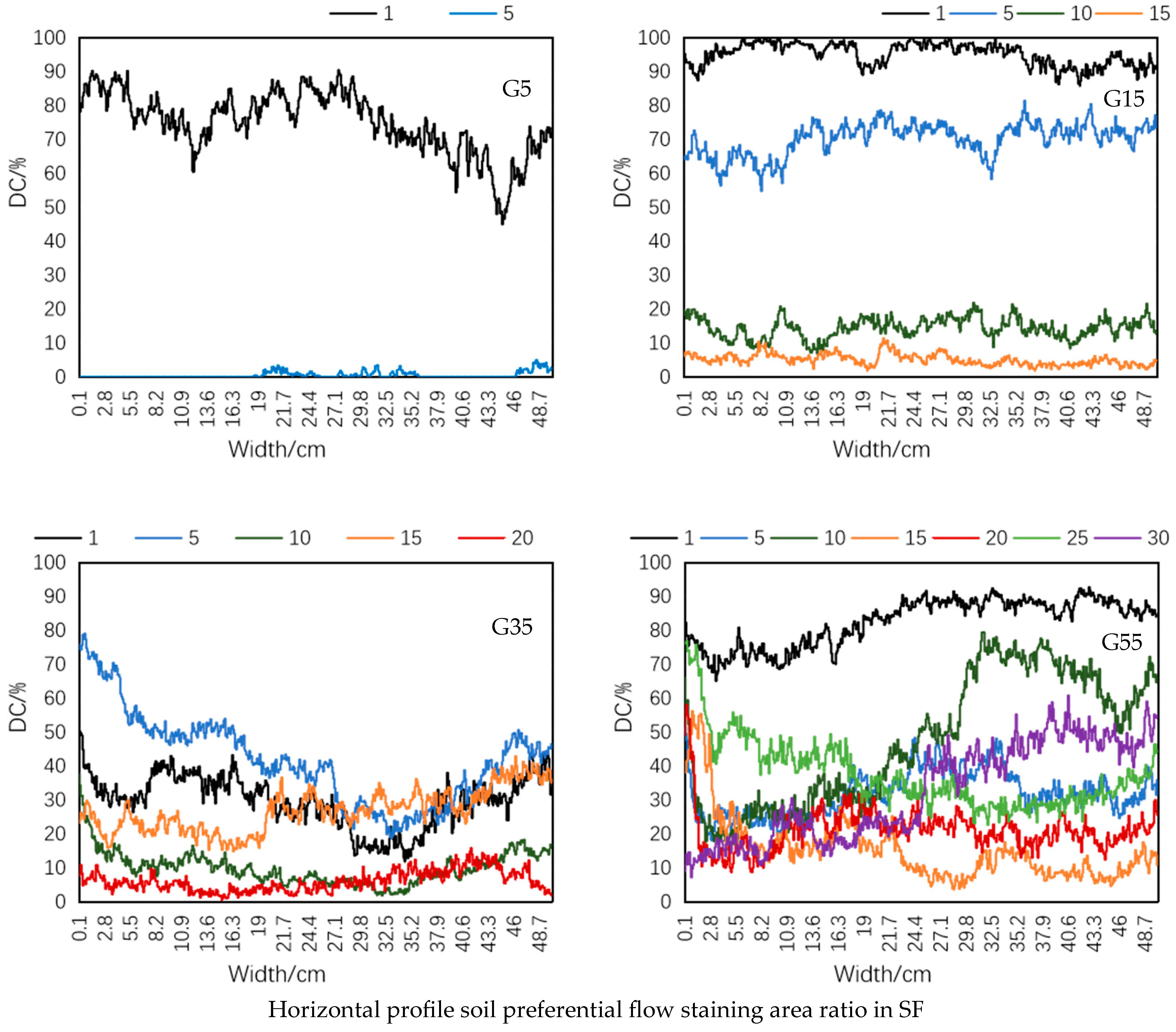
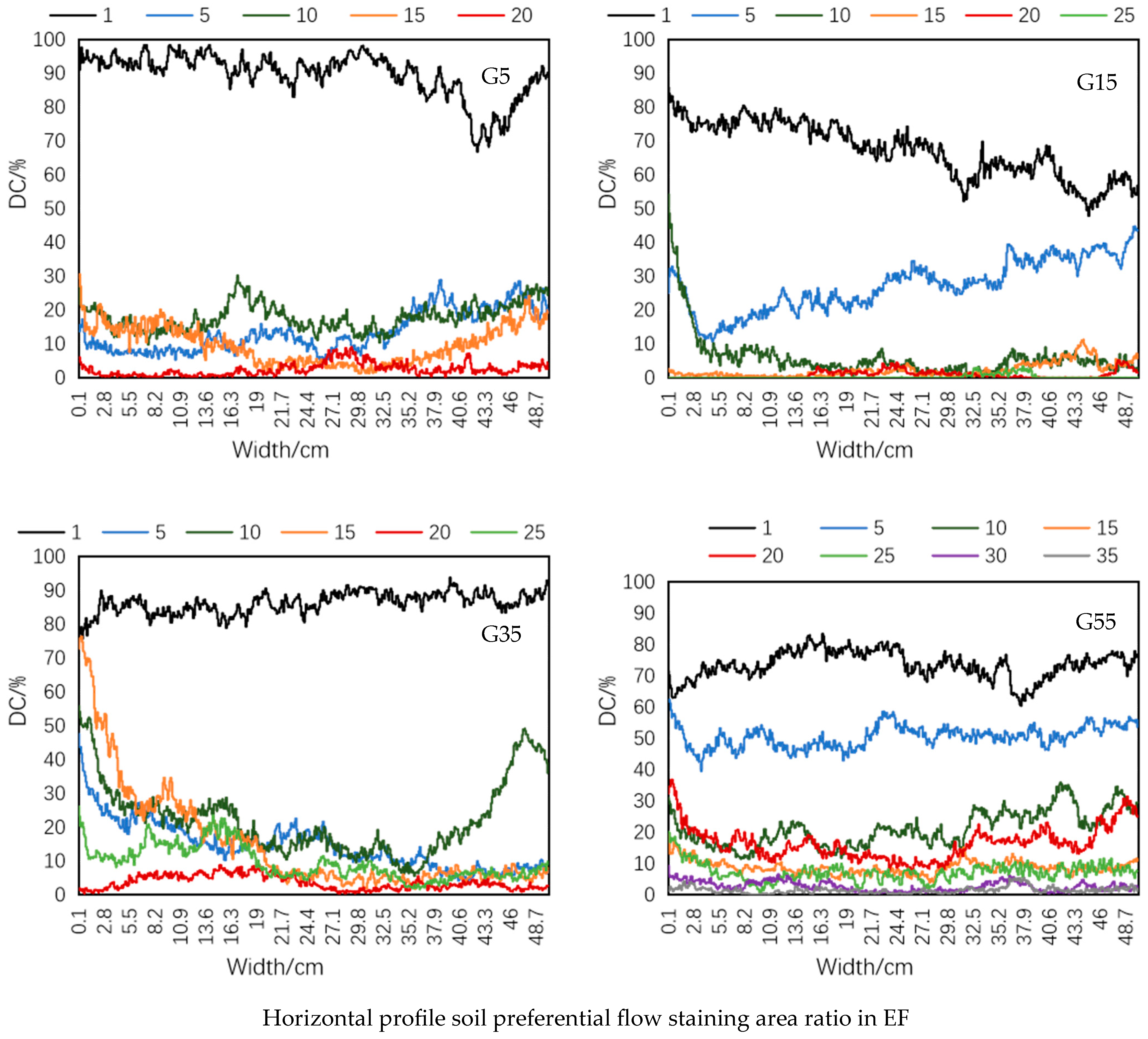
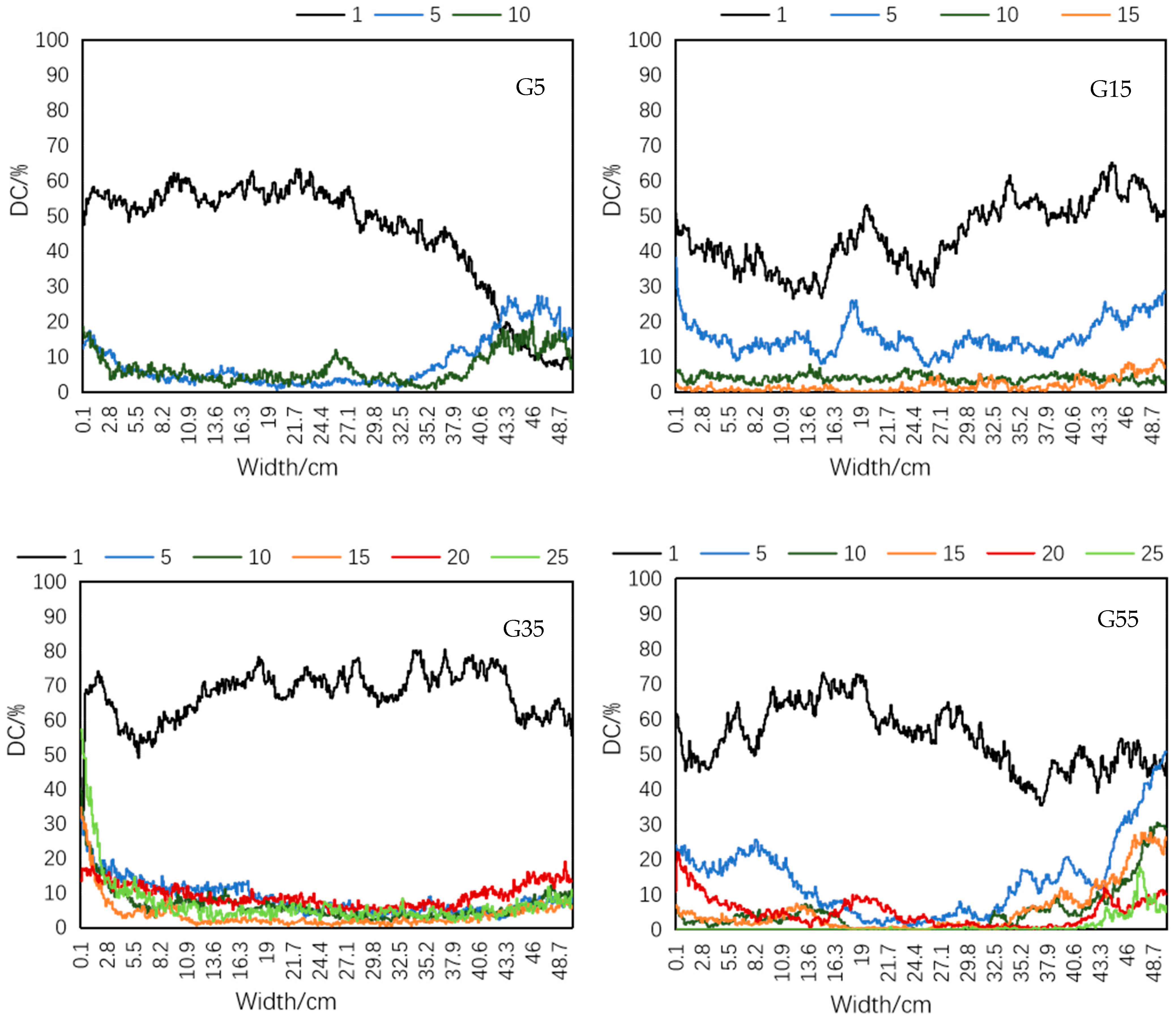
3.2. Dye Tracing Experiment
3.3. CT Scanning Results
3.4. HYDRUS-2D Simulation of Different Flow Motions
3.5. Statistical Analysis
4. Discussion
4.1. Comparison of the Physical Properties of Soil
4.2. Relationship between Macropores and Preferential Flow
4.3. Influence of Different Vegetation Types on the Wetting Front of Preferential Flow
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hou, F.; Cheng, J.; Zhang, H.; Wang, X.; Shi, D.; Guan, N. Response of preferential flow to soil–root–rock fragment system in karst rocky desertification areas. Ecol. Indic. 2024, 165, 112234. [Google Scholar] [CrossRef]
- Jordán, A.; Martínez-Zavala, L.; Bellinfante, N. Heterogeneity in soil hydrological response from different land cover types in southern Spain. Catena 2008, 74, 137–143. [Google Scholar] [CrossRef]
- Yeshaneh, E.; Salinas, J.L.; Blöschl, G. Decadal trends of soil loss and runoff in the Koga catchment, northwestern Ethiopia. Land Degrad. Dev. 2015, 28, 1806–1819. [Google Scholar] [CrossRef]
- Hu, L.; Zhou, Q.; Peng, D. Effects of vegetation restoration on the temporal variability of soil moisture in the humid karst region of southwest China. J. Hydrol. Reg. Stud. 2024, 53, 101852. [Google Scholar] [CrossRef]
- Macias-Fauria, M. Satellite images show China going green. Nature 2018, 553, 411–413. [Google Scholar] [CrossRef] [PubMed]
- Breshears, D.D.; Myers, O.B.; Barnes, F.J. Horizontal heterogeneity in the frequency of plant-available water with woodland intercanopy-canopy vegetation patch type rivals that occuring vertically by soil depth. Ecohydrology 2009, 2, 503–519. [Google Scholar] [CrossRef]
- Iqbal, S.; Guber, A.K.; Khan, H.Z. Estimating nitrogen leaching losses after compost application in furrow irrigated soils of Pakistan using HYDRUS-2D software. Agric. Water Manag. 2016, 168, 85–95. [Google Scholar] [CrossRef]
- Sohrt, J.; Ries, F.; Sauter, M.; Lange, J. Significance of preferential flow at the rock soil interface in a semi-arid karst environment. CATENA 2014, 123, 1–10. [Google Scholar] [CrossRef]
- Dasgupta, S.; Mohanty, B.P.; Kohne, J.M. Impacts of juniper vegetation and karst geology on subsurface flow processes in the Edwards Plateau, Texas. Vadose Zone J. 2006, 5, 1076–1085. [Google Scholar] [CrossRef]
- Verachtert, E.; Eeckhaut, M.V.D.; Poesen, J.; Deckers, J. Spatial interaction between collapsed pipes and landslides in hilly regions with loess-derived soils. Earth Surf. Process. Landf. 2013, 38, 826–835. [Google Scholar] [CrossRef]
- McDonnell, J.J. A rationale for old water discharge through macropores in a steep, humid catchment. Water Resour. Res. 1990, 26, 2821–2832. [Google Scholar] [CrossRef]
- Kogovsek, J.; Petric, M. Solute transport processes in a karst vadose zone characterized by long-term tracer tests (the cave system of Postojnska Jama, Slovenia). J. Hydrol. 2014, 519, 1205–1213. [Google Scholar] [CrossRef]
- Avanzi, F.; Petrucci, G.; Matzl, M.; Schneebeli, M.; De Michele, C. Early formation of preferential flow in a homogeneous snowpack observed by micro-CT. Water Resour. Res. 2017, 53, 3713–3729. [Google Scholar] [CrossRef]
- Guo, L.; Liu, Y.; Wu, G.-L.; Huang, Z.; Cui, Z.; Cheng, Z.; Zhang, R.-Q.; Tian, F.-P.; He, H. Preferential water flow: Influence of alfalfa (Medicago sativa L.) decayed root channels on soil water infiltration. J. Hydrol. 2019, 578, 124019. [Google Scholar] [CrossRef]
- Yao, J.; Cheng, J.; Sun, L. Effect of Antecedent Soil Water on Preferential Flow in Four Soybean Plots in Southwestern China. Soil Sci. 2017, 182, 83–93. [Google Scholar] [CrossRef]
- Rongier, G.; Collon-Drouaillet, P.; Filipponi, M. Simulation of 3D karst conduits with an object-distance based method integrating geological knowledge. Geomorphology 2014, 217, 152–164. [Google Scholar] [CrossRef]
- Kaufmann, G. Modelling karst aquifer evolution in fractured, porous rocks. J. Hydrol. 2016, 543, 796–807. [Google Scholar] [CrossRef]
- Flury, M.; Flühler, H. Tracer characteristics of brilliant blue FCF. Soil Sci. Soc. Am. J. 1995, 59, 22–27. [Google Scholar] [CrossRef]
- Ghodrati, M.; Jury, W.A. A field study using dyes to characterize preferential flow of water. Soil Sci. Soc. Am. J. 1990, 54, 1558–1563. [Google Scholar] [CrossRef]
- Katuwal, S.; Norgaard, T.; Moldrup, P.; Lamandé, M.; Wildenschild, D.; de Jonge, L.W. Linking air and water transport in intact soils to macropore characteristics inferred from X-ray computed tomography. Geoderma 2015, 237, 9–20. [Google Scholar] [CrossRef]
- Navin, K.C.; Twarakavi, J.S.; Sophia, S. Evaluating Interactions between Groundwater and Vadose Zone Using the HYDRUS-Based Flow Package for MODFLOW. Vadose Zone J. 2008, 7, 757–768. [Google Scholar]
- El-Nesr, M.N.; Alazba, A.A.; Šimůnek, J. HYDRUS simulations of the effects of dualdrip subsurface irrigation and a physical barrier on water movement and solute transport in soils. Irrig. Sci. 2014, 32, 111–125. [Google Scholar] [CrossRef]
- Karandish, F.; Šimůnek, J. A comparison of the HYDRUS (2D/3D) and SALTMED models to investigate the influence of various water-saving irrigation strategies on the maize water footprint. Agric. Water Manag. 2019, 213, 809–820. [Google Scholar] [CrossRef]
- Nohra, J.S.A.; Madramootoo, C.A.; Hendershot, W.H. Modeling Phosphorus Transport in Soil and Water. In Proceedings of the 2004 ASAE Annual Meeting, Ottawa, ON, Canada, 1–4 August 2004. [Google Scholar]
- Kan, X.; Cheng, J.; Hu, X.; Zhu, F.; Li, M. Effects of Grass and Forests and the Infiltration Amount on Preferential Flow in Karst Regions of China. Water 2019, 11, 1634. [Google Scholar] [CrossRef]
- Dexter, A.R. Advances in Characterization of Soil Structure. Soil Tillage Res. 1988, 11, 199–238. [Google Scholar] [CrossRef]
- Dexter, A.R.; Richard, G.; Arrouays, D.; Czyż, E.A.; Jolivet, C.; Duval, O. Complexed organic matter controls soil physical properties. Geoderma 2008, 144, 620–627. [Google Scholar] [CrossRef]
- Klute, A.; Dirksen, C. Methods of soil analysis: Part 1—Physical and mineralogical methods. In Hydraulic Conductivity and Diffusivity: Laboratory Methods; American Society of Agronomy: Madison, WI, USA, 1986; pp. 687–734. [Google Scholar]
- Williams, J.R. EPIC-Erosion/Productivity Impact Calculator: 2. User Manual; USDA. Agricultural Research Service: Beltsville, MD, USA, 1990.
- Bronick, C.J.; Lal, R. Soil structure and management: A review. Geoderma 2005, 124, 3–22. [Google Scholar] [CrossRef]
- Kutílek, M. Soil hydraulic properties as related to soil structure. Soil Tillage Res. 2004, 79, 175–184. [Google Scholar] [CrossRef]
- Meng, C.; Niu, J.; Li, X.; Luo, Z.; Du, X.; Du, J.; Lin, X.; Yu, X. Quantifying soil macropore networks in different forest communities using industrial computed tomography in a mountainous area of North China. J. Soil Sediments 2017, 17, 2357–2370. [Google Scholar] [CrossRef]
- Kan, X.; Cheng, J.; Hou, F. Response of Preferential Soil Flow to Different Infiltration Rates and Vegetation Types in the Karst Region of Southwest China. Water 2020, 12, 1778. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; van Genuchten, M.T. The HYDRUS Software Package for Simulating Two and Three-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media. Technical Manual, Version 1.0. 2006. Available online: https://www.pc-progress.com/en/Default.aspx?hydrus (accessed on 15 August 2024).
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Recent developments and applications of the HYDRUS computer software packages. Vadose Zone J. 2016, 15, 7. [Google Scholar] [CrossRef]
- Celia, M.A.; Bouloutas, E.T.; Zarba, R.L. A general mass-conservative numerical solution for the unsaturated flow equation. Water Resour. Res. 1990, 26, 1483–1496. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. ROSETTA: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Flury, M.; Flühler, H. Brilliant Blue FCF as a dye tracer for solute transport studies—A toxicological overview. J. Environ. Qual. 1994, 23, 1108–1112. [Google Scholar] [CrossRef] [PubMed]
- Van Ommen, H.C.; Dijksma, R.; Hendrickx, J.M.H. Experimental assessment of preferential flow paths in a field soil. J. Hydrol. 1989, 105, 253–262. [Google Scholar] [CrossRef]
- Bargués, T.A.; Reese, H.; Almaw, A. The effect of trees on preferential flow and soil infiltrability in an agroforestry parkland in semiarid Burkina Faso. Water Resour. Res. 2014, 50, 3342–3354. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, W.D.; Drury, C.F.; Tan, C.S.; Fox, C.A.; Yang, X.M. Use of indicators and pore volume-function characteristics to quantify soil physical quality. Geoderma 2009, 152, 252–263. [Google Scholar] [CrossRef]
- Pulido-Moncada, M.; Ball, B.C.; Gabriels, D.; Lobo, D.; Cornelis, W.M. Evaluation of soil physical quality index S for some tropical and temperate medium-textured soils. Soil Sci. Soc. Am. J. 2014, 79, 9–19. [Google Scholar] [CrossRef]
- Edwards, W.M.; Van, D.P.R.R.; Ehlers, W. A Numerical Study of the Effects of Noncapillary-Sized Pores Upon Infiltration1. Soil Sci. Soc. Am. J. 1979, 43, 851. [Google Scholar] [CrossRef]
- Karsanina, M.V.; Gerke, K.M.; Skvortsova, E.B.; Mallants, D. Universal spatial correlation functions for describing and reconstructing soil microstructure. PLoS ONE 2015, 10, e0126515. [Google Scholar] [CrossRef] [PubMed]
- Jarvis, N.J. A review of non-equilibrium water flow and solute transport in soil macropores: Principles, controlling factors and consequences for water quality. Eur. J. Soil Sci. 2007, 58, 523–546. [Google Scholar] [CrossRef]
- Givi, J.; Prasher, S.O.; Patel, R.M. Evaluation of pedotransfer functions in predicting the soil water contents at field capacity and wilting point. Agric. Water Manag. 2004, 70, 83–96. [Google Scholar] [CrossRef]
- Jiang, X.J.; Chen, C.; Zhu, X.; Zakari, S.; Singh, A.K.; Zhang, W.; Zeng, H.; Yuan, Z.-Q.; He, C.; Yu, S.; et al. Use of dye infiltration experiments and HYDRUS-3D to interpret preferential flow in soil in a rubber-based agroforestry systems in Xishuangbanna, China. Catena 2019, 178, 120–131. [Google Scholar] [CrossRef]
- Bottinelli, N.; Zhou, H.; Boivin, P.; Zhang, Z.B.; Jouquet, P.; Hartmann, C.; Peng, X. Macropores generated during shrinkage in two paddy soils using X-ray micro-computed tomography. Geoderma 2016, 265, 78–86. [Google Scholar] [CrossRef]
- Zhang, Z.; Peng, X.; Zhou, H.; Lin, H.; Sun, H. Characterizing preferential flow in cracked paddy soils using computed tomography and breakthrough curve. Soil Tillage Res. 2015, 146, 53–65. [Google Scholar] [CrossRef]
- Noriaki, W.; Hikaru, K.; Takashi, S.; Yagi, M. Local non-vuggy modeling and relations among porosity, permeability and preferential flow for vuggy carbonates. Eng. Geol. 2018, 248, 197–206. [Google Scholar]
- Niemeyer, R.J.; Fremier, A.K.; Heinse, R.; Chávez, W.; DeClerck, F.A. Woody vegetation increases saturated hydraulic conductivity in dry tropical Nicaragua. Vadose Zone J. 2014, 13, vzj2013-01. [Google Scholar] [CrossRef]
- Germann, P.F.; Zimmermann, M. Directions of preferential flow in a hillslope soil. Quasi-steady flow. Hydrol. Process. 2005, 19, 887–899. [Google Scholar] [CrossRef]
- Koestel, J.K.; Moeys, J.; Jarvis, N.J. Meta-analysis of the effects of soil properties, site factors and experimental conditions on solute transport. Hydrol. Earth Syst. Sci. 2012, 16, 1647–1665. [Google Scholar] [CrossRef]
- Rousseva, S.; Kercheva, M.; Shishkov, T.; Lair, G.J.; Nikolaidis, N.P.; Moraetis, D.; Krám, P.; Bernasconi, S.M.; Blum, W.E.H.; Menon, M.; et al. Soil water characteristics of European SoilTrEC critical zone observatories. Adv. Agron. 2017, 142, 29–72. [Google Scholar]
- Buttle, J.M.; McDonald, D.J. Coupled vertical and lateral preferential flow on a forested slope. Water Resour. Res. 2002, 38, 1–16. [Google Scholar] [CrossRef]


| Vegetation Type | Sample Number | Altitude (m.a.s.l.) | Latitude (N) | Longitude (E) | Slope (°) | Canopy Density (%) | Sand Content (%) | Silt Content (%) | Clay Content (%) |
|---|---|---|---|---|---|---|---|---|---|
| Secondary forest | SF1 | 1370 | 23°43′55″ | 102°54′54″ | 7 | 75 | 1.26 ± 0.61 | 20.34 ± 3.35 | 78.40 ± 3.63 |
| SF2 | 1370 | 23°43′53″ | 102°54′55″ | 7 | 80 | 0.52 ± 3.74 | 28.61 ± 5.62 | 70.87 ± 18.05 | |
| SF3 | 1371 | 23°43′57″ | 102°54′52″ | 6 | 70 | 0.05 ± 4.82 | 21.20 ± 4.18 | 78.75 ± 7.57 | |
| SF4 | 1371 | 23°43′57″ | 102°54′57″ | 9 | 80 | 1.15 ± 1.03 | 25.38 ± 3.39 | 75.54 ± 8.85 | |
| Eucalyptus robusta Smith plantation forestland | EF1 | 1370 | 23°37′21″ | 102°54′16″ | 4 | 82 | 2.82 ± 1.17 | 26.86 ± 2.27 | 70.32 ± 4.38 |
| EF2 | 1370 | 23°37′23″ | 102°54′13″ | 3 | 77 | 2.34 ± 1.58 | 42.93 ± 5.69 | 54.73 ± 1.06 | |
| EF3 | 1370 | 23°37′20″ | 102°54′18″ | 3 | 80 | 3.41 ± 0.56 | 42.76 ± 8.08 | 53.83 ± 5.49 | |
| EF4 | 1370 | 23°37′24″ | 102°54′25″ | 4 | 81 | 3.13 ± 2.73 | 38.94 ± 7.54 | 59.67 ± 0.78 | |
| Platycladus orientalis (L.) Francoptmxjjkmsc cypress plantation forestland | CF1 | 1370 | 23°37′13″ | 102°53′53″ | 2 | 60 | 9.86 ± 1.05 | 26.54 ± 5.77 | 63.6 ± 7.79 |
| CF2 | 1370 | 23°37′17″ | 102°53′48″ | 2 | 67 | 0.37 ± 1.84 | 14.48 ± 0.95 | 85.15 ± 4.41 | |
| CF3 | 1370 | 23°37′20″ | 102°53′51″ | 2 | 65 | 0.77 ± 1.65 | 26.92 ± 0.50 | 72.31 ± 17.16 | |
| CF4 | 1369 | 23°37′16″ | 102°53′56″ | 1 | 68 | 1.55 ± 2.91 | 23.21 ± 8.15 | 75.54 ± 1.06 |
| Site Type | Depth (cm) | P (%) | P1 (%) | P2 (%) | P3 (%) | P4 (%) | P5 (%) | P6 (%) | BD (%) |
|---|---|---|---|---|---|---|---|---|---|
| SF | 0–15 | 38.93% ± 2.61% | 35.76% ± 2.96% | 3.17% ± 0.35% | 31.07% ± 3.37% | 28.56% ± 3.54% | 26.68% ± 2.94% | 22.67% ± 1.52% | 1.26 ± 0.05 |
| 15–30 | 34.82% ± 3.78% | 33.32% ± 3.88% | 1.50% ± 0.10% | 31.51% ± 4.84% | 30.16% ± 4.87% | 27.95% ± 3.83% | 24.49% ± 0.54% | 1.11 ± 0.05 | |
| 30–50 | 44.63% ± 0.03% | 38.62% ± 2.92% | 6.02% ± 2.89% | 44.90% ± 0.29% | 38.83% ± 2.66% | 36.35% ± 2.81% | 22.04% ± 0.15% | 0.99 ± 0.01 | |
| EF | 0–15 | 37.30% ± 1.94% | 35.97% ± 1.40% | 1.33% ± 0.54% | 31.00% ± 2.71% | 29.88% ± 2.22% | 27.60% ± 1.75% | 29.24% ± 2.77% | 1.05 ± 0.03 |
| 15–30 | 39.15% ± 0.01% | 37.08% ± 0.08% | 2.07% ± 0.07% | 40.51% ± 0.01% | 38.37% ± 0.06% | 36.74% ± 0.03% | 35.13% ± 0.06% | 0.98 ± 0.09 | |
| 30–50 | 40.20% ± 0.01% | 39.92% ± 0.01% | 0.28% ± 0.01% | 40.07% ± 0.00% | 39.79% ± 0.01% | 36.77% ± 0.01% | 35.39% ± 0.02% | 1.04 ± 0.09 | |
| CF | 0–15 | 44.17% ± 0.01% | 41.50% ± 0.02% | 2.67% ± 0.01% | 38.38% ± 0.00% | 36.06% ± 0.01% | 33.74% ± 0.01% | 27.46% ± 0.02% | 1.15 ± 0.00 |
| 15–30 | 37.46% ± 1.72% | 35.76% ± 0.79% | 1.70% ± 0.93% | 33.59% ± 0.38% | 32.10% ± 1.13% | 29.99% ± 1.46% | 27.70% ± 0.69% | 1.12 ± 0.06 | |
| 30–50 | 40.80% ± 0.01% | 36.72% ± 0.00% | 4.08% ± 0.01% | 33.77% ± 0.00% | 30.39% ± 0.00% | 28.61% ± 0.01% | 27.94% ± 0.01% | 1.21 ± 0.00 |
| Site Type | Waterhead | Sample Number | UF/cm | ID/cm | DC/% | PF | Li/% | CV | Cμ |
|---|---|---|---|---|---|---|---|---|---|
| SF | G5 | 1 | 0.12 ± 0.04 | 5.10 ± 0.66 | 2.94 ± 1.30 | 0.99 ± 0.00 | 5.31 ± 2.16 | 0.41 ± 0.09 | 0.0020 ± 0.0012 |
| 2 | 0.10 ± 0.06 | 7.26 ± 2.68 | 2.19 ± 0.62 | 0.99 ± 0.00 | |||||
| G15 | 1 | 2.08 ± 1.13 | 22.78 ± 8.97 | 10.17 ± 1.98 | 0.96 ± 0.01 | 17.65 ± 4.51 | 0.42 ± 0.21 | 0.0028 ± 0.0002 | |
| 2 | 0.10 ± 0.06 | 11.72 ± 3.29 | 3.77 ± 2.12 | 0.99 ± 0.01 | |||||
| G35 | 1 | 0.40 ± 0.60 | 17.34 ± 2.65 | 9.16 ± 3.52 | 0.99 ± 0.01 | 26.42 ± 0.59 | 0.37 ± 0.06 | 0.0012 ± 0.0001 | |
| 2 | 0.12 ± 0.04 | 16.7 ± 1.95 | 10.33 ± 2.92 | 1.00 ± 0.00 | |||||
| G55 | 1 | 0.56 ± 0.74 | 25.94 ± 3.52 | 18.39 ± 3.41 | 0.99 ± 0.01 | 26.85 ± 1.46 | 0.21 ± 0.01 | 0.0010 ± 0.0001 | |
| 2 | 0.40 ± 0.28 | 25.40 ± 3.30 | 19.48 ± 3.86 | 1.00 ± 0.00 | |||||
| EF | G5 | 1 | 0.10 ± 0.00 | 14.70 ± 12.73 | 2.76 ± 2.10 | 0.98 ± 0.03 | 15.31 ± 4.64 | 0.48 ± 0.27 | 0.0037 ± 0.0023 |
| 2 | 0.90 ± 1.41 | 8.36 ± 2.73 | 7.94 ± 2.54 | 0.98 ± 0.02 | |||||
| 3 | 0.40 ± 0.33 | 6.72 ± 1.05 | 5.29 ± 1.06 | 0.98 ± 0.01 | |||||
| G15 | 1 | 1.48 ± 1.40 | 13.20 ± 2.98 | 7.76 ± 2.22 | 0.97 ± 0.03 | 17.94 ± 3.24 | 0.40 ± 0.17 | 0.0019 ± 0.0003 | |
| 2 | 0.46 ± 0.46 | 16.72 ± 2.69 | 7.60 ± 1.74 | 0.99 ± 0.01 | |||||
| 3 | 1.88 ± 1.81 | 14.12 ± 3.63 | 7.14 ± 4.05 | 0.96 ± 0.03 | |||||
| G35 | 1 | 1.80 ± 1.20 | 7.24 ± 1.78 | 7.05 ± 0.97 | 0.95 ± 0.03 | 11.84 ± 6.01 | 0.27 ± 0.13 | 0.0026 ± 0.0008 | |
| 2 | 0.88 ± 0.39 | 10.20 ± 2.60 | 4.77 ± 0.82 | 0.96 ± 0.01 | |||||
| 3 | 0.88 ± 0.78 | 6.92 ± 3.45 | 5.48 ± 2.24 | 0.97 ± 0.02 | |||||
| G55 | 1 | 0.44 ± 0.68 | 9.66 ± 3.25 | 6.67 ± 2.23 | 0.99 ± 0.01 | 21.14 ± 11.60 | 0.38 ± 0.15 | 0.0032 ± 0.0014 | |
| 2 | 0.10 ± 0.00 | 8.04 ± 1.35 | 4.15 ± 0.77 | 1.00 ± 0.00 | |||||
| 3 | 0.62 ± 0.85 | 13.34 ± 7.42 | 7.46 ± 3.78 | 0.99 ± 0.01 | |||||
| CF | G5 | 1 | 0.10 ± 0.00 | 8.36 ± 2.95 | 3.12 ± 1.81 | 0.98 ± 0.02 | 11.37 ± 4.92 | 0.66 ± 0.01 | 0.0034 ± 0.0006 |
| 2 | 0.10 ± 0.00 | 4.68 ± 2.02 | 1.47 ± 0.88 | 0.97 ± 0.04 | |||||
| G15 | 1 | 0.18 ± 0.16 | 15.40 ± 3.88 | 5.30 ± 2.12 | 0.99 ± 0.00 | 13.57 ± 3.87 | 0.41 ± 0.04 | 0.0029 ± 0.0006 | |
| 2 | 0.94 ± 0.72 | 7.98 ± 3.25 | 5.06 ± 1.68 | 0.97 ± 0.02 | |||||
| G35 | 1 | 0.14 ± 0.08 | 5.10 ± 2.04 | 3.75 ± 0.73 | 0.99 ± 0.00 | 8.04 ± 0.13 | 0.18 ± 0.04 | 0.0033 ± 0.0002 | |
| 2 | 0.28 ± 0.22 | 6.78 ± 2.37 | 4.46 ± 0.57 | 0.99 ± 0.01 | |||||
| G55 | 1 | 0.14 ± 0.08 | 3.86 ± 0.89 | 2.05 ± 0.77 | 0.98 ± 0.01 | 6.78 ± 1.79 | 0.39 ± 0.03 | 0.0032 ± 0.0012 | |
| 2 | 0.10 ± 0.00 | 7.28 ± 3.35 | 2.94 ± 0.93 | 0.99 ± 0.00 |
| Samples | SF | EF | CF | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | ||
| d (mm) | 1.26 | 1.18 | 1.24 | 1.15 | 1.23 | 1.25 | 1.27 | 1.19 | 1.20 | |
| Vm (104 mm3) | 20.97 | 25.16 | 33.26 | 51.65 | 40.05 | 18.46 | 15.41 | 16.42 | 24.17 | |
| Sm (105 mm3) | 11.65 | 17.76 | 20.43 | 37.55 | 20.38 | 10.99 | 9.03 | 14.06 | 18.34 | |
| L | 0.55 | 0.53 | 0.86 | 0.56 | 0.47 | 0.51 | 0.48 | 0.62 | 0.55 | |
| Volume ratio (%) | <5 mm3 | 3.90% | 4.79% | 2.86% | 2.71% | 2.67% | 6.53% | 2.50% | 14.61% | 8.37% |
| 5–105 mm3 | 1.20% | 0.58% | 0.62% | 0.14% | 8.50% | 8.05% | 4.63% | 4.78% | 1.29% | |
| >105 mm3 | 94.89% | 94.64% | 96.52% | 97.15% | 88.83% | 85.42% | 92.87% | 80.62% | 90.35% | |
| Plot | Depth | Qr (cm3 cm−3) | Qs (cm3 cm−3) | Alpha (mm−1) | n (-) | Ks-S (cm day−1) | K (10−10) | Particle Size | Ks (cm·min−1) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SAN (%) | SIL (%) | CLA (%) | |||||||||
| SF | 0–15 | 0.1068 | 0.5233 | 0.0198 | 1.1822 | 17.36 | 19.58 | 1.26 | 20.34 | 78.40 | 17.57 |
| 15–30 | 0.1075 | 0.5269 | 0.0192 | 1.2117 | 19.04 | 14.37 | 0.52 | 28.61 | 70.87 | 13.54 | |
| 30–50 | 0.1077 | 0.5257 | 0.0199 | 1.1838 | 16.95 | 9.81 | 0.05 | 21.20 | 78.75 | 29.38 | |
| EF | 0–15 | 0.1060 | 0.5223 | 0.0192 | 1.2082 | 19.03 | 29.11 | 2.82 | 26.86 | 70.32 | 48.67 |
| 15–30 | 0.1063 | 0.5183 | 0.0155 | 1.3008 | 20.37 | 31.02 | 2.34 | 42.93 | 54.73 | 22.61 | |
| 30–50 | 0.1055 | 0.5156 | 0.0152 | 1.3050 | 20.05 | 38.90 | 3.41 | 42.76 | 53.83 | 35.14 | |
| CF | 0–15 | 0.1019 | 0.5075 | 0.0189 | 1.2206 | 21.93 | 2.20 | 9.86 | 26.54 | 63.60 | 5.62 |
| 15–30 | 0.1072 | 0.5206 | 0.0196 | 1.1657 | 17.67 | 4.09 | 0.37 | 14.48 | 85.15 | 6.05 | |
| 30–50 | 0.1073 | 0.5262 | 0.0194 | 1.2051 | 17.91 | 1.69 | 0.77 | 26.92 | 72.31 | 8.35 | |
| V | δ | τ | S | ξ | Ss | P | P1 | P2 | RF | TCR | P3 | P4 | P5 | Ks | P6 | Sa | Si | SCv | UF | ID | DC | PF | Li | CV | Cμ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| V | 1 | 0.281 * | −0.508 ** | 0.950 ** | −0.590 ** | 0.545 ** | 0.423 ** | 0.369 ** | 0.261 * | −0.106 | 0.125 | 0.455 ** | 0.449 ** | 0.466 ** | 0.379 ** | −0.203 | −0.206 | −0.013 | 0.151 | 0.041 | 0.164 | 0.147 | 0.065 | 0.081 | −0.066 | −0.095 |
| δ | 1 | −0.279 * | 0.336 ** | −0.0629 ** | 0.292 * | 0.107 | −0.035 | 0.430 ** | 0.145 | 0.298 * | 0.170 | 0.092 | 0.086 | 0.027 | −0.126 | −0.198 | −0.150 | 0.256 | −0.116 | 0.274 * | 0.217 | 0.385 ** | 0.132 | −0.212 | −0.052 | |
| τ | 1 | −0.397 ** | 0.461 ** | −0.072 | −0.366 ** | −0.317 * | −0.326 * | −0.026 | −0.771 ** | −0.313 * | −0.300 * | −0.330 * | 0.027 | 0.293 * | 0.315 * | 0.254 | −0.0421 ** | 0.407 ** | 0.091 | 0.254 | −0.386 ** | 0.231 | −0.157 | 0.106 | ||
| S | 1 | −0.590 ** | 0.484 ** | 0.353 ** | 0.296 * | 0.247 | −0.194 | 0.078 | 0.421 ** | 0.414 ** | 0.424 ** | 0.414 ** | −0.144 | −0.237 | −0.005 | 0.166 | 0.053 | 0.179 | 0.164 | 0.076 | 0.076 | −0.136 | −0.146 | |||
| ξ | 1 | −0.184 | −0.280 * | −0.197 | −0.322 * | −0.240 | −0.0433 ** | −0.403 ** | −0.374 ** | −0.385 ** | −0.296 * | 0.012 | 0.375 ** | −0.033 | −0.230 | 0.078 | −0.170 | −0.145 | −0.265 * | −0.059 | 0.249 | 0.161 | ||||
| Ss | 1 | −0.047 | −0.065 | −0.027 | −0.150 | −0.097 | 0.005 | −0.014 | −0.009 | 0.235 | −0.167 | 0.105 | 0.121 | −0.170 | 0.306 * | 0.461 ** | 0.362 ** | −0.188 | 0.312 * | 0.019 | 0.175 | |||||
| P | 1 | 0.948 ** | 0.477 ** | 0.107 | 0.153 | 0.856 ** | 0.863 ** | 0.858 ** | 0.090 | 0.339 ** | −0.037 | −0.195 | 0.183 | −0.295 * | −0.158 | −0.127 | .281 * | −0.071 | 0.012 | −0.077 | ||||||
| P1 | 1 | 0.189 | 0.084 | 0.154 | 0.752 ** | 0.808 ** | 0.800 ** | 0.148 | 0.392 ** | −0.061 | −0.163 | 0.173 | −0.285 * | −0.184 | −0.172 | 0.229 | −0.097 | 0.077 | −0.064 | |||||||
| P2 | 1 | 0.131 | 0.145 | 0.562 ** | 0.430 ** | 0.438 ** | −0.138 | −0.042 | 0.051 | −0.190 | 0.118 | −0.206 | 0.011 | 0.048 | 0.330 * | 0.000 | −0.114 | −0.065 | ||||||||
| RF | 1 | 0.037 | 0.155 | 0.142 | 0.138 | −0.055 | 0.102 | −0.085 | −0.032 | 0.084 | 0.157 | 0.348 ** | 0.410 ** | 0.283 * | 0.325 * | −0.132 | 0.183 | |||||||||
| TCR | 1 | 0.191 | 0.200 | 0.220 | −0.144 | 0.055 | −0.444 ** | −0.189 | 0.457 ** | −0.503 ** | −0.178 | −0.373 ** | 0.436 ** | −0.358 ** | 0.143 | −0.158 | ||||||||||
| P3 | 1 | 0.987 ** | 0.983 ** | 0.275 * | 0.466 ** | −0.172 | −0.034 | 0.145 | −0.206 | 0.030 | 0.058 | 0.331 * | 0.032 | −0.201 | −0.141 | |||||||||||
| P4 | 1 | 0.993 ** | 0.314 * | 0.510 ** | −0.194 | −0.016 | 0.146 | −0.211 | 0.006 | 0.030 | 0.307 * | 0.013 | −0.179 | −0.149 | ||||||||||||
| P5 | 1 | 0.296 * | 0.478 ** | −0.207 | −0.018 | 0.157 | −0.228 | −0.034 | −0.016 | 0.312 * | −0.024 | −0.163 | −0.141 | |||||||||||||
| Ks | 1 | 0.151 | −0.123 | 0.395 ** | −0.235 | 0.275 * | 0.240 | 0.338 ** | −0.041 | 0.283 * | −0.209 | −0.097 | ||||||||||||||
| P6 | 1 | −0.128 | −0.023 | 0.106 | −0.087 | −0.039 | −0.009 | 0.130 | −0.018 | −0.112 | −0.076 | |||||||||||||||
| Sa | 1 | −0.108 | −0.597 ** | 0.206 | −0.057 | 0.028 | −0.434 ** | 0.111 | 0.042 | 0.168 | ||||||||||||||||
| Si | 1 | −0.733 ** | 0.145 | 0.094 | 0.147 | −0.095 | 0.094 | −0.221 | 0.019 | |||||||||||||||||
| SCv | 1 | −0.259 * | −0.037 | −0.138 | 0.374 ** | −0.152 | 0.149 | −0.130 | ||||||||||||||||||
| UF | 1 | 0.581 ** | 0.742 ** | −0.669 ** | 0.711 ** | −0.192 | 0.175 | |||||||||||||||||||
| ID | 1 | 0.885 ** | −0.051 | 0.778 ** | −0.155 | 0.178 | ||||||||||||||||||||
| DC | 1 | −0.173 | 0.853 ** | −0.0374 ** | 0.125 | |||||||||||||||||||||
| PF | 1 | −0.216 | 0.050 | −0.102 | ||||||||||||||||||||||
| Li | 1 | −0.095 | 0.115 | |||||||||||||||||||||||
| CV | 1 | 0.171 | ||||||||||||||||||||||||
| Cμ | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kan, X.; Cheng, J.; Zheng, W.; Zhangzhong, L.; Li, J.; Liu, C.; Zhang, X. Interpretation of Soil Characteristics and Preferential Water Flow in Different Forest Covers of Karst Areas of China. Water 2024, 16, 2319. https://doi.org/10.3390/w16162319
Kan X, Cheng J, Zheng W, Zhangzhong L, Li J, Liu C, Zhang X. Interpretation of Soil Characteristics and Preferential Water Flow in Different Forest Covers of Karst Areas of China. Water. 2024; 16(16):2319. https://doi.org/10.3390/w16162319
Chicago/Turabian StyleKan, Xiaoqing, Jinhua Cheng, Wengang Zheng, Lili Zhangzhong, Jing Li, Changbin Liu, and Xin Zhang. 2024. "Interpretation of Soil Characteristics and Preferential Water Flow in Different Forest Covers of Karst Areas of China" Water 16, no. 16: 2319. https://doi.org/10.3390/w16162319
APA StyleKan, X., Cheng, J., Zheng, W., Zhangzhong, L., Li, J., Liu, C., & Zhang, X. (2024). Interpretation of Soil Characteristics and Preferential Water Flow in Different Forest Covers of Karst Areas of China. Water, 16(16), 2319. https://doi.org/10.3390/w16162319





