Identification of the Runoff Evolutions and Driving Forces during the Dry Season in the Xijiang River Basin
Abstract
1. Introduction
2. Study Area and Dataset
2.1. Study Area Description
2.2. Dataset
3. Methodology
3.1. Extreme-Point Symmetric Mode Decomposition
3.2. Bayesian Estimator of Abrupt Seasonal and Trend Change Algorithm
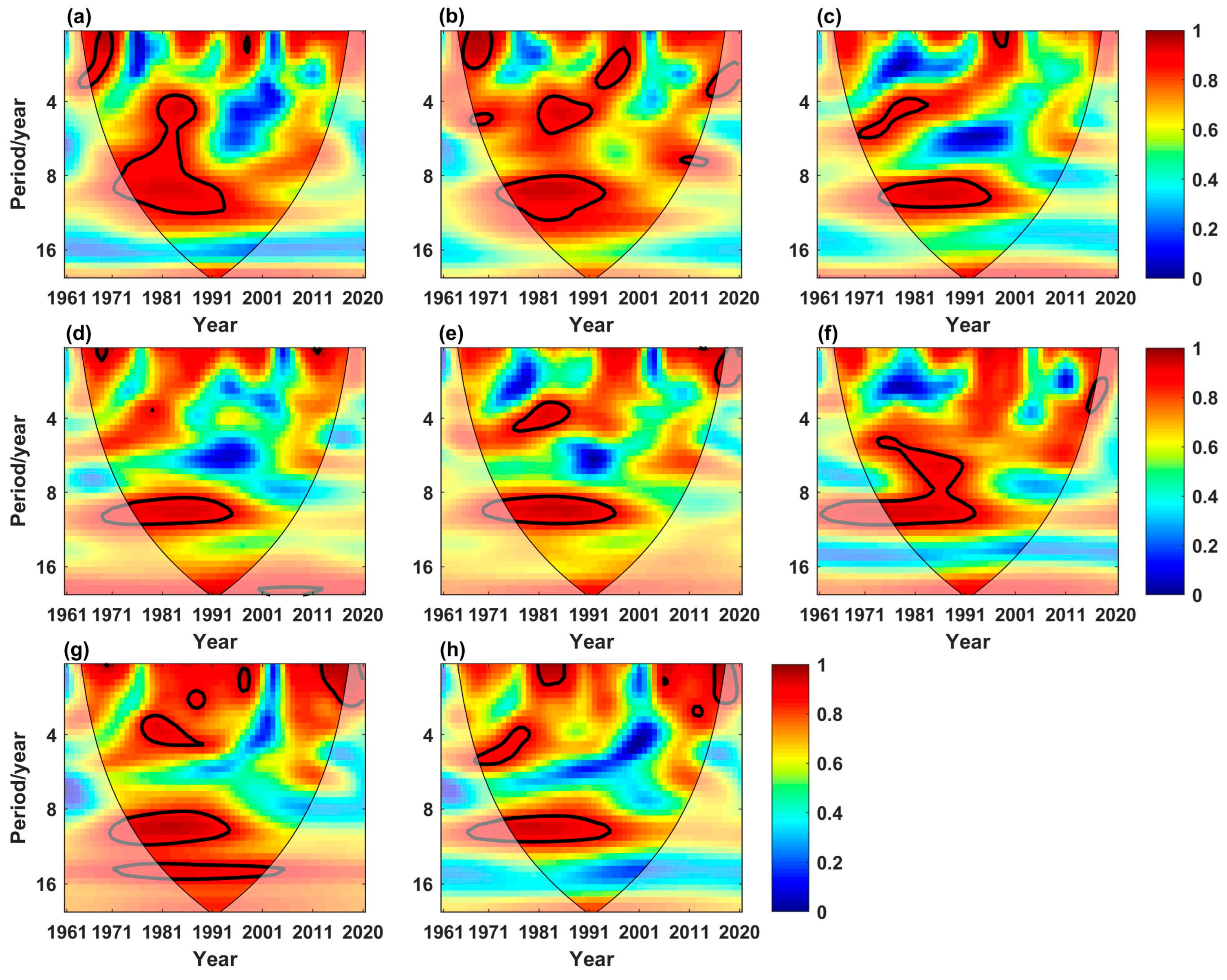
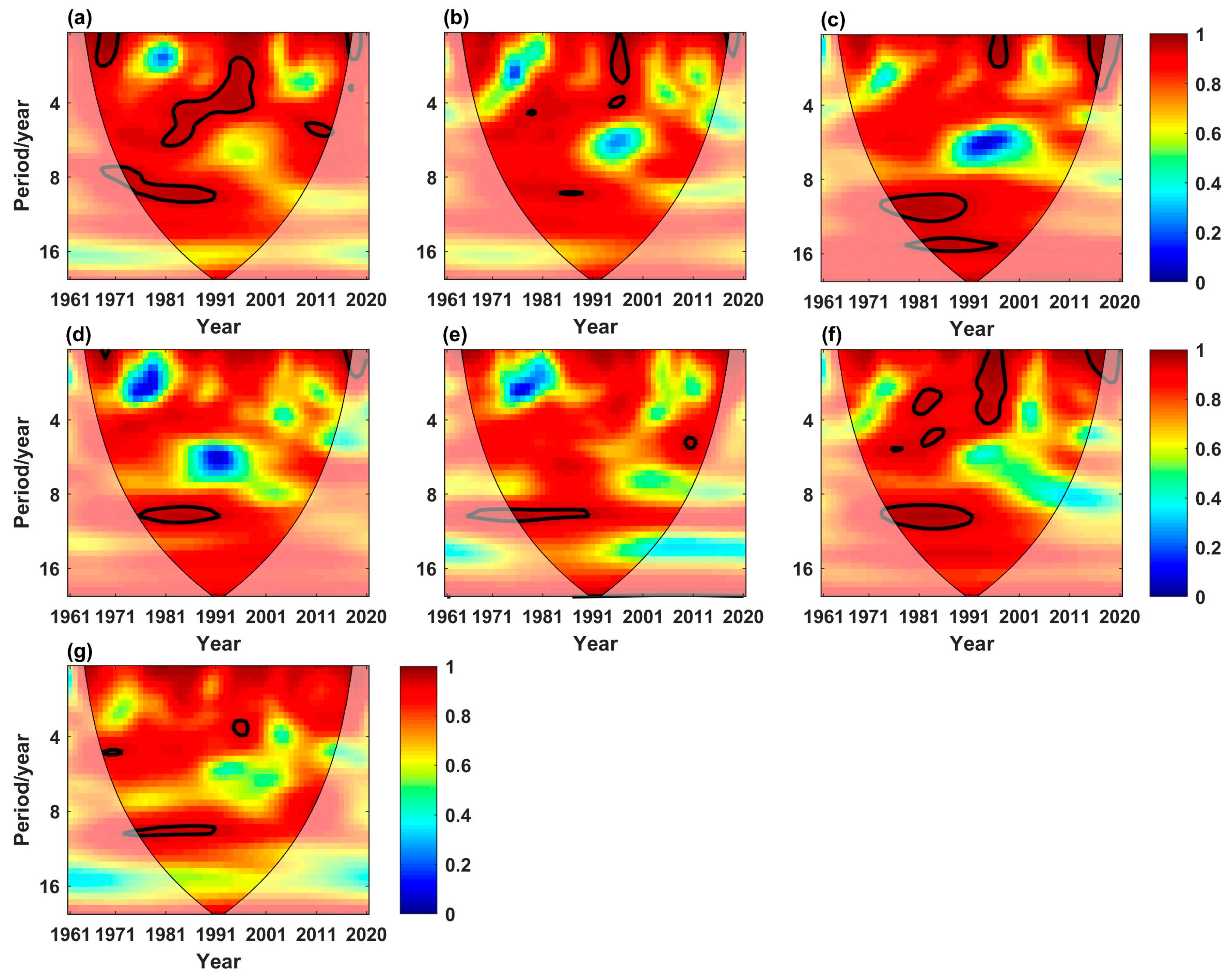
3.3. Cross Wavelet Transform Technology
4. Results
4.1. Analysis of Monthly Runoff Evolution
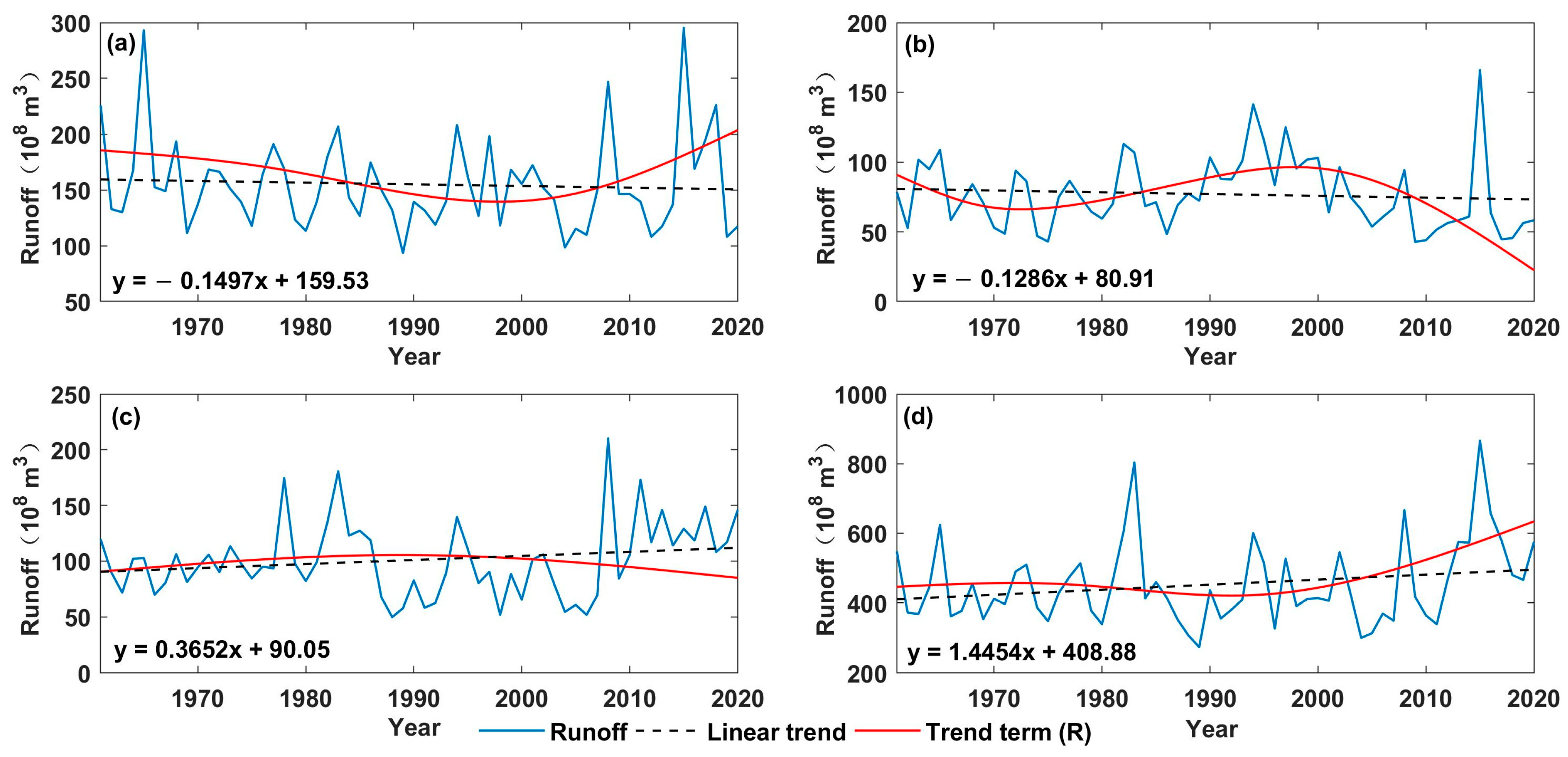
4.2. Identification of Trends, Periodicity, and Variability
4.3. Runoff Variation Characteristics during the Dry Season
4.4. The Driving Force of Circulation Factors
5. Discussion
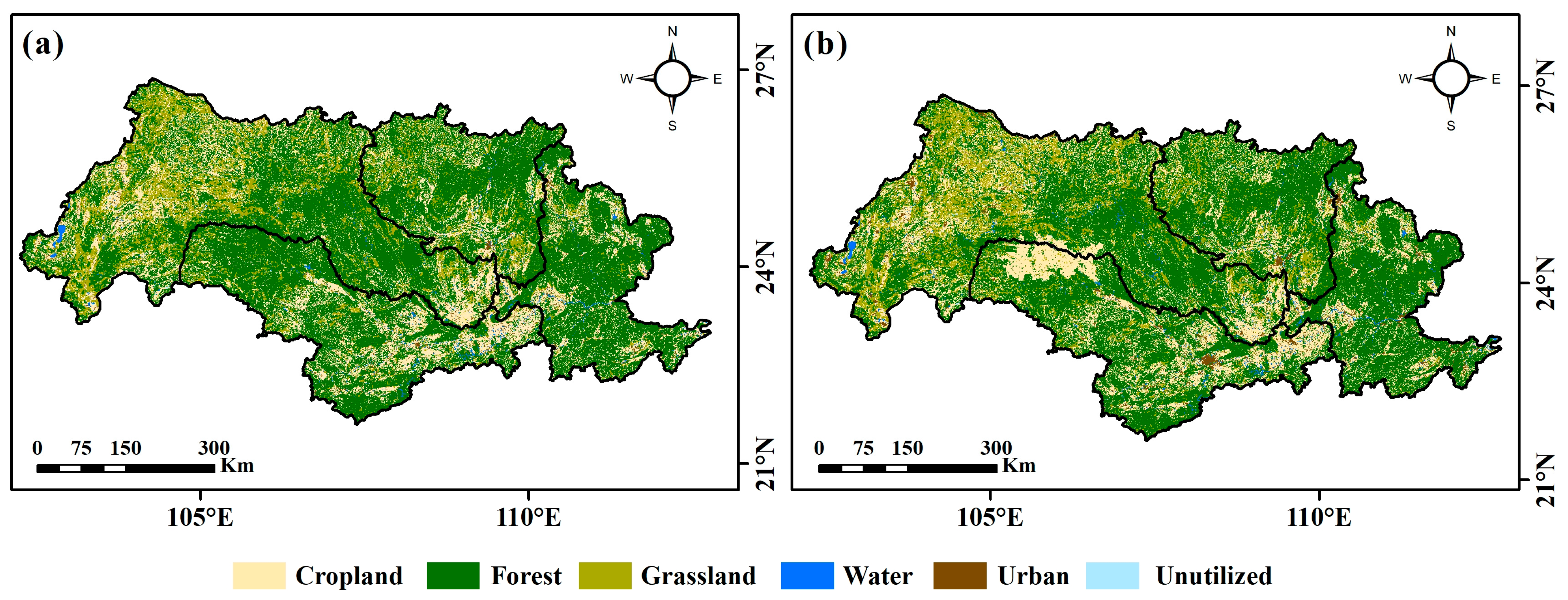
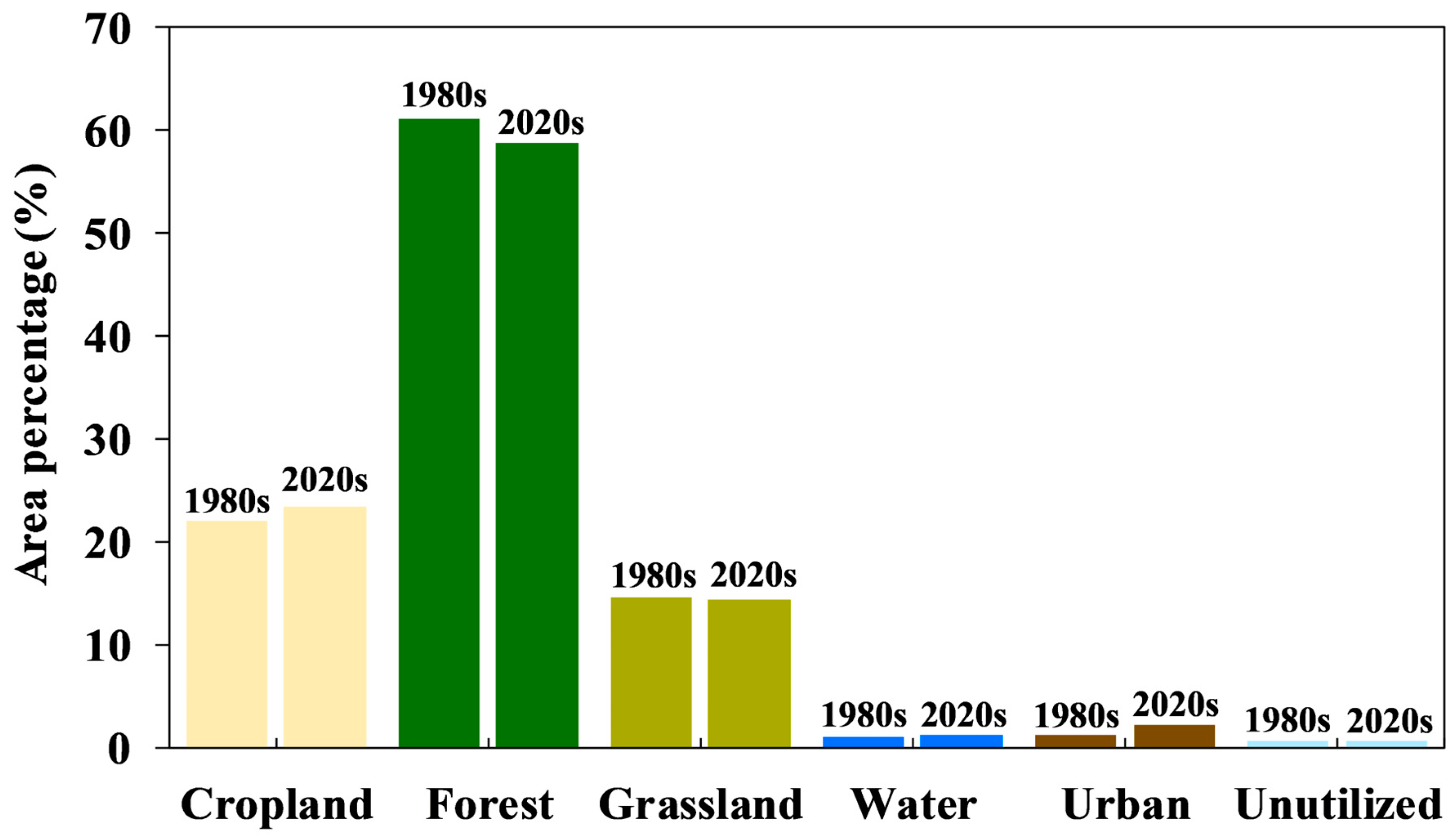
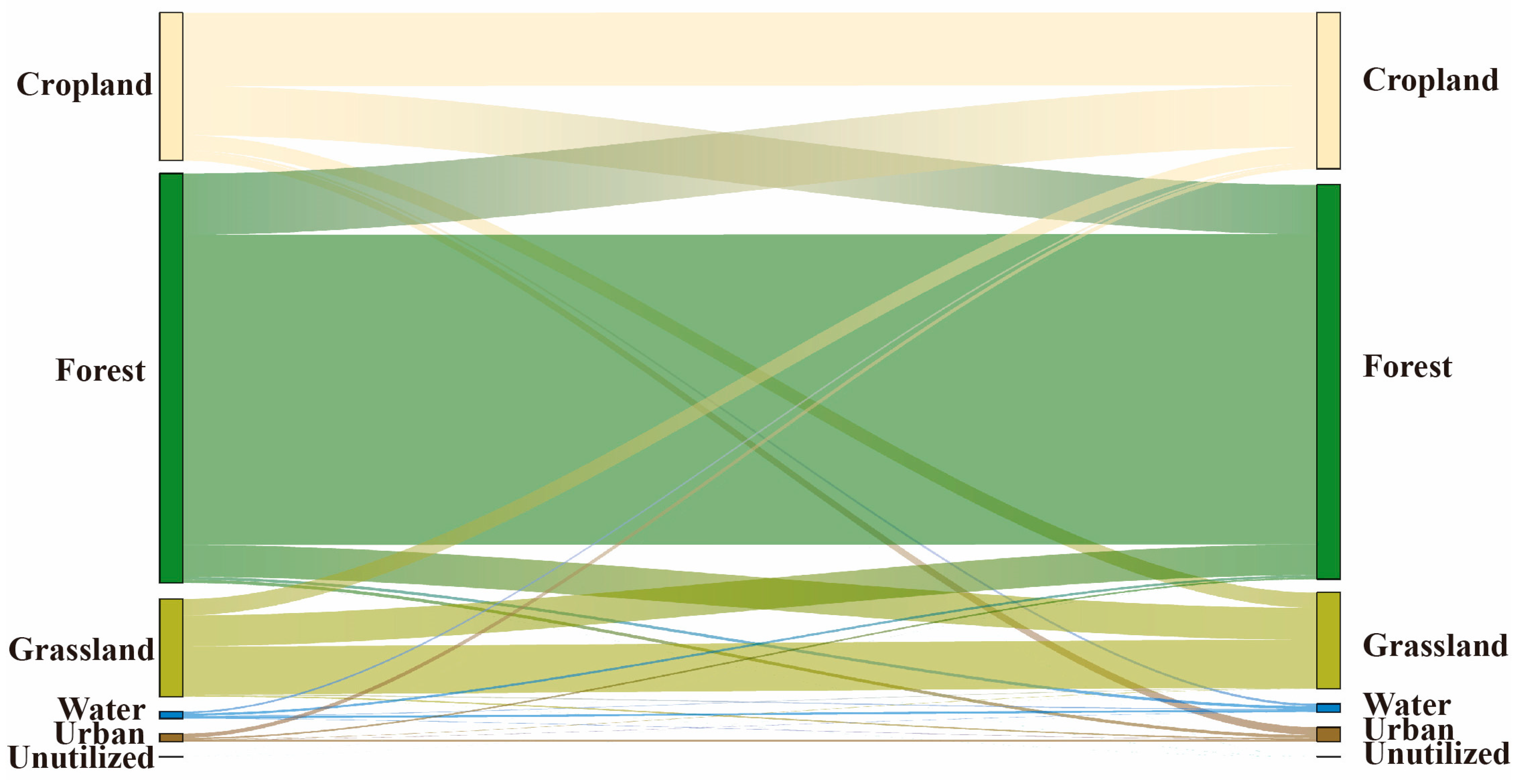
5.1. The Impact of Land Use on Runoff
5.2. Advantages and Limitations
5.3. Future Prospects
6. Conclusions
- (1)
- During the research period, the characteristics of runoff changes were generally consistent during the dry season in the XRB and each sub-basin. The minimum and maximum monthly runoff occurred in February and October, respectively. On an interannual scale, dry-season runoff exhibited periodicity of 3.53 years and 7.5 years.
- (2)
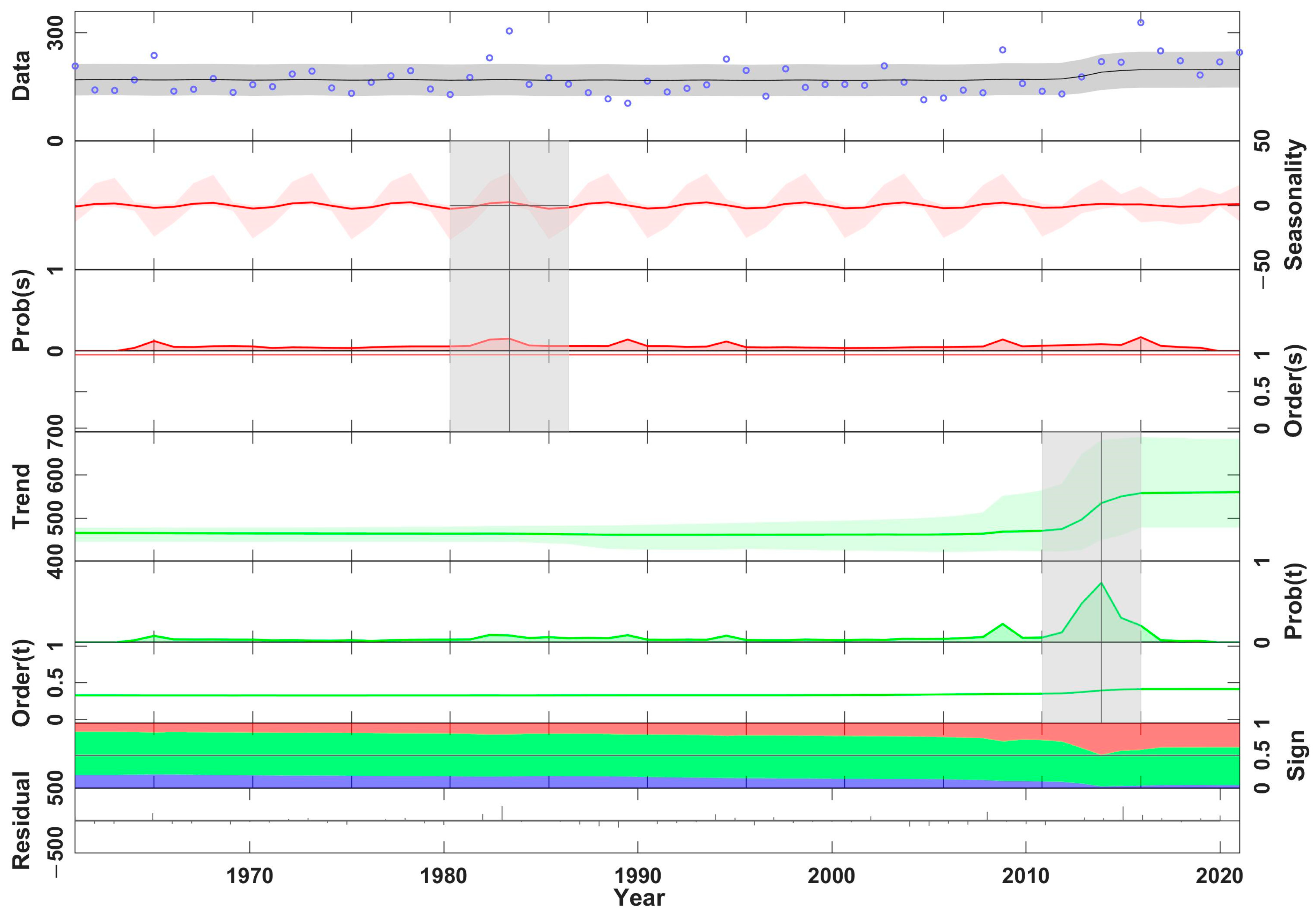
- Based on the BEAST algorithm, the seasonal abrupt point occurred in 1983, with a confidence interval from 1980 to 1986. Additionally, the trend abrupt point occurred in 2013, with a confidence interval from 2010 to 2015.
- (3)
- The evolution characteristics of dry-season runoff in the XRB were significantly influenced by atmospheric circulation anomaly factors. Overall, SSI-ENSO-PDO had the greatest impact on the changes in dry-season runoff in the XRB.
- (4)
- Land use change has had an impact on runoff in the XRB. Specifically, the increase in urban land area had an obvious impact on runoff. In addition, an increase in forest area may contribute to a decrease in runoff.
- (5)
- Based on seasonal and long-term trends of runoff, water resource allocation policies can be proposed. Advanced hydrological models and remote sensing technology can be utilized to improve the accuracy of dry-season runoff prediction and provide scientific basis for real-time water resource management.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Risva, K.; Nikolopoulos, D.; Efstratiadis, A.; Nalbantis, L. A Framework for Dry Period Low Flow Forecasting in Mediterranean Streams. Water Resour. Manag. 2018, 32, 4911–4932. [Google Scholar] [CrossRef]
- Li, Z.J.; Liu, M.Q.; Li, Z.X.; Feng, Q.; Song, L.L.; Xu, B.; Liu, X.Y.; Gui, J. Where does the runoff come from in dry season in the source region of the Yangtze River? Agr. For. Meteorol. 2023, 330, 109314. [Google Scholar]
- Singh, R.; Mishra, V. Atmospheric and Land Drivers of Streamflow Flash Droughts in India. J. Geophys. Res.-Atmos. 2024, 129, e2023JD040257. [Google Scholar] [CrossRef]
- Duan, Y.; Xu, G.B.; Liu, Y.; Liu, Y.J.; Zhao, S.X.; Fan, X.L. Tendency of Runoff and Sediment Variety and Multiple Time Scale Wavelet Analysis in Hongze Lake during 1975–2015. Water 2020, 12, 999. [Google Scholar] [CrossRef]
- Lin, Q.X.; Wu, Z.Y.; Zhang, Y.L.; Peng, T.; Chang, W.J.; Guo, J.L. Propagation from meteorological to hydrological drought and its application to drought prediction in the Xijiang River basin, South China. J. Hydrol. 2023, 617, 128889. [Google Scholar] [CrossRef]
- Jiang, K.; Mo, S.; Yu, K.; Li, P.; Li, Z. Analysis on the relationship between runoff erosion power and sediment transport in the Fujiang River basin and its response to land use change. Ecol. Indic. 2024, 159, 111690. [Google Scholar] [CrossRef]
- Bing, L.F.; Shao, Q.Q.; Liu, J.Y. Runoff characteristics in flood and dry seasons based on wavelet analysis in the source regions of the Yangtze and Yellow rivers. J. Geogr. Sci. 2012, 22, 261–272. [Google Scholar] [CrossRef]
- Mallakpour, I.; Sadegh, M.; AghaKouchak, A. A new normal for streamflow in California in a warming climate: Wetter wet seasons and drier dry seasons. J. Hydrol. 2018, 567, 203–211. [Google Scholar] [CrossRef]
- Niu, J.; Chen, J.; Sun, L.Q. Exploration of drought evolution using numerical simulations over the Xijiang (West River) basin in South China. J. Hydrol. 2015, 526, 68–77. [Google Scholar] [CrossRef]
- Smakhtin, V.U. Low flow hydrology: A review. J. Hydrol. 2001, 240, 147–186. [Google Scholar] [CrossRef]
- Guan, B.T.; Wright, W.E.; Chiang, L.H.; Cook, E.R. A dry season streamflow reconstruction of the critically endangered Formosan landlocked salmon habitat. Dendrochronologia 2018, 52, 152–161. [Google Scholar] [CrossRef]
- Tian, J.X.; Chang, J.; Zhang, Z.X.; Wang, Y.J.; Wu, Y.F.; Jiang, T. Influence of Three Gorges Dam on Downstream Low Flow. Water 2019, 11, 65. [Google Scholar] [CrossRef]
- Wang, F.E.; Xie, X.H. Practice and thinking on “Three Defense Lines” of water supply system regulation in the Pearl River Basin during 2022–2023 dry season. China Flood Drought Manag. 2024, 34, 32–35. [Google Scholar]
- Palmer, T.A.; Montagna, P.A. Impacts of droughts and low flows on estuarine water quality and benthic fauna. Hydrobiologia 2015, 753, 111–129. [Google Scholar] [CrossRef]
- Wang, W.Z.; Dong, Z.C.; Zhu, F.L.; Cao, Q.; Chen, J.; Yu, X. A Stochastic Simulation Model for Monthly River Flow in Dry Season. Water 2018, 10, 1654. [Google Scholar] [CrossRef]
- Cingolani, A.M.; Poca, M.; Whitworth-Hulse, J.I.; Giorgis, M.A.; Vaieretti, M.V.; Herrero, L.; Ramos, S.N.; Renison, D. Fire reduces dry season low flows in a subtropical highland of central Argentina. J. Hydrol. 2020, 590, 125538. [Google Scholar] [CrossRef]
- Mosley, L.M.; Zammit, B.; Leyden, E.; Heneker, T.M.; Hipsey, M.R.; Skinner, D.; Aldridge, K.T. The Impact of Extreme Low Flows on the Water Quality of the Lower Murray River and Lakes (South Australia). Water Resour. Manag. 2012, 26, 3923–3946. [Google Scholar] [CrossRef]
- Zhou, Z.; Ouyang, Y.; Qiu, Z.; Zhou, G.; Lin, M.; Li, Y. Evidence of climate change impact on stream low flow from the tropical mountain rainforest watershed in Hainan Island, China. J. Water Clim. Chang. 2017, 8, 293–302. [Google Scholar] [CrossRef]
- Wu, G.D.; Zhang, J.Y.; Li, Y.L.; Ren, H.Z.; Yang, M.Z. Revealing temporal variation of baseflow and its underlying causes in the source region of the Yangtze River (China). Int. J. Climatol. 2024, 41, 2045–2059. [Google Scholar] [CrossRef]
- Moreido, V.M.; Kalugin, A.S. Assessing possible changes in Selenga R. water regime in the XXI century based on a runoff formation model. Water Resour. 2017, 44, 390–398. [Google Scholar] [CrossRef]
- Ogden, F.L.; Crouch, T.D.; Stallard, R.F.; Hall, J.S. Effect of land cover and use on dry season river runoff, runoff efficiency, and peak storm runoff in the seasonal tropics of Central Panama. Water Resour. Res. 2013, 49, 8443–8462. [Google Scholar] [CrossRef]
- Yuan, F.; Zhao, C.; Jiang, Y.; Ren, L.; Shan, H.; Zhang, L.; Zhu, Y.; Chen, T.; Jiang, S.; Yang, X.; et al. Evaluation on uncertainty sources in projecting hydrological changes over the Xijiang River basin in South China. J. Hydrol. 2017, 554, 434–450. [Google Scholar] [CrossRef]
- Huang, F.; Xia, Z.Q.; Li, F.; Guo, L.D.; Yang, F.C. Hydrological Changes of the Irtysh River and the Possible Causes. Water Resour. Manag. 2012, 26, 3195–3280. [Google Scholar] [CrossRef]
- Ji, X.; Li, Y.G.; Luo, X.; He, D.M. Changes in the Lake Area of Tonle Sap: Possible Linkage to Runoff Alterations in the Lancang River? Remote Sens. 2018, 10, 866. [Google Scholar] [CrossRef]
- Wu, H.; Xue, H.Z.; Dong, G.T.; Gao, J.J.; Lian, Y.K.; Li, Z.C. Runoff variation in midstream Hei River, northwest China: Characteristics and driving factors analysis. J. Hydrol. Reg. Stud. 2024, 53, 101764. [Google Scholar] [CrossRef]
- Feng, Z.; Liu, S.; Guo, Y.; Liu, X. Runoff responses of various driving factors in a typical basin in Beijing-Tianjin-Hebei area. Remote Sens. 2023, 15, 1027. [Google Scholar] [CrossRef]
- Dalla Torre, D.; Di Marco, N.; Menapace, A.; Avesani, D.; Righetti, M.; Majone, B. Suitability of ERA5-Land reanalysis dataset for hydrological modelling in the Alpine region. J. Hydrol. Reg. Stud. 2024, 52, 101718. [Google Scholar] [CrossRef]
- Li, B.; Chen, Y.; Xiong, H. Quantitatively evaluating the effects of climate factors on runoff change for Aksu River in northwestern China. Theor. Appl. Climatol. 2016, 123, 97–105. [Google Scholar] [CrossRef]
- Luo, K.; Tao, F.; Deng, X.; Moiwo, J.P. Changes in potential evapotranspiration and surface runoff in 1981–2010 and the driving factors in Upper Heihe River Basin in Northwest China. Hydrol. Process. 2017, 31, 90–103. [Google Scholar] [CrossRef]
- Fu, T.G.; Liu, J.T.; Gao, H.; Qi, F.; Wang, F.; Zhang, M. Surface and subsurface runoff generation processes and their influencing factors on a hillslope in northern China. Sci. Total Environ. 2024, 906, 167372. [Google Scholar] [CrossRef]
- Xue, D.; Zhou, J.; Zhao, X.; Liu, C.; Wei, W.; Yang, X.; Li, Q.; Zhao, Y. Impacts of climate change and human activities on runoff change in a typical arid watershed, NW China. Ecol. Indic. 2021, 121, 107013. [Google Scholar] [CrossRef]
- Xu, G.C.; Cheng, Y.T.; Zhao, C.Z.; Mao, J.S.; Li, Z.B.; Jia, L.; Zhang, Y.X.; Wang, B. Effects of driving factors at multi-spatial scales on seasonal runoff and sediment changes. Catena 2023, 222, 106867. [Google Scholar] [CrossRef]
- Rasouli, K.; Scharold, K.; Mahmood, T.H.; Glenn, N.F.; Marks, D. Linking hydrological variations at local scales to regional climate teleconnection patterns. Hydrol. Process. 2020, 34, 5624–5641. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Lei, X.H.; Wang, H.; Zhang, X.H.; You, J.J.; Tan, Q.F.; Liu, X.L. Teleconnection analysis of monthly streamflow using ensemble empirical mode decomposition. J. Hydrol. 2020, 582, 124411. [Google Scholar] [CrossRef]
- Yang, W.C.; Jin, F.M.; Si, Y.J.; Li, Z. Runoff change controlled by combined effects of multiple environmental factors in a headwater catchment with cold and arid climate in northwest China. Sci. Total Environ. 2021, 756, 143995. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Gan, T.Y.; Bush, A.B.G.; Liu, J.G.; Zolina, O.; Gelfan, A. Changes of the streamflow of northern river basins of Siberia and their teleconnections to climate patterns. Int. J. Climatol. 2023, 43, 6114–6130. [Google Scholar] [CrossRef]
- Zhao, X.H.; Huang, G.H.; Li, Y.P.; Lu, C. Responses of hydroelectricity generation to streamflow drought under climate change. Renew. Sust. Energ. Rev. 2023, 174, 113141. [Google Scholar] [CrossRef]
- Xu, C.J.; Zhu, D.; Guo, W.; Ouyang, S.; Li, L.P.; Bu, H.; Wang, L.; Zuo, J.; Chen, J.H. Multi-Objective Ecological Long-Term Operation of Cascade Reservoirs Considering Hydrological Regime Alteration. Water 2024, 16, 1849. [Google Scholar] [CrossRef]
- Jakimavičius, D.; Adžgauskas, G.; Šarauskienė, D.; Kriaučiūnienė, J. Climate Change Impact on Hydropower Resources in Gauged and Ungauged Lithuanian River Catchments. Water 2020, 12, 3265. [Google Scholar] [CrossRef]
- Lin, Q.X.; Wu, Z.Y.; Singh, V.P.; Sadeghi, S.H.R.; He, H.; Lu, G.H. Correlation between hydrological drought, climatic factors, reservoir operation, and vegetation cover in the Xijiang Basin, South China. J. Hydrol. 2017, 549, 512–524. [Google Scholar] [CrossRef]
- Tian, Q.Q.; Wang, F.; Tian, Y.; Jiang, Y.Z.; Weng, P.Y.; Li, J.B. Copula-based comprehensive drought identification and evaluation over the Xijiang River Basin in South China. Ecol. Indic. 2023, 154, 110503. [Google Scholar] [CrossRef]
- Weng, P.Y.; Tian, Y.; Jiang, Y.Z.; Chen, D.X.; Kang, J. Assessment of GPM IMERG and GSMaP daily precipitation products and their utility in droughts and floods monitoring across Xijiang River Basin. Atmos. Res. 2023, 286, 106673. [Google Scholar] [CrossRef]
- Fei, K.; Chen, M.Y.; Zhou, Y.Y.; Du, H.X.; Deng, S.C.; Gao, L. Streamflow and surface soil moisture simulation capacity of high-resolution Satellite-derived precipitation estimate datasets: A case study in Xijiang river basin, China. J. Hydrol. Reg. Stud. 2022, 42, 101163. [Google Scholar] [CrossRef]
- White, J.H.R.; Walsh, J.E.; Thoman, R.L., Jr. Using Bayesian statistics to detect trends in Alaskan precipitation. Int. J. Climatol. 2021, 41, 2045–2059. [Google Scholar] [CrossRef]
- Hadad, M.A.; González-Reyes, Á.; Roig, F.A.; Matskovsky, M.; Cherubini, P. Tree-ring-based hydroclimatic reconstruction for the northwest Argentine Patagonia since 1055 CE and its teleconnection to large-scale atmospheric circulation. Glob. Planet. Chang. 2021, 202, 103496. [Google Scholar] [CrossRef]
- Wang, F.; Lai, H.X.; Li, Y.B.; Feng, K.; Zhang, Z.Z.; Tian, Q.Q.; Zhu, X.M.; Yang, H.B. Dynamic variation of meteorological drought and its relationships with agricultural drought across China. Agr. Water Manag. 2022, 261, 107301. [Google Scholar] [CrossRef]
- Ahmad, M.H.; Abubakar, A.; Ishak, M.Y.; Danhassan, S.S.; Zhang, J.H.; Alatalo, J.M. Modeling the influence of daily temperature and precipitation extreme indices on vegetation dynamics in Katsina State using statistical downscaling model (SDM). Ecol. Indic. 2023, 155, 110979. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X. The 30 m annual land cover dataset and its dynamics in China from 1990 to 2019. Earth Syst. Sci. Data. 2021, 13, 3907–3925. [Google Scholar] [CrossRef]
- Wang, J.L.; Li, Z.J. Extreme-point symmetric mode decomposition method for data analysis. Adv. Adapt. Data Anal. 2013, 5, 1350015. [Google Scholar] [CrossRef]
- Cai, Y.T.; Liu, S.T.; Lin, H. Monitoring the vegetation dynamics in the Dongting lake wetland from 2000 to 2019 using the BEAST algorithm based on dense Landsat time series. Appl. Sci. 2020, 10, 4209. [Google Scholar] [CrossRef]
- Nalley, D.; Adamowski, J.; Biswas, A.; Gharabaghi, B.; Hu, W. A multiscale and multivariate analysis of precipitation and streamflow variability in relation to ENSO, NAO and PDO. J. Hydrol. 2019, 574, 288–307. [Google Scholar] [CrossRef]
- Hu, W.; Si, B.C. Technical Note: Multiple wavelet coherence for untangling scale-specific and localized multivariate relationships in geosciences. Hydrol. Earth Syst. Sci. 2016, 20, 3183–3191. [Google Scholar] [CrossRef]
- Zheng, J.H.; Wang, H.L.; Liu, B.J. Impact of the long-term precipitation and land use changes on runoff variations in a humid subtropical river basin of China. J. Hydrol. Reg. Stud. 2022, 42, 101136. [Google Scholar] [CrossRef]
- Chen, Q.H.; Chen, H.; Zhang, J.; Hou, Y.K.; Shen, M.X.; Chen, J.; Xu, C.Y. Impacts of climate change and LULC change on runoff in the Jinsha River Basin. J. Geogr. Sci. 2020, 30, 85–102. [Google Scholar] [CrossRef]
- Khorn, N.; Ismail, M.H.; Nurhidayu, S.; Kamarudin, N.; Sulaiman, M.S. Land use/land cover changes and its impact on runoff using SWAT model in the upper Prek Thnot watershed in Cambodia. Environ. Earth Sci. 2022, 81, 466. [Google Scholar] [CrossRef]
- Zare, M.; Samani, A.A.N.; Mohammady, M. The impact of land use change on runoff generation in an urbanizing watershed in the north of Iran. Environ. Earth Sci. 2016, 75, 1279. [Google Scholar] [CrossRef]
- Liu, W.C.; Wu, J.H.; Xu, F.; Mu, D.W.; Zhang, P.B. Modeling the effects of land use/land cover changes on river runoff using SWAT models: A case study of the Danjiang River source area, China. Environ. Res. 2024, 242, 117810. [Google Scholar] [CrossRef] [PubMed]
- Li, J.Q.; Peng, Z.; Zhao, Y.Y.; Yang, L. Temporal and spatial evolution characteristics of runoff in the Xijiang River Basin in recent 60 years under the changing environment. J. Lake Sci. 2023, 35, 1033–1046. [Google Scholar]
- Feng, K.; Su, X.L. Spatiotemporal characteristics of drought in the Heihe River Basin based on the extreme-point symmetric mode decomposition method. Int. J. Disast. Risk Sc. 2019, 10, 591–603. [Google Scholar] [CrossRef]
- Zhao, K.; Wulder, M.A.; Hu, T.; Bright, R.; Wu, Q.; Qin, H.; Li, Y.; Toman, E.; Mallick, B.; Zhang, X.; et al. Detecting change-point, trend, and seasonality in satellite time series data to track abrupt changes and nonlinear dynamics: A Bayesian ensemble algorithm. Remote Sens. Environ. 2019, 232, 111181. [Google Scholar] [CrossRef]
- Hu, T.X.; Toman, E.M.; Chen, G.; Shao, G.; Zhou, Y.Y.; Li, Y.; Zhao, K.G.; Feng, Y.N. Mapping fine-scale human disturbances in a working landscape with Landsat time series on Google Earth Engine. ISPRS J. Photogramm. 2021, 176, 250–261. [Google Scholar] [CrossRef]
- Wang, F.; Lai, H.X.; Li, Y.B.; Feng, K.; Tian, Q.Q.; Guo, W.X.; Qu, Y.P.; Yang, H.B. Spatio-temporal evolution and teleconnection factor analysis of groundwater drought based on the GRACE mascon model in the Yellow River Basin. J. Hydrol. 2023, 626, 130349. [Google Scholar] [CrossRef]
- Su, L.; Miao, C.; Duan, Q.; Lei, X.; Li, H. Multiple-Wavelet Coherence of World’s Large Rivers with Meteorological Factors and Ocean Signals. J. Geophys. Res.-Atmos. 2019, 124, 4932–4954. [Google Scholar] [CrossRef]
- Ng, E.K.W.; Chan, J.C.L. Geophysical applications of partial wavelet coherence and multiple wavelet coherence. J. Atmos. Ocean. Tech. 2012, 29, 1845–1853. [Google Scholar] [CrossRef]
- Gao, C.; Ruan, T. The influence of climate change and human activities on runoff in the middle reaches of the Huaihe River Basin, China. J. Geogr. Sci. 2017, 28, 79–92. [Google Scholar] [CrossRef]
- Lv, C.M.; Wang, X.R.; Ling, M.H.; Xu, W.J.; Yan, D.H. Effects of Precipitation Concentration and Human Activities on City Runoff Changes. Water Resour. Manag. 2023, 37, 5023–5036. [Google Scholar] [CrossRef]
- Kriauciuniene, J.; Jakimavicius, D.; Sarauskiene, D.; Kaliatka, T. Estimation of uncertainty sources in the projections of Lithuanian river runoff. Stoch. Environ. Res. Risk Assess. 2012, 27, 769–784. [Google Scholar] [CrossRef]
- Ravindranath, A.; Devineni, N. Quantifying streamflow regime behavior and its sensitivity to demand. J. Hydrol. 2020, 582, 124423. [Google Scholar] [CrossRef]
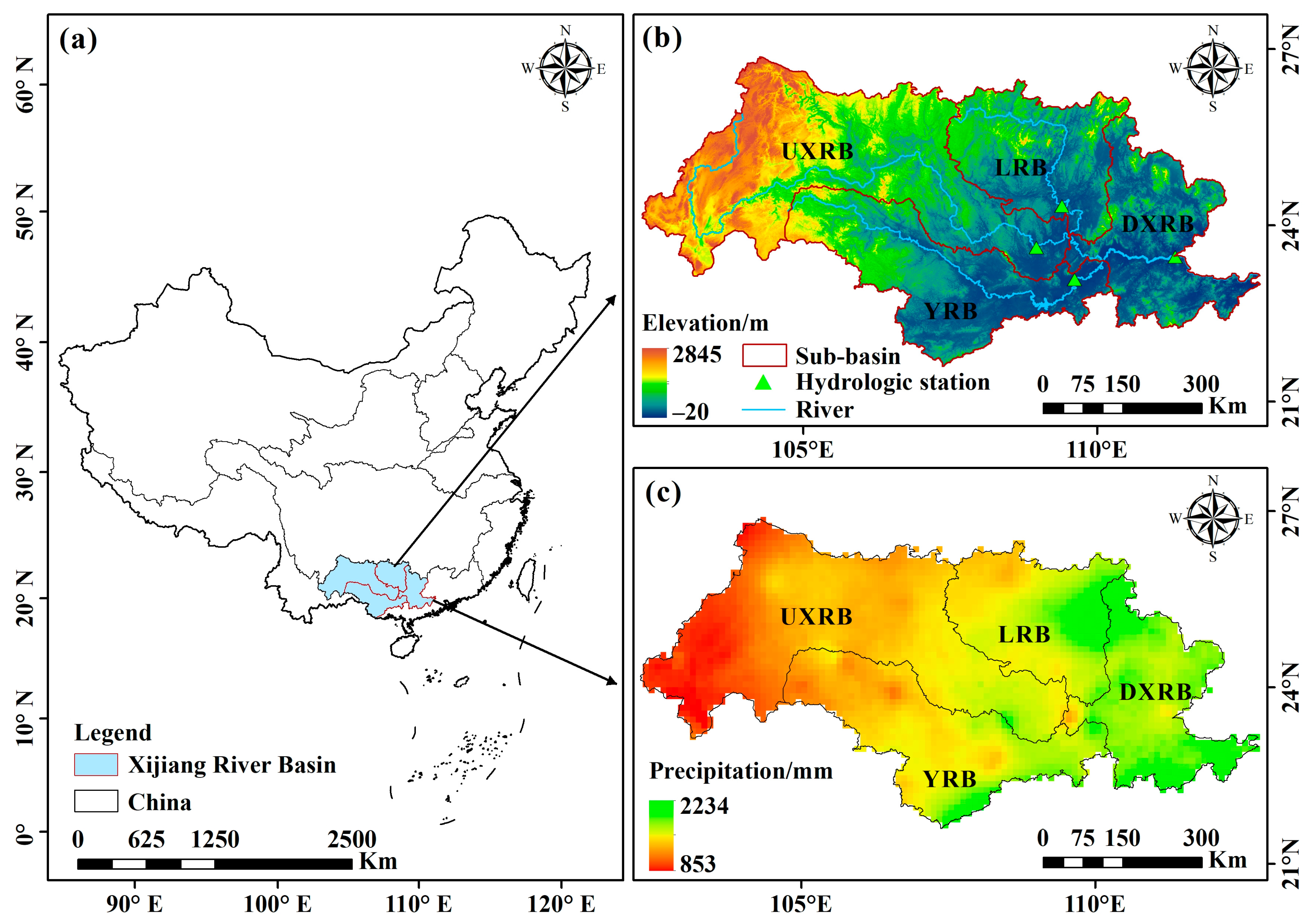
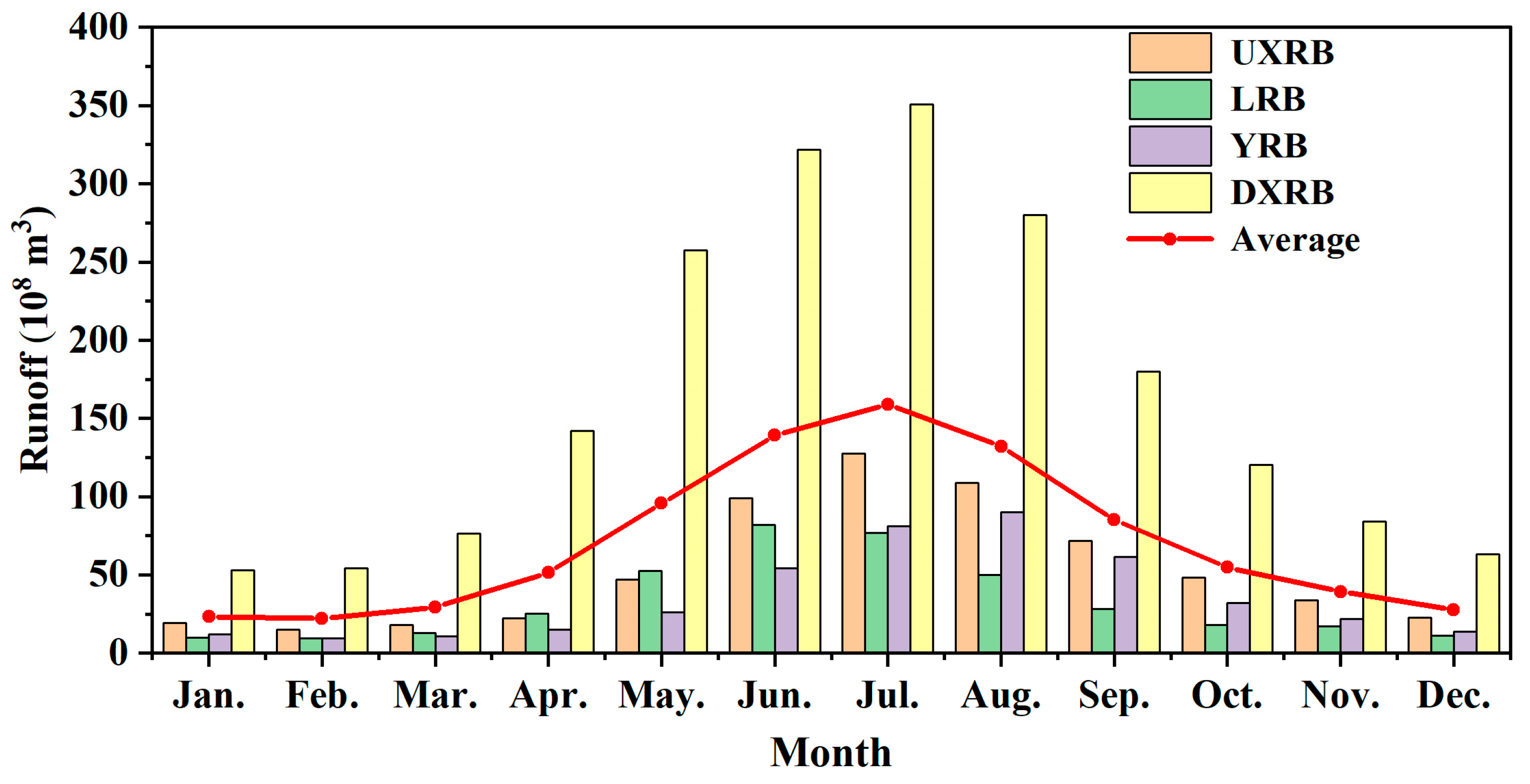
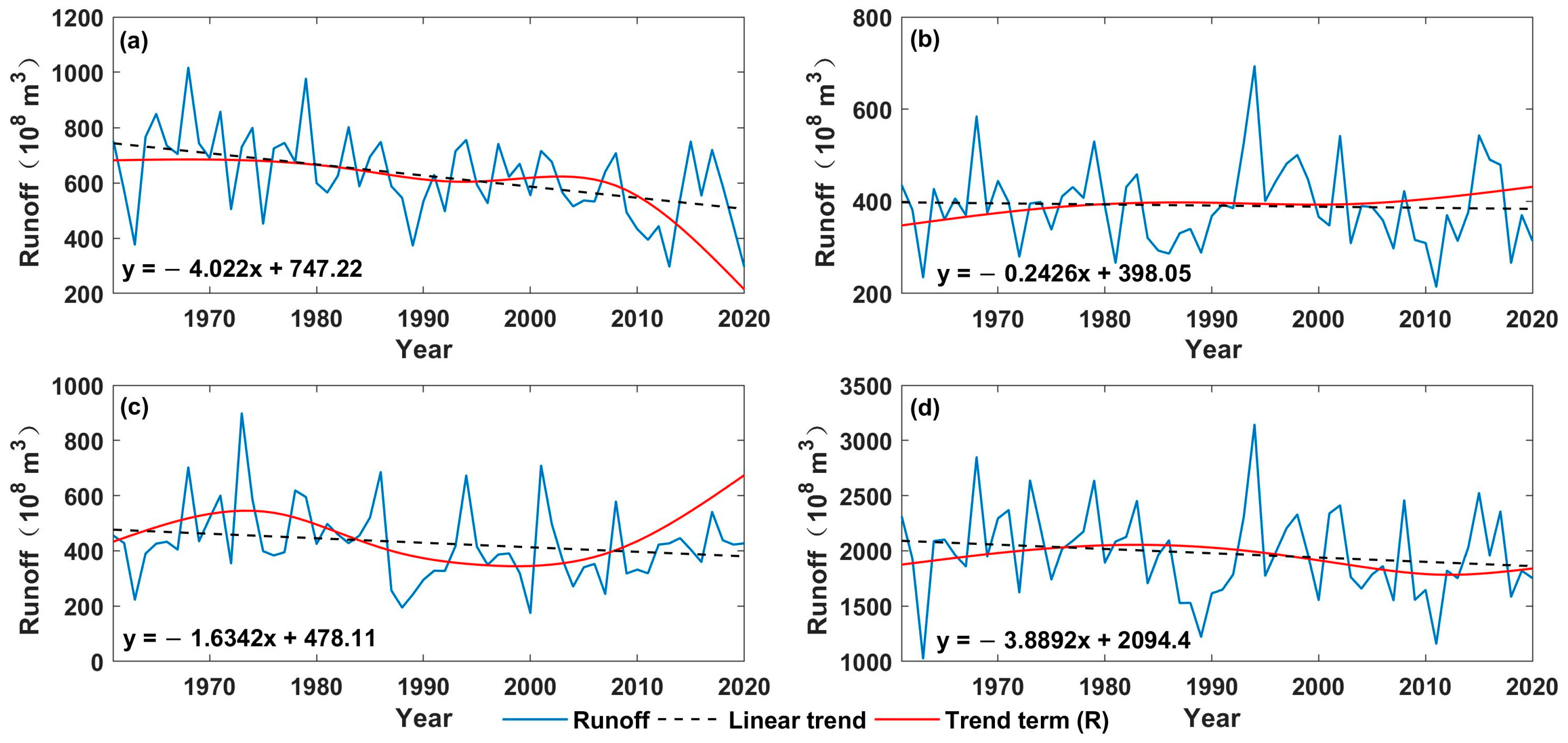
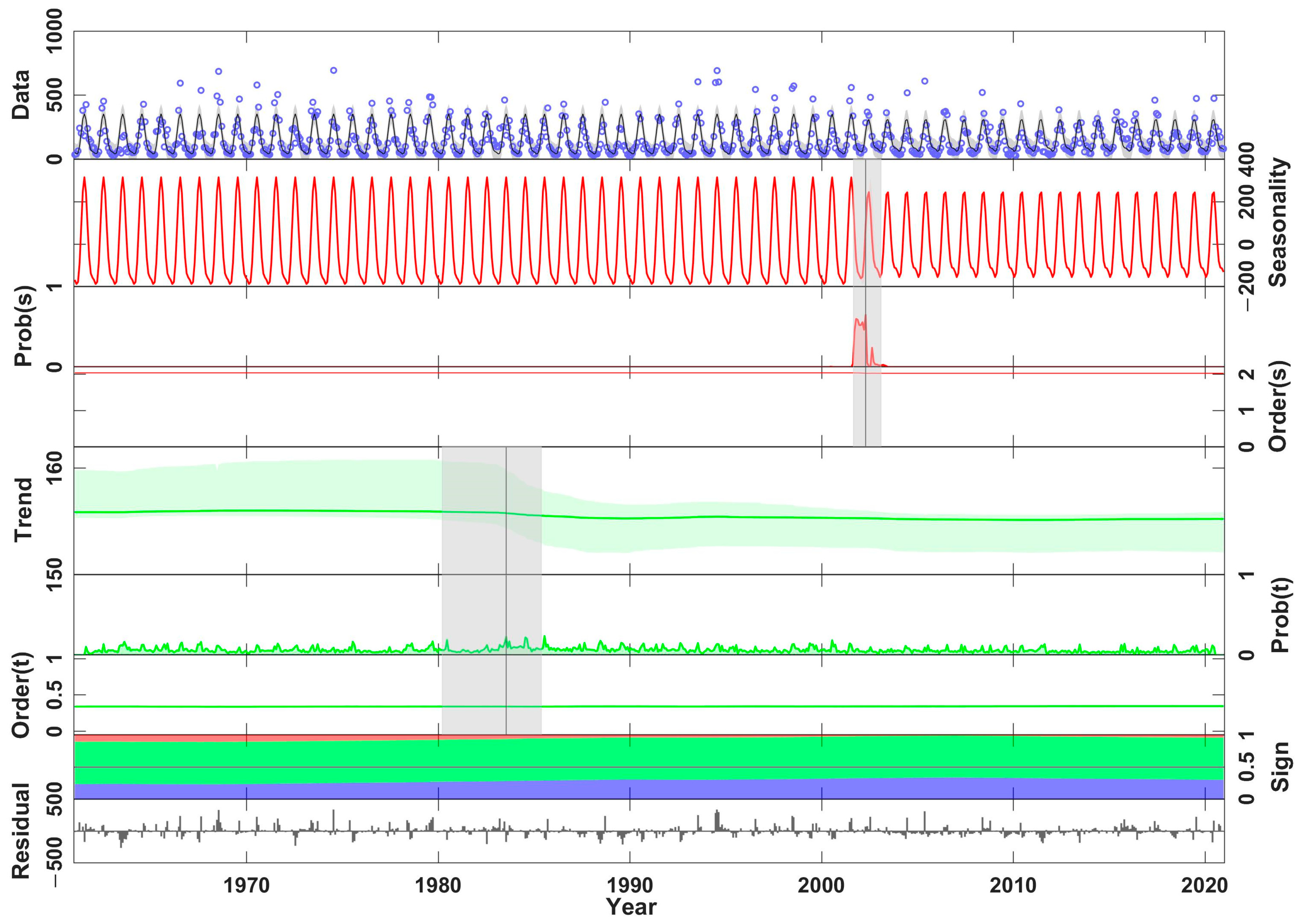
| Name | Date | Temporal Resolution | Spatial Resolution | Reference |
|---|---|---|---|---|
| Runoff | 1961–2020 | monthly | – | Tian et al. [41] |
| Large-scale climate circulation factors | 1961–2020 | monthly | – | Hadad et al. [45] |
| Digital elevation model | 2020 | – | 1 km | Ahmad et al. [47] |
| Land use | 1980–2020 | yearly | 30 m | Yang and Huang [48] |
| Stations Names | Coordinates | Elevation (m) | Period | Temporal Resolution |
|---|---|---|---|---|
| Qianjiang | 23°38′ N, 108°58′ E | 77 | 1961–2020 | monthly |
| Liuzhou | 24°19′ N, 109°24′ E | 101 | 1961–2020 | monthly |
| Guigang | 23°5′ N, 109°37′ E | 48 | 1961–2020 | monthly |
| Wuzhou | 23°29′ N, 111°18′ E | 16 | 1961–2020 | monthly |
| Sub-Basins | Whole Year | Dry Season | Dry-Season Runoff/Whole Year Runoff (%) | ||
|---|---|---|---|---|---|
| Runoff (108 m3) | Coefficient of Variation | Runoff (108 m3) | Coefficient of Variation | ||
| UXRB | 633.32 | 0.23 | 156.42 | 0.27 | 24.7 |
| LRB | 392.33 | 0.23 | 77.67 | 0.33 | 19.8 |
| YRB | 428.39 | 0.32 | 100.15 | 0.34 | 23.4 |
| DXRB | 1982.29 | 0.20 | 450.63 | 0.26 | 22.7 |
| Sub-Basins | IMF Component | IMF1 | IMF2 | IMF3 | IMF4 | R |
|---|---|---|---|---|---|---|
| UXRB | Period (year) | 2.90 | 9.67 | 14.50 | 29.00 | |
| Variance contribution rate (%) | 37.41 | 22.14 | 13.73 | 4.76 | 21.96 | |
| Correlation coefficient | 0.58 ** | 0.42 ** | 0.26 | 0.19 | 0.32 * | |
| LRB | Period (year) | 2.90 | 7.25 | 11.60 | 29.00 | |
| Variance contribution rate (%) | 41.90 | 25.37 | 25.85 | 4.11 | 2.77 | |
| Correlation coefficient | 0.60 ** | 0.43 ** | 0.48 ** | 0.13 | 0.10 | |
| YRB | Period (year) | 3.87 | 8.29 | 29.00 | \ | |
| Variance contribution rate (%) | 39.28 | 36.14 | 9.48 | \ | 15.10 | |
| Correlation coefficient | 0.49 ** | 0.48 ** | 0.14 | \ | 0.38 ** | |
| DXRB | Period (year) | 3.75 | 6.67 | 15.00 | 30.00 | |
| Variance contribution rate (%) | 51.50 | 22.05 | 10.38 | 11.46 | 4.61 | |
| Correlation coefficient | 0.67 ** | 0.42 ** | 0.25 | 0.35 ** | 0.12 |
| Sub-Basins | IMF Component | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | R |
|---|---|---|---|---|---|---|---|
| UXRB | Period (year) | 3.53 | 7.50 | 15.00 | 30.00 | \ | |
| Variance contribution rate (%) | 43.46 | 35.76 | 3.06 | 4.73 | \ | 13.00 | |
| Correlation coefficient | 0.66 ** | 0.40 ** | 0.12 | 0.12 | \ | 0.18 | |
| LRB | Period (year) | 4.29 | 8.57 | 20.00 | \ | \ | |
| Variance contribution rate (%) | 39.12 | 25.84 | 12.28 | \ | \ | 22.76 | |
| Correlation coefficient | 0.39 ** | 0.28 * | 0.28 * | \ | \ | 0.36 ** | |
| YRB | Period (year) | 2.31 | 8.57 | 15.00 | 30.00 | 30.00 | |
| Variance contribution rate (%) | 36.58 | 23.14 | 13.84 | 25.86 | 0.31 | 0.27 | |
| Correlation coefficient | 0.60 ** | 0.45 ** | 0.28 * | 0.49 ** | 0.17 | 0.06 | |
| DXRB | Period (year) | 4.29 | 8.57 | 15.00 | 20.00 | 30.00 | |
| Variance contribution rate (%) | 30.63 | 33.98 | 5.85 | 3.48 | 6.92 | 19.14 | |
| Correlation coefficient | 0.50 ** | 0.31 * | 0.13 | 0.17 | 0.28 * | 0.44 ** |
| Univariate | AWC | POSP (%) | Bivariate | AWC | POSP (%) | Trivariate | AWC | POSP (%) |
|---|---|---|---|---|---|---|---|---|
| ENSO | 0.92 | 12.98 | SSI-ENSO | 0.95 | 18.68 | SSI-ENSO-PDO | 0.97 | 20.13 |
| PDO | 0.92 | 11.47 | SSI-PDO | 0.94 | 15.74 | SSI-ENSO-NAO | 0.94 | 14.63 |
| NAO | 0.90 | 2.43 | SSI-NAO | 0.93 | 10.41 | SSI-ENSO-AO | 0.95 | 15.62 |
| AO | 0.91 | 6.87 | SSI-AO | 0.92 | 8.54 | SSI-ENSO-AMO | 0.95 | 15.48 |
| AMO | 0.91 | 5.03 | SSI-AMO | 0.93 | 11.54 | SSI-ENSO-DMI | 0.95 | 16.21 |
| DMI | 0.91 | 5.64 | SSI-DMI | 0.93 | 10.78 | SSI-ENSO-NPI | 0.96 | 18.67 |
| NPI | 0.92 | 9.67 | SSI-NPI | 0.94 | 14.20 | SSI-ENSO-PNA | 0.95 | 16.78 |
| PNA | 0.92 | 9.45 | SSI-PNA | 0.93 | 9.63 | |||
| SSI | 0.93 | 13.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Men, R.; Yan, S.; Wang, Z.; Lai, H.; Feng, K.; Gao, S.; Li, Y.; Guo, W.; Tian, Q. Identification of the Runoff Evolutions and Driving Forces during the Dry Season in the Xijiang River Basin. Water 2024, 16, 2317. https://doi.org/10.3390/w16162317
Wang F, Men R, Yan S, Wang Z, Lai H, Feng K, Gao S, Li Y, Guo W, Tian Q. Identification of the Runoff Evolutions and Driving Forces during the Dry Season in the Xijiang River Basin. Water. 2024; 16(16):2317. https://doi.org/10.3390/w16162317
Chicago/Turabian StyleWang, Fei, Ruyi Men, Shaofeng Yan, Zipeng Wang, Hexin Lai, Kai Feng, Shikai Gao, Yanbin Li, Wenxian Guo, and Qingqing Tian. 2024. "Identification of the Runoff Evolutions and Driving Forces during the Dry Season in the Xijiang River Basin" Water 16, no. 16: 2317. https://doi.org/10.3390/w16162317
APA StyleWang, F., Men, R., Yan, S., Wang, Z., Lai, H., Feng, K., Gao, S., Li, Y., Guo, W., & Tian, Q. (2024). Identification of the Runoff Evolutions and Driving Forces during the Dry Season in the Xijiang River Basin. Water, 16(16), 2317. https://doi.org/10.3390/w16162317







