Volume-Mediated Lake-Ice Phenology in Southwest Alaska Revealed through Remote Sensing and Survival Analysis
Abstract
1. Introduction
2. Methods
2.1. Study Area
2.2. Ice Phenology Observations
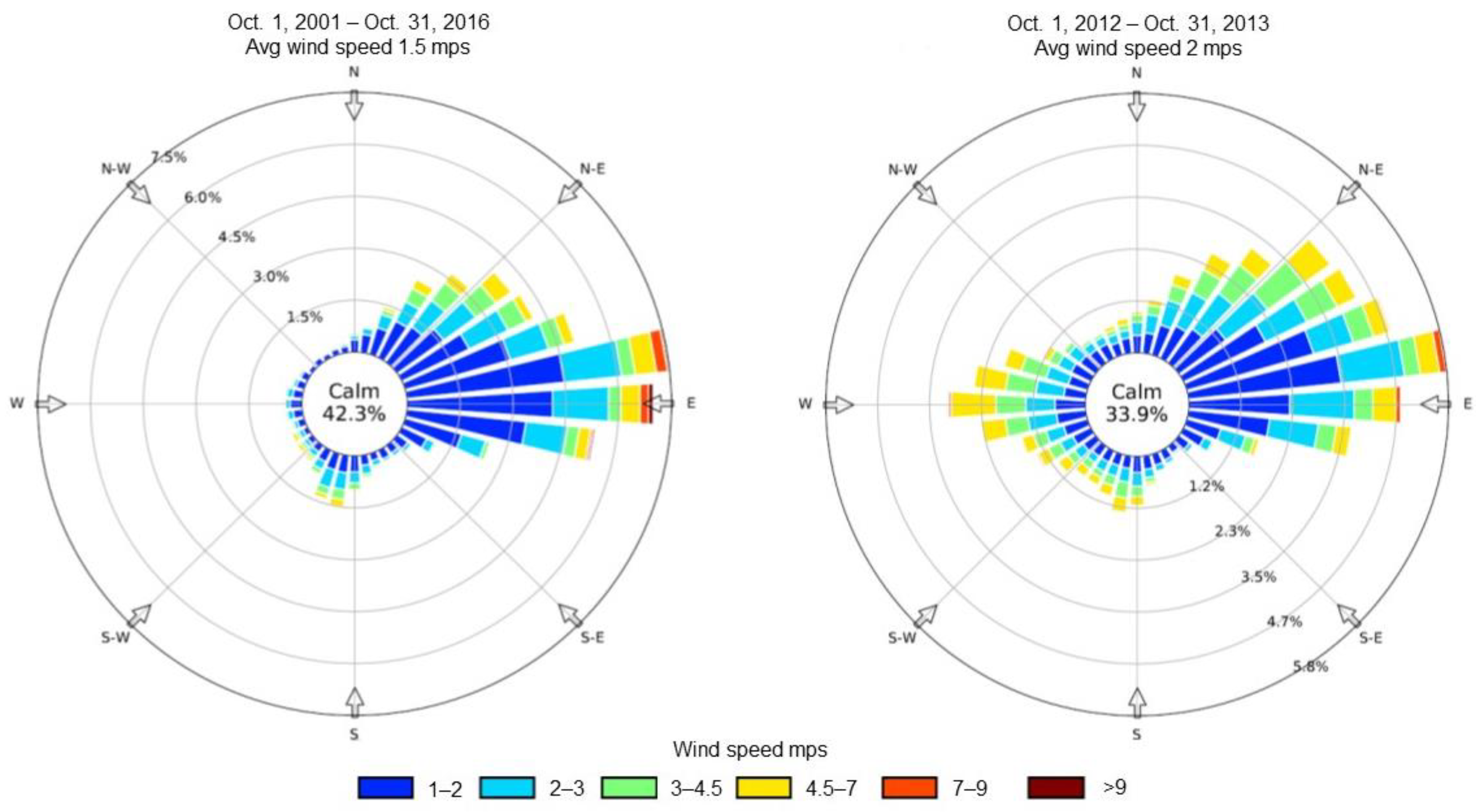
2.3. Meteorologic Data
2.4. Survival Model
3. Results
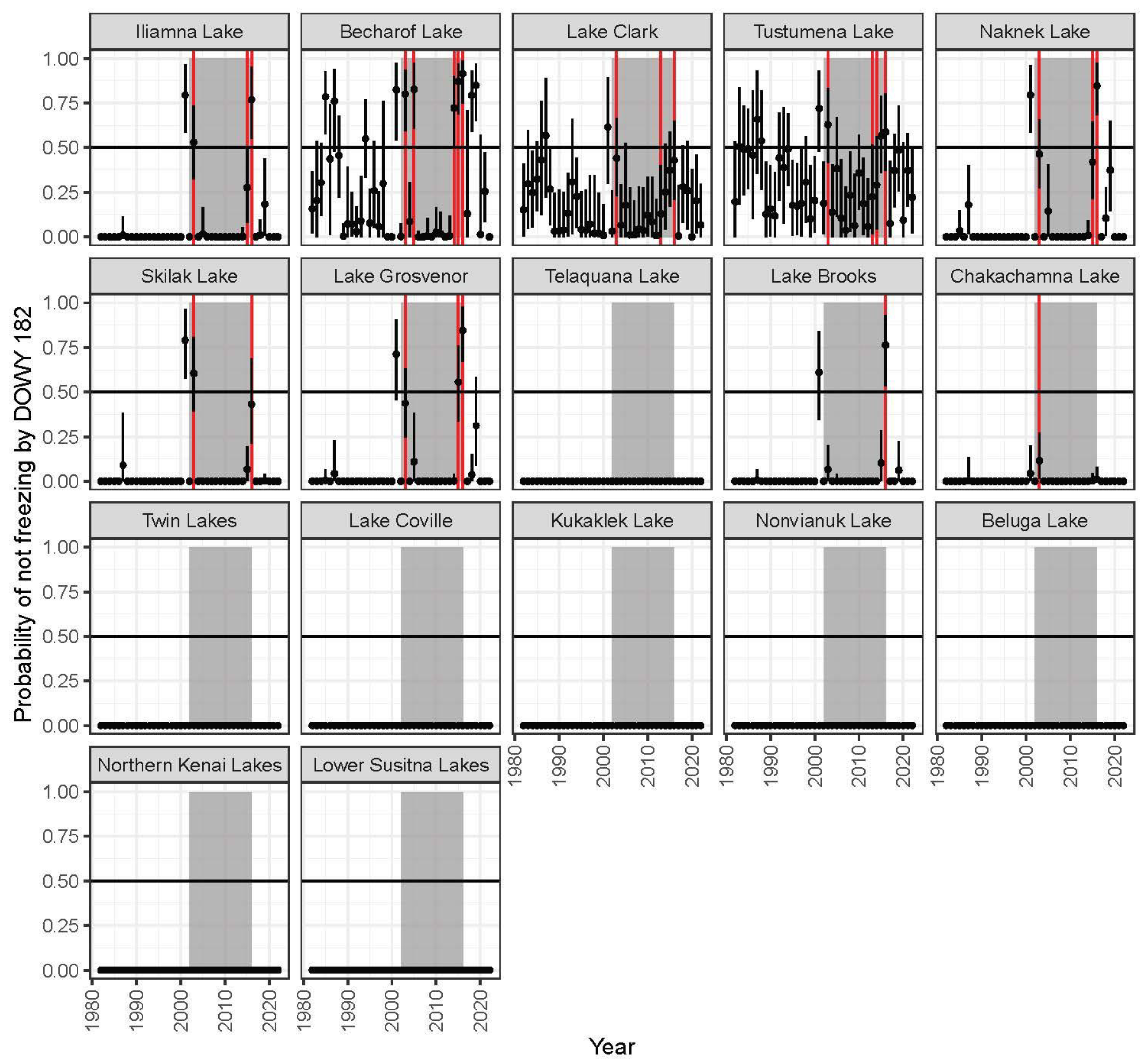
3.1. Satellite Observations
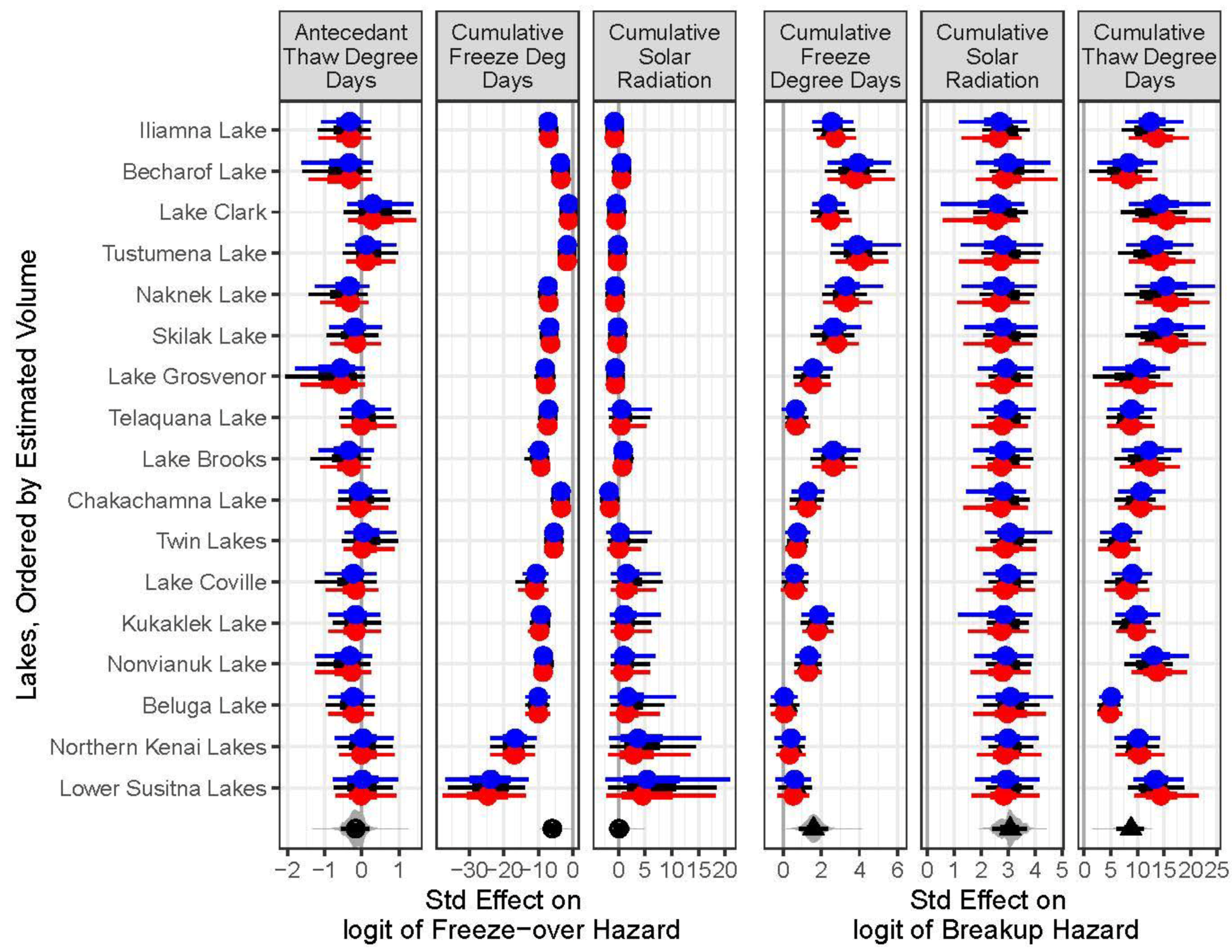
3.2. Survival Model
3.3. Lake Volumes
3.4. Validation against In Situ Observations
3.5. Long-Term Climate Record
4. Discussion
4.1. Variability
4.2. Threshold Response
4.3. Trend
4.4. Future Efforts
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Detailed Model Description
| Parameter | Prior Distribution | Characteristics |
|---|---|---|
| Weakly informative on logit scale | ||
| Weakly informative on logit scale | ||
| for sd |
Appendix B
Observed versus Predicted Figures for Freeze-Over and Breakup
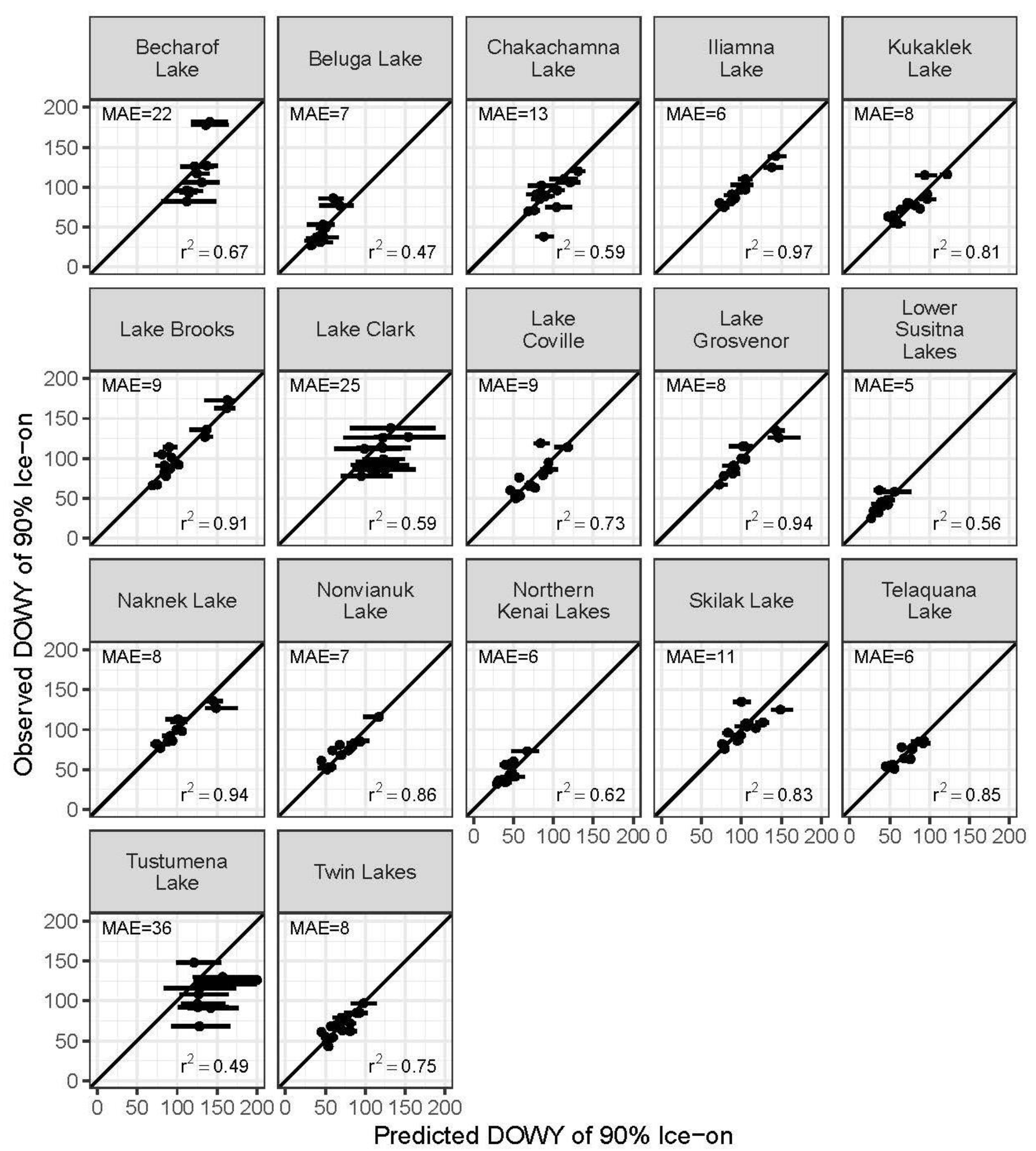

Appendix C
Appendix C.1. Bayesian Prior Sensitivity Analysis
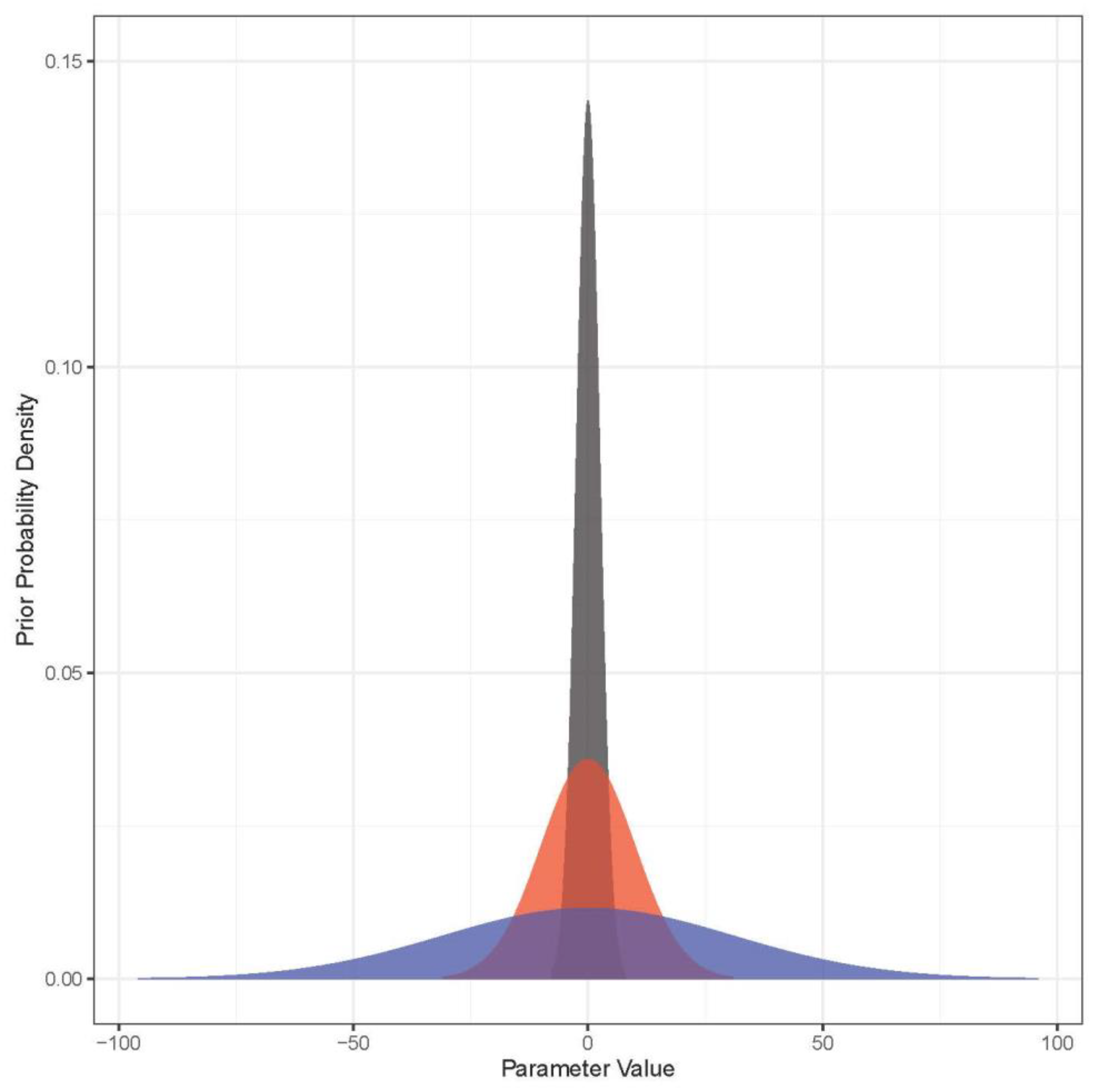
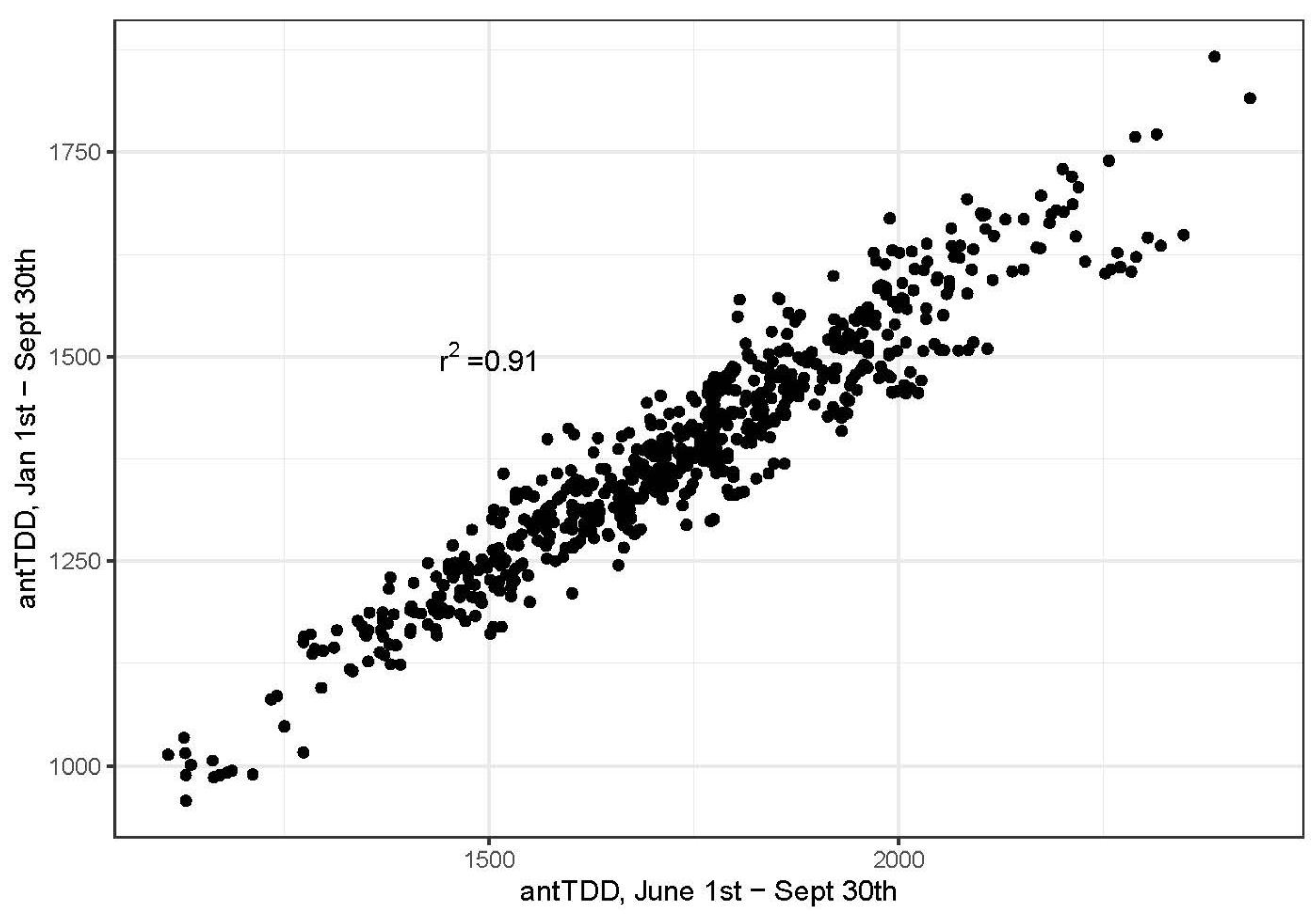
Appendix C.2. Climate Accumulation Periods
References
- Magnuson, J.J.; Robertson, D.M.; Benson, B.J.; Wynne, R.H.; Livingstone, D.M.; Arai, T.; Assel, R.A.; Barry, R.G.; Card, V.; Kuusisto, E.; et al. Historical Trends in Lake and River Ice Cover in the Northern Hemisphere. Science 2000, 289, 1743–1746. [Google Scholar] [CrossRef] [PubMed]
- Newton, A.M.W.; Mullan, D.J. Climate Change and Northern Hemisphere Lake and River Ice Phenology from 1931–2005. Cryosphere 2021, 15, 2211–2234. [Google Scholar] [CrossRef]
- Adrian, R.; Walz, N.; Hintze, T.; Hoeg, S.; Rusche, R. Effects of Ice Duration on Plankton Succession during Spring in a Shallow Polymictic Lake. Freshw. Biol. 1999, 41, 621–634. [Google Scholar] [CrossRef]
- Cai, Y.; Duguay, C.R.; Ke, C.-Q. A 41-Year (1979–2019) Passive-Microwave-Derived Lake Ice Phenology Data Record of the Northern Hemisphere. Earth Syst. Sci. Data 2022, 14, 3329–3347. [Google Scholar] [CrossRef]
- Serreze, M.C.; Francis, J.A. The Arctic Amplification Debate. Clim. Chang. 2006, 76, 241–264. [Google Scholar] [CrossRef]
- Prowse, T.; Alfredsen, K.; Beltaos, S.; Bonsal, B.; Duguay, C.; Korhola, A.; McNamara, J.; Pienitz, R.; Vincent, W.F.; Vuglinsky, V.; et al. Past and Future Changes in Arctic Lake and River Ice. Ambio 2011, 40, 53–62. [Google Scholar] [CrossRef]
- Cohen, J.; Screen, J.A.; Furtado, J.C.; Barlow, M.; Whittleston, D.; Coumou, D.; Francis, J.; Dethloff, K.; Entekhabi, D.; Overland, J.; et al. Recent Arctic Amplification and Extreme Mid-Latitude Weather. Nat. Geosci. 2014, 7, 627–637. [Google Scholar] [CrossRef]
- Woolway, R.I.; Merchant, C.J. Worldwide Alteration of Lake Mixing Regimes in Response to Climate Change. Nat. Geosci. 2019, 12, 271–276. [Google Scholar] [CrossRef]
- Sharma, S.; Blagrave, K.; Magnuson, J.J.; O’Reilly, C.M.; Oliver, S.; Batt, R.D.; Magee, M.R.; Straile, D.; Weyhenmeyer, G.A.; Winslow, L.; et al. Widespread Loss of Lake Ice around the Northern Hemisphere in a Warming World. Nat. Clim. Chang. 2019, 9, 227–231. [Google Scholar] [CrossRef]
- Gaul, K. Nanutset ch’u Q’udi Gu, before Our Time and Now, An Ethnohistory of Lake Clark National Park and Preserve. USDOI, NPS, Lake Clark National Park and Preserve, 179. 2007. Available online: https://nps.gov/lacl/learn/historyculture/upload/Nanutset-Gaul-508.pdf (accessed on 20 October 2023).
- Cold, H.S.; Brinkman, T.J.; Brown, C.L.; Hollingsworth, T.N.; Brown, D.R.N.; Heeringa, K.M. Assessing Vulnerability of Subsistence Travel to Effects of Environmental Change in Interior Alaska. Ecol. Soc. 2020, 25, 20. [Google Scholar] [CrossRef]
- Bogdanova, E.; Lobanov, A.; Andronov, S.V.; Soromotin, A.; Popov, A.; Skalny, A.V.; Shaduyko, O.; Callaghan, T.V. Challenges of Changing Water Sources for Human Wellbeing in the Arctic Zone of Western Siberia. Water 2023, 15, 1577. [Google Scholar] [CrossRef]
- Bengtsson, L.; Herschy, R.W.; Fairbridge, R.W. (Eds.) Ice Formation on Lakes and Ice Growth. In Encyclopedia of Lakes and Reservoirs; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Leppäranta, M. Modelling the Formation and Decay of Lake Ice. In The Impact of Climate Change on European Lakes; George, G., Ed.; Springer Science & Business Media: Dordrecht, The Netherlands, 2009; Volume 4. [Google Scholar]
- Leppäranta, M. Ice Phenology and Thickness Modelling for Lake Ice Climatology. Water 2023, 15, 2951. [Google Scholar] [CrossRef]
- Kirillin, G.; Leppäranta, M.; Terzhevik, A.; Granin, N.; Bernhardt, J.; Engelhardt, C.; Efremova, T.; Golosov, S.; Palshin, N.; Sherstyankin, P.; et al. Physics of Seasonally Ice-Covered Lakes: A Review. Aquat. Sci. 2012, 74, 659–682. [Google Scholar] [CrossRef]
- Launiainen, J.; Cheng, B. Modelling of Ice Thermodynamics in Natural Water Bodies. Cold Reg. Sci. Technol. 1998, 27, 153–178. [Google Scholar] [CrossRef]
- Brown, L.C.; Duguay, C.R. A Comparison of Simulated and Measured Lake Ice Thickness Using a Shallow Water Ice Profiler. Hydrol. Process. 2011, 25, 2932–2941. [Google Scholar] [CrossRef]
- Rafat, A.; Pour, H.K.; Spence, C.; Palmer, M.J.; MacLean, A. An Analysis of Ice Growth and Temperature Dynamics in Two Canadian Subarctic Lakes. Cold Reg. Sci. Technol. 2023, 210, 103808. [Google Scholar] [CrossRef]
- Golub, M.; Thiery, W.; Marcé, R.; Pierson, D.; Vanderkelen, I.; Mercado, D.; Woolway, R.I.; Grant, L.; Jennings, E.; Schewe, J.; et al. A framework for ensemble modelling of climate change impacts on lakes worldwide: The ISIMIP Lake Sector. Geosci. Model Dev. Discuss. 2022, 15, 4597–4623. [Google Scholar] [CrossRef]
- Wynne, R.H. Statistical Modeling of Lake Ice Phenology: Issues and Implications. SIL Proc. 2000, 27, 2820–2825. [Google Scholar] [CrossRef]
- Preston, D.L.; Caine, N.; McKnight, D.M.; Williams, M.W.; Hell, K.; Miller, M.P.; Hart, S.J.; Johnson, P.T.J. Climate Regulates Alpine Lake Ice Cover Phenology and Aquatic Ecosystem Structure. Geophys. Res. Let. 2016, 43, 5353–5360. [Google Scholar] [CrossRef]
- Beyene, M.T.; Jain, S.; Gupta, R.C. Linear-Circular Statistical Modeling of Lake Ice-Out Dates. Water Resour. Res. 2018, 54, 7841–7858. [Google Scholar] [CrossRef]
- Terres, M.A.; Gelfand, A.E.; Allen, J.M.; Silander, J.A. Analyzing First Flowering Event Data Using Survival Models with Space and Time-varying Covariates. Environmetrics 2013, 24, 317–331. [Google Scholar] [CrossRef]
- Diez, J.M.; Pulliam, H.R. Hierarchical Analysis of Species Distributions and Abundance Across Environmental Gradients. Ecology 2007, 88, 3144–3152. [Google Scholar] [CrossRef] [PubMed]
- Elmendorf, S.C.; Crimmins, T.M.; Gerst, K.L.; Weltzin, J.F. Time to Branch out? Application of Hierarchical Survival Models in Plant Phenology. Agric. For. Meteorol. 2019, 279, 107694. [Google Scholar] [CrossRef]
- USGS Publications Warehouse, 1992, 1:2,000,000-Scale Digital Line Graph (DLG) Data. Available online: https://pubs.usgs.gov/publication/ds4 (accessed on 30 July 2009).
- McCabe, S.; Bartz, K.; Young, D.; Gabriel, P. GIS bathymetry of selected southwest Alaska Lakes, from field measurements. In GIS Data Layer, in Preparation; National Park Service Southwest Alaska Inventory and Monitoring Network: Anchorage, AK, USA, 2024. [Google Scholar]
- U.S. Bureau of Reclamation. Chakachamna Project, Alaska Status Report; Alaska District Office: Juneau, AK, USA, 1962; 21p. [Google Scholar]
- Spafard, M.A.; Edmonson, J.A. A Morphometric Atlas of Alaskan Lakes: Cook Inlet, Prince William Sound, and Bristol Bay Areas; Alaska Department of Fish and Game, Commercial Fisheries Division: Anchorage, AK, USA, 2000. Available online: www.adfg.alaska.gov/fedaidpdfs/RIR.2A.2000.23.pdf (accessed on 20 June 2024).
- Hollister, J.; Milstead, W.B. Using GIS to Estimate Lake Volume from Limited Data. Lake Reserv. Manag. 2010, 26, 194–199. [Google Scholar] [CrossRef]
- Reed, B.; Budde, M.; Spencer, P.; Miller, A.E. Integration of MODIS-Derived Metrics to Assess Interannual Variability in Snowpack, Lake Ice, and NDVI in Southwest Alaska. Remote Sens. Environ. 2009, 113, 1443–1452. [Google Scholar] [CrossRef]
- Verrier, M.; Shepherd, T.; Spencer, P.; Lindsay, C.; Kirchner, P. Southwest Alaska Remote Sensing Lake Ice Phenology for 17 Lakes and Lake Clusters for 2002–2016 Water Years; National Park Service—Southwest Alaska Inventory and Monitoring Network: Anchorage, AK, USA, 2024. [Google Scholar] [CrossRef]
- Thorton, M.M.; Shrestha, R.; Wei, Y.; Thornton, P.E.; Kao, S.-C.; Wilson, B.E. Daymet: Daily Surface Weather Data on a 1-km Grid for North America, Version 4R1; ORNL DAAC: Oak Ridge, TN, USA, 2022. [Google Scholar] [CrossRef]
- Plummer, M. JAGS Version 4.3.0 User Manual 2017, 73. Available online: https://sourceforge.net/projects/mcmc-jags/ (accessed on 20 September 2023).
- Kellner, K. jagsUI: A Wrapper around “rjags” to Streamline “JAGS” Analyses 2018. Available online: https://CRAN.R-project.org/package=jagsUI (accessed on 1 April 2024).
- Kay, M. Tidybayes: Tidy Data and Geoms for Bayesian Models 2022. Available online: https://mjskay.github.io/tidybayes/ (accessed on 1 April 2024).
- R Core Team. R: A Language and Environment for Statistical Computing 2019. Available online: https://R-project.org/ (accessed on 20 September 2023).
- Gelman, A.; Rubin, D.B. Inference from Iterative Simulation Using Multiple Sequences. Stat. Sci. 1992, 7, 457–511. [Google Scholar] [CrossRef]
- Gelman, A.; Goodrich, B.; Gabry, J.; Vehtari, A. R-Squared for Bayesian Regression Models. Am. Stat. 2019, 73, 307–309. [Google Scholar] [CrossRef]
- Nakagawa, S.; Schielzeth, H. A General and Simple Method for Obtaining R2 from Generalized Linear Mixed-effects Models. Methods Ecol. Evol. 2012, 4, 133–142. [Google Scholar] [CrossRef]
- Eggleston, K. xmACIS Version 1.0.69a, NOAA Northeast Regional Climate Center Released 4-Dec-2023. Available online: https://xmacis.rcc-acis.org (accessed on 1 May 2023).
- Zhang, S.; Pavelsky, T.M. Remote Sensing of Lake Ice Phenology across a Range of Lakes Sizes, ME, USA. Remote Sens. 2019, 11, 1718. [Google Scholar] [CrossRef]
- Tuttle, S.E.; Roof, S.R.; Retelle, M.J.; Werner, A.; Gunn, G.E.; Bunting, E.L. Evaluation of Satellite-Derived Estimates of Lake Ice Cover Timing on Linnévatnet, Kapp Linné, Svalbard Using In-Situ Data. Remote Sens. 2022, 14, 1311. [Google Scholar] [CrossRef]
- Bartz, K.; Gabriel, P. Lake Temperature Monitoring in Southwest Alaska Parks: A Synthesis of Year-Round, Multi-Depth Data from 2006 through 2018; National Park Service: Fort Collins, CO, USA, 2020. [Google Scholar] [CrossRef]
- Ashton, G.D. Lake Ice Decay. Cold Reg. Sci. Technol. 1983, 8, 83–86. [Google Scholar] [CrossRef]
- Ashton, G.D. River and Lake Ice Thickening, Thinning, and Snow Ice Formation. Cold Reg. Sci. Technol. 2011, 68, 3–19. [Google Scholar] [CrossRef]
- Woolway, R.I.; Albergel, C.; Frölicher, T.L.; Perroud, M. Severe Lake Heatwaves Attributable to Human-Induced Global Warming. Geophys. Res. Lett. 2022, 49, e2021GL097031. [Google Scholar] [CrossRef]
- Zhou, J.; Leavitt, P.R.; Rose, K.C.; Wang, X.; Zhang, Y.; Shi, K.; Qin, B. Controls of Thermal Response of Temperate Lakes to Atmospheric Warming. Nat. Commun. 2023, 14, 6503. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.; Thorne, P.; Banzon, V.; Boyer, T.; Chepurin, G.; Lawrimore, J.; Menne, J.; Smith, T.; Vose, S.; Zhang, H. NOAA Extended Reconstructed Sea Surface Temperature (ERSST), Version 5. NOAA National Centers for Environmental Information. 2017. Available online: https://ncei.noaa.gov/access/ (accessed on 29 December 2023).
- Hartmann, B.; Wendler, G. The Significance of the 1976 Pacific Climate Shift in the Climatology of Alaska. J. Clim. 2005, 18, 4824–4839. [Google Scholar] [CrossRef]
- Litzow, M.A.; Mueter, F.J. Assessing the Ecological Importance of Climate Regime Shifts: An Approach from the North Pacific Ocean. Prog. Oceanogr. 2014, 120, 110–119. [Google Scholar] [CrossRef]
- Danielson, S.L.; Hennon, T.D.; Monson, D.H.; Suryan, R.M.; Campbell, R.W.; Baird, S.J.; Holderied, K.; Weingartner, T.J. Temperature Variations in the Northern Gulf of Alaska across Synoptic to Century-Long Time Scales. Deep-sea Research. Part 2. Topical Studies in Oceanography/Deep Sea Research. Part II Top. Stud. Oceanogr. 2022, 203, 105155. [Google Scholar] [CrossRef]
- Benson, B.J.; Magnuson, J.J.; Jacob, R.L.; Fuenger, S.L. Response of Lake Ice Breakup in the Northern Hemisphere to the 1976 Interdecadal Shift in the North Pacific. Verh. Int. Ver. Theor. Angew. Limnol. 2000, 27, 2770–2774. [Google Scholar] [CrossRef]
- Robertson, D.M.; Wynne, R.H.; Chang, W.Y.B. Influence of El Niño on Lake and River Ice Cover in the Northern Hemisphere from 1900 to 1995. Verh. Int. Ver. Theor. Angew. Limnol. 2000, 27, 2784–2788. [Google Scholar] [CrossRef]
- Benson, B.J.; Magnuson, J.J.; Jensen, O.P.; Card, V.M.; Hodgkins, G.; Korhonen, J.; Livingstone, D.M.; Stewart, K.M.; Weyhenmeyer, G.A.; Granin, N.G. Extreme Events, Trends, and Variability in Northern Hemisphere Lake-Ice Phenology (1855–2005). Clim. Chang. 2011, 112, 299–323. [Google Scholar] [CrossRef]
- Dauginis, A.A.; Brown, L.C. Recent Changes in Pan-Arctic Sea Ice, Lake Ice, and Snow-on/off Timing. Cryosphere 2021, 15, 4781–4805. [Google Scholar] [CrossRef]
- Dibike, Y.; Prowse, T.; Saloranta, T.; Ahmed, R. Response of Northern Hemisphere Lake-ice Cover and Lake-water Thermal Structure Patterns to a Changing Climate. Hydrol. Process. 2011, 25, 2942–2953. [Google Scholar] [CrossRef]
- Weyhenmeyer, G.A.; Livingstone, D.M.; Meili, M.; Jensen, O.; Benson, B.; Magnuson, J.J. Large Geographical Differences in the Sensitivity of Ice-Covered Lakes and Rivers in the Northern Hemisphere to Temperature Changes. Global Chang. Biol. 2010, 17, 268–275. [Google Scholar] [CrossRef]
- Wang, X.; Feng, L.; Qi, W.; Cai, X.; Zheng, Y.; Gibson, L.; Tang, J.; Song, X.; Liu, J.; Zheng, C.; et al. Continuous Loss of Global Lake Ice Across Two Centuries Revealed by Satellite Observations and Numerical Modeling. Geophys. Res. Lett. 2022, 49, e2022GL099022. [Google Scholar] [CrossRef]
- Warren, K.; Margaret, W. U.S. Fish & Wildlife Service, Region 7, Water Resources Branch, Egegik River/Becharof Lake Watershed Navigability Research Report, October 1997. Available online: https://dnr.alaska.gov/mlw/paad/nav/rdi/gegik_becharof/becharof_draft_report.pdf (accessed on 21 February 2024).
- Lindsay, C.; Zhu, J.; Miller, A.E.; Kirchner, P.; Wilson, T.L. Deriving Snow Cover Metrics for Alaska from MODIS. Remote Sens. 2015, 7, 12961–12985. [Google Scholar] [CrossRef]
- LaPerriere, J.D. Limnological Monitoring of Lake Becharof, Final Report to the U.S. Fish and Wildlife Service, Research Work Order 58, Alaska Cooperative Fish and Wildlife Research Unit April l998. Available online: https://ecos.fws.gov/ServCat/DownloadFile/108087 (accessed on 15 February 2024).
- Gelman, A.; Jakulin, A.; Pittau, M.G.; Su, Y.S. A Weakly Informative Default Prior Distribution for Logistic and Other Regression Models. Ann. Appl. Stat. 2008, 2, 1360–1383. [Google Scholar] [CrossRef]



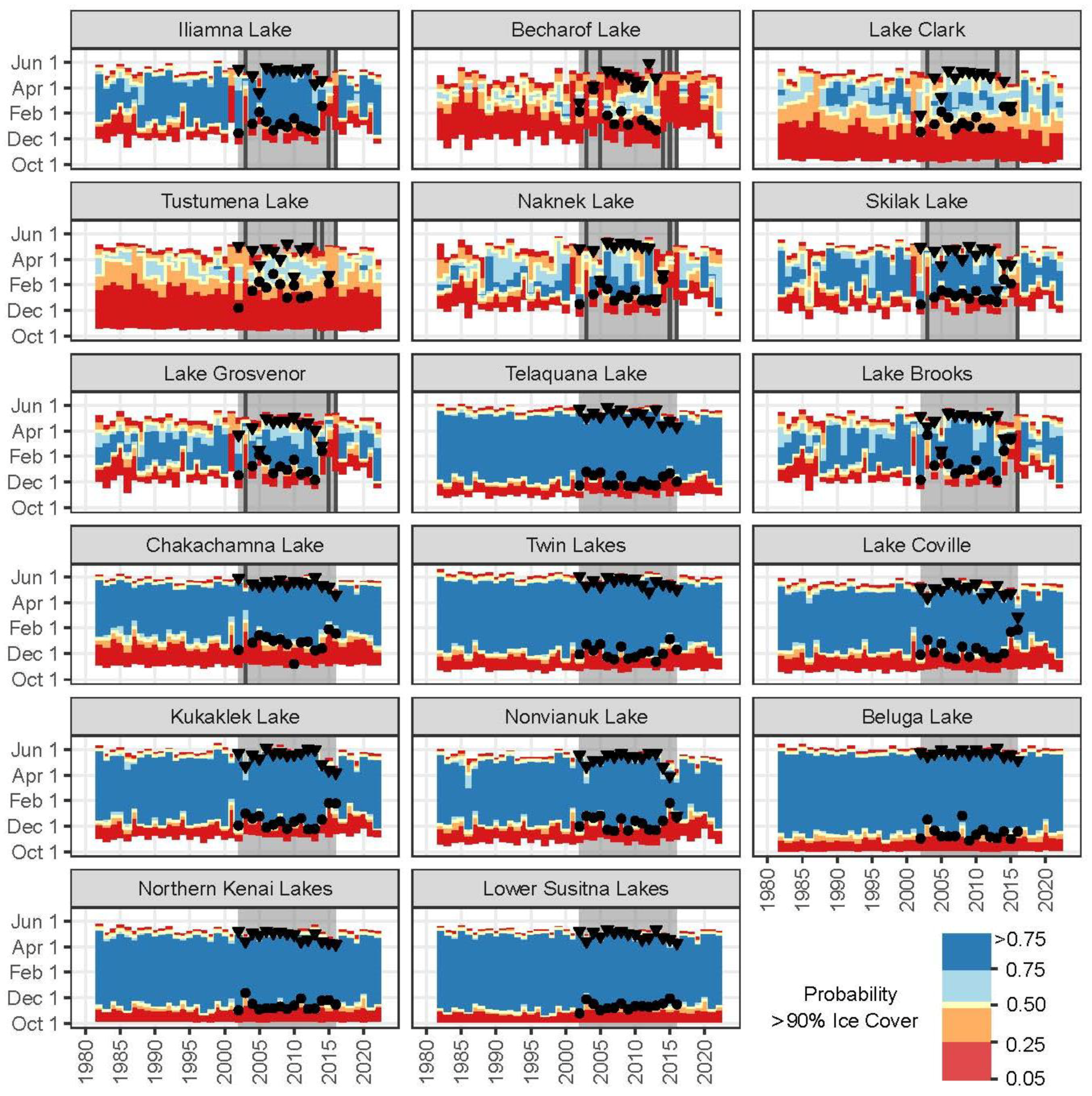
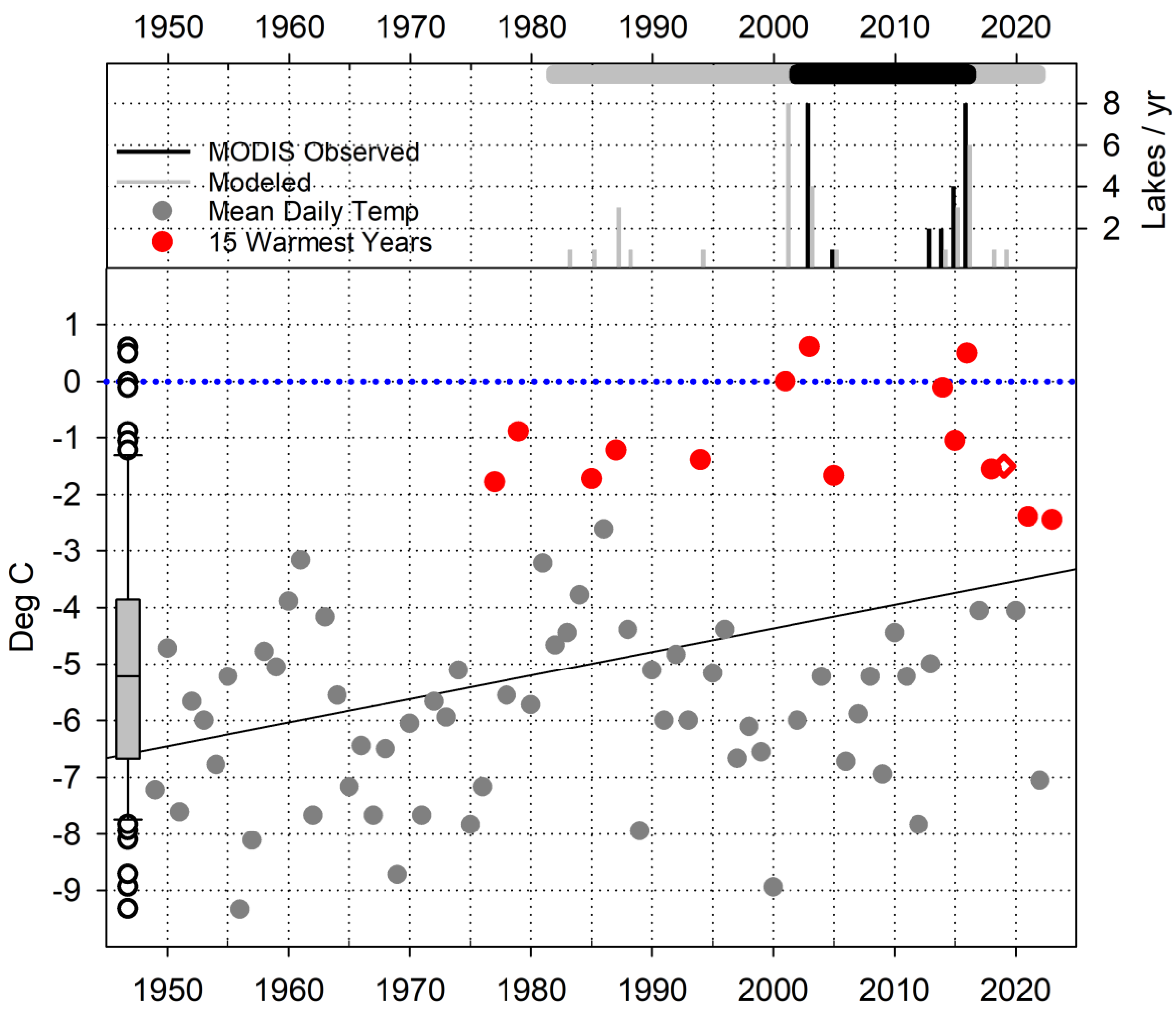
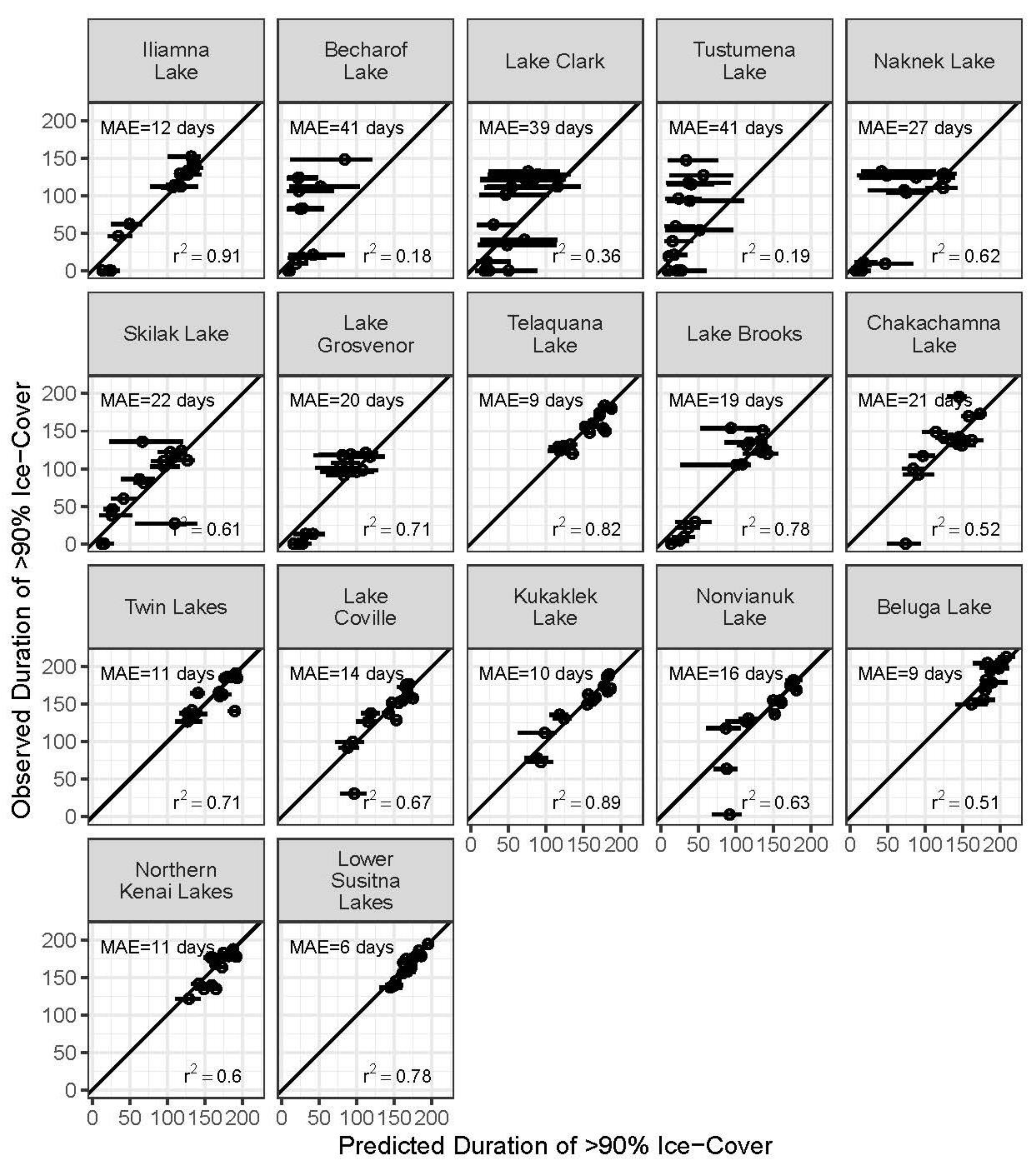
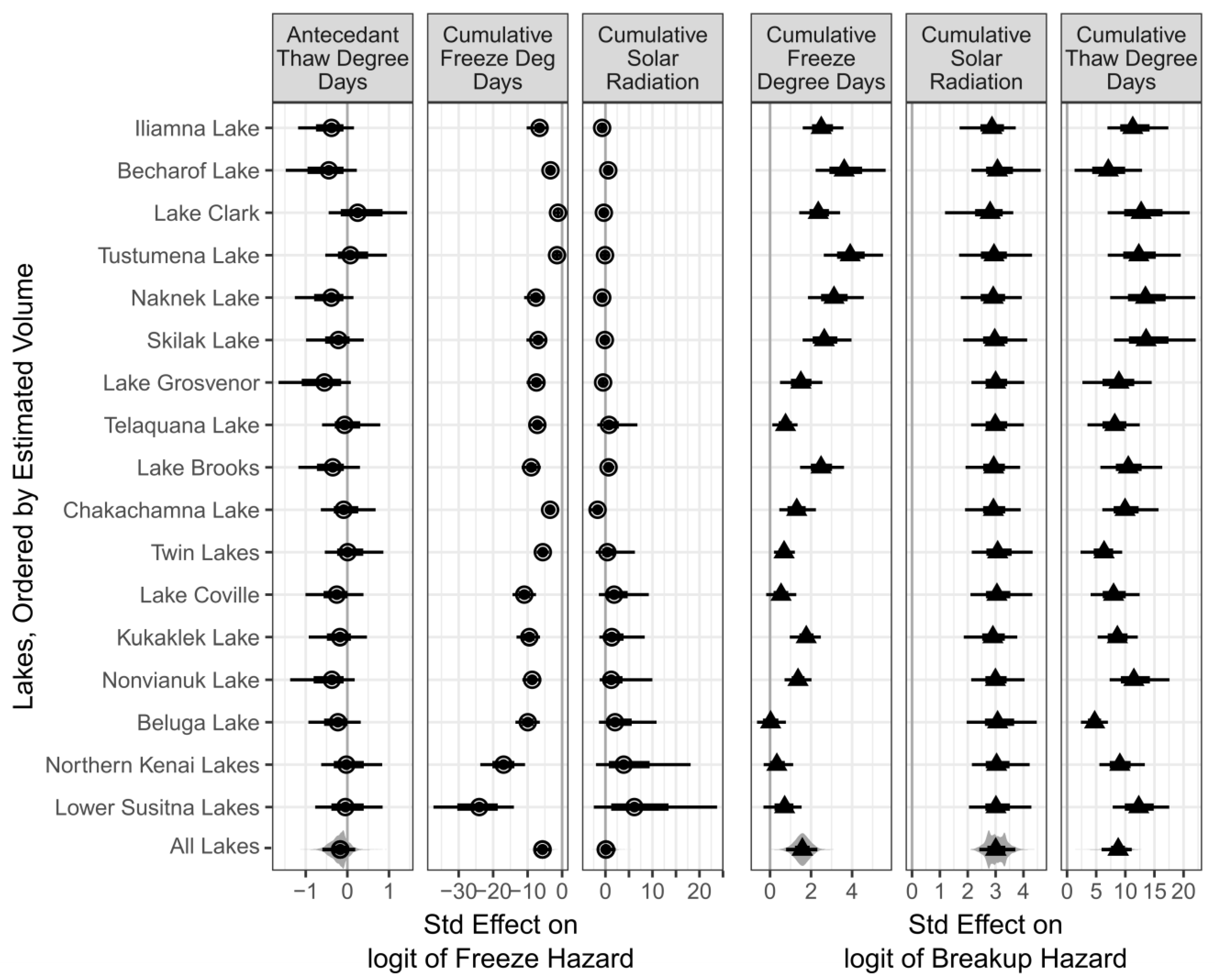

| Lake A | Area km2 | Lake Elev. m | Max. Depth m B | Conical Volume est. km3 | Known Volumes km3 | No-Freeze Years n = 15 MODIS C | No-Freeze Years n = 40 Model D | Duration Trend Days/Year E | MAD Days F | RMAD G |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 Iliamna Lake | 2637 | 11 | 301 | 264.58 | 115.3 | 3 | 6 | −0.5 * [−0.8,−0.2] | 40 | 0.43 |
| 2 Becharof Lake | 1195 | 4 | 92 | 36.65 | 44.0 | 5 | 11 | 0.2 * [0.0,0.6] | 31 | 0.57 |
| 3 Lake Clark | 336 | 75 | 266 | 29.79 | 32.3 | 3 | 3 | 0.2 [−0.8,0.8] | 46 | 0.63 |
| 4 Tustumena Lake | 298 | 34 | 290 | 28.81 | - | 4 | 11 | 0.2 [−0.4,0.9] | 80 | 1.35 |
| 5 Naknek Lake | 458 | 13 | 160 | 24.43 | - | 4 | 6 | 0.2 [−0.1,0.5] | 33 | 0.44 |
| 6 Skilak Lake | 99 | 58 | 174 | 5.74 | 7.2 | 2 | 2 | −0.1 [−0.1,−0.4] | 53 | 0.69 |
| 7 Lake Grosvenor | 73 | 35 | 112 | 2.73 | - | 3 | 3 | −0.2 [−0.2,−0.4] | 30 | 0.40 |
| 8 Telaquana Lake | 48 | 376 | 132 | 2.11 | 2.9 | 0 | 0 | −0.5 * [−0.7,−0.1] | 23 | 0.21 |
| 9 Lake Brooks | 75 | 20 | 82 | 2.05 | - | 1 | 2 | 0.0 [−0.3,0.4] | 25 | 0.28 |
| 10 Chakachamna | 74 | 346 | 80 | 1.97 | - | 1 | 0 | −0.1 [−0.8,0.4] | 15 | 0.11 |
| 11 Twin Lakes | 27 | 601 | 103 | 0.93 | - | 0 | 0 | −0.5 * [−0.8,−0.2] | 33 | 0.20 |
| 12 Lake Coville | 33 | 35 | 62 | 0.68 | - | 0 | 0 | −0.6 * [−0.7,−0.3] | 31 | 0.23 |
| 13 Kukaklek Lake | 173 | 247 | - | - | - | 0 | 0 | −0.6 * [−0.7,−0.4] | 20 | 0.23 |
| 14 Nonvianuk Lake | 133 | 191 | - | - | - | 0 | 0 | −0.6 * [−0.7,−0.4] | 34 | 0.24 |
| 15 Beluga Lake | 44 | 75 | - | - | - | 0 | 0 | −0.3 * [−0.5,−0.2] | 10 | 0.06 |
| 16 Northern Kenai | 88 | 60 | - | - | - | 0 | 0 | −0.3 * [−0.5,−0.1] | 16 | 0.10 |
| 17 Lower Susitna | 61 | 39 | - | - | - | 0 | 0 | −0.6 * [−0.9,−0.3] | 15 | 0.09 |
| Lake | Validation Data A | Years B | Model Correlation | Mean Duration Obs. | Mean Duration Model | SD Obs. | SD Model | n Years | Conical Volume Estimate | Ranking by Proxy Volume |
|---|---|---|---|---|---|---|---|---|---|---|
| Lake Clark | T, Array, 100 m | 2006–2022 | 0.84 | 60 | 60 | 47 | 27 | 16 | 29.79 | 3 |
| Naknek Lake | T, Array, 70 m | 2008–2022 | 0.89 | 87 | 74 | 45 | 47 | 14 | 24.43 | 5 |
| Telaquana Lake | Ice obs. | 2002–2020 * | 0.85 | 150 | 157 | 21 | 21 | 12 | 2.73 | 7 |
| Lake Brooks | T, Array, 50 m | 2010–2022 | 0.83 | 73 | 77 | 46 | 44 | 12 | 2.05 | 9 |
| Twin Lakes | Ice obs. | 1982–1996 * | 0.95 | 177 | 172 | 17 | 12 | 14 | 0.93 | 11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kirchner, P.B.; Hannam, M.P. Volume-Mediated Lake-Ice Phenology in Southwest Alaska Revealed through Remote Sensing and Survival Analysis. Water 2024, 16, 2309. https://doi.org/10.3390/w16162309
Kirchner PB, Hannam MP. Volume-Mediated Lake-Ice Phenology in Southwest Alaska Revealed through Remote Sensing and Survival Analysis. Water. 2024; 16(16):2309. https://doi.org/10.3390/w16162309
Chicago/Turabian StyleKirchner, Peter B., and Michael P. Hannam. 2024. "Volume-Mediated Lake-Ice Phenology in Southwest Alaska Revealed through Remote Sensing and Survival Analysis" Water 16, no. 16: 2309. https://doi.org/10.3390/w16162309
APA StyleKirchner, P. B., & Hannam, M. P. (2024). Volume-Mediated Lake-Ice Phenology in Southwest Alaska Revealed through Remote Sensing and Survival Analysis. Water, 16(16), 2309. https://doi.org/10.3390/w16162309










