Numerical Simulation Study on Three-Dimensional Flow Characteristics and Probability Density Distribution of Water-Permeable Gabion Backflow Zone in Different Curvature Bends
Abstract
:1. Introduction
2. Methods
2.1. Physical Model
2.2. Mathematical Model
2.2.1. Continuity Equation and Momentum Equation
2.2.2. Turbulence Model
2.3. Boundary Conditions and Solution Setup
2.4. Model Validation
3. Results Analysis
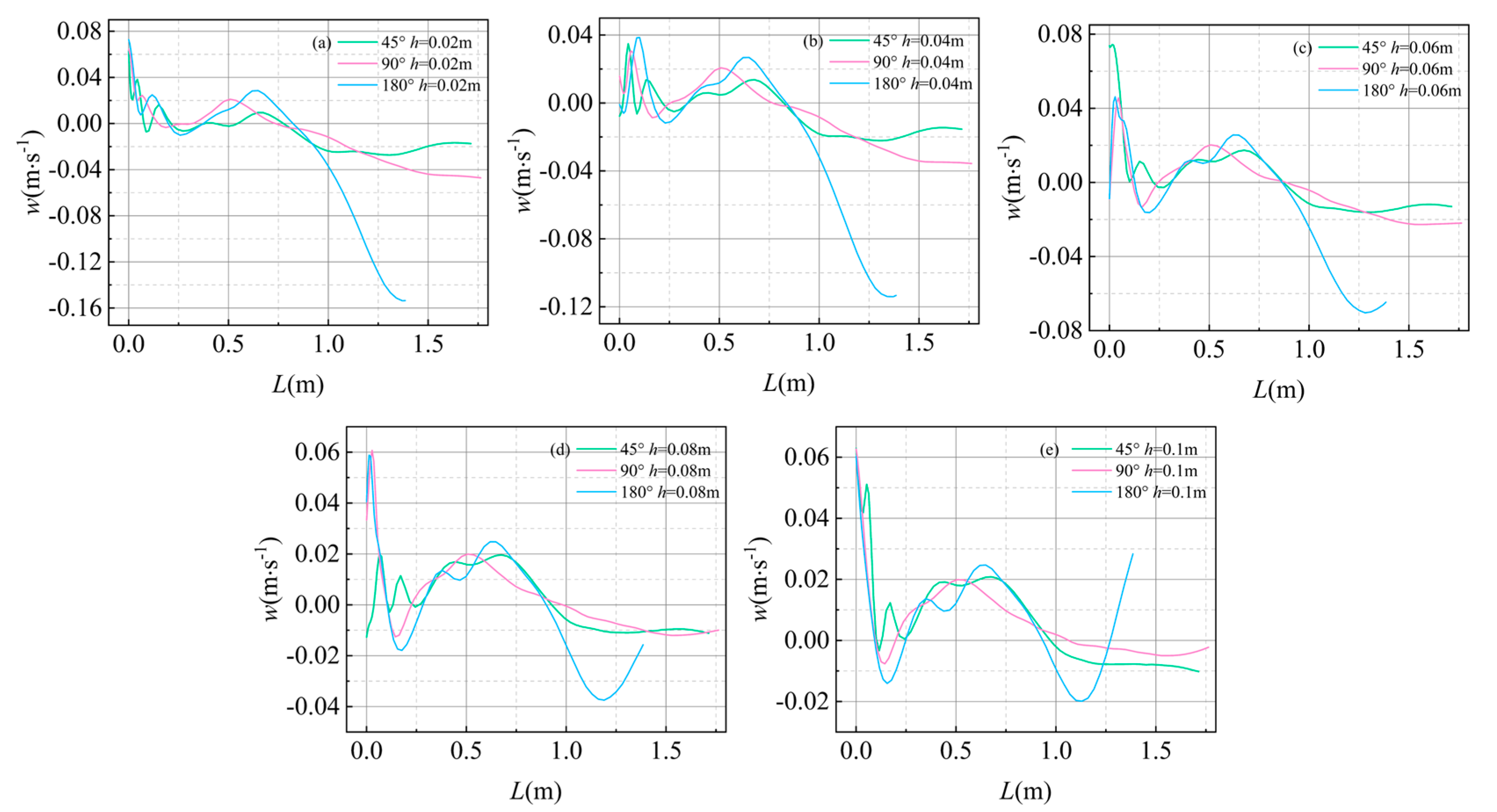
3.1. Velocity Distribution along the Axis of the Recirculation Zone
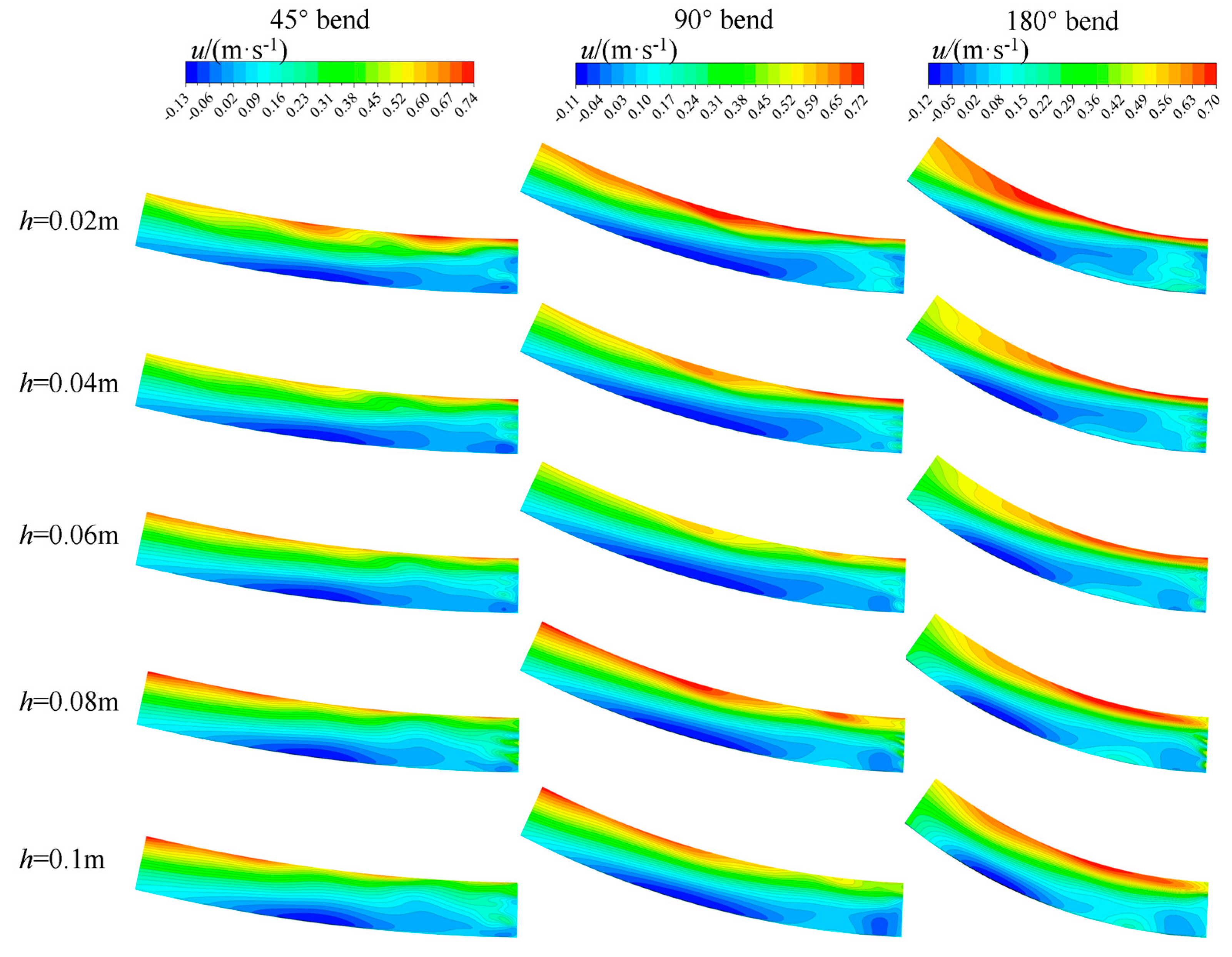
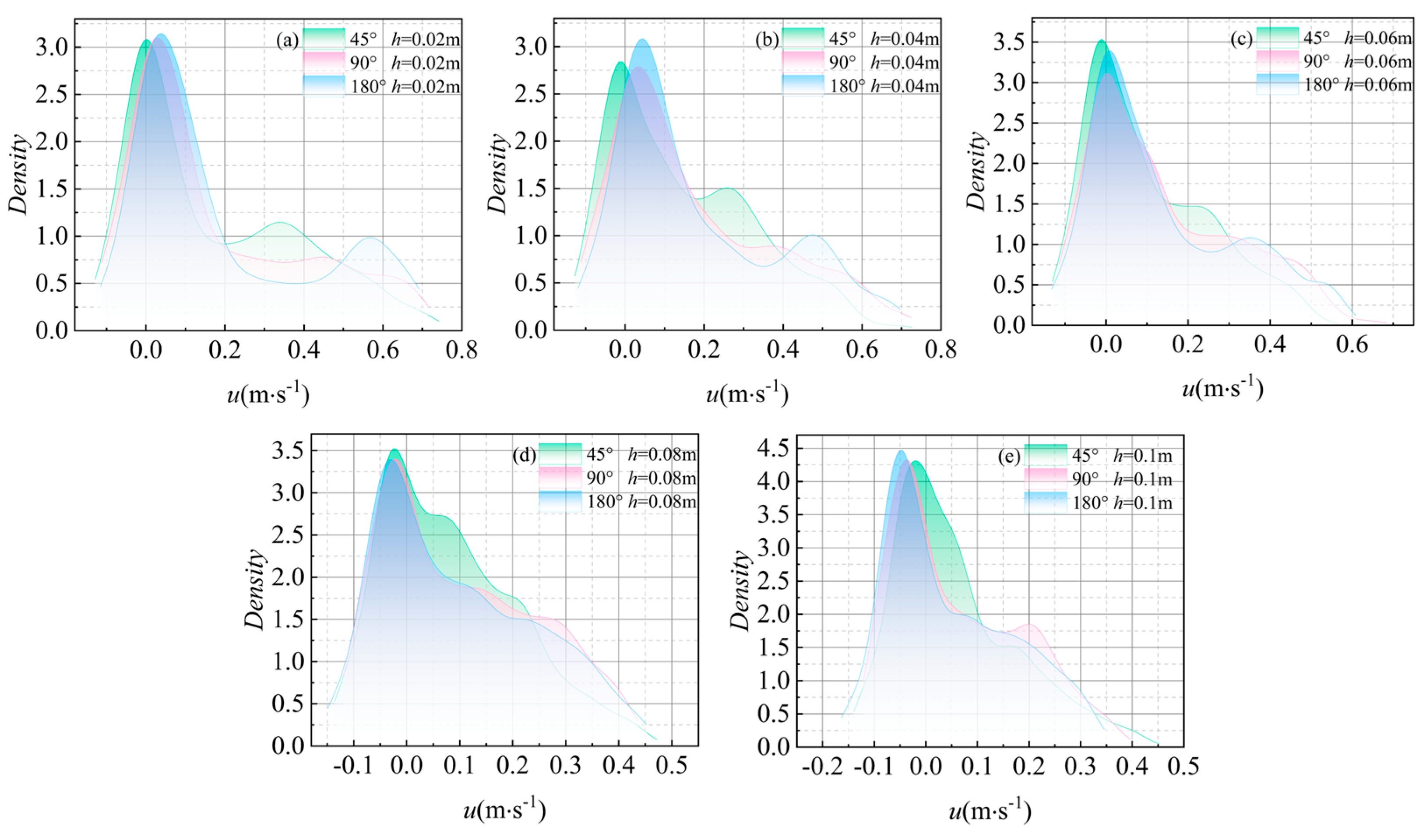
3.2. Two-Dimensional Velocity Distribution in the Recirculation Zone
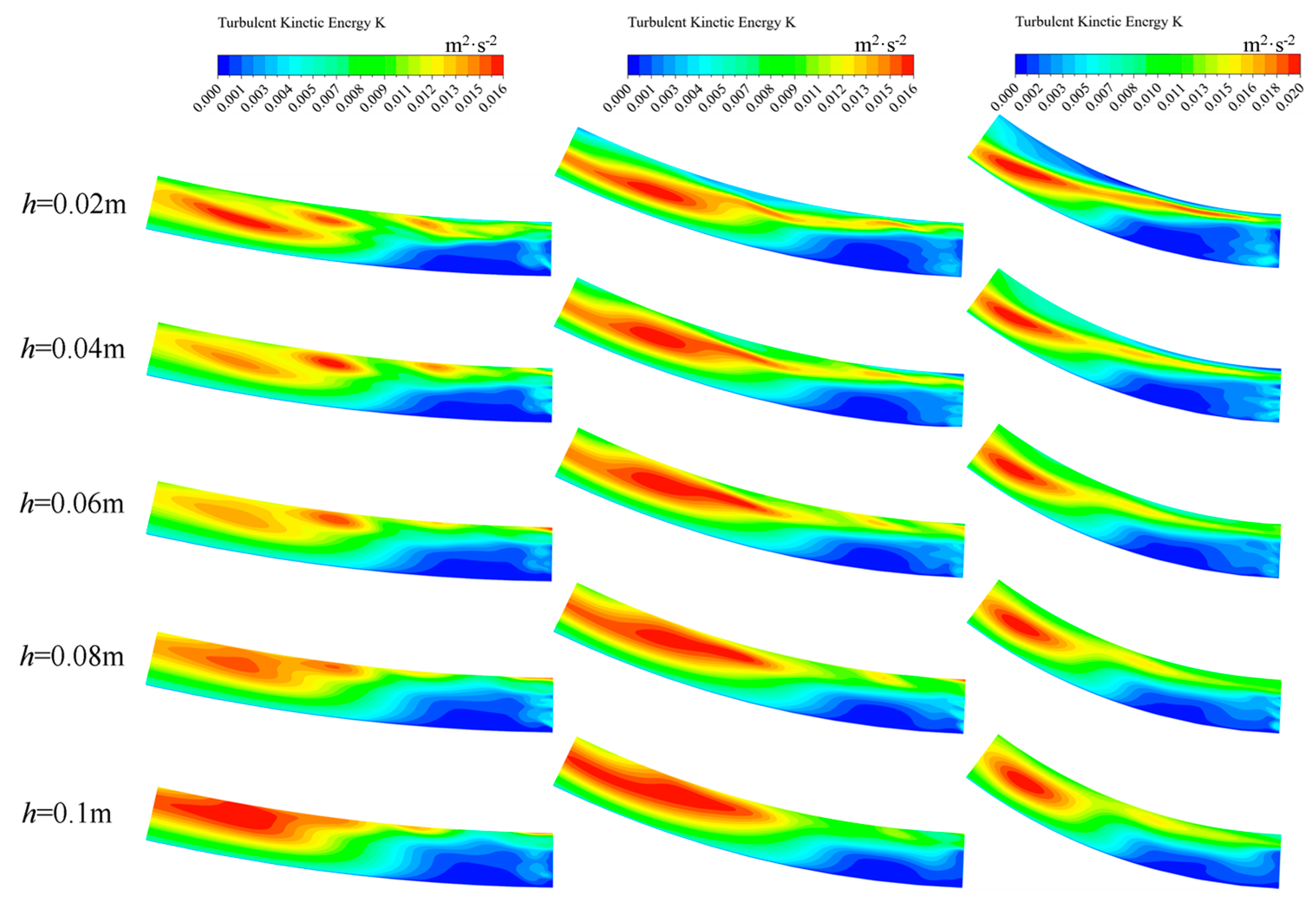
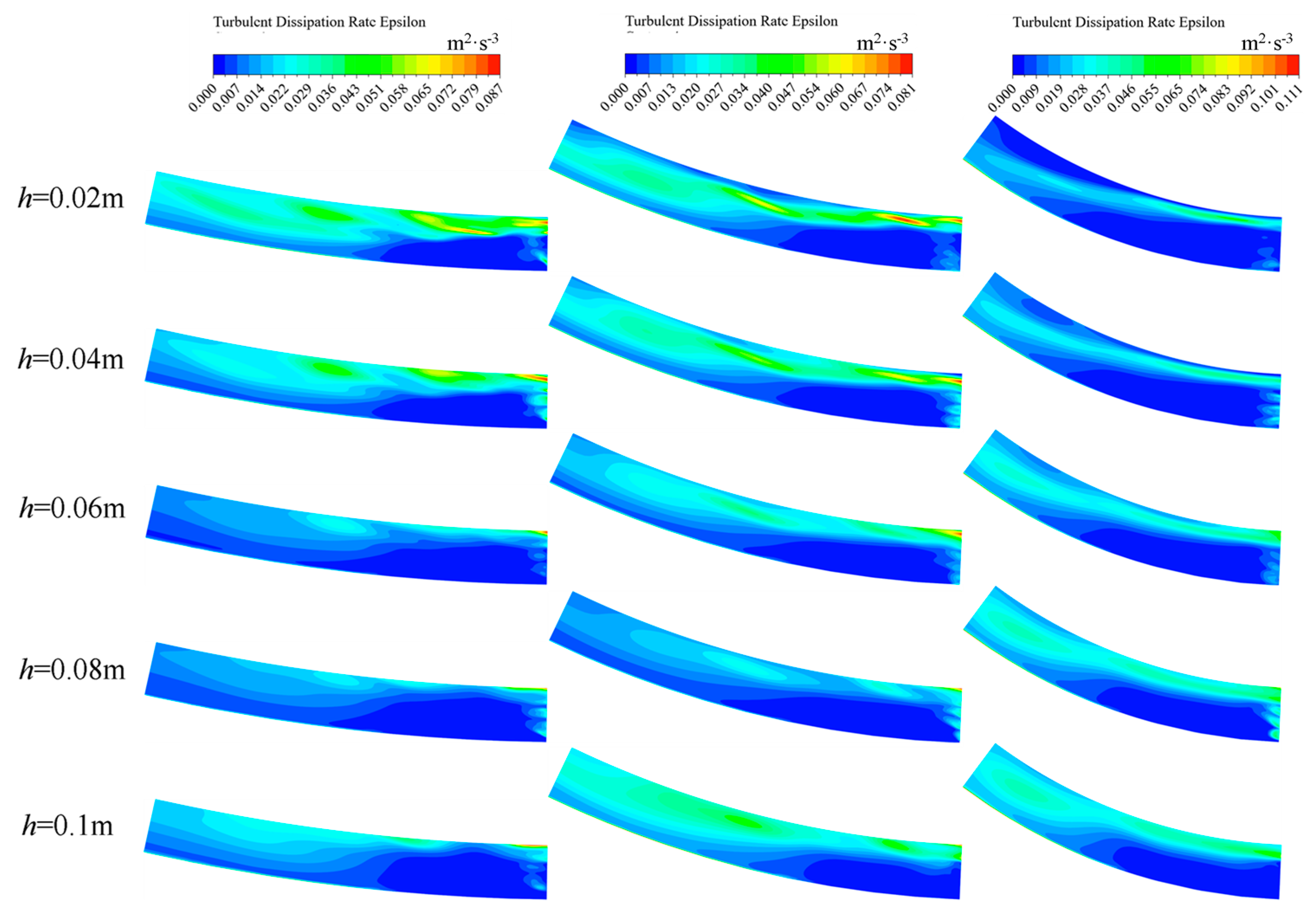
3.3. Turbulent Kinetic Energy and Turbulent Kinetic Energy Dissipation Rate
3.4. Flowlines of the Return Flow Area
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Charlton, R.O. Fundamentals of Fluvial Geomorphology, 1st ed.; Routledge: London, UK, 2007. [Google Scholar]
- Duan, J.G.; He, L.; Fu, X.; Wang, Q. Mean flow and turbulence around experimental spur dike. Adv. Water Resour. 2009, 32, 1717–1725. [Google Scholar] [CrossRef]
- Azinfar, H.; Kells, J.A. Flow resistance due to a single spur dike in an open channel. J. Hydraul. Res. 2009, 47, 755–763. [Google Scholar] [CrossRef]
- Teraguchi, H.; Nakagawa, H.; Kawaike, K.; Baba, Y.; Zhang, H. Effects of hydraulic structures on river morphological processes. Int. J. Sediment Res. 2011, 26, 283–303. [Google Scholar] [CrossRef]
- Iqbal, S.; Pasha, G.A.; Ghani, U.; Ullah, M.K.; Ahmed, A. Flow dynamics around permeable spur dike in a rectangular channel. Arab. J. Sci. Eng. 2021, 46, 4999–5011. [Google Scholar] [CrossRef]
- Fujita, I.; Muto, Y.; Shimazu, Y.; Tsubaki, R. Velocity measurements around non-submerged and submerged spur dykes by means of large-scale particle image velocimetry. J. Hydrosci. Hydraul. Eng. 2004, 22, 51–61. [Google Scholar] [CrossRef]
- Gu, Z.; Akahori, R.; Ikeda, S. Study on the transport of suspended sediment in an open channel flow with permeable spur dikes. Int. J. Sediment Res. 2011, 26, 96–111. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.S.Y. Application of a depth-averaged 2-D model in river restoration. In Proceedings of the World Environmental and Water Resources Congress: Examining Confluence of Environmental and Water Concerns, Omaha, NE, USA, 21–25 May 2006; pp. 1–10. [Google Scholar]
- Hartman, K.J.; Titus, J.L. Fish use of artificial dike structures in a navigable river. River Res. Appl. 2010, 26, 1170–1186. [Google Scholar] [CrossRef]
- King, H.E. River stabilization with groynes in the Western Cape, South Africa. In Proceedings of the International Conference on Fluvial Hydraulics River Flow, Lausanne, Switzerland, 3–5 September 2014; pp. 2145–2150. [Google Scholar]
- Zha, W.; Huang, M.; Zeng, Y. Swimming behavior of crucian carp in an open channel with sudden expansion. River Res. Appl. 2019, 35, 1499–1510. [Google Scholar] [CrossRef]
- Gao, F.; Ma, W.; Zambonini, G.; Boudet, J. Large-eddy simulation of 3-D corner separation in a linear compressor cascade. Phys. Fluids 2015, 27, 085105. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Nwachukwu, B.A. Erosion near groyne-like structures. J. Hydraul. Res. 1983, 21, 277–287. [Google Scholar] [CrossRef]
- Ikeda, S.; Sugimoto, T.; Yoshiike, T. Study on the characteristics of flow in channels with impermeable spur dikes. Doboku Gakkai Ronbunshu 2000, 2000, 145–155. [Google Scholar] [CrossRef] [PubMed]
- Fazli, M.; Ghodsian, M.; Neyshabouri, S.A.A.S. Scour and flow field around a spur dike in a 90 bend. Int. J. Sediment Res. 2008, 23, 56–68. [Google Scholar] [CrossRef]
- Haghnazar, H.; Hashemzadeh Ansar, B.; Asadzadeh, F.; Salehi Neyshabouri, A.A. Experimental study on the effect of single spur-dike with slope sides on local scour pattern. J. Civ. Eng. Mater. Appl. 2018, 2, 111–120. [Google Scholar]
- Fukuoka, S.; Watanabe, A.; Kawaguchi, H.; Yasutake, Y. A study of permeable groins in series installed in a straight channel. Proc. Hydraul. Eng. 2000, 44, 1047–1052. [Google Scholar] [CrossRef]
- Li, Z.; Michioku, K.; Maeno, S.; Ushita, T. Hydraulic characteristics of a group of permeable groins constructed in an open channel flow. J. Appl. Mech. 2005, 8, 773–782. [Google Scholar] [CrossRef]
- Han, L.; Riviere, N.; Chatelain, M.; Mignot, E. Recirculation zone downstream lateral expansions of open channel flow. Phys. Fluids 2020, 32, 115119. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. CFD simulation of near-field pollutant dispersion in the urban environment: A review of current modeling techniques. Atmos. Environ. 2013, 79, 716–730. [Google Scholar] [CrossRef]
- Blocken, B.; Stathopoulos, T.; Van Beeck, J. Pedestrian-level wind conditions around buildings: Review of wind-tunnel and CFD techniques and their accuracy for wind comfort assessment. Build. Environ. 2016, 100, 50–81. [Google Scholar] [CrossRef]
- Thordal, M.S.; Bennetsen, J.C.; Koss, H.H.H. Review for practical application of CFD for the determination of wind load on high-rise buildings. J. Wind Eng. Ind. Aerodyn. 2019, 186, 155–168. [Google Scholar] [CrossRef]
- Moin, P.; Mahesh, K. Direct numerical simulation: A tool in turbulence research. Annu. Rev. Fluid Mech. 1998, 30, 539–578. [Google Scholar] [CrossRef]
- Ishihara, T.; Gotoh, T.; Kaneda, Y. Study of high–Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 2009, 41, 165–180. [Google Scholar] [CrossRef]
- Koken, M.; Constantinescu, G. An investigation of the flow and scour mechanisms around isolated spur dikes in a shallow open channel: 1. Conditions corresponding to the initiation of the erosion and deposition process. Water Resour. Res. 2008, 44, W08406. [Google Scholar] [CrossRef]
- Li, S.; Cain, S.; Wosnik, M.; Miller, C.; Kocahan, H.; Wyckoff, R. Numerical modeling of probable maximum flood flowing through a system of spillways. J. Hydraul. Eng. 2011, 137, 66–74. [Google Scholar] [CrossRef]
- Olsen, N.R.B. CFD Algorithms for Hydraulic Engineering; The Norvegian University of Science and Technology: Trondheim, Norway, 2000. [Google Scholar]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence. I. Basic theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Bulat, M.P.; Bulat, P.V.; Tian, C.; Lu, Y.; Goldberg, U.; Peroomian, O.; Chakravarthy, S. Comparison of turbulence models in the calculation of supersonic separated flows. World Appl. Sci. J. 2013, 27, 1263–1266. [Google Scholar]
- Choi, S.U.; Kang, H. Reynolds stress modeling of vegetated open-channel flows. J. Hydraul. Res. 2004, 42, 3–11. [Google Scholar] [CrossRef]
- Anjum, N.; Tanaka, N. Hydrodynamics of longitudinally discontinuous, vertically double layered and partially covered rigid vegetation patches in open channel flow. River Res. Appl. 2020, 36, 115–127. [Google Scholar] [CrossRef]
- Ghani, U.; Anjum, N.; Pasha, G.A.; Ahmad, M. Numerical investigation of the flow characteristics through discontinuous and layered vegetation patches of finite width in an open channel. Environ. Fluid Mech. 2019, 19, 1469–1495. [Google Scholar] [CrossRef]
- Kumar, M.; Malik, A. 3D simulation of flow around different types of groyne using ANSYS Fluent. Imp. J. Interdiscip. Res. 2016, 2. Available online: https://www.semanticscholar.org/paper/3D-Simulation-of-Flow-around-Different-Types-of-Kumar-Malik/be8645a521701e679e620bd4124f9fa78352f9bf (accessed on 26 June 2024).
- Tang, X.; Ding, X.; Chen, Z. Large eddy simulations of three-dimensional flows around a spur dike. Tsinghua Sci. Technol. 2006, 11, 117–123. [Google Scholar] [CrossRef]
- Choi, S.; Oh, D. Finite element modeling of shallow water equations for numerical simulation of flows near spur–dike. Adv. Hydro-Sci. Eng. 2004, 6, 1–9. [Google Scholar]
- Mostafa, M.M.; Ahmed, H.S.; Ahmed, A.A.; Abdel-Raheem, G.A.; Ali, N.A. Experimental study of flow characteristics around floodplain single groyne. J. Hydro-Environ. Res. 2019, 22, 1–13. [Google Scholar] [CrossRef]
- Giglou, A.N.; Mccorquodale, J.A.; Solari, L. Numerical study on the effect of the spur dikes on sedimentation pattern. Ain Shams Eng. J. 2018, 9, 2057–2066. [Google Scholar] [CrossRef]
- Zhang, H.; Nakagawa, H.; Kawaike, K.; Baba, Y. Experiment and simulation of turbulent flow in local scour around a spur dyke. Int. J. Sediment Res. 2009, 24, 33–45. [Google Scholar] [CrossRef]
- Shin, J.; Lee, S.; Park, I. Analysis of storage effects in the recirculation zone based on the junction angle of channel confluence. Appl. Sci. 2021, 11, 11607. [Google Scholar] [CrossRef]
- Jenkins, S.A.; Inman, D.L.; Richardson, M.D.; Wever, T.F.; Wasyl, J. Scour and burial mechanics of objects in the nearshore. IEEE J. Ocean. Eng. 2007, 32, 78–90. [Google Scholar] [CrossRef]
- Cataño-Lopera, Y.A.; Landry, B.J.; Abad, J.D.; García, M.H. Experimental and numerical study of the flow structure around two partially buried objects on a deformed bed. J. Hydraul. Eng. 2013, 139, 269–283. [Google Scholar] [CrossRef]
- McCoy, A.; Constantinescu, G.; Weber, L.J. Numerical investigation of flow hydrodynamics in a channel with a series of groynes. J. Hydraul. Eng. 2008, 134, 157–172. [Google Scholar] [CrossRef]
- Zhu, H.; Gao, X.; Liu, Y. Experimental study of velocity fluctuations in inlet/outlet under outflow diffusion. J. Hydraul. Eng. 2022, 41, 129–139. [Google Scholar]
- Fu, C.J.; Wang, J.G.; Zhao, T.L.; Yi, L. Experimental research on the flow structure in the open channel with bionic grass. China Rural Water Hydropower 2021, 10, 55–65. [Google Scholar]
- Yang, L.; Liu, B.; Xu, H.; Zhang, S.; Zhang, H. Experimental study on oscillating pressure characteristics of overtopped cofferdam with monolithic protection slab. J. Hydraul. Eng. 2015, 34, 103–108. [Google Scholar]
- Cheng, N.S.; Adrian, W.K.L.; Lin, S.Y. Probability distribution of bed particle instability. Adv. Water. Resour. 2003, 26, 427–433. [Google Scholar] [CrossRef]
- El-Raheem, A.; Ali, N.A.; Tominaga, A.; Khodary, S.M. Flow analysis around groyne with different permeability in compound channel floodplains. JES J. Eng. Sci. 2013, 41, 302–320. [Google Scholar]
- Yun, B.G.; Yu, T.; Wang, P.Y. Experiment research on energy variation around the permeable spur dike. Sci. Technol. Eng. 2021, 21, 3783–3789. [Google Scholar]
- Fan, X.J.; He, W.J.; Zhao, W.J.; Yan, C.F. Study on variation law of flow structure of hydraulic flashboard permeable spur dike along with water permeability. Water Res. Hydropower Eng. 2018, 49, 120–126. [Google Scholar]
- Fukuoka, S.; Nakagawa, H.; Sumi, T.; Zhang, H. Advances in River Sediment Research, 1st ed.; Taylor & Francis Group: London, UK, 2013. [Google Scholar]
- Futian, C.; Wei, F. Experiment at Investigation of Reasonable Spacing among Spur Dikes. J. Hohai Univ. (Nat. Sci.) 1992, 4, 7–14. [Google Scholar]
- Karami, H.; Ardeshir, A.; Saneie, M.; Behzadian, K.; Jalilsani, F. Reduction of local scouring with protective spur dike. In Proceedings of the World Environmental and Water Resources Congress 2008: Ahupua’A, Honolulu, HI, USA, 12–16 May 2008; pp. 1–9. [Google Scholar]
- Ning, J.; Li, G.D.; Li, S.S. Experimental study on the influence of spur dikes spacing on local scouring. In Proceedings of the 2018 International Conference on Energy Development and Environmental Protection (EDEP 2018), Nanjing, China, 17–19 August 2018; pp. 298–303. [Google Scholar]
- Tajnesaie, M.; Jafari Nodoushan, E.; Barati, R.; Azhdary Moghadam, M. Performance comparison of four turbulence models for modeling of secondary flow cells in simple trapezoidal channels. ISH J. Hydraul. Eng. 2020, 26, 187–197. [Google Scholar] [CrossRef]
- Gildeh, H.K. Numerical Modeling of Thermal/Saline Discharges in Coastal Waters. Master’s Thesis, University of Ottawa, Ottawa, ON, Canada, 2013. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fuid Dynamics, 1st ed.; Longman Science & Technical: Harlow, UK, 1995. [Google Scholar]
- Shih, T.H.; Zhu, J.; Lumley, J.L. A new Reynolds stress algebraic equation model. Comput. Methods Appl. Mech. Eng. 1995, 125, 287–302. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Qian, S.; Sun, N.N. Application of permeable spur dike in mountain river training. Appl. Mech. Mater. 2014, 641, 236–240. [Google Scholar] [CrossRef]
- Jeon, J.; Lee, J.Y.; Kang, S. Experimental investigation of three-dimensional flow structure and turbulent flow mechanisms around a nonsubmerged spur dike with a low length-to-depth ratio. Water Res. Res. 2018, 54, 3530–3556. [Google Scholar] [CrossRef]
- Meinders, E.R.; Hanjalic, K.; Martinuzzi, R.J. Experimental study of the local convection heat transfer from a wall-mounted cube in turbulent channel flow. J. Heat Transf. 1999, 121, 564–573. [Google Scholar] [CrossRef]
- Yakhot, A.; Liu, H.; Nikitin, N. Turbulent flow around a wall-mounted cube: A direct numerical simulation. Int. J. Heat Fluid Flow 2006, 27, 994–1009. [Google Scholar] [CrossRef]
- Higham, J.E.; Brevis, W.; Keylock, C.J.; Safarzadeh, A. Using modal decompositions to explain the sudden expansion of the mixing layer in the wake of a groyne in a shallow flow. Adv. Water Res. 2017, 107, 451–459. [Google Scholar] [CrossRef]
- Paik, J.; Sotiropoulos, F. Coherent structure dynamics upstream of a long rectangular block at the side of a large aspect ratio channel. Phys. Fluids 2005, 17, 115104. [Google Scholar] [CrossRef]
- Devenport, W.J.; Simpson, R.L. Time-depeiident and time-averaged turbulence structure near the nose of a wing-body junction. J. Fluid Mech. 1990, 210, 23–55. [Google Scholar] [CrossRef]
- Paik, J.; Escauriaza, C.; Sotiropoulos, F. Coherent structure dynamics in turbulent flows past in-stream structures: Some insights gained via numerical simulation. J. Hydraul. Eng. 2010, 136, 981–993. [Google Scholar] [CrossRef]



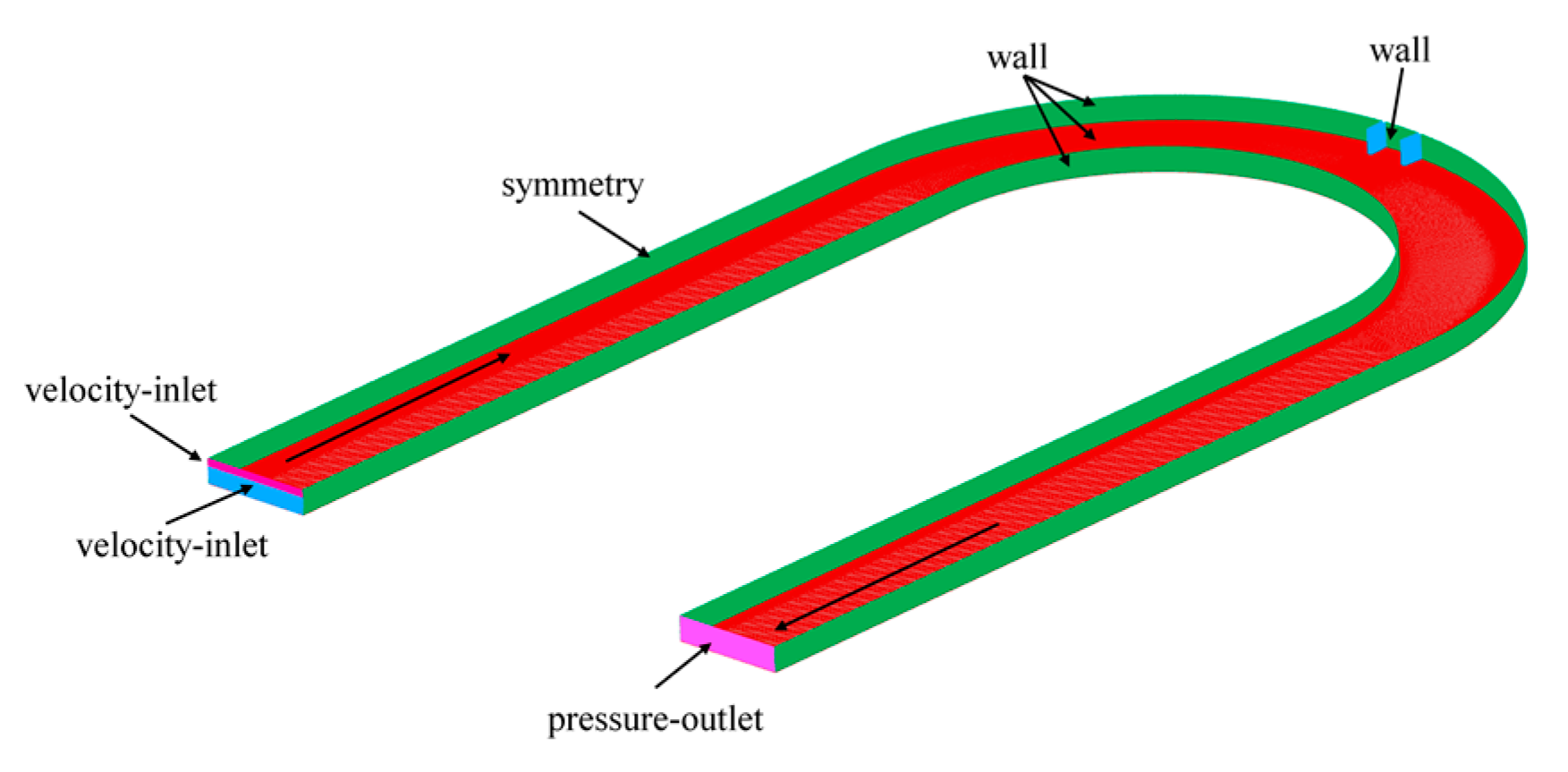
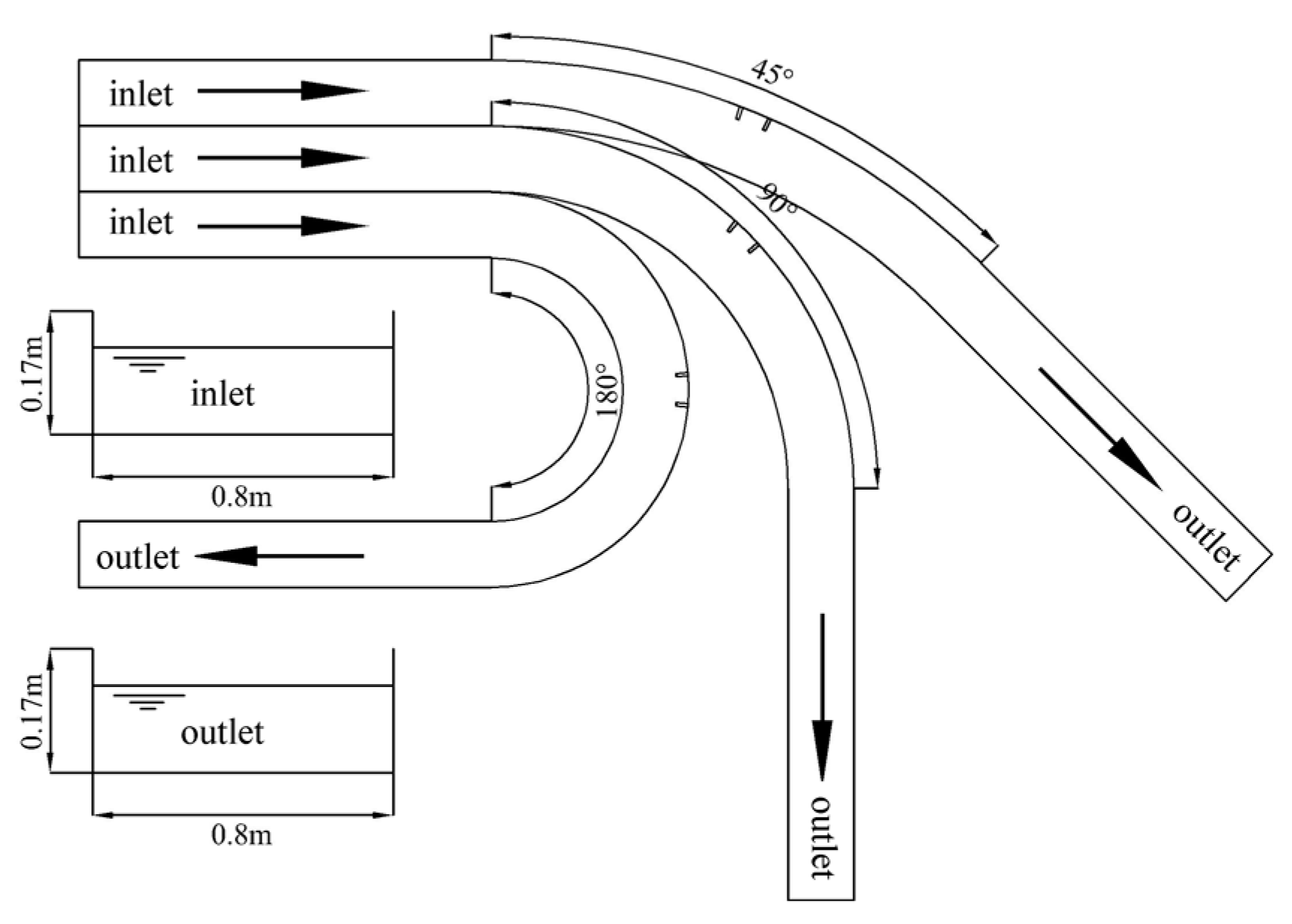
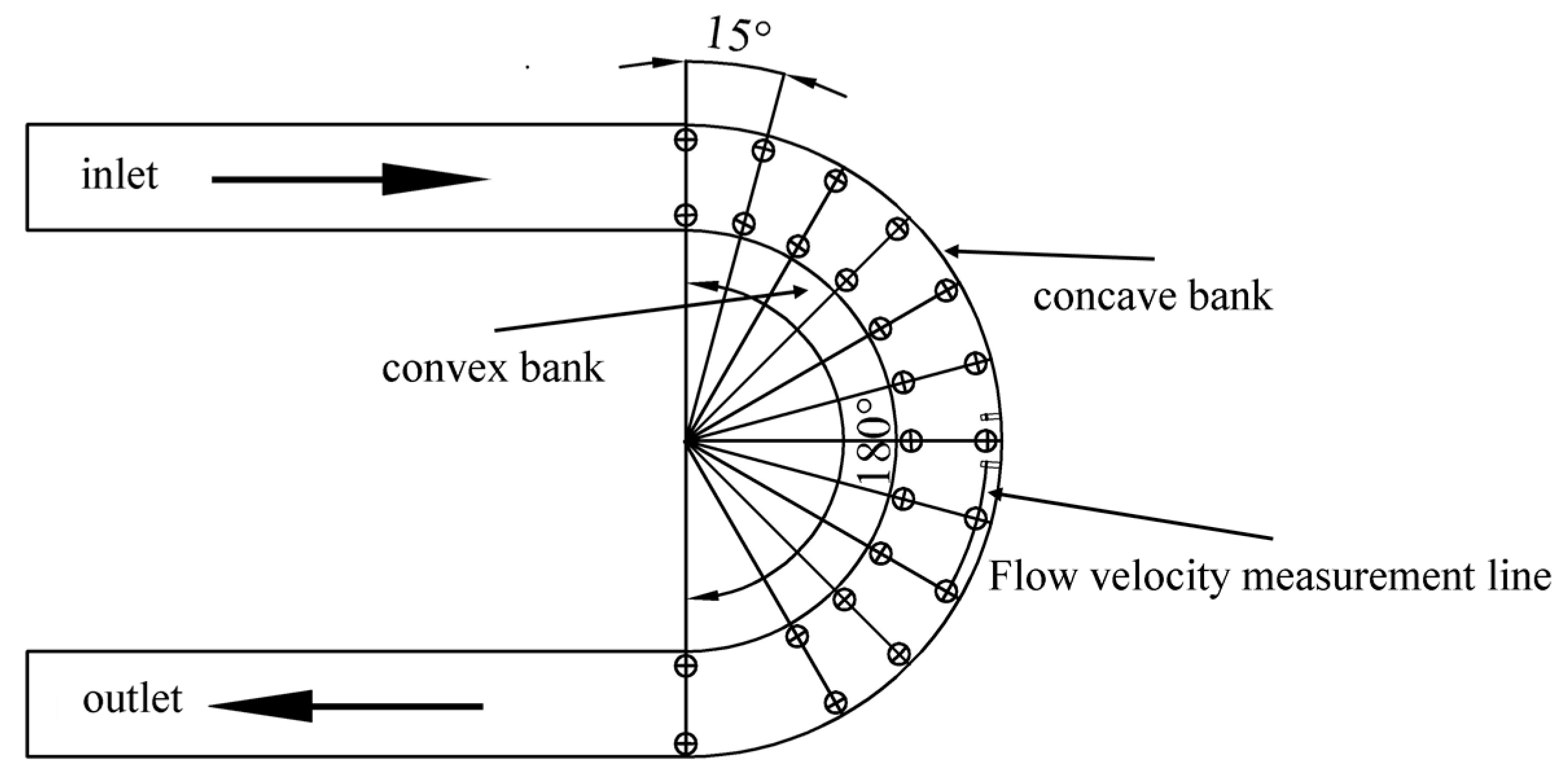
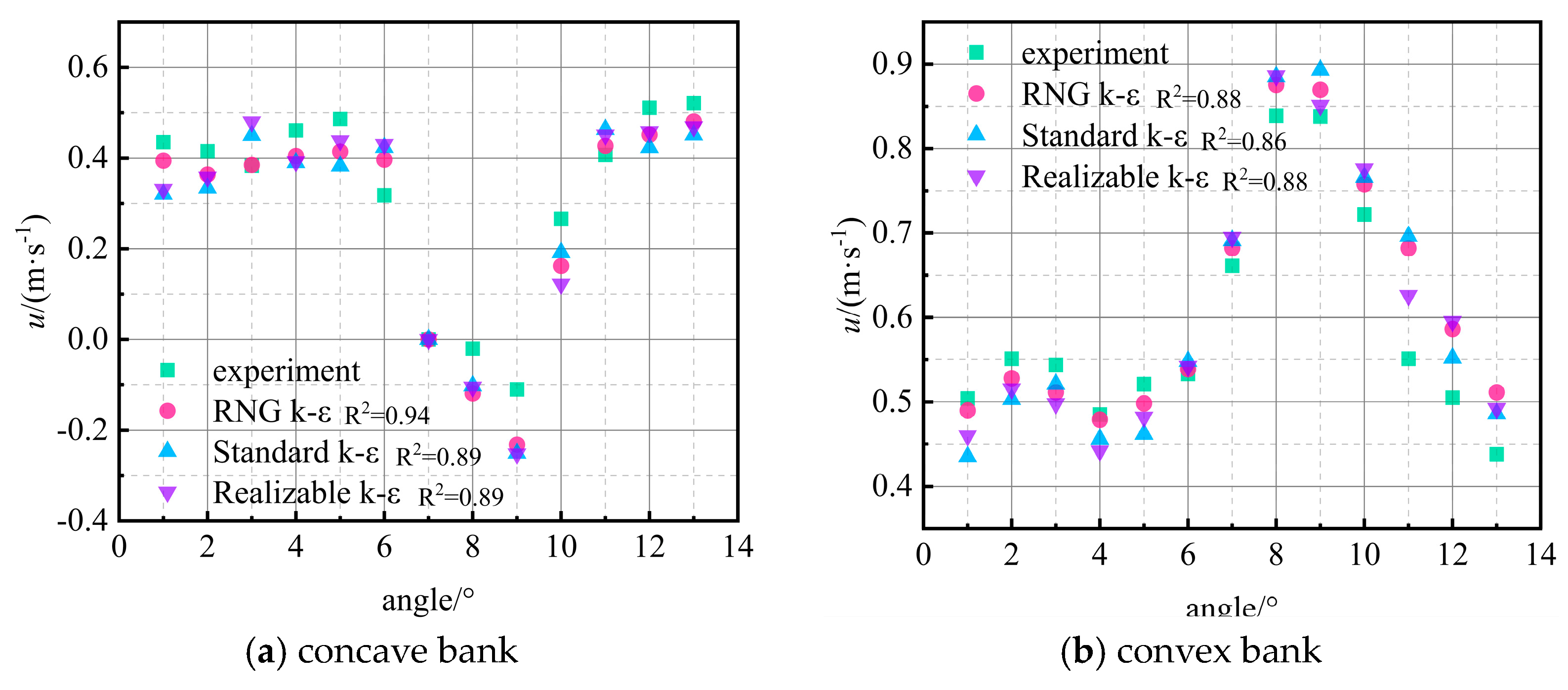






| Model Parameters | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| , | 0.12 | |||
| , | 0.8 | |||
| , | 0.02 | |||
| , | 0.15 | |||
| The ratio of the width of the sink to the water depth of the tailgate, | 6.67 | |||
| The ratio of the length of the spur dike to the water depth of the tailgate, | 1.25 | |||
| The ratio of the length of the spur dike to the width of the tank, | 0.19 | |||
| Flow rate, | 0.05 | |||
| 0.52 | ||||
| 0.48 | ||||
| 24 | ||||
| ) | 0.9 × 10−6 | |||
| 6.9 × 104 | ||||
| 8 | 4 | 2 | 2 | |
| Center angle of the curve, (°) | 45 | 90 | 180 | 180 |
| Curvature of a curve | 0.125 | 0.25 | 0.5 | 0.5 |
| Research methods | Numerical simulation | Numerical simulation | Numerical simulation | Physical experiment |
| Curvature | h (m) | Skewness Coefficient | |
|---|---|---|---|
| longitudinal | Horizontal | ||
| 0.125 | 0.02 | 0.702017 | 0.789333 |
| 0.25 | 0.02 | 0.856053 | −0.38265 |
| 0.5 | 0.02 | 0.850755 | −1.03391 |
| 0.125 | 0.04 | 0.647329 | 0.128103 |
| 0.25 | 0.04 | 0.790334 | −0.55784 |
| 0.5 | 0.04 | 0.779543 | −0.96054 |
| 0.125 | 0.06 | 0.717472 | 0.993362 |
| 0.25 | 0.06 | 0.710017 | −0.27714 |
| 0.5 | 0.06 | 0.756787 | −0.46314 |
| 0.125 | 0.08 | 0.616826 | 0.848162 |
| 0.25 | 0.08 | 0.451669 | 1.210951 |
| 0.5 | 0.08 | 0.508694 | 0.714217 |
| 0.125 | 0.1 | 0.867849 | 1.410127 |
| 0.25 | 0.1 | 0.590159 | 1.873173 |
| 0.5 | 0.1 | 0.562967 | 1.443221 |
| Curvature | h (m) | Skewness Coefficient | |
|---|---|---|---|
| k | ε | ||
| 0.125 | 0.02 | −0.02814 | 0.918754 |
| 0.25 | 0.02 | 0.246802 | 1.242032 |
| 0.5 | 0.02 | 0.745532 | 3.142222 |
| 0.125 | 0.04 | 0.037977 | 1.395058 |
| 0.25 | 0.04 | 0.136417 | 1.05524 |
| 0.5 | 0.04 | 0.473628 | 2.250936 |
| 0.125 | 0.06 | 0.178807 | 3.530223 |
| 0.25 | 0.06 | 0.05045 | 1.569564 |
| 0.5 | 0.06 | 0.290631 | 1.553615 |
| 0.125 | 0.08 | 0.282487 | 3.151887 |
| 0.25 | 0.08 | 0.055616 | 2.293563 |
| 0.5 | 0.08 | 0.208776 | 1.047833 |
| 0.125 | 0.1 | 0.353097 | 2.812622 |
| 0.25 | 0.1 | 0.114305 | 0.962738 |
| 0.5 | 0.1 | 0.154631 | 1.290174 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, P.; Lv, S.; Li, Z.; Zhang, Y.; Lv, J. Numerical Simulation Study on Three-Dimensional Flow Characteristics and Probability Density Distribution of Water-Permeable Gabion Backflow Zone in Different Curvature Bends. Water 2024, 16, 2247. https://doi.org/10.3390/w16162247
Xie P, Lv S, Li Z, Zhang Y, Lv J. Numerical Simulation Study on Three-Dimensional Flow Characteristics and Probability Density Distribution of Water-Permeable Gabion Backflow Zone in Different Curvature Bends. Water. 2024; 16(16):2247. https://doi.org/10.3390/w16162247
Chicago/Turabian StyleXie, Peng, Suiju Lv, Zelin Li, Ying Zhang, and Jianping Lv. 2024. "Numerical Simulation Study on Three-Dimensional Flow Characteristics and Probability Density Distribution of Water-Permeable Gabion Backflow Zone in Different Curvature Bends" Water 16, no. 16: 2247. https://doi.org/10.3390/w16162247
APA StyleXie, P., Lv, S., Li, Z., Zhang, Y., & Lv, J. (2024). Numerical Simulation Study on Three-Dimensional Flow Characteristics and Probability Density Distribution of Water-Permeable Gabion Backflow Zone in Different Curvature Bends. Water, 16(16), 2247. https://doi.org/10.3390/w16162247





