Daily Runoff Prediction Based on FA-LSTM Model
Abstract
1. Introduction
2. Study Area and Data
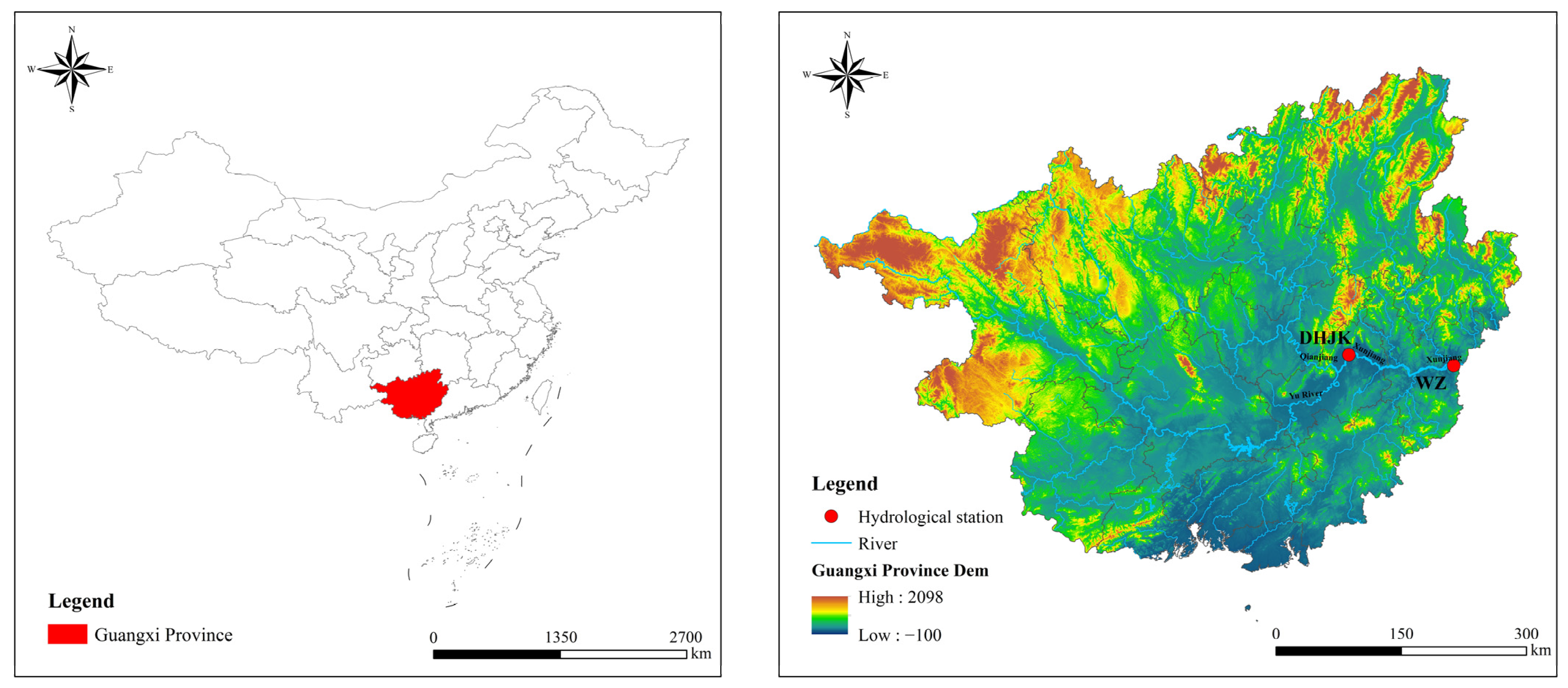
2.1. Overview of the Study Area
2.2. Data Sources
3. Research Methods
3.1. RNN Model Introduction
3.2. LSTM Model Introduction
3.3. GRU Model Introduction
3.4. SVM Model Introduction
3.5. RF Model Introduction
3.6. Firefly Algorithm
3.7. Model Construction and Parameter Setting
3.7.1. Model Construction
3.7.2. Model Parameter Setting
4. Case Analysis
4.1. Model Evaluation Index
4.2. Comparison and Analysis of Model Results
4.2.1. Runoff Prediction Results of the Model
4.2.2. Model Generalization Experiment
4.2.3. The Prediction Performance of the Optimal Model under Different Prediction Periods
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Solaimani, K. Rainfall-runoff prediction based on artificial neural network (a case study: Jarahi watershed). Am.-Eurasian J. Agric. Environ. Sci. 2009, 5, 856–865. [Google Scholar]
- Li, F.F.; Cao, H.; Hao, C.F.; Qiu, J. Daily streamflow forecasting based on flow pattern recognition. Water Resour. Manag. 2021, 35, 4601–4620. [Google Scholar] [CrossRef]
- Wu, J.H.; Wang, Z.C.; Dong, J.H.; Cui, X.F.; Tao, S.; Chen, X. Robust runoff prediction with explainable artificial intelligence and meteorological variables from deep learning ensemble model. Water Resour. Res. 2023, 59, e2023WR035676. [Google Scholar] [CrossRef]
- Mao, G.Q.; Wang, M.; Liu, J.G.; Wang, Z.F.; Wang, K.; Meng, Y.; Zhong, R.; Li, Y. Comprehensive comparison of artificial neural networks and long short-term memory networks for rainfall-runoff simulation. Phys. Chem. Earth Parts A/B/C 2021, 123, 103026. [Google Scholar] [CrossRef]
- Han, H.; Morrison, R.R. Improved runoff forecasting performance through error predictions using a deep-learning approach. J. Hydrol. 2022, 608, 127653. [Google Scholar] [CrossRef]
- Lei, X.H.; Wang, H.; Yang, M.X.; Gui, Z.L. Research Progress on Meteorological Hydrological Forecasting under Changing Environments. J. Hydraul. Eng. 2018, 49, 9–18. (In Chinese) [Google Scholar]
- Zhu, S.; Zhou, J.Z.; Ye, L.; Meng, C.Q. Streamflow estimation by support vector machine coupled with different methods of time series decomposition in the upper reaches of Yangtze River, China. Environ. Earth Sci. 2016, 75, 531. [Google Scholar] [CrossRef]
- Wu, J.H.; Wang, Z.C.; Hu, Y.; Tao, S.; Dong, J.H. Runoff forecasting using convolutional neural networks and optimized bi-directional long short-term memory. Water Resour. Manag. 2023, 37, 937–953. [Google Scholar] [CrossRef]
- Kalra, A.; Miller, W.P.; Lamb, K.W.; Ahmad, S.; Piechota, T. Using large-scale climatic patterns for improving long lead time streamflow forecasts for Gunnison and San Juan River Basins. Hydrol. Process. 2013, 27, 1543–1559. [Google Scholar] [CrossRef]
- Lin, G.F.; Chou, Y.C.; Wu, M.C. Typhoon flood forecasting using integrated two-stage support vector machine approach. J. Hydrol. 2013, 486, 334–342. [Google Scholar] [CrossRef]
- Xu, X.Y.; Yang, D.; Yang, H.; Lei, H. Attribution analysis based on the Budyko hypothesis for detecting the dominant cause of runoff decline in Haihe basin. J. Hydrol. 2014, 510, 530–540. [Google Scholar] [CrossRef]
- Van, S.P.; Le, H.M.; Thanh, D.V.; Dang, T.D.; Loc, H.H.; Anh, D.T. Deep learning convolutional neural network in rainfall–runoff modelling. J. Hydroinform. 2020, 22, 541–561. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, T.; Kang, A.Q.; Li, J.Z.; Lei, X.H. Research on runoff simulations using deep-learning methods. Sustainability 2021, 13, 1336. [Google Scholar] [CrossRef]
- Osman, A.; Afan, H.A.; Allawi, M.F.; Jaafar, O.; Noureldin, A.; Hamzah, F.M.; Ahmed, A.N.; El-Shafie, A. Adaptive Fast Orthogonal Search (FOS) algorithm for forecasting streamflow. J. Hydrol. 2020, 586, 124896. [Google Scholar] [CrossRef]
- Wu, Y.Q.; Wang, Q.H.; Li, G.; Li, J.D. Data-driven runoff forecasting for Minjiang River: A case study. Water Supply 2020, 20, 2284–2295. [Google Scholar] [CrossRef]
- Moosavi, V.; Fard, Z.G.; Vafakhah, M. Which one is more important in daily runoff forecasting using data driven models: Input data, model type, preprocessing or data length? J. Hydrol. 2022, 606, 127429. [Google Scholar] [CrossRef]
- Wang, J.J.; Shi, P.; Jiang, P.; Hu, J.W.; Qu, S.; Chen, X.Y.; Chen, Y.B.; Dai, Y.Q.; Xiao, Z.W. Application of BP neural network algorithm in traditional hydrological model for flood forecasting. Water 2017, 9, 48. [Google Scholar] [CrossRef]
- Sivapragasam, C.; Liong, S.Y.; Pasha, M.F.K. Rainfall and runoff forecasting with SSA–SVM approach. J. Hydroinform. 2001, 3, 141–152. [Google Scholar] [CrossRef]
- Li, M.; Zhang, Y.Q.; Wallace, J.; Campbell, E. Estimating annual runoff in response to forest change: A statistical method based on random forest. J. Hydrol. 2020, 589, 125168. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Khan, A.; Zhang, Y.K.; Kuang, X.; Liang, X.; Taccari, M.; Nuttall, J. Daily runoff forecasting by deep recursive neural network. J. Hydrol. 2021, 596, 126067. [Google Scholar] [CrossRef]
- He, F.F.; Wan, Q.J.; Wang, Y.Q.; Wu, J.; Zhang, X.Q.; Feng, Y. Daily Runoff Prediction with a Seasonal Decomposition-Based Deep GRU Method. Water 2024, 16, 618. [Google Scholar] [CrossRef]
- Tabas, S.S.; Samadi, S. Variational Bayesian dropout with a Gaussian prior for recurrent neural networks application in rainfall–runoff modeling. Environ. Res. Lett. 2022, 17, 065012. [Google Scholar] [CrossRef]
- Gao, S.; Huang, Y.F.; Zhang, S.; Han, J.C.; Wang, G.Q.; Zhang, M.X.; Lin, Q.S. Short-term runoff prediction with GRU and LSTM networks without requiring time step optimization during sample generation. J. Hydrol. 2020, 589, 125188. [Google Scholar] [CrossRef]
- Sheng, Z.Y.; Wen, S.P.; Feng, Z.K.; Shi, K.B.; Huang, T.W. A Novel Residual Gated Recurrent Unit Framework for Runoff Forecasting. IEEE Internet Things J. 2023, 10, 12736–12748. [Google Scholar] [CrossRef]
- Ayzel, G.; Heistermann, M. The effect of calibration data length on the performance of a conceptual hydrological model versus LSTM and GRU: A case study for six basins from the CAMELS dataset. Comput. Geosci. 2021, 149, 104708. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Li, W.; Kiaghadi, A.; Dawson, C. High temporal resolution rainfall–runoff modeling using long-short-term-memory (LSTM) networks. Neural Comput. Appl. 2021, 33, 1261–1278. [Google Scholar] [CrossRef]
- Sabzipour, B.; Arsenault, R.; Troin, M.; Martel, J.L.; Brissette, F.; Brunet, F.; Mai, J. Comparing a long short-term memory (LSTM) neural network with a physically-based hydrological model for streamflow forecasting over a Canadian catchment. J. Hydrol. 2023, 627, 130380. [Google Scholar] [CrossRef]
- Yin, Z.K.; Liao, W.H.; Wang, R.J.; Lei, X.H. Rainfall-Runoff Simulation and Forecasting Based on Long Short-Term Memory Neural Network (LSTM). South—North Water Divers. Water Sci. Technol. 2019, 17, 1–9. (In Chinese) [Google Scholar]
- Li, J.X.; Qian, K.X.; Liu, Y.; Yan, W.; Yang, X.Y.; Luo, G.P.; Ma, X.F. LSTM-based model for predicting inland river runoff in arid region: A case study on Yarkant River, Northwest China. Water 2022, 14, 1745. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Luo, G. A review of automatic selection methods for machine learning algorithms and hyper-parameter values. Netw. Model. Anal. Health Inform. Bioinform. 2016, 5, 1–16. [Google Scholar] [CrossRef]
- Wu, J.W.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Chu, H.B.; Wang, Z.Q.; Nie, C. Monthly Streamflow Prediction of the Source Region of the Yellow River Based on Long Short-Term Memory Considering Different Lagged Months. Water 2021, 16, 593. [Google Scholar] [CrossRef]
- Alqahtani, F. AI-driven improvement of monthly average rainfall forecasting in Mecca using grid search optimization for LSTM networks. J. Water Clim. Chang. 2024, 15, 1439–1458. [Google Scholar] [CrossRef]
- Yang, X.Z.; Maihemuti, B.; Simayi, Z.; Saydi, M.; Na, L. Prediction of glacially derived runoff in the muzati river watershed based on the PSO-LSTM model. Water 2022, 14, 2018. [Google Scholar] [CrossRef]
- Xu, Y.H.; Hu, C.H.; Wu, Q.; Jian, S.Q.; Li, Z.H.; Chen, Y.Q.; Zhang, G.D.; Zhang, Z.X.; Wang, S. Research on particle swarm optimization in LSTM neural networks for rainfall-runoff simulation. J. Hydrol. 2022, 608, 127553. [Google Scholar] [CrossRef]
- Aderyani, F.R.; Mousavi, S.J.; Jafari, F. Short-term rainfall forecasting using machine learning-based approaches of PSO-SVR, LSTM and CNN. J. Hydrol. 2022, 614, 128463. [Google Scholar] [CrossRef]
- Wang, X.J.; Wang, Y.P.; Yuan, P.X.; Wang, L.; Cheng, D.L. An adaptive daily runoff forecast model using VMD-LSTM-PSO hybrid approach. Hydrol. Sci. J. 2021, 66, 1488–1502. [Google Scholar] [CrossRef]
- Li, W.Z.; Liu, C.S.; Hu, C.H.; Niu, C.J.; Li, R.X.; Li, M.; Xu, Y.Y.; Tian, L. Application of a hybrid algorithm of LSTM and Transformer based on random search optimization for improving rainfall-runoff simulation. Sci. Rep. 2021, 14, 11184. [Google Scholar] [CrossRef]
- Naganna, S.R.; Marulasiddappa, S.B.; Balreddy, M.S.; Yaseen, Z.M. Daily scale streamflow forecasting in multiple stream orders of Cauvery River, India: Application of advanced ensemble and deep learning models. J. Hydrol. 2023, 626, 130320. [Google Scholar] [CrossRef]
- Cong, Y.; Zhao, X.M.; Tang, K.; Wang, G.; Hu, Y.F.; Jiao, Y.K. FA-LSTM: A novel toxic gas concentration prediction model in pollutant environment. IEEE Access 2021, 10, 1591–1602. [Google Scholar] [CrossRef]
- Luo, G.; Wang, X.Y.; Zhu, J.M.; Zhou, Y.Q. Quantitative detection of composite defects based on infrared technology and FA-LSTM. J. Phys. Conf. Ser. 2024, 2770, 012012. [Google Scholar] [CrossRef]
- Zhu, L.Z. Short-term power load forecasting based on FA-LSTM with similar day selection. In Proceedings of the 2023 IEEE 3rd International Conference on Electronic Technology, Communication and Information, Qingdao, China, 21–24 July 2023; IEEE: Piscataway, NJ. USA, 2023; pp. 1110–1115. [Google Scholar]
- Zhang, R.; Zheng, X. Short-term wind power prediction based on the combination of firefly optimization and LSTM. Adv. Control Appl. Eng. Ind. Syst. 2024, 6, e161. [Google Scholar] [CrossRef]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arxiv 2014, arXiv:1406.1078. [Google Scholar]
- Gunn, S.R. Support Vector Machines for Classification and Regression. Technical Report, Image Speech and Intelligent Systems Research Group, University of Southampton. 1997. Available online: http://www.isis.ecs.soton.ac.uk/isystems/kernel/ (accessed on 28 April 2024).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly algorithms for multimodal optimization. In International Symposium on Stochastic Algorithms; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Chen, Y.; Zhang, P.; Zhao, Y.; Qu, L.Q.; Du, P.F.; Wang, Y.G. Factors Affecting Runoff and Sediment Load Changes in the Wuding River Basin from 1960 to 2020. Hydrology 2022, 9, 198. [Google Scholar] [CrossRef]
- Yin, L.; Wang, L.; Keim, B.D.; Konsoer, K.; Yin, Z.; Liu, M.; Zheng, W. Spatial and wavelet analysis of precipitation and river discharge during operation of the Three Gorges Dam, China. Ecol. Indic. 2023, 154, 110837. [Google Scholar] [CrossRef]
















| Station | Sequence Length/d | Daily Runoff Series Statistics (m3/s) | |||
|---|---|---|---|---|---|
| Maximum Value | Minimum Value | Mean Value | Standard Deviation | ||
| DHJK | 1826 | 42,400 | 576 | 4552 | 4943 |
| WZ | 1826 | 53,300 | 964 | 5463 | 5786 |
| Station | Model | Training Set | Test Set | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE (103 m3/s) | RMSE (103 m3/s) | R2 | KGE | MAE (103 m3/s) | RMSE (103 m3/s) | R2 | KGE | ||
| DHJK | FA-LSTM | 0.426 | 0.850 | 0.972 | 0.965 | 0.455 | 0.871 | 0.966 | 0.965 |
| RNN | 0.564 | 1.214 | 0.935 | 0.917 | 0.596 | 1.283 | 0.933 | 0.917 | |
| LSTM | 0.490 | 1.046 | 0.952 | 0.952 | 0.495 | 1.101 | 0.950 | 0.953 | |
| GRU | 0.560 | 1.130 | 0.949 | 0.943 | 0.574 | 1.141 | 0.942 | 0.942 | |
| SVM | 0.651 | 1.248 | 0.932 | 0.908 | 0.663 | 1.319 | 0.929 | 0.891 | |
| RF | 0.562 | 1.164 | 0.943 | 0.940 | 0.575 | 1.208 | 0.939 | 0.938 | |
| WZ | FA-LSTM | 0.445 | 1.117 | 0.968 | 0.956 | 0.330 | 0.748 | 0.971 | 0.960 |
| RNN | 0.704 | 1.581 | 0.936 | 0.933 | 0.465 | 1.027 | 0.946 | 0.935 | |
| LSTM | 0.615 | 1.454 | 0.946 | 0.945 | 0.427 | 0.949 | 0.954 | 0.947 | |
| GRU | 0.638 | 1.507 | 0.942 | 0.938 | 0.454 | 0.988 | 0.950 | 0.940 | |
| SVM | 0.766 | 1.665 | 0.929 | 0.916 | 0.541 | 1.090 | 0.939 | 0.908 | |
| RF | 0.733 | 1.614 | 0.934 | 0.929 | 0.516 | 1.053 | 0.943 | 0.929 | |
| Station | Model | Training Set | Test Set | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE (103 m3/s) | RMSE (103 m3/s) | R2 | KGE | MAE (103 m3/s) | RMSE (103 m3/s) | R2 | KGE | ||
| QJ | FA-LSTM | 0.198 | 0.484 | 0.970 | 0.984 | 0.157 | 0.411 | 0.973 | 0.985 |
| WX | FA-LSTM | 0.309 | 0.850 | 0.963 | 0.980 | 0.426 | 1.105 | 0.960 | 0.978 |
| GG | FA-LSTM | 0.099 | 0.224 | 0.977 | 0.962 | 0.183 | 0.345 | 0.975 | 0.961 |
| Station | Model | Error Indicator | Forecast Period | ||||
|---|---|---|---|---|---|---|---|
| 1 Day | 2 Days | 3 Days | 4 Days | 5 Days | |||
| DHJK | FA-LSTM | MAE (103 m3/s) | 0.455 | 0.699 | 0.803 | 0.980 | 1.072 |
| RMSE (103 m3/s) | 0.871 | 1.360 | 1.747 | 2.042 | 2.304 | ||
| R2 | 0.966 | 0.916 | 0.862 | 0.811 | 0.760 | ||
| KGE | 0.965 | 0.930 | 0.915 | 0.837 | 0.811 | ||
| WZ | FA-LSTM | MAE (103 m3/s) | 0.330 | 0.520 | 0.650 | 0.769 | 0.843 |
| RMSE (103 m3/s) | 0.748 | 1.128 | 1.475 | 1.751 | 1.995 | ||
| R2 | 0.971 | 0.935 | 0.888 | 0.843 | 0.796 | ||
| KGE | 0.960 | 0.939 | 0.885 | 0.861 | 0.821 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, Q.; Zhang, S.; Tian, Q.; Yang, C.; Guo, L. Daily Runoff Prediction Based on FA-LSTM Model. Water 2024, 16, 2216. https://doi.org/10.3390/w16162216
Chai Q, Zhang S, Tian Q, Yang C, Guo L. Daily Runoff Prediction Based on FA-LSTM Model. Water. 2024; 16(16):2216. https://doi.org/10.3390/w16162216
Chicago/Turabian StyleChai, Qihui, Shuting Zhang, Qingqing Tian, Chaoqiang Yang, and Lei Guo. 2024. "Daily Runoff Prediction Based on FA-LSTM Model" Water 16, no. 16: 2216. https://doi.org/10.3390/w16162216
APA StyleChai, Q., Zhang, S., Tian, Q., Yang, C., & Guo, L. (2024). Daily Runoff Prediction Based on FA-LSTM Model. Water, 16(16), 2216. https://doi.org/10.3390/w16162216





