Construction Stability Analysis and Field Monitoring of Shallowly Buried Large-Section Tunnels in Loess Strata
Abstract
1. Introduction
2. Project Overview
3. Numerical Model and Parameter Determination
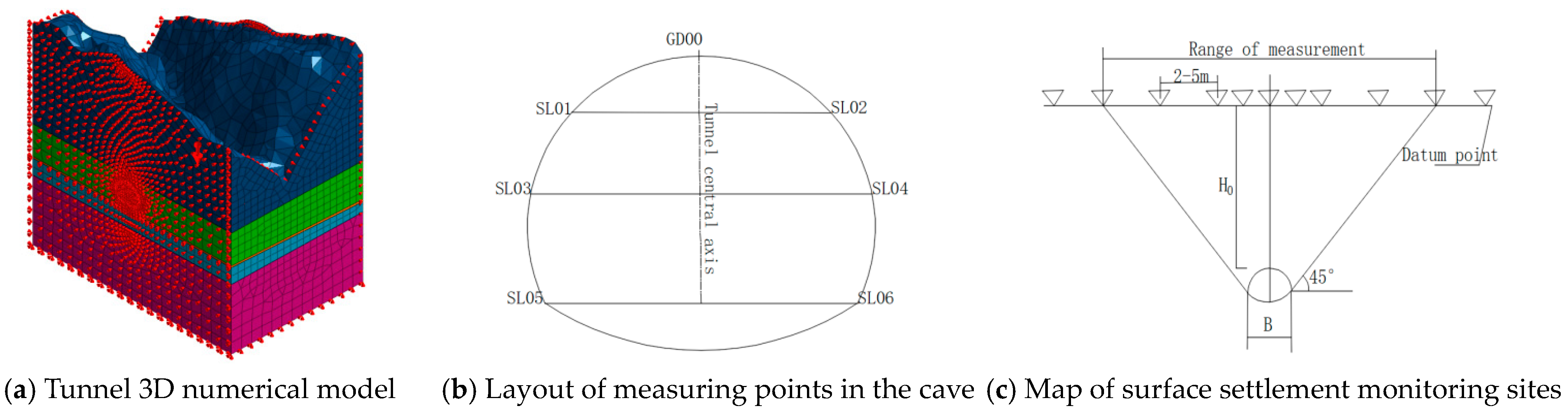
3.1. Numerical Model
3.2. Simulation of the Construction Scheme
4. Simulation Study on the Optimization of the Excavation Footage
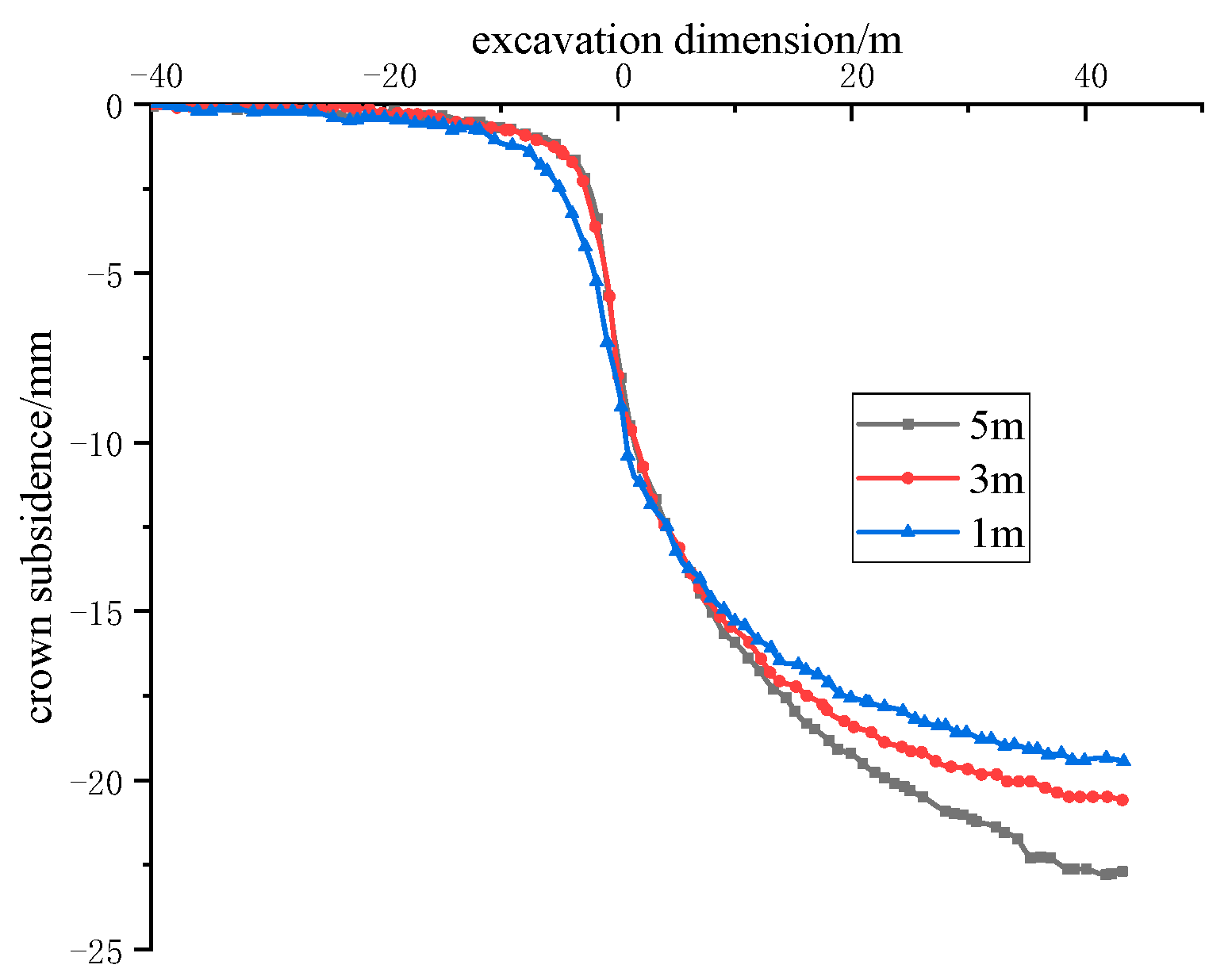
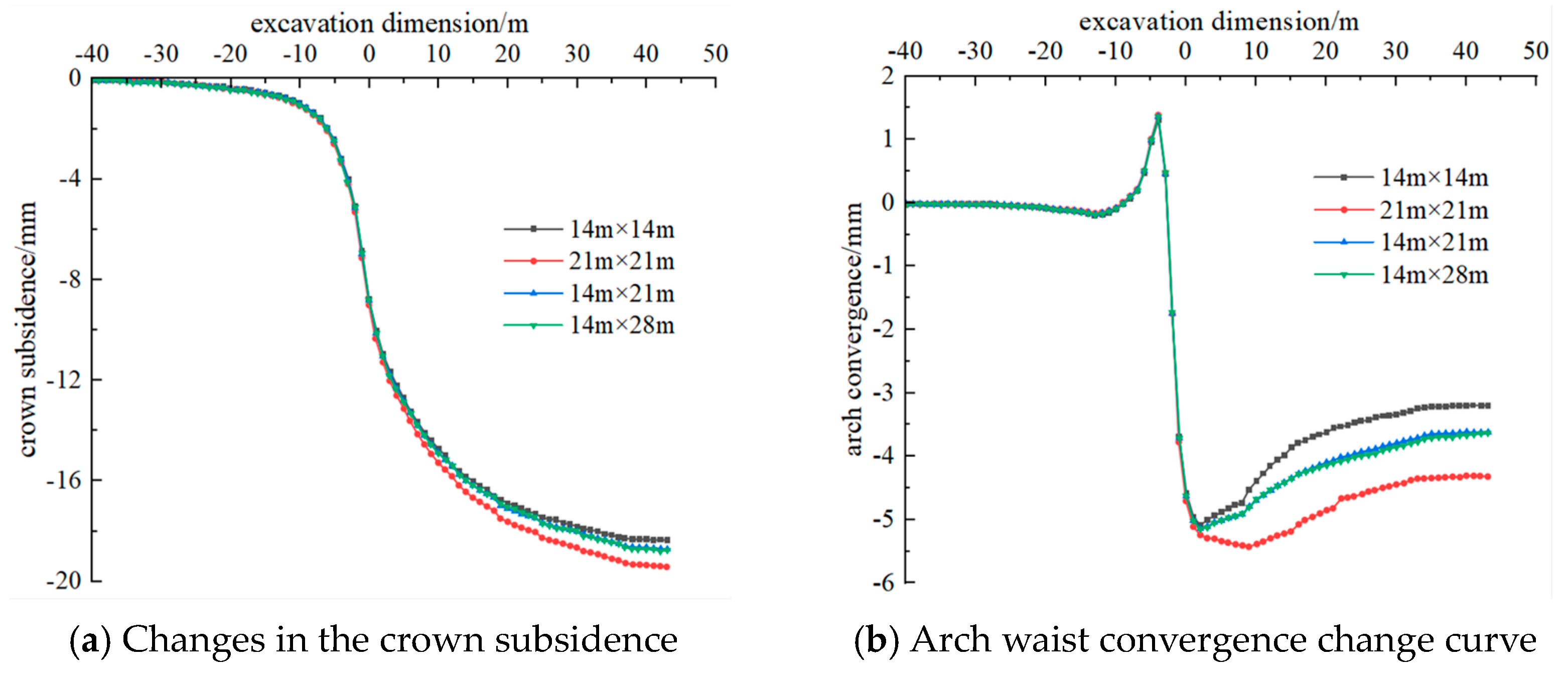
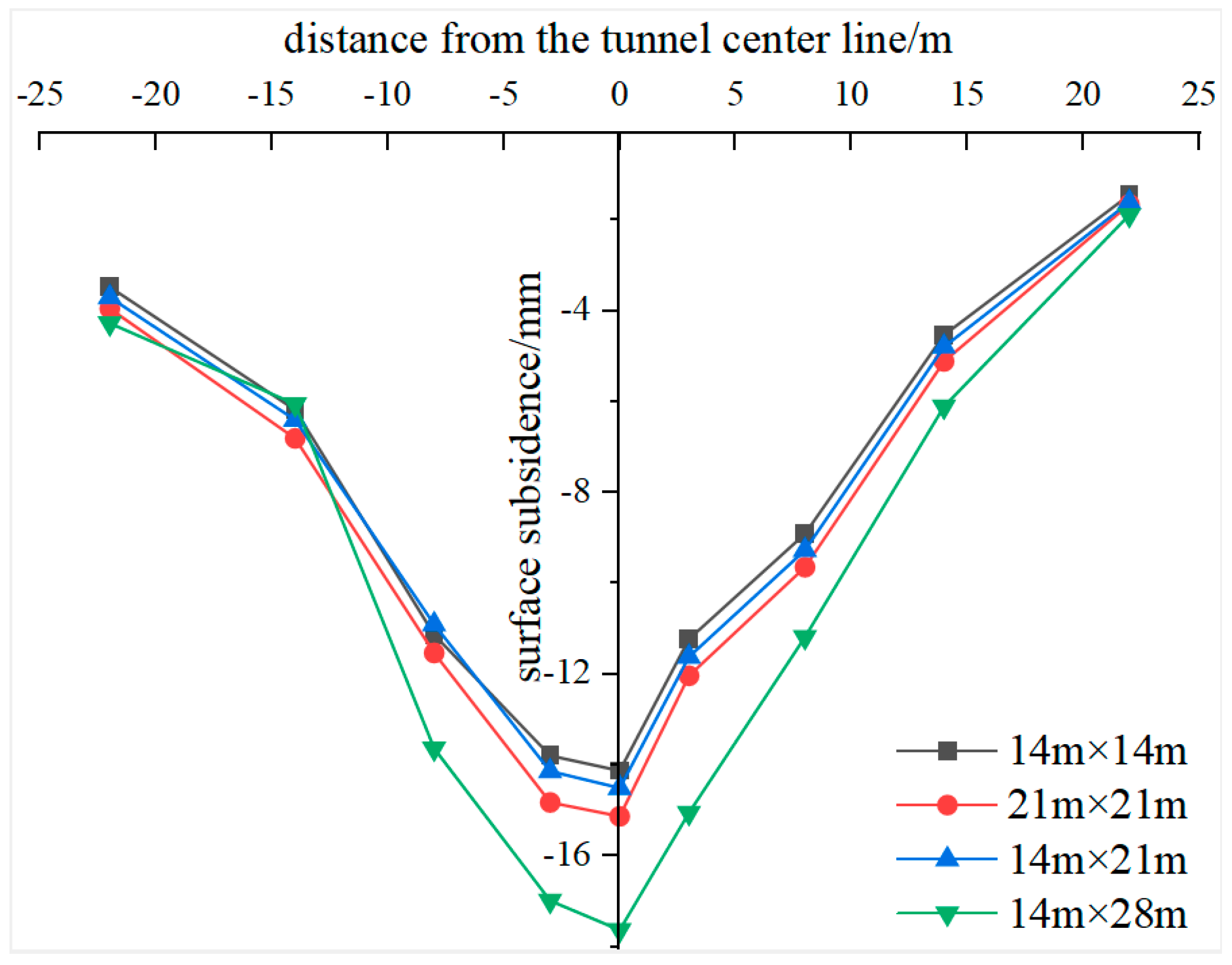
4.1. Deformation Analysis of the Surrounding Rock
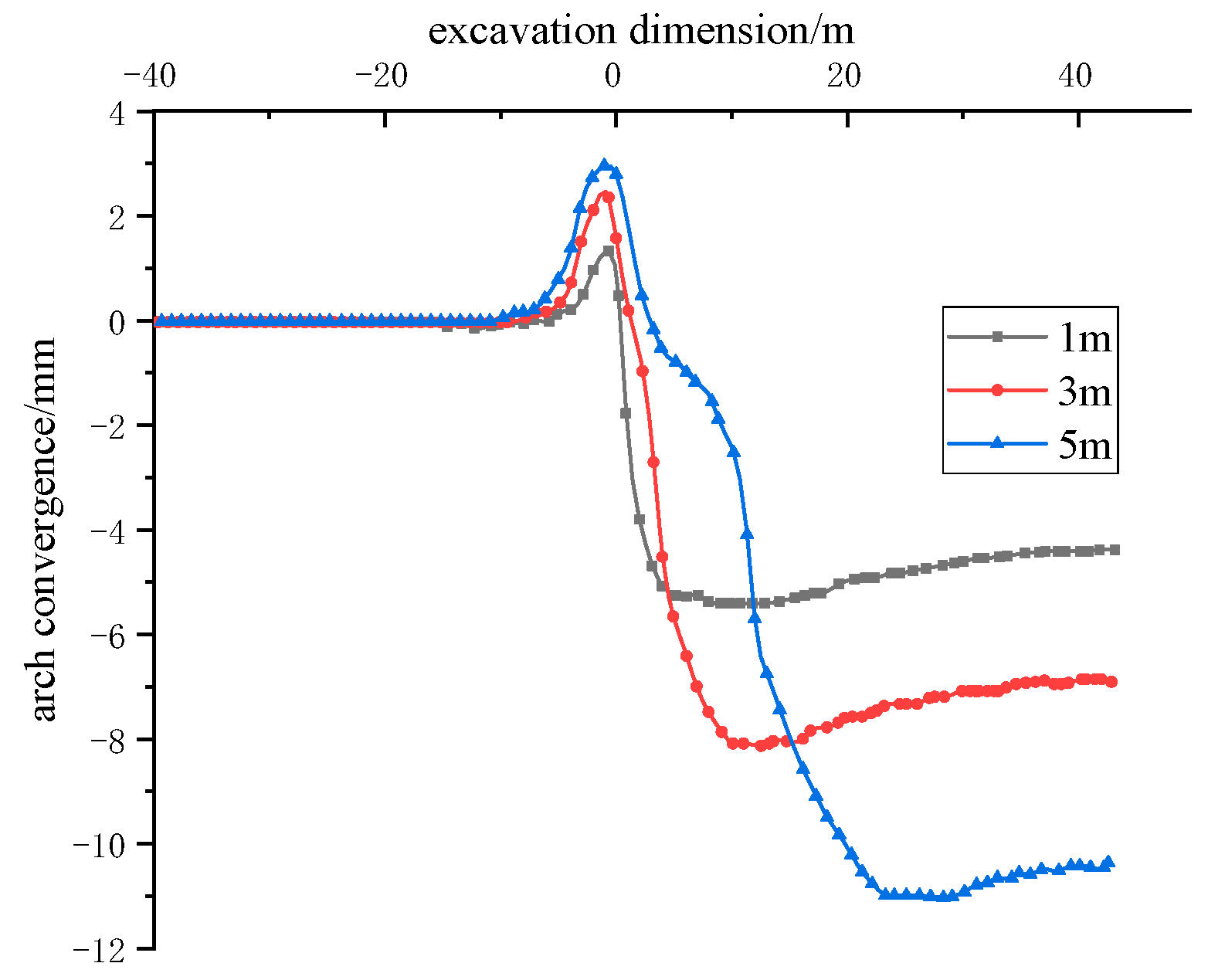
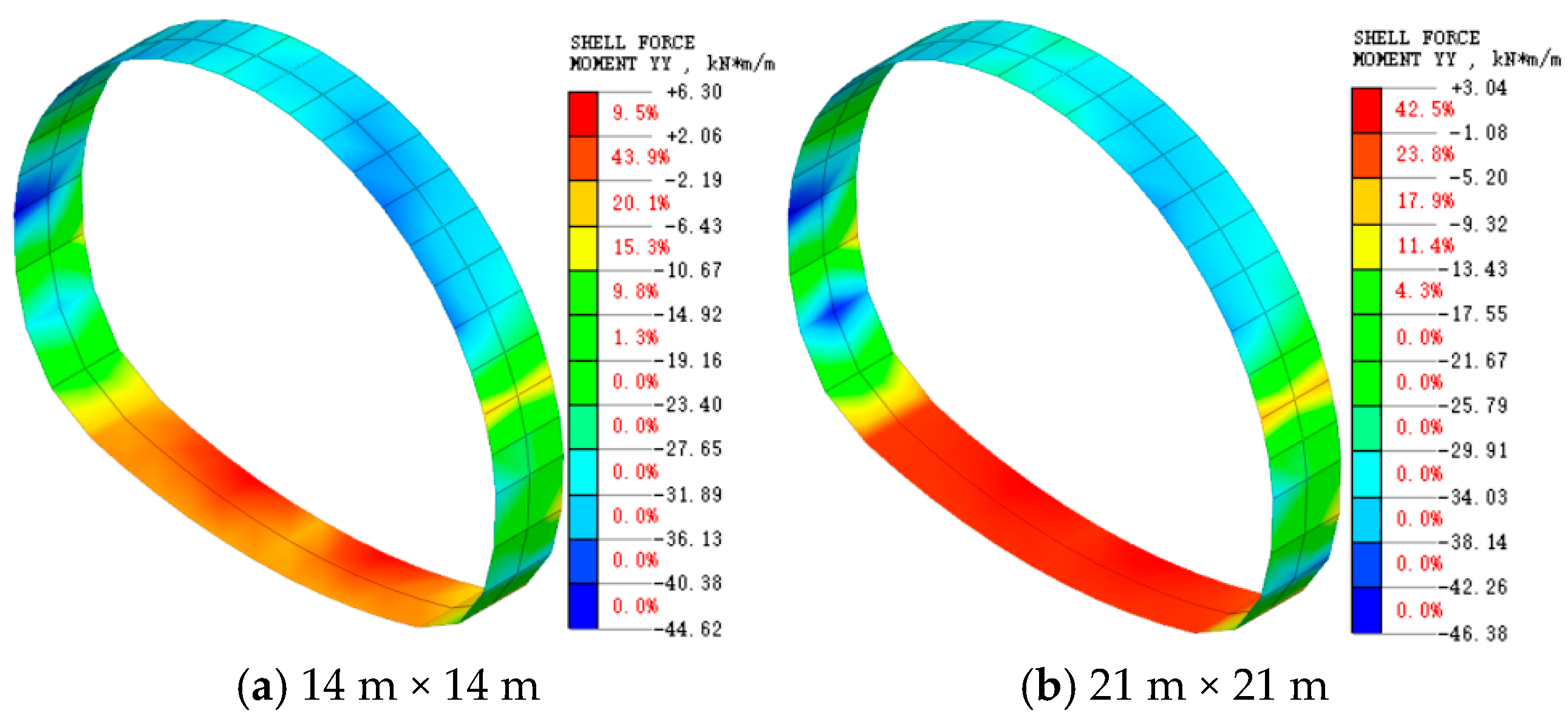
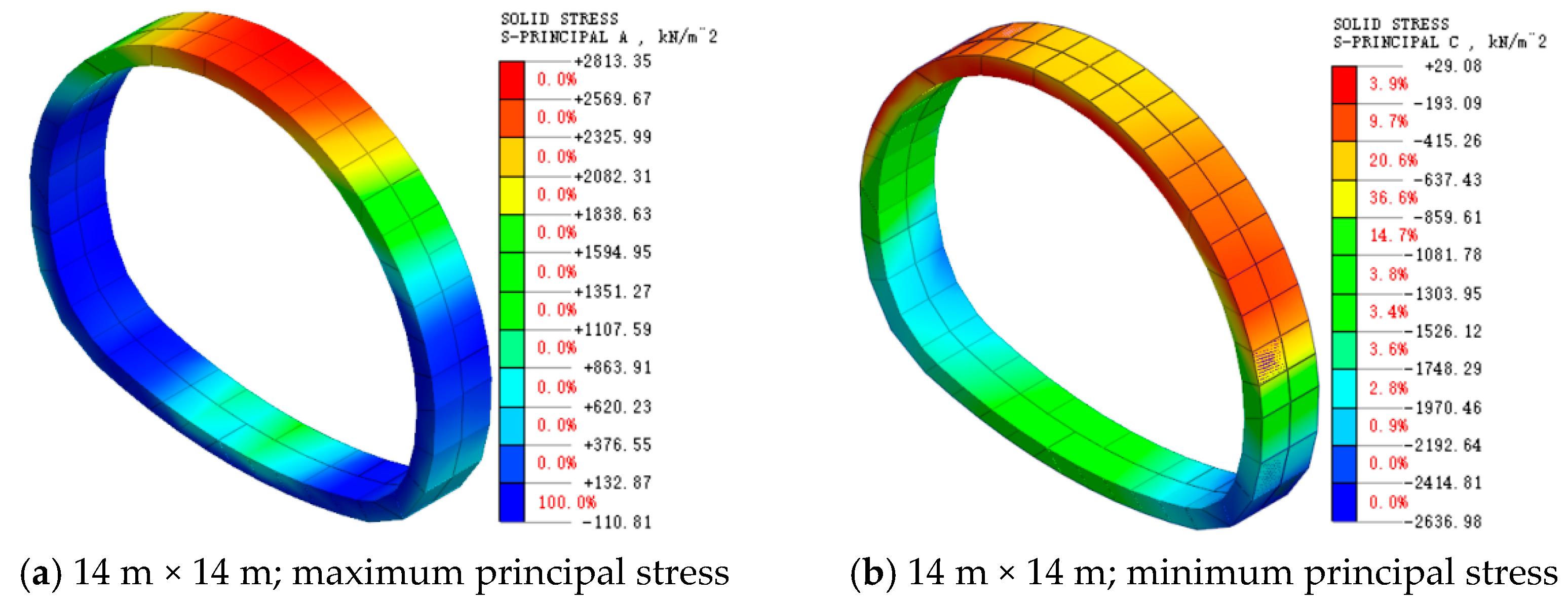
4.2. Initial Support Force Analysis
5. Simulation Study on Lining Time Optimization
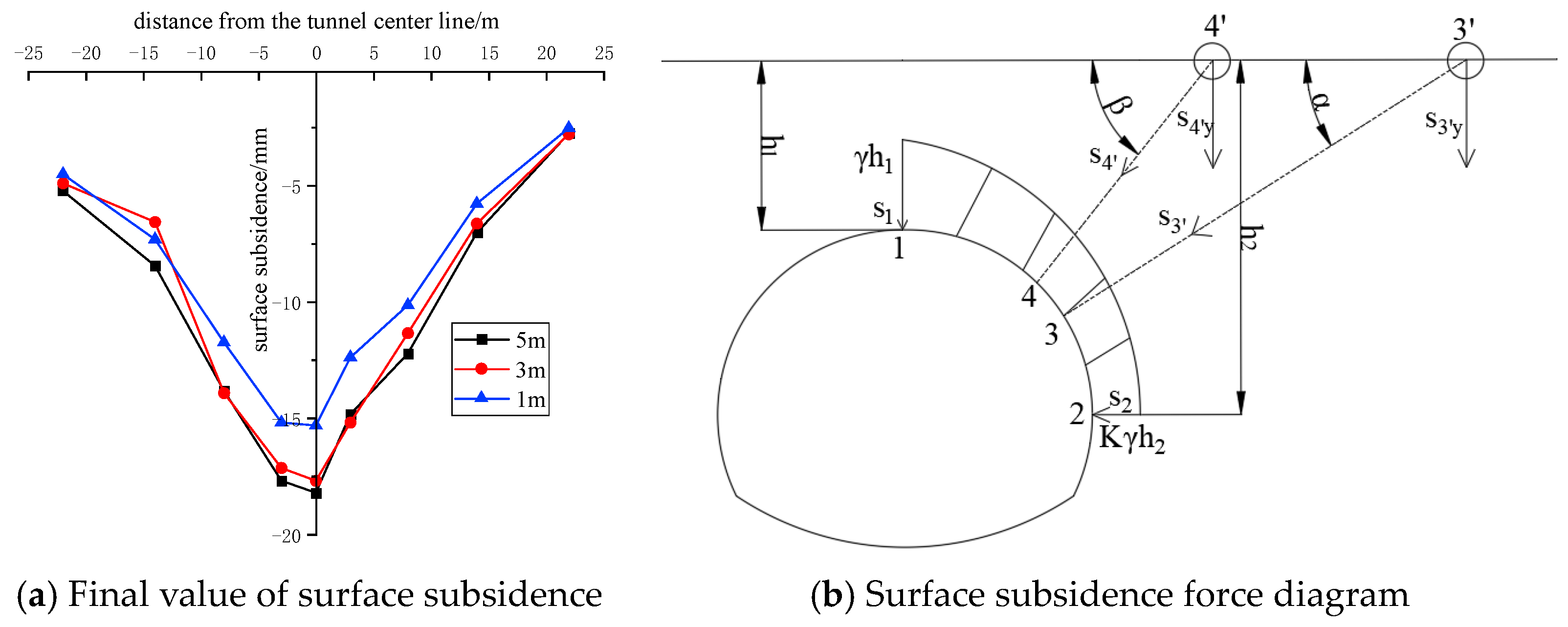
5.1. Deformation Analysis of the Surrounding Rock
5.2. Analysis of the Initial Support Force
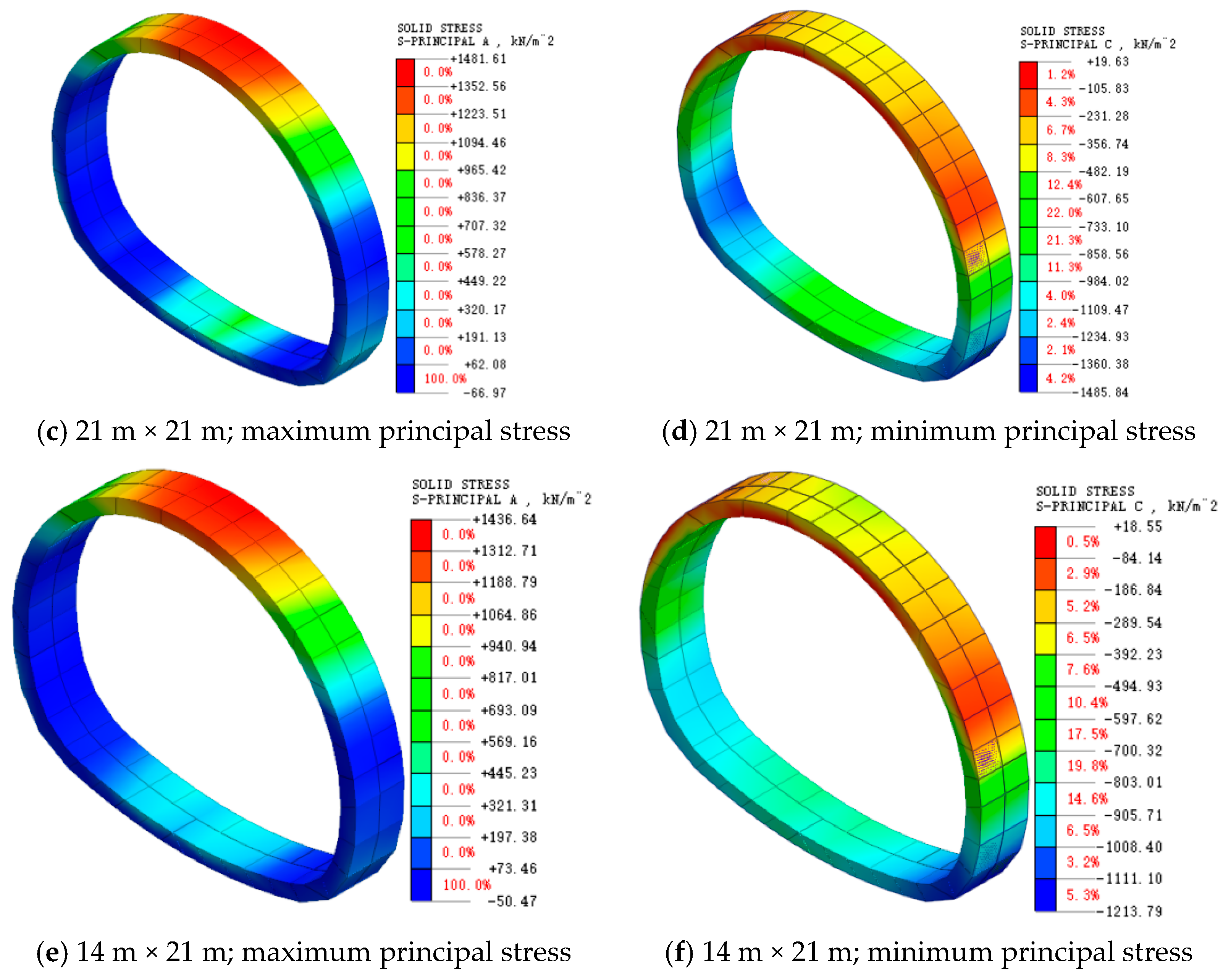
5.3. Secondary Lining Force Analysis
6. Site Construction Monitoring
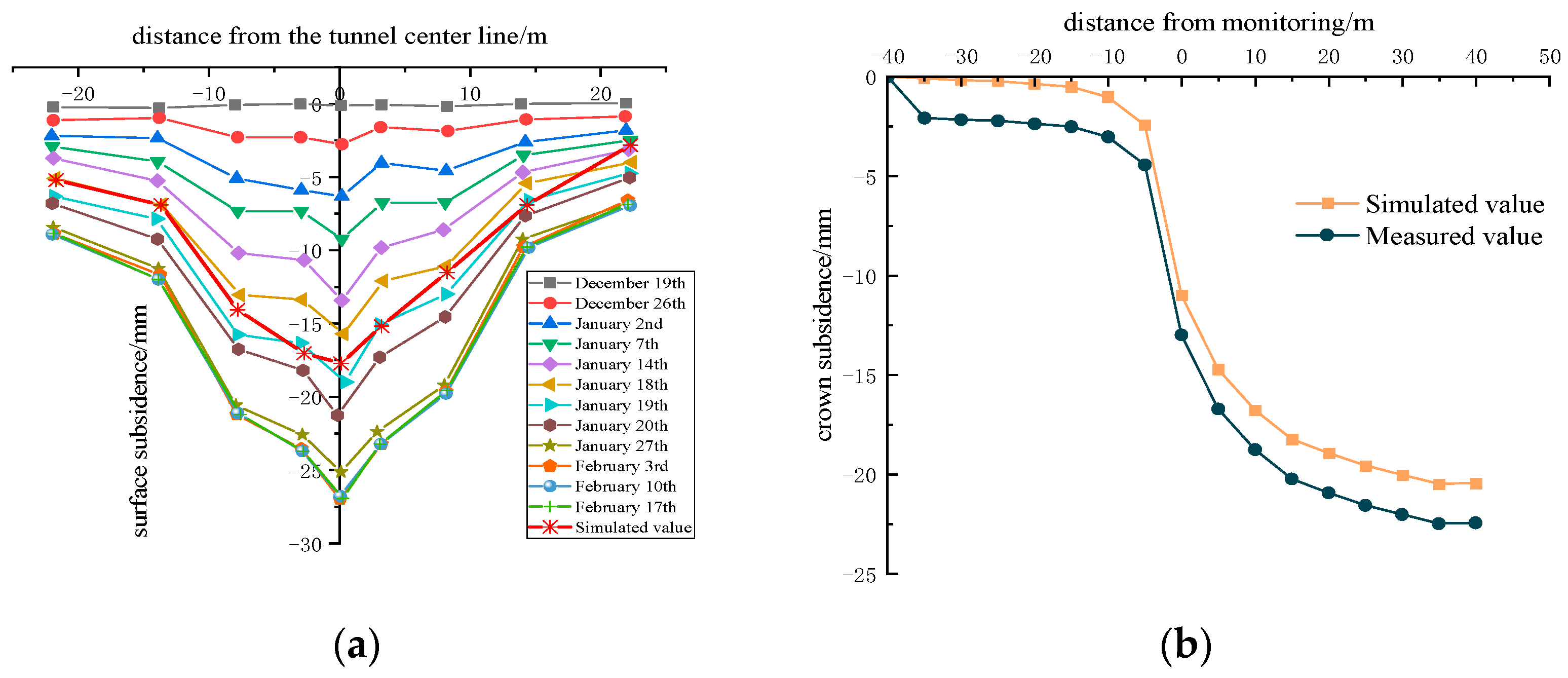
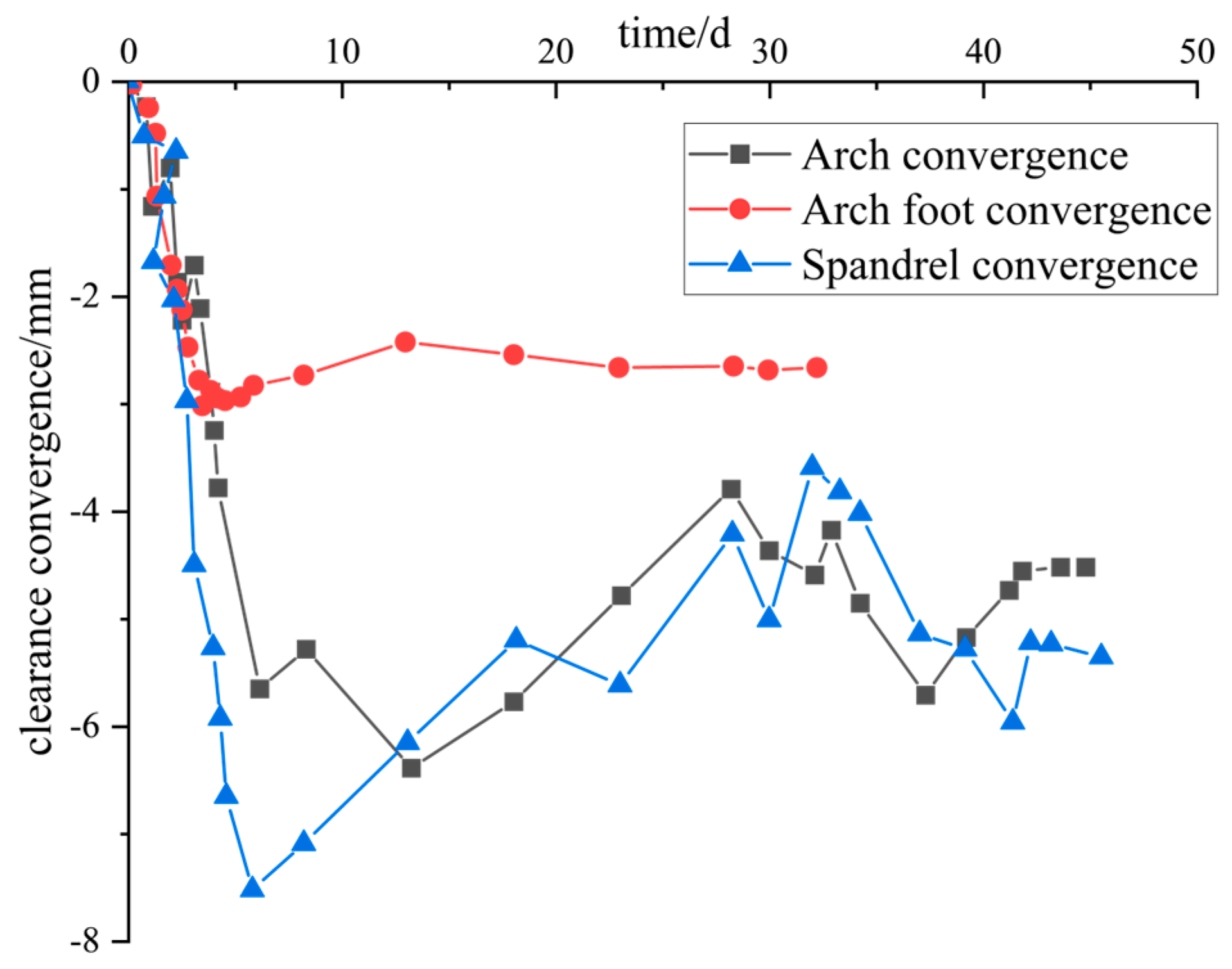
6.1. Analysis of the Monitoring Results of Surrounding Rock Deformation
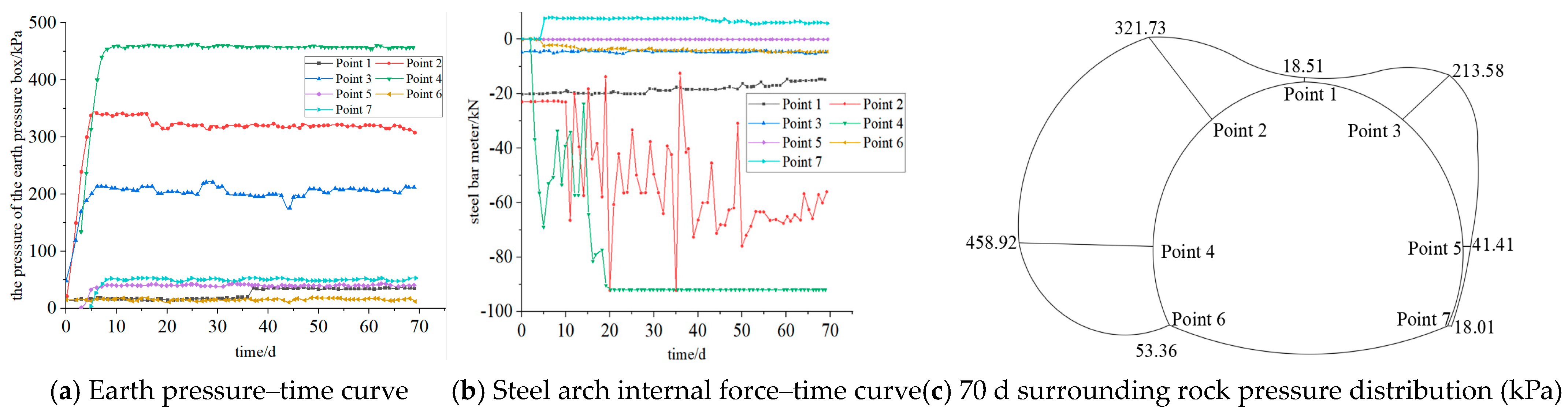
6.2. Analysis of the Monitoring Results of Surrounding Rock Pressure
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, Z.; Liu, Y.; Zhang, Y. Research and prospect of demarcation of deep and shallow buried in loess tunnel. Hazard Comtrol Tunn. Undergr. Eng. 2021, 3, 1–15. [Google Scholar] [CrossRef]
- Zhao, Y.; Bai, M.; Ma, X.; Xie, J.; Mi, W. Application research on the surface grouting in shallow buried loess tunnel with large section. J. Railw. Eng. Soc. 2019, 36, 48–51+99. [Google Scholar]
- Zhang, Y.; Zhang, Z.; Hu, W.; Zhang, Y.; Shi, G.; Wang, Y. Shear Strength of Loess in the Yili Region and Corresponding Degradation Mechanisms under Different Cycling Modes. Water 2023, 15, 3382. [Google Scholar] [CrossRef]
- Ma, J.; Qiu, Y.; Gao, Y.; An, Y.; Duan, Z.; Li, S. Effects of Sample Preparation Methods on Permeability and Microstructure of Remolded Loess. Water 2023, 15, 3469. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, Z.; Xu, C.; Hao, R.; Lv, Q.; Jia, J.; Liang, S.; Zhu, H. Destabilization Mechanism of Rainfall-Induced Loess Landslides in the Kara Haisu Gully, Xinyuan County, Ili River Valley, China: Physical Simulation. Water 2023, 15, 3775. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Wang, W.; Mi, W. Research on the instability mechanism of tunnel face of shallow buried and large section tunnel in loess tableland. J. Railw. Eng. Soc. 2020, 37, 67–72. [Google Scholar]
- Song, Z.; Wu, Y.; Zhou, G.; Pan, H.; Xiao, K. Statistical constitutive model of loess damage and its application in tunnel stability analysis. Chin. J. Undergr. Space Eng. 2023, 19, 640–649. [Google Scholar]
- Tong, J. General formulas for calculating surrounding rock pressure of tunnels and underground spaces. KSCE J. Civ. Eng. 2020, 24, 1348–1356. [Google Scholar] [CrossRef]
- Xue, Y.; Zhang, X.; Li, S.; Qiu, D.; Su, M.; Xu, Z.; Zhou, B.; Xia, T. Sensitivity analysis of loess stability to physical and mechanical properties: Assessment model. Int. J. Geomech. 2019, 19, 06019012. [Google Scholar] [CrossRef]
- Wang, B.; Ye, F.; Guo, H.; Ji, Y.; Lei, P. Research on the mechanical properties of surrounding rock of deep shield tunnel in structural loess. Chin. J. Undergr. Space Eng. 2022, 18, 751–758. [Google Scholar]
- Lee, I.M.; Nam, S.W. The study of seepage forces acting on the tunnel lining and tunnel face in shallow tunnels. Tunn. Undergr. Space Technol. 2001, 16, 31–40. [Google Scholar] [CrossRef]
- Song, Z.; Wang, S.; Su, C.; Pan, H.; Wei, S. Optimization of construction scheme for shallow buried tunnel with small spacing asymmetric section in loess stratum. J. Xi’an Univ. Archit. Technol. 2022, 54, 646–656. [Google Scholar] [CrossRef]
- Yuan, L.; He, W. Study on the application of double-side heading method in the construction of shallow and large section loess tunnel. Chin. J. Undergr. Space Eng. 2022, 18, 289–295. [Google Scholar]
- Hu, S.; Zhang, D. DEM analysis of failure modes of surrounding rock for large-section loess tunnel. J. Beijing Jiaotong Univ. 2013, 37, 13–18. [Google Scholar]
- Lan, H.; Gao, Y.; Li, H. Analysis of settlement deformation of complex geological tunnel construction. Highw. Eng. 2021, 46, 142–148. [Google Scholar] [CrossRef]
- Thomas, K.; Gunther, M. A numerical study of the effect of soil and grout material properties and cover depth in shield tunneling. Comput. Geotech. 2006, 33, 234–247. [Google Scholar] [CrossRef]
- Zhu, T.; Liu, Y. Evaluating construction parameters of HB and CD methods for super large section tunnel: A case study. Sci. Rep. 2023, 13, 15812. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Ding, C.; Dou, S.; Wu, X.; Shu, J. Analysis on deformation characteristics of surrounding rock in large section shallow loess tunnels. Chin. J. Undergr. Space Eng. 2014, 10, 1623–1628. [Google Scholar]
- Liu, Q.; Li, Y.; Li, W.; Zhao, J.; Qin, Z.; Yang, X.; Feng, Q.; Jiang, B.; Wang, K.; Li, Y. Primary support optimization of large-span and shallow buried hard rock tunnels based on the active support concept. Sci. Rep. 2022, 12, 7918. [Google Scholar] [CrossRef]
- Xue, Y.; Ma, X.; Yang, W.; Ma, L.; Qiu, D.; Li, Z.; Li, X.; Zhou, B. Total deformation prediction of the typical loess tunnels. Bull. Eng. Geol. Environ. 2020, 79, 3621–3634. [Google Scholar] [CrossRef]
- Yang, J.; Yu, Y.; Tan, Z.; Zhao, H. Experimental research on the surrounding rock pressure of large sectional loess tunnel under deep and shallow submersion. J. Railw. Eng. Soc. 2009, 2, 76–79. [Google Scholar] [CrossRef]
- Cui, G.; Ma, J.; Wang, D. A large 3D laboratory test on the deformation characteristic of shallow loess tunnel under different plastic states. Bull. Eng. Geol. Environ. 2021, 80, 7577–7590. [Google Scholar] [CrossRef]
- Tan, Z.; Yu, Y.; Wang, M.; Yang, J. Experimental study on bolt effect on large section shallow depth loess tunnels. Rock Soil Mech. 2008, 29, 491–495+506. [Google Scholar] [CrossRef]
- Liu, Y.; Lai, H. Experimental study on lining cracking of shallow buried loess tunnel under the simulation of effect of slide surface immersion. Appl. Sci. 2020, 10, 6080. [Google Scholar] [CrossRef]
- Shinichiro, I.; Toshiyuki, H.; Kenji, M. Settlement trough above a model shield observed in a centrifuge. In Proceedings of the International Conference Centrifuge, Tokyo, Japan, 23–25 September 1998; Volume 9, pp. 23–25. [Google Scholar]
- Xue, X.; Su, Z.; Sun, Z.; Song, F. Analysis of the tunnel disease considering the unsaturated loess matric suction effects. Adv. Mater. Res. 2014, 859, 182–185. [Google Scholar] [CrossRef]
- Chen, P.; Wang, W.; Wu, Z.; Yuan, Q.; Jiang, H.; Zhai, S. Study on deformation characteristics and control measures of shallow large-span loess tunnels. Mod. Tunn. Technol. 2021, 58, 203–211. [Google Scholar] [CrossRef]
- Zhang, Z. Analysis of the influence of different advanced support of shallow railway tunnel with large-section in loess area. Munic. Eng. Technol. 2023, 41, 176–181. [Google Scholar] [CrossRef]
- Luo, Y.; Wu, Y.; Chen, J.; Dong, F.; Liu, W.; Chen, L.; Li, Y.; Shi, Z. Back-calculation method of rock mass pressure in a shallow-buried super large-span tunnel using upper-bench CD method. KSCE J. Civ. Eng. 2022, 26, 433–447. [Google Scholar] [CrossRef]
- Sun, W.; Liang, Q.; Qin, S.; Yuan, Y.; Zhang, T. Evaluation of groundwater effects on tunnel engineering in loess. Bull. Eng. Geol. Environ. 2021, 80, 1947–1962. [Google Scholar] [CrossRef]
- Li, Q.; Su, Z. Analysis of difference in axial force of anchor in shallow-buried loess tunnel with large cross-section. Appl. Mech. Mater. 2012, 204, 1343–1346. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, J.; Gao, S.; Deng, X.; Diao, P. Stability analysis of super-large-section tunnel in loess ground considering water infiltration caused by irrigation. Environ. Earth Sci. 2017, 76, 763. [Google Scholar] [CrossRef]
- TB 10121-2007; Technical Specification for Monitoring Measurement of Railway Tunnel. China Railway Publishing House: Beijing, China, 2007.




| Name of the Material | Gravity/(kN/m3) | Elastic Modulus/kPa | Poisson’s Ratio | Angle of Internal Friction/° | Cohesive Force/kPa | Unloading Elastic Modulus/kPa |
|---|---|---|---|---|---|---|
| Clay loess | 18.40 | 3.50 × 104 | 0.44 | 33.10 | 35.30 | 1.60 × 105 |
| Silt | 18.80 | 2.00 × 104 | 0.23 | 32.00 | 3.00 | 1.00 × 105 |
| Silty loess | 17.50 | 3.00 × 104 | 0.30 | 24.00 | 25.00 | 2.00 × 105 |
| Sandstone | 25.40 | 1.93 × 108 | 0.25 | 27.80 | 27,200.00 | 5.00 × 108 |
| Pipe roof | 4.15 | 1.06 × 108 | 0.30 | - | - | - |
| Initial support | 25.94 | 3.29 × 108 | 0.21 | - | - | - |
| Temporary support | 27.54 | 3.70 × 108 | 0.21 | - | - | - |
| Secondary lining | 24.83 | 3.36 × 108 | 0.21 | - | - | - |
| Advanced small pipe | 0.42 | 1.06 × 106 | 0.30 | - | - | - |
| Lining Time | Final Arch Waist Convergence Deformation (SL03-04)/mm | Final Crown Subsidence/Convergence Deformation (GD00)/mm |
|---|---|---|
| 14 m × 14 m | −3.19 | −18.29 |
| 21 m × 21 m | −4.30 | −19.34 |
| 14 m × 21 m | −3.62 | −18.67 |
| 14 m × 28 m | −3.62 | −18.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, F.; Li, W.; Song, Z.; Wang, J.; Zhang, Y.; Liu, N.; Xiao, K.; Wang, Y. Construction Stability Analysis and Field Monitoring of Shallowly Buried Large-Section Tunnels in Loess Strata. Water 2024, 16, 2192. https://doi.org/10.3390/w16152192
Zheng F, Li W, Song Z, Wang J, Zhang Y, Liu N, Xiao K, Wang Y. Construction Stability Analysis and Field Monitoring of Shallowly Buried Large-Section Tunnels in Loess Strata. Water. 2024; 16(15):2192. https://doi.org/10.3390/w16152192
Chicago/Turabian StyleZheng, Fang, Wenqiang Li, Zhanping Song, Jiahui Wang, Yuwei Zhang, Naifei Liu, Kehui Xiao, and Yan Wang. 2024. "Construction Stability Analysis and Field Monitoring of Shallowly Buried Large-Section Tunnels in Loess Strata" Water 16, no. 15: 2192. https://doi.org/10.3390/w16152192
APA StyleZheng, F., Li, W., Song, Z., Wang, J., Zhang, Y., Liu, N., Xiao, K., & Wang, Y. (2024). Construction Stability Analysis and Field Monitoring of Shallowly Buried Large-Section Tunnels in Loess Strata. Water, 16(15), 2192. https://doi.org/10.3390/w16152192






