Abstract
The regulation of upstream cascade reservoirs has significantly altered the downstream hydrologic regime and should be taken into account in design flood estimation. The current flood regional composition (FRC) methods do not consider the unfavorable situations for reservoir flood control operation. In this paper, a novel framework, the most unfavorable flood regional composition (MUFRC) method, was proposed based on flood risk analysis to estimate design flood in the cascade reservoir operation period. The cascade reservoirs in the Yalong River basin were selected as a case study. The results indicated that (1) the proposed MUFRC method would allocate more flood volume to the downstream uncontrolled sub-basin, and the precise definition of flood disaster loss could have a significant impact on the MUFRC method for the rational estimation of design flood. (2) The 1000-year design flood peak, and 3-day and 7-day flood volumes at the outlet section estimated by the MUFRC method are 15,400 m3/s, 3.91, and 8.42 billion m3, respectively, which are higher than the values estimated by other FRC methods. (3) The flood control water level in the downstream reservoir can be adjusted for the reduction in design floods in the operation period, which can additionally generate 460 million kW·h (+1.82%) of hydropower during the flood season. A comparison study and sensitivity analysis further proved that the MUFRC method can rationally allocate flood volume while balancing the flood risk and comprehensive utilization benefits, which is worth further study and practical application.
1. Introduction
The operation of cascade reservoirs has altered the downstream hydrologic regime, and the flow discharge hydrograph has also undergone considerable temporal and spatial changes [,]. In the reservoir planning and construction periods, design flood is typically estimated based on natural annual maximum flood data series []. Hence, how to consider the regulation of upstream reservoirs and estimation of the “design flood in cascade reservoir operation period” has become a hot research topic for the effective utilization of flood water resources []. Meanwhile, reservoir operation should always consider and balance the flood hazard risk and comprehensive utilization benefits [,], which is well worth including in the estimation of unfavorable downstream design flood [,].
Two approaches, i.e., the non-stationary flood frequency analysis (NFFA) method and flood regional composition (FRC) method, have been widely used to estimate design flood considering the impact of climate change and human activities (primarily reservoir regulation) [,,,]. The former requires measured flood data series in the design section, while the latter needs restored natural flood data series. The NFFA method defines time-varying covariates relevant to design flood factors and fits a time-varying distribution model []. With recent values of covariates input into the fitted model, the characteristic feature of design flood in the operation period could be derived []. The selection of covariates would significantly influence the accuracy and rationality of the NFFA method. For example, reservoir index (RI), defined by reservoir capacity and catchment area, has been widely applied and has successfully recognized the downward trend of the downstream flood []. However, the RI indicator was unable to explain why and how the design flood was reduced and which hydrological mechanism corresponded to the RI-caused reduction in frequency analysis, let alone derive an hourly design flood hydrograph after flood control operation and channel flow routing [,]. Thus, the NFFA method might be more suitable for large and complex basins with massive reservoirs, where the natural flood data series are very difficult to restore.
Based on the mechanism of runoff generation and the flow concentration process, the FRC method allocates the downstream design flood to each sub-basin []. With the allocated floods controlled and regulated by hydraulic structures, the design flood in the operation period can be estimated using reservoir outflow discharge, river channel flow routing, and inter-basin inflow discharge []. In this way, the complicated operation rules and flood routing pattern can be constrained, and the design flood in the operation period influenced by cascade reservoirs can be derived in the design section level by level. The FRC method has been widely applied in design flood estimation in China [], whose key point is the rational allocation of flood volume to each sub-basin.
The Ministry of Water Resources (MWR) of China has recommended some methods for downstream design flood estimation, among which the equivalent-frequency flood regional composition (EFFRC) method was the most classic and practical one []. The EFFRC method assumed that the flood frequency of the upstream reservoir or inter-basins was identical to that of the downstream design section. In other words, it implicitly suggested that the flood data series in the designative sub-basin and design section were fully related, with a correlation coefficient equal to one, so their cumulative distribution function (CDF) all responded to the design frequency p. This basic assumption obviously neglected the uneven rainfall distribution and randomness in flood magnitudes, which limited the EFFRC method to only being suitable for highly correlated basins []. Besides, the number of EFFRC schemes exponentially increased with the number of reservoirs, which also made the selection of a representative EFFRC scheme more difficult. Guo et al. [] proposed the most likely flood regional composition method (MLFRC) with the maximum probability of flood allocation to investigate the downstream design flood, which was proved to be more reasonable and practical through statistical experiments. The copula functions were also introduced into the MLFRC method to describe the joint distribution of flood volumes from various sub-basins. The application of the EFFRC and MLFRC methods suggested that the upstream reservoir regulation has significantly reduced the peak discharge and flood volume in the downstream section, and thus the flood control water level in the reservoir operation period might need a re-evaluation owing to the differences between the design flood hydrographs in the reservoir construction and operation periods [,].
The current FRC methods tend to derive a rational flood volume allocation scheme in view of a probability and statistics analysis, and neglect to consider flood risk under unfavorable situations. Hence, this paper proposed a novel FRC method, i.e., the most unfavorable flood regional composition (MUFRC) method, which considers the flood occurrence probability and flood disaster loss. The flood occurrence probability can be effectively estimated by copula functions [,], while the flood disaster loss still requires a reasonable definition. Since flood damage is tightly associated with peak discharge and flooding duration [,], the additional suffered flood volume was selected and used to symbolize flood disaster loss in this study. The additional suffered flood volume is further categorized as excessive flood volume from the uncontrolled inter-basin, where there are no reservoirs to regulate the flow discharge from the ungagged sub-basin adjacent to the design section.
The aim of this study was to propose a novel framework for the investigation of the most unfavorable design flood in the cascade reservoir operation period. The novelty of this work included (1) the most unfavorable flood regional composition (MUFRC) method, which was proposed based on flood risk analysis to estimate design flood in cascade reservoir operation period. (2) All aspects of performance and applicable conditions for different FRC methods were quantitatively analyzed and compared by statistical experiments. A similar study has not been reported in the literature until now. The rest of the paper is organized as follows: Section 2 introduces the methodology of the FRC framework and proposes a novel MUFRC method. In Section 3, the cascade reservoirs in the Yalong River basin are selected as a case study to demonstrate the effectiveness of the proposed approach in real-world conditions, in which the design flood and flood limit water level in the operation period are derived, and their corresponding power generation benefits are estimated. Section 4 discusses and compares different FRC methods via statistical experiment schemes. Finally, the conclusion is given in Section 5.
2. Methodology
2.1. Copula Function
Assuming that there are random variables X1, X2, …, Xn, whose marginal distribution functions can be expressed as F1(x1), F2(x2), …, Fn(xn), respectively, and the joint distribution function is expressed as H(x1, x2, …, xn), then according to Sklar’s theorem, there is a function C satisfying the following equation []:
Function C is called the copula function. Representing F1(x1), F2(x2), …, Fn(xn) with u1, u2, …, un, and letting xi = Fi−1(ui), Equation (1) can be rewritten as [,]:
Hence, the joint probability density function of H can be derived as:
where c denotes the mixed partial derivative of C. In flood frequency analysis, Archimedean copulas were always applied to bivariate simulation, while t-copula and vine copula were more recommended for high-dimensional systems [].
2.2. Flood Regional Composition (FRC) Method
Cascade reservoirs have significantly altered the downstream hydrologic regime and have had a sizeable impact on the design flood hydrograph. The FRC method can reallocate the original design flood in the construction period into each sub-basin according to representative flood volume rates. Additionally, with the simulation of flood control and routing from upstream to downstream, the design flood hydrograph in the operation period can finally be derived.
A sketch diagram of the FRC method is shown in Figure 1. A cascade reservoir system composed of n reservoirs divides the basin into n + 1 sub-basins. As shown in Figure 1, Ai, Bi, and C represent the i-th upstream reservoir, the i-th inter-basin, and the design section, respectively, whose inflows are represented as random variables Xi, Yi, and Z with corresponding values of xi, yi, and z, respectively.
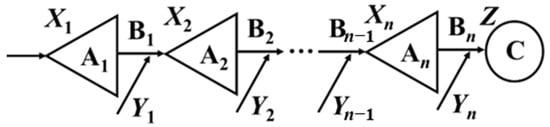
Figure 1.
Sketch diagram of flood regional composition framework.
2.3. Equivalent-Frequency Flood Regional Composition (EFFRC) Method
The EFFRC method assumes that equivalent-frequency floods are more likely to occur among highly correlated adjacent sub-basins, which has been recommended by the MWR and proved to be a convenient reference in practice []. Taking a single reservoir system as an example for illustration:
- (1)
- If both design floods in the downstream section and upstream reservoir are equal in design frequency p, and their flood volumes are represented as zp and xp, then according to the principle of water balance, the flood volume y at inter-basin B is given by zp − xp. So, [xp, zp − xp] was one of the EFFRC schemes for a single reservoir system.
- (2)
- If design floods in the downstream section and interval basin B are equal in frequency, then similarly, the flood volume X at the upstream reservoir A site is given by x = zp − yp, and [zp − yp, yp] was the other EFFRC scheme for a single reservoir system.
[xp, zp − xp] and [zp − yp, yp] serves as the basic schemes for the EFFRC method. For the cascade reservoir system, as the number of reservoirs (n) increases, the research basin can be divided into n single reservoir sub-systems from downstream to upstream one by one, and then the number of EFFRC schemes (2n) increases dramatically based on the possible choice of basic schemes in each sub-system.
2.4. Most Likely Flood Regional Composition (MLFRC) Method
The probability density of the FRC scheme (x1, y1, y2, …, yn) is estimated by copulas, and its higher value is considered more reasonable and representative in the MLFRC method. Hence, the MLFRC scheme can be obtained when the copula-fitted joint distribution f(x1, y1, y2, …, yn) is maximized within the principle of water balance []:
where u1 and vi denote the corresponding cumulative distribution functions (CDFs) of x1 and yi; fX1(x1) and fYi(yi) denote the marginal distributions of floods at upstream reservoir A1 and each inter-basin Bi, respectively; c(·) denotes the derivative of the copula function.
Xiong et al. (2020) recommended the genetic algorithm (GA) to solve the MLFRC method for a high-dimensional cascade reservoir system with the flood volumes in each sub-basin coded and optimized, in which the principle of water balance served as the constraint condition to prevent unrealistic solutions [].
2.5. Most Unfavorable Flood Regional Composition (MUFRC) Method
The EFFRC method searches the composition of flood volumes whose CDFs are equal to the design frequency, implicitly assuming that the flood data series in all sub-basins are completely linearly correlated. The MLFRC method tends to search for the scheme with the highest probability density, which is able to fully consider the correlation of flood generation []. This section proposes the MUFRC method based on flood risk analysis, which is aimed at solving FRC schemes with the maximum product of excessive flood volume and its probability of occurrence.
There are various mathematical definitions of risk R. The United Nations Department of Humanitarian Affairs [], now reorganized as the United Nations Office for the Coordination of Humanitarian Affairs, stated that risk is the product of hazard and vulnerability. Sun et al. [] and Qi [] pointed out that for flood risk, the hazard is usually described by the probability of occurrence PR, and the vulnerability is embodied by the disaster loss DR. Hence, the risk for a specific flood disaster event can be quantified as R = PR × DR.
The probability of occurrence PR can be effectively estimated by Equation (4), similar to the MLFRC method, while the disaster loss DR is very difficult to accurately estimate. Generally, the flood disaster loss is tightly associated with the additional suffered flood volume at the downstream flood control section. Since the essence of the FRC method is the rational allocation of flood volumes, the flood vulnerability is set as the excessive flood volume from the uncontrolled sub-basins in this paper. As shown in Figure 1, the flood volumes X1, Y1, …, Yn−1 from the upstream basins are regulated by cascade reservoirs, while Yn directly threatens the flood security of the downstream section []. Hence, the more the flood volume is allocated to the uncontrolled sub-basins, the larger the uncontrolled flood loss is. Therefore, disaster loss DR is defined as follows:
where denotes the flood volume assigned to the n-th uncontrolled sub-basin in the EFFRC method, which is exactly regarded as the designed controllable flood volume for the downstream section; Δyn denotes the additional suffered uncontrolled flood volume.
Then, the MUFRC scheme (, , , …,) can be maximized within the principle of water balance in following equation:
2.6. Design Flood Estimation in Cascade Reservoir Operation Period
Figure 2 represents the estimation procedure of the most unfavorable design flood in the reservoir operation period. Firstly, similar to the traditional frequency analysis, the marginal distributions should be fitted with P-III curves based on the natural annual maximum flood series []. Then, the joint distributions are fitted with copulas [,], and the MUFRC method is solved based on the assumption that additional suffered flood volume from uncontrolled sub-basin would threaten downstream security. Flood volume is allocated by the MUFRC method for each sub-basin based on the principle of water balance []. Finally, design flood in the reservoir operation period is estimated and the flood control water level is derived using an unchanged flood control standard (the highest water level in reservoir operation) [].
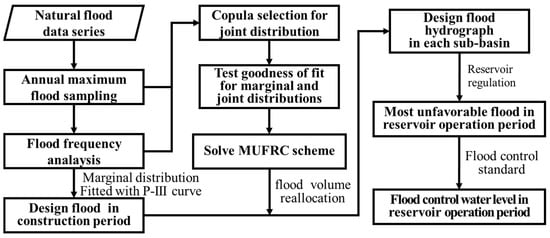
Figure 2.
Flow chart of design flood estimated by MUFRC method in cascade reservoir operation period.
3. Case Study
3.1. Cascade Reservoirs in the Yalong River Basin
The Yalong River is located in the east of the Qinghai–Tibet Plateau, China, with a geographical location between 26°32′ and 33°58′ N, and 96°52′ and 102°48′ E. As the largest tributary of the upper Yangtze River, its entire basin is shaped like a north–south strip, with an average width of about 137 km. The elevation varies from 5400 m to 980 m above sea level, which gathers 33.72 million kW theoretical hydropower resources for development and utilization. The Yalong River hydropower base ranks third in “China’s Thirteen Largest Hydropower Base Plan”. Figure 3 shows the location of seven reservoirs that have been built in the middle and low reaches of the Yalong River along the mainstream, and Table 1 lists their basic information, namely Lianghekou (LHK), Yangfanggou (YFG), Jinping-1 (JP1), Jinping-2 (JP2), Guandi (GD), Ertan (ET), and Tongzilin (TZL). All seven reservoirs were constructed for the purpose of hydropower generation, among which LHK, JP1, and ET are the main controlled reservoirs additionally designed for flood control. A total of 4.5 billion m3 flood control storage capacity is allocated as 2.0, 1.6, and 0.9 billion m3 for LHK, JP1, ET, respectively.
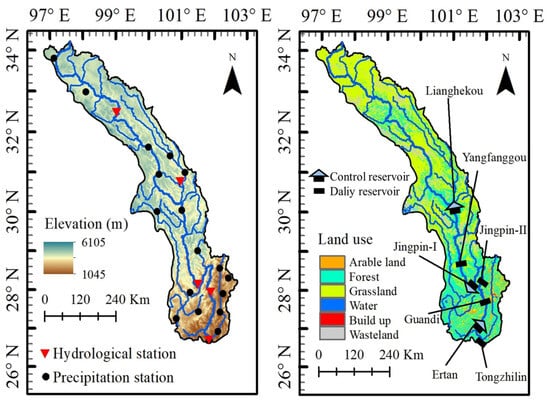
Figure 3.
Sketch location map of cascade reservoirs in the Yalong River.

Table 1.
Basic information of cascade reservoirs in the Yalong River.
The flood volume of the Yalong River basin is distributed into the LHK reservoir, L-J inter-basin, J-E inter-basin, and E-T inter-basin according to the three controlled reservoirs and downstream outlet section TZL. The 1000-year design flood was estimated and compared with original values designed in the reservoir construction period.
3.2. The Marginal Distribution of Flood Data Series
According to the characteristics of runoff and cascade reservoirs in the Yalong River basin, the annual maximum 7-day (abbreviated as 7 d below) flood volume data series from the TZL section is important for flood control. The P-III distribution was chosen to fit the marginal distribution of the 7 d flood volume data series, which was commonly used in China for design floods in the construction period []. The density function of P-III distribution was expressed as follows:
where a0, α, and β are the location, shape, and scale parameters of the P-III distribution, respectively.
For illustration only, the marginal CDF of the 7 d flood volume data series for LHK, JP1, ET, and TZL are plotted in Figure 4, respectively. The sample points (blue point) fell within a narrow range of the theoretical distribution curve (black line), and all passed the Kolmogorov–Smirnov test within the 5% significance level (PKS > 0.05), both of which confirmed that the P-III distribution could adequately match the marginal distribution of the annual maximum 7 d flood volume data series.
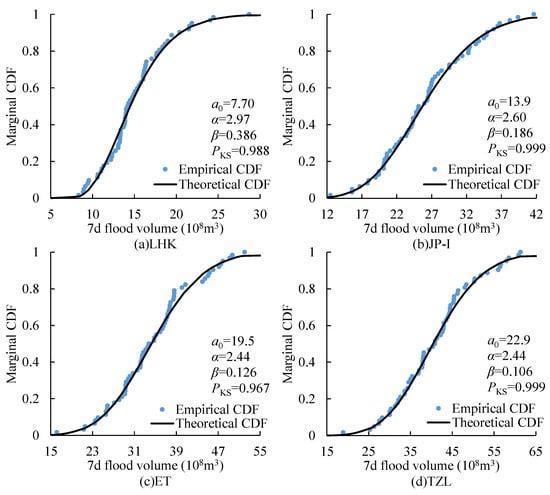
Figure 4.
Cumulative distribution of annual maximum 7 d flood volume data series fitted by P-III distributions at four (LHK, JP, ET, and TZL) cascade reservoirs. PKS denotes the result of Kolmogorov–Smirnov test.
3.3. The Joint Distribution of Flood Data Series
Archimedean copulas, t-copula, and vine copula were sequentially applied to fit the joint distributions of the 7 d flood volume data series at the TZL section. The functions of Gumbel copula (CG), Clayton copula (CC), Frank copula (CF), and t-copula (CT) were expressed by the following equations, respectively:
where τ denotes Kendall’s tau coefficient and θ denotes the parameter of the copula function; Tv−1 and TΣ,v−1 denote the inverse functions of the t-distribution for univariate and multivariable, respectively; v denotes the degree of freedom; Σ denotes the correlation matrix. Vine copula can be expressed as the topological connections among other basic copulas.
The primary criterion for evaluating the goodness of fit was the lowest value of the Akaike Information Criterion (AIC), which is defined as follows:
where k denotes the count of copula parameters; MLK denotes the maximum likelihood function. Meanwhile, the root mean square error (RMSE) between empirical and theoretical frequencies and the Kolmogorov–Smirnov test were also used for goodness of fit.
As shown in Table 2, vine copula described the joint distribution of the 7 d flood volume data series precisely for each sub-basin with minimum AIC and RMSE values, and the Kolmogorov–Smirnov test also presented an excellent goodness of fit. The P-P plot of the theoretical and empirical CDFs shown in Figure 5 also indicated that the 7 d flood volume data series conformed to the specified vine copula with the scatters narrowed around the 1:1 line.

Table 2.
The goodness of fit for 7 d flood volume joint distribution with different copulas.
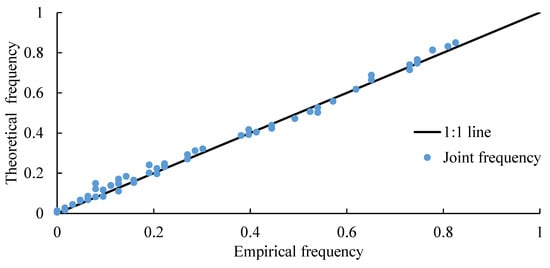
Figure 5.
The scatters of empirical frequency and theoretical frequency of annual maximum 7 d flood volume data series fitted by vine copula.
3.4. Design Flood Estimated by Three FRC Methods
After selected the marginal and joint distributions, the GA algorithm was applied to solve the FRC methods, whose parameters were set as follows: population size = 100, generation = 500, crossover rate = 0.95, and mutation rate = 0.05. The EFFRC, MLFRC, and MUFRC methods were used to estimate design flood at the TZL section. Figure 6 compares the 1000-year design 7 d flood volumes estimated by the three FRC methods at the TZL section. It is worth mentioning that the Yalong River is located in a mountain region with a high correlation between floods in adjacent sub-basins, with a Pearson correlation between 0.72 and 0.97. As a result, there were not any notable differences between those FRC methods. Details about FRC differences and Pearson’s correlation will be further discussed in Section 4.3.
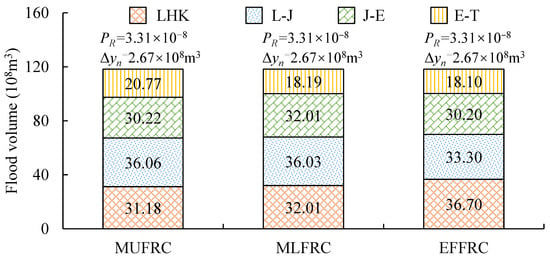
Figure 6.
Comparison of 1000-year design 7 d flood volumes estimated by three FRC methods at the TZL section, where PR and Δyn denote the probability of occurrence and flood disaster loss indicators.
In the case study of the Yalong River basin, the EFFRC method tended to allocate more flood volume to the upstream reservoir (LHK) and less to the downstream inter-basin (E-T sub-basin). Meanwhile, the MLFRC allocated more flood volume to the J-E and E-T sub-basins within the correlation and occurrence pattern of floods in each sub-basin. As defined in Equation (6), MUFRC modifies the MLFRC method with the weight of additional suffered flood volume at the downstream section. Hence, the MUFRC scheme allocated more flood volume to the E-T inter-basin, which was unfavorable for flood control operation at the basin outlet.
As shown in Figure 6, the flood risk in the MLFRC scheme was also insignificant, with a small value of Δyn, and its probability density was not significantly higher than other FRC schemes, which still failed to satisfy the security requirement of design flood. As its definition suggests, MUFRC schemes would result in the greatest flood hazard risk and allocated the largest 7 d flood volume to the E-T sub-basin, whose R = PR × Δyn was almost 17 times that of MLFRC.
Table 3 compares the 1000-year design floods estimated by the three FRC methods with the original values designed in the construction period at the TZL section. Figure 7 plots the 1000-year design flood hydrographs derived by the three FRC methods and the original hydrograph designed in the construction period at the TZL section. The results indicated the following:

Table 3.
Comparison of 1000-year design floods estimated by three FRC methods with original values designed in construction period at TZL section.
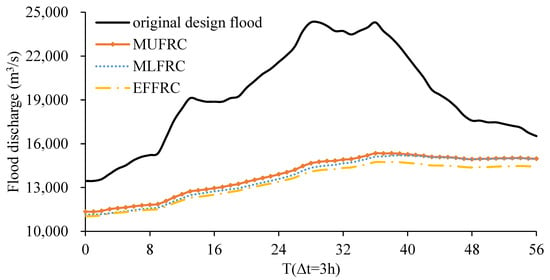
Figure 7.
Comparison of 1000-year design flood hydrographs derived by three FRC methods with original hydrograph designed in construction period at TZL section.
- (1)
- The full utilization of flood control storage in upstream reservoirs has significantly changed the flood characteristic features at the downstream section. Compared with the originally designed values, the annual maximum peak discharge and maximum 1 d, 3 d, and 7 d flood volumes estimated by the MUFRC method at the TZL design section decreased by 36.6%, 36.1%, 33.0%, and 28.7%, respectively.
- (2)
- Traditionally, flood control standards define the highest water level for flood control during reservoir operation using a design flood hydrograph, which starts from the flood limit water level. Since the downstream flood control pressure has been lessened by the regulation of upper cascade reservoirs, the originally designed flood limit water level might fail to adapt to these alterations and could be redesigned for more benefits. Through reservoir operation and flood routing calculation, the flood control water levels of downstream controlled reservoirs like JP1 and ET could be appropriately derived with the flood prevention standard unchanged. Compared with the originally designed flood limit water level, the flood control water levels were increased by 3.39 m and 2.59 m, respectively.
- (3)
- The rise in flood control water level would correspondingly increase the net head of hydropower generator units. The redesigned water level could increase the total of hydropower generation (HG) in the Yalong River basin from 45.58 to 46.22 billion kW·h (+1.82%) during the flood season, indicating a significant increase in economic benefits.
As shown in Figure 7, the flood volumes of the LHK, L-J, and E-T sub-basins estimated by MUFRC were similar to those estimated by MLFRC and EFFRC. The additional flood volume in the E-T inter-basin made the difference in those FRC schemes. Meanwhile, the probability remained acceptable, which was just slightly less than that of the EFFRC method. Hence, the MUFRC scheme was preferred for the estimation of design flood in the cascade reservoir operation period.
4. Discussion and Comparison
4.1. Influence of Flood Disaster Loss
The flood disaster loss DR distinguished the MUFRC method from the MLFRC method, and an unsensitive definition of DR would make the MUFRC scheme similar to MLFRC. This section aimed to investigate how flood disaster loss DR and relevant definition indicator would influence the results of the MUFRC method.
As shown in Figure 8, the controllable flood volume had a significant impact on the MUFRC method. When < 1.5 billion m3, little fluctuation could be recognized for different MUFRC schemes, and their probability densities were approximated to that of MLFRC, which indicated that the quantification of uncontrolled flood risk is mostly determined by probability rather than magnitude. On the contrary, when > 2.0 billion m3, the steep decreases in allocated flood volume to the LHK reservoir and the occurrence probability suggest unsatisfying MUFRC results, which became worse when > 2.9 billion m3 and the downstream J-E and E-T sub-basins carved up more than 80% flood volume. Stringent flood security requirements might lead to a high , indicating that the downstream section could suffer more flood volume, then flood hazard events in the downstream section would be less likely to occur (f/fMLFRC < 0.2); therefore, the MUFRC schemes tended to extreme solutions that allocated the most flood volume for the J-E and E-T inter-basins and especially less for the LHK reservoir, whose flood volume would be controlled and reduced by all three cascade reservoirs. When 1.5 billion m3 < < 2.0 billion m3, the flood volumes were allocated slightly more for E-T and less for the other upstream basins, which were more acceptable, at 0.3~0.8 f/fMLFRC, since the flood data series were highly correlated in the Yalong River basin. Anyway, the practical = 1.81 billion m3 in the case study, and the MUFRC scheme differed from MLFRC and presented a reasonable possibility (f/fMLFRC = 0.55), so the case study remained rational and applicable.
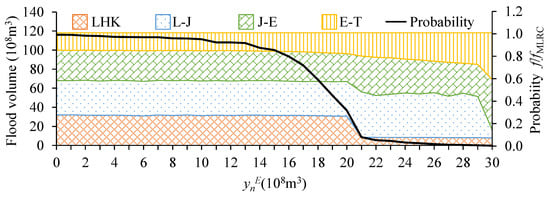
Figure 8.
Influence of controllable flood volume on 7 d flood volume allocation in MUFRC method.
4.2. Sensitivity Analysis
The Bootstrap method [,,] was applied for the sensitivity analysis of the FRC methods: Firstly, we generated the flood data series based on the fitted distributions for the Yalong River basin. Then, we reassessed the marginal and joint distributions with generated sample data series and derived the corresponding FRC schemes. Finally, we repeated the above two steps a sufficient number of times and analyzed the statistical features of all the FRC results.
The boxplot in Figure 9 presents the flood volumes in each sub-basin for the three FRC methods. Overall, the results of the Bootstrap method still followed the pattern of the case study. The EFFRC method preferred to allocate more flood volume to the upstream, the MLFRC method tended to derive proportionate results, and the MUFRC method focused more on downstream sub-basins. Meanwhile the inter-quartile ranges (IQRs) were also proportional to the magnitude of floods from the inter-basins, except for LHK. The upper and lower edges of the LHK boxes were even close to the feasible region (1~5 billion m3) set in the GA algorithm, since the principle of the water balance constraint x1 = zp − y1 − y2 − y3 mathematically led to a higher statistical variance.
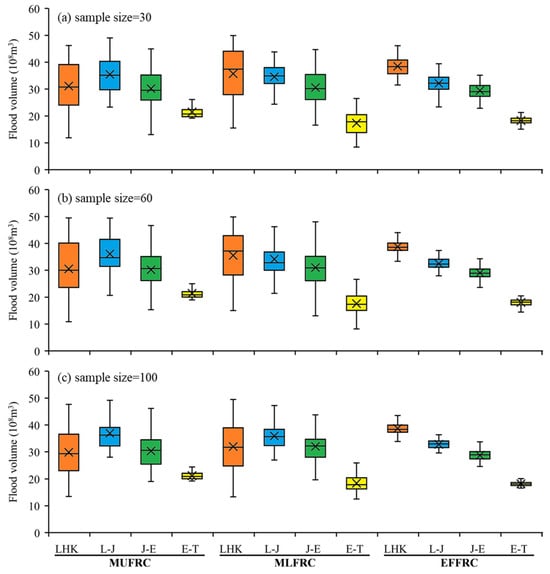
Figure 9.
Sensitivity analysis of 7 d flood volume regional composition schemes with different sample sizes. The boxplot indicates the statistical characteristics of the flood volume distribution in all loops of Bootstrap, and the results of different basins marked with different colors.
The sample sizes were set as 30, 62, and 100, which symbolized the minimum series length requirement [], the actual value in the case study, and an abundant sample size, respectively. Obviously, the larger the sample size, the narrower the box, especially for the J-E and E-T inter-basins, as shown in Figure 9. Additionally, the flood volume distribution of the EFFRC method was centralized with the least IQR, suggesting less reliance on large sample sizes, which contributed to the concise mathematical definition of the EFFRC method, which is only concerned with marginal distributions, except for the copula-fitted joint distribution and complex flood loss. The simple calculation procedure could make the EFFRC method a convenient means of rough but steady design flood estimation.
The MLFRC and MUFRC methods were highly sensitive to the uncertainty from the copula function. In the sample size of the case study shown in Figure 9b, the IQR of the E-T inter-basin was 0.20, 0.53, and 0.18 billion m3, respectively, for the MUFRC, MLFRC and EFFRC methods. The difference in joint distributions in the Bootstrap loops directly influenced the MLFRC results, whose variable amplitude was nearly three times more than that of EFFRC. However, the MUFRC method presented better results, as its flood loss in Equation (5) constrained the flood volume in the E-T inter-basin and made it strictly greater than . Therefore, its lower edge and lower quartile were both close to 1.81 billion m3. In other words, the uncontrolled flood risk narrowed the feasible region of the MUFRC method for the GA algorithm, and the uncertainty of MUFRC was relatively smaller.
For the MLFRC and MUFRC methods, the similar median value under LHK and J-E confirmed that MUFRC differed from MLFRC with the introduction of the downstream uncontrolled basin. The LHK and J-E sub-basins were in the upper reaches of the study area, which would not be involved in the flood loss computation in our proposed MUFRC method. Hence, a more likely upstream flood allocation was preferred for higher flood risk, as defined in Equation (6), which was exactly the aim of MLFRC. So, their similar result could also prove the rationality of MUFRC.
The relative error RE was used to assess the accuracy of the Bootstrap results and expressed as follows:
where x1 and yi are the FRC schemes derived in the case study; and are the FRC schemes estimated in each loop of the Bootstrap. The average RE in the MUFRC, MLFRC, and EFFRC methods was, respectively, 0.20, 0.23, and 0.07, with sample size of 62, so the instability of the copula fit also led to a significant RE in the MUFRC and MLFRC methods. Meanwhile, the risk definition helped MUFRC to present better accuracy than MLFRC. Further, we estimated design flood using all the generated FRC schemes, as shown in Figure 10. The average Euclidean distances between the Bootstrap results and the case study results were 6350 m3/s, 7500 m3/s, and 2070 m3/s for the three FRC methods. Additionally, a higher discharge corresponded to a wider fluctuation range, especially around the flood peak. The range of the MUFRC method was always narrower than that of the MLFRC method, and their overlap during the flood reduction period (T > 50 × 3 h) in Figure 10d shows consistent reservoir flood control operation at the end of flood events.
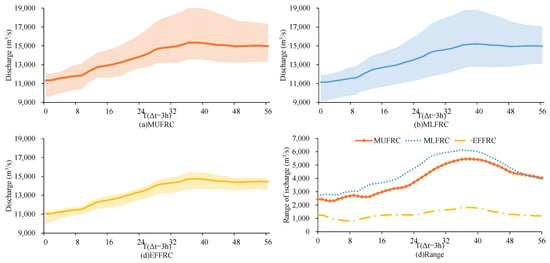
Figure 10.
Design floods estimated using the Bootstrap method. The filled areas in (a–c) present the range of results in all Bootstrap loops and the solid lines present results in the Yalong River case study. The ranges in (d) were calculated with the difference between the upper and lower boundaries of the filled areas.
In summary, though the EFFRC method presented optimal stability, its allocation scheme made full use of the upstream reservoir capacities and derived a minimum design flood, which failed to fit the unfavorable security requirement. The MLFRC method allocated flood volume according to the correlation, but its probability density was the highest, together with instability. The MUFRC method reasonably focused on the uncontrolled basin and led to the most threatening flood risk; meanwhile, it overcame the incorrect assumption in EFFRC and reduced the fluctuation from copulas like MLFRC to some extent. Thus, MUFRC was more suitable for the reference of design flood estimation.
4.3. Theoretical Derivation
To further discuss the rationality of the flood risk in MUFRC, we compared the analytical solutions of the EFFRC, MLFRC, and MUFRC methods based on the theoretical derivation. A two-dimensional case was taken as an example for simplification, assuming that there were floods from reservoir X and design section Z, which both obeyed a normal distribution, respectively, while their joint density function obeyed bivariate normal distribution []:
where ux, uz and σx, σz denote the average and standard deviation of X and Z, respectively; r denotes the Pearson’s correlation coefficient between X and Z.
Assuming that the allocation schemes for EFFRC and MLFRC were (xE, yE) and (xL, yL), respectively, then Xiong et al. derived the following equation []
where tz denotes the normalization value of variable Z. Since the design flood volume zp in the design frequency p was far greater than the constant value uz, tz > 0, with the principle of water balance, Equations (16) and (17) could be derived:
According to the definition of the MUFRC method, the flood risk of the MUFRC scheme (xU, yU) reached the maximum when its first derivative with respect to x was equal to 0:
Obviously, f(x, z) was always greater than 0, so Equation (19) could be derived by solving the univariate quadratic equation with respect to xU in Equation (18):
For Equations (18) and (19), the other solution failed to satisfy the constraint xU < zp-yE and was therefore discarded. Since ux, σx, and tz were all constants greater than 0, it could be deduced that MUFRC always allocated the most flood volume into the uncontrolled basin:
Assuming that the average of flood volumes for the upstream reservoir and the design section were 5 and 10 billion m3, respectively, and the coefficients of variation were both 0.25, the relationship between the correlation coefficient r and the downstream uncontrolled flood volume was further analyzed, as shown in Figure 11. The uncontrolled flood volume in EFFRC was unchanged with r since it was unable to account for the correlation of sub-basins under the assumption that r ≡ 1. The MUFRC method assigned a nonlinear decline to the uncontrolled interval basin flood, and the greater r was, the faster it decreased. Overall, the smaller r was, the larger the gap among the different FRC methods was, while r = 1 meant that X and Z were completely linearly correlated, and the FRC scheme (xp, zp − xp) was uniquely determined with the known constant, design flood volume zp, which was not related to the equal frequency, the probability density, the flood risk, or any other factors. In summary, the MUFRC method allocated more flood volume to the downstream uncontrolled sub-basin, followed by the MLFRC method, and the EFFRC method with the least.
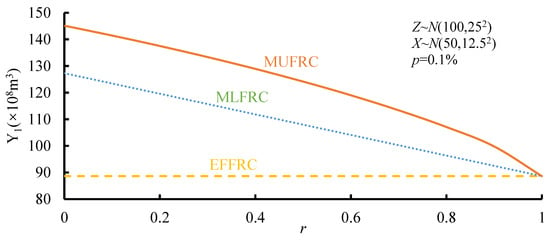
Figure 11.
Comparison of flood volumes in uncontrolled sub-basin allocated by three FRC methods under different correlation coefficients.
5. Conclusions
In this study, a novel FRC method, i.e., the most unfavorable flood regional composition (MUFRC) method, was proposed to estimate design floods in the cascade reservoir operation period. The case study in the Yalong River cascade reservoirs has clarified its practicality. The rationality of the proposed method was further proven by theoretical derivation. The main conclusions are summarized as follows:
- (1)
- The proposed MUFRC method would allocate more flood volume to the downstream uncontrolled sub-basin, and the precise definition of flood disaster loss could have a significant impact on the MUFRC method for the rational estimation of design flood.
- (2)
- The most unfavorable design flood of the Yalong River basin in the cascade reservoir operation period could be derived by MUFRC, and its peak discharge and maximum 1 d, 3 d, and 7 d flood volumes decreased by 36.6%, 36.1%, 33.0%, and 28.7%, respectively, compared with the originally designed values in the reservoir construction period.
- (3)
- The decrease in design flood would lessen the downstream flood control pressure. Hence, redesigned flood control water levels of JP1 and ET reservoirs could be raised to 1862.39 m and 1192.59 m, respectively, under the condition of the original flood prevention standards remaining unchanged. The rise in water level could generate 640 million kW·h (+1.82%) more hydropower during the flood season annually.
The proposed MUFRC method would serve as an important reference for flood control and hydropower generation during the flood season. In the reservoir operation period, the MUFRC method could provide a conservative assessment of the flood control water level and the effective utilization of flood resources. However, there are still some limitations of the current study. The joint distribution of the annual maximum flood volume data series should be fitted more accurately, and the flood disaster loss needs a more practical and intuitive definition. What is more, flood risk also deserves further discussion regarding the most unfavorable flood situation. Overall, the proposed MUFRC method is worth further study and practical application.
Author Contributions
Conceptualization, S.Z. and S.G.; methodology, S.Z.; software, S.Z.; validation, Y.X. and Y.H.; formal analysis, S.G.; investigation, Y.X.; resources, Y.H.; data curation, S.Z.; writing—original draft preparation, S.Z.; writing—review and editing, S.G.; visualization, S.Z.; supervision, Y.X.; project administration, S.G.; funding acquisition, Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financially supported by the National Natural Science Found of China (U2340205) and the National Key Research and Development Plan (2022YFC3202801).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to thank the editor and anonymous reviewers whose comments and suggestions helped to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Duan, W.; Guo, S.; Wang, J.; Liu, D. Impact of cascaded reservoirs group on flow regime in the middle and lower reaches of the Yangtze River. Water 2016, 8, 218. [Google Scholar] [CrossRef]
- Volpi, E.; Lazzaro, D.M.; Bertola, M.; Viglione, A.; Fiori, A. Reservoir effects on flood peak discharge at the catchment scale. Water Resour. Res. 2018, 54, 9623–9636. [Google Scholar] [CrossRef]
- MWR (Ministry of Water Resources). Regulation for Calculating Design Flood of Water Resources and Hydropower Projects; Water Resources and Hydropower Press: Beijing, China, 2006. (In Chinese)
- Guo, S.; Rizwan, M.; Liu, Z.; Xiong, F.; Yin, J. Design flood estimation methods for cascade reservoirs based on copulas. Water 2018, 10, 560. [Google Scholar] [CrossRef]
- Qi, W.; Liu, J. A non-stationary cost-benefit based bivariate extreme flood estimation approach. J. Hydrol. 2018, 557, 589–599. [Google Scholar] [CrossRef]
- Qi, W. A non-stationary cost-benefit analysis approach for extreme flood estimation to explore the nexus of risk, cost and non-stationarity. J. Hydrol. 2017, 554, 128–136. [Google Scholar] [CrossRef]
- Liu, P.; Lin, K.; Wei, X. A two-stage method of quantitative flood risk analysis for reservoir real-time operation using ensemble-based hydrologic forecasts. Stoch. Environ. Res. Risk Assess. 2015, 29, 803–813. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, P.; Xu, C.; Gong, Y.; Cheng, L.; He, S. Real-time reservoir flood control operation for cascade reservoirs using a two-stage flood risk analysis method. J. Hydrol. 2019, 577, 123954. [Google Scholar] [CrossRef]
- Xie, Y.; Guo, S.; Xiong, L.; Tian, J.; Xiong, F. Nonstationary design flood estimation in response to climate change, population growth and cascade reservoir regulation. Water 2021, 13, 2687. [Google Scholar] [CrossRef]
- Xiong, F.; Guo, S.; Liu, P.; Xu, C.-Y.; Zhong, Y.; Yin, J.; He, S. A general framework of design flood estimation for cascade reservoirs in operation period. J. Hydrol. 2019, 577, 124003. [Google Scholar] [CrossRef]
- Xiong, F.; Guo, S.; Yin, J.; Tian, J.; Rizwan, M. Comparative study of flood regional composition methods for design flood estimation in cascade reservoir system. J. Hydrol. 2020, 590, 125530. [Google Scholar] [CrossRef]
- Jiang, C.; Xiong, L.; Xu, C.; Yan, L. A river network-based hierarchical model for deriving flood frequency distributions and its application to the upper Yangtze basin. Water Resour. Res. 2021, 57, e2020WR029374. [Google Scholar] [CrossRef]
- Rigby, A.; Stasinopoulos, M. Generalized additive models for location, scale and shape. J. R. Stat. Soc. Ser. C Appl. Stat. 2005, 54, 507–554. [Google Scholar] [CrossRef]
- López, J.; Francés, F. Non-stationary flood frequency analysis in continental Spanish rivers, using climate and reservoir indices as external covariates. Hydrol. Earth Syst. Sci. 2013, 17, 3189–3203. [Google Scholar] [CrossRef]
- Su, C.; Chen, X. Assessing the effects of reservoirs on extreme flows using nonstationary flood frequency models with the modified reservoir index as a covariate. Adv. Water Resour. 2018, 124, 29–40. [Google Scholar] [CrossRef]
- Wang, W.; Li, H.-Y.; Leung, L.R.; Yigzaw, W.; Zhao, J.; Lu, H.; Deng, Z.; Demisie, Y.; Blöschl, G. Nonlinear filtering effects of reservoirs on flood frequency curves at the regional scale. Water Resour. Res. 2017, 53, 8277–8292. [Google Scholar] [CrossRef]
- Lee, D.; Ward, P.J.; Block, P. Attribution of large-scale climate patterns to seasonal peak-flow and prospects for prediction globally. Water Resour. Res. 2018, 54, 916–938. [Google Scholar] [CrossRef]
- Yin, J.; Guo, S.; Liu, Z.; Yang, G.; Zhong, Y.; Liu, D. Uncertainty analysis of bivariate design flood estimation and its impacts on reservoir routing. Water Resour. Manag. 2018, 32, 1795–1809. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, P.; Chen, J.; Xu, J.; Wang, Y.; Yao, L.; Hong, X. Research on the synergistic effect of multi-reservoir flood control capacity by considering the conditional value-at-risk. Adv. Water Sci. 2022, 33, 298–305. (In Chinese) [Google Scholar]
- Zhao, L.; Li, J.; Zhang, T.; Feng, P.; Wang, X.; Shen, J. Multi-method combined analysis of urban flood risks and its influencing factors under low impact development. J. Hydrol. 2024, 632, 130927. [Google Scholar] [CrossRef]
- Nelsen, R. An Introduction to Copulas, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Salvadori, G.; Durante, F.; Michele, C.; Bernardi, M.; Petrella, L. A multivariate copula-based framework for dealing with hazard scenarios and failure probabilities. Water Resour. Res. 2016, 52, 3701–3721. [Google Scholar] [CrossRef]
- Salvadori, G.; Michele, C. Frequency analysis via copulas: Theoretical aspects and applications to hydrological events. Water Resour. Res. 2004, 40, 12511. [Google Scholar] [CrossRef]
- UNDHA (United Nations Department of Humanitarian Affairs). Internationally Agreed Glossary of Basic Terms Related to Disaster Management; United Nations Department of Humanitarian Affairs: Geneva, Switzerland, 1992. [Google Scholar]
- Sun, Z.; Zhu, X.; Pan, Y.; Liu, X.F. Flood risk analysis: Progress, challenges and prospect. J. Catastrophology 2017, 32, 125–130+136. (In Chinese) [Google Scholar]
- Gopalan, P.S.; Kawamura, A.; Amaguchi, H.; Takasaki, T.; Azhikodan, G. A bootstrap approach for the parameter uncertainty of an urban-specific rainfall-runoff model. J. Hydrol. 2019, 579, 124195. [Google Scholar] [CrossRef]
- Bomers, A.; Schielen, J.M.R.; Hulscher, H.M.J.S. Decreasing uncertainty in flood frequency analyses by including historic flood events in an efficient bootstrap approach. Nat. Hazards Earth Syst. Sci. 2019, 19, 1895–1908. [Google Scholar] [CrossRef]
- Arnaud, P.; Cantet, P.; Odry, J. Uncertainties of flood frequency estimation approaches based on continuous simulation using data resampling. J. Hydrol. 2017, 554, 360–369. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).