Abstract
Pressure management is a fundamental and highly effective method for the management of real losses in water distribution networks and therefore reducing non-revenue water. In this work, a methodology is developed to assess leakages in the water distribution networks of small settlements. The settlement of Agios Germanos in the Municipality of Prespes is selected as a representative case study. The hydraulic modeling of the water distribution network in the study area is used to assess the hydraulic behavior of the existing infrastructure in its current state of operation and to find critical locations to install the necessary measuring equipment (pressure sensors, flow meters, water level sensors, and pressure reducing valves). This equipment is used to calibrate the hydraulic model, estimate leakages, and manage them effectively. Minimum night flow analysis is utilized to assess leakages in the studied network based on measurements of the hydraulic parameters from the equipment installed. The effects of pressure management on leakages are then examined by assessing the relationship between the pressure and leak flow rate in the selected settlement.
1. Introduction
Non-revenue water refers to the volume of water for which the water utility does not generate revenue, representing a discrepancy between the volume of water introduced into a distribution network (net production) and the billed authorized consumption. According to the International Water Association (IWA), non-revenue water encompasses both water losses and unbilled authorized consumption [1]. Water losses are further classified by the IWA into real losses and apparent losses [2]. Real losses are primarily due to leakages in transmission or distribution mains, valves, service connections up to the water meter, and leakages or overflows in storage tanks. Apparent losses stem from unauthorized consumption, metering inaccuracies, and data handling errors. While real losses generally account for a larger volume, the financial impact of apparent losses is often higher because the cost of unmeasured water is based on the retail price rather than just the production cost [3].
Real losses in water supply networks, arising from leaks and breaks in pipelines and overflows in tanks, have significant environmental, economic, and public health consequences. Leaking pipes can lead to contamination risks due to pressure drops (suctions) [4,5], environmental impacts from water and energy waste, and an increased carbon footprint [6,7,8]. Financial losses occur due to the treatment and transport costs of lost water. Additionally, societal costs include disruptions in the water supply, property damage, and road traffic interruptions caused by pipeline repairs. These losses can necessitate premature investments in infrastructure to meet the water demand [8,9,10].
The rate of real losses increases with the age and usage of the water supply network but can be mitigated through integrated management strategies. These include (i) active leakage control (ALC), (ii) pressure management, (iii) rapid and high-quality repairs, and (iv) effective pipeline and asset management [10,11]. Real losses, and consequently non-revenue water, exhibit daily fluctuations due to pressure variations within the system. Hence, pressure management stands out as one of the most fundamental and effective strategies for the control of real losses in water distribution networks (WDNs) and is frequently one of the most impactful measures of minimizing leakages [12]. It is the sole preventive leakage management technique that can reduce base leaks without resorting to equipment replacement [13,14,15]. Pressure management has demonstrated its efficacy as a leakage management tool over short-, medium-, and long-term periods [16,17,18,19,20,21,22,23]. Advances in electronic and hydraulic regulators have enabled the reduction of leaks to minimal levels in a cost-effective manner, particularly through the use of flow-modulated pressure reducing valves [14,24,25].
To determine whether pressure management can effectively reduce real losses, particularly leaks in water pipelines, it is essential to introduce models that explain how leakages are influenced by and evolve with pressure variations. A common approach employed by water utilities to assess leakage evolution involves determining the water balance, which evaluates the total input volume and water consumption in a specific area over a given period [12]. In the absence of detailed consumption data or when the data span long periods (e.g., four to six months), the minimum night flow (MNF) method is applied. This method utilizes the minimum inflow in a district metered area (DMA), typically observed during night-time hours when user consumption is minimal and the leakage flow constitutes a significant portion of the total inflow [12,26,27,28,29,30].
Water- and energy-saving strategies in WDNs often progress concurrently, given the close interrelationship between water use and energy consumption. Globally, water demand control and the efficient design of water supply networks are standard strategies for the achievement of these goals [31,32,33,34,35,36]. In recent years, model-based techniques combining hydraulic modeling with various optimization algorithms have been developed to enhance leakage reduction efforts in WDNs. These advanced methods enable more efficient water management strategies. Additionally, the optimal positioning of pressure monitoring devices within a WDN can significantly aid in the detection and localization of leaks or pipe breaks, ensuring the effective and cost-efficient management of real water losses [37,38,39,40,41,42].
This study develops a systematic methodology for the quantification of leakages in the WDNs of small settlements and explores cost-effective strategies for their reduction and management. The analysis is specifically targeted at small settlements, which typically meet the principal design criteria of DMAs, forming hydraulically isolated zones that can be effectively monitored with limited resources. This methodology is applied in Agios Germanos, located in the Prespes Municipality of Greece, an environmentally critical region where the conservation of natural resources is of paramount importance. The approach for small settlements relies on simplified assumptions to approximate leakages, employing the water balance and MNF methods. Typically, only a small portion (approximately 6%) of the population is active during the night [29,43,44], translating into a minimal number of inhabitants in small settlements like Agios Germanos. Non-residential activities, such as night irrigation, are considered negligible, allowing the MNF to be confidently assumed to be equivalent to the leakage amount. The literature indicates that smaller-diameter pipes, common in the WDNs of small settlements, exhibit lower water pressure and moments of inertia, rendering them more susceptible to leakages and pipe failures [29].
This study integrates a modern, minimal-pressure sensor placement methodology, an estimation approach for leakages based on MNF analysis, and a pressure management strategy to efficiently reduce leakages. To determine the optimal number of pressure sensors with the maximum isolability, leakage information is obtained using a pressure sensitivity matrix, which is assessed by simulating the network with and without leaks in each pipe. These data are combined with budgetary constraints, ensuring that the installed sensors reliably calibrate the hydraulic model of the WDN and facilitate the implementation of pressure management alternatives to estimate their impact on leakages. The presented methodology is both straightforward and comprehensive, contributing to the quantification and improved management of leakages and unreported bursts within the system, as well as enhancing pressure management in the DMA. Additionally, the study evaluates the energy savings resulting from leakage reduction through the implementation of pressure management strategies.
2. Materials and Methods
2.1. Study Area
The Municipality of Prespes is situated within the Prespa Cross-Border Park (Figure 1), recognized as the first transboundary protected area in the Balkans. This park was established in February 2000 pursuant to a joint declaration by the Prime Ministers of Greece, Albania, and North Macedonia. The “International Agreement on the Protection and Sustainable Development of the Prespa Park Area”, signed on February 2010 between the three countries and the European Union, significantly strengthened the institutional operation of the protected area. The abovementioned agreement prioritizes water management in the area and creates a legal obligation among the three states to develop a common strategy to protect the natural environment. The Prespa basin in the Greek territory consists of two high-altitude tectonic lakes, namely the Micro Prespa Lake and Macro Prespa Lake, mountains with high peaks and part of the valley of Korestia. The total area of the Prespa region, encompassing both the drainage basins and the lakes, is 2519.1 km2. The Micro Prespa Lake, with a total surface area of 47.4 km2, is predominantly situated within the jurisdiction of Greece, covering 43.5 km2, while a smaller segment, approximately 4 km2, falls within the territorial bounds of Albania. The Macro Prespa Lake, having a total surface area of 259.4 km2, is allocated among the three countries, with the majority share belonging to North Macedonia. Notably, both the Micro and Macro Prespa Lakes are positioned at an elevation of approximately 850 m a.s.l., encompassed by mountainous regions that ascend to heights exceeding 2000 m a.s.l.
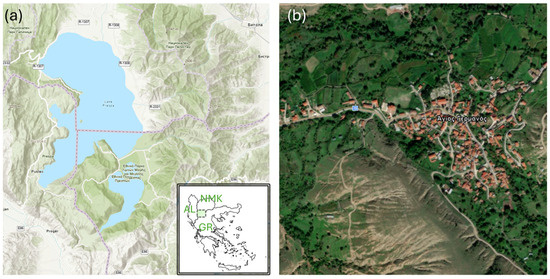
Figure 1.
(a) Prespa National Park, shared between Greece (GR), Albania (AL), and North Macedonia (NMK), and (b) pilot area of Agios Germanos.
The Municipality of Prespes is located in the northwest of Greece (in the region of Western Macedonia), in the Regional Unit of Florina, and it is almost 50 km away from the city of Florina and 45 km from the city of Kastoria. The municipality covers an area of 504.19 km2, including inland waters, and has a population of 1560 inhabitants, according to the census of the year 2011. The settlements of Vrontero, Laimos, Milionas, Lefkonas, Platy, Pyli, Agios Achillios, and Psarades are supplied by water supply boreholes and associated pumping stations, while the other settlements are supplied by surface springs. Neither the springs’ outlets nor the water supply boreholes are equipped with metering equipment, so it is not possible to accurately determine the flow of each water intake. For the considered water supply networks, there exists a severe problem in the water supply and management of the available water reserves, resulting in the marginal coverage of the water supply needs of all municipal units, especially in the summer months. A large number of the WDNs in the study area are very old and were designed without following certain standards and restrictions, resulting in many problems and failures, even during the normal operating conditions of the networks. It should be noted that there are also parts of some WDNs considered harmful to public health, as there still exist pipes constructed from asbestos.
The municipal unit of Agios Germanos occupies an area of 60,500 acres. The largest community of the municipal unit is the village of Agios Germanos (see Figure 1b), which belongs to the Municipality of Prespes. Agios Germanos is located at the western end of a valley at the toe of Mount Varnoudas, at the borders of Greece and North Macedonia. It can be found around 54 km from Kastoria and it is built at an elevation of about 1050 m. Water in the municipal unit of Agios Germanos is supplied by a water tank fed by springs in the wider area of the settlement.
The WDN in Agios Germanos settlement consists of a water head tank and a pipe network with a total length exceeding 4.2 km. All pipes of the WDN are composed of polyvinyl chloride (PVC), a cost-effective and durable option for potable water networks. The water main from the water tank is a DN110 PVC pipe, with a total length of 256 m. The DN110 pipe is followed by a DN90 PVC pipe having a length of 427.5 m. The rest of the network consists of DN63 PVC pipes, having a total length of 3578.5 m. Figure 2 presents the WDN of the Agios Germanos settlement. The majority of the WDN pipes were replaced in the early 2000s. However, a few pipes at the western end of the network have been constructed quite recently.
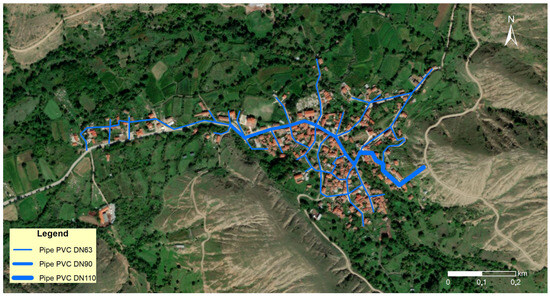
Figure 2.
Water distribution network of Agios Germanos settlement in Prespes Municipality.
In this work, a ground survey was conducted in the Agios Germanos settlement, resulting in a sample of elevation data for a number of selected points. All points were selected close to the detected pipes of the WDN and in areas that were easy to access. The selected points were first georeferenced (assigned map coordinates), while, afterwards, an elevation was assigned to them. The data collected were then digitized in the ArcGIS Pro v.3.2.2 Geographic Information System (GIS) software and the measured elevation values were interpolated to produce an elevation map covering the entire study area. The elevation map developed is not equivalent to a digital elevation model (DEM) in the purest definition of the term, because the selected points are not regularly spaced. The National Cadastre map of the area, including the road map of the studied settlements, was used as a reference feature. Interpolation was performed using the selected sample points, implementing the geostatistical procedure of kriging to generate ground surface elevations [45]. This procedure can generate a surface from a scattered set of data point elevations. The main advantage of the method is that it performs optimization to find the best estimation method to generate the elevation surface. This method is recommended when the selected data points are characterized by a known spatially correlated distance or directional bias [46].
2.2. Methodological Framework
The presented methodology (Figure 3) outlines a systematic approach aimed at optimizing the management and efficiency of WDNs, crucial in mitigating existing leakage issues and enhancing the overall network performance. Initially, the methodology relies on community feedback to identify potential leakage areas, particularly focusing on susceptible zones of low elevation or structural vulnerabilities. This citizen-driven approach plays a pivotal role in identifying areas requiring improvement. Subsequently, a strategically positioned flow meter is installed at the WDN inlet to precisely monitor the water flow dynamics within the study area. A comprehensive hydraulic model of the settlement’s WDN is then developed, meticulously integrating all customer meters into the network framework. This detailed model serves as a fundamental tool for simulation and analysis, enabling informed decision-making regarding network operations and maintenance. Furthermore, a network of pressure sensors is strategically deployed across the WDN. These sensors fulfill dual roles: ensuring the accuracy and reliability of the hydraulic model through calibration and employing advanced model-based diagnostic techniques for leak detection. The sensor placement is optimized to balance technical effectiveness with budgetary constraints. The MNF analysis is subsequently employed to quantitatively evaluate leakages throughout the study area. Lastly, proactive pressure management strategies are implemented throughout the WDN. These measures aim to optimize the pressure levels network-wide, thereby reducing the occurrence and impact of leaks. The integration of these pressure management practices enhances the network’s resilience and efficiency, promoting sustainable water resource management practices. Together, these methodological steps establish a comprehensive framework to address leakage challenges, enhancing the operational efficiency and ensuring the long-term sustainability of WDNs.
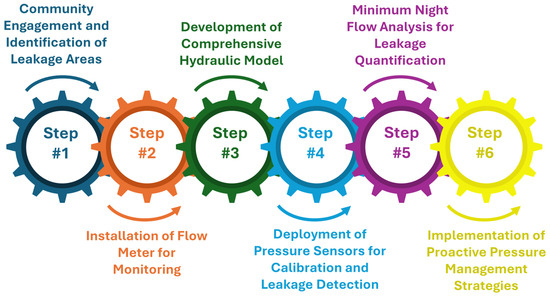
Figure 3.
Methodological framework for water distribution network optimization.
2.3. Hydraulic Modeling of a Water Distribution Network
WDNs are designed to meet diverse consumer demands while ensuring adequate pressure levels at critical nodes and maintaining water quality standards. The hydraulic simulation of pressurized pipe systems plays a pivotal role in the management and decision-making processes for WDNs, encompassing both routine and emergency scenarios. These simulations are essential for system planning, operational optimization, the design of contamination warning systems, the detection of contaminants, and responses to disasters [47,48]. The OpenFlows WaterGEMs v.23 software [49], built upon the hydraulic engine of the EPANET v. 2.2 software [50], provides a versatile modeling environment for the design, analysis, and optimization of WDNs. It offers advanced hydraulic capabilities, geospatial model-building tools, optimization features, and asset management functionalities [51,52,53,54].
To establish a hydraulic model of the WDN within a small settlement, it is imperative to systematically gather the crucial topological features and hydraulic properties of the pipes, as well as dimensional and hydraulic data pertaining to the system’s head tank. In this study, the specific parameters obtained for the tank include the (i) base elevation, (ii) minimum water level elevation (typically corresponding to the top of the outlet pipe), (iii) maximum water level elevation (typically considered slightly lower than the overflow pipe elevation), (iv) cross-sectional shape, and (v) dimensions of the tank’s cross-section. These data were meticulously sourced from existing drawings and field measurements. Fundamental input parameters concerning pipe characteristics such as the length, diameter, and pipe roughness are essential for accurate simulations. In this investigation, the pipe roughness is quantified using the Hazen–Williams coefficient C [54], a critical determinant in hydraulic modeling. Furthermore, nodal elevations crucial in formulating the WDN model were derived from a dedicated GIS database tailored specifically to the WDN in the studied settlement. This comprehensive approach ensures that the hydraulic model integrates precise spatial data and hydraulic parameters, enabling the robust analysis and simulation of the WDN’s performance and efficiency.
The precision of a hydraulic model for a WDN relies significantly on two pivotal parameters, the nodal demands and pipe roughness coefficients [55,56], both of which present challenges as they are not directly measurable. The calibration of pipe roughness coefficients has evolved through various techniques over recent years, encompassing simple methods like trial-and-error and empirical approaches [57], as well as more sophisticated explicit [58] and implicit optimization methods [59,60,61,62,63]. In this study, the calibration of the pipe roughness coefficients was executed manually, leveraging pressure data collected from strategically positioned sensors within the network’s nodes (refer to Section 3.1). This approach ensures that the hydraulic model incorporates accurate and site-specific adjustments to the roughness coefficients, thereby enhancing the model’s fidelity in simulating the actual hydraulic behavior of the WDN. Such meticulous calibration procedures are essential in validating the model’s reliability and effectiveness in predicting the flow dynamics and operational characteristics of the network under varying conditions.
The estimation of the water demand in the selected settlement was approached through the combination of a theoretical methodology and measured consumption data. The theoretical estimation of the water demand primarily relied on demographic data (permanent residents and tourists) and specific water consumption data (assumed equal to 200 L/c/day) in the selected settlement. Population data were obtained from the 2011 census in the Municipality of Prespes. To estimate the water demand of each consumer in the settlement, water consumption data for all water meters installed in the settlement were collected from recent bills. The annual water consumption (total volume recorded in a year) of all water meters was collected, together with their geographical coordinates. The water meters were first geo-allocated and the water consumption was then transformed into the mean and maximum (multiplying the mean daily consumption with a coefficient equal to 3) daily consumption. The theoretical coefficient of the hourly water demand initially used in the simulations was obtained from the literature and is presented in Figure 4. The water meter demands estimated using the abovementioned methodology were utilized in the hydraulic model of the WDN, created to locate the pressure sensors based on the methodology described in Section 2.4.
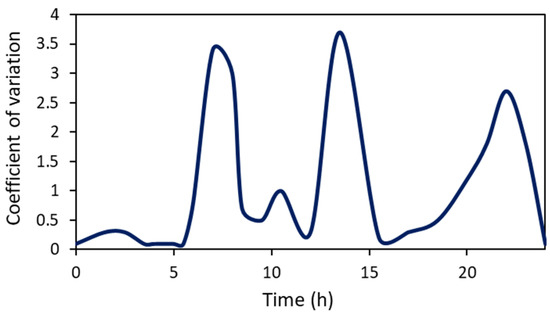
Figure 4.
Theoretical coefficient of hourly water demand in the studied settlement [64].
The calibration of a hydraulic model necessitates the accurate simulation of the observed pressure and flow values within a WDN. This process involves two primary steps: firstly, comparing the simulated and measured flows, nodal pressures, and tank levels under defined operational conditions; secondly, adjusting the input parameters to minimize the disparities between the simulation and observation. It should be noted that a hydraulic model is not considered to be calibrated until it can predict, with reasonable accuracy, the system parameters for a variety of conditions. In the present work, differences of ±5% between the measured and modeled pressure are considered allowable in the calibration process.
To assess the maximum daily demand at each water meter of the settlement, together with the coefficient of the hourly water demand, flow measurements acquired from a flow meter installed after the system’s head tank (see Section 3.1) were used in this work. Initial water levels, as well as the minimum and maximum water level values for the system’s head tank, were sourced from the installed Supervisory Control and Data Acquisition (SCADA) system in the settlement, which includes sensors for the flow, pressure, and water level (refer to Section 3.1). By integrating the measured data from this comprehensive monitoring system, the accuracy and reliability of the hydraulic model calibration process are achieved. This approach ensures that the model accurately represents the dynamic behavior of the WDN under varying operational conditions, thereby supporting effective water management and infrastructure planning initiatives.
2.4. Pressure Sensor Positioning
To select appropriate nodes to monitor the pressure for leakage detection in a WDN, the hydraulic modeling of the network is usually coupled with a pressure sensitivity analysis. More specifically, the methodology followed in this work identifies the WDN nodes that are most sensitive to different leakage positions, conditional on avoiding node combinations that can lead to uneconomical solutions that scarcely contribute to the optimal leakage monitoring of the network. The leak sensitivity matrix, S, is defined with elements sij, measuring the effect of a leak at element j on the pressure at node i, representing variations in the nodal pressure between the no-leak and leak scenarios. Considering that y = f(θ) is a set of equations describing the hydraulic model of a WDN, with y corresponding to a vector of n output variables and θ to a vector of m independent input variables, the elements of the leak sensitivity matrix are defined as [39]
where Δθj represents the variation range of the jth input parameter and ysi is the reference value of the output variable yi. Therefore, considering n nodes and m leak positions placed halfway along the network pipes, the leak/pressure sensitivity matrix is defined as follows [65]:
where sij measures the effect of leak fj on the pressure at junction pi. The average sensitivity index results from averaging the sensitivities of the modeling output yi to the variations in the input parameters, m [39]:
The ranking of the average sensitivity indices of all nodes of the network reveals the nodes most sensitive to different leakage positions. In the studied WDN, leakages are modeled as new nodes, placed in the middle of all system pipes (except for the pipes connected to the network’s tank). The elevations of the leak nodes are assessed as the average values of the elevations of the pipe start and end nodes. An emitter flow of 0.2 L/s is selected to perform each analysis to assess the elements of the pressure sensitivity matrix of Equation (2).
Blesa et al. [66] combined a robustness percentage index with the pressure sensitivity matrix for different leak magnitudes and changes in demands, to optimally define the number and positions of sensors in a WDN. Puleo et al. [39] used the identifiability index, defined based on the pressure sensitivity matrix of a WDN, to finally select the nodes’ combination to be utilized as the monitoring subset for pressure sensors’ installation. Pérez et al. [65] binarized the pressure sensitivity matrix of a WDN using a threshold independent of the node and combined it with genetic algorithms to form a complete methodology for optimal pressure sensor placement. The constrained budget allocated for sensor procurement and installation imposes limitations on the total number of pressure sensors deployed within the investigated WDN, restricting it to three sensors. This financial constraint necessitates the strategic placement and prioritization of sensor locations to maximize the coverage and effectiveness in monitoring the hydraulic parameters that are critical for the network’s operation and modeling accuracy. Therefore, it was decided to select appropriate locations for the installation of the pressure sensors by combining the results of the pressure sensitivity matrix with the preferred locations for the calibration of the hydraulic model of the network, as well as for the purposes of pressure management. The studied WDN features a single inlet, designated for both pressure measurement and control purposes; hence, one pressure sensor is placed after the water head tank of the network. A pressure sensor is also located close to the most remote from the inlet node of the network, mostly appropriate for the calibration of the hydraulic model of the network. The remaining third sensor is located based on the results of the methodology described above. Any pipe burst or leakage in the network can be therefore identified by the turbulence in the pressure monitoring data of the abovementioned three pressure sensors.
2.5. Minimum Night Flow Analysis
In a WDN, the hydraulic pressure dynamically fluctuates with varying flow rates. During peak demand periods, such as the early morning, noon, and the afternoon, the pressure reduces as the flow rate increases. Leaks are well known as pressure-dependent water flows [15], where higher pipeline pressure correlates with increased leak flow rates. The drop in pressure during peak demand periods can also reduce the leakage rate of the network. On the other hand, the leakage rate increases during the night, when the flow rate of the network is significantly reduced. MNF analysis is an important tool to detect existing leaks. As detected from field campaigns, the MNF is usually measured between 12:00 pm and 5:00 am, as, during the night, the flow takes the lowest values within the entire day. The MNF is composed of the minimum night use, background losses, and burst leakages [10]:
The background leakage, DB, includes all minor leaks from fittings and connections that are generally imperceptible through visual or acoustic inspection, while the burst leakage includes water lost from bursts on the WDN. The empirical equation used by the IWA to estimate the background leakage, DB (L/h), is [64]
where L is the total length of the pipes (m), N is the number of consumer connections, and s is the total length (m) of the consumer connections to the network. It should be mentioned that the abovementioned formula holds for a WDN in good condition and for a night-time operation pressure of about 5 atm. For a different night-time pressure (atm), Equation (5) becomes [64]
Hunaidi [43] developed the following empirical model for the estimation of night-time background leakage (L/h) for PVC pipes:
where Lm represents the aggregate length of the primary pipes within the network (km), Nc signifies the total count of service connections, Lp denotes the mean length of the service connection pipes extending from curb stops to customer meters (m), and P is the average pressure within the pipes (atm), factoring in the service connection pipes of 15 m post curb stops.
Leaks generally constitute a significant proportion of the real losses. The relationship between the leakage and pressure can be described by Toricelli’s equation, defining the actual flow rate through an orifice as [12]
where Q represents the leakage flow rate (m3/s), Cq stands for the flow coefficient (dimensionless), A denotes the orifice area (m2), g signifies the acceleration due to gravity (m/s2), and h refers to the pressure head (m). May [67] proposed the Fixed and Variable Discharge (FAVAD) approach based on the correlation between the leak flow rate and pressure. The FAVAD equation results from Equation (8) by substituting the leak area, A, as the sum of a fixed area at a zero head differential, A0 (m2), and a variable area defined as a product of the head area slope, m (m2/m), and the pressure head, h (m):
In hydraulic engineering practice, a generalized power equation is commonly employed to characterize the relationship between the system leakage and pressure [29]:
where C represents the leakage coefficient (m3-N1/s), and N1 denotes the leakage exponent (dimensionless). Van Zyl and Cassa [68] conducted research into the relationship between the FAVAD method and power equations, defining a pure number, the leakage number (LN), defined as the ratio of the variable leakage area to the fixed leakage area. A simplified expression relating the leakage coefficient, N1, and the leakage number, LN, is given below [12,68]:
The influence of the pressure on a water leakage is well established in hydraulic studies. An increase in pressure typically results in higher leakage rates. The pipe material also affects the relationship between the pressure and leakages [10]. Following Lambert and Fantozzi [69], this influence can be expressed by
where P0 and L0 denote the initial pressure and leak flow rate in the network, respectively, and P1 and L1 represent their respective values under revised pressure conditions. The factor (P1/P0)N1 is known as the pressure correction factor (PCF), assisting in estimating the leakage rate L1 at pressure P1, by measuring or estimating leakage rate L0 at pressure P0. The exponent N1 typically ranges from 0.5 to 1.5 for different DMAs, contingent upon the nature of the leaks and the material composition of the pipes, whether rigid or flexible. In some cases, the values of N1 can reach 2.5. The larger the values of N1, the more sensitive the leak flow rate to the pressure variation [10]. Background leakages and reported and unreported leaks at non-metal pipes are usually associated with values of N1 equal to 1.5 and are usually sensitive to pressure changes. Detectable leaks (reported and unreported) at metal pipes are associated with values of N1 equal to 0.5 and are less sensitive to pressure changes [10]. A linear relationship between the pressure and leak flow rate results when the value of N1 is considered equal to 1.0.
The pressure–leakage relationship used in the literature [2,70,71] to estimate the total leakage is
where L (L/s) represents the leakage rate, denotes the average pressure (m) across the network, and k and n are coefficients requiring evaluation. The coefficient n usually varies in the interval from 0.5 to 2.5, while higher values are sometimes assessed [70,71]. Values of n greater than 1.0 are usually assessed for leakages from joints and fittings, while lower values of n are assumed for leaks from holes in pipes [71]. For n > 1, a water leakage will be highly sensitive to the water pressure [71]. In the absence of experimental data, Farley and Trow [11] advocate for adopting a n = 1.0 exponent in Equation (13), implying that a 10% reduction in the network’s average pressure results in a proportional 10% reduction in leakages. An exponent significantly larger than n = 1.0 signifies the increased sensitivity of the leakage rates to the pressure management strategies, highlighting the critical role of pressure control in minimizing water losses within the distribution system.
To characterize the relationship between the inlet pressure and leakage, the following equation, which is similar to Equation (13), is used:
where P is the inlet pressure (m), L is the leakage (L/s), and and are parameters to be calibrated. The MNF is used in this work to assess the coefficients and . Equations (13) and (14) use different values of pressure (the average pressure is used in Equation (13), while the inlet pressure is used in Equation (14)); therefore, the direct comparison of n and is not possible. However, an estimated exponent in Equation (14) for that is much larger than 1.0 signifies that the water leakage is highly sensitive to the water pressure.
3. Results
3.1. Installing Measurement Equipment
To estimate leakages in the WDN of the Agios Germanos settlement, a small-scale SCADA system was installed on the studied network. The monitoring network installed comprised pressure sensors, a flow sensor located at the watermain of the settlement, and a water level sensor installed at its head tank. The network was equipped with three pressure sensors (see Section 2.4), considering the small scale of the settlement, primarily subject to budgetary constraints. To assess the pressure sensitivity matrix (Equation (2)) of the WDN, the hydraulic model of the network was constructed in OpenFlows WaterGEMs [49]. The water consumption of all customer meters was assessed from existing bills obtained from the Prespes Municipality. The mean daily water consumption was assessed from the annual water consumption in the Agios Germanos settlement and then multiplied by a factor of 3 to assess the maximum daily demand and by the maximum coefficient of variation in Figure 4 to estimate the peak hourly water demands for all customer meters. Based on the methodology presented in Section 2.4, in the studied WDN, leakages were modeled as new nodes, placed in the middle of all system pipes (except for the pipes connected to the network’s tank, with no customer meters connected). The elevations of the leak nodes were assessed as the average values of the elevations of the pipe start and end nodes. An emitter flow of 0.2 L/s was selected to simulate each leakage and a hydraulic analysis was performed in steady-state mode. The simulated leakage nodes totaled 87. The pressure sensitivity matrix (Equation (2)) and average sensitivity index (Equation (3)) were then assessed for all network nodes. Table 1 presents the first eight nodes of the WDN with the highest estimates of the index (used instead of for presentation purposes). Figure 5 presents the locations of the eight nodes of Table 1 in the WDN of the Agios Germanos settlement.

Table 1.
The average sensitivity index for the first eight nodes of the network.
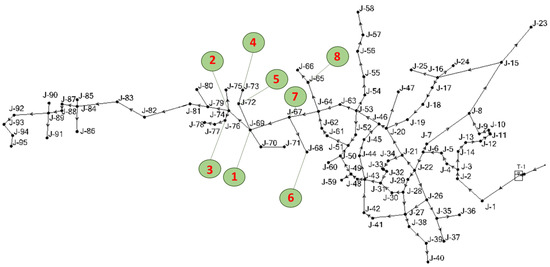
Figure 5.
Locations of eight nodes with the highest average sensitivity indices in the water distribution network of the Agios Germanos settlement.
The proposed methodology of this research is primarily based on detecting possible leakage hotspots in the network according to citizens’ and experts’ experience. Communication with the local population in the Agios Germanos settlement revealed observations of quite frequent pipe breaks and bursts in the lowest-elevation area of the settlement, which comprises the most remote part of the network from the system’s head tank. The elevation difference in this part of the network from the WDN’s tank is about 100 m or even higher. Due to the large elevation differences and subsequent high pressure developed in this part of the network, a decision was made to initially install a pressure reducing valve (PRV) upstream of this area (see Section 3.2). It should be noted that the nodes of the network downstream of the location of this PRV were found to exhibit very low average sensitivity indexes and were therefore not considered possible locations for the installation of pressure sensors based on the methodology described in Section 2.4. However, it should be emphasized that, as described in Section 2.4, a pressure sensor (one of the three to be installed in the Agios Germanos settlement) is to be placed at the most remote from the tank part of the network, close to a node located downstream of the installed PRV (see Figure 6).
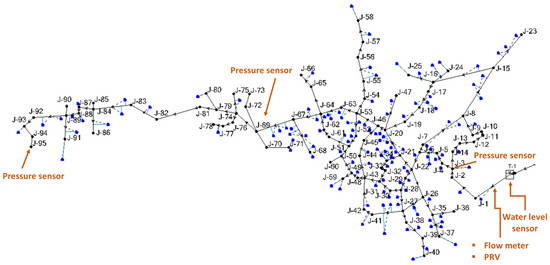
Figure 6.
Locations of measuring equipment installed in Agios Germanos settlement.
The results in Table 1 manifest that the most sensitive node to leakages is node J-69, and therefore a pressure sensor was decided to be installed there. Node J-69 is located on the central pipeline of the settlement (on the DN90 PVC pipe), making the installation of the pressure sensor and the collection of measurements more convenient. Since a total of three pressure sensors was to be installed on the network, the other two were placed after the head tank of the settlement (J-3), at the entrance of the WND, to manage the pressure in the network, and at the most remote node of the network (J-95), which could significantly assist in the calibration of the system’s hydraulic model. The exact locations of the pressure sensors were also determined by the topographic features of the settlement and the ability to locate equipment at specific points/junctions. A flow meter was also installed at the entrance of the settlement, after its head tank, to measure the incoming flow in the WDN. Moreover, a fixed outlet PRV was placed upstream of the WDN after Agios Germanos’ tank to enable the implementation of pressure management in the network. The water level in the studied settlement’s tank is measured by a water level sensor. Figure 6 presents the locations of the measuring equipment installed in the settlement of Agios Germanos.
The SCADA system installed in the settlement of Agios Germanos provided available data, such as water level data at the system’s head tank, flow measurements downstream of the system’s tank, and pressure measurements at the three selected locations within the WDN. The hydraulic model calibration was performed manually in Extended Period Simulation (EPS) mode over a 24 h period, with the primary calibration parameters being the roughness coefficients of the system’s pipes. The simulation began at midnight, with the tank’s water level set to its maximum observed value. The calibration of the WDN was performed for the day that the maximum water demand in the study period was measured, ensuring that the maximum water demand of all customer meters matched the highest measured value and considering the pattern of the hourly variation in the water demand recorded by the flow meter, valid for all water meters in the study area. The calibration of the pipe roughness coefficients was conducted through an iterative trial-and-error methodology, utilizing pressure data acquired from the SCADA system. The trial-and-error method is well established in the domain of water distribution network calibration, and it has been extensively documented in numerous studies [72,73,74,75]. The iterative nature of the trial-and-error method means that it inherently involves numerous cycles of adjustment and comparison based on engineering experience and domain knowledge, a process that can be time-consuming and computationally demanding. As a result, this method is typically more suited to addressing small-scale problems [73], such as those exemplified by the Agios Germanos settlement.
In our study, this approach involved systematically updating and adjusting the roughness parameter at each iteration and comparing the resulting pressure simulations with the observed data to minimize discrepancies. Its effectiveness lies in its ability to refine the model parameters iteratively, thereby enhancing the accuracy of the hydraulic simulations. Following the trial-and-error methodology, the Hazen–Williams coefficient was determined to be approximately 100 for most pipes in the network. Exceptions were noted for a few recently constructed DN63 PVC pipes at the western end of the settlement, where the coefficient was found to be around 120. The accuracy of this calibration was confirmed by comparing the pressure estimates at the three junctions with the available pressure measurements, resulting in a very satisfactory match, within ±5% of the observed values [76], and thus the hydraulic model’s calibration was deemed successful. Furthermore, the model’s reliability was validated using flow data from three different days. During validation, the demands for all customer meters were assigned following a predefined procedure, and the pressure measurements were found to match within ±8% of the measured values, further affirming the model’s accuracy and robustness.
Flow measurements acquired from the SCADA system assisted in extracting the coefficient of variation of the daily demand applied to all customer meters in the study area. The patterns of daily variation in the water demand were extracted using the recorded 30 min flow measurements for an extended period of more than four months. To extract the daily pattern of the coefficient of flow variation in the settlement, each recorded 30 min measurement was divided by the average flow of the respective measuring interval. The pattern extracted for the day of the maximum water demand was applied to all customer meters, while the demand of all customer meters (at peak demand time) was adjusted to equal the maximum daily demand recorded by the flow meter. The mean pattern of the daily variation in flow was also assessed by dividing the average value of each 30 min interval by the average flow of the entire measuring period. Figure 7 presents the mean pattern of the coefficient of flow variation for the Agios Germanos settlement, as well as the coefficient of variation for the day that the maximum flow rate during the study period was recorded.
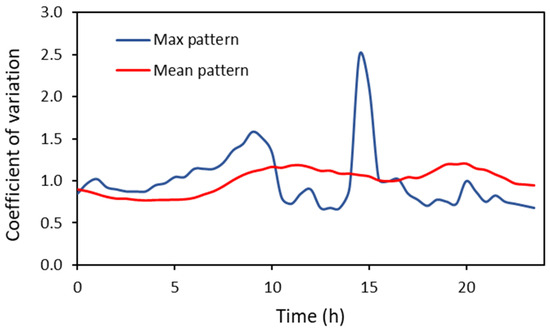
Figure 7.
Coefficient of hourly water demand in the settlement of Agios Germanos extracted from measured data.
The calibration of the hydraulic model in the Agios Germanos settlement was conducted for the day of the maximum water demand measured during the studied period, adjusting the customer meters’ demands accordingly and using the pattern of the flow coefficient of variation extracted from the measurements as described above, i.e., see the blue pattern in Figure 7. The highest flow rates were observed at the watermain of the network starting from the system’s tank, while the lowest flows were observed at the most remote and low-altitude part of the network, as well as in the majority of the network’s secondary branches. It should be noted that a large part of the network is characterized by high pressure, even during the period of maximum water consumption. Figure 8 presents the water pressure in the Agios Germanos WDN during the period of minimum flow on the day that the maximum flow rate was measured. The area of the network after node J-81 is characterized by a significant drop in elevation (marked as the “area of critical pressures” in Figure 8), leading to the development of high pressure, especially during the MNF.
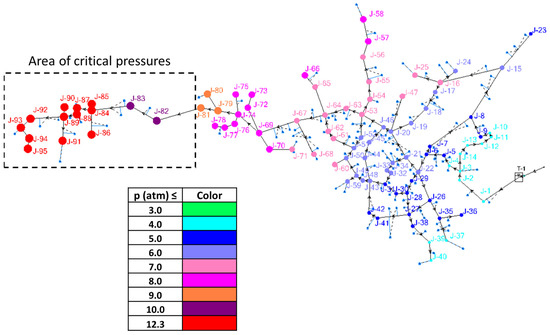
Figure 8.
Water pressure in the Agios Germanos water distribution network during the time of minimum flow on the day of the maximum measured flow rate.
The highest velocities in the network approached 1 m/s and were assessed at the watermain of the system. However, the water velocities were found to be low in some parts of the network. Low velocities in pipes result in extended travel times, leading to sections where sediments can collect and accumulate, providing environments for microbial growth. Extended detention times can also significantly diminish the corrosion control effectiveness by affecting phosphate inhibitors and pH management. Pipe deterioration, manifesting as leaks or breaks, compromises the hydraulic integrity of the system. The loss of hydraulic integrity has several detrimental consequences, including the contamination of the distribution system through intrusion, sedimentation, a reduction in hydraulic capacity, the loosening of scale, and a prolonged water age, all of which can have significant water quality implications.
3.2. MNF and Leakage Assessment
In the Agios Germanos settlement, the minimum elevations are observed at the most remote nodes of the network, leading to high pressure in a quite large area of the network. This part of the network is, as observed also by field measurements and ALC operations, the most prone to frequent pipe breaches and sometimes even pipe breaks. At this part of the network, the pressure even exceeds the nominal pipe resistance. The high pressure observed in the network intensifies the wear on valves and fittings, consequently amplifying the leakage rates and potentially leading to additional leaks or breaks with subsequent repercussions for the water quality. This part of the network is characterized by low elevation, with the difference in altitude from the system’s tank exceeding 100 m. Figure 8 presents the critical area of the Agios Germanos WDN in a black box. To provide evidence of this matter, pressure and flow measurements were conducted at the existing WDN for a one-month period. The flow was recorded at 30 min intervals and the MNF was assessed for each 24 h interval, both between 12:00 pm and 5:00 am and between 2:00 am and 4:00 am (see Section 2.5). The minimum value observed for the entire period of measurements and for both intervals was considered equal to the MNF and therefore represented the leakages of the studied WDN.
To reduce the risk of new pipe breaks in the critical area of the network—but, most importantly, to reduce the existing leakages of the entire network—a fixed-outlet PRV was located at the beginning of the critical branch. Fixed-outlet valves aim to maintain the outlet pressure from the valve at a constant and defined value. This somewhat limits their effectiveness in reducing base leaks, especially when the water demand is low [12]. The downstream pressure of the PRV was fixed at 4 atm. After placing the additional PRV in the WDN of the Agios Germanos settlement, the pressure and flow in the network and the water level in the network’s tank were measured for more than three months at 30 min intervals. Figure 9 presents the water pressure in the Agios Germanos settlement at the time of the minimum flow, after placing a fixed-outlet PRV upstream of the critical area of the network shown in Figure 8. The hydraulic simulation was again conducted for the day of the maximum water demand measured during the studied period (see Figure 7 for the coefficient of the hourly water demand). The MNF was again assessed as the minimum value observed for the entire interval of measurements (three months) and for both the 12:00 pm to 5:00 am and 2:00 am to 4:00 am periods. Figure 10 presents the water flow variation in the Agios Germanos settlement for the measurement period from 27 July 2022 to 12 September 2022, after installing a PRV (see Figure 9) upstream of the area of critical pressure of the WDN. The MNF, occurring twice during the time interval presented in Figure 10, is marked in green.
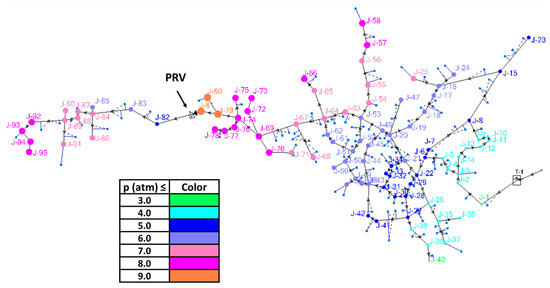
Figure 9.
Water pressure in the Agios Germanos water distribution network at the time of minimum flow after placing a pressure reducing valve (PRV) upstream of the critical area of the existing network.
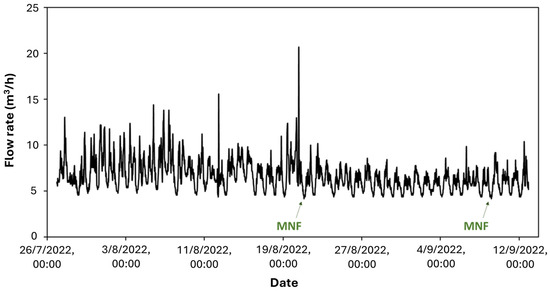
Figure 10.
Water flow variation in Agios Germanos water distribution network and minimum night flow (MNF) after placing a pressure reducing valve (PRV) upstream of the critical low-elevation area of the existing network.
Based on Equation (4), the MNF is composed of the minimum night use, background losses, and burst leakage, with the latter two representing the total leakage of the WDN. As mentioned earlier in this work, in small settlements, such as Agios Germanos in the Prespes Municipality, the MNF can be confidently assumed to equal the leakage amount. During night-time hours, approximately 6% of the population is actively engaged [29,43,44], corresponding to a very small number of inhabitants in the Agios Germanos settlement. It is also noted that non-residential activities, such as night irrigation, are considered negligible in the area, and home leakages are assumed to be limited owing to information campaigns conducted by the Municipality of Prespes to assist in water saving in the broader area. Therefore, the minimum night-time use is considered to be almost zero in Equation (4). The background leakage, also present in Equation (4), usually refers to very small leaks and could be assessed using Equations (5)–(7).
The installation of the fixed-outlet PRV upstream of the critical low-elevation area of the Agios Germanos settlement significantly reduced the water pressure in this area. This reduction almost reached 35% for the lowest-elevation nodes of the network (nodes that are farther from the system’s tank). As mentioned earlier, the MNF of the WDN was measured for a one-month period before installing the PRV shown in Figure 9. The MNF during this interval was measured at 5.36 m3/h (case a). After installing the PRV upstream of the low-elevation area of the settlement (case b), the MNF was measured at 4.13 m3/h. Table 2 presents the MNF, representing the sum of background losses and burst leakages, in the Agios Germanos settlement before and after installing the fixed-outlet PRV upstream of the low-elevation part of the network. It should be noted that the MNF with the aforementioned PRV is estimated to be about 23% lower compared to the previous condition (without the PRV). The background losses were also assessed for the WDN of the Agios Germanos settlement with a total length of pipes L = 4.26 km, N = 104 consumer connections, and a total length of consumer connections s = 0.60 km. For case (a) and an average pnight = 6.3 atm, the background losses were DB = 332.4 L/h based on Equation (6). For case (b) and an average pnight = 5.5 atm, the background losses were assessed to be DB = 271.1 L/h. Considering Equation (7), the background losses were assessed to be DB = 409.3 L/h for case (a) and DB = 333.9 L/h for case (b).

Table 2.
Minimum night flow in Agios Germanos settlement using different management schemes.
After assessing the MNF for the existing pressure regime and leakages of the system, a pressure reduction scheme was implemented. The pressure was reduced at the inlet of the settlement by adjusting the fixed-outlet PRV, installed together with the rest of the measuring equipment (SCADA system) after the system’s head tank (see Section 2.4), at a pressure lower than the one existing during the maximum daily flow observed during the four-month period (one month without and three months with the PRV installed upstream of the low-elevation area of the network) of measurements. This PRV is referred to as PRVPM, as it is used to implement pressure management in the entire WDN of the settlement. In the Agios Germanos settlement, the initial pressure measured at the inlet of the WDN is 1.26 atm. The reduction in the inlet pressure is found to be around 12.7%. The pressure reduction scheme was implemented for almost twenty days and the MNF in the settlement was measured and extracted for this interval. The MNF measured for this pressure reduction scheme in the Agios Germanos settlement is also included in Table 2 (case c). Therefore, the reduction in MNF when implementing a pressure management scheme directly after the system’s head tank reaches 17% (with respect to case b).
After implementing the pressure management scheme described above, Equation (12) is used to assess the leakage exponent N1 of the WDN of the Agios Germanos settlement. Table 3 presents the estimated value of the leakage exponent N1, together with other pressure–leakage coefficients estimated for the studied WDN of the Agios Germanos settlement. The estimated value of N1 exceeds 1.0, signifying that, for a 10% reduction in the inlet pressure, the leakages are reduced by more than 10%. Equation (11) is then used to estimate the leakage number, LN, of the WDN. To further estimate the coefficients and of Equation (14), more pressure management schemes for the WDN should be considered. In this work, an attempt was also made to approximate these coefficients by further reducing the inlet pressure of the Agios Germanos settlement at total proportions of ≈16.5% and ≈20.5% (from the initial inlet pressure). Each pressure reduction scheme was monitored for a period of almost ten days and the MNF was assessed from measurements of each such period. Equation (14) was then fitted using the least squares method to assess the coefficients and for the Agios Germanos WDN. The above coefficients are also presented in Table 3. The estimated exponent in Equation (14) was found to be larger than 1.0, indicating that the water leakage is sensitive to the water pressure. However, the results extracted for the two coefficients of Equation (14) should be considered with caution, as the measurement intervals for the two additional inlet pressure reduction schemes were quite short so as to produce MNF results with high confidence.

Table 3.
Pressure–leakage coefficients assessed when implementing pressure management.
Leakage reduction in WDNs can lead to savings in energy consumption and reductions in greenhouse gas emissions. Stokes and Horvarth [77] used a hybrid life-cycle assessment (LCA) to evaluate the energy implications of water supply systems in the U.S. to aid the decision-making process in LCAs for U.S. water provision systems. Four water sources were analyzed in this research, namely imported water, seawater desalination, brackish groundwater desalination, and recycled water (producing non-potable water). According to the LCA findings of this study, a defined quantity of 1 m3 of imported water needs 18 MJ of energy to be treated and distributed. Table 4 presents the energy consumption due to leakages in the WDN of the Agios Germanos settlement, based on the results presented in [77] for imported water, after installing a PRV upstream of the low-elevation area of the network (case b) and after implementing a pressure management scheme by reducing the inlet pressure of the settlement by 12.7% (case c). Table 4 also includes the energy savings with respect to the initial condition of the network (case a).

Table 4.
Energy consumption due to leakages and energy savings using different management schemes.
In the present work, a minimum pressure of 2 atm has to be retained at all nodes of the WDN associated with the demands. However, based on the results of the hydraulic modeling and also based on the pressure monitoring conducted in the network, the actual minimum pressure at the network is always higher than the aforementioned limiting value. This also holds for the pressure management scheme presented in Table 2 (case c). This implies that there remains significant potential for further reduction in the inlet pressure of the settlement. Even the boundary pressure of 2 atm could be considered quite high for small settlements with low-rise buildings; however, the firefighting requirements do not allow further reductions. Unbilled authorized water consumption and possible unauthorized consumption could form part of the total remaining MNF of the settlement. However, it should be noted that pressure management for WDNs is quite a complex process, as the distribution of pressure both in space and in time is influenced by the local topography, the water use characteristics, the age and condition of the WDN, and other factors that need to be further investigated.
4. Conclusions
Reducing non-revenue water in WDNs has multiple benefits for the global community. First of all, a precious natural resource is protected, while, at the same time, the energy consumption throughout the water supply chain is reduced. The reduction of non-revenue water significantly contributes to economically sustainable water utilities, with increased incomes and reduced costs of energy and rehabilitation. The sustainability of water utilities contributes to energy savings and reductions in greenhouse gas emissions, thus contributing to mitigating climate change’s impacts on societies and assisting global sustainability.
In the present work, hydraulic modeling was combined with the installation of pressure and flow measuring equipment on the WDN of a small DMA, to assess and manage leakages using MNF analysis. After installing the necessary equipment on the WDN of the Agios Germanos settlement, a critical area of very high pressure was detected, rendering this part of the network vulnerable to leakages. A PRV was installed upstream of this area to reduce leakages in the network, resulting in a significant reduction in real losses (about 23%). Pressure and flow data were then acquired for a three-month period to assess the MNF, assumed to represent leakages in the study area. The pressure was then reduced upstream of the WDN to assess the relationship between the pressure and leak flow rate in the selected settlement. The leakage exponent N1, describing the influence of the pressure on water leakages in the Agios Germanos settlement, was found to exceed one, signifying that, for a 10% reduction in the inlet pressure, leakages are reduced by more than 10%. The implemented pressure management scheme resulted in a reduction in the MNF and therefore a reduction in leakages, reaching 17%.
Pressure management is judged to be an efficient method of managing real losses in the WDNs of quite small settlements and therefore of reducing non-revenue water. Besides reducing leaks and pipe breaks in the network, pressure management can also significantly contribute to improvements in costumers’ service due to fewer water supply interruptions, the suspension of network deterioration, and the reduction of social costs caused by pipe failures, as well as the reduction of maintenance costs for the responsible water utility due to fewer repairs and ALC actions.
Author Contributions
Conceptualization, P.G. (Panagiota Galiatsatou), D.M. and P.P.; methodology, P.G. (Panagiota Galiatsatou), D.M. and P.G. (Philipos Ganoulis); software, P.G. (Panagiota Galiatsatou); validation, P.G. (Panagiota Galiatsatou), D.M., P.G. (Philipos Ganoulis) and P.P.; formal analysis, P.G. (Panagiota Galiatsatou) and P.G. (Philipos Ganoulis); investigation, P.G. (Panagiota Galiatsatou), D.M. and P.G. (Philipos Ganoulis); resources, P.G. (Panagiota Galiatsatou) and P.P.; data curation, P.G. (Panagiota Galiatsatou), D.M. and P.G. (Philipos Ganoulis); writing—original draft preparation, P.G. (Panagiota Galiatsatou); writing—review and editing, P.G. (Panagiota Galiatsatou), D.M., P.G. (Philipos Ganoulis) and P.P.; visualization, P.G. (Panagiota Galiatsatou) and D.M.; supervision, P.G. (Panagiota Galiatsatou) and P.P.; project administration, P.P.; funding acquisition, P.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was conducted within the Interreg IPA CBC (CCI 2014 TC 16 I5CB 009) Smart-WaterSave “A Real Time Monitoring and Leakage Detection System in Water Distribution Networks” project (Subsidy Contract No. CN1-S.O.2.3.-SC011) between Greece and the Republic of North Macedonia.
Data Availability Statement
The datasets presented in this article are not readily available because they are measured and managed by the Municipality of Prespes, Greece.
Acknowledgments
We gratefully acknowledge the support of the Prespes Municipality in conducting this research.
Conflicts of Interest
The authors declare no conflicts of interest. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- IWA. Best Practice Water Balance. Available online: https://www.leakssuitelibrary.com/iwa-water-balance/ (accessed on 23 May 2024).
- Lambert, A.O. International report: Water losses management and techniques. Water Supply 2002, 2, 1–20. [Google Scholar] [CrossRef]
- Arregui, F.J.; Gavara, F.J.; Soriano, J.; Pastor-Jabaloyes, L. Performance analysis of ageing single-jet water meters for measuring residential water consumption. Water 2018, 10, 612. [Google Scholar] [CrossRef]
- Karim, M.R.; Abbaszadegan, M.; Le Chevallier, M. Potential for Pathogen Intrusion during Pressure Transients. J. AWWA 2003, 95, 134–146. [Google Scholar] [CrossRef]
- Boulos, P.F.; Aboujaoude, A.S. Managing leaks using flow step-testing, network modeling, and field measurement. J. AWWA 2011, 103, 90–97. [Google Scholar] [CrossRef]
- Colombo, A.F.; Karney, B.W. Impacts of Leaks on Energy Consumption in Pumped Systems with Storage. J. Water Resour. Plan. Manag. 2005, 131, 146–155. [Google Scholar] [CrossRef]
- Cabrera, E.; Pardo, M.A.; Cobacho, R.; Cabrera, E., Jr. Energy Audit of Water Networks. J. Water Resour. Plan. Manag. 2010, 136, 669–677. [Google Scholar] [CrossRef]
- Mutikanga, H.E. Waterloss Management: Tools and Methods for Developing Countries. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2012. [Google Scholar]
- Jowitt, P.W.; Xu, C. Optimal Valve Control in Water-Distribution Networks. J. Water Resour. Plan. Manag. 1990, 116, 455–472. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Tsitsifli, S. Integrated Management of Urban Water Distribution Networks; Kallipos Open Academic Publications: Athens, Greece, 2015; p. 323. Available online: https://repository.kallipos.gr/handle/11419/3415 (accessed on 5 February 2024). (In Greek)
- Farley, M.; Trow, S. Losses in Water Distribution Networks—A practitioner’s Guide to Assessment, Monitoring and Control; IWA Publishing: London, UK, 2003; p. 273. [Google Scholar]
- Marzola, I.; Alvisi, S.; Franchini, M. Analysis of MNF and FAVAD model for leakage characterization by exploiting smart-metered data: The case of the Gorino Ferrarese (FE-Italy) district. Water 2021, 13, 643. [Google Scholar] [CrossRef]
- Savic, D.A.; Walters, G.A. An Evolution Program for Optimal Pressure Regulation in Water Distribution Networks. Eng. Optim. 1995, 24, 197–219. [Google Scholar] [CrossRef]
- Ulanicki, B.; Bounds, P.L.M.; Rance, J.P.; Reynolds, L. Open and Closed Loop Pressure Control for Leakage Reduction. Urban Water 2000, 2, 105–114. [Google Scholar] [CrossRef]
- Thornton, J.; Sturm, R.; Kunkel, G. Water Loss Control Manual, 2nd ed.; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Fanner, P.; Sturm, R.; Thornton, J.; Liemberger, R. Leakage Management Technologies; AWWA Research Foundation: Denver, CO, USA, 2007; p. 345. [Google Scholar]
- Nazif, S.; Karamouz, M.; Tabesh, M.; Moridi, A. Pressure management model for urban water distribution networks. Water Resour. Manag. 2010, 24, 437–458. [Google Scholar] [CrossRef]
- Gomes, R.; Marques, A.S.; Sousa, J. Estimation of the benefits yielded by pressure management in water distribution systems. Urban Water J. 2011, 8, 65–77. [Google Scholar] [CrossRef]
- Karadirek, I.E.; Kara, S.; Yilmaz, G.; Muhammetoglu, A.; Muhammetoglu, H. Implementation of hydraulic modelling for water-loss reduction through pressure management. Water Resour. Manag. 2012, 26, 2555–2568. [Google Scholar] [CrossRef]
- Martínez-Codina, A.; Castillo, M.; González-Zeas, D.; Garrote, L. Pressure as a predictor of occurrence of pipe breaks in water distribution networks. Urban Water J. 2016, 13, 676–686. [Google Scholar] [CrossRef]
- Vicente, D.J.; Garrote, L.; Sánchez, R.; Santillán, D. Pressure management in water distribution systems: Current status, proposals, and future trends. J. Water Resour. Plan. Manag. 2016, 142, 1–13. [Google Scholar] [CrossRef]
- Creaco, E.; Walski, T. Economic analysis of pressure control for leakage and pipe burst reduction. J. Water Resour. Plan. Manag. 2017, 143, 04017074. [Google Scholar] [CrossRef]
- Fontana, N.; Giugni, M.; Glielmo, L.; Marini, G.; Zollo, R. Real-time control of pressure for leakage reduction in water distribution network: Field experiments. J. Water Resour. Plan. Manag. 2018, 144, 04017096. [Google Scholar] [CrossRef]
- Trow, S.W.; Payne, A. Intelligent Pressure Management—A New Development for Monitoring and Control of Water Distribution Systems. In Proceedings of the 5th IWA Water Loss Reduction Specialist Conference, Cape Town, South Africa, 26–30 April 2009; pp. 302–314. [Google Scholar]
- Giustolisi, O.; Ugarelli, R.; Berardi, L.; Laucelli, D. Strategies for the electric regulation of pressure control valves. J. Hydroinform. 2017, 19, 621–639. [Google Scholar] [CrossRef]
- Butler, D. Leakage Detection and Management; Palmer Environmental: Cwmbran, UK, 2009. [Google Scholar]
- Hamilton, S.; McKenzie, R. Water Management and Water Loss; IWA Publishing: London, UK, 2014. [Google Scholar]
- Alkasseh, J.M.; Adlan, M.N.; Abustan, I.; Aziz, H.A.; Hanif, A.B.M. Applying minimum night flow to estimate water loss using statistical modeling: A case study in Kinta Valley, Malaysia. Water Resour. Manag. 2013, 27, 1439–1455. [Google Scholar] [CrossRef]
- Deyi, M.; Van Zyl, J.; Shepherd, M. Applying the FAVAD concept and leakage number to real networks: A case study in Kwadabeka, South Africa. Procedia Eng. 2014, 89, 1537–1544. [Google Scholar] [CrossRef]
- Özdemir, Ö.; Fırat, M.; Yılmaz, S.; Usluer, M. Analysis of the effect of pressure control on leakages in distribution systems by FAVAD equation and field applications. Water Pract. Technol. 2021, 16, 320–332. [Google Scholar] [CrossRef]
- Fan, L.; Wang, F.; Liu, G.; Yang, X.; Qin, W. Public perception of water consumption and its effects on water conservation behavior. Water 2014, 6, 1771–1784. [Google Scholar] [CrossRef]
- Byeon, S.; Choi, G.; Maeng, S.; Gourbesville, P. Sustainable water distribution strategy with smart water grid. Sustainability 2015, 7, 4240–4259. [Google Scholar] [CrossRef]
- Gorev, N.B.; Kodzhespirova, I.F. Noniterative implementation of pressure-dependent demands using the hydraulic analysis engine of EPANET 2. Water Resour. Manag. 2013, 27, 3623–3630. [Google Scholar] [CrossRef]
- Muranho, J.; Ferreira, A.; Sousa, J.; Gomes, A.J.; Marques, A.S. Pressure-dependent demand and leakage modelling with an EPANET extension—WaterNetGen. Procedia Eng. 2014, 89, 632–639. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Tsitsifli, S. Using the bimonthly water balance of a non-fully monitored water distribution network with seasonal water demand peaks to define its actual NRW level: The case of Kos town, Greece. Urban Water J. 2013, 11, 348–360. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Gonelas, K. Analysis and calculation of the short and long run economic leakage level in a water distribution system. Water Util. J. 2016, 12, 57–66. [Google Scholar]
- Sarrate, R.; Nejjari, F.; Rosich, A. Sensor placement for fault diagnosis performance maximization in distribution networks. In Proceedings of the 20th Mediterranean Conference on Control & Automation, Barcelona, Spain, 3–6 July 2012; pp. 110–115. [Google Scholar]
- Li, C.; Du, K.; Tu, J.-P.; Dong, W.-X. Optimal placement of pressure sensors in water distribution system based on clustering analysis of pressure sensitive matrix. Procedia Eng. 2017, 186, 405–411. [Google Scholar]
- Puleo, V.; Freni, G.; La Loggia, G. Pressure sensors positioning for leakages detection under uncertain demands. In Proceedings of the 13th International Conference on Hydroinformatics, Palermo, Italy, 1–6 July 2018; pp. 1713–1717. [Google Scholar]
- Soroush, F.; Abedini, M.J. Optimal selection of number and location of pressure sensors in water distribution systems using geostatistical tools coupled with genetic algorithm. J. Hydroinform. 2019, 21, 1030–1047. [Google Scholar] [CrossRef]
- Francés-Chust, J.; Brentan, B.M.; Carpitella, S.; Izquierdo, J.; Montalvo, I. Optimal placement of pressure sensors using fuzzy DEMATEL-based sensor influence. Water 2020, 12, 493. [Google Scholar] [CrossRef]
- Peng, S.; Cheng, J.; Wu, X.; Fang, X.; Wu, Q. Pressure sensor placement in water supply network based on graph neural network clustering method. Water 2022, 14, 150. [Google Scholar] [CrossRef]
- Hunaidi, O.; Brothers, K. Night flow analysis of pilot DMAs in Ottawa. In Proceedings of the Water Loss Specialist Conference, Bucharest, Romania, 23–26 September 2007; pp. 32–46. [Google Scholar]
- Tabesh, M.; Yekta, A.A.; Burrows, R. An integrated model to evaluate losses in water distribution systems. Water Resour. Manag. 2009, 23, 477–492. [Google Scholar] [CrossRef]
- Childs, C. Interpolating Surfaces in ArcGIS Spatial Analyst, ESRI Education Services 2004. Available online: https://www.esri.com/news/arcuser/0704/files/interpolating.pdf (accessed on 31 May 2024).
- Murayama, Y.; Estoque, R.C. Creating a Digital Elevation Model (DEM): A GIS Lecture Tutorial; Division of Spatial Information Science, Graduate School of Life and Environmental Sciences, National University of Tsukuba: Tsukuba, Japan, 2011; Available online: http://giswin.geo.tsukuba.ac.jp/sis/tutorial/Creating%20a%20DEM%20from%20a%20Topographic%20Map_RCEstoque.pdf (accessed on 31 May 2024).
- Annan, M.; Gooda, E.A. Effect of minor losses during steady flow in transmission pipelines–Case study “water transmission system upgrade in northern Saudi Arabia”. Alex. Eng. J. 2018, 57, 4299–4305. [Google Scholar] [CrossRef]
- AL-Washali, T.M.; Elkhider, M.E.; Sharma, S.K.; Kennedy, M.D. A review of nonrevenue water assessment software tools. WIREs Water 2020, 7, e1413. [Google Scholar] [CrossRef] [PubMed]
- OpenFlows WaterGEMs. Water Distribution Analysis and Design Software. Available online: https://www.bentley.com/software/openflows-watergems/ (accessed on 31 May 2024).
- Rossman, L.A. EPANET 2: Users’ Manual; EPA/600/R-00/057; National Risk Management Research Laboratory, Office of Research and Development, United Sates Environmental Protection Agency (EPA): Cincinnati, OH, USA, 2000.
- Hou, Y.-K.; Zhao, C.-H.; Huang, Y.-C. A GIS-based water distribution model for Zhengzhou city, China. Water Supply 2011, 11, 497–503. [Google Scholar]
- Świtnicka, K.; Suchorab, P.; Kowalska, B. The optimisation of a water distribution system using Bentley WaterGEMS software. In Proceedings of the 2nd International Conference of Computational Methods in Engineering Science (CMES’17), ITM Web of Conferences, EDP Sciences, Lublin, Poland, 23–25 November 2017; p. 03009. [Google Scholar]
- Chatzivasili, S.; Papadimitriou, K.; Kanakoudis, V. Optimizing the formation of DMAs in a Water Distribution Network through Advanced Modelling. Water 2019, 11, 278. [Google Scholar] [CrossRef]
- Mentes, A.; Galiatsatou, P.; Spyrou, D.; Samaras, A.; Stournara, P. Hydraulic simulation and analysis of an urban center’s aqueducts using emergency scenarios for network operation: The case of Thessaloniki City in Greece. Water 2020, 12, 1627. [Google Scholar] [CrossRef]
- Kang, D.; Lansey, K. Demand and roughness estimation in water distribution systems. J. Water Resour. Plan. Manag. 2011, 137, 20–30. [Google Scholar] [CrossRef]
- Do, N.C.; Simpson, A.R.; Deuerlein, J.W.; Piller, O. Calibration of water demand multipliers in water distribution systems using genetic algorithms. J. Water Resour. Plan. Manag. 2016, 142, 04016044. [Google Scholar] [CrossRef]
- Bhave, P.R. Calibrating water distribution network models. J. Hydraul. Eng. 1988, 114, 120–136. [Google Scholar] [CrossRef]
- Boulos, P.F.; Wood, D.J. Explicit calculation of pipe-network parameters. J. Hydraul. Eng. 1990, 116, 1329–1344. [Google Scholar] [CrossRef]
- Ormsbee, L.E. Implicit network calibration. J. Water Resour. Plan. Manag. 1989, 115, 243–257. [Google Scholar] [CrossRef]
- Kapelan, Z.S.; Savic, D.A.; Walters, G.A. Calibration of water distribution hydraulic models using a Bayesian-type procedure. J. Hydraul. Eng. 2007, 133, 927–936. [Google Scholar] [CrossRef]
- Koppel, T.; Vassiljev, A. Calibration of a model of an operational water distribution system containing pipes of different age. Adv. Eng. Softw. 2009, 40, 659–664. [Google Scholar] [CrossRef]
- Dini, M.; Tabesh, M. A new method for simultaneous calibration of demand pattern and Hazen-Williams coefficients in water distribution systems. Water Resour. Manag. 2014, 28, 2021–2034. [Google Scholar] [CrossRef]
- Zhang, Q.; Zheng, F.; Duan, H.F.; Jia, Y.; Zhang, T.; Guo, X. Efficient numerical approach for simultaneous calibration of pipe roughness coefficients and nodal demands for water distribution systems. J. Water Resour. Plan. Manag. 2018, 144, 04018063. [Google Scholar] [CrossRef]
- Tsakiris, G.; Charalambous, P. Management of Water Networks. In Hydraulic Works—Design and Management; Tsakiris, G., Ed.; Symmetry: Athens, Greece, 2010; Volume I: Urban Hydraulic Works, pp. 445–482. (In Greek) [Google Scholar]
- Pérez, R.; Puig, V.; Pascual, J.; Quevedo, J.; Landeros, E.; Peralta, A. Methodology for leakage isolation using pressure sensitivity analysis in water distribution networks. Control Eng. Pract. 2011, 19, 1157–1167. [Google Scholar] [CrossRef]
- Blesa, J.; Nejjari, F.; Sarrate, R. Robustness analysis of sensor placement for leak detection and location under uncertain operating conditions. Procedia Eng. 2014, 89, 1553–1560. [Google Scholar] [CrossRef]
- May, J. Pressure Dependent Leakage. World Water Environ. Eng. 1994, 10, 15–19. [Google Scholar]
- van Zyl, J.E.; Cassa, A.M. Modeling elastically deforming leaks in water distribution pipes. J. Hydraul. Eng. 2014, 140, 182–189. [Google Scholar] [CrossRef]
- Lambert, A.O.; Fantozzi, M. Recent Developments in Pressure Management. In Proceedings of the 6th IWA Water Loss reduction Specialist Conference, Sao Paulo, Brazil, 6–9 June 2010. [Google Scholar]
- Thornton, J.; Lambert, A. Managing pressures to reduce new breaks. Water 2006, 21, 24–26. [Google Scholar]
- Xu, Q.; Chen, Q.; Ma, J.; Blanckaert, K.; Wan, Z. Water saving and energy reduction through pressure management in urban water distribution networks. Water Resour. Manag. 2014, 28, 3715–3726. [Google Scholar] [CrossRef]
- Savic, D.A.; Kapelan, Z.S.; Jonkergouw, P.M. Quo vadis water distribution model calibration? Urban Water J. 2009, 6, 3–22. [Google Scholar] [CrossRef]
- Zanfei, A.; Menapace, A.; Santopietro, S.; Righetti, M. Calibration procedure for water distribution systems: Comparison among hydraulic models. Water 2020, 12, 1421. [Google Scholar] [CrossRef]
- Chu, S.; Zhang, T.; Yu, T.; Wang, Q.J.; Shao, Y. A noise adaptive approach for nodal water demand estimation in water distribution systems. Water Res. 2021, 192, 116837. [Google Scholar] [CrossRef]
- Marlim, M.S.; Kang, D. Contaminant flushing in water distribution networks incorporating customer faucet control. Sustainability 2022, 14, 2249. [Google Scholar] [CrossRef]
- Hossain, S.; Hewa, G.A.; Chow, C.W.; Cook, D. Modelling and incorporating the variable demand patterns to the calibration of water distribution system hydraulic model. Water 2021, 13, 2890. [Google Scholar] [CrossRef]
- Stokes, J.R.; Horvath, A. Energy and air emission effects of water supply. Environ. Sci. Technol. 2009, 43, 2680–2687. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).