Abstract
The treatment of pharmaceutical wastewater is a critical environmental challenge, necessitating efficient removal methods. This study investigates the adsorption of a synthetic multicomponent pharmaceutical wastewater (SPWW) containing methanol, benzene, methylene chloride, 4-aminophenol, aniline, and sulfanilic acid onto charcoal-based activated carbon (AC). Batch experiments were conducted to study the effects of pH, contact time, and initial concentrations of the adsorbates. The results show that longer contact time and higher initial concentrations increase the adsorption capacity, whereas pH shows no significant effect on the adsorption capacity at a value of less than 10, eliminating the need for pH adjustment and reducing process costs. The pseudo-second order (PSO) kinetic model best describes the adsorption process, with intraparticle diffusion playing a key role, as confirmed by the Weber and Morris (W-M) model. Six models describing the adsorption at equilibrium are applied to experimental data, and their parameters are estimated with a nonlinear regression model. Among isotherm models, the Langmuir-Freundlich model provides the best fit, suggesting multilayer adsorption on a heterogeneous granular activated carbon (GAC) surface. The maximum adsorption capacity is estimated to be 522.3 mgC/gAC. Experimental results confirm that GAC could effectively treat highly concentrated pharmaceutical wastewater, achieving up to 52% removal efficiency.
1. Introduction
The growing demand for pharmaceuticals and personal care products (PPCP) has surged wastewater production from drug manufacturing facilities. Higher production volumes, complex manufacturing processes, stringent cleaning protocols, and facility expansions contribute to increased water usage and, subsequently, wastewater generation. In pharmaceutical manufacturing facilities, wastewater is produced during various activities such as equipment cleaning, cooling, and development of new PPCPs. Moreover, the technologies used in producing pharmaceuticals generate large quantities of highly polluted wastewater. As a result, in response to wastewater management policies, industries are required to minimize wastewater production at the source of generation, which subsequently necessitates end-of-pipe treatment methods [1,2,3].
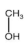
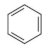
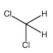
Methanol is a volatile organic compound (VOC) produced worldwide for various industrial purposes, including insecticide production. During plant start-up and shut-down, large quantities of water containing methanol are released into the environment, making it a major focus of regulation categorized in class 3 (flammability) and 6.1 (toxicity) of hazardous material as per Globally Harmonized System (GHS) of classification and labelling of chemicals [4]. Prolonged exposure to methanol can cause nerve impairment and vision loss [5,6]. Other major VOCs found in water resources include benzene and dichloromethane (DCM), which are used as solvents and raw materials in pharmaceuticals and personal care products [7]. Benzene is a definite carcinogen that is categorized as a group A chemical by the Environmental Protection Agency (EPA), and DCM can lead to health issues and environmental pollution, which is included in group B2 chemicals as per EPA evaluation [8,9,10,11]. The EPA’s drinking water guidelines limit the concentration of benzene and DCM to a maximum of 5 μg/L [12].
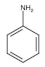
Among aromatic amines and sulfa drugs, aniline, 4-aminophenol, and sulfanilic acid are widely used in pesticide production or as intermediates/raw materials in the chemical synthesis of pharmaceuticals [13]. However, they are highly toxic and carcinogenic, and due to the complex degradation pathway, they can enter the water stream and impose risks to public health [14,15,16,17]. Therefore, removing these compounds from water and wastewater is essential to maintain a healthy environment.
Various methods, including biological treatment, adsorption, advanced oxidation processes, membrane or filtration technologies, and coagulation/flocculation techniques, have been implemented for the removal of PPCP from wastewater [18,19,20,21,22]. Furthermore, to increase the removal efficiency, one or two treatment processes are merged into one as a hybrid process or used as a sequence which has been the focus of recent studies [23,24,25,26,27,28].
The utilization of Activated carbon (AC) in removing PPCPs stands out among various treatment methods due to its highly effective adsorption capacity. This process efficiently eliminates pharmaceuticals without generating any by-products or toxic intermediates [8,29,30,31] and is able to remove persistent pollutants from the wastewater where biological treatment fails to degrade them [32,33]. The adsorption process is the migration of molecules from bulk gaseous or aqueous media onto a solid surface and is commonly utilized in the water treatment sector since the process is reported to be efficient, economically viable, and have low maintenance, simple design with social acceptance [34,35]. Among all adsorbents, activated carbon is relatively efficient for removing various organic and inorganic materials. In removing pharmaceuticals, the low-cost preparation, regeneration possibility, highly porous structure, large surface area, and the thermal stability of activated carbon are primary reasons for its application [36,37].
Several researchers studied the removal of pharmaceuticals by activated carbon under batch [38,39,40,41,42,43] and continuous conditions [1,44,45,46,47,48,49]. A comprehensive review, focusing on the removal of pharmaceuticals from wastewater, reported the quantitative portion of advanced treatment technologies implemented in Switzerland and Germany [50]. As per their studies, 65% and 81% of the wastewater treatment facilities in Switzerland and Germany have applied or are planning to upgrade their facilities by activated carbon adsorption process to meet the required target of pharmaceutical removal from the wastewater.
The pharmaceutical removal by adsorption process using activated carbon have been reviewed [37,51]. They reported that the performance of the adsorption process under the experimental conditions that simulate the actual industrial scenarios using various types of pharmaceutical wastewater needs further investigation. Many studies have shown prospects of implementing activated carbon for PPCP removal and have focused on developing a low-cost activated carbon, investigating the optimum operating condition, and modelling the adsorption behaviour [52,53,54]. A thorough literature review indicates that despite extensive studies on removing PPCP from wastewater, further investigation into the performance of the adsorption process under conditions that closely mimics real-world scenarios is needed. Most studies focus on a single pollutant removal at very low concentrations (), which does not fully represent the complexity of actual industrial effluents. This allows further investigations focusing on the adsorption behaviour and optimization for treating medium-high organic strength multicomponent wastewater under batch conditions. This better mimic real industrial effluents and considers the negative effects that multicomponent pollutants might have on adsorption performance.
Therefore, the novelty of this work lies on the comprehensive evaluation of a mixture of pharmaceutical compounds rather than individual compounds. Additionally, this study utilizes total organic carbon (TOC) as a parameter to evaluate the adsorption mechanisms. Compound-specific analytical methods often focus on single pollutants, providing a detailed but narrow perspective on adsorption performance. In contrast, TOC measurement offers a general insight into overall process performance without the deficiencies of chemical oxygen demand (COD) analysis, which can overestimate or underestimate pollutant concentrations. Additionally, the TOC can be measured online, making it a faster and cheaper alternative compared to mass spectrometry and high-performance liquid chromatography. This approach allows for a comprehensive assessment of the adsorption process in real wastewater treatment scenarios.
The data interpretation on the adsorption kinetics and isotherm provides information about the adsorption mechanism and pollutant removal rate [55]. Moreover, it provides a base for comparing the predicted model parameters to experimental adsorption behaviour under different experimental conditions and verifying theoretical assumptions. The model parameters also allow us to express the dependence of surface properties on sorption results, quantify the distribution of the pharmaceuticals on the adsorbent, and determine the adsorbent capacity to design an effective adsorption system [56,57,58].
Therefore, it is desired to study the pharmaceutical removal and the adsorption behaviour of charcoal-based activated carbon for multicomponent wastewater. Hence, the objectives of this study are as follows:
- Treatment of high-strength multicomponent pharmaceutical wastewater under batch conditions along with the optimization of the adsorption process by studying the effects of pH, contact time, and initial concentration of organics;
- Investigating the adsorption mechanism by analysis of dynamic and equilibrium behaviour using experimental data and various kinetic and isotherm models; and
- Developing an isotherm and kinetic model with potential application for predicting a continuous flow adsorption system.
This study represents the adsorption behaviour by addressing the simultaneous removal of multiple pharmaceuticals from wastewater using granular activated carbon (GAC). To investigate the adsorption mechanism, it introduces a novel assessment method based on TOC reduction, providing a holistic view of pharmaceutical removal. By applying various isotherm and kinetic models to multicomponent wastewater under batch conditions, this study not only unveils adsorption mechanisms but also offers practical insights for efficient pharmaceutical contaminant removal in real-world scenarios.
2. Materials and Methods
2.1. Preparation of Wastewater
The composition of the synthetic pharmaceutical wastewater (SPWW) is shown in Table 1. The chemical concentrations were selected by studying the wastewater properties from the pharmaceutical manufacturing sector reported in the open literature, including the most prevalent solvents used in this industry [59,60,61]. A specific amount of each compound was measured and added to distilled water to make a solution with the desired total organic carbon content ranging between 990 to 2200 mgC/L. For pH adjustment, liquid sodium hydroxide (NaOH, 40 g/mol, ≥97%, VWR Chemicals BDH, Mississauga, ON, Canada), liquid hydrochloric acid (HCl, 36.46 g/mol, 36.5–38.0% ACS, VWR Chemicals BDH, Mississauga, ON, Canada), and liquid sulfuric acid (H2SO4, 98.08 g/mol, 1 N, EMD Millipore, Etobicoke, ON, Canada) were used.

Table 1.
Physical and chemical properties of pharmaceuticals used to prepare synthetic wastewater.
Table 2 shows compounds and their concentrations used in preparing synthetic pharmaceutical wastewater.

Table 2.
Composition, concentration, and bulk properties of synthetic pharmaceutical wastewater and their reported range in the open literature.
2.2. Preparation and Characterization of the Activated Carbon
The charcoal-based GAC (Anachemia Science, Mississauga, ON, Canada) is physically activated by steam with a 4–12 mesh particle size. Prior to the adsorption experiments, the GAC was rinsed using distilled water to wash off the potential impurities and subsequently dried in an oven at a temperature of 100 °C for a duration of two days to make sure the water on the surface and inside the pores was removed prior to the experiments.
The GAC texture was analyzed using the Nova 11.0 Quantochrome gas sorption apparatus (Ashland, VA, USA), where nitrogen gas adsorption at the temperature of 77 K was used to measure the surface properties of the GAC. In advance of the adsorption measurements, approximately 0.2 g of the sample underwent an outgassing process at 300 °C for 3 h. Various parameters, including the BET surface area (Brunauer-Emmett-Teller), the BJH (Barrett–Joyner–Halenda) pore size distribution, the Horvath-Kawazoe (HK) pore size distribution, the t-method of De Boer micropore volume, and the mesopore volume of the GAC were calculated from the N2 adsorption and desorption isotherms [81,82,83,84]. The difference between the total pore volume (volume of N2 adsorbed at a relative pressure of P/P0 = 0.99) and micropore volume was used to calculate the mesopore volume.
The point of zero charge (pzc) for GAC was determined using the pH drift method in a 0.01 M NaCl electrolyte solution with a total volume of 100 mL [85]. First, the pH of the solutions was adjusted between 4 and 12 using NaOH or HCl solutions of 0.1 M, and then 0.3 g of GAC was added to each solution. The solutions were then shaken in a shaker until equilibrium was obtained. Later, the GAC was separated from the solution, and the pH of the solution was measured. The pzc value was obtained by plotting the initial pH versus the changes in pH (). When the resulting change in pH is zero, the surface is considered electrically neutral, and that pH value is taken as the pzc. At the pzc, the GAC’s surface has a net charge of zero as an equal number of positively and negatively charged functional groups are present [86].
2.3. Batch Adsorption Experiments
The uptake of pharmaceuticals from wastewater was investigated by changing the mass of activated carbon from 0.05 gAC to 75 gAC, using 100 mL of SPWW which is equivalent to an activated carbon dosage ranging from 0.5 gAC/L to 750 gAC/L. Throughout the experiments, the temperature was maintained at 23 °C to match the ambient temperature and the agitation speed was kept at 150 rpm. This constant agitation rate was selected to overcome potential external mass transfer limitation, ensuring adequate homogenization of the solution and continuous accessibility of the adsorption sites to the pharmaceuticals throughout the process. The amount of pharmaceuticals adsorbed was assessed by calculating the change in the concentration at a specific sampling time (TOC) from the initial concentration (TOC0) using Equations (1) and (2):
where q (mgC/gAC) is the capacity of GAC, V [L] is the volume of the solution in contact with the GAC, m (gAC) is the mass of dry GAC, and TOC (mgC/L) is the total organic carbon. To study the effect of pH, 0.1 g of GAC was added to 100 mL of synthetic pharmaceutical wastewater and agitated at 150 rpm for one day under a controlled temperature of 23 °C. The pH was adjusted to the values in the range of 4 to 11. To adjust the pH, 5N sodium hydroxide (NaOH) and 1N sulfuric acid (H2SO4) were used.
2.4. Analytical Technique
Samples were collected at various times, and the solution was filtered with a Whatman filter paper No. 44 to separate the GAC. The TOC (mgC/L) and TN (mgN/L) were determined by catalytic combustion TOC analyzer (Apollo 9000, Teledyne Tekmar, Mason, OH, USA) at 700 °C using an STS-8000 autosampler (Teledyne Tekmar, Mason, OH, USA). The analyzer is equipped with a non-dispersive infrared detector to measure the TOC and chemiluminescence detector to measure the TN. Method 132 of Orbeco-Hellige MC500 colorimeter (Sarasota, FL, USA) was used for COD (mgO2/L) measurements. A pH meter (model 230A, Thermo Scientific Orion Star, Mississauga, ON, Canada) was used to measure the pH of the solutions.
2.5. Error Analysis
The best model selection for experimental data has conventionally relied on the coefficient of determination (R2), with linearized models being preferred, and the one with the R2 closest to unity is considered the best model. However, it is shown that linear regression alters the models’ error structure [87]. Although the linearized form of the models is easier to calculate, it can introduce propagating errors that lead to incorrect parameter predictions [88]. Therefore, it is recommended to use nonlinear regression and curve-fitting tools to estimate the model parameters [89]. The advancement in computer technology has led to an increased adaptation of the nonlinear regression approach. This approach minimizes the quadratic error between the experimental data and the model’s outputs to obtain the model parameters [90]. In this study, MATLAB software, version 9.14 (R2023a) and its built-in curve fitting toolbox were used to obtain model parameters [91]. Various methods are employed to determine the goodness of fit, including the coefficient of determination, residual norm (RN), the average relative error (ARE), and the statistical Fisher test (F-test), which are presented in Table 3.

Table 3.
Error functions used to compare various isotherm and kinetic models used in this study.
Table 3.
Error functions used to compare various isotherm and kinetic models used in this study.
| Error Function | Definition | References | |
|---|---|---|---|
| Coefficient of determination (R2) | (3) | [92,93] | |
| Residual norm (RN) | (4) | [55,94] | |
| Average relative error (ARE) | (5) | [95,96] | |
| Degree of freedom | (6) | [97] | |
| F-Value | (7) | [98] | |
| p-value | (8) | [56] |
3. Results and Discussion
3.1. Surface Properties of the GAC
Analyzing the equilibrium and mechanism of adsorption can be improved by conducting surface characterization of activated carbon. This involves measuring the mesopore, micropore, and total pore volume of activated carbon [99]. Figure 1 illustrates the nitrogen adsorption and desorption isotherms based on the data obtained from the surface analyzer. In Figure 1, the data points from nitrogen adsorption revealed that activated carbon conforms to an isotherm of type-III, which is indicative of weak interactions between the adsorbent and the adsorbate and that the interactions between the adsorbate molecules itself have a considerable impact on the adsorption [100]. This implies that as the pressure increases, the adsorption capacity continues to rise, indicating a multilayer adsorption. In this scenario, the adsorbate molecules tend to aggregate on the surface of the adsorbent rather than forming a uniform monolayer, as observed with type I and II isotherms. This was supported by isotherm studies (Section 3.6), which demonstrated that the adsorption process most accurately followed a multilayer adsorption model. Moreover, the isotherm suggests that to optimize the use of granular activated carbon (GAC) in wastewater treatment applications, higher pollutant concentrations might be needed for effective adsorption. This aligns with the use of medium-high strength wastewater in this study. Furthermore, as per the classification of the International Union of Pure and Applied Chemistry (IUPAC) for hysteresis, the activated carbon showed the type H4 on desorption isotherm, which is related to slit-like pores with micropore region [101].
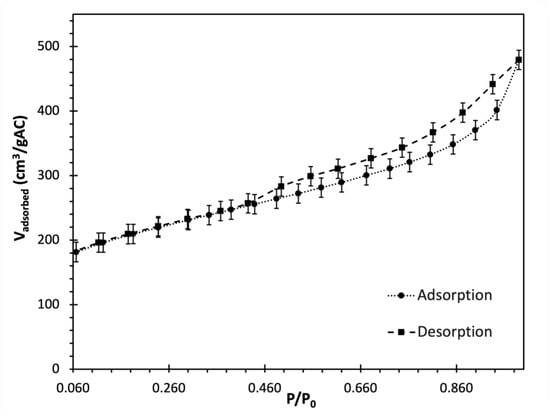
Figure 1.
Variation in the adjusted volume of adsorbed nitrogen (Vadsorbed) on granular activated carbon (GAC) by changing nitrogen gas pressures (P) at 273 K and 1 atm. The adsorption and desorption isotherms are obtained from Brunauer-Emmett-Teller (BET) surface analyzer at saturation pressure (P0) of 101.8 kPa and temperature of 77 K.
Table 4 presents the results obtained from the Quantochrome gas sorption analyzer for the calculation of total pore volume, t-plot micropore volume, BET surface area, BJH and HK average pore diameter. For the calculation of the surface area, the relative pressure was gradually increased within the range of 0.05 to 0.35 using the Brunauer–Emmett–Teller (SBET) method with the saturation pressure (P0) equal to 101.8 kPa. According to BET surface analysis, the total specific surface area available for the adsorption of pollutants on GAC is 763.0 m2/gAC.

Table 4.
Characteristics of GAC by nitrogen adsorption and desorption isotherms obtained from BET surface analyzer at T = 77 K.
The total pore volume was determined by measuring the nitrogen volume adsorbed on the surface of the GAC, which corresponds to a value of 0.6924 cm3/gAC. At a relative pressure of 0.99, it is assumed that all pores are already filled with nitrogen. Then, considering a slit-like geometry based on the type of isotherm, the calculated micropore volume by the t-method was equal to 0.2042 cm3/gAC, contributing to 30% of the total pore volume.
The GAC pore size distribution was measured with 16 desorption points over the 1.5–200 nm range. The average pore diameter and size distribution were determined using the BJH method, as shown in Figure 2. The figure shows the differential pore volume as a function of pore width (dV/dlog(D)) obtained from desorption isotherm on the y-axis and the pore diameter (D [μm]) on the x-axis. It displays that most pores fall within the range of 3–5 nm in diameter with the calculated average pore diameter of 3.631 nm, indicative of the GAC’s narrow mesoporous structure. The results are in agreement with the calculated average pore diameter using the Horvath-Kawazoe method. The HK method is utilized in the determination of pore size distribution for compounds with microporous structures assuming slit-like geometry and successfully predicted the structural properties of the studied activated carbon.
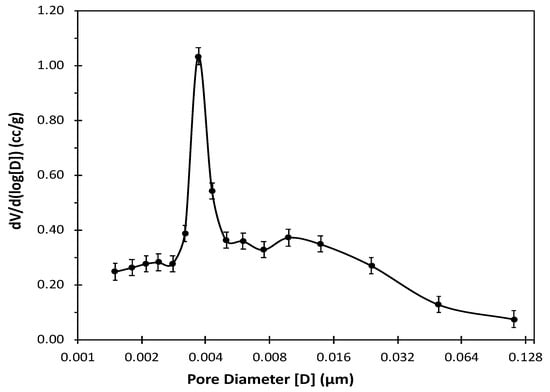
Figure 2.
Distribution of differential GAC pore volume with respect to its pore width (D) obtained from BET surface analyzer with BJH method using nitrogen gas desorption at .
The pH drift method, as described in the previous section, was used for the determination of pzc. From the data points presented in Figure 3, it is inferred that the GAC surface is electrically neutral at pH 7.1. In the pH range of 4.0 to 7.1, the final pH of the solution is always higher than the initial value, meaning that the surface functional groups of the GAC exist in a protonated state, so the surface carries a positive charge. At a pH higher than 7.1, the summation of charges on the GAC surface changes to negative as the functional groups on the surface deprotonate, resulting in a reduced final pH compared to the initial one. The presence of protonated and deprotonated functional groups on the surface of GAC at pH between 4.0 and 7.1 led to the increment of the solution pH, which stabilized at the final pH of about 7. This means that the functional groups on the surface of the GAC act as a buffer system, which keeps the pH of the solution constant. Similar results were reported in another study for the removal of endocrine disruptors by commercial activated carbon [102].
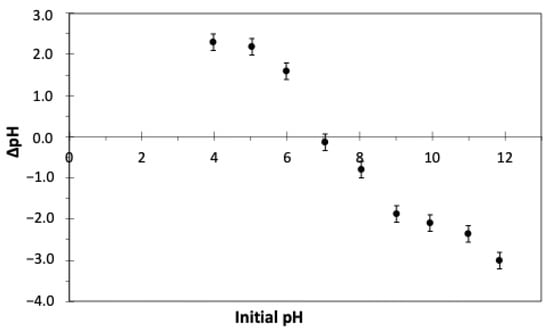
Figure 3.
The observed change in pH () of 0.01 M NaCl solution after 24 h by varying its initial pH, following the pH drift method to determine the point zero charge (pHPZC) of GAC. GAC dosage = 3 gAC/L, T = 23 °C, shaking speed = 150 rpm.
In summary, the activated carbon surface carries a positive charge in this study since the initial pH of the SPWW is approximately 4. This indicates the protonation of the GAC surface functional group, potentially leading to increased removal of anions such as sulfanilic acid. Nonetheless, the competition between the positively charged 4-aminophenol and aniline with H+ ions for adsorption on the GAC surface cannot be overlooked. This will be further elaborated in the next section to describe the pH effect on pharmaceutical removal.
3.2. Effect of pH
The pH level affects the adsorption process by changing the ionization state of functional groups on the activated carbon surface, as well as the charge on the adsorbate molecules. At low pH, functional groups on activated carbon tend to protonate, which in turn increases the competition between other positively charged compounds in the solution and H+ ions for adsorption sites. However, this protonation favours the adsorption of anions owing to the presence of H+ ions. In contrast, at elevated pH levels, the deprotonation of the functional groups due to the prevalence of OH- ions creates a negatively charged surface that enhances the attraction forces and adsorbs cations [103].
Figure 4 shows the pH effect on the TOC removal percentage. The range of solution pH in this study varied from 4 to 11 with a GAC dosage of 1 gAC/L and an initial TOC concentration of 1170.7 mgC/L in batch mode. The change in the pharmaceutical removal with pH can be attributed to the final pH of the solution after reaching the equilibrium, which typically falls within the range of 6 to 7, as expected. At this pH, all the components in the SPWW are electrically neutral except sulfanilic acid, which carries a negative charge. This means that neither repulsion nor attractive forces favour the removal of components by GAC except for sulfanilic acid. As activated carbon tends to adsorb H+ ions at pH values less than 7, it is anticipated that the adsorption of sulfanilic acid is higher at lower pH values, owning to the accumulation of positive charge on the GAC surface. In the opposite scenario, where the initial pH is higher than 7, and deprotonation of GAC surface functional groups occurs, the higher density of negative charge on the surface is expected to reduce the favorability of sulfanilic acid adsorption.
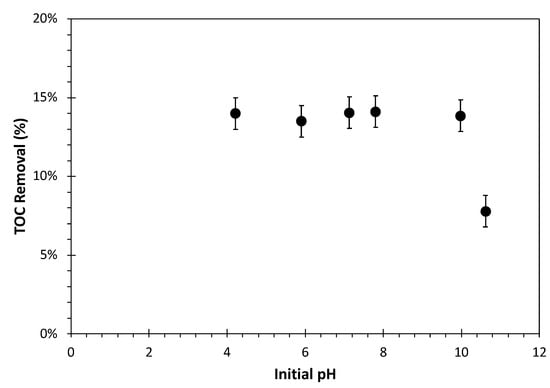
Figure 4.
Effect of synthetic pharmaceutical wastewater initial pH on TOC removal by adsorption on GAC under batch mode after 24 h. TOC0 = 1170.7 mgC/L, adsorbent dosage = 1 gAC/L, T = 23 °C, shaking speed = 150 rpm.
Increasing the pH from 4 to 7 decreases the density of the positive charge on the GAC’s surface. Therefore, the attraction forces to adsorb the negatively charged sulfanilic acid decreases, which leads to a reduction in its removal rate. However, from pH 4 to 10, no significant changes in the removal of pharmaceuticals were observed. The findings indicated that the adsorption remained relatively constant throughout the selected pH range as the densities of positive and negative charges on the GAC’s surface were limited.
At initial pH values less than 5, aniline and 4-aminophenol carried a positive charge competing with H+ ions for adsorption on the GAC surface. Since the final pH of the solution was around 7, it suggested that H+ ions are primarily adsorbed on the GAC, limiting the adsorption of aniline and 4-aminophenol. However, not all the surface functional groups underwent protonation, explaining the lack of increase in the sulfanilic acid and total TOC removal. As the adsorption progressed towards equilibrium, the adsorption of H+ ions onto the GAC raised the solution pH, causing the dissociation of non-adsorbed aniline and 4-aminophenol. Hence, neither attraction nor repulsion forces favoured the adsorption of remaining aniline and 4-aminophenol when the solution pH passed the value of 5.
As the pH increased towards 7, fewer H+ ions were adsorbed on the GAC, leaving more adsorption sites available for other neutral components. However, since the density of positively charged functional groups was reduced, less sulfanilic acid was removed from the solution. This balance explains why the adsorption remains relatively constant in the pH range of 4 to 7. Overall, it can be said that as the pH increases, the adsorption of sulfanilic acid decreases while the adsorption of other components increases due to the availability of adsorption sites. From pH 7 to 10, The adsorption sites continued to deprotonate, leading to an increase in the density of the negatively charged functional groups on the GAC surface, which further reduced the adsorption of sulfanilic acid. However, other neutral components in the solution continued to adsorb onto the GAC.
By increasing the pH to values more than 10, the activated carbon surface deprotonates, contributing to an increase in the negative charge density. At pH 11, sulfanilic acid and 4-aminophenol carried negative charges, which led to decreased adsorption because of repulsive forces between the surface and these components. In a study of atenolol adsorption on activated carbon, a similar trend is observed [102]. This analysis showed that the competitive adsorption dynamics and the pH dependent changes in the surface charge are critical factors influencing the adsorption efficiency of different compounds. To summarize the findings, it was noticed that by increasing the pH of the solution, there was no change in the removal rate of the selected compounds in the range of pH 4 to 10, and since the SPWW has an initial pH of approximately 4, no pH adjustment was made for further experiments. This is advantageous for several reasons. First, it indicates that the adsorption process does not require pH adjustment, which reduces operational costs by eliminating the need for additional chemicals. Second, this robustness ensures that the performance of the studied GAC is reliable even in real-world scenarios where wastewater pH might fluctuate. As a result, the model predictions for adsorption capacity and TOC removal are valid across varying pH levels within this range, confirming the efficacy and economic viability of the process in wastewater treatment applications.
3.3. Effect of Contact Time
Figure 5 illustrates how the contact time affects the pharmaceuticals’ adsorption onto activated carbon, considering two distinct initial concentrations of the pollutants. The adsorption process is affected by the operating conditions as well as the adsorbent physical and chemical properties. The increase in the contact time leads to a higher quantity of pharmaceuticals being adsorbed. The equilibrium time for activated carbon is considered when the concentration in the liquid phase changes to less than 1% between two sampling intervals. In this regard, batch experiments under a controlled temperature of 23 °C and GAC dosage of 1 gAC/L showed that the time to reach equilibrium is 8 h and 24 h for 956.9 and 2162.4 mgC/L initial TOC concentrations, respectively, which can be justified as the initial concentration increased, the number of available sites per molecule of pharmaceuticals decreased; subsequently, the time to reach to equilibrium increased. Similar behaviour was observed for sulfamethoxazole and metronidazole removal using activated carbon [104].
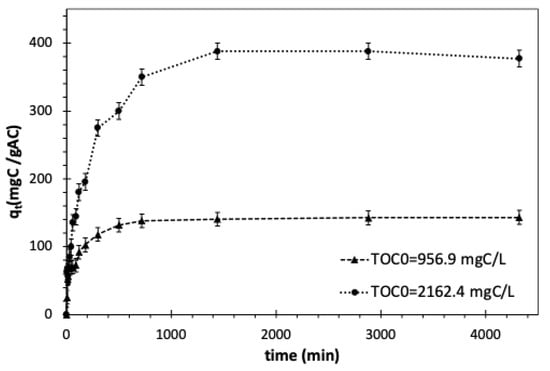
Figure 5.
Effect of contact time and initial TOC of synthetic pharmaceutical wastewater on adsorption capacity of GAC in batch mode. Adsorbent dosage = 1 gAC/L, T = 23 °C, and shaking speed = 150 rpm.
The enlarged first portion of Figure 5 shows the initial rapid adsorption of pharmaceuticals within the first 45 min of the process. Subsequently, there is a gradual reduction in the adsorption rate until it reaches a state of equilibrium. The fluctuations observed over the 300-min period can be attributed to the initial competitive adsorption of pharmaceuticals. Additionally, the abundance of readily accessible adsorption sites at the onset of the process could be the reason for the initial fast removal of pharmaceuticals. As the adsorption proceeds, the number of vacant sites gradually diminishes, leading to a reduced adsorption rate caused by the saturation of the activated carbon surface [105].
3.4. Effect of Initial Concentration on Adsorption
Figure 5 displays the change in the adsorption capacity of activated carbon resulting from variations in the initial pharmaceutical concentration in batch mode with a controlled temperature of T = 23 °C and a GAC dosage of 1 gAC/L. The results showed that by increasing the initial TOC concentration from 956.9 to 2162.4 mgC/L, the capacity of GAC was increased to 144.3 and 384.9 mgC/gAC, respectively. Moreover, the removal rate was increased with higher initial TOC loads, meaning that the removal rate was more rapid at the start of the adsorption process. This happens as a larger load of organics increases the driving force for the pharmaceuticals to dominate the mass transfer resistance between the solid and liquid phases.
3.5. Adsorption Kinetic Studies
The rate of pharmaceutical removal from the wastewater is affected by several factors, including external mass transfer resistance. In this study, to ensure the elimination of the external mass transfer layer, the shaking speed was chosen as such an increment did not affect the rate of pharmaceutical removal. This aligns with the finding of Al-Qodah et al. [106], who demonstrated that increasing the agitation speed enhances the mass transfer rate by reducing the external boundary layer thickness. To further study the effect of intra-particle diffusion and the rate of pharmaceutical attachment, four types of adsorption kinetic models were examined. Weber and Morris’ model (W-M) falls in the diffusion-based class as the model explains the adsorbate uptake by intraparticle diffusion mechanism. On the other hand, in the reaction-based models such as Langmuir, Pseudo-first order (PFO), and Pseudo-second order (PSO), the adsorbate removal is mainly controlled by the rate at which the adsorbate attaches to the solid surface [56]. Table 5 summarizes all the tested kinetic models, independent variables, and their constant parameters found by the nonlinear least square regression method using MATLAB software, version 9.14 (R2023a). The average relative error, R2, and the residual norm associated with each model were also calculated to find the best model.

Table 5.
Adsorption kinetic models, their estimated parameters, and calculated error for pharmaceutical removal from multicomponent wastewater by adsorption on GAC in batch mode. The PSO model was identified as the best one to describe the adsorption process. TOC0 = 963.3 mgC/L, adsorbent dosage = 1 gAC/L, T = 23 °C, and shaking speed = 150 rpm.
Table 5.
Adsorption kinetic models, their estimated parameters, and calculated error for pharmaceutical removal from multicomponent wastewater by adsorption on GAC in batch mode. The PSO model was identified as the best one to describe the adsorption process. TOC0 = 963.3 mgC/L, adsorbent dosage = 1 gAC/L, T = 23 °C, and shaking speed = 150 rpm.
| Model | Correlation | Estimated Parameters | Error Analysis | |||
|---|---|---|---|---|---|---|
| ARE | R2 (%) | |||||
| W-M 1 | (9) | 3.66 | 66.5 | 9.90 | ||
| PFO 2 | (10) | 84.2 | 4.66 | |||
| Langmuir | (11) | 84.2 | 4.66 | |||
| PSO 3 | (12) | 99.9 | 2.29 | |||
Note: 1 Weber and Morris, 2 Pseudo-First Order, 3 Pseudo-Second Order.
Figure 6 illustrates all models by showing the experimental data under the batch conditions with the activated carbon dosage of 1 gAC/L, T = 23 °C, and initial TOC of 963.3 mgC/L. As indicated by error analysis, PFO deviated from the experimental data, displaying an estimated equilibrium adsorption capacity of 131.6 mgC/gAC and an adsorption constant of 1.43 × 10−2 min−1. The errors obtained for PFO were the highest compared to other models, as shown in Table 5. The Langmuir model, which assumes reversible adsorption between pharmaceuticals in the liquid and on the GAC surface, aligns with the PFO model when the desorption rate constant is very low. This is expected during the kinetic studies since the effective removal of pharmaceuticals from wastewater necessitates a higher adsorption rate. The predicted equilibrium capacity and adsorption rate constant of the Langmuir model are consistent with those of the PFO model.
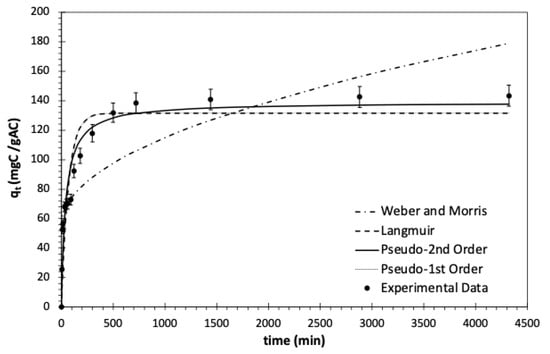
Figure 6.
Experimental data and kinetic models showing GAC capacity (qt) by varying the contact time for pharmaceutical removal from wastewater in batch mode. TOC0 = 963.3 mgC/L, adsorbent dosage = 1 gAC/L, T = 23 °C, and shaking speed = 150 rpm.
Figure 6 shows a close alignment between the experimental data and the PSO model. The model predicted the uptake of pharmaceuticals with the minimum discrepancy between the experimental and calculated capacity, indicating a good agreement between the PSO model and the mechanism of pharmaceutical removal. Upon comparing the adsorption-controlled models based on F-test and error functions considering a 95% confidence interval, it became evident that the PSO gave a more accurate fit to the experimental data [107,108,109]. Although PSO predicts the experimental data well, it falls short in describing the intraparticle diffusion, particularly in the early stages of the adsorption process [110]. Thus, this study aimed to assess whether intraparticle diffusion serves as the limiting factor in determining the rate of the adsorption process. The experimental data was fitted using the linear Weber and Morris model, and it showed multilinearity, as depicted in Figure 7. Similar results were observed by Kaur et al. [109]. The multilinearity indicates that the intraparticle diffusion does not exclusively control the adsorption rate. Thus, it is concluded that two steps, including the intraparticle diffusion and rate of attachment of pharmaceuticals to the GAC surface, regulated the adsorption process.
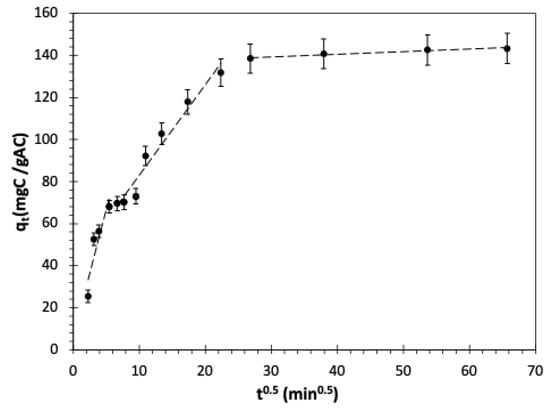
Figure 7.
Weber and Morris intraparticle diffusion model for pharmaceutical adsorption from wastewater on GAC under batch mode. Average TOC0 = 963.3 mgC/L, adsorbent dosage = 1 gAC/L, T = 23 °C, and shaking speed = 150 rpm.
3.6. Adsorption Isotherms
Several isotherm models have been utilized to understand the adsorption process and effectively plan an adsorption system. In this study, eleven experimental equilibrium points were obtained under a controlled temperature of and the initial TOC concentration of 911.8 mgC/L by changing the activated carbon dosage in batch mode, as described in the following sections.
3.6.1. Langmuir Isotherm
The model assumes no interaction between adsorbed molecules and a constant binding energy between the adsorbate and the adsorbent. The Langmuir isotherm explains the removal of many micropollutants by activated carbon [1,93,107,111], as shown in Equation (13).
where is the capacity of activated carbon at equilibrium, is the liquid phase TOC concentration at equilibrium, constant relates to the adsorption energy, and is the maximum monolayer adsorption capacity. The feasibility of the adsorption process, indicating whether adsorption occurs through the interaction of adsorbates and adsorbent, and favorability of adsorption, determining if it is a spontaneous process, are assessed using a dimensionless number known as the separation factor (RL), as shown in Equation (14).
where is the initial TOC of the solution. A value of indicates favourable adsorption, and an value equal to 0 indicates irreversible adsorption [112,113]. In this study, the RL is close to zero due to the large value estimated for the Langmuir constant (). This implies that the adsorption is strongly favourable or potentially irreversible; however, the small value of could be attributed to the inadequacy of the Langmuir model in fitting the experimental data.
The linear plot of the model with a negative intercept showed that the adsorbent did not follow the Langmuir model behaviour over the whole concentration range. Ghafoori et al. [1] reported a maximum adsorption capacity of 1.85 mgC/gAC to remove the same pharmaceuticals by activated carbon. However, in this study, it was observed that the Langmuir model, by linear regression, could not describe the adsorption behaviour, which is due to increased initial concentration and experimental data points at activated carbon dosage of less than 10 gAC/L. The results from linear regression varied significantly from the ones obtained by nonlinear regression as experimental data did not follow the Langmuir model, and the linear fit was not an accurate estimation of the isotherm behaviour; nonetheless, the nonlinear regression could predict the maximum monolayer adsorption which was estimated to be 47.00 mgC/gAC. The adsorption constants estimated by nonlinear regression for the Langmuir model are summarized in Table 6.

Table 6.
Isotherm parameters and calculated error for the treatment of a multicomponent pharmaceutical wastewater by adsorption on GAC under batch mode after 24 h of contact time. TOC0 = 911.8 mgC/L, T = 23 °C, and shaking speed = 150 rpm.
3.6.2. Freundlich Isotherm
Freundlich isotherm (Equation (15)), is an empirical model utilized for adsorption on heterogeneous sites with multilayer adsorption. It assumes a nonuniform distribution of the energy on the adsorption sites. However, its applicability does not extend across the entire range of adsorption data [89].
where is the capacity of activated carbon at equilibrium, is the liquid phase TOC concentration at equilibrium, KF represents the Freundlich constant associated with the adsorption capacity, and shows the surface energetic heterogeneity or adsorption intensity which for values , adsorption is considered favourable and large n values are interpreted as stronger interaction [103,114]. The linear Freundlich plot for the isotherm batch studies with GAC mass ranging from 0.05–75 gAC with initial TOC of 911.8 mgC/L is shown in Figure 8, and a good linearity for the adsorption data is observed. The KF and nF values calculated by nonlinear curve fitting are also shown in Table 6.
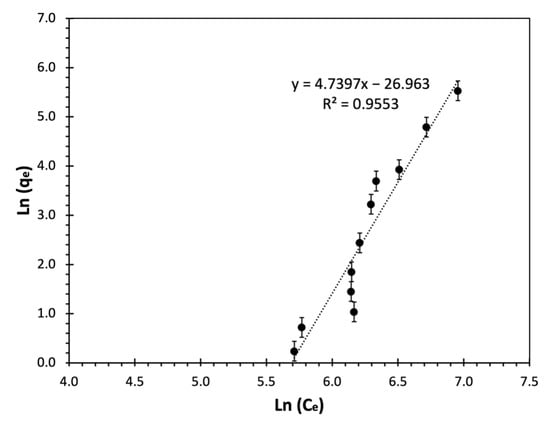
Figure 8.
Freundlich isotherm linear plot for treatment of multicomponent synthetic pharmaceutical wastewater by adsorption on GAC after 24 h in batch mode. Average TOC0 = 911.8 mgC/L, T = 23 °C, and shaking speed = 150 rpm.
From Figure 8, it can be observed that there is a linearity between the experimental data. The n value predicted by linearization was less than one (), indicating the adsorption process is unfavourable at lower concentrations of pharmaceuticals. Nevertheless, the adsorption is more favourable at higher concentrations of wastewater. Moreover, the value of n indicated weak interactions between the pharmaceuticals and the activated carbon [92]. The nF value obtained by nonlinear regression is the value of 0.28. The KF calculated by linearization () and nonlinear regression () are different in four orders of magnitude, highlighting the importance of regression method and error induced by linearization. The very small value of indicates a low adsorption capacity for the selected pharmaceuticals. Yaneva et al. [115], studied p-nitrophenol removal by biosorption using five isotherm models, including Langmuir, Freundlich, Redlich-Peterson, and Fritz-Schlunder isotherm models. They concluded that the adsorption on Rhizopus oryzae fungi for removal of p-nitrophenol was better fitted to Freundlich isotherm. Their results showed that p-aminophenol biosorption was favourable with an value of 0.3. The results were not comparable as the operating condition and presence of fungi changed the adsorption behaviour.
3.6.3. Dubinin-Radushkevich (D-R) Isotherm
This isotherm expresses the distribution of the adsorbate on the heterogenous surface with Gaussian energy distribution. It is temperature dependent, and by plotting the equilibrium data, the mean adsorption energy can be obtained [57]. This isotherm is expressed as follows:
and
where relates to the adsorption energy per mole of adsorbate (E (kJ/mol)), is Polanyi potential, R is the gas constant , and T (K) is the temperature at which adsorption occurs. The graph of isotherm fitted to experimental data obtained at T = under batch operating conditions is illustrated in Figure 9. Table 6 represents the isotherm constants where the energy of adsorption for the studied adsorption system was estimated to be equal to 1.65 kJ/mol, which indicated weak interactions between the activated carbon and the pharmaceuticals as predicted by Freundlich isotherm [116]. The estimated maximum adsorption capacity is equal to 678.5 mgC/gAC, which is higher than the maximum capacity predicted by Langmuir-Freundlich isotherm.
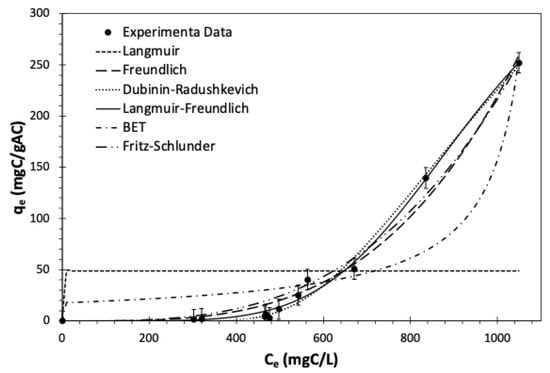
Figure 9.
Change in the GAC equilibrium adsorption capacity by varying the equilibrium TOC of multicomponent synthetic pharmaceutical wastewater for the Experimental data points and six fitted isotherm models for batch-mode treatment after 24 h of contact time. Average TOC0 = 911.8 mgC/L, T = 23 °C, and shaking speed = 150 rpm.
3.6.4. Langmuir-Freundlich Isotherm
This isotherm is a three-parameter model describing the adsorption on heterogeneous surfaces. It exhibits Freundlich-like behaviour at low adsorbate concentrations and Langmuir-like behaviour at high adsorbate concentrations [117]. The model deviates from the Langmuir isotherm to get a closer fit to the experimental data. It assumes adsorption sites are made of energetically different patches with finite adsorption capacity. The isotherm can be shown as [118]:
where is the maximum adsorption capacity (mgC/gAC), stands for the equilibrium constant (L/mgC), and denotes the heterogeneity intensity. The isotherm parameters are found by nonlinear regression, and the plot of the experimental data and fitted model is shown in Figure 9. Table 6 summarizes the parameters obtained from the MATLAB (2023a). The error analysis showed that the model in the study range explains the adsorption system well. An n value exceeding one implies a heterogeneous adsorption surface, indicating that 4.70 adsorbate molecules cooperate in their adsorption onto the activated carbon surface [119]. This model estimates the maximum adsorption capacity at 522.3 mgC/gAC for GAC dosage ranging from 0.05–75 gAC with an initial TOC of 911.8 mgC/L at the temperature of 23 , which falls within the range reported by Hamdaoui and Naffrechoux. [120] for the removal of phenolic compounds by granular activated carbon. As per their study, the maximum adsorption capacity ranged from 300 to 850 mgC/gAC for the five different phenolic compounds, including phenol, 2-chlorophenol, 4-chlorophenol, 2,4-dichlorophenol, and 2,4,6-trichlorophenol.
Furthermore, Bolong et al. [121], discussed that an effective adsorption technology achieves 40–60% removal in the effluent of wastewater treatment plants. The adsorption capacity predicted by the model in this study showed that a maximum reduction of 52% could be achieved for pharmaceutical wastewater over the range of the study, which proved an effective adsorption system.
3.6.5. Brunauer-Emmett-Teller Isotherm
The isotherm is a generalized form of Langmuir isotherm. It describes monolayer adsorption with infinite adsorption capacity due to multilayer interaction between the adsorbate molecules. The BET isotherm is generally used for solid-gas systems; however, it is modified to describe the liquid-solid system [122]. The isotherm can be expressed by
where b1 and b2 are the BET isotherm constants (L/mgC) and (mgC/gAC) is the monolayer adsorption capacity. In this isotherm, b1 is the surface binding energy, and b2 represents the monolayer saturation concentration [123]. The fitted isotherm model is plotted in Figure 9, and its constants are reported in Table 6 for batch-mode adsorption studies at T = using GAC. The results from modelling showed that the saturation concentration in the liquid for activated carbon was at 1120.1 mgC/L, and the monolayer maximum adsorption capacity was at 16.38 mgC/gAC. The predicted monolayer capacity is almost three times less than the capacity predicted by the Langmuir model. However, the isotherm predicted the experimental data better than Langmuir as it fitted better. The error analysis showed that the BET model after Langmuir is the least adequate to the experimental data, with R2 equal to 89.3%.
3.6.6. Fritz-Schlunder Isotherm
The model applies to a wide range of experimental isotherm data because it has four parameters in its definition. The isotherm can be expressed by
where K1 and K2 are the equilibrium constants with p and s as model exponents [87]. The isotherm at reduces to Langmuir, and for high adsorbate concentration, it behaves as a Freundlich isotherm [124]. The result of the modelling is shown in Figure 9 for batch equilibrium studies with TOC0 = 911.8 mgC/L and , and the estimated parameters are presented in Table 6.
Figure 9 shows that the isotherm fitted to experimental data with a good fit with ; however, the residual norm and ARE are higher compared to those of the Langmuir-Freundlich and Freundlich model. The isotherm equilibrium constants ratio ) corresponds to the Freundlich constant (4.89 ), and the difference of the exponents () is equal to the power of Freundlich model 1/nF (3.55).
3.6.7. Selection of the Best Isotherm
Figure 9 displays all six isotherm models alongside the experimental data for pharmaceutical adsorption from wastewater on GAC in batch mode. This plot visualizes the degree of fit between the models and the actual experimental data; yet the choice of the optimal isotherm for replicating the experimental data was based on the coefficient of determination, residual norm, average relative error, and F-test. Considering the 95% confidence interval and degree of freedom for each isotherm, the p-value of every two models was calculated. Therefore, for the p-values more than 0.05, it can be considered that the isotherm adequately fits the experimental data. The F value and degree of freedom for every two isotherms were incorporated in calculating the cumulative distribution function. Table 6 represents the isotherm constants and the error associated with each isotherm model.
The F-test analysis between all isotherms indicated that the Freundlich isotherm and Langmuir-Freundlich isotherm provide the most accurate representation of the experimental data. Table 6 validates this conclusion as these models had the lowest ARE and RN. Furthermore, a comparison between the Freundlich and Langmuir-Freundlich also showed that Langmuir-Freundlich isotherm was the best fit to describe the pharmaceutical adsorption on activated carbon over the study range. Therefore, the isotherm models based on the most adequate to the least one could be arranged in the order of Langmuir-Freundlich > Freundlich > Dubinin-Radushkevich > Fritz-Schlunder > Brunauer-Emmett-Teller > Langmuir.
4. Conclusions
The removal rates of six pharmaceuticals in a multicomponent mixture by commercial granular activated carbon were studied under batch operating conditions. The results showed that multiple steps limit the rate of pharmaceutical removal. Moreover, six isotherm models were studied for the equilibrium behaviour of the GAC. The selection of the kinetic and equilibrium models was based on residual norm, average relative error, coefficient of determination functions, and the statistical F-test to account for the degree of freedom of all models. The following conclusions were made by this study:
- From the textural and surface analysis, commercial GAC is characterized by a narrow mesoporous structure, showing an average pore diameter of 3.63 nm and making it a proper candidate for removing pharmaceuticals as most have a molecular size of less than 2 nm. In addition, the zero net charge on the studied GAC was measured to be at a pH of 7.1.
- The findings from varying contact times and initial concentrations indicated that higher initial concentrations and longer content times resulted in greater pharmaceutical adsorption. This can be attributed to an increased driving force and sufficient time for the adsorbates to diffuse and bind to the activated carbon surface, leading to an enhanced adsorption capacity. The removal of pharmaceuticals remained unaffected by the change in the solution’s pH at values below 10. Beyond that, a substantial drop in the removal was observed due to the repulsion that exists between the negatively charged compounds and the surface of activated carbon. Consequently, no pH adjustment is required to favour the removal, which is beneficial in scale-up cost as no raw material for pH adjustment is needed.
- The dynamic studies showed that the Pseudo-second order reaction kinetic model provided the most accurate results over the entire adsorption time with an adsorption rate of for synthetic wastewater with initial TOC of . This model indicates that the removal of pharmaceuticals is mainly dependent on the rate at which the pharmaceuticals bind to the surface of the activated carbon. Furthermore, the multilinearity obtained by the Weber and Morris model confirmed the intraparticle diffusion, as well as the adsorption rate, determined the rate of pharmaceutical removal with the diffusion effect more dominant at the initial stages of the adsorption.
- Among the six investigated isotherm models explaining adsorption equilibrium behaviour, the Langmuir-Freundlich model provided the most accurate prediction of the experimental data, which could be inferred as multilayer adsorption and heterogeneous adsorption surface. The studied adsorption system was estimated to have a maximum adsorption capacity of 522.3 mgC/gAC following heterogeneity intensity of 4.70 and equilibrium constant equal to .
The batch adsorption studies proved that the granular activated carbon is effective in treating highly concentrated pharmaceutical wastewater, with up to 52% removal achievable as per Langmuir-Freundlich isotherm prediction. The use of synthetic wastewater closely mimic real-world conditions, offering valuable insights into the adsorption process. However, using real industrial effluent in future studies is crucial for validating the effectiveness of GAC under practical conditions [125]. This study highlighted the potential use of TOC analysis as a more cost-effective, accurate, and sustainable assessment of the removal process compared to compound-specific analysis.
Future research should explore the continuous adsorption process to monitor the removal of pharmaceuticals, verify the isotherm capacity prediction and adsorption mechanism and evaluate the long-term performance of GAC. The integration of adsorption with other advanced treatment methods, such as bioaugmentation, membrane filtration, advanced oxidation, electrocoagulation, etc., has shown promise in enhancing treatment efficiency and should be considered for future research [27,125,126]. These research directions will further enhance the understanding and optimization of GAC for wastewater treatment.
Author Contributions
This review article was a collaborative effort. The conceptualization was led by research supervisor M.M., while the extensive review, analysis, summarization, and literature comparison were carried out by M.A., guided by M.M. M.A. took the lead in drafting the manuscript, with contributions and feedback from M.M. during critical revisions. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Sciences and Engineering Research Council of Canada (NSERC), Toronto Metropolitan University Graduate Scholarship, and Toronto Metropolitan University Faculty of Engineering and Architectural Science.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design, execution, interpretation, or writing of the study.
Nomenclature
| Acronyms | |
| AC | Activated Carbon |
| ARE | Average Relative Error |
| BET | Brunauer–Emmett–Teller model |
| BJH | Barrett–Joyner–Halenda model |
| COD | Chemical Oxygen Demand |
| D-R | Dubinin-Radushkevich isotherm model |
| DCM | Dichloromethane |
| EPA | Environmental Protection Agency |
| F-test | Statistical Fisher test |
| GAC | Granular Activated Carbon |
| GHS | Globally Harmonized System |
| HK | Horvath-Kawazoe model |
| IUPAC | International Union of Pure and Applied Chemistry |
| PFO | Pseudo-First Order kinetic model |
| PPCP | Pharmaceuticals and Personal Care Products |
| PSO | Pseudo-Second Order kinetic model |
| PZC | Point of Zero Charge |
| RN | Residual Norm error |
| SPWW | Synthetic Pharmaceutical Wastewater |
| TN | Total Nitrogen |
| TOC | Total Organic Carbon |
| VOC | Volatile Organic Compound |
| W-M | Weber and Morris kinetic model |
| Greek letters | |
| Dubinin-Radushkevich isotherm constant | |
| Polanyi potential | |
| Special symbols | |
| b1 | BET isotherm constants |
| b2 | BET isotherm constants |
| C0 | Initial concentration |
| Ce | Concentration at equilibrium |
| WM | Weber and Morris constant |
| df | Degree of freedom |
| E | Energy of adsorption |
| K1 | Fritz-Schlunder isotherm constant |
| K2 | Fritz-Schlunder isotherm constant |
| KAd | Adsorption rate constant |
| KD | Desorption rate constant |
| KF | Freundlich isotherm constant |
| KL | Langmuir isotherm constant |
| KLF | Langmuir-Freundlich isotherm constant |
| KPFO | Pseudo-first order rate constant |
| KPSO | Pseudo-second order rate constant |
| KWM | Weber and Morris coefficient |
| m | Mass dry of activated carbon [g] |
| n | Langmuir-Freundlich isotherm power |
| nF | Freundlich isotherm power |
| p | Fritz-Schlunder isotherm power |
| P0 | Nitrogen saturation pressure at 77 K (kPa) |
| q | Activated carbon capacity |
| qe | Equilibrium adsorption capacity |
| qm | Maximum monolayer adsorption capacity |
| qs | Maximum adsorption capacity |
| R | Universal gas constant |
| R2 | Coefficient of determination |
| RL | Separation factor |
| s | Fritz-Schlunder isotherm power |
| T | Temperature () |
| t | Time (min) |
| TOC0 | Initial total organic carbon |
| V | Volume of solution (L) |
References
- Ghafoori, S.; Shah Kiran, K.; Mehrvar, M.; Chan, P.K. Pharmaceutical Wastewater Treatment Using Granular Activated Carbon and UV/H2O2 Processes: Experimental Analysis and Modelling. Can. J. Chem. Eng. 2014, 92, 1163–1173. [Google Scholar] [CrossRef]
- Johnson, M.B.; Mehrvar, M. Treatment of Actual Winery Wastewater by Fenton-like Process: Optimization to Improve Organic Removal, Reduce Inorganic Sludge Production and Enhance Co-Treatment at Municipal Wastewater Treatment Facilities. Water 2021, 14, 39. [Google Scholar] [CrossRef]
- Gadipelly, C.; Pérez-González, A.; Yadav, G.D.; Ortiz, I.; Ibáñez, R.; Rathod, V.K.; Marathe, K.V. Pharmaceutical Industry Wastewater: Review of the Technologies for Water Treatment and Reuse. Ind. Eng. Chem. Res. 2014, 53, 11571–11592. [Google Scholar] [CrossRef]
- Methanol Institute Methanol Safe Handling Technical Bulletin. Available online: https://www.methanol.org/safe-handling/ (accessed on 21 February 2024).
- Al-Dawery, S.K. Adsorption of Methanol from Methanol–Water Mixture by Activated Carbon and Its Regeneration Using Photo-Oxidation Process. Desalination Water Treat. 2016, 57, 3065–3073. [Google Scholar] [CrossRef]
- Han, Y.; Zhao, J.; Guo, X.; Jiao, T. Removal of Methanol from Water by Capacitive Deionization System Combined with Functional Nanoporous Graphene Membrane. Chemosphere 2023, 311, 137011. [Google Scholar] [CrossRef] [PubMed]
- Shestakova, M.; Sillanpää, M. Removal of Dichloromethane from Ground and Wastewater: A Review. Chemosphere 2013, 93, 1258–1267. [Google Scholar] [CrossRef] [PubMed]
- Teimoori, S.; Hassani, A.H.; Panahi, M.; Mansouri, N. A Review, Methods for Removal and Adsorption of Volatile Organic Compounds from Environmental Matrixes. Anal. Methods Environ. Chem. J. 2020, 3, 34–58. [Google Scholar] [CrossRef]
- Su, Y.; Fu, K.; Zheng, Y.; Ji, N.; Song, C.; Ma, D.; Lu, X.; Han, R.; Liu, Q. Catalytic Oxidation of Dichloromethane over Pt-Co/HZSM-5 Catalyst: Synergistic Effect of Single-Atom Pt, Co3O4, and HZSM-5. Appl. Catal. B Environ. 2021, 288, 119980. [Google Scholar] [CrossRef]
- Kyzas, G.Z.; McKay, G.; Al-Musawi, T.J.; Salehi, S.; Balarak, D. Removal of Benzene and Toluene from Synthetic Wastewater by Adsorption onto Magnetic Zeolitic Imidazole Framework Nanocomposites. Nanomaterials 2022, 12, 3049. [Google Scholar] [CrossRef]
- Ravindran, C.; Panayam Parambil Kunnathulli, A.; Kunhikrishnan Maniath, J. Polyvinyl Alcohol-Polyvinylpyrrolidone-Hydroxy Apatite (PVA-PVP-Hap) Membrane for Effective Removal of Benzene from Aqueous Solutions:-Kinetic, Isotherm, and Thermodynamic Studies. Mater. Today Proc. 2022, 66, 2422–2430. [Google Scholar] [CrossRef]
- US EPA National Primary Drinking Water Regulations. Available online: https://www.epa.gov/ground-water-and-drinking-water/national-primary-drinking-water-regulations (accessed on 25 April 2023).
- Mohajerani, M.; Mehrvar, M.; Ein-Mozaffari, F. Optimization of Aqueous P-Aminophenol Degradation by External-Loop Airlift Sonophotoreactor Using Response Surface Methodology. Chem. Eng. Res. Des. 2012, 90, 1221–1234. [Google Scholar] [CrossRef]
- Koyuncu, H.; Kul, A.R. Removal of Aniline from Aqueous Solution by Activated Kaolinite: Kinetic, Equilibrium and Thermodynamic Studies. Colloids Surf. A Physicochem. Eng. Asp. 2019, 569, 59–66. [Google Scholar] [CrossRef]
- Li, N.; Zhang, F.; Wang, H.; Hou, S. Catalytic Degradation of 4-Nitrophenol in Polluted Water by Three-Dimensional Gold Nanoparticles/Reduced Graphene Oxide Microspheres. Eng. Sci. 2019, 7, 72–79. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, Y.; Peng, Z.; Liu, Y. Treatment of High Salinity Sulfanilic Acid Wastewater by Bipolar Membrane Electrodialysis. Sep. Purif. Technol. 2022, 281, 119842. [Google Scholar] [CrossRef]
- Karimi-Maleh, H.; Darabi, R.; Karimi, F.; Karaman, C.; Shahidi, S.A.; Zare, N.; Baghayeri, M.; Fu, L.; Rostamnia, S.; Rouhi, J.; et al. State-of-Art Advances on Removal, Degradation and Electrochemical Monitoring of 4-Aminophenol Pollutants in Real Samples: A Review. Environ. Res. 2023, 222, 115338. [Google Scholar] [CrossRef] [PubMed]
- Mowla, A.; Mehrvar, M.; Dhib, R. Combination of Sonophotolysis and Aerobic Activated Sludge Processes for Treatment of Synthetic Pharmaceutical Wastewater. Chem. Eng. J. 2014, 255, 411–423. [Google Scholar] [CrossRef]
- Shojaee Nasirabadi, P.; Saljoughi, E.; Mousavi, S.M. Membrane Processes Used for Removal of Pharmaceuticals, Hormones, Endocrine Disruptors and Their Metabolites from Wastewaters: A Review. Desalination Water Treat. 2016, 57, 24146–24175. [Google Scholar] [CrossRef]
- Jahani, R.; Dhib, R.; Mehrvar, M. Photochemical Degradation of Aqueous Artificial Sweeteners by UV/H2O2 and Their Biodegradability Studies. J. Chem. Technol. Biotechnol. 2020, 95, 2509–2521. [Google Scholar] [CrossRef]
- Wang, J.; Zhuan, R. Degradation of Antibiotics by Advanced Oxidation Processes: An Overview. Sci. Total Environ. 2020, 701, 135023. [Google Scholar] [CrossRef] [PubMed]
- Alfonso-Muniozguren, P.; Serna-Galvis, E.A.; Bussemaker, M.; Torres-Palma, R.A.; Lee, J. A Review on Pharmaceuticals Removal from Waters by Single and Combined Biological, Membrane Filtration and Ultrasound Systems. Ultrason. Sonochem. 2021, 76, 105656. [Google Scholar] [CrossRef]
- Martínez, F.; Molina, R.; Rodríguez, I.; Pariente, M.I.; Segura, Y.; Melero, J.A. Techno-Economical Assessment of Coupling Fenton/Biological Processes for the Treatment of a Pharmaceutical Wastewater. J. Environ. Chem. Eng. 2018, 6, 485–494. [Google Scholar] [CrossRef]
- Schneider, I.; Abbas, A.; Bollmann, A.; Dombrowski, A.; Knopp, G.; Schulte-Oehlmann, U.; Seitz, W.; Wagner, M.; Oehlmann, J. Post-Treatment of Ozonated Wastewater with Activated Carbon and Biofiltration Compared to Membrane Bioreactors: Toxicity Removal In Vitro and in Potamopyrgus Antipodarum. Water Res. 2020, 185, 116104. [Google Scholar] [CrossRef]
- Della-Flora, A.; Wilde, M.L.; Thue, P.S.; Lima, D.; Lima, E.C.; Sirtori, C. Combination of Solar Photo-Fenton and Adsorption Process for Removal of the Anticancer Drug Flutamide and Its Transformation Products from Hospital Wastewater. J. Hazard. Mater. 2020, 396, 122699. [Google Scholar] [CrossRef]
- Ricky, R.; Shanthakumar, S. Phycoremediation Integrated Approach for the Removal of Pharmaceuticals and Personal Care Products from Wastewater—A Review. J. Environ. Manag. 2022, 302, 113998. [Google Scholar] [CrossRef] [PubMed]
- Asheghmoalla, M.; Mehrvar, M. Integrated and Hybrid Processes for the Treatment of Actual Wastewaters Containing Micropollutants: A Review on Recent Advances. Processes 2024, 12, 339. [Google Scholar] [CrossRef]
- Al-Zghoul, T.M.; Al-Qodah, Z.; Al-Jamrah, A. Performance, Modeling, and Cost Analysis of Chemical Coagulation-Assisted Solar Powered Electrocoagulation Treatment System for Pharmaceutical Wastewater. Water 2023, 15, 980. [Google Scholar] [CrossRef]
- Jayawardhana, Y.; Mayakaduwa, S.S.; Kumarathilaka, P.; Gamage, S.; Vithanage, M. Municipal Solid Waste-Derived Biochar for the Removal of Benzene from Landfill Leachate. Env. Geochem. Health 2019, 41, 1739–1753. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Tian, M.; He, C.; Li, L.; Shi, J.-W.; Yu, Y.; Cheng, J. Yolk-Shell-like Mesoporous CoCrOx with Superior Activity and Chlorine Resistance in Dichloromethane Destruction. Appl. Catal. B Environ. 2020, 264, 118493. [Google Scholar] [CrossRef]
- Shahid, M.K.; Kashif, A.; Fuwad, A.; Choi, Y. Current Advances in Treatment Technologies for Removal of Emerging Contaminants from Water—A Critical Review. Coord. Chem. Rev. 2021, 442, 213993. [Google Scholar] [CrossRef]
- Parsa, Z.; Dhib, R.; Mehrvar, M. Dynamic Modelling, Process Control, and Monitoring of Selected Biological and Advanced Oxidation Processes for Wastewater Treatment: A Review of Recent Developments. Bioengineering 2024, 11, 189. [Google Scholar] [CrossRef]
- Lin, Y.P.; Dhib, R.; Mehrvar, M. Nonlinear System Identification for Aqueous PVA Degradation in a Continuous UV/H2O2 Tubular Photoreactor. Ind. Eng. Chem. Res. 2021, 60, 1302–1315. [Google Scholar] [CrossRef]
- Patiño-Ruiz, D.; Rehmann, L.; Mehrvar, M.; Quiñones-Bolaños, E.; Herrera, A. Synthesis of FeO@SiO2–DNA Core–Shell Engineered Nanostructures for Rapid Adsorption of Heavy Metals in Aqueous Solutions. RSC Adv. 2020, 10, 39284–39294. [Google Scholar] [CrossRef]
- Zamiri, M.A.; Niu, C.H. Development and Characterization of Novel Activated Carbons Based on Reed Canary Grass. Ind. Crops Prod. 2022, 187, 115316. [Google Scholar] [CrossRef]
- De Andrade, J.R.; Oliveira, M.F.; Da Silva, M.G.C.; Vieira, M.G.A. Adsorption of Pharmaceuticals from Water and Wastewater Using Nonconventional Low-Cost Materials: A Review. Ind. Eng. Chem. Res. 2018, 57, 3103–3127. [Google Scholar] [CrossRef]
- Mansour, F.; Al-Hindi, M.; Yahfoufi, R.; Ayoub, G.M.; Ahmad, M.N. The Use of Activated Carbon for the Removal of Pharmaceuticals from Aqueous Solutions: A Review. Rev. Environ. Sci. Biotechnol. 2018, 17, 109–145. [Google Scholar] [CrossRef]
- Jatmiko, T.H. Optimization of Production Activated Carbon for Removal of Pharmaceuticals Wastewater Using Taguchi Method and Grey Relational Analysis. J. Ris. Teknol. Pencegah. Pencemaran Ind. 2020, 11, 11–18. [Google Scholar] [CrossRef]
- Pirvu, F.; Covaliu-Mierlă, C.I.; Paun, I.; Paraschiv, G.; Iancu, V. Treatment of Wastewater Containing Nonsteroidal Anti-Inflammatory Drugs Using Activated Carbon Material. Materials 2022, 15, 559. [Google Scholar] [CrossRef] [PubMed]
- Mestre, A.S.; Viegas, R.M.C.; Mesquita, E.; Rosa, M.J.; Carvalho, A.P. Engineered Pine Nut Shell Derived Activated Carbons for Improved Removal of Recalcitrant Pharmaceuticals in Urban Wastewater Treatment. J. Hazard. Mater. 2022, 437, 129319. [Google Scholar] [CrossRef]
- Hu, W.; Niu, Y.; Dong, K.; Wang, D. Removal of Sulfamethoxazole from Aqueous Solution onto Bagasse-Derived Activated Carbon: Response Surface Methodology, Isotherm and Kinetics Studies. J. Mol. Liq. 2022, 347, 118141. [Google Scholar] [CrossRef]
- Hörsing, M.; Andersen, H.R.; Grabic, R.; Jansen, J.L.C.; Ledin, A. Sorption of 71 Pharmaceuticals to Powder Activated Carbon for Improved Wastewater Treatment. Clean Technol. 2022, 4, 296–308. [Google Scholar] [CrossRef]
- Zhang, Y.; Dou, B.; Liu, X.; Fan, H.; Geng, C.; Liu, X.; Chang, J.; Hao, Q.; Hu, X.; Yang, Y.; et al. Experimental and Theoretical Study of the Adsorption of Mixed Low Carbon Alcohols and Acids from Fischer Tropsch Synthesis Wastewater by Activated Carbon. Fuel 2023, 339, 126928. [Google Scholar] [CrossRef]
- Eljaiek-Urzola, M.; Guardiola-Meza, L.; Ghafoori, S.; Mehrvar, M. Treatment of Mature Landfill Leachate Using Hybrid Processes of Hydrogen Peroxide and Adsorption in an Activated Carbon Fixed Bed Column. J. Environ. Sci. Health Part A 2018, 53, 238–243. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.H.; Shon, H.K.; Ngo, H.H. Adsorption Characteristics of Antibiotics Trimethoprim on Powdered and Granular Activated Carbon. J. Ind. Eng. Chem. 2010, 16, 344–349. [Google Scholar] [CrossRef]
- Awwad, M.; Al-Rimawi, F.; Dajani, K.J.K.; Khamis, M.; Nir, S.; Karaman, R. Removal of Amoxicillin and Cefuroxime Axetil by Advanced Membranes Technology, Activated Carbon and Micelle–Clay Complex. Environ. Technol. 2015, 36, 2069–2078. [Google Scholar] [CrossRef] [PubMed]
- Al-Dawery, S.K.; Aljundi, I.H. Methanol Removal from Methanol-Water Mixture Using Activated Sludge, Air Stripping and Adsorption Process: Comparative Study. J. Eng. Sci. Technol. 2015, 10, 1615–1627. [Google Scholar]
- Kennedy, A.M.; Reinert, A.M.; Knappe, D.R.U.; Ferrer, I.; Summers, R.S. Full- and Pilot-Scale GAC Adsorption of Organic Micropollutants. Water Res. 2015, 68, 238–248. [Google Scholar] [CrossRef] [PubMed]
- Sgroi, M.; Anumol, T.; Roccaro, P.; Vagliasindi, F.G.A.; Snyder, S.A. Modeling Emerging Contaminants Breakthrough in Packed Bed Adsorption Columns by UV Absorbance and Fluorescing Components of Dissolved Organic Matter. Water Res. 2018, 145, 667–677. [Google Scholar] [CrossRef]
- Krahnstöver, T.; Santos, N.; Georges, K.; Campos, L.; Antizar-Ladislao, B. Low-Carbon Technologies to Remove Organic Micropollutants from Wastewater: A Focus on Pharmaceuticals. Sustainability 2022, 14, 11686. [Google Scholar] [CrossRef]
- Aljeboree, A.M.; Alshirifi, A.N. Adsorption of Pharmaceuticals as Emerging Contaminants from Aqueous Solutions on to Friendly Surfaces Such as Activated Carbon: A Review. J. Pharm. Sci. Res 2018, 10, 2252–2257. [Google Scholar]
- Metcalf, L.; Eddy, H.; Tchobanoglous, G. Wastewater Engineering: Treatment, Disposal, and Reuse, 4th ed.; Tchobanoglous, G., Stensel, H.D., Burton, F.L., Eds.; McGraw-Hill: New York, NY, USA, 1991; ISBN 0-07-124140-X. [Google Scholar]
- Rodgers, M.; Healy, M.G.; Mulqueen, J. Organic Carbon Removal and Nitrification of High Strength Wastewaters Using Stratified Sand Filters. Water Res. 2005, 39, 3279–3286. [Google Scholar] [CrossRef]
- Vanerkar, A.P.; Satyanarayan, S.; Dharmadhikari, D.M. Enhancement of Organic Removals in High Strength Herbal Pharmaceutical Wastewater. Environ. Technol. 2005, 26, 389–396. [Google Scholar] [CrossRef]
- Wang, J.; Guo, X. Adsorption Kinetic Models: Physical Meanings, Applications, and Solving Methods. J. Hazard. Mater. 2020, 390, 122156. [Google Scholar] [CrossRef] [PubMed]
- Largitte, L.; Pasquier, R. A Review of the Kinetics Adsorption Models and Their Application to the Adsorption of Lead by an Activated Carbon. Chem. Eng. Res. Des. 2016, 109, 495–504. [Google Scholar] [CrossRef]
- Ayawei, N.; Ebelegi, A.N.; Wankasi, D. Modelling and Interpretation of Adsorption Isotherms. J. Chem. 2017, 2017, 3039817. [Google Scholar] [CrossRef]
- Behjoee, M.; Zamiri, M.A.; Tabil, L.G.; Baik, O.-D.; Niu, C.H. Equilibrium, Thermodynamics, and Regeneration and Reuse of Biosorbents Developed from Pelletized Agricultural Residues for Gas Dehydration. Energy Fuels 2023, 37, 1451–1463. [Google Scholar] [CrossRef]
- Priya, V.S.; Philip, L. Biodegradation of Dichloromethane Along with Other VOCs from Pharmaceutical Wastewater. Appl. Biochem. Biotechnol. 2013, 169, 1197–1218. [Google Scholar] [CrossRef] [PubMed]
- Ghafoori, S.; Mowla, A.; Jahani, R.; Mehrvar, M.; Chan, P.K. Sonophotolytic Degradation of Synthetic Pharmaceutical Wastewater: Statistical Experimental Design and Modeling. J. Environ. Manag. 2015, 150, 128–137. [Google Scholar] [CrossRef]
- Gupta, A.; Garg, A. Adsorption and Oxidation of Ciprofloxacin in a Fixed Bed Column Using Activated Sludge Derived Activated Carbon. J. Environ. Manag. 2019, 250, 109474. [Google Scholar] [CrossRef]
- Kaya, Y.; Bacaksiz, A.M.; Bayrak, H.; Gönder, Z.B.; Vergili, I.; Hasar, H.; Yilmaz, G. Treatment of Chemical Synthesis-Based Pharmaceutical Wastewater in an Ozonation-Anaerobic Membrane Bioreactor (AnMBR) System. Chem. Eng. J. 2017, 322, 293–301. [Google Scholar] [CrossRef]
- Ganzenko, O.; Trellu, C.; Papirio, S.; Oturan, N.; Huguenot, D.; van Hullebusch, E.D.; Esposito, G.; Oturan, M.A. Bioelectro-Fenton: Evaluation of a Combined Biological—Advanced Oxidation Treatment for Pharmaceutical Wastewater. Environ. Sci. Pollut. Res. 2018, 25, 20283–20292. [Google Scholar] [CrossRef]
- Ng, K.K.; Shi, X.; Tang, M.K.Y.; Ng, H.Y. A Novel Application of Anaerobic Bio-Entrapped Membrane Reactor for the Treatment of Chemical Synthesis-Based Pharmaceutical Wastewater. Sep. Purif. Technol. 2014, 132, 634–643. [Google Scholar] [CrossRef]
- Gupta, R.; Sati, B.; Gupta, A. Treatment and Recycling of Wastewater from Pharmaceutical Industry. In Advances in Biological Treatment of Industrial Wastewater and their Recycling for a Sustainable Future, Applied Environmental Science and Engineering for a Sustainable Future; Singh, R.L., Singh, R.P., Eds.; Applied Environmental Science and Engineering for a Sustainable Future; Springer: Singapore, 2019; pp. 267–302. ISBN 9789811314681. [Google Scholar]
- Wang, K.; Liu, S.; Zhang, Q.; He, Y. Pharmaceutical Wastewater Treatment by Internal Micro-electrolysis–Coagulation, Biological Treatment and Activated Carbon Adsorption. Environ. Technol. 2009, 30, 1469–1474. [Google Scholar] [CrossRef] [PubMed]
- Kavitha, R.V.; Murthy, V.K.; Makam, R.; Asith, K. a Physico-Chemical Analysis of Effluents from Pharmaceutical Industry and Its Efficiency Study. Int. J. Eng. Res. Appl. 2012, 2, 103–110. [Google Scholar]
- Wu, Z.; Cong, Y.; Zhou, M.; Tan, T. P-Nitrophenol Abatement by the Combination of Electrocatalysis and Activated Carbon. Chem. Eng. J. 2005, 106, 83–90. [Google Scholar] [CrossRef]
- Obiri-Nyarko, F.; Kwiatkowska-Malina, J.; Kumahor, S.K.; Malina, G. Evaluating Low-Cost Permeable Adsorptive Barriers for the Removal of Benzene from Groundwater: Laboratory Experiments and Numerical Modelling. J. Contam. Hydrol. 2022, 250, 104054. [Google Scholar] [CrossRef]
- Rineksa, G.; Bustomy, A.; Park, D.-H.; Gozan, M. Isotherm Coefficient for Benzene and Toluene Adsorption on Granular Activated Carbon for Preparation of Biobarrier. IOP Conf. Ser. Earth Environ. Sci. 2022, 1111, 012049. [Google Scholar] [CrossRef]
- Melaphi, K.; Sadare, O.O.; Simate, G.S.; Wagenaar, S.; Moothi, K. Adsorptive Removal of BTEX Compounds from Wastewater Using Activated Carbon Derived from Macadamia Nut Shells. WSA 2023, 49, 36–45. [Google Scholar] [CrossRef]
- Zeinali, F.; Ghoreyshi, A.A.; Najafpour, G. Removal of toluene and dichloromethane from aqueous phase by granular activated carbon (GAC). Chem. Eng. Commun. 2012, 199, 203–220. [Google Scholar] [CrossRef]
- Alhooshani, K.R. Adsorption of Chlorinated Organic Compounds from Water with Cerium Oxide-Activated Carbon Composite. Arab. J. Chem. 2019, 12, 2585–2596. [Google Scholar] [CrossRef]
- Mangotra, A.; Singh, S.K.; Mohan, A. Preparation, Characterization and Assessment of Low Cost Green Adsorbent Prepared from Coconut Shell for Removal of Toxic Dichloromethane. Ann. Biol. 2023, 39, 41–48. [Google Scholar]
- Chen, C.; Geng, X.; Huang, W. Adsorption of 4-Chlorophenol and Aniline by Nanosized Activated Carbons. Chem. Eng. J. 2017, 327, 941–952. [Google Scholar] [CrossRef]
- Li, H.; Liu, L.; Cui, J.; Cui, J.; Wang, F.; Zhang, F. High-Efficiency Adsorption and Regeneration of Methylene Blue and Aniline onto Activated Carbon from Waste Edible Fungus Residue and Its Possible Mechanism. RSC Adv. 2020, 10, 14262–14273. [Google Scholar] [CrossRef]
- Celarek, M. Sorptive Removal of 4-Aminophenol from Water Using a Polymeric Sorbent. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2017. [Google Scholar]
- Abdul Ameer, A.M. Removal of Mixture of Phenolic Compounds from Aqueous Solution by Tire Char Adsorption. IOP Conf. Ser. Mater. Sci. Eng. 2019, 518, 062011. [Google Scholar] [CrossRef]
- Mishra, P.; Singh, K.; Dixit, U.; Agarwal, A.; Ahmad Bhat, R. Effective Removal of 4-Aminophenol from Aqueous Environment by Pea (Pisum sativum) Shells Activated with Sulfuric Acid: Characterization, Isotherm, Kinetics and Thermodynamics. J. Indian Chem. Soc. 2022, 99, 100528. [Google Scholar] [CrossRef]
- Al-Amrani, W.A.; Hanafiah, M.A.K.M.; Lim, P.-E. Influence of Hydrophilicity/Hydrophobicity on Adsorption/Desorption of Sulfanilic Acid Using Amine-Modified Silicas and Granular Activated Carbon. DWT 2022, 249, 109–118. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Dubinin, M.M. The Potential Theory of Adsorption of Gases and Vapors for Adsorbents with Energetically Nonuniform Surfaces. Chem. Rev. 1960, 60, 235–241. [Google Scholar] [CrossRef]
- de Boer, J.H.; Linsen, B.G.; van der Plas, T.; Zondervan, G.J. Studies on Pore Systems in Catalysts: VII. Description of the Pore Dimensions of Carbon Blacks by the t Method. J. Catal. 1965, 4, 649–653. [Google Scholar] [CrossRef]
- Ravikovitch, P.I.; Haller, G.L.; Neimark, A.V. Density Functional Theory Model for Calculating Pore Size Distributions: Pore Structure of Nanoporous Catalysts. Adv. Colloid Interface Sci. 1998, 76–77, 203–226. [Google Scholar] [CrossRef]
- Rivera-Utrilla, J.; Bautista-Toledo, I.; Ferro-García, M.A.; Moreno-Castilla, C. Activated Carbon Surface Modifications by Adsorption of Bacteria and Their Effect on Aqueous Lead Adsorption. J. Chem. Tech. Biotech. 2001, 76, 1209–1215. [Google Scholar] [CrossRef]
- Órfão, J.J.M.; Silva, A.I.M.; Pereira, J.C.V.; Barata, S.A.; Fonseca, I.M.; Faria, P.C.C.; Pereira, M.F.R. Adsorption of a Reactive Dye on Chemically Modified Activated Carbons—Influence of pH. J. Colloid Interface Sci. 2006, 296, 480–489. [Google Scholar] [CrossRef] [PubMed]
- Ehiomogue, P.; Ahuchaogu, I.; Ahaneku, E. A Review of Bioreremediation of Hydrocarbon Contaminated Soils in Niger Delta Area of Nigeria. Poljopr. Teh. 2021, 46, 23–39. [Google Scholar] [CrossRef]
- Qureshi, U.A.; Hameed, B.H.; Ahmed, M.J. Adsorption of Endocrine Disrupting Compounds and Other Emerging Contaminants Using Lignocellulosic Biomass-Derived Porous Carbons: A Review. J. Water Process Eng. 2020, 38, 101380. [Google Scholar] [CrossRef]
- Kalam, S.; Abu-Khamsin, S.A.; Kamal, M.S.; Patil, S. Surfactant Adsorption Isotherms: A Review. ACS Omega 2021, 6, 32342–32348. [Google Scholar] [CrossRef] [PubMed]
- Marković, D.D.; Lekić, B.M.; Rajaković-Ognjanović, V.N.; Onjia, A.E.; Rajaković, L.V. A New Approach in Regression Analysis for Modeling Adsorption Isotherms. Sci. World J. 2014, 2014, 930879. [Google Scholar] [CrossRef] [PubMed]
- MATLAB and Curve Fitting Toolbox. Version 9.14 (R2023a); The MathWorks Inc.: Natick, MA, USA, 2023; Available online: https://www.mathworks.com (accessed on 12 December 2023).
- Podder, M.S.; Majumder, C.B. Sequestering of As(III) and As(V) from Wastewater Using a Novel Neem Leaves/MnFe 2 O 4 Composite Biosorbent. Int. J. Phytoremediation 2016, 18, 1237–1257. [Google Scholar] [CrossRef] [PubMed]
- Pauletto, P.S.; Lütke, S.F.; Dotto, G.L.; Salau, N.P.G. Adsorption Mechanisms of Single and Simultaneous Removal of Pharmaceutical Compounds onto Activated Carbon: Isotherm and Thermodynamic Modeling. J. Mol. Liq. 2021, 336, 116203. [Google Scholar] [CrossRef]
- Allen, S.J.; Gan, Q.; Matthews, R.; Johnson, P.A. Comparison of Optimised Isotherm Models for Basic Dye Adsorption by Kudzu. Bioresour. Technol. 2003, 88, 143–152. [Google Scholar] [CrossRef] [PubMed]
- Hashem, A.; Al-Anwar, A.; Nagy, N.M.; Hussein, D.M.; Eisa, S. Isotherms and Kinetic Studies on Adsorption of Hg(II) Ions onto Ziziphus Spina-Christi L. from Aqueous Solutions. Green Process. Synth. 2016, 5, 213–224. [Google Scholar] [CrossRef]
- Revellame, E.D.; Fortela, D.L.; Sharp, W.; Hernandez, R.; Zappi, M.E. Adsorption Kinetic Modeling Using Pseudo-First Order and Pseudo-Second Order Rate Laws: A Review. Clean. Eng. Technol. 2020, 1, 100032. [Google Scholar] [CrossRef]
- Foo, K.Y.; Hameed, B.H. Insights into the Modeling of Adsorption Isotherm Systems. Chem. Eng. J. 2010, 156, 2–10. [Google Scholar] [CrossRef]
- Kletting, P.; Glatting, G. Model Selection for Time-Activity Curves: The Corrected Akaike Information Criterion and the F-Test. Z. Med. Phys. 2009, 19, 200–206. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Yang, F.-C.; Hung, W.-N.; Liu, C.-L.; Yang, M.; Lin, T.-F. Prediction of Powdered Activated Carbon Doses for 2-MIB Removal in Drinking Water Treatment Using a Simplified HSDM Approach. Chemosphere 2016, 156, 374–382. [Google Scholar] [CrossRef] [PubMed]
- Connelly, A. BET Surface Area—Andy Connelly. Available online: https://andyjconnelly.wordpress.com/2017/03/13/bet-surface-area/ (accessed on 27 September 2022).
- Sing, K.S.W.; Everett, D.H.; Haul, R.A.W.; Moscou, L.; Pierotti, R.A.; Rouquerol, J.; Siemieniewska, T. Reporting Physisorption Data for Gas/Solid Systems with Special Reference to the Determination of Surface Area and Porosity (Recommendations 1984). Pure Appl. Chem. 1985, 57, 603–619. [Google Scholar] [CrossRef]
- Sotelo, J.L.; Rodríguez, A.R.; Mateos, M.M.; Hernández, S.D.; Torrellas, S.A.; Rodríguez, J.G. Adsorption of Pharmaceutical Compounds and an Endocrine Disruptor from Aqueous Solutions by Carbon Materials. J. Environ. Sci. Health Part B 2012, 47, 640–652. [Google Scholar] [CrossRef] [PubMed]
- Sumanjit; Rani, S.; Mahajan, R.K. Equilibrium, Kinetics and Thermodynamic Parameters for Adsorptive Removal of Dye Basic Blue 9 by Ground Nut Shells and Eichhornia. Arab. J. Chem. 2016, 9, S1464–S1477. [Google Scholar] [CrossRef]
- Çalışkan, E.; Göktürk, S. Adsorption Characteristics of Sulfamethoxazole and Metronidazole on Activated Carbon. Sep. Sci. Technol. 2010, 45, 244–255. [Google Scholar] [CrossRef]
- Sajid, M.; Bari, S.; Saif Ur Rehman, M.; Ashfaq, M.; Guoliang, Y.; Mustafa, G. Adsorption Characteristics of Paracetamol Removal onto Activated Carbon Prepared from Cannabis Sativum Hemp. Alex. Eng. J. 2022, 61, 7203–7212. [Google Scholar] [CrossRef]
- Al-Qodah, Z.; Shawaqfeh, A.T.; Lafi, W.K. Two-Resistance Mass Transfer Model for the Adsorption of the Pesticide Deltamethrin Using Acid Treated Oil Shale Ash. Adsorption 2007, 13, 73–82. [Google Scholar] [CrossRef]
- Baccar, R.; Sarrà, M.; Bouzid, J.; Feki, M.; Blánquez, P. Removal of Pharmaceutical Compounds by Activated Carbon Prepared from Agricultural By-Product. Chem. Eng. J. 2012, 211–212, 310–317. [Google Scholar] [CrossRef]
- Mohammed, R.R.; Ketabachi, M.R.; McKay, G. Combined Magnetic Field and Adsorption Process for Treatment of Biologically Treated Palm Oil Mill Effluent (POME). Chem. Eng. J. 2014, 243, 31–42. [Google Scholar] [CrossRef]
- Kaur, H.; Bansiwal, A.; Hippargi, G.; Pophali, G.R. Effect of Hydrophobicity of Pharmaceuticals and Personal Care Products for Adsorption on Activated Carbon: Adsorption Isotherms, Kinetics and Mechanism. Environ. Sci. Pollut. Res. 2018, 25, 20473–20485. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Kong, D.; Wang, Y.; Wu, J.; Sun, S.; Xu, P. Production of Mesoporous Activated Carbon from Tea Fruit Peel Residues and Its Evaluation of Methylene Blue Removal from Aqueous Solutions. BioResources 2013, 8, 2145–2160. [Google Scholar] [CrossRef]
- Song, X.; Zhang, Y.; Yan, C.; Jiang, W.; Chang, C. The Langmuir Monolayer Adsorption Model of Organic Matter into Effective Pores in Activated Carbon. J. Colloid Interface Sci. 2013, 389, 213–219. [Google Scholar] [CrossRef] [PubMed]
- Lyubchik, S.; Lyubchik, A.; Lygina, O.; Lyubchik, S.; Fonsec, I. Comparison of the Thermodynamic Parameters Estimation for the Adsorption Process of the Metals from Liquid Phase on Activated Carbons. In Thermodynamics—Interaction Studies—Solids, Liquids and Gases; Moreno Pirajn, J.C., Ed.; InTech: London, UK, 2011; p. 932. ISBN 978-953-307-563-1. [Google Scholar]
- Álvarez-Torrellas, S.; Peres, J.A.; Gil-Álvarez, V.; Ovejero, G.; García, J. Effective Adsorption of Non-Biodegradable Pharmaceuticals from Hospital Wastewater with Different Carbon Materials. Chem. Eng. J. 2017, 320, 319–329. [Google Scholar] [CrossRef]
- Batool, F.; Akbar, J.; Iqbal, S.; Noreen, S.; Bukhari, S.N.A. Study of Isothermal, Kinetic, and Thermodynamic Parameters for Adsorption of Cadmium: An Overview of Linear and Nonlinear Approach and Error Analysis. Bioinorg. Chem. Appl. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Yaneva, Z.L.; Koumanova, B.K.; Georgieva, N.V. Linear and Nonlinear Regression Methods for Equilibrium Modelling of p-Nitrophenol Biosorption by Rhizopus Oryzae: Comparison of Error Analysis Criteria. J. Chem. 2013, 2013, 1–10. [Google Scholar] [CrossRef]
- Ramadoss, R.; Subramaniam, D. Removal of Divalent Nickel from Aqueous Solution Using Blue-Green Marine Algae: Adsorption Modeling and Applicability of Various Isotherm Models. Sep. Sci. Technol. 2019, 54, 943–961. [Google Scholar] [CrossRef]
- Brião, G.D.V.; Hashim, M.A.; Chu, K.H. The Sips Isotherm Equation: Often Used and Sometimes Misused. Sep. Sci. Technol. 2023, 58, 884–892. [Google Scholar] [CrossRef]
- Girish, C.R. Various Isotherm Models for Multicomponent Adsorption: A Review. Int. J. Civ. Eng. Technol. 2017, 8, 80–86. [Google Scholar]
- Shimizu, S.; Matubayasi, N. Cooperative Sorption on Porous Materials. Langmuir 2021, 37, 10279–10290. [Google Scholar] [CrossRef] [PubMed]
- Hamdaoui, O.; Naffrechoux, E. Modeling of Adsorption Isotherms of Phenol and Chlorophenols onto Granular Activated carbonPart II. Models with More than Two Parameters. J. Hazard. Mater. 2007, 147, 401–411. [Google Scholar] [CrossRef] [PubMed]
- Bolong, N.; Ismail, A.F.; Salim, M.R.; Matsuura, T. A Review of the Effects of Emerging Contaminants in Wastewater and Options for Their Removal. Desalination 2009, 239, 229–246. [Google Scholar] [CrossRef]
- Brião, G.D.V.; Da Silva, M.G.C.; Vieira, M.G.A.; Chu, K.H. Correlation of Type II Adsorption Isotherms of Water Contaminants Using Modified BET Equations. Colloid Interface Sci. Commun. 2022, 46, 100557. [Google Scholar] [CrossRef]
- Al-Ghouti, M.A.; Da’ana, D.A. Guidelines for the Use and Interpretation of Adsorption Isotherm Models: A Review. J. Hazard. Mater. 2020, 393, 122383. [Google Scholar] [CrossRef] [PubMed]
- Isiuku, B.O.; Okonkwo, P.C.; Emeagwara, C.D. Batch Adsorption Isotherm Models Applied in Single and Multicomponent Adsorption Systems—A Review. J. Dispers. Sci. Technol. 2021, 42, 1879–1897. [Google Scholar] [CrossRef]
- Al-Qodah, Z.; Al-Shannag, M.; Hudaib, B.; Bani-Salameh, W. Enhancement of Dairy Wastewater Treatment Efficiency in Batch Chemical-Assisted Solar-Powered Electrocoagulation-Adsorption System. Case Stud. Chem. Environ. Eng. 2024, 9, 100760. [Google Scholar] [CrossRef]
- Al-Qodah, Z.; Al-Zghoul, T.M.; Jamrah, A. The Performance of Pharmaceutical Wastewater Treatment System of Electrocoagulation Assisted Adsorption Using Perforated Electrodes to Reduce Passivation. Env. Sci. Pollut. Res. 2024, 31, 20434–20448. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).