Two-Dimensional Hydrodynamic Simulation of the Effect of Stormwater Inlet Blockage on Urban Waterlogging
Abstract
1. Introduction
2. Materials and Methods
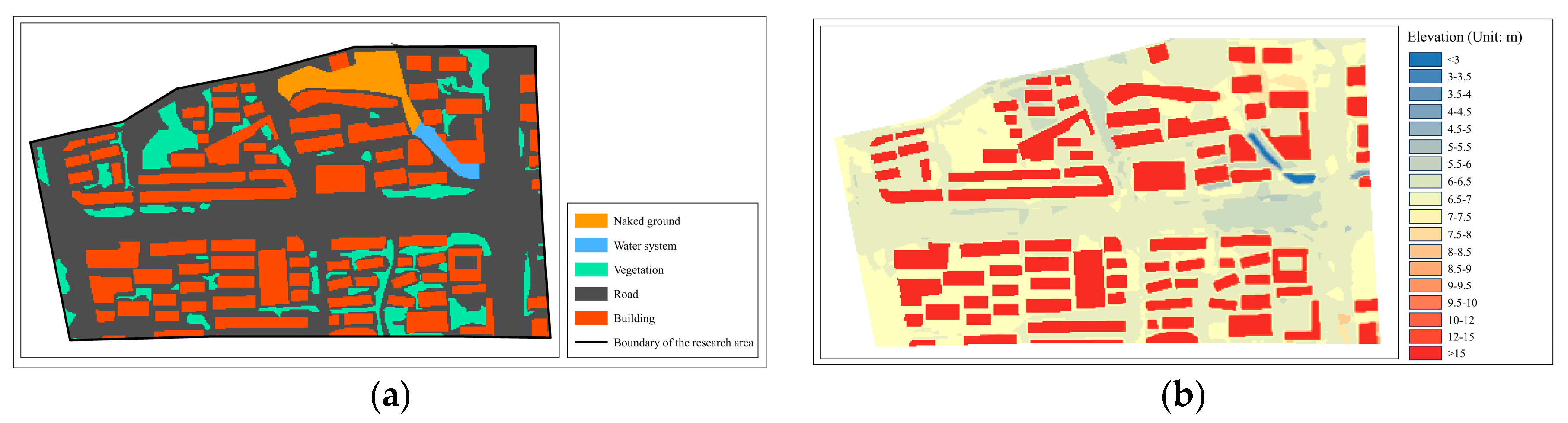
2.1. Research Area and Data
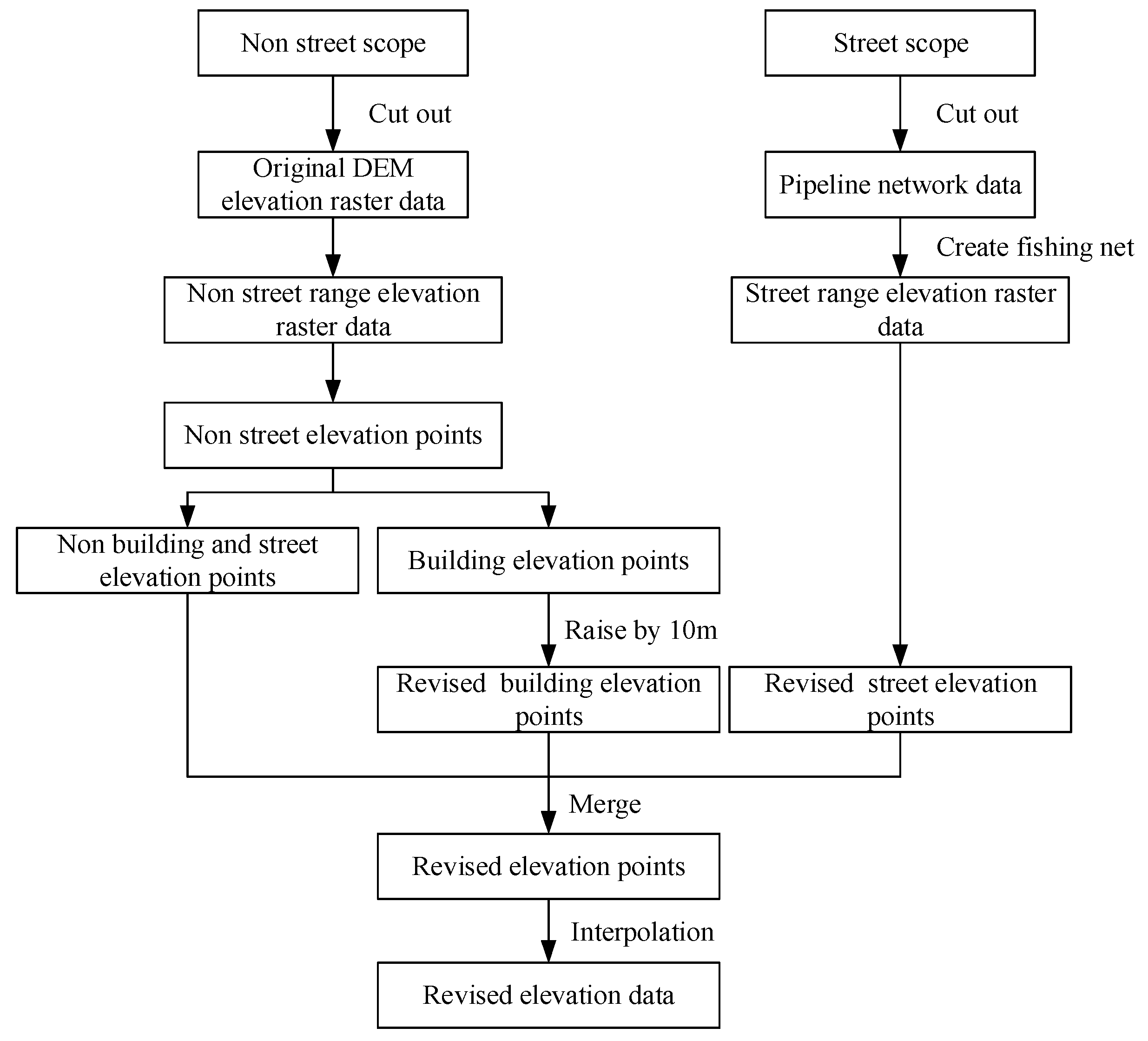
2.2. DEM Reconstruction
2.2.1. DEM Reconstruction Process
2.2.2. Spatial Interpolation
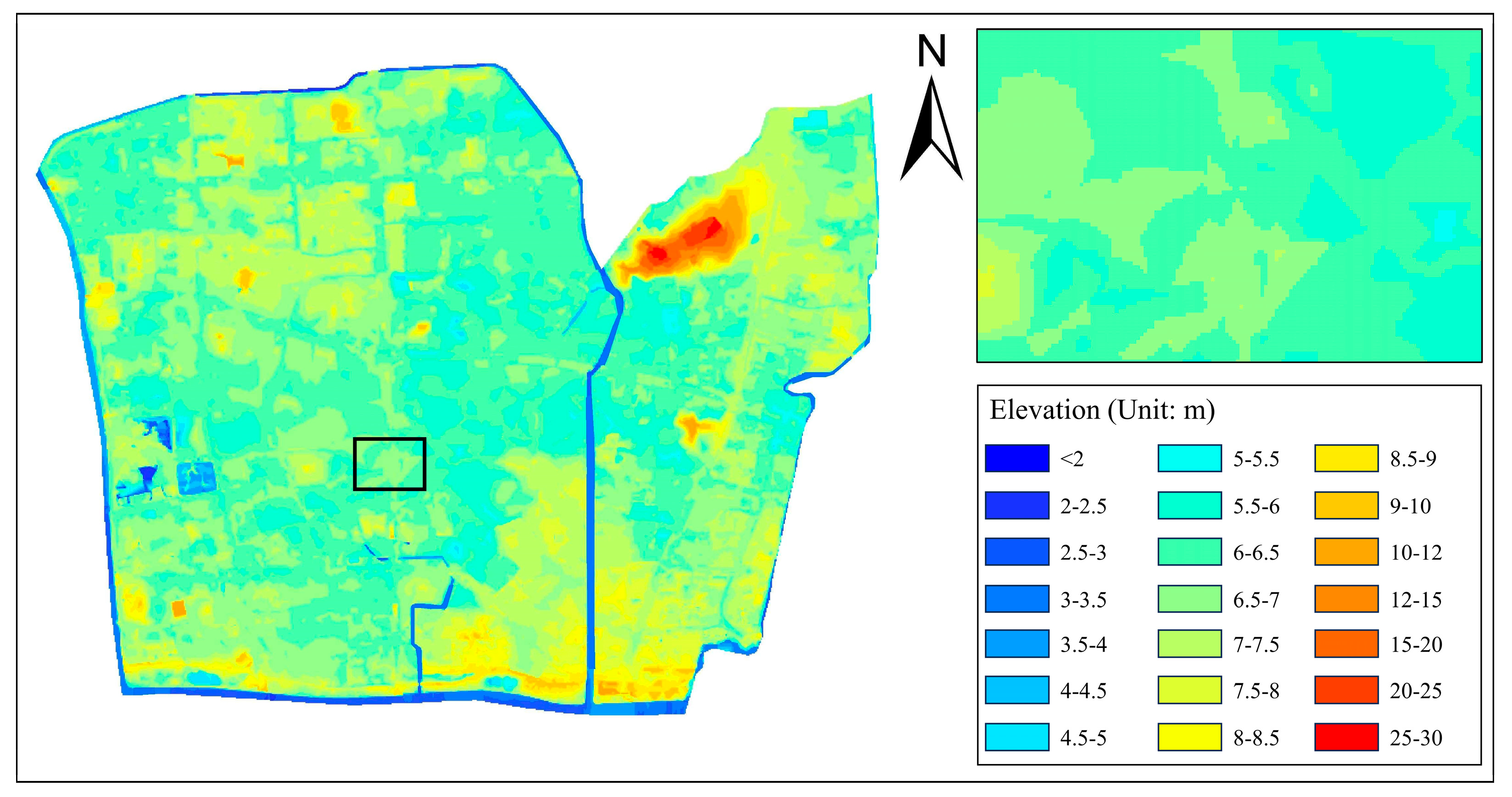
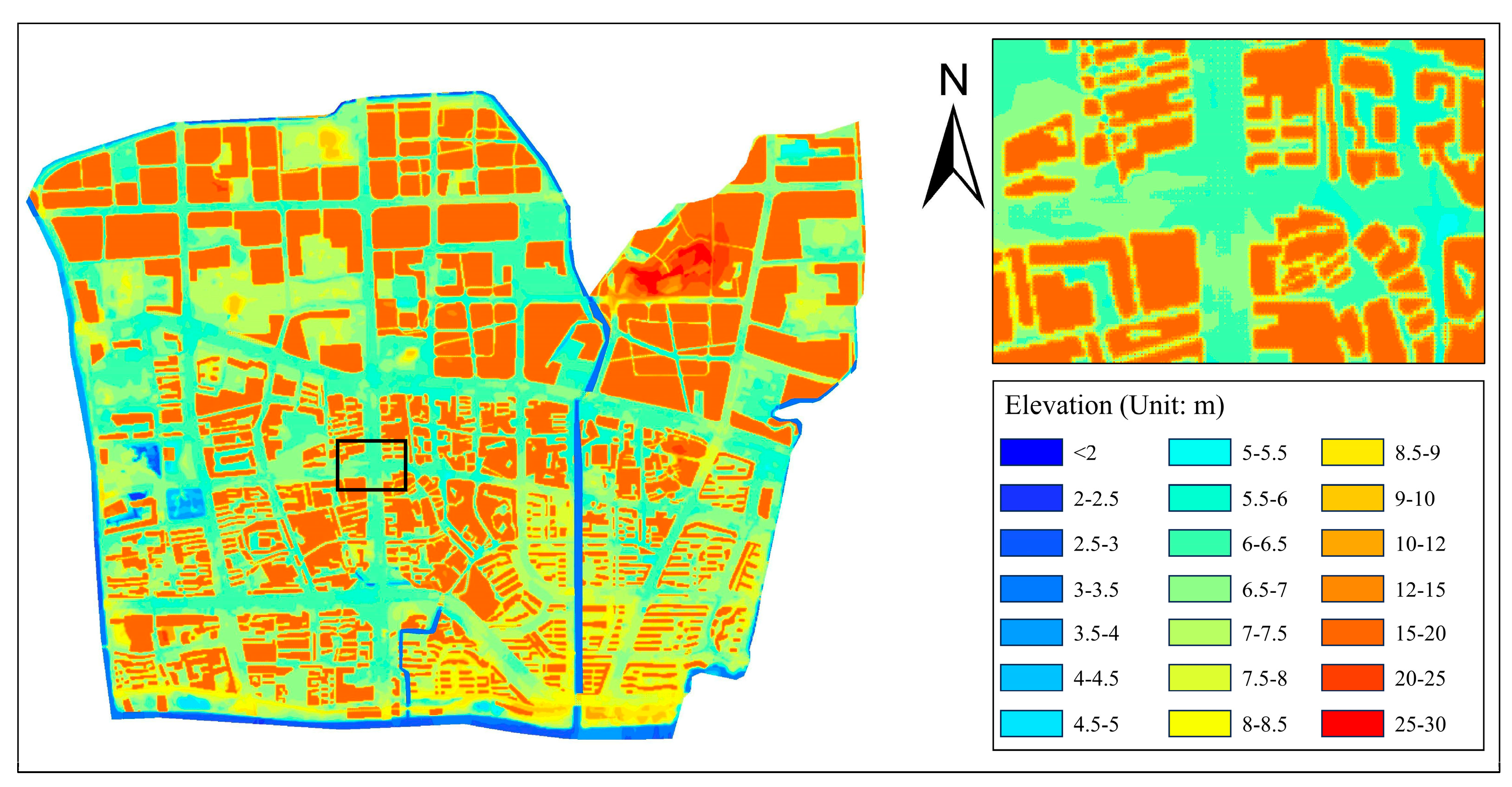
2.2.3. Comparison of the DEM Reconstruction Results
2.3. Methodology
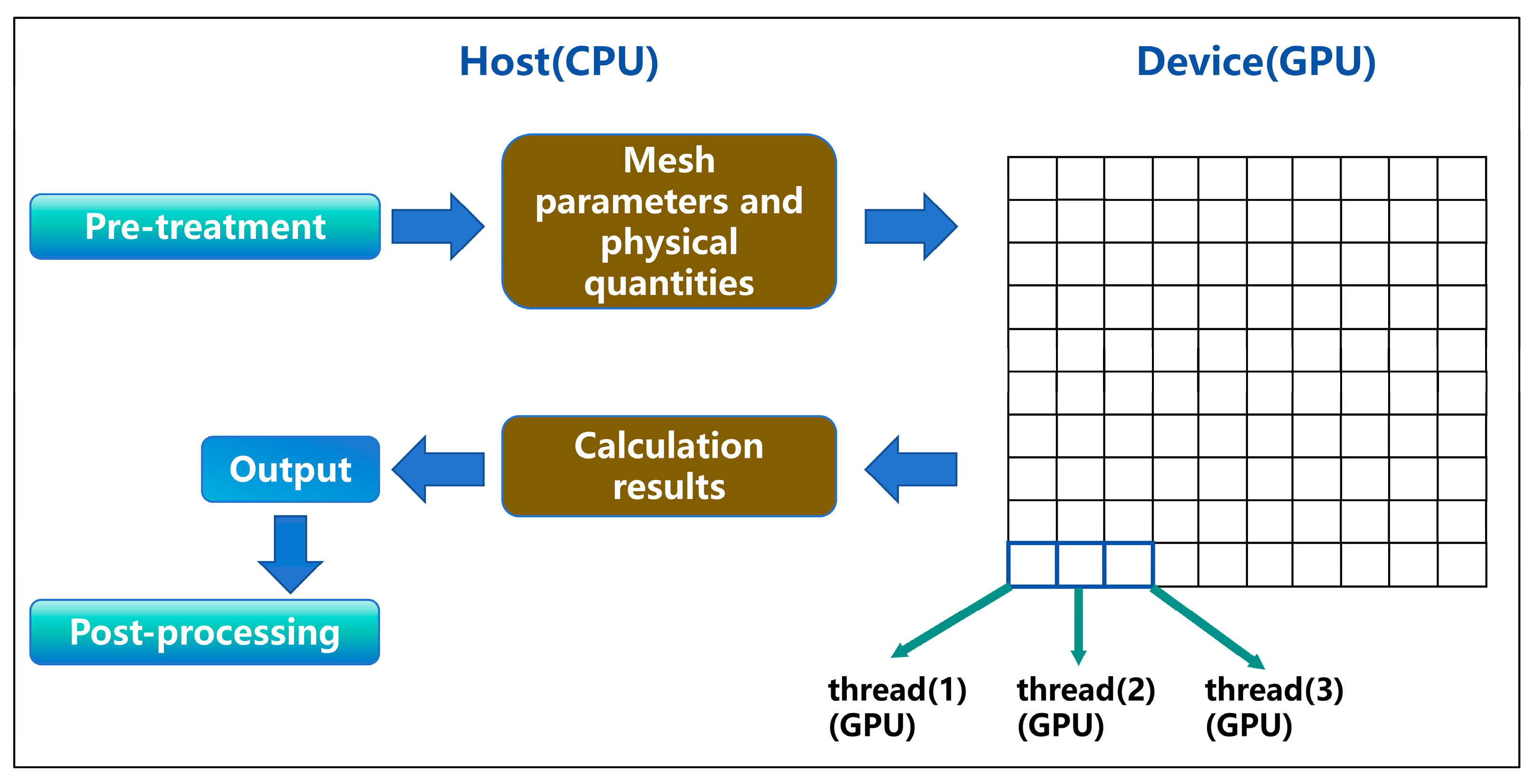
2.3.1. ITF-FLOOD Model
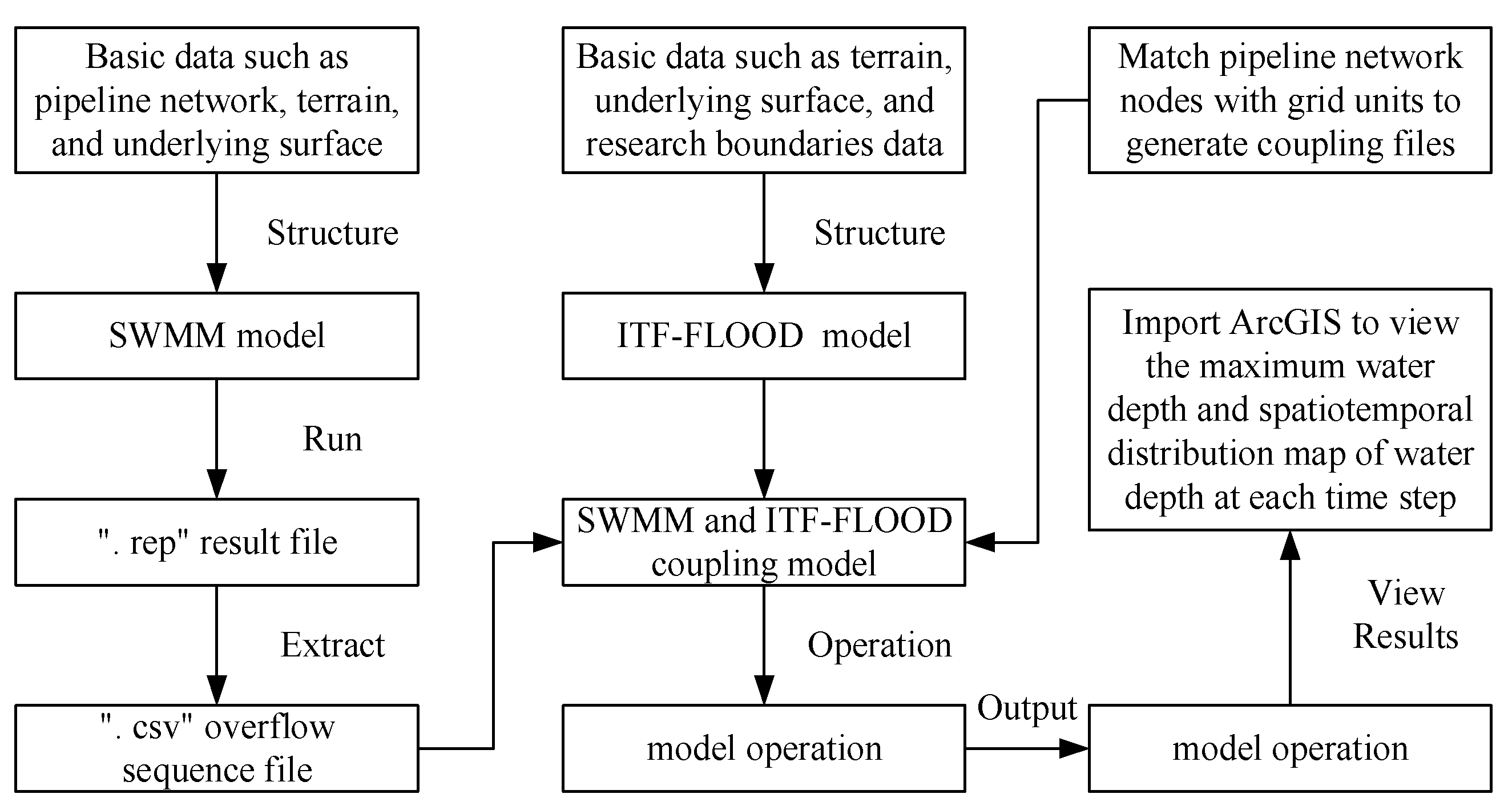
2.3.2. SWMM and ITF-FLOOD Coupling Model
2.3.3. Generalized Drainage Capacity of Pipe Network
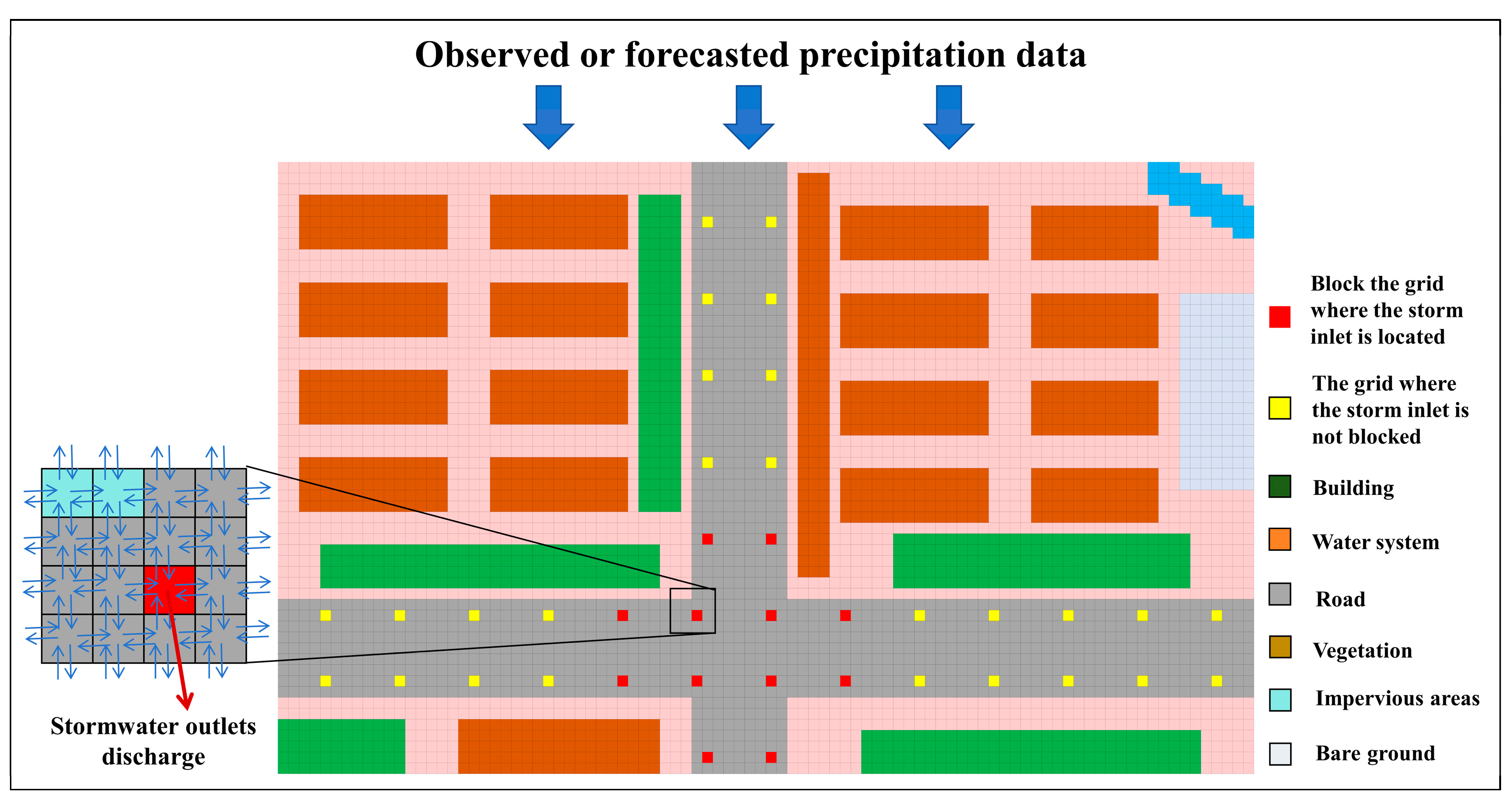
2.3.4. Simulation of STORMWATER Inlet Blockage
- (1)
- Calculation equation for the stormwater inlet discharge capacity
- (2)
- Control of the stormwater inlet blockage state
2.4. Model Building
2.4.1. Construction of a Two-Dimensional Hydrodynamic Model Coupled with the Stormwater Inlet Discharge
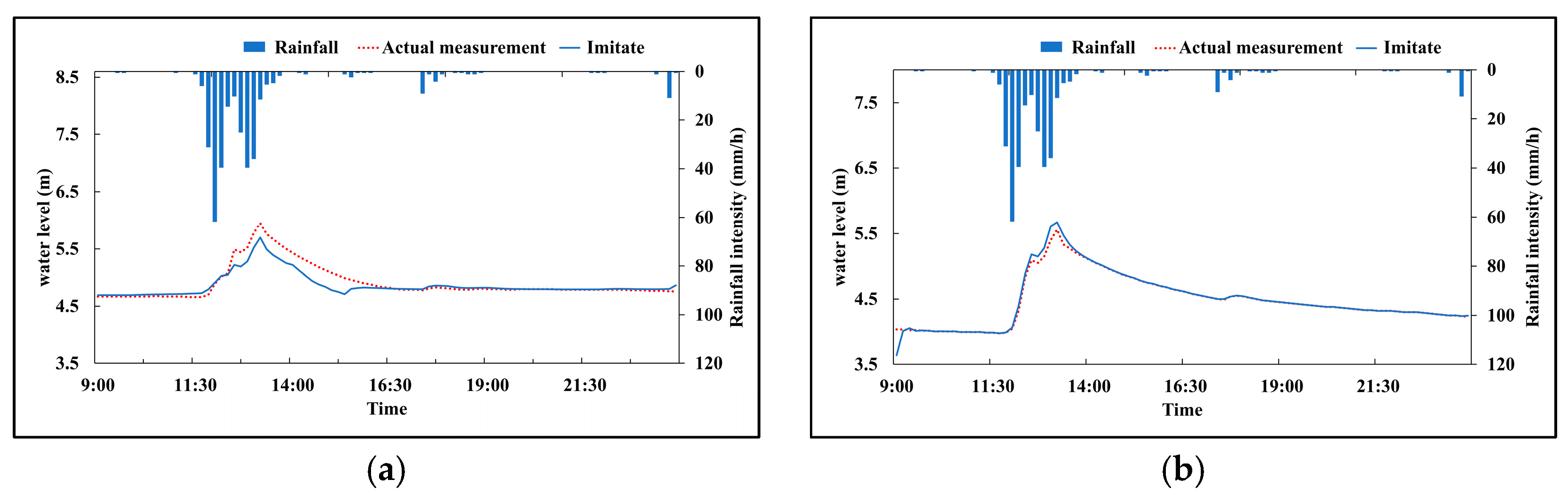
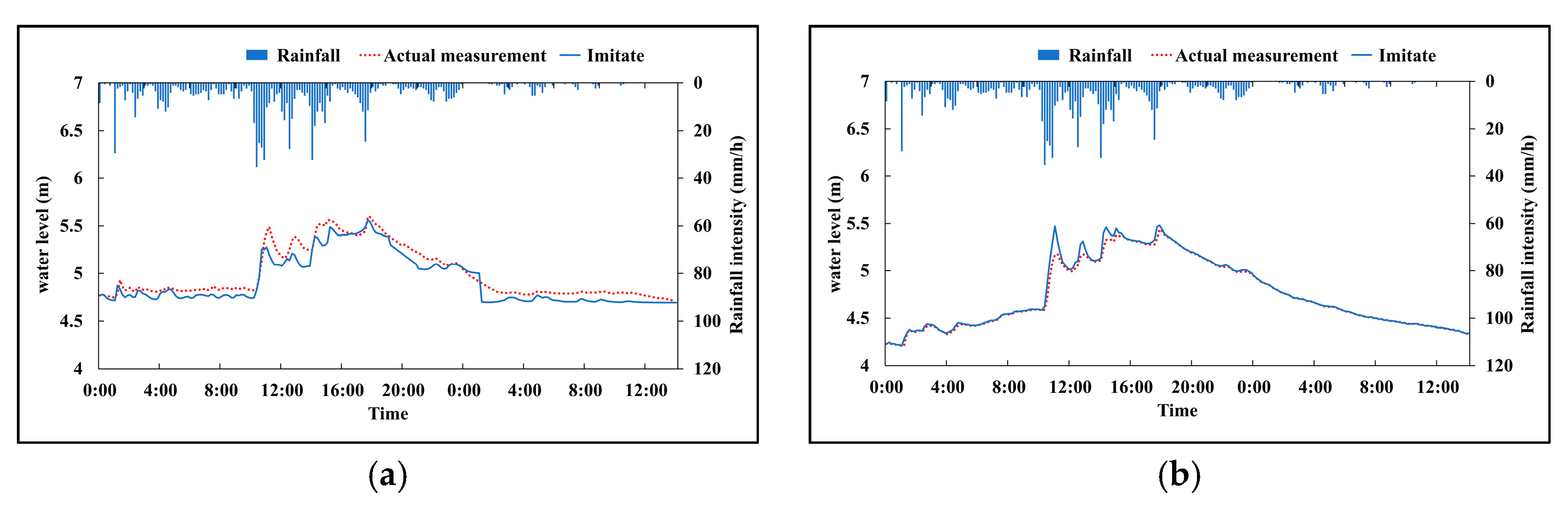
2.4.2. Parameter Calibration and Validation
3. Analysis of the Impact of Stormwater Inlet Blockage on Waterlogging
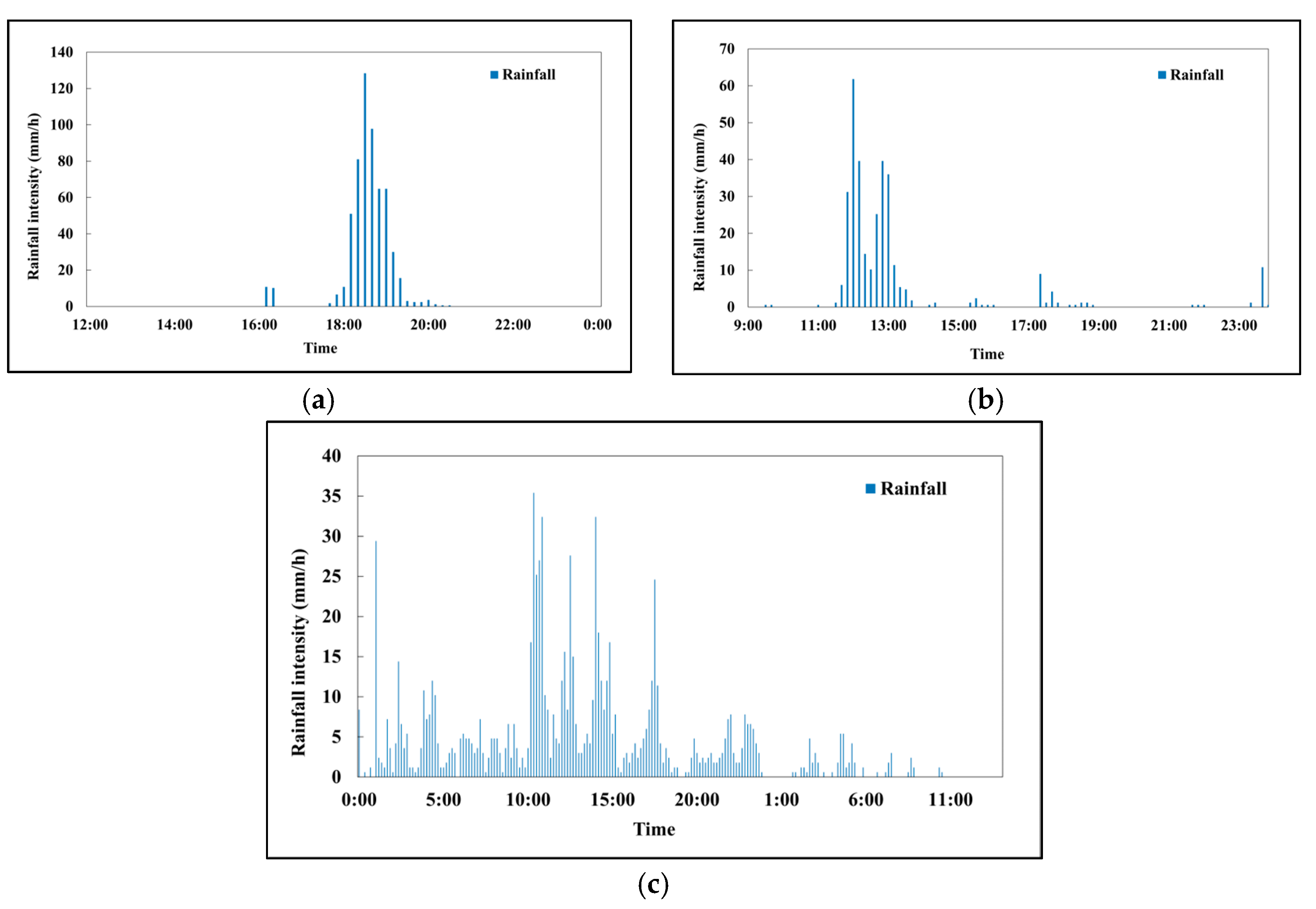
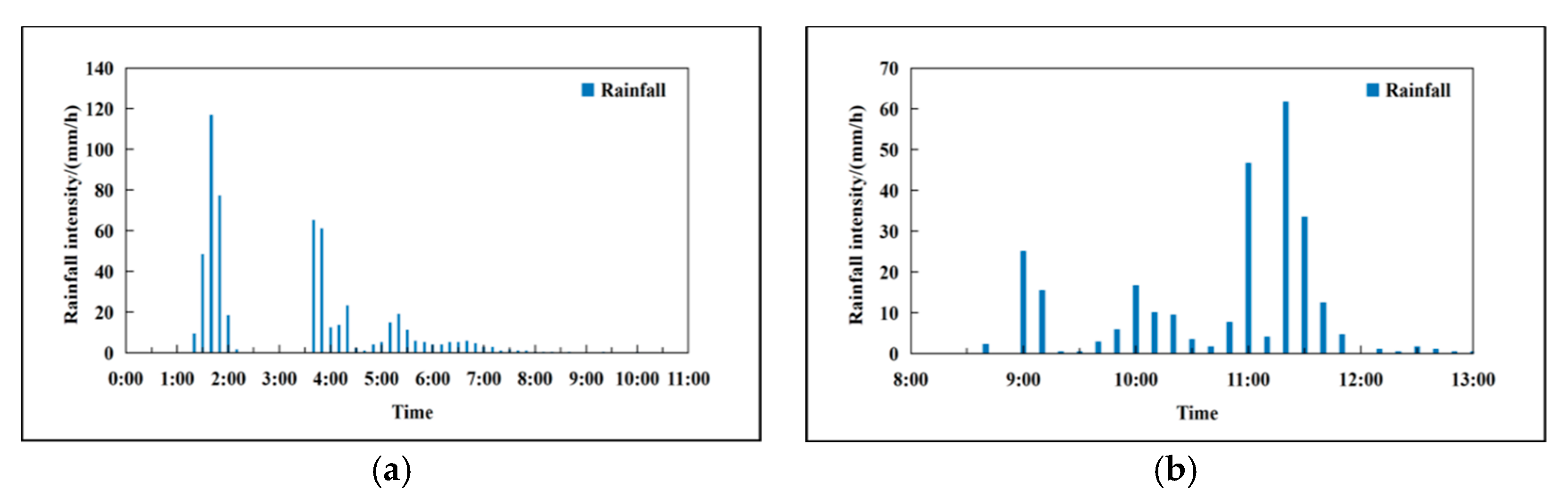
3.1. Different Rainfall Scenarios
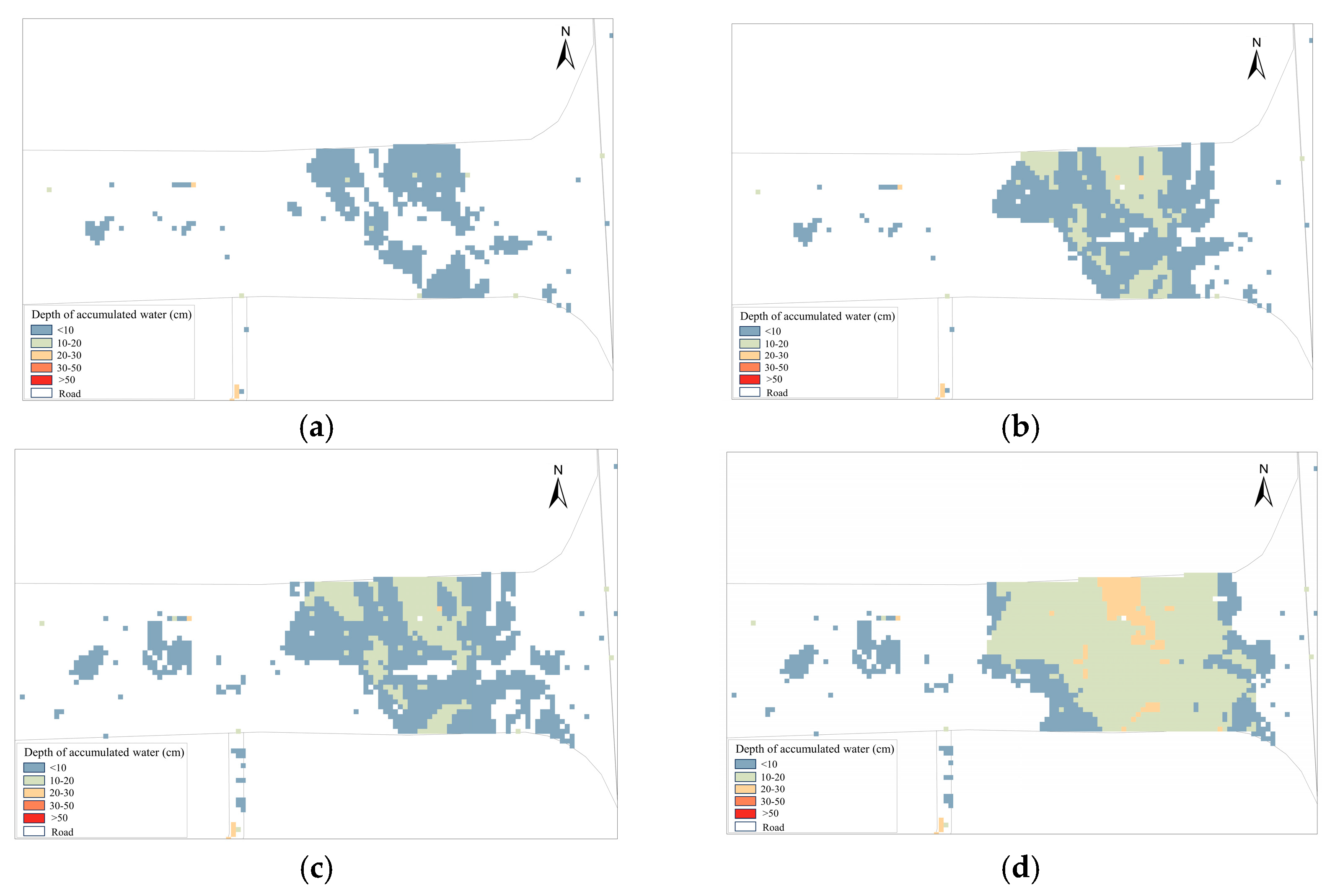
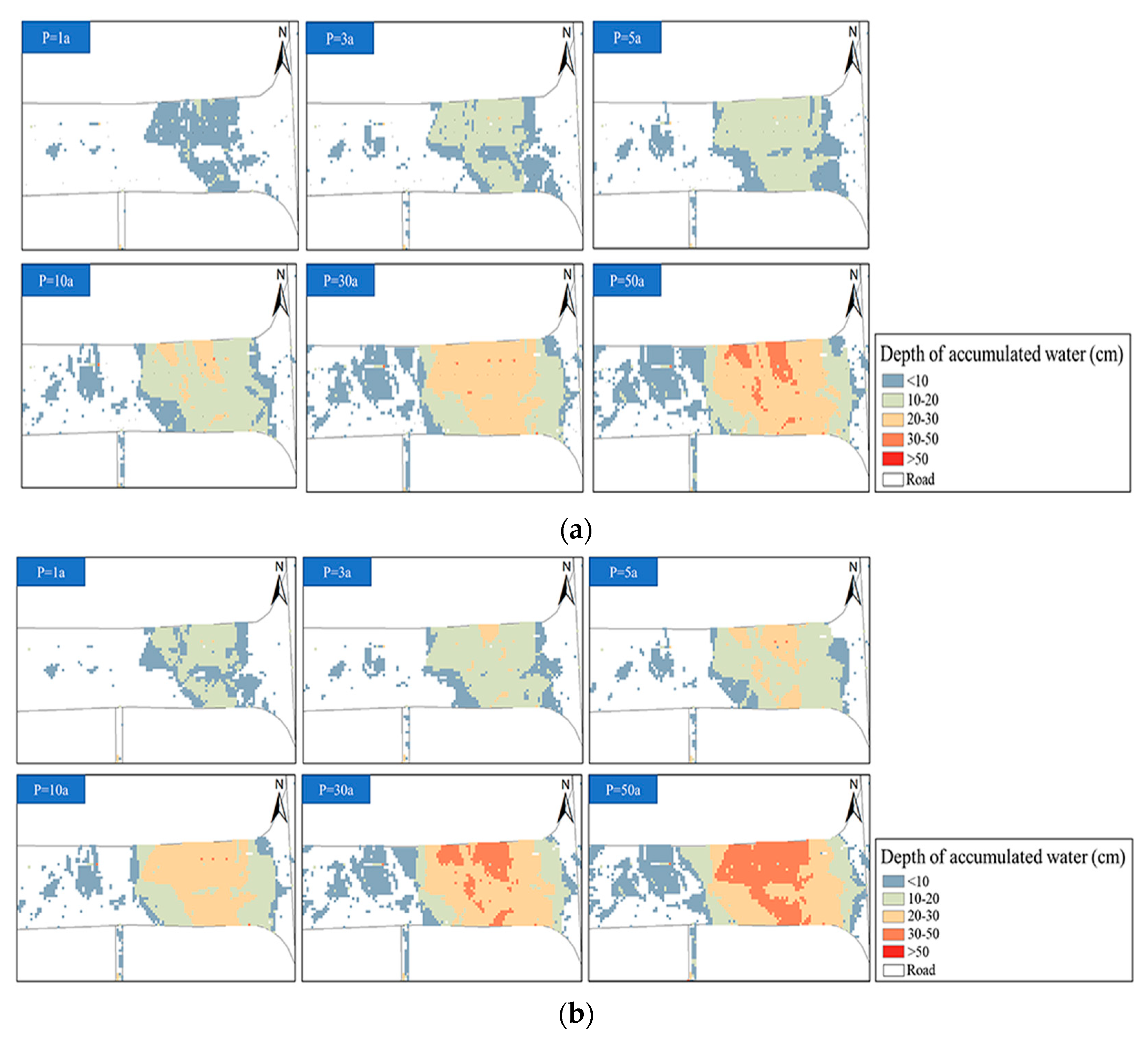
3.2. Analysis of the Simulation Results
4. Discussion
- (1)
- Replace aged or easily clogged stormwater grates
- (2)
- Implement a stormwater inlet subcontracting system
- (3)
- Combining other measures to address accumulated water
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qi, G.Z.; Wang, Z.B.; Wei, L.J.; Wang, Z.X. Multidimensional effects of urbanization on PM2.5 concentration in China. Environ. Sci. Pollut. Res. 2022, 29, 77081–77096. [Google Scholar] [CrossRef] [PubMed]
- Duan, C.Y.; Zhang, J.Q.; Chen, Y.N.; Lang, Q.L.; Zhang, Y.C.; Wu, C.Y.; Zhang, Z. Comprehensive Risk Assessment of Urban Waterlogging Disaster Based on MCDA-GIS Integration: The Case Study of Changchun, China. Remote Sens. 2022, 14, 3101. [Google Scholar] [CrossRef]
- Yu, H.F.; Zhao, Y.L.; Fu, Y.C.; Li, L. Spatiotemporal Variance Assessment of Urban Rainstorm Waterlogging Affected by Impervious Surface Expansion: A Case Study of Guangzhou, China. Sustainability 2018, 10, 3761. [Google Scholar] [CrossRef]
- Chen, X.S.; Jiang, S.L.; Xu, L.S.; Xu, H.G.; Guan, N.N. Resilience assessment and obstacle factor analysis of urban areas facing waterlogging disasters: A case study of Shanghai, China. Environ. Sci. Pollut. Res. 2023, 30, 65455–65469. [Google Scholar] [CrossRef] [PubMed]
- Xie, S.; Liu, W.; Yuan, Z.; Zhang, H.Y.; Lin, H.; Wang, Y.Q. Integrated Risk Assessment of Waterlogging in Guangzhou Based on Runoff Modeling, AHP, GIS and Scenario Analysis. Water 2022, 14, 2899. [Google Scholar] [CrossRef]
- Qi, W.C.; Ma, C.; Xu, H.S.; Zhao, K. Urban flood response analysis for designed rainstorms with different characteristics based on a tracer-aided modelling simulation. J. Clean. Prod. 2022, 335, 131797. [Google Scholar] [CrossRef]
- Zhang, Q.F.; Wu, Z.F.; Zhang, H.; Dalla Fontana, G.; Tarolli, P. Identifying dominant factors of waterlogging events in metropolitan coastal cities: The case study of Guangzhou, China. Environ. Manag. 2020, 271, 110951. [Google Scholar] [CrossRef]
- Merz, B.; Blöschl, G.; Vorogushyn, S.; Dottori, F.; Aerts, J.C.J.H.; Bates, P.; Bertola, M.; Kemter, M.; Kreibich, H.; Lall, U.; et al. Causes, impacts and patterns of disastrous river floods. Nat. Rev. Earth. Environ. 2021, 2, 592–609. [Google Scholar] [CrossRef]
- Bryndal, T.; Franczak, P.; Kroczak, R.; Cabaj, W.; Kołodziej, A. The impact of extreme rainfall and flash floods on the flood risk management process and geomorphological changes in small Carpathian catchments: A case study of the Kasiniczanka river (Outer Carpathians, Poland). Nat. Hazards 2017, 88, 95–120. [Google Scholar] [CrossRef]
- Zhao, X.F.; Li, H.M.; Cai, Q.; Pan, Y.; Qi, Y. Managing Extreme Rainfall and Flooding Events: A Case Study of the 20 July 2021 Zhengzhou Flood in China. Climate 2023, 11, 228. [Google Scholar] [CrossRef]
- Alemaw, B.F.; Tafesse, N.T. Urban Stormwater and Sewerage Modelling: An Approach for Peak Runoff and Volume Assessment. J. Water Resour. Prot. 2021, 13, 855–880. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.H.; Su, H.D.; Wang, D.; Gu, Q.H. Modelling and Application of Urban Drainage Based on Mike Urban Model. IOP Conf. Ser. Earth Environ. Sci. 2020, 474, 062003. [Google Scholar] [CrossRef]
- Komori, D.; Nakaguchi, K.; Inomata, R.; Oyatsu, Y.; Tachikawa, R.; Kazama, S. Topographical Characteristics of Frequent Urban Pluvial Flooding Areas in Osaka and Nagoya Cities, Japan. Water 2022, 14, 2795. [Google Scholar] [CrossRef]
- Zhang, Q.F.; Wu, Z.F.; Tarolli, P. Investigating the Role of Green Infrastructure on Urban WaterLogging: Evidence from Metropolitan Coastal Cities. Remote Sens. 2021, 13, 2341. [Google Scholar] [CrossRef]
- Wu, J.S.; Sha, W.; Zhang, P.H.; Wang, Z.Y. The spatial non-stationary effect of urban landscape pattern on urban waterlogging: A case study of Shenzhen City. Sci. Rep. 2020, 10, 7369. [Google Scholar] [CrossRef]
- Zhao, Y.J.; Xia, J.; Xu, Z.X.; Zou, L.; Qiao, Y.F.; Li, P. Impact of Urban Expansion on Rain Island Effect in Jinan City, North China. Remote Sens. 2021, 13, 2989. [Google Scholar] [CrossRef]
- Hu, M.C.; Zhang, X.Q.; Siu, Y.L.; Li, Y.; Tanaka, K.; Yang, H.; Xu, Y.P. Flood Mitigation by Permeable Pavements in Chinese Sponge City Construction. Water 2018, 10, 172. [Google Scholar] [CrossRef]
- Ahmad, T.; Pandey, A.C.; Kumar, A. Evaluating urban growth and its implication on flood hazard and vulnerability in Srinagar city, Kashmir Valley, using geoinformatics. Arab. J. Geosci. 2019, 12, 308. [Google Scholar] [CrossRef]
- Wang, L.Y.; Li, Y.; Hou, H.; Chen, Y.; Fan, J.J.; Wang, P.; Hu, T.G. Analyzing spatial variance of urban waterlogging disaster at multiple scales based on a hydrological and hydrodynamic model. Nat. Hazards 2022, 114, 1915–1938. [Google Scholar] [CrossRef]
- Zhang, K.; Li, J.K.; Ning, L.Z.; Xie, W.F.; Li, Y.F.; Ullah, Z.; Peng, K. Three-Dimensional Numerical Simulation Research on Discharge Characteristics of Storm-Drain Inlet in Low-Lying Areas. Water Resour. Manag. 2023, 37, 5273–5287. [Google Scholar] [CrossRef]
- Yu, S.; Zhang, S.H.; Di, S.C.; Zhou, X.; Ge, J.; Xiao, B.Q. Effect of combined flat and vertical renovation of urban road gullies on surface water flooding prevention based on physical model experiments. J. Hydraul. Eng. 2022, 53, 854–861. [Google Scholar]
- Harada, S. Application of Porous Concrete Infiltration Techniques to Street Stormwater Inlets That Simultaneously Mitigate against Non-Point Heavy Metal Pollution and Stormwater Runoff Reduction in Urban Areas: Catchment-Scale Evaluation of the Potential of Discrete and Small-Scale Techniques. Water 2023, 15, 1998. [Google Scholar] [CrossRef]
- Kim, J.S.; Kwak, C.J.; Jo, J.B. Enhanced method for estimation of flow intercepted by drainage grate inlets on roads. J. Environ. Manag. 2021, 279, 111546. [Google Scholar] [CrossRef] [PubMed]
- Noh, S.J.; Lee, S.; An, H.; Kawaike, K.; Nakagawa, H. Ensemble urban flood simulation in comparison with laboratory-scale experiments: Impact of interaction models for manhole, sewer pipe, and surface flow. Adv. Water Resour. 2016, 97, 25–37. [Google Scholar] [CrossRef]
- Martins, R.; Leandro, J.; Carvalho, R.F.D. Characterization of the hydraulic performance of a gully under drainage conditions. Water Sci. Technol. 2014, 69, 2423–2430. [Google Scholar] [CrossRef] [PubMed]
- Martins, R.; Rubinato, M.; Kesserwani, G.; Leandro, J.; Djordjević, S.; Shucksmith, J.D. On the characteristics of velocities fields on the vicinity of manhole inlet grates during flood events. Water Resour. Res. 2018, 54, 6408–6422. [Google Scholar] [CrossRef]
- Rubinato, M.; Lee, S.; Martins, R.; Shucksmith, J.D. Surface to sewer flow exchange through circular inlets during urban flood conditions. J. Hydroinform. 2018, 20, 564–576. [Google Scholar] [CrossRef]
- Santoso, B.P.; Yanto, M.; Apriyono, A. Inverse distance weighting interpolated soil properties and their related landslide occurrences. MATEC Web Conf. 2018, 195, 03013. [Google Scholar] [CrossRef]
- Tügel, F.; Hassan, A.; Hou, J.; Hinkelmann, R. Applicability of Literature Values for Green–Ampt Parameters to Account for Infiltration in Hydrodynamic Rainfall–Runoff Simulations in Ungauged Basins. Environ. Model. Assess. 2022, 27, 205–231. [Google Scholar] [CrossRef]
- Yang, D.; Hou, J.M.; Li, B.R.; Li, D.L.; Li, Y.Q.; Fu, D.Y.; Ji, G.Q. Generalized simulation of drainage process in urban networks without data. J. Water Res. Water Eng. 2020, 31, 139–144. [Google Scholar]
- Xia, J.Q.; Cheng, Q.; Dong, B.L.; Zhang, X.L. Experimental study on the effect of clogging on the inlet discharge capacity. Adv. Water Sci. 2020, 31, 843–851. [Google Scholar]
- Chen, J.; Li, Y.; Zhang, C. The Effect of Design Rainfall Patterns on Urban Flooding Based on the Chicago Method. Int. J. Environ. Res. Public Health 2023, 20, 4245. [Google Scholar] [CrossRef] [PubMed]



| Serial Number | Example of the File Name | Description |
|---|---|---|
| 1 | ctrl.itf.bmh.201017-1.csv | Control parameter file |
| 2 | i01_mask3_geo_bmh190927.asc | Program-controlled grid |
| 3 | i02_surfWatBody_bmh201014.asc | Surface drainage grid |
| 4 | i03_demRevRv_bmh190926.asc | DEM elevation data grid |
| 5 | i04_ldcvFineGeo_bmh190926.asc | Land cover grid |
| 6 | i05_soilPoly_bmh201015.asc | Soil distribution grid |
| 7 | i06_soilPoly2type_bmh201015.csv | Soil polygon ID and soil type ID |
| 8 | i07_bndryWatLvl_2days_bmh201015.csv | Time series of boundary water levels |
| 9 | i08_prec_1gauge_1day_200612.csv | Rainfall time series |
| 10 | i09_strmGaugePara_bmh200903_2.csv | Number of river gauging sections |
| 11 | i10_gaugeUpDnZonesClip_bmh190927.asc | Cross-sectional grid for river gauging |
| Serial Number | Rainfall Duration (h) | Time Interval (min) | Rainfall Scenarios | Maximum Rainfall Intensity (mm/h) | Total Rainfall (mm) |
|---|---|---|---|---|---|
| 1 | 6 | 10 | P = 1a | 89.68 | 69.28 |
| 2 | 6 | 10 | P = 3a | 119.63 | 92.66 |
| 3 | 6 | 10 | P = 5a | 133.55 | 103.18 |
| 4 | 6 | 10 | P = 10a | 152.45 | 117.78 |
| 5 | 6 | 10 | P = 30a | 182.40 | 140.91 |
| 6 | 6 | 10 | P = 50a | 196.33 | 151.67 |
| Serial Number | Rainfall Scenario | Area of Accumulated Water (m2) | Depth of Accumulated Water (cm) | ||||
|---|---|---|---|---|---|---|---|
| No Blockage | Block up | Growth Ratio (%) | No Blockage | Block up | Growth Ratio (%) | ||
| 1 | P = 1a | 3580 | 5132 | 43.35 | 19 | 25 | 31.58 |
| 2 | P = 3a | 5880 | 7016 | 19.32 | 25 | 30 | 20.00 |
| 3 | P = 5a | 7124 | 7968 | 11.85 | 27 | 33 | 22.22 |
| 4 | P = 10a | 8104 | 9028 | 11.40 | 31 | 37 | 19.35 |
| 5 | P = 30a | 10,304 | 10,720 | 4.04 | 38 | 42 | 10.53 |
| 6 | P = 50a | 11,032 | 11,400 | 3.34 | 41 | 45 | 9.76 |
| Rainfall Scenarios | Waterlogging Level (cm) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Area at Each Accumulated Water Level under the Scenario of Nonblocked Stormwater Inlet (m2) | Area at Each Accumulated Water Level under the Scenario of Stormwater Inlet Blockage (m2) | |||||||||
| <10 | 10~20 | 20~30 | 30~50 | >50 | <10 | 10~20 | 20~30 | 30~50 | >50 | |
| P = 1a | 3292 | 184 | 0 | 0 | 0 | 2388 | 2732 | 12 | 0 | 0 |
| P = 3a | 2608 | 3256 | 16 | 0 | 0 | 2008 | 4688 | 320 | 0 | 0 |
| P = 5a | 2668 | 4436 | 20 | 0 | 0 | 1848 | 4564 | 1548 | 8 | 0 |
| P = 10a | 2416 | 4808 | 872 | 8 | 0 | 1820 | 2920 | 4268 | 20 | 0 |
| P = 30a | 2832 | 2780 | 4660 | 32 | 0 | 2648 | 1876 | 4792 | 1404 | 0 |
| P = 50a | 3124 | 2300 | 4720 | 888 | 0 | 2888 | 1868 | 3572 | 3072 | 0 |
| Waterlogging Level (cm) | <10 | 10~20 | 20~30 | 30~50 | >50 | |
|---|---|---|---|---|---|---|
| Rainfall Scenarios | ||||||
| P = 1a | −27.46 | 1384.78 | - | 0 | 0 | |
| P = 3a | −23.01 | 43.98 | 1900 | 0 | 0 | |
| P = 5a | −30.73 | 2.89 | 7640 | - | 0 | |
| P = 10a | −24.67 | −39.27 | 389.45 | 150 | 0 | |
| P = 30a | −6.5 | −32.52 | 2.83 | 4287.5 | 0 | |
| P = 50a | −7.55 | −18.78 | −24.32 | 245.95 | 0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, W.; Zhai, M.; Lei, X.; Huang, H.; Long, Y.; Li, S. Two-Dimensional Hydrodynamic Simulation of the Effect of Stormwater Inlet Blockage on Urban Waterlogging. Water 2024, 16, 2029. https://doi.org/10.3390/w16142029
Guo W, Zhai M, Lei X, Huang H, Long Y, Li S. Two-Dimensional Hydrodynamic Simulation of the Effect of Stormwater Inlet Blockage on Urban Waterlogging. Water. 2024; 16(14):2029. https://doi.org/10.3390/w16142029
Chicago/Turabian StyleGuo, Weiwei, Mingshuo Zhai, Xiaohui Lei, Haocheng Huang, Yan Long, and Shusen Li. 2024. "Two-Dimensional Hydrodynamic Simulation of the Effect of Stormwater Inlet Blockage on Urban Waterlogging" Water 16, no. 14: 2029. https://doi.org/10.3390/w16142029
APA StyleGuo, W., Zhai, M., Lei, X., Huang, H., Long, Y., & Li, S. (2024). Two-Dimensional Hydrodynamic Simulation of the Effect of Stormwater Inlet Blockage on Urban Waterlogging. Water, 16(14), 2029. https://doi.org/10.3390/w16142029







