1. Introduction and objective
The Water Framework Directive (WFD) requires comprehensive protection of both surface waters and groundwater [
1]. The environmental objectives for the chemical status of groundwater under the EU-WFD are further specified in the Groundwater Directive [
2]. To achieve the environmental protection objectives for groundwater and surface waters whose good status cannot be guaranteed, management plans and programmes of measures were established in 2012 and have since been updated every six years. At present, we are at the beginning of the third EU-WFD cycle, which will last until 2027.
According to an assessment of the chemical status of groundwater bodies carried out in 2021, 67.3% of all groundwater bodies are currently in good chemical status, while 32.7% are at risk, mainly due to high nitrate concentrations [
3]. The achievement of a good status for about 90% of surface waters is considered an unclear, or rather, unlikely goal, as a consequence of the high nutrient levels and insufficient hydromorphology [
3].
Inputs from diffuse sources and most nitrate losses from agricultural land have remained the main reasons for exceeding the groundwater quality standard of nitrate (50 mg NO
3/L) and for not achieving the “good qualitative status” of groundwater [
3]. High phosphorus concentrations exceeding orientation values occur, e.g., in river basins with high population density. Against this background, the drafting and implementation of a programme of measures according to the EU-WFD in Germany must include actions against nutrient pollution [
3]. Orientation values in the context of the WFD are target values to achieve a higher “natural” status.
In this context, it should be remembered that the physicochemical properties of N and P compounds are very different. While nitrate and ammonia are easily soluble and chemically almost inert [
4,
5], phosphates are poorly soluble and are easily adsorbed into soil particles [
6,
7]. For this reason, the input pathways for N and P are quite different. The transport of diffuse N compounds (especially nitrate) occurs in a dissolved form and is coupled to the runoff components of natural interflow, drainage runoff, or groundwater runoff as input pathways [
8,
9]. The transport of diffuse P compounds, on the other hand, is coupled with soil particles, and so the input pathway erosion is very significant [
10,
11].
Against this background, the development and implementation of programmes against nutrient pollution in the framework of the EU-WFD implementation process includes both N-specific and P-specific measures. Supporting the development and implementation of action programmes at a national level requires the determination of the different N and P sources, their input pathways, and the resulting N and P inputs to groundwater and surface waters in a consistent and comparable way. For this purpose, nutrient flux models are applied not only in many EU Member States [
12,
13,
14,
15], but also beyond [
16,
17,
18].
In the case of smaller countries like Denmark or the Netherlands, the site conditions can be regarded as relatively homogeneous. Also, the derivation rules of input data generation and their degree of detail do not hinder a consistent and uniform model application. In contrast, for large countries like Germany (approx. 357,000 km
2), the establishment of an integrated nutrient flux model entails a particular challenge as the complex and heterogeneous climatic, pedological, and hydrogeological site conditions must be simultaneously represented by a hydrological sub-model [
19]. The same applies to both (1) an agro-economic sub-model that accounts for the N and P pressures on groundwater and surface water quality from diffuse sources, and (2) a sub-model that quantifies the N and P emissions arising from urban water management. For these reasons, in some large countries, integrated nutrient flux models have only been established within regions or provinces [
20,
21,
22].
In Germany, the establishment of an integrated nutrient flux model is further complicated by the federal political structure, as the 16 Federal German states are not only independently responsible for the implementation of EU directives [
23], but also for the management of their natural resources, such as soil and groundwater. The latter led, among other aspects, to the state-specific creation of non-harmonized databases, e.g., concerning soil parameters. Consequently, in the past, not only the heterogeneous site conditions, but also the heterogeneous databases considerably aggravated the development of an integrated German nutrient flux model, jointly supported and accepted by all federal states.
This explains why in Germany, despite the nationwide prevailing nutrient problems [
3,
24,
25], so far, only unharmonized, state-specific nutrient models have been developed to support the implementation of the EU-WFD. Because of these “isolated solutions”, the EU accused Germany in the year 2013 because of insufficient action concerning the abatement of nitrate pollution. Following a 2018 ruling by the European Court of Justice, Germany was finally threatened with fines in the billions [
26]. Against the background of this strong pressure from the EU, the LAWA (German Working Group on water issues of the federal states and the Federal Government represented by the Federal Environment Ministry) initiated the development of a harmonized integrated German nutrient model based on the AGRUM model network in 2018, i.e., five years after the first accusation.
The AGRUM model network was developed for quantifying macro-scale nitrogen and phosphorus inputs to groundwater and surface waters [
19]. It consists of three independently developed and applicable sub-models including the regionalized agricultural and environmental information system for Germany (RAUMIS) of the Thünen Institute in Braunschweig [
27], the hydrological/hydrogeological model system mGROWA-DENUZ-WEKU-MEPhos of Research Centre Jülich [
28,
29], and the nutrient input model MONERIS of the Institute for freshwater ecology and inland fisheries in Berlin [
30,
31].
This contribution focuses on the use of the AGRUM model network for quantifying nutrient inputs into groundwater and surface waters throughout Germany. This paper comprises the following:
Brief introductions to the models RAUMIS, mGROWA, DENUZ, WeKu, MEPhos, and MONERIS, with a focus on the Germany-wide consistent and uniform determination of nutrient inputs according to pathways.
A comparison of the importance of selected input pathways for the status quo N and P input into groundwater and surface waters in Germany.
A statistical evaluation of the N and P model results with respect to observed N and P loads at gauging stations and thus the regional representativity of the modelled nutrient inputs.
A concluding discussion of the modelled nutrient inputs with regard to the delineation of priority areas for the implementation of reduction measures.
2. AGRUM Model Approach for Determining Status Quo Nutrient Fluxes and Demand for Input Data
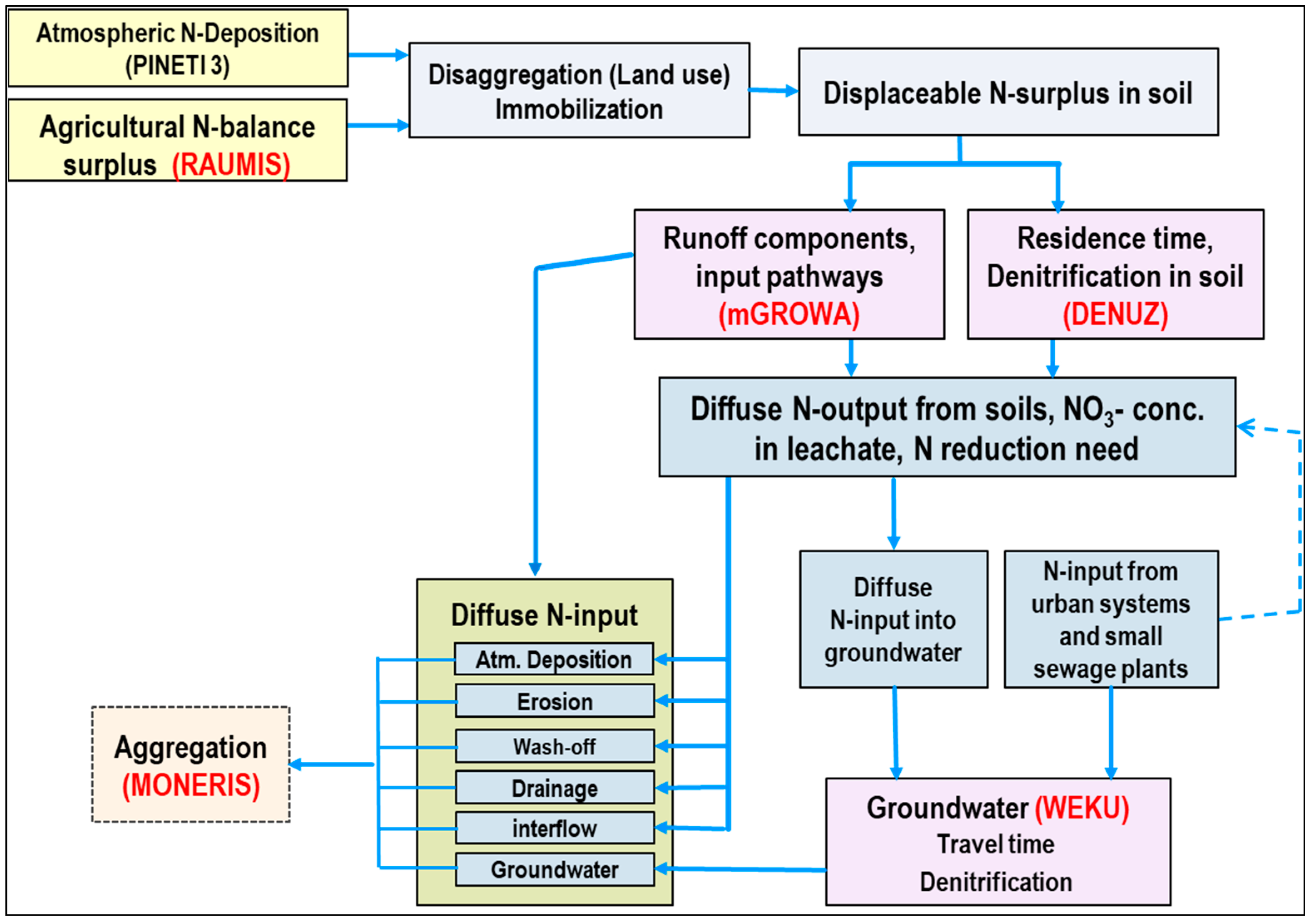
The general procedure of the AGRUM model approach for determining the status quo of nutrient emissions and inputs to groundwater, surface waters, and oceans is illustrated in
Figure 1 for the diffuse nitrogen fluxes and in
Figure 2 for the diffuse phosphorus fluxes. The corresponding procedure for determining non-agricultural nutrient inputs is shown in
Figure 3. More detailed descriptions of the individual models would have been beyond the scope of this publication and can be found in the relevant literature cited in the next sections.
2.1. Modelling Nitrogen Balance Surplus on Agricultural Land
Nitrogen soil surface budgets on utilized agricultural area (UAA) are modelled with the spatial agro-economic optimization model RAUMIS. The model has been designed as a regional agricultural sector model for Germany, depicting the entire agricultural production (land use, livestock, and biogas production) at the NUTS-3 level. In addition to this optimization model, RAUMIS consists of several modules with higher spatial resolution to depict agri-environmental indicators such as nutrient budgets or irrigation requirement at the municipality level. These modules can be used stand-alone or coupled with the core optimization model.
In this contribution, the nutrient module from RAUMIS was used to calculate mean nitrogen surpluses on UAA for the period 2014–2016 at the municipality level [
32,
33].
2.2. Modelling of Diffuse N-Fluxes
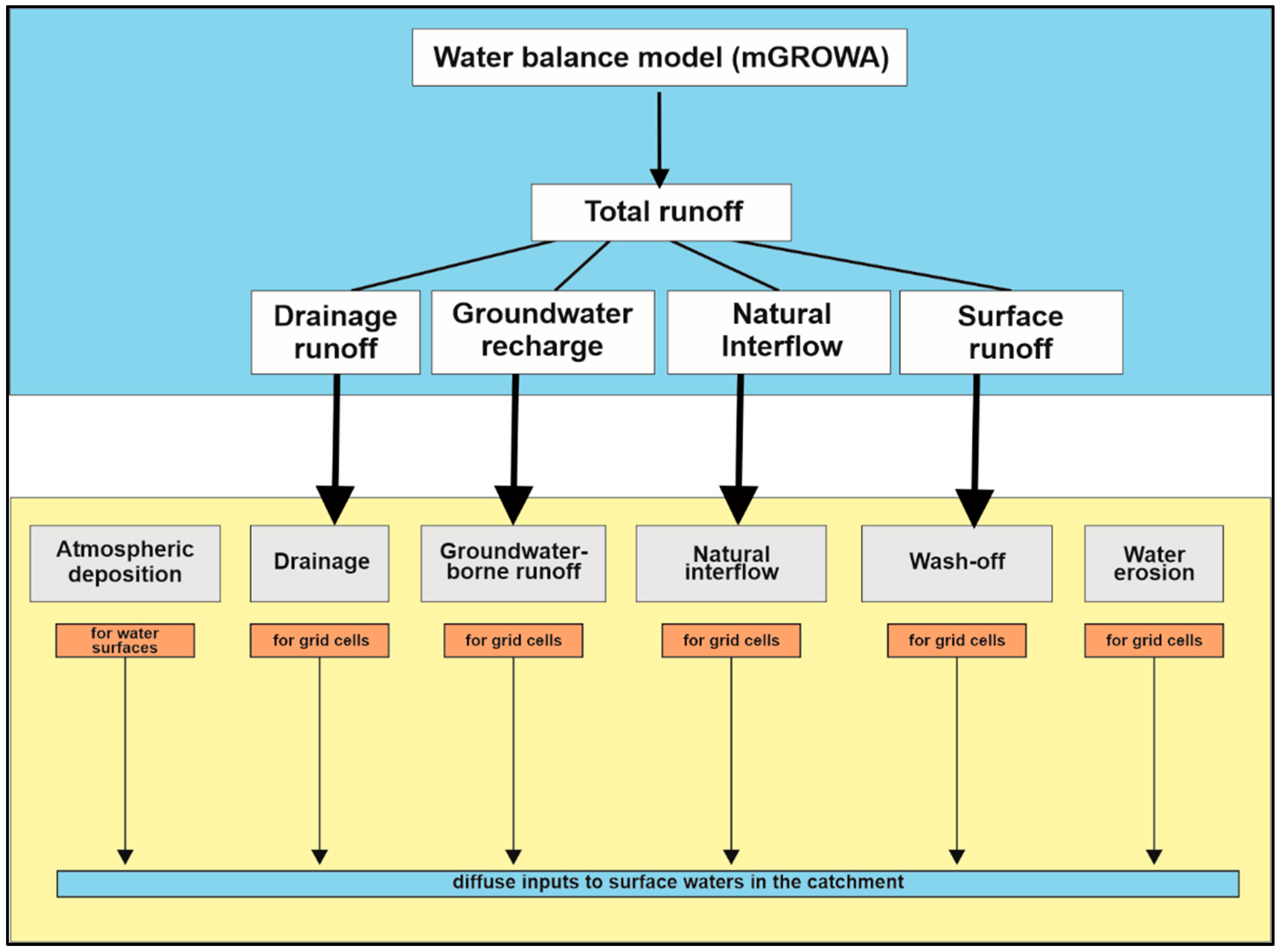
In order to quantify the multi-year mean diffuse nitrogen inputs to groundwater and surface waters from area-differentiated diffuse sources, the runoff components/input pathways simulated with the mGROWA model and the N soil surface budget surpluses simulated with the RAUMIS model were linked with the DENUZ-WEKU model [
34,
35]. Modelling is carried out with a spatial resolution of 100 m × 100 m, so that all model results are presented for approx. 35.7 million grid cells.
N sources for simulating diffuse N inputs to groundwater and surface waters included the N balance surpluses determined by the RAUMIS model for agriculturally used land [
34] and the Germany-wide available data set for atmospheric N deposition from the PINETI-3 model [
36] (see
Figure 1). In addition, for urban areas, the N inputs to groundwater from leaking sewer systems assessed by the MONERIS model [
31] was considered.
At first, the N loads from the individual N sources are disaggregated to the 100 m grid cells according to land use, whereas atmospheric N deposition rates are applied based on area covered, i.e., irrespective of the land use; N balance surpluses are exclusively applied to the agriculturally used land and N inputs to groundwater from leaking sewer systems to the urban areas only.
Subsequently, N immobilization in soil and in plants is considered, but exclusively for the land-use classes grassland and forests [
37,
38,
39]. Then, the extent of microbiological denitrification in soil is accounted for in the DENUZ model by the Michaelis–Menten kinetics depending on the residence time of the leachate in the soil, the amount of N input into the soil, and the nitrate degradation capacity of the soil [
34,
35]. Additionally, the N inputs from leaking sewage systems [
40] are applied to the groundwater covering layers below the root zone of urban areas from where they are dislocated, so that neither N immobilization nor denitrification in soil is considered.
For the grid-cell-specific modelling of diffuse N inputs to groundwater and surface waters, the N emissions from the soil are linked to the runoff components and input pathways according to ratio of direct runoff/groundwater recharge simulated by the mGROWA model [
41]. N outputs from the soil that do not reach surface waters via drainage or natural interflow enter the aquifer and are transported through the aquifer to a surface water body. Along this pathway, denitrification processes are considered in the WeKu model as a function of groundwater travel times [
42], the nitrate inputs to the aquifer, and the denitrification conditions in the aquifer [
43].
2.3. Modelling of Diffuse P-Fluxes
For the area-differentiated modelling of multi-year mean diffuse P inputs to surface waters, the runoff components simulated with the mGROWA model were linked to the input pathways in the MEPhos model. MEPhos is based on a pathway- and area-differentiated emission approach, which uses so-called phosphotopes [
44] (see
Figure 2), i.e., types of homogeneous sub-areas with defined properties, representing georeferenced source areas of P inputs [
45].
Multiplying the P contents of the phosphotopes with the mean long-term mGROWA discharge rates per grid provides the mean annual P inputs in kg/(hectare∙yr) per 100 m × 100 m grid cell as defined by the runoff components determined by the mGROWA model. As mostly larger, contiguous areas, the phosphotopes have the character of raster clusters.
Phosphotopes representing drainage systems are of particular importance for the determination of diffuse P emissions [
45]. However, information on the location of artificially drained agricultural land in Germany is neither available for large areas nor in a positionally precise nor officially documented form. For this reason, potentially artificially drained areas were determined using a method that incorporates area-wide data on land use and soil conditions as well as relief characteristics [
46].
The modelling of P inputs via water erosion is performed based on the USLE [
47] and its adaptation to German site conditions [
48] for the land uses of cropland and permanent crops at a resolution of 25 m × 25 m. The spatially higher resolution for modelling P inputs via water erosion is necessary because the slope, which is the most sensitive factor to determine soil losses via water erosion, is not represented adequately in the 100 m × 100 m grids. To further limit the source areas of erosive P inputs, the areas showing cropland and permanent crops with a direct connection to a water body are identified [
44,
49]. Urban areas, forests, and areas displaying permanent grassland are excluded from modelling water erosion because soils are permanently covered, so that the dislocation of soil particles is rather improbable.
The modelling of P input via natural interflow and groundwater follows a different approach. Based on observed P concentrations in groundwater and runoff values (interflow, groundwater discharge) P input is assessed based on larger sub-units according to aquifer typologies [
50].
All P inputs into receiving waters are simulated in the MEPhos model as total P. However, in order to make statements on the eutrophication relevance of phosphorus inputs in inland waters, total P is of limited relevance only, since total P is partially adsorbed to soil particles and does not have a direct eutrophic effect in this form. For this reason, the orthophosphate-phosphorus fraction directly affecting eutrophication was estimated from the amount of total phosphorus following [
51].
2.4. Modelling of Point Source N and P Emissions
The MONERIS model enables the process-oriented modelling of diffuse and point source inputs via various input pathways, retention in surface waters, and resulting loads on an annual and monthly basis. In this study, however, the model was only used for modelling inputs from urban sources and retention in surface waters. A detailed description of the model and application examples can be found in [
52,
53].
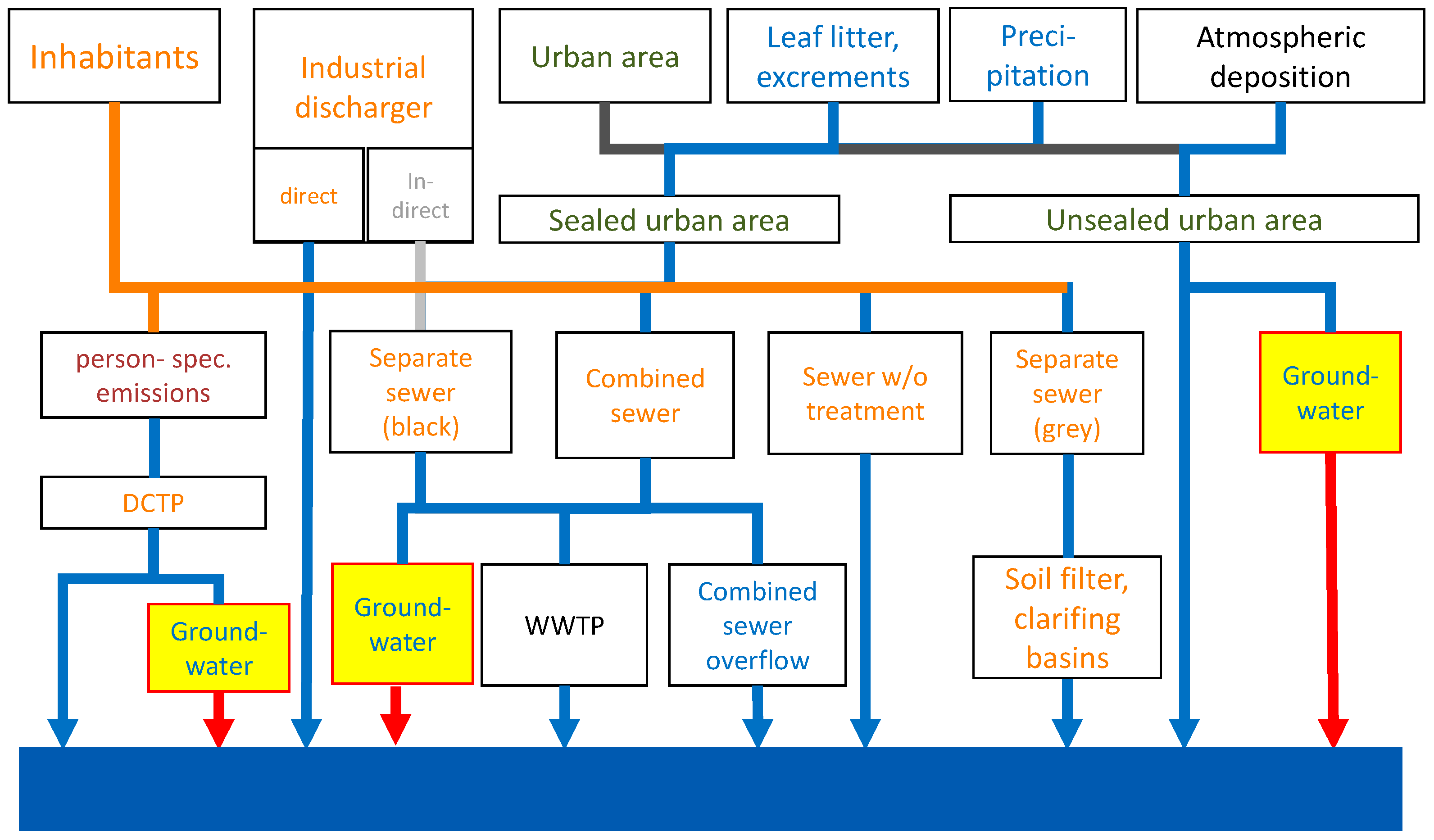
The point source inputs (municipal wastewater treatment plants and industrial direct dischargers) were provided by the Federal Environment Agency (UBA) with coordinates of the discharge points and as annual totals. After a consistency check, these could be used directly in the model. The inputs from urban systems comprise a number of different sub-pathways that were derived based on different influencing variables (
Figure 3).
First of all, official data on wastewater collection and treatment as well as on the length and age of the separate and combined sewer systems at the municipal level, i.e., the highest-resolution data source for Germany, were processed and checked for consistency. These figures were used to derive a harmonized data set with shares of the connected population and sealed urban areas to the separate and combined sewer system and to municipal (>50 inhabitants) and decentralized (≤50 inhabitants) wastewater treatment plants.
For sealed urban areas and commercial areas, the runoff component was estimated as a function of the runoff coefficient and the annual precipitation. In addition, the per capita water consumption was used for the calculations for the combined sewer system and decentralized wastewater treatment plants.
For sealed urban areas, nutrient inputs were estimated on the basis of atmospheric deposition and the additional accumulation of leaves and animal excrement. Household-related discharges into the combined sewer system and small sewage treatment plants were taken into account as person-specific nutrient discharges.
In principle, the input is calculated using the sub-pathway-specific concentrations and discharge components. In the combined sewer system, the concentration during overflow events is determined as the ratio of the total nutrients from connected sealed surfaces and households and the volume of water contained in the sewer system. For all other partial discharge paths, the calculated discharges and the nutrient quantities discharged were considered. In addition, sub-pathways and wastewater-type-specific treatment capacities in sand filters or clarifying basins, for example, were taken into account. For decentralized wastewater treatment plants, a distinction is made between the type of discharge (direct discharge into surface waters or discharge via a soil–groundwater passage) in addition to the plant’s own treatment capacity. Soil–groundwater passage only occurs if the subsoil has suitable permeability and can lead to considerable additional retention before the nutrients reach a surface water body.
In addition to these “planned” inputs from urban systems, nutrient inputs via seepage from leaking sewer pipes were identified as a further input pathway. Based on observed data from various studies, this empirical approach assumes an average age-dependent rate of damage. The amount of exfiltrating wastewater depends on the type of sewer (separate or combined sewer system) and the frequency of stormwater events. The duration of exfiltration depends on the rebuilding of a colmation layer in the pipe, which closes the leakage again. Further details of this approach can be found in [
40,
52]. The retention of nutrients during the soil–groundwater passage is carried out using the models and approaches described above for modelling groundwater inputs.
For the sum of all diffuse, point source and urban nutrient inputs, the subsequent transport and retention in surface waters was modelled as a basis for the subsequent model validation. The retention calculation and routing through the water network was based on 2819 sub-catchment areas. For this purpose, the water surfaces of receiving watercourses and main courses (including lakes) through which water flows were determined for each sub-catchment area. Taking into account runoff, water surface area, and water temperature (nitrogen only), retention was described according to the approaches of [
31,
53]. While nitrogen retention (mainly denitrification) can in principle occur in all surface waters, phosphorus retention only occurs if the phosphorus adsorbed on particles sediments at corresponding particle-size-dependent flow velocities. Under average conditions, it is assumed that the flow velocity in receiving waters is lower than in main courses (in the absence of lakes), so the retention in main courses was considered to be negligible for loads originating from receiving waters.
3. Input Data
Essentially, the model input data can be divided into georeferenced data, statistical records (agricultural production), or monitoring data (measured discharges or concentrations). The complete databases used for modelling with the RAUMIS, mGROWA, DENUZ, WEKU, MEPhos, and MONERIS models are summarized in [
33] and in the supplementary materials of this publication. At this point, only a few basic aspects regarding the data basis are mentioned.
For the RAUMIS model, land use and livestock data from the Integrated Administration and Control System (IACS) were used for the first time for all the federal states. The IACS administers agricultural subsidies from the Common Agricultural Policy and contains plot-specific data on agricultural land use for all funded farms in Germany. In addition, data from the Animal Origin Assurance and Information System, the animal disease funds, the manure reporting databases, and the sewage sludge registers of the Länder were used. The databases are merged, checked for plausibility, supplemented with information from the official state statistics, and aggregated to the municipality level, so that the agricultural production in Germany is represented completely and regionally differentiated.
The data required on climate, topography, land cover, soil parameters, hydrogeological parameters, and groundwater quality for the mGROWA-DENUZ/WEKU-MEPhos models were provided Germany-wide. In order to keep biases in the input data between the federal states as low as possible, one of the premises under which the AGRUM-DE project started was the use of databases that are consistently available throughout Germany. Against this background, digital maps at a scale of 1:200,000 (soil, geology, etc.) were used on the one hand, and georeferenced point data (e.g., water quality data) on the other. The climate data originated from the climate data centre and was made available for the period 1981–2010.
In addition, area-wide data on municipal wastewater treatment plants, industrial direct dischargers, type of sewer system, and connected inhabitants were provided for the modelling with MONERIS. All calculations of inputs from urban systems were carried out at the municipal level. In addition, municipal wastewater treatment plants and industrial direct dischargers were taken into account via the location of the discharge point.
Both the use of more detailed databases provided by the federal states and the consideration of validated model results from projects in the federal states were excluded from the outset. Consequently, there were discrepancies between the modelling at the national level and the modelling at the state level, which were accepted on purpose.
For the exchange of data, parameters and results between the different models, GIS-based interfaces were developed, guaranteeing that the different regional differentiations of the models (RAUMIS: municipalities; mGROWA-DENUZ-WEKU-MEPhos: 100 m × 100 m grid; MONERIS: water bodies) could be adjusted without loss of information.
4. Model Results on N and P Inputs into Groundwater and Surface Waters
For the modelling of N and P inputs to groundwater and surface waters, the N and P emissions are linked to the runoff components and input pathways simulated by the mGROWA model Germany-wide in a spatial resolution of 100 m × 100 m. The input pathways include both the direct runoff components (above all drainage runoff, natural interflow, and direct runoff from urban areas) and baseflow, which can be considered equivalent to long-term groundwater recharge within catchments [
41]. In this way, the N and P emissions calculated with separate models are coupled to the same grid-wise determined runoff volumes for the individual runoff components. However, the same runoff volume for a specific runoff component in a specific grid cell has a different impact on the N and P export from this grid. In this chapter, input pathway-related differences between N and P inputs to surface waters are discussed and interpreted in more detail using several examples.
The selection comprises results on diffuse N and P sources in
Section 4.1, diffuse N and P inputs into surface waters via the input pathway water erosion in
Section 4.2, diffuse P inputs into surface waters via natural interflow and drainage systems in
Section 4.3, and the N and P inputs into surface waters from selected point sources and urban systems in
Section 4.4. Conclusively,
Section 4.5 gives an overview about the total N and P inputs and the outcome of their validation against loads estimated from measured water quality and discharge data.
4.1. Comparison of Data on N Sources and P Sources in Soil
The most important N sources for simulating diffuse N inputs to groundwater and surface waters are the agricultural N-soil-surface surpluses modelled by RAUMIS and the atmospheric N deposition from the PINETI-3 model [
36].
Figure 4 (left) shows the N-soil-surface surplus for UAA in Germany calculated by the RAUMIS model for the period 2014–2016 on a municipality level. UAA stands for utilized agricultural area. The total Germany-wide N balance surplus (960,000 tonnes N/yr) shows considerable regional differences between 20 and 100 kg N/(hectare UAA × yr). The highest N surpluses can be observed in the Northern German lowland regions with high livestock numbers and large (often plant-based) biogas production capacities. Areas with lower N surpluses are found in regions where extensive agriculture predominates, i.e., in Brandenburg. The Germany-wide average of the N balance surplus is around 58 kg N/(hectare UAA × yr).
Atmospheric N deposition per grid (100 m × 100 m) is in general at a lower level and sums up to 520,000 t N/yr. It is, however, a nationwide N source that is also effective on non-agricultural land. As
Figure 4 (right) shows, an atmospheric N deposition of more than 20 kg N (hectare×yr) occurs especially in the northwestern German regions with high livestock density and in the ridge regions of the low mountain ranges with larger forested areas and high precipitation. With decreasing livestock density and decreasing precipitation, atmospheric N deposition decreases towards the east to values between 10 and 15 kg N (hectare×yr).
In contrast to most nitrogen compounds added to the soil as fertilizer, phosphorus compounds have a very low soil mobility on most sites. As a result, a P pool has accumulated in the soil since the 1960s due to P fertilization, from which nowadays plant-available P is released into the soil solution [
54]. Since plants can cover most of their current P demand in Germany from the remobilized P in soil [
55], only very small amounts of P fertilizers are currently added to the soil or even no P fertilization at all [
56]. The main source of P contributing to surface water pollution is therefore the P content in the topsoil. However, an area-covering publicly available database about the P content in the topsoil in Germany does not exist. Therefore, the P contents in the topsoil shown in
Figure 5 were adopted or derived from heterogeneous federal-state-specific data in terms of actuality, resolution, and genesis (
Figure 5).
As
Figure 5 shows, the results vary between approx. 200 mg/kg and approx. 2500 mg/kg. The nationwide mean value is 660 mg/kg. The large differences in total P content along the federal state borders are mainly a consequence of the non-harmonized determination methods (e.g., P
CAL: calcium acetate lactate extract and P
DL: double lactate extract) and the conversion methods used in the federal states to derive the total P content. The total P contents in the topsoil shown in
Figure 5 are then used as initial values for modelling the P inputs via the water erosion input pathway.
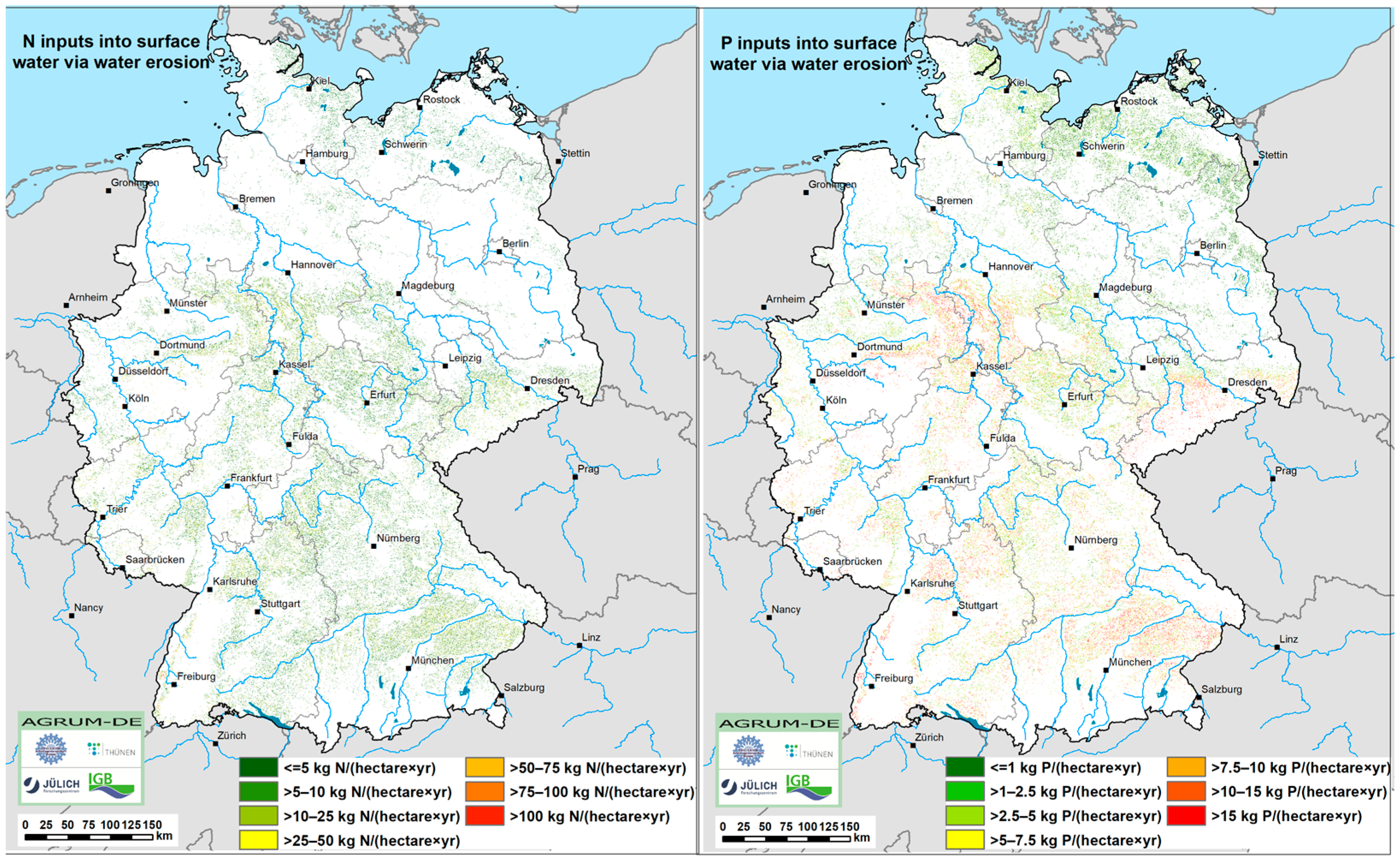
4.2. Diffuse P and N Inputs into Surface Waters via Water Erosion
The modelling of the N and P inputs via water erosion is shown in
Figure 6. By multiplication of the N and P content in the topsoil with the discharge levels according to mGROWA, the mean annual erosive N and P inputs were calculated for individual pixels with a resolution of 25 m × 25 m. Since the sites contributing to input via water erosion are characterized by a slope >2% and, in addition, arable land use, lack of drainage, and a hydraulic connection to surface waters, the number of grids from which sediment input to surface waters can take place is relatively small.
The P input via water erosion (
Figure 6, right) per grid cell is on average approx. 8 kg P/(hectare×yr). Below-average P inputs between <1 and approx. 5 kg/(hectare×yr) occur widespread in the Northern German lowlands and are here mainly as a consequence of the low soil erosion risk due to low slope gradients. Above-average P inputs via water erosion of over 10 kg P/(hectare×yr) are typical for low mountain ranges with a high risk of soil erosion. Water erosion-related N inputs to surface waters (
Figure 6, left) per grid cell are generally 10 kg N/(hectare×yr) or below.
Germany-wide, the total P input to surface waters through water erosion per year is about 4400 t/yr Pges, i.e., three times lower than the total N input (approx. 14,000 t N/yr). Yet, almost 25% of the total P inputs to surface waters are discharged via the water erosion pathway, while N inputs to surface waters through water erosion account for only about 3%. If the share of water erosion is related exclusively to the total diffuse N and P inputs, the difference is even more pronounced. While water erosion contributes about 4% to the diffuse N input into surface waters, about 41% of the diffuse P input into surface waters is attributable to this input pathway. Water erosion is thus the most dominant input pathway for diffuse P inputs to surface waters.
4.3. Immobilization and Microbiological Degradation of Nitrogen Compounds in Soil
In contrast to the P compounds in the soil, agricultural nitrogen balance surpluses and atmospheric N deposition (Germany-wide in total 890,000 t N/yr) are partly immobilized and/or microbially degraded in soil (
Figure 7, left). N losses by denitrification of up to 50 kg N/(hectare×yr) and more occur in regions where groundwater-influenced soils with a high proportion of organic matter occur and in regions with long residence times of the leachate. The same applies in regions in which high proportions of pasture occur, so that immobilization is high. In contrast, N immobilization and microbiological degradation of nitrogen compounds is less than 2 kg N/(hectare×yr) in low mountain regions.
The resulting N outputs from soil in
Figure 7 (right) sum up to 590,000 t N/yr, i.e., 35% of the N input into soils. In regions where unfavourable denitrification conditions and low N immobilization rates in the soil coincide with short residence times of the leachate in the soil, N discharges from the soil of 50 kg N/(hectare×yr) and more can occur. Examples of this can be found in the regions with high livestock numbers in northwest Germany. In many low mountain regions, not only the immobilization rates but also the denitrification rates are low. As a result, N emissions from the soil in these low mountain regions are often less than 25 kg N/(hectare×yr). In many unconsolidated regions, N losses from the soil are between less than 5 and 25 kg N/(hectare×yr). The residence time of the leachate in the soil is the main reason why a high proportion of the N inputs to the soil is degraded.
4.4. Diffuse P and N Inputs into Surface Waters via Natural Interflow and Drainage Systems
The geographical reference for the quantification of diffuse N and P inputs to surface waters via the input pathways of natural runoff and drainage systems was determined using the mGROWA water balance model [
40]. To quantify the N input via these two pathways, it is assumed that the grid-wise determined share of natural interflow and artificial drainage runoff in total runoff determines the amount of N input from the soil via these pathways. If, for example, the natural interflow was identified as 40% of the total runoff, it is assumed that 40% of the N discharge from the soil reaches the surface waters via this input pathway. The same applies if the direct runoff component identified is drainage runoff.
Natural interflow is the main runoff component of consolidated rock regions, so that, due to the high proportion of solid rocks in Germany, the share of natural interflow in total runoff is significant (
Figure 7, left). Accordingly, the N input into surface waters via natural interflow is high and sums up to a total of approx. 190,000 t N/yr. In most low mountain regions, the N inputs via natural interflow are in the range between <5 and 25 kg N/(hectare×yr), as can be seen from
Figure 7 (left). In low mountain regions with a high proportion of forests, the N inputs via natural interflow are generally less than 10 kg N/(hectare×yr) due to the relatively low N inputs into the soil originating exclusively from atmospheric N deposition. In regions with a high proportion of livestock, the N inputs via natural interflow are significantly higher and can reach 25 kg N/(hectare×yr).
As phosphate compounds are poorly soluble in soils, the model approach to quantify dissolved P input into surface waters via natural runoff is different. As there are hardly any measured values for P concentrations in natural interflow that can be used as a reference for estimating the P input via natural interflow Germany-wide, for the first approximation, measured P concentrations in near-surface groundwater [
57,
58] were considered as reference values for the P concentrations in natural interflow. By multiplying these P concentrations with the grid-wise calculated rate of natural interflow, the mean annual P inputs in kg/(hectare×yr) are derived.
P inputs via natural interflow are mainly found in low mountain areas displaying steep gradients and, additionally, in the young moraine deposits at the foothills of the Alps (
Figure 8, right). At higher elevations with higher precipitation and runoff levels, P inputs between 0.1 and 0.25 kg P/(hectare×yr) are achieved; in other areas, the inputs do not exceed 0.1 kg P/(hectare×yr). On average, they amount to approx. 0.05 kg P/(hectare×yr), while the nationwide total of P inputs via interflow amounts to approx. 1100 tonnes per year.
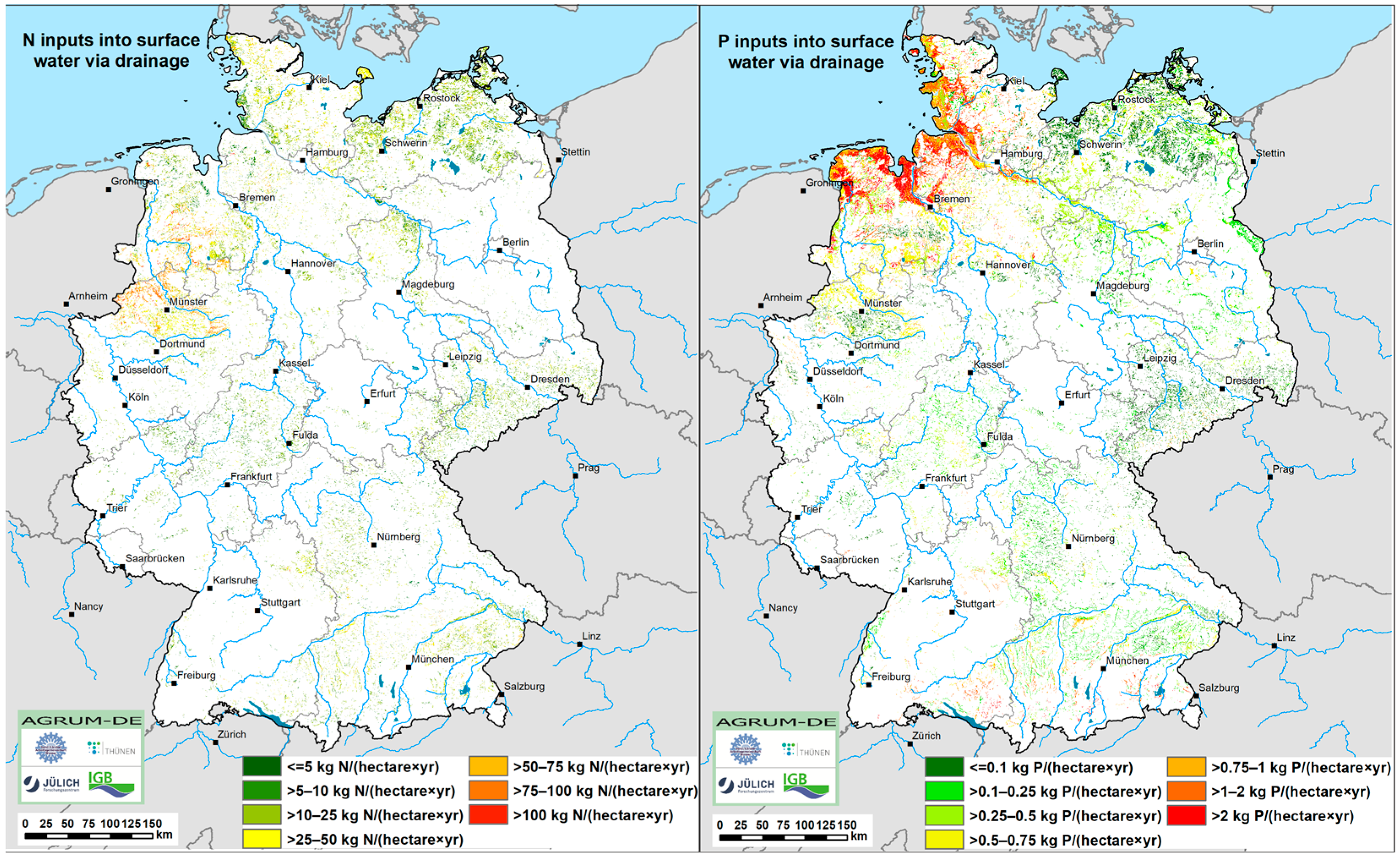
In contrast to natural interflow, runoff from drainage systems is the most important component of direct runoff in unconsolidated rock regions. N and P inputs to surface waters via drainage systems therefore occur primarily in the North German Plain.
Figure 9 (left) shows the N inputs to surface waters via drainage runoff. The model results indicate that N inputs via drainage systems are widespread in the lowland regions near the North and Baltic Seas. However, due to very effective denitrification and immobilization processes (
Figure 7, left), N inputs hardly exceed 10 kg N/(hectare×yr) despite high N inputs into the soil. There are particularly high N inputs via drainage systems (up to 75 kg N/(hectare×yr)) from agricultural soils in the Münsterland, where the denitrification and immobilization processes in the soil are less intensive. The total N inputs to surface waters over the entire drained areas in Germany amount to approx. 33,000 t N/yr.
The total P inputs via drainage systems amount to approx. 2600 t/yr. The average input is approx. 1 kg/(hectare×yr) per hectare and year and is related to the potentially drained agricultural land. The P inputs vary greatly between <0.1 and >2 kg/(hectare×yr), as can be seen in
Figure 9 (right). P inputs via drainage systems above-average are calculated for the marshlands near the North Sea coast, which is a consequence of the high P enrichment in the marshland soils and the corresponding high concentrations of dissolved P in the drainage runoff there. The hot spots of P inputs via drainage are, in particular, raised bog soils under grassland use, low bog soils under agricultural use, and marsh soils under grassland use. Otherwise, low P inputs via drainage systems of less than 0.5 kg/(hectare×yr) are typical for clayey and loamy sites, e.g., for the Beckumer Berge south of Münster or the boulder clay distribution areas in the young moraine country of Mecklenburg–Western Pomerania with strong sorption capacities for P.
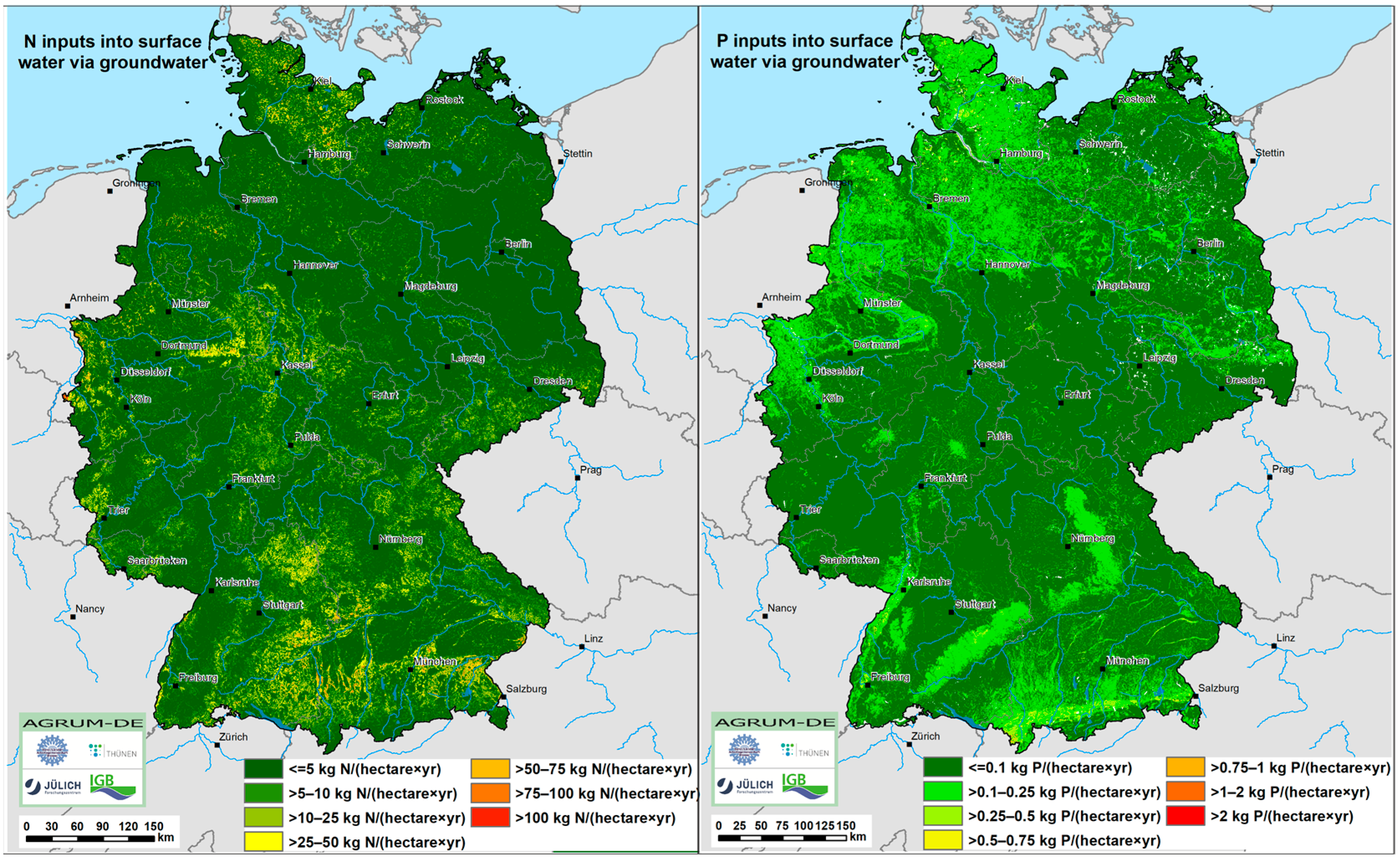
4.5. Diffuse P and N Inputs into Surface Waters via Groundwater Runoff
The N output from soil, which is not discharged via direct runoff, is percolating into the aquifer. The N loads denitrified in groundwater during their passage from the entry point into the groundwater to the river, depending on the hydrogeochemical conditions and groundwater travel times, have been calculated based on the WEKU model. Germany-wide, the amount of nitrate entering the groundwater of about 390,000 t N/yr is reduced to about 120,000 t N/yr by the processes taking place in the aquifer, which corresponds to about 44% of the amount of N entering the aquifer.
Figure 10 (left) shows the resulting groundwater-borne N inputs into surface waters. In the northern part of Germany, unconsolidated rock aquifers with nitrate-reducing conditions and long groundwater residence times are typical. Consequently, most of the nitrate input into the groundwater is denitrified and—although groundwater flow dominates the regional hydrology—the map reveals nitrate inputs from the groundwater into surface waters of less than 1 kg N/(hectare×yr). There, higher groundwater-borne nitrate input into rivers occur only in close vicinity to the rivers. In the bedrock regions in the southern and central parts of Germany, the groundwater-borne N inputs to surface waters largely correspond to the N inputs to groundwater due to the predominantly unfavourable denitrification conditions and the short travel times in the aquifer.
The multi-year average P input into surface waters via groundwater is controlled by groundwater runoff, which corresponds to the mean long-term groundwater recharge, and its concentration of total P. The latter depends largely on the sorption capacity of the soil and geochemistry of the groundwater-bearing rock units [
59].
Total P concentrations from 5687 monitoring sites were available for the AGRUM-DE project. The monitoring sites were assigned to hydrogeological units and the concentration measurements were analysed using primary statistics. The median P concentrations derived for each unit were combined with the groundwater recharge rate to calculate the P loads in the groundwater runoff.
The modelled mean P inputs via groundwater runoff amount to approx. 2500 t/yr nationwide. P inputs > 0.1 kg/(hectare×yr) occur mainly in the North German Geest and parts of the Pleistocene moraine country and are the result of groundwater recharge of more than 150 mm/yr here and the high P content of the soils in this region. In addition, P inputs > 0.1 kg/(hectare×yr) occur in some low mountain ranges, like in the Swabian and Franconian Alb.
4.6. N and P Inputs into Surface Waters from Wastewater Treatment and Urban Systems
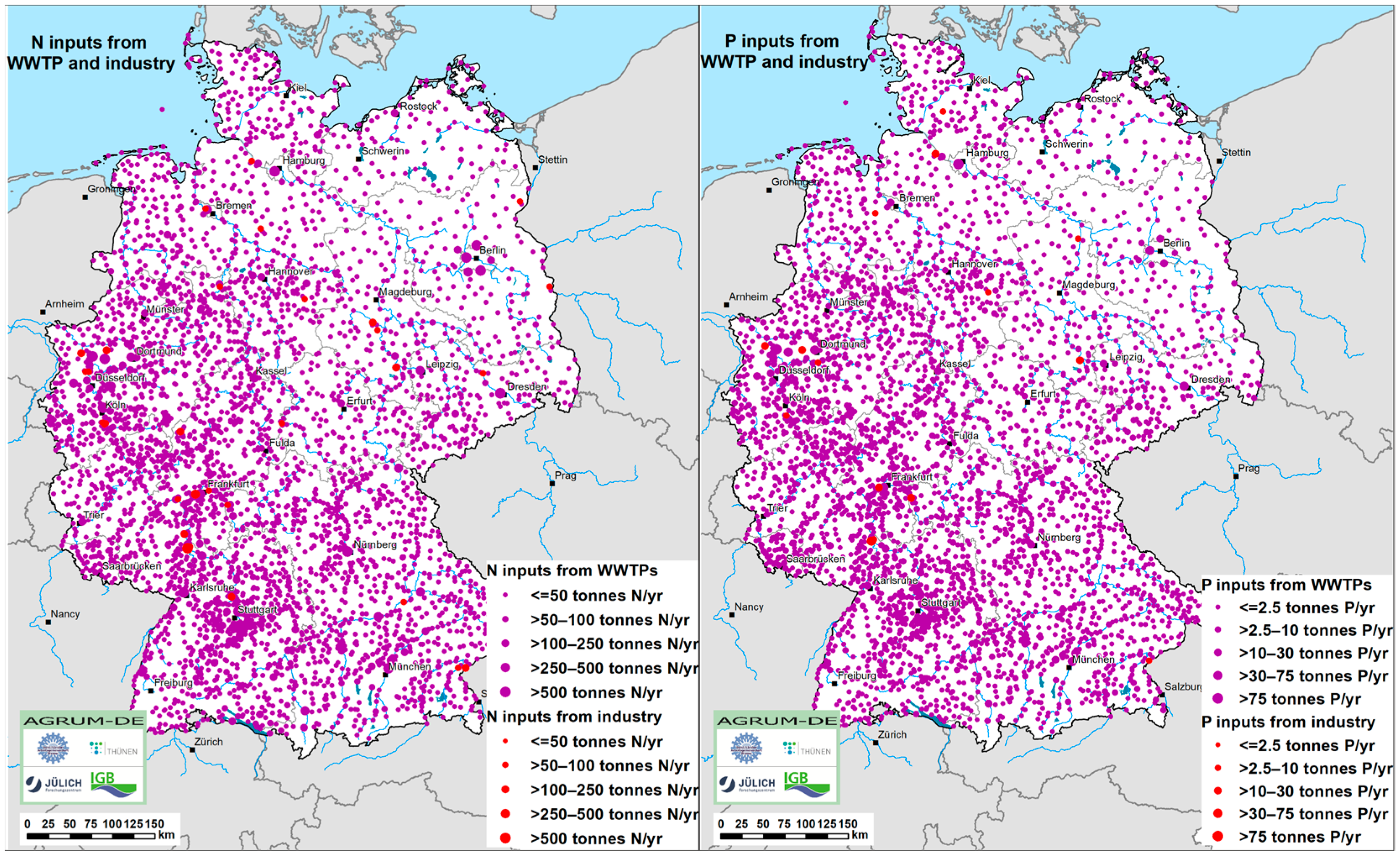
Point source discharges (municipal wastewater treatment plants and industrial direct dischargers) contribute by far the largest share of discharges from urban systems. This can be explained by the high connection rate of households to wastewater treatment plants, which means that the dominant share of urban wastewater is collected, treated, and discharged via this pathway. The inputs from point sources contribute 78,500 t N/yr (82%) of the N inputs and 5100 t P/yr (64%) of the P inputs from point sources (
Figure 11).
We differentiated between inputs from urban areas according to whether they discharge directly into surface waters or via a soil–groundwater passage. For inputs from urban systems into the groundwater, retention via FZJ approaches was taken into account. At a good 16,500 t/a (TN) and 3000 t/a (TP), almost 80% of which originate from exfiltration from canal leachates, the inputs into the groundwater exceed the direct inputs from urban systems. Due to degradation during transportation in soil and groundwater, these are in some cases considerably reduced and contribute on average only a minor role to urban inputs throughout Germany. Locally, however, especially in regions where groundwater retention is lower, there can be significant contributions. On average, around 60% of the direct inputs from urban areas into surface waters of 12,000 t/a (TN) and 1900 t/a (TP) originate from the separate sewer system. Their share is greatly reduced in regions with hard rock and in the old towns of agglomerations where combined sewers are increasingly being installed. Inputs from the combined sewer system are 3–4 times lower than those from the separate sewer system because wastewater in the combined sewer system is treated in wastewater treatment plants during dry weather conditions and is mapped via this input path. The inputs from combined sewer overflows, which occur on the order of 10–30 times a year, lead to temporary but intensive inputs that can cause significant local problems for aquatic fauna or bathing water quality. Decentralized wastewater treatment plants with fewer than 50 connected inhabitants contribute 22% (TN) or 15% (TP) to urban direct discharges into surface waters. This type of wastewater treatment mainly takes place in rural areas with a low population density. The total of 95,000 t/yr (TN) and 8100 t/yr (TP) from urban systems and point sources, i.e., 20% and 41% of total inputs, respectively, originate mainly from densely populated large cities and their peripheries. However, it should be noted that rural areas contribute a disproportionately high share of total inputs due to a less comprehensive collection and less efficient treatment of wastewater.
4.7. Total N and P Inputs into Surface Water
Figure 12 shows the modelled N and P inputs to surface waters via diffuse and point source input pathways. The sum of diffuse N inputs to surface waters is about 380,000 t N/yr. The total P input from diffuse sources is 11,530 t/yr. Taking into account all diffuse and urban input pathways, the total inputs to surface waters for the base year amount to 477,000 t N/yr and 19,100 t P/yr. The diffuse input paths quantified by FZJ contribute a total of 80% (TN) and 59% (TP) to the total inputs.
As can be seen from
Figure 12 (above), the majority of diffuse N inputs occur via interflow and groundwater runoff, whereas the majority of the diffuse P discharge into surface waters (
Figure 12, below) occurs via water erosion, drainage systems, and groundwater runoff.
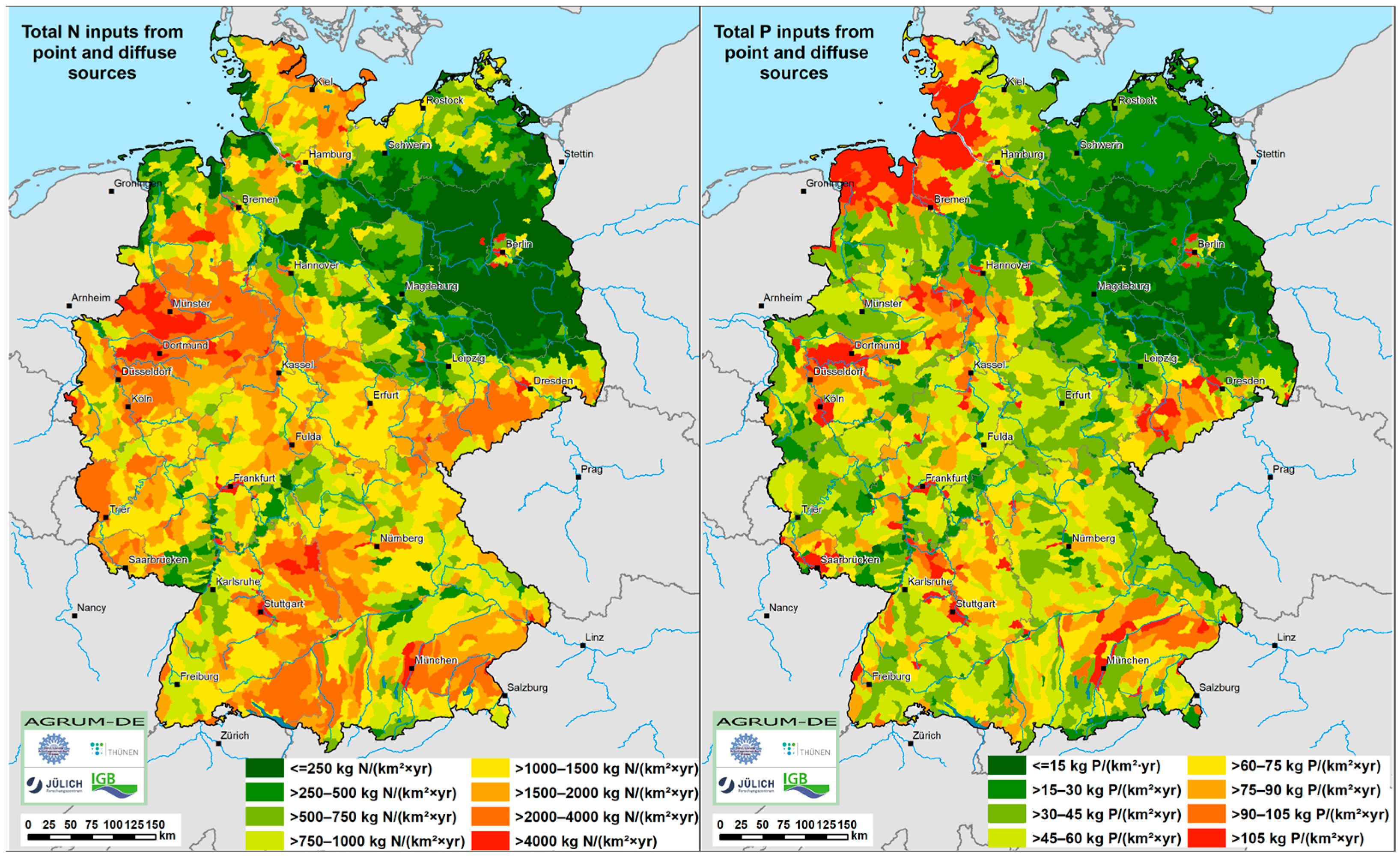
Figure 13 shows the corresponding total N input into surface waters (left) and total P input into surface waters (right) aggregated at the sub-basin level. As expected, the regional distribution of nutrient inputs shows significant differences in Germany.
These total N input vary between <200 t N/(hectare×yr) for large parts of Brandenburg and >4000 t N/(hectare×yr) for large parts of NRW and some regions in Lower Saxony, Saxony, Baden-Württemberg, and Bavaria. Total P input is on a much lower level and varies between <15 kg P/(hectare×yr) for large parts of Brandenburg and >105 kg P/(hectare×yr) for large parts of the marshes along the North Sea coast in Lower Saxony and Schleswig-Holstein.
4.8. Validation of Total N and P Inputs into Surface Waters
The modelled N and P inputs to surface waters via the diffuse input pathways were aggregated at sub-basin level and used, after plausibility check, to model nutrient retention and the total N and P loads in the surface waters. The validation was carried out on the basis of a comparison of observed and modelled loads. The modelled loads were calculated by taking into account the total diffuse, urban, and point inputs. In addition, the internal retention of water bodies and the transport through the water network were considered. For the calculation of the loads in the main courses, the load shares from the foreign upstream reaches were considered as well.
The comparison of observed and modelled loads showed an overall very good statistical agreement (
Figure 14). Thus, the mean absolute deviation (MMA) was 18% (total N) and 23% (total P), the PBIAS [
60] for TN and TP was less than 5%, and the coefficient of determination (r
2) and the NSE [
61] were >0.99. For the comparison based on concentrations, MMA and PBIAS yielded similar good values, whereby only r
2 and NSE decreased, but this is partly due to the fact that the value ranges for concentrations are much narrower than for loads, and thus the statistical correlations are weaker.
Some of the deviations (load) can also be explained by the use of long-term mean modelled discharges, wherein there is not always a complete coverage of the comparison period 2010–2016 or partly different reference years in the input data (e.g., FDZ data for the year 2013). However, since the load comparison does not show any systematic deviation, it can be assumed that the load and concentration ratios are basically well represented.
5. Discussion and Conclusions
The aim of the project was to develop a tool that can be used consistently throughout Germany for determining the nutrient pollution of groundwater and surface waters with input pathway-related and regional differentiation. In this project, available nationwide databases were used, which were provided by authorities of water management, agriculture, and the statistical offices of the federal and state governments. Germany is a federal system comprising 16 different states that are responsible, e.g., for the collection of environmental and geo data. As a consequence, a wide range of scales and resolutions exist, for example, between 1:25,000 and 1:300,000 for soil data at the state level. The objective of the AGRUM project was to use the “best” data, which are harmonized and consistently available at the federal level (e.g., soil map 1:200,000) in order to avoid breaks of values at the state borders. Therefore, it is critical that the data basis for model approaches on state level is far better than on the federal level. It is obvious that the identification of critical source areas for the N and P pollution is more realistic on the state than on the federal level so far. To overcome this limitation, the succeeding project RELAS build up on state data and initiatives are planned to harmonize data at state boundaries.
Information on model validity is crucial to enhance the acceptance of model results. The model is validated if a concrete model result is in the value ranges of appropriate measurements. For nationwide review, this presupposes that model results are suitable for this purpose and that suitable measuring networks exist at the federal or state level. In the project, modelled outflows as well as modelled nutrient concentrations and nutrient loads are compared with measured values from corresponding surface waters monitoring networks. The separate evaluation of the modelled runoff components’ total runoff and net groundwater recharge showed a good agreement of 0.89 with NSE and of −4.0% with PBIAS for total runoff and an NSE of 0.70 and PBIAS of 13.9% for net groundwater recharge [
41]. The comparison of modelled nutrient loads showed acceptable-to-good agreement, with a PBIAS of less than 5% for both N and P. In addition, modelled nitrate concentrations in the leachate are compared with measured nitrate concentrations in shallow groundwater, with an acceptable agreement.
In principle, the possibility of calibration and validation of the models of the AGRUM model network would improve if the federal states both enlarge the number of discharge and water quality measuring points as well as increase the sampling frequency and make these data available centrally. Checking the validity of modelled nitrate concentrations in the leachate would benefit from a denser groundwater monitoring network and depends also on the willingness of all states to supply these data.
Although there is still considerable potential for improving the data basis, the plausibility checks have shown that the instrument created by AGRUM-DE is fundamentally suitable for representing nutrient inputs to groundwater and surface waters on a nationwide basis.
The exemplary model results have shown that the relevance of the input pathways for N and P must be assessed differently. While the input pathways “natural interflow” and “groundwater runoff” are particularly significant for diffuse total N inputs, the input pathways “water erosion” and “drainage” dominate the diffuse total P inputs, especially in less populated regions.
The input of N always occurs in dissolved form, i.e., primarily as NO3 and to a lesser extent as NH4. Regions in which the nitrate inputs into groundwater exceed the groundwater threshold of 50 mg NO3/L can be regarded as the priority areas for the implementation of protection measures against increased nitrate inputs. In the areas concerned, measures are implemented that aim to reduce the (dissolved) nitrate emissions from soil to groundwater. As a kind of side-effect, the groundwater protection measures implemented in such priority areas also contribute to the protection of surface waters from eutrophication-effective nitrate inputs via drainage systems and natural interflow.
The risk posed by P must be regarded differently compared to N. To provide indications of the eutrophication relevance of phosphorus inputs in inland waters, the parameter total P is only of limited relevance, since P partially adsorbs into soil particles, i.e., it does not have a direct eutrophicating effect in this form. The direct input of dissolved orthophosphate-phosphorus, which is bioavailable, has been estimated based on the dissolved share of total phosphorus. Following [
51], the following proportions of orthophosphate-phosphorus in total P were used: drainage 70%, groundwater runoff, interflow and alluvium 100%, erosion 10%, and atmospheric deposition on water surfaces 80%. Accordingly, the total dissolved P inputs sum up to 6700 t/yr or 58% of the diffuse total P input for Germany. The relevance of the individual input pathways thus changes significantly. The most important input pathway for dissolved o-PO
4-P is then groundwater, followed by drainage and interflow. Besides atmospheric deposition, water erosion is of least importance. Accordingly, protection measures to avoid soil erosion have only a limited effect for reducing eutrophication-relevant P inputs to surface waters. However, this should not prevent us from realizing that the implementation of erosion control measures is important in order to prevent sediment transfer, colmation in water bodies, and the input of particle-bound pesticides.
A look at the result maps shows discrepancies at some state borders (see map of P content in topsoil (
Figure 5) and map of total N inputs (
Figure 13, left)). On the one hand, these can be attributed to unharmonized databases with inconsistent scale ranges in the individual federal states. On the other hand, it was a premise of the AGRUM-DE project to primarily use databases that are consistently available nationwide in order to prove that the development of a nationwide, uniform nutrient model is possible. For this reason, there is in some cases a weak consistency with the results of modelling nutrient inputs into groundwater and surface waters at the federal state level [
34,
62].
The AGRUM-DE model is continued in the RELAS project, in which the best available databases at federal-state scale will be applied to achieve a better harmonization with model approaches at the federal state level. By means of the RELAS project, the AGRUM-DE model is embedded in the monitoring system for the Fertilizer Application Ordinance’s impact on groundwater and surface waters. The task of the model network in impact-monitoring is to connect short-run changes in agricultural practices with medium- and long-run impacts on water quality. Accordingly, in the future, it will be possible to make more reliable statements about the regional nutrient situation as well as its development over time.