Hydrological Drought Risk Assessment and Its Spatial Transmission Based on the Three-Dimensional Copula Function in the Yellow River Basin
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Research methods
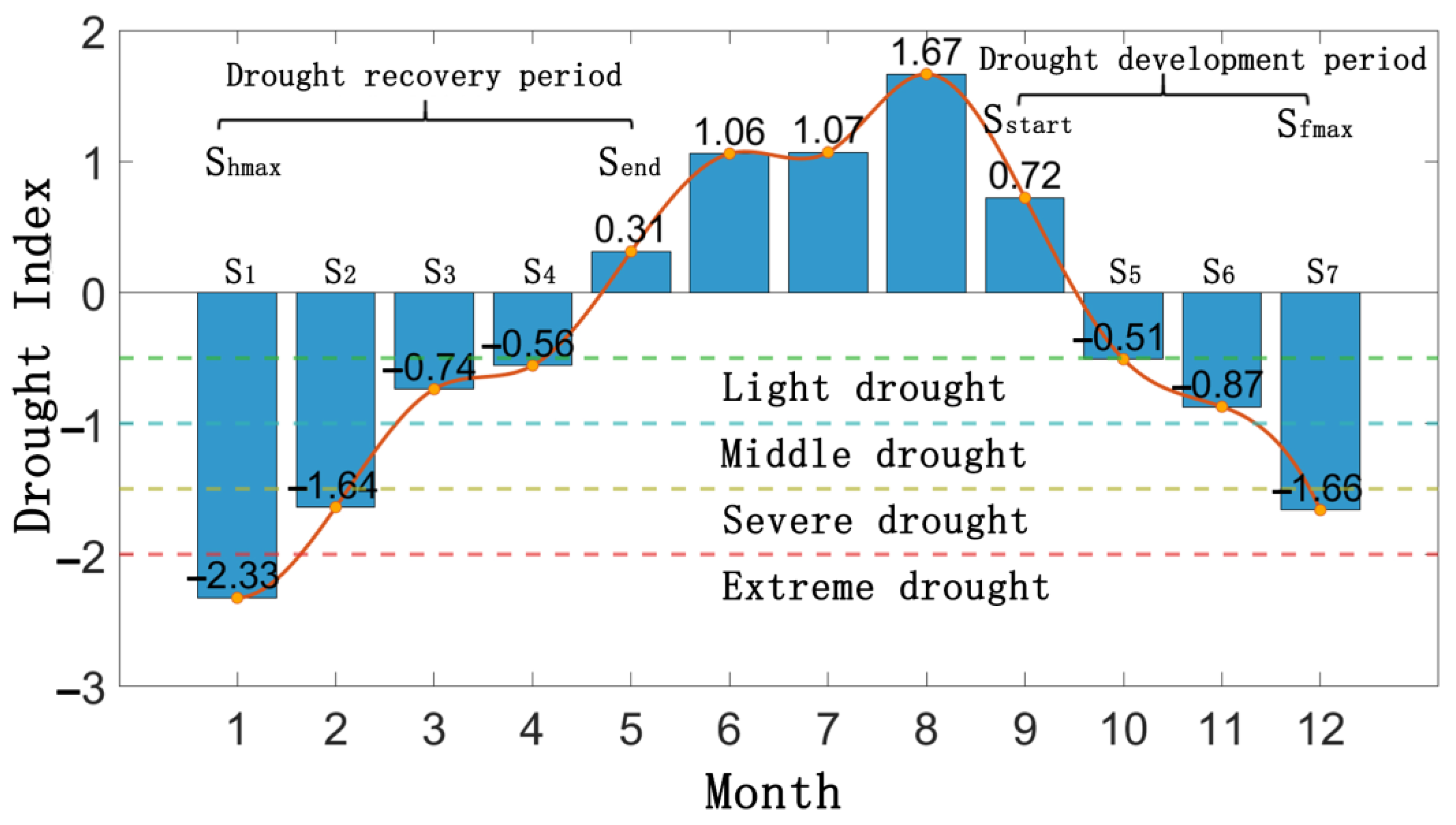
2.2.1. Drought identification and feature quantification
- Drought index calculation
- 2.
- Run theory
2.2.2. Drought Risk Assessment Method Based on Three-Dimensional Copula Function
- where are sample observations; are the corresponding edge distribution functions.
2.2.3. Quantitative Methods of Drought Risk Transmission Law
- 3.
- Equal frequency discrete method
- 4.
- Bayesian network
3. Results
3.1. Hydrological Drought Characteristics of the Yellow River Basin
3.1.1. Hydrological Drought Severity
3.1.2. Hydrological Drought Duration
3.1.3. Hydrological Drought Development Speed
3.2. Hydrological Drought Risk Assessment in the Yellow River Basin
3.2.1. Temporal Variation Characteristics of Hydrological Drought Risk
3.2.2. Spatial Distribution Characteristics of Hydrological Drought Risk
3.3. Risk Transfer Law of Hydrological Drought in the Yellow River Basin
4. Discussion
5. Conclusions
- (1)
- The hydrological drought characteristics of each region in the Yellow River Basin were quantified. In general, the severity of hydrological drought in the Yellow River Basin has increased, the duration has increased and the development has accelerated. The HYK and LJ regions are used to represent the situation of the whole Yellow River Basin. The rate at which the hydrological drought is increasing in the two regions is 0.063/10a and 0.117/10a, respectively. This suggests that the hydrological drought in the Yellow River Basin is intensifying.
- (2)
- The risk of hydrological drought in the Yellow River Basin was assessed. On the whole, the hydrological drought risk in all regions of the Yellow River Basin, except BJC and WH, showed an upward trend. The risk in the BJC region decreased rapidly, about −0.038/10a, while in the WH region, it changed slowly. The hydrological drought risk in the HYK and LJ regions increased rapidly, about 0.025/10a and 0.029/10a, respectively. At the same time, the annual average hydrological drought risk in the upper reaches was high, while that in the middle and lower reaches was relatively low, with the highest value of 0.533 in the TDG area, in the upper reaches, and the lowest value of 0.393 in the HJ area.
- (3)
- The risk transfer law of hydrological drought in the Yellow River Basin was explored. The risk transmission types of hydrological drought in each region can be roughly divided into unchanged types. For example, the transmission probabilities of the low, medium and high risks of hydrological drought from the HYK region to the low, medium and high risks of hydrological drought in the LJ region are 0.68, 0.66 and 0.78, respectively. The risk transfer probability from the low risk of hydrological drought in the TDG region to the middle risk in the LM region is 0.56. The probability of risk transfer from the TDG hydrological drought to the low risk in the LM region is 0.47.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ault, T.R. On the essentials of drought in a changing climate. Science 2020, 368, 256–260. [Google Scholar] [CrossRef]
- Schwalm, C.R.; Anderegg, W.R.L.; Michalak, A.M.; Fisher, J.B.; Biondi, F.; Koch, G.; Litvak, M.; Ogle, K.; Shaw, J.D.; Wolf, A.; et al. Global patterns of drought recovery. Nature 2017, 548, 202. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W. Extreme weather and climate events in China under changing climate. Natl. Sci. Rev. 2020, 7, 938–943. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Hao, Z.; Singh, V.P.; Zhang, Y.; Feng, S.; Xu, Y.; Hao, F. Drought propagation under global warming: Characteristics, approaches, processes, and controlling factors. Sci. Total Environ. 2022, 838, 156021. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhu, Y.; Qin, T.; Zhang, X. Study on the propagation probability characteristics and prediction model of meteorological drought to hydrological drought in basin based on copula function. Front. Earth Sci. 2022, 10, 961871. [Google Scholar] [CrossRef]
- Graw, V.; Dubovyk, O.; Ghazaryan, G.; Schreier, J.; Gonzalez, J.; Abdel-Hamid, A.; Walz, Y.; Dall, K.; Post, J.; Jordaan, A. Timing is everything—Drought classification for risk assessment. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 428–433. [Google Scholar] [CrossRef]
- Zhu, S.; Huang, W.; Luo, X.; Guo, J.; Yuan, Z. The spread of multiple droughts in different seasons and its dynamic changes. Remote Sens. 2023, 15, 3848. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Laaha, G. Hydrological drought severity explained by climate and catchment characteristics. J. Hydrol. 2015, 526, 3–14. [Google Scholar] [CrossRef]
- Li, P.; Jia, L.; Lu, J.; Jiang, M.; Zheng, C. A new evapotranspiration-based drought index for flash drought identification and monitoring. Remote Sens. 2024, 16, 780. [Google Scholar] [CrossRef]
- Chianeh, F.N.; Anaraki, M.V.; Mahmoudian, F.; Farzin, S. A new methodology for the prediction of optimal conditions for dyes’ electrochemical removal; Application of copula function, machine learning, deep learning, and multi-objective optimization. Process Saf. Environ. Protect. 2024, 182, 298–313. [Google Scholar] [CrossRef]
- Farrokhi, A.; Farzin, S.; Mousavi, S. Meteorological drought analysis in response to climate change conditions, based on combined four-dimensional vine copulas and data mining (VC-DM). J. Hydrol. 2021, 603, 127135. [Google Scholar] [CrossRef]
- Reddy, M.J.; Ganguli, P. Application of copulas for derivation of drought severity-duration-frequency curves. Hydrol. Process. 2012, 26, 1672–1685. [Google Scholar]
- Mirabbasi, R.; Fakheri-Fard, A.; Dinpashoh, Y. Bivariate drought frequency analysis using the copula method. Theor. Appl. Climatol. 2012, 108, 191–206. [Google Scholar] [CrossRef]
- Apurv, T.; Cai, X. Evaluation of the stationarity assumption for meteorological drought risk estimation at the multidecadal scale in contiguous united states. Water Resour. Res. 2019, 55, 5074–5101. [Google Scholar]
- Yang, X.; Li, Y.P.; Liu, Y.R.; Gao, P.P. A mcmc-based maximum entropy copula method for bivariate drought risk analysis of the amu darya river basin. J. Hydrol. 2020, 590, 125502. [Google Scholar] [CrossRef]
- Tsakiris, G. Drought risk assessment and management. Water Resour. Manag. 2017, 31, 3083–3095. [Google Scholar] [CrossRef]
- Dunne, A.; Kuleshov, Y. Drought risk assessment and mapping for the murray-darling basin, australia. Nat. Hazards 2023, 115, 839–863. [Google Scholar] [CrossRef]
- Hagenlocher, M.; Meza, I.; Anderson, C.C.; Min, A.; Renaud, F.G.; Walz, Y.; Siebert, S.; Sebesvari, Z. Drought vulnerability and risk assessments: State of the art, persistent gaps, and research agenda. Environ. Res. Lett. 2019, 14, 083002. [Google Scholar] [CrossRef]
- Li, X.; Jiao, Y.; Liu, J. Changes in drought characteristics in the yellow river basin during the carbon-neutral period under low-emission scenarios. Water 2024, 16, 1045. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Z.; Yang, H.; Di, D.; Zhao, Y.; Liang, Q.; Hussain, Z. Comprehensive evaluation of hydrological drought and its relationships with meteorological drought in the yellow river basin, China. J. Hydrol. 2020, 584, 124751. [Google Scholar] [CrossRef]
- Dabanli, I.; Mishra, A.K.; Sen, Z. Long-term spatio-temporal drought variability in turkey. J. Hydrol. 2017, 552, 779–792. [Google Scholar] [CrossRef]
- Qiu, J.; Shen, Z.; Xie, H. Drought impacts on hydrology and water quality under climate change. Sci. Environ. 2023, 858, 159854. [Google Scholar] [CrossRef] [PubMed]
- Burnham, K.P.; Anderson, D.R. Multimodel inference—Understanding aic and bic in model selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Jahangir, M.H.; Yarahmadi, Y. Hydrological drought analyzing and monitoring by using streamflow drought index (SDI) (case study: Lorestan, Iran). Arab. J. Geosci. 2020, 13, 110. [Google Scholar] [CrossRef]
- Yevjevich, V. An objective approach to definitions and investigations of continental hydrologic droughts: Vujica yevjevich: Fort Collins, Colorado State University, 1967, 19 p. (Hydrology paper no. 23). J. Hydrol. 1969, 7, 353. [Google Scholar]
- Herbst, P.H.; Bredenkamp, D.B.; Barker, H.M.G. A technique for the evaluation of drought from rainfall data. J. Hydrol. 1966, 4, 264–272. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Yao, H.; Zhang, D. Multi-timescale assessment of propagation thresholds from meteorological to hydrological drought. Sci. Total Environ. 2021, 765, 144232. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Yao, H.; Chen, X.; Wang, G.; Bai, X.; Zhang, D. A framework for assessing compound drought events from a drought propagation perspective. J. Hydrol. 2022, 604, 127228. [Google Scholar] [CrossRef]
- Boulle, M. Optimal bin number for equal frequency discretizations in supervized learning. Intell. Data Anal. 2005, 9, 175–188. [Google Scholar] [CrossRef]
- Cao, F.; Ge, Y.; Wang, J. Spatial data discretization methods for geocomputation. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 432–440. [Google Scholar] [CrossRef]
- Zhou, Z.; Tu, X.; Wang, T.; Singh, V.P.; Chen, X.; Lin, K. Bivariate socioeconomic drought assessment based on a hybrid framework and impact of human activities. J. Clean. Prod. 2023, 409, 137150. [Google Scholar] [CrossRef]
- Hao, Z.; Hao, F.; Singh, V.P.; Xia, Y.; Ouyang, W.; Shen, X. A theoretical drought classification method for the multivariate drought index based on distribution properties of standardized drought indices. Adv. Water Resour. 2016, 92, 240–247. [Google Scholar] [CrossRef]
- Abbas, A.; Waseem, M.; Ullah, W.; Zhao, C.; Zhu, J. Spatiotemporal analysis of meteorological and hydrological droughts and their propagations. Water 2021, 13, 2237. [Google Scholar] [CrossRef]
- Chen, N.; Li, R.; Zhang, X.; Yang, C.; Wang, X.; Zeng, L.; Tang, S.; Wang, W.; Li, D.; Niyogi, D. Drought propagation in northern China plain: A comparative analysis of gldas and merra-2 datasets. J. Hydrol. 2020, 588, 125026. [Google Scholar] [CrossRef]
- Vaziri, H.; Karami, H.; Mousavi, S.; Hadiani, M. Analysis of hydrological drought characteristics using copula function approach. Paddy Water Environ. 2018, 16, 153–161. [Google Scholar] [CrossRef]
- Tao, Y.; Meng, E.; Huang, Q. Spatiotemporal changes and hazard assessment of hydrological drought in China using big data. Water 2024, 16, 106. [Google Scholar] [CrossRef]
- Zhang, Q.; Peng, J.; Singh, V.P.; Li, J.; Chen, Y.D. Spatio-temporal variations of precipitation in arid and semiarid regions of China: The yellow river basin as a case study. Glob. Planet. Chang. 2014, 114, 38–49. [Google Scholar] [CrossRef]
- Kay, J.E. Early climate models successfully predicted global warming. Nature 2020, 578, 45–46. [Google Scholar] [CrossRef]
- Niu, Z.; Wang, L.; Fang, L.; Li, J.; Yao, R. Analysis of spatiotemporal variability in temperature extremes in the yellow and Yangtze river basins during 1961–2014 based on high-density gauge observations. Int. J. Climatol. 2020, 40, 1–21. [Google Scholar] [CrossRef]
- Dang, S.; Liu, X.; Yin, H.; Guo, X. Prediction of sediment yield in the middle reaches of the yellow river basin under extreme precipitation. Front. Earth Sci. 2020, 8, 542686. [Google Scholar] [CrossRef]
- Zhao, Y.; Cao, W.; Hu, C.; Wang, Y.; Wang, Z.; Zhang, X.; Zhu, B.; Cheng, C.; Yin, X.; Liu, B.; et al. Analysis of changes in characteristics of flood and sediment yield in typical basins of the yellow river under extreme rainfall events. Catena 2019, 177, 31–40. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, Y.; Li, Z.; Chang, J.; Guo, A.; Zhou, K. Characterizing spatio-temporal patterns of multi-scalar drought risk in mainland China. Ecol. Indic. 2021, 131, 108189. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Leng, G.; Huang, Q. Integrated index for drought assessment based on variable fuzzy set theory: A case study in the yellow river basin, China. J. Hydrol. 2015, 527, 608–618. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Zhang, Q. Analysis of ecological drought risk characteristics and leading factors in the yellow river basin. Theor. Appl. Climatol. 2024, 155, 1739–1757. [Google Scholar] [CrossRef]
- Lee, S.; Moriasi, D.N.; Mehr, A.D.; Mirchi, A. Sensitivity of standardized precipitation and evapotranspiration index (SPEI) to the choice of SPEI probability distribution and evapotranspiration method. J. Hydrol.-Reg. Stud. 2024, 53, 101761. [Google Scholar] [CrossRef]
- Zhong, Z.; He, B.; Guo, L.; Zhang, Y. Performance of various forms of the palmer drought severity index in China from 1961 to 2013. J. Hydrometeorol. 2019, 20, 1867–1885. [Google Scholar] [CrossRef]












| Year | Hydrological Station | Longitude | Latitude | Data |
|---|---|---|---|---|
| 1960–2018 | Tangnaihai | 100°09′ | 35°30′ | Monthly runoff |
| 1960–2018 | Lanzhou | 103°49′ | 36°04′ | Monthly runoff |
| 1960–2018 | Shizuishan | 106°47′ | 39°15′ | Monthly runoff |
| 1960–2018 | Toudaoguai | 111°5′ | 40°15′ | Monthly runoff |
| 1960–2018 | Baijiachuan | 110°25′ | 37°14′ | Monthly runoff |
| 1960–2018 | Huaxian | 109°46′ | 34°35′ | Monthly runoff |
| 1960–2018 | Zhuangtou | 109°50′ | 35°02′ | Monthly runoff |
| 1960–2018 | Longmen | 110°35′ | 35°40′ | Monthly runoff |
| 1960–2018 | Hejin | 110°48′ | 35°34′ | Monthly runoff |
| 1960–2018 | Huayuankou | 113°40′ | 34°54′ | Monthly runoff |
| 1960–2018 | Lijin | 118°18′ | 37°31′ | Monthly runoff |
| SRI | Drought Grade |
|---|---|
| SRI > −0.5 | No drought |
| −1.0 < SRI ≤ −0.5 | Light drought |
| −1.5 < SRI ≤ −1.0 | Moderate drought |
| −2.0 < SRI ≤ −1.5 | Severe drought |
| SRI ≤ −2.0 | Extreme drought |
| Risk Grade | Drought Risk Values in Various Regions | ||||
|---|---|---|---|---|---|
| TNH | LZ | SZS | TDG | BJC | |
| Low | 0 ≤ R < 0.367 | 0 ≤ R < 0.381 | 0 ≤ R < 0.324 | 0 ≤ R < 0.48 | 0 ≤ R < 0.388 |
| Medium | 0.367 ≤ R < 0.412 | 0.381 ≤ R< 0.457 | 0.324 ≤ R< 0.6 | 0.48 ≤ R < 0.71 | 0.388 ≤ R < 0.496 |
| High | 0.412 ≤ R ≤ 1 | 0.457 ≤ R ≤ 1 | 0.6 ≤ R ≤ 1 | 0.71 ≤ R ≤ 1 | 0.496 ≤ R ≤ 1 |
| Risk Grade | Drought Risk Values in Various Regions | ||||
| WH | LM | HJ | HYK | LJ | |
| Low | 0 ≤ R < 0.4 | 0 ≤ R < 0.299 | 0 ≤ R < 0.375 | 0 ≤ R < 0.332 | 0 ≤ R< 0.39 |
| Medium | 0.4 ≤ R < 0.619 | 0.299 ≤ R < 0.516 | 0.375 ≤ R < 0.467 | 0.332 ≤ R < 0.59 | 0.39 ≤ R < 0.56 |
| High | 0.619 ≤ R ≤ 1 | 0.516 ≤ R ≤ 1 | 0.467 ≤ R ≤ 1 | 0.59 ≤ R ≤ 1 | 0.56 ≤ R ≤ 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Guo, J.; Yan, D.; Wang, H.; Jiang, X. Hydrological Drought Risk Assessment and Its Spatial Transmission Based on the Three-Dimensional Copula Function in the Yellow River Basin. Water 2024, 16, 1873. https://doi.org/10.3390/w16131873
Li H, Guo J, Yan D, Wang H, Jiang X. Hydrological Drought Risk Assessment and Its Spatial Transmission Based on the Three-Dimensional Copula Function in the Yellow River Basin. Water. 2024; 16(13):1873. https://doi.org/10.3390/w16131873
Chicago/Turabian StyleLi, Hui, Jiamei Guo, Dengming Yan, Huiliang Wang, and Xiujuan Jiang. 2024. "Hydrological Drought Risk Assessment and Its Spatial Transmission Based on the Three-Dimensional Copula Function in the Yellow River Basin" Water 16, no. 13: 1873. https://doi.org/10.3390/w16131873
APA StyleLi, H., Guo, J., Yan, D., Wang, H., & Jiang, X. (2024). Hydrological Drought Risk Assessment and Its Spatial Transmission Based on the Three-Dimensional Copula Function in the Yellow River Basin. Water, 16(13), 1873. https://doi.org/10.3390/w16131873








