A Structural Optimization of Urban Drainage Systems: An Optimization Approach for Mitigating Urban Floods
Abstract
1. Introduction
2. Materials and Methods
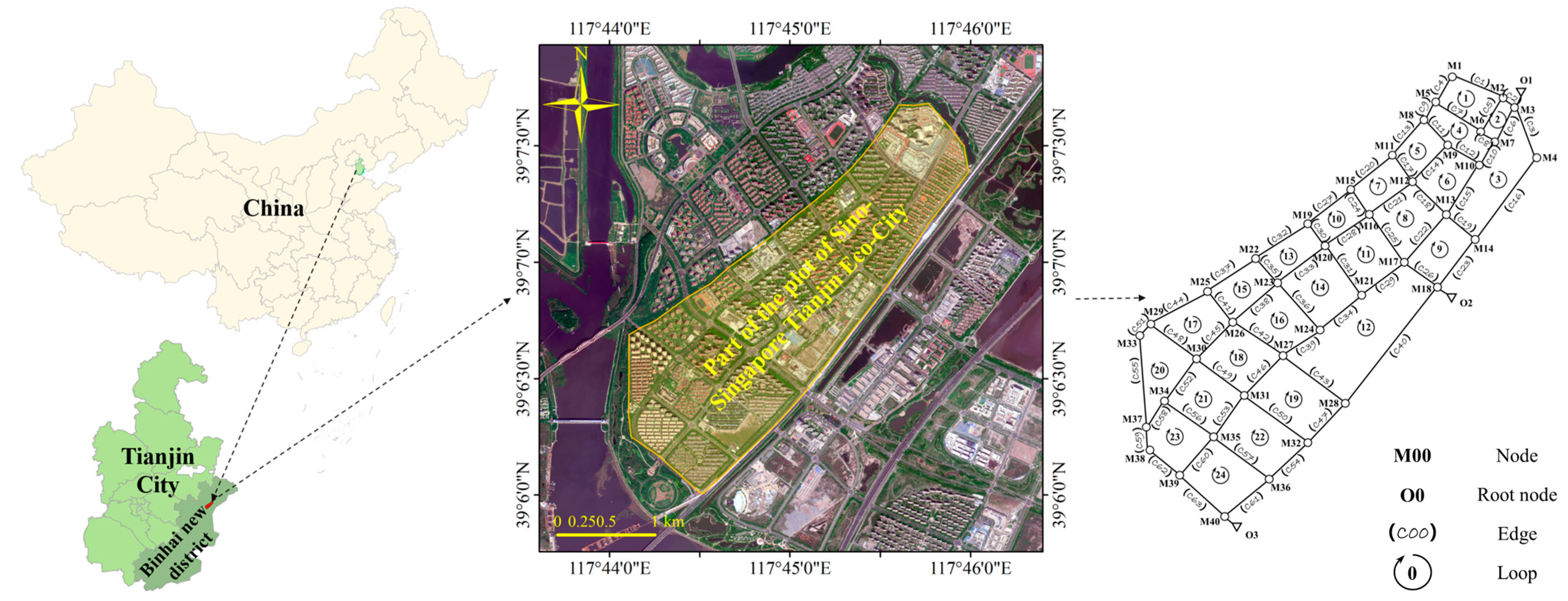
2.1. Study Area
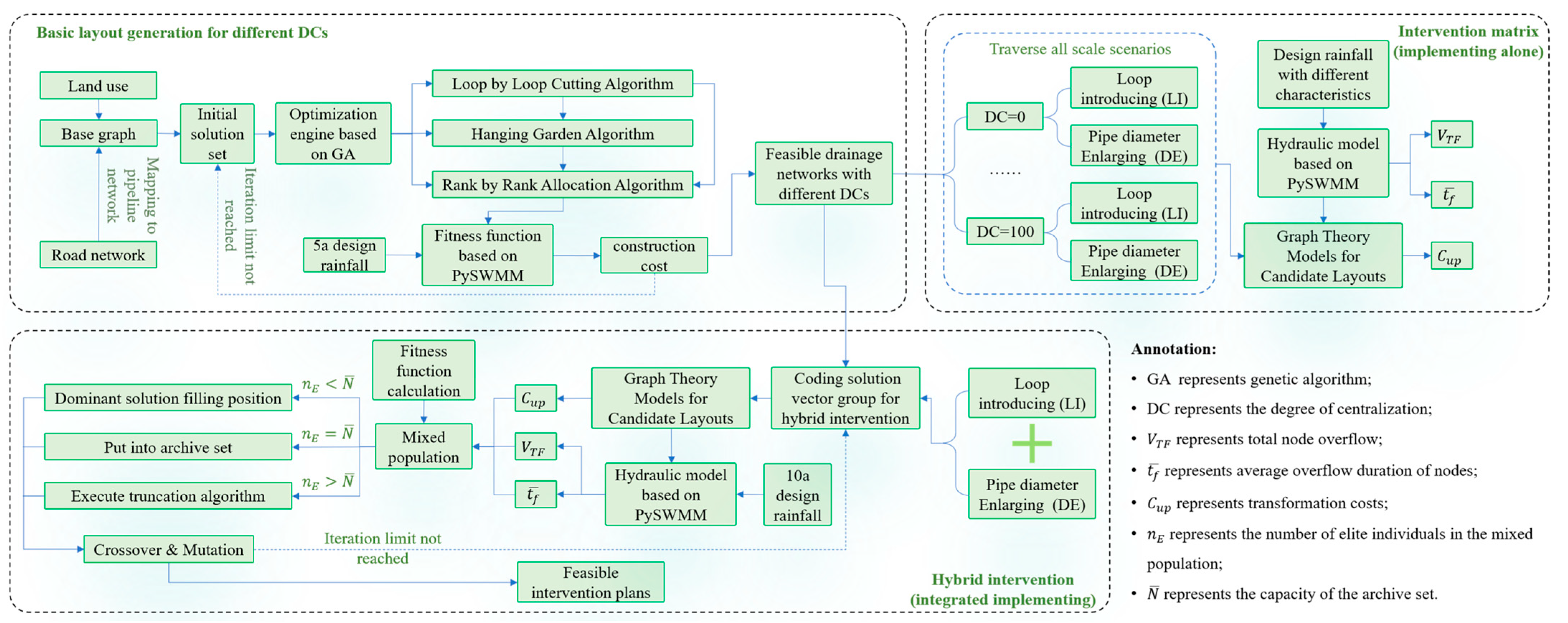
2.2. Layout Generation of the Optimized Network
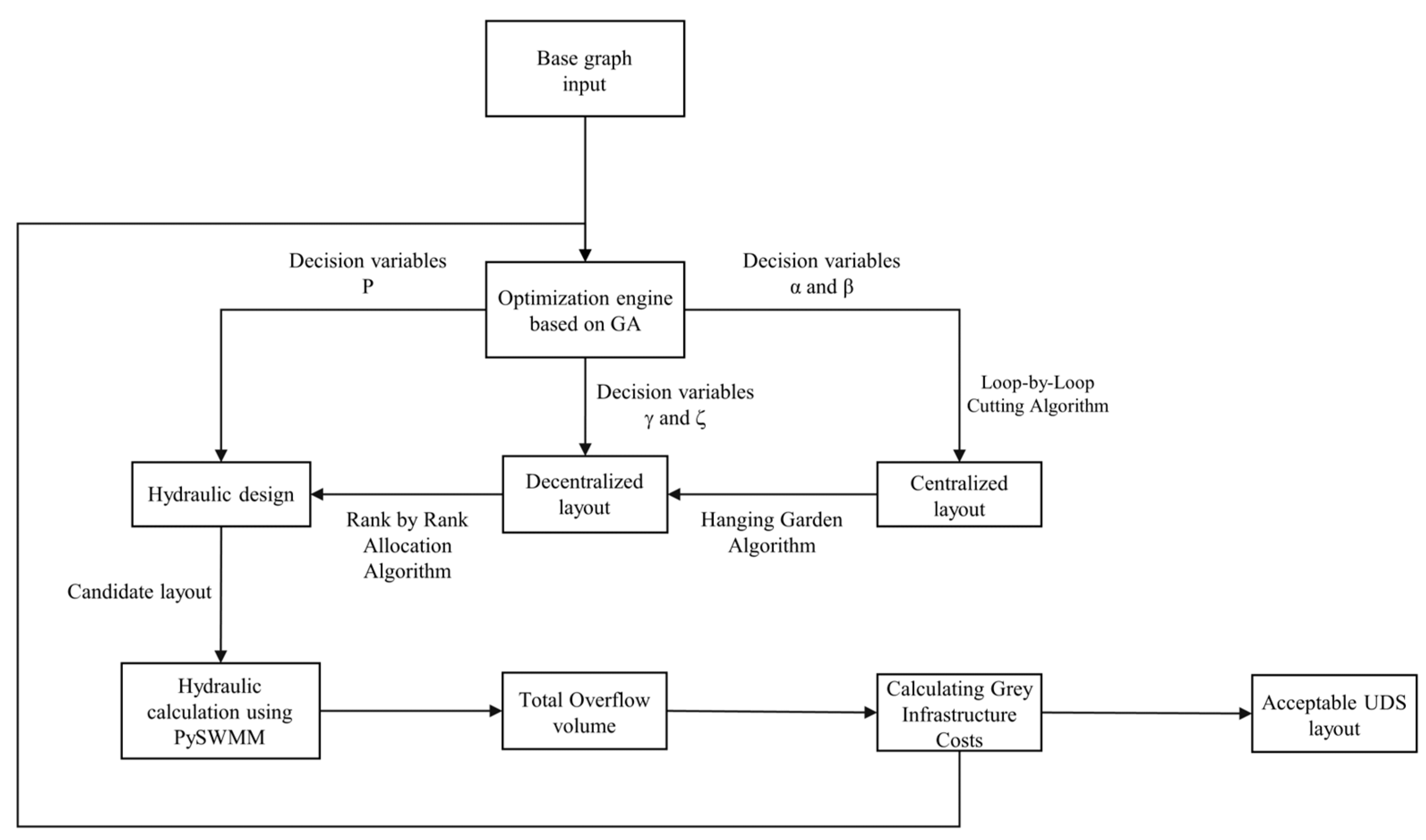
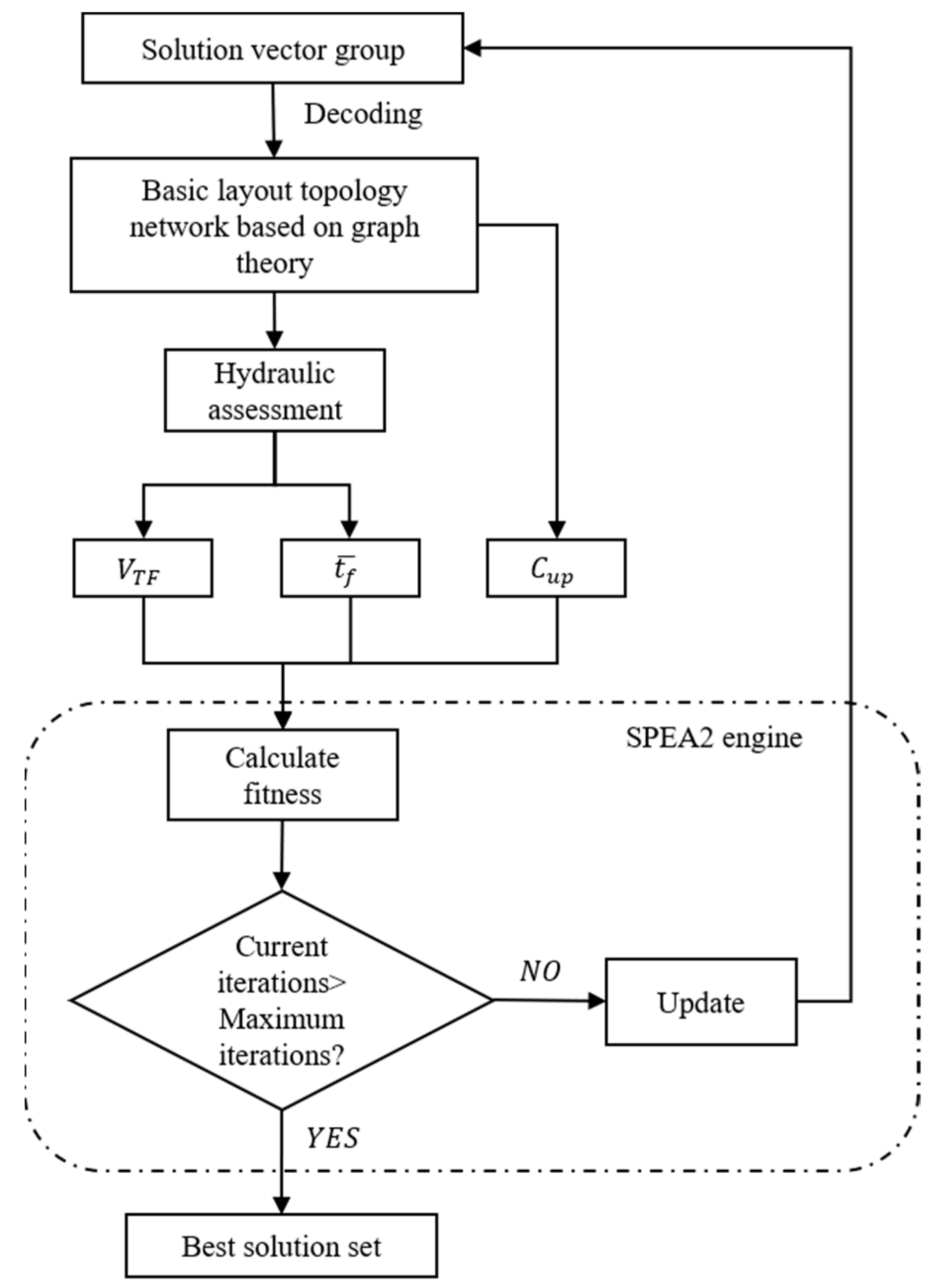
2.2.1. (De)centralized Layout Generator
2.2.2. Hydraulic Component Designer
- The pipe diameters fall within the range between the maximum and minimum pipe diameters.
- The downstream pipe diameter must not be smaller than the upstream pipe diameter.
- Feasible commercial pipe diameters selected.
- The flow velocity within the pipe must lie between the maximum and minimum allowable velocities.
- The pipes must meet the minimum burial depth requirements.
2.2.3. Optimization Engine
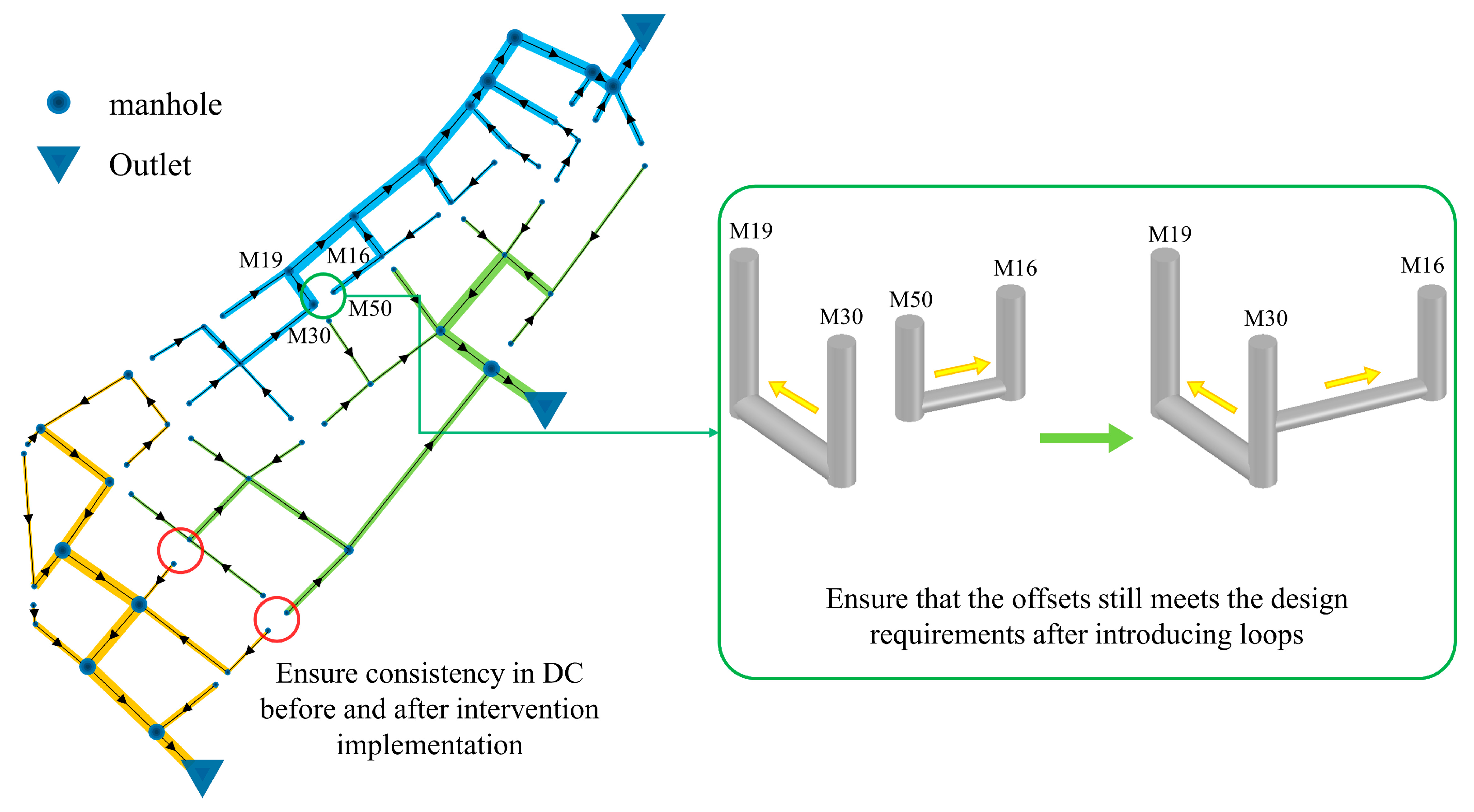
2.3. Redundancy Intervention
2.3.1. Loop-Introducing
2.3.2. Pipe Diameter Enlarging
2.3.3. Hybrid Mode
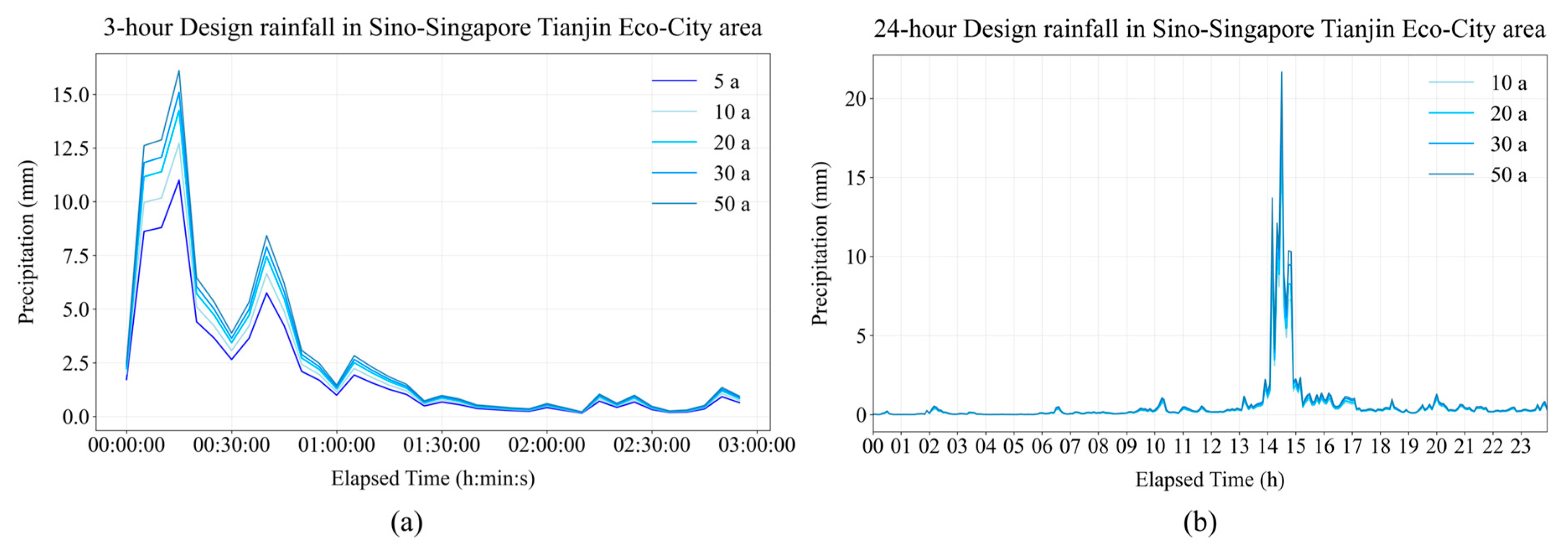
2.3.4. Analysis Method
- Total Overflow Volume ():
- 2.
- Average Node Flooding Duration ():
- 3.
- Intervention and Transformation Cost ():
- The scheme must include at least 1 loop-introducing intervention measure and at least 1 pipe diameter enlarging intervention measure, which implies that the minimum scale of intervention is 2;
- To facilitate a comparison between the hybrid scheme and the individual effects of the 2 intervention measures, the implementation scale of the 3 intervention schemes must be consistent. If the upper limits of the implementation scale for the LI scenario and the DE scenario are and (with ), respectively, then the total scale of LI and DE in the hybrid scheme must not exceed (which means ).
3. Results and Discussion
3.1. Layout of Drainage Systems with Different Degree of (De)centralization
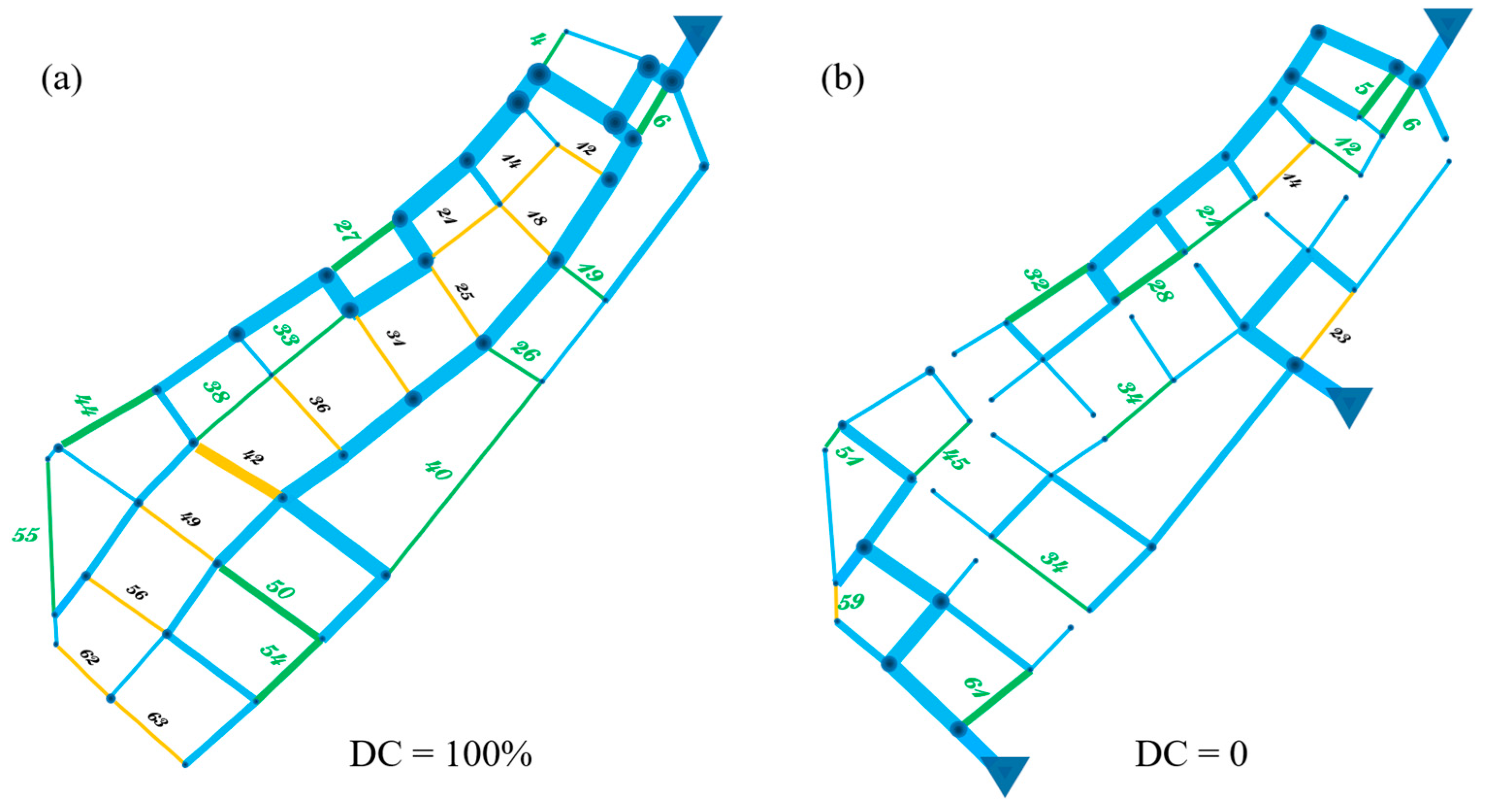
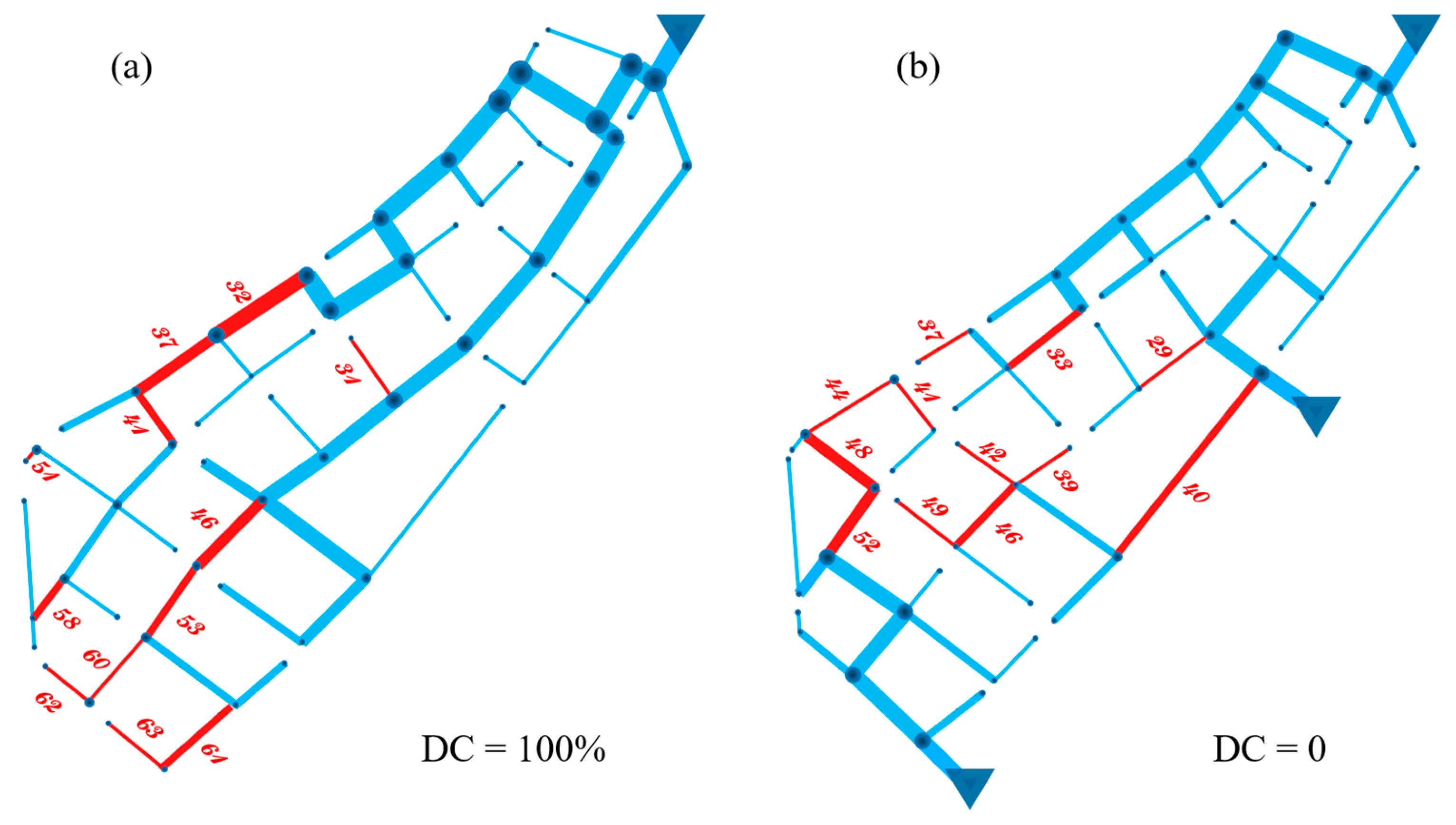
3.2. Candidate Addition (Replacement) Pipelines for Redundancy Intervention
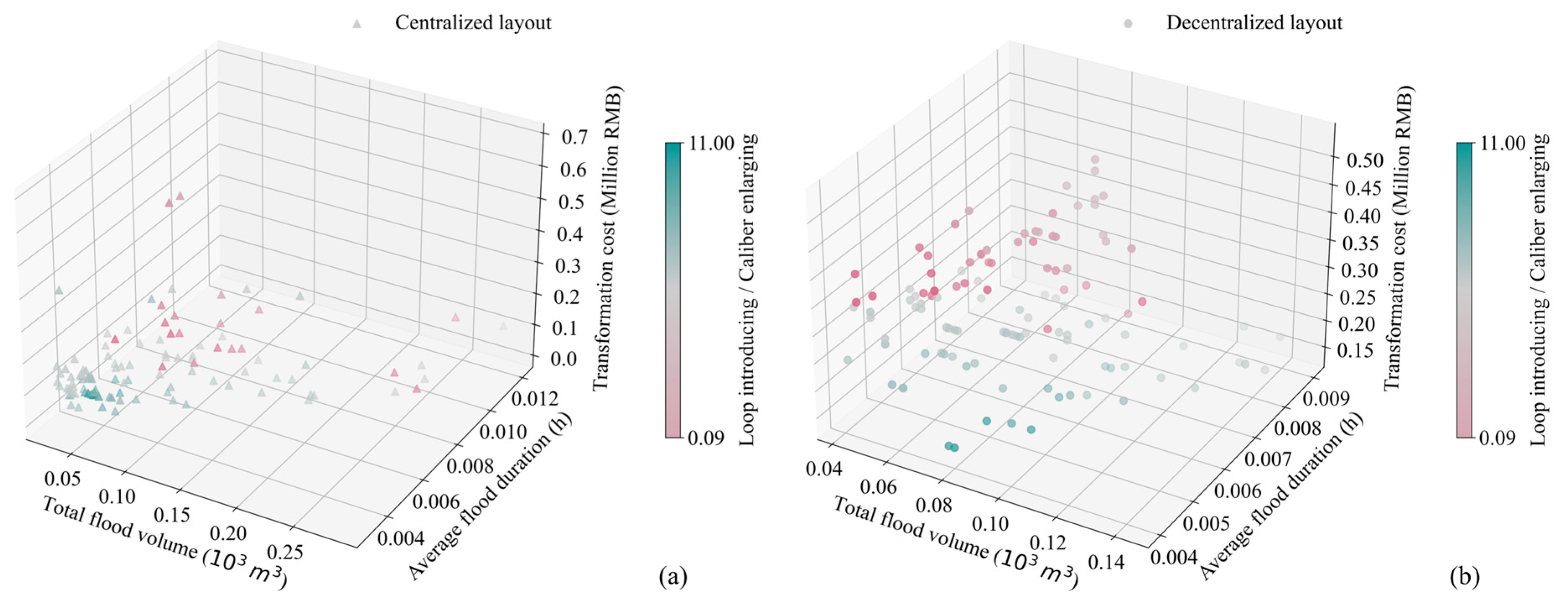
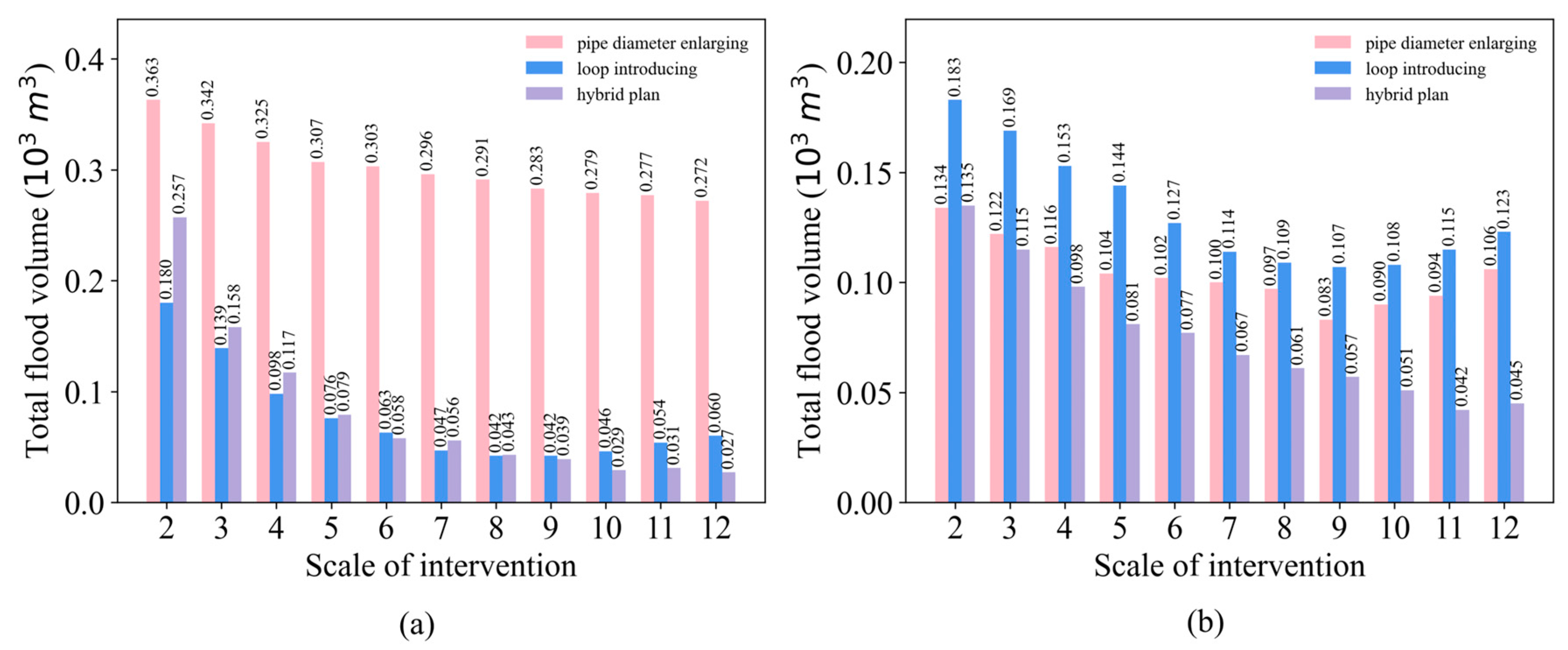
- Mitigation effect of loop-introducing and pipe diameter enlarging
- b.
- The edges of hybrid mode
4. Conclusions
- For intervention measures involving the replacement or upgrading of components within the drainage network, not all intervention combinations provide positive support to the performance of the UDS. The interplay among different solutions results in varying UDS performance, indicating that precise deployment of grey infrastructure is crucial for urban water management practices.
- The structural variations in UDS, arising from differences in degree of centralization, confer distinct improvement preferences to the two categories of redundant intervention measures. The strategy of loop introduction offers enhanced resilience and significant, robust improvements for centralized UDS layouts across almost all rainfall scenarios. Conversely, for decentralized UDS layouts, the hydraulic improvements provided by both intervention measures are very similar.
- Considering that most built-up urban areas (watersheds) feature centralized UDS layouts, the transformation to decentralized layouts may involve extensive pipe redirection projects due to hydraulic constraints, including changes in pipe diameter, slope, and burial depth, although decentralized layouts can significantly alleviate V_TF (total overflow volume). Constructing loop redundancy structures is clearly a more economical choice. For newly planned construction sites, decentralized layouts are a novel and competitive option, depending on feasibility. For watersheds that have already adopted decentralized layouts, the replacement of key pipe diameters may further enhance their performance.
- Compared to the two intervention modes that act independently, the hybrid scheme provides the UDS with flood risk adaptation support that combines effective runoff distribution and increased flow capacity, thus promising optimal intervention outcomes. However, as the scale of intervention increases, the hybrid intervention may also encounter conflicts in the effectiveness of the effects between components. It is necessary to determine an appropriate upper limit for the scale of intervention.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Miller, J.D.; Hutchins, M. The impacts of urbanisation and climate change on urban flooding and urban water quality: A review of the evidence concerning the United Kingdom. J. Hydrol. Reg. Stud. 2017, 12, 345–362. [Google Scholar] [CrossRef]
- Lu, M.; Yu, Z.; Hua, J.; Kang, C.; Lin, Z. Spatial dependence of floods shaped by extreme rainfall under the influence of urbanization. Sci. Total Environ. 2023, 857, 159134. [Google Scholar] [CrossRef] [PubMed]
- Dharmarathne, G.; Waduge, A.O.; Bogahawaththa, M.; Rathnayake, U.; Meddage, D.P.P. Adapting cities to the surge: A comprehensive review of climate-induced urban flooding. Results Eng. 2024, 22, 102123. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, P.; Li, Y.; Sheng, Y.; Wang, B.; Popovych, N.; Hu, T. Contributions of climate change and urbanization to urban flood hazard changes in China’s 293 major cities since 1980. J. Environ. Manag. 2024, 353, 120113. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Zevenbergen, C.; Ma, Y. Urban pluvial flooding and stormwater management: A contemporary review of China’s challenges and “sponge cities” strategy. Environ. Sci. Policy 2018, 80, 132–143. [Google Scholar] [CrossRef]
- Zhou, Q.; Leng, G.; Su, J.; Ren, Y. Comparison of urbanization and climate change impacts on urban flood volumes: Importance of urban planning and drainage adaptation. Sci. Total Environ. 2019, 658, 24–33. [Google Scholar] [CrossRef] [PubMed]
- Tellman, B.; Sullivan, J.A.; Kuhn, C.; Kettner, A.J.; Doyle, C.S.; Brakenridge, G.R.; Erickson, T.A.; Slayback, D.A. Satellite imaging reveals increased proportion of population exposed to floods. Nature 2021, 596, 80–86. [Google Scholar] [CrossRef] [PubMed]
- Jovanovic, T.; Hale, R.L.; Gironás, J.; Mejia, A. Hydrological Functioning of an Evolving Urban Stormwater Network. Water Resour. Res. 2019, 55, 6517–6533. [Google Scholar] [CrossRef]
- Eggimann, S.; Truffer, B.; Maurer, M. To connect or not to connect? Modelling the optimal degree of centralisation for wastewater infrastructures. Water Res. 2015, 84, 218–231. [Google Scholar] [CrossRef]
- Fortunato, A.; Oliveri, E.; Mazzola, M.R. Selection of the Optimal Design Rainfall Return Period of Urban Drainage Systems. Procedia Eng. 2014, 89, 742–749. [Google Scholar] [CrossRef]
- Bieker, S.; Cornel, P.; Wagner, M. Semicentralised supply and treatment systems: Integrated infrastructure solutions for fast growing urban areas. Water Sci. Technol. 2010, 61, 2905–2913. [Google Scholar] [CrossRef]
- Obando, G.; Poveda, J.I.; Quijano, N. Replicator dynamics under perturbations and time delays. Math. Control. Signals Syst. 2016, 28, 20. [Google Scholar] [CrossRef]
- Bakhshipour, A.E.; Bakhshizadeh, M.; Dittmer, U.; Haghighi, A.; Nowak, W. Hanging Gardens Algorithm to Generate Decentralized Layouts for the Optimization of Urban Drainage Systems. J. Water Resour. Plan. Manag. 2019, 145, 04019034. [Google Scholar] [CrossRef]
- Hesarkazzazi, S.; Hajibabaei, M.; Bakhshipour, A.E.; Dittmer, U.; Haghighi, A.; Sitzenfrei, R. Generation of optimal (de)centralized layouts for urban drainage systems: A graph-theory-based combinatorial multi-objective optimization framework. Sustain. Cities Soc. 2022, 81, 103827. [Google Scholar] [CrossRef]
- Wang, M.; Chen, B.; Zhang, D.; Yuan, H.; Rao, Q.; Zhou, S.; Li, J.; Wang, W.; Tan, S.K. Comparative life cycle assessment and life cycle cost analysis of centralized and decentralized urban drainage systems: A case study in Zhujiang New Town, Guangzhou, China. J. Clean. Prod. 2023, 426, 139173. [Google Scholar] [CrossRef]
- Mugume, S.N.; Gomez, D.E.; Fu, G.; Farmani, R.; Butler, D. A global analysis approach for investigating structural resilience in urban drainage systems. Water Res. 2015, 81, 15–26. [Google Scholar] [CrossRef] [PubMed]
- Ahern, J. From fail-safe to safe-to-fail: Sustainability and resilience in the new urban world. Landsc. Urban Plan. 2011, 100, 341–343. [Google Scholar] [CrossRef]
- Haghbin, S.; Mahjouri, N. Quantifying and improving flood resilience of urban drainage systems based on socio-ecological criteria. J. Environ. Manag. 2023, 339, 117799. [Google Scholar] [CrossRef] [PubMed]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Varela, J.M.R.; Santonastaso, G.F.; Simone, A.; Tzatchkov, V. Redundancy Features of Water Distribution Systems. Procedia Eng. 2017, 186, 412–419. [Google Scholar] [CrossRef]
- Yazdi, J. Improving Urban Drainage Systems Resiliency Against Unexpected Blockages: A Probabilistic Approach. Water Resour. Manag. 2018, 32, 4561–4573. [Google Scholar] [CrossRef]
- Lu, J.; Liu, J.; Fu, X.; Wang, J. Stormwater hydrographs simulated for different structures of urban drainage network: Dendritic and looped sewer networks. Urban Water J. 2021, 18, 522–529. [Google Scholar] [CrossRef]
- Lu, J.; Liu, J.; Yu, Y.; Liu, C.; Su, X. Network Structure Optimization Method for Urban Drainage Systems Considering Pipeline Redundancies. Int. J. Disaster Risk Sci. 2022, 13, 793–809. [Google Scholar] [CrossRef]
- Reyes-Silva, J.D.; Bangura, E.; Helm, B.; Benisch, J.; Krebs, P. The Role of Sewer Network Structure on the Occurrence and Magnitude of Combined Sewer Overflows (CSOs). Water 2020, 12, 2675. [Google Scholar] [CrossRef]
- Hesarkazzazi, S.; Bakhshipour, A.E.; Hajibabaei, M.; Dittmer, U.; Haghighi, A.; Sitzenfrei, R. Battle of centralized and decentralized urban stormwater networks: From redundancy perspective. Water Res. 2022, 222, 118910. [Google Scholar] [CrossRef]
- Kwon, S.H.; Jung, D.; Kim, J.H. Optimal Layout and Pipe Sizing of Urban Drainage Networks to Improve Robustness and Rapidity. J. Water Resour. Plan. Manag. 2021, 147, 06021003. [Google Scholar] [CrossRef]
- Alfaisal, F.M.; Mays, L.W. Optimization Models for Layout and Pipe Design for Storm Sewer Systems. Water Resour. Manag. 2021, 35, 4841–4854. [Google Scholar] [CrossRef]
- Ogidan, O.; Giacomoni, M. Multiobjective Genetic Optimization Approach to Identify Pipe Segment Replacements and Inline Storages to Reduce Sanitary Sewer Overflows. Water Resour. Manag. 2016, 30, 3707–3722. [Google Scholar] [CrossRef]
- Hesarkazzazi, S.; Hajibabaei, M.; Diao, K.; Sitzenfrei, R. Implication of Different Pipe-Sizing Strategies for the Resilience of Stormwater Networks. In Proceedings of the World Environmental and Water Resources Congress 2021, virtual, 7–11 June 2021; pp. 244–252. [Google Scholar]
- Liu, Y.; Zhao, W.; Wei, Y.; Sebastian, F.S.M.; Wang, M. Urban waterlogging control: A novel method to urban drainage pipes reconstruction, systematic and automated. J. Clean. Prod. 2023, 418, 137950. [Google Scholar] [CrossRef]
- Mair, M.; Zischg, J.; Rauch, W.; Sitzenfrei, R. Where to Find Water Pipes and Sewers?—On the Correlation of Infrastructure Networks in the Urban Environment. Water 2017, 9, 146. [Google Scholar] [CrossRef]
- Haghighi, A. Loop-by-Loop Cutting Algorithm to Generate Layouts for Urban Drainage Systems. J. Water Resour. Plan. Manag. 2013, 139, 693–703. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Leitão, J.P.; Wang, Z.; Bach, P.M. A drainage network-based impact matrix to support targeted blue-green-grey stormwater management solutions. Sci. Total Environ. 2024, 912, 168623. [Google Scholar] [CrossRef] [PubMed]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; ETH Zurich, Computer Engineering and Networks Laboratory: Zurich, Switzerland, 2001. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Wang, M.; Fang, Y.; Sweetapple, C. Assessing flood resilience of urban drainage system based on a ‘do-nothing’ benchmark. J. Environ. Manag. 2021, 288, 112472. [Google Scholar] [CrossRef] [PubMed]
- Sweetapple, C.; Fu, G.; Farmani, R.; Meng, F.; Ward, S.; Butler, D. Attribute-based intervention development for increasing resilience of urban drainage systems. Water Sci. Technol. 2018, 77, 1757–1764. [Google Scholar] [CrossRef] [PubMed]
- Moon, H.-T.; Kim, J.-S.; Chen, J.; Yoon, S.-K.; Moon, Y.-I. Mitigating urban flood Hazards: Hybrid strategy of structural measures. Int. J. Disaster Risk Reduct. 2024, 108, 104542. [Google Scholar] [CrossRef]
- Yin, D.; Zhang, X.; Cheng, Y.; Jia, H.; Jia, Q.; Yang, Y. Can flood resilience of green-grey-blue system cope with future uncertainty? Water Res. 2023, 242, 120315. [Google Scholar] [CrossRef]


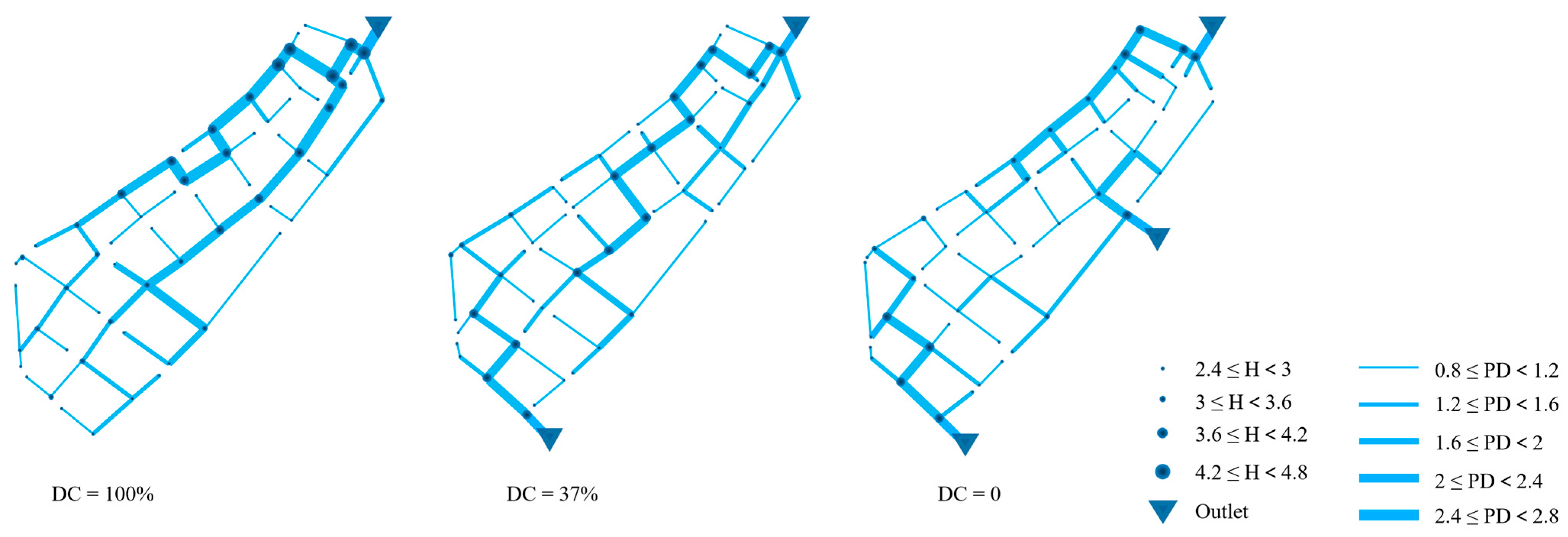

| Degree of Centralization (%) | Total Length of Pipes (m) | Average Diameter (m) | Maximum Diameter (m) | Maximum Depth of Manholes (m) | Cost (10 Million RMB) | Storage Capacity (m3) |
|---|---|---|---|---|---|---|
| 100 | 22,956.96 | 1.66 | 2.6 | 4.51 | 2.28 | 51,503.50 |
| 37 | 22,965.78 | 1.46 | 2.4 | 4.72 | 1.57 | 40,446.29 |
| 0 | 22,999.94 | 1.42 | 2.2 | 3.97 | 1.43 | 36,808.73 |
| Degree of Centralization (%) | Candidate Addition Pipelines for Loop-Introducing | Effect Proportion | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 26 | 6 | 50 | 40 | 19 | 54 | 27 | 44 | 38 | 33 | 55 | 4 | 112.14% |
| 0 | 50 | 34 | 5 | 32 | 6 | 28 | 21 | 59 | 51 | 45 | 12 | 61 | 106.80% |
| Degree of Centralization (%) | Candidate Replacement Pipelines for Pipe Diameter Enlarging | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 41 | 53 | 63 | 37 | 60 | 46 | 58 | 62 | 61 | 32 | 51 | 31 |
| 0 | 33 | 46 | 40 | 37 | 44 | 39 | 42 | 41 | 49 | 29 | 48 | 52 |
| Intervention Mode | Candidate Addition (Replacement) Pipelines | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Loop-introducing | 26 | 6 | 50 | 40 | 19 | 54 | 27 | 44 | 38 | 33 | 55 | 4 |
| Caliber enlarging | 41 | 53 | 63 | 37 | 60 | 46 | 58 | 62 | 61 | 32 | 51 | 31 |
| Intervention Mode | Candidate Addition (Replacement) Pipelines | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Loop-introducing | 50 | 34 | 5 | 32 | 6 | 28 | 21 | 59 | 51 | 45 | 12 | 61 |
| Caliber enlarging | 33 | 46 | 40 | 37 | 44 | 39 | 42 | 41 | 49 | 29 | 48 | 52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, E.; Gong, Y. A Structural Optimization of Urban Drainage Systems: An Optimization Approach for Mitigating Urban Floods. Water 2024, 16, 1696. https://doi.org/10.3390/w16121696
Zhang Y, Wang E, Gong Y. A Structural Optimization of Urban Drainage Systems: An Optimization Approach for Mitigating Urban Floods. Water. 2024; 16(12):1696. https://doi.org/10.3390/w16121696
Chicago/Turabian StyleZhang, Yukun, Ersong Wang, and Yongwei Gong. 2024. "A Structural Optimization of Urban Drainage Systems: An Optimization Approach for Mitigating Urban Floods" Water 16, no. 12: 1696. https://doi.org/10.3390/w16121696
APA StyleZhang, Y., Wang, E., & Gong, Y. (2024). A Structural Optimization of Urban Drainage Systems: An Optimization Approach for Mitigating Urban Floods. Water, 16(12), 1696. https://doi.org/10.3390/w16121696







