Constructing a Machine Learning Model for Rapid Urban Flooding Forecast in Sloping Cities along the Yangtze River: A Case Study in Jiujiang
Abstract
1. Introduction
2. Research Methods
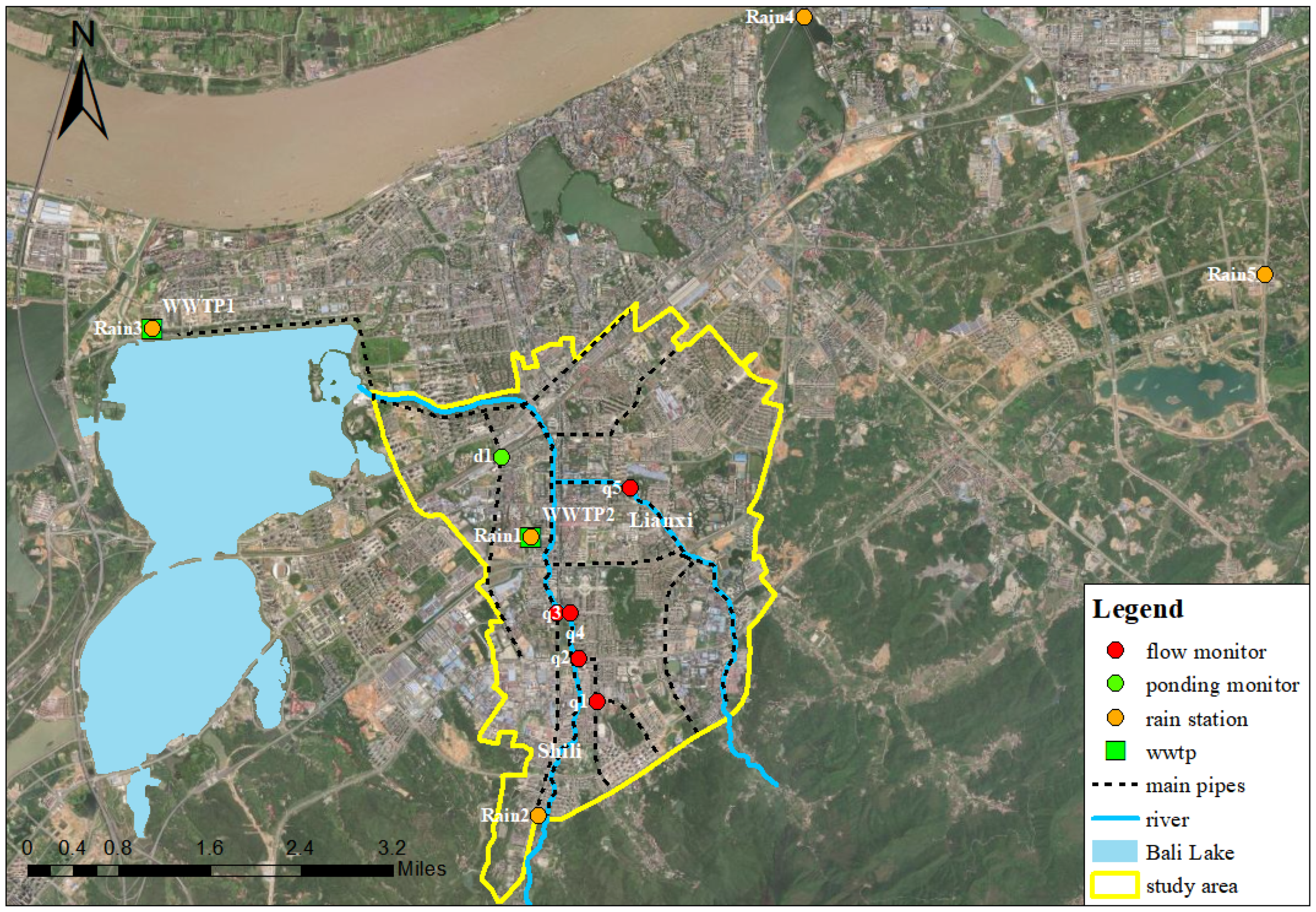
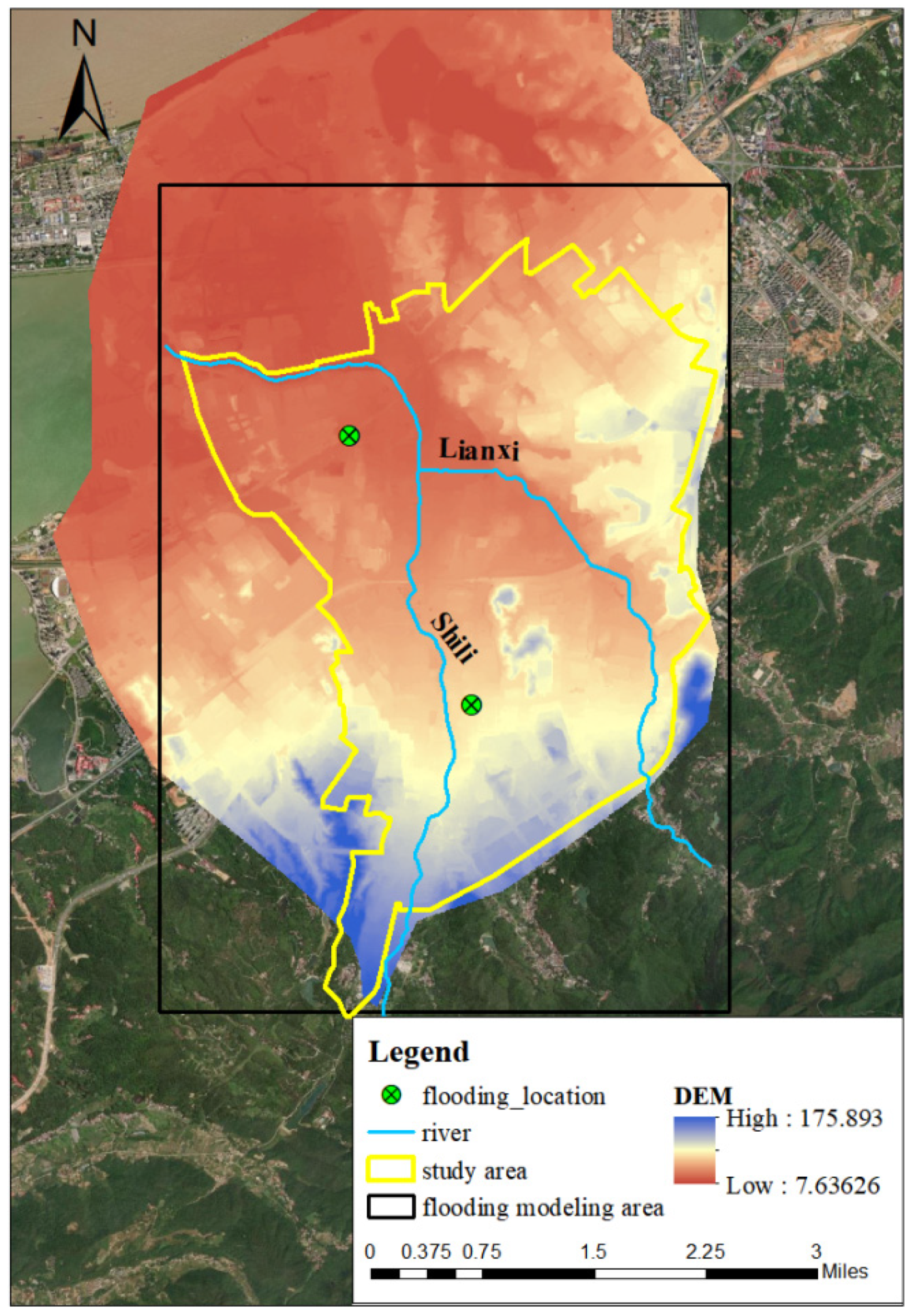
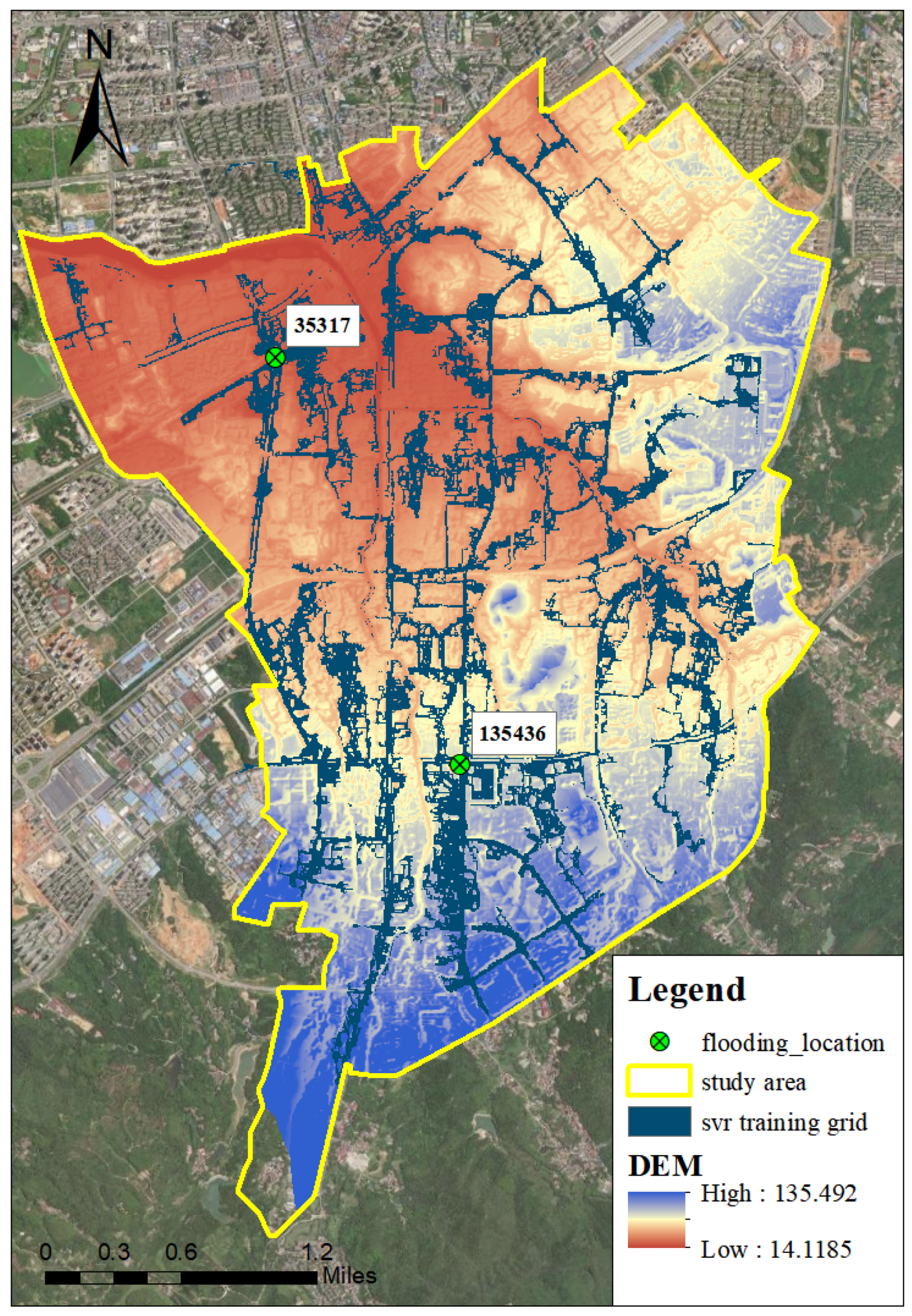
2.1. Study Area
2.2. Methodology
2.2.1. 1D Drainage System Model and 2D Overland Flow Model
2.2.2. Coupling of 1D and 2D Models
- ①
- Depth1d > Depth2d, while the junction water level was higher than the surface water level at the corresponding position. At present, the water flow in the pipe network system was outflowing through the junctions into the surface flow, and the water flow was transitioning from the 1D model to the 2D model.
- ②
- Depth1d < Depth2d, while the water level at the junctions was lower than the surface water level at the corresponding position. The water flowed from the surface to the underground drainage pipe network, and the water flow entered the 1Dmodel from the 2D.
- ③
- Depth1d = Depth2d, while the surface water level was equal to the junction water level, or there was no water on the surface and the junction water level was lower than the surface elevation, the surface and groundwater flow did not exchange.
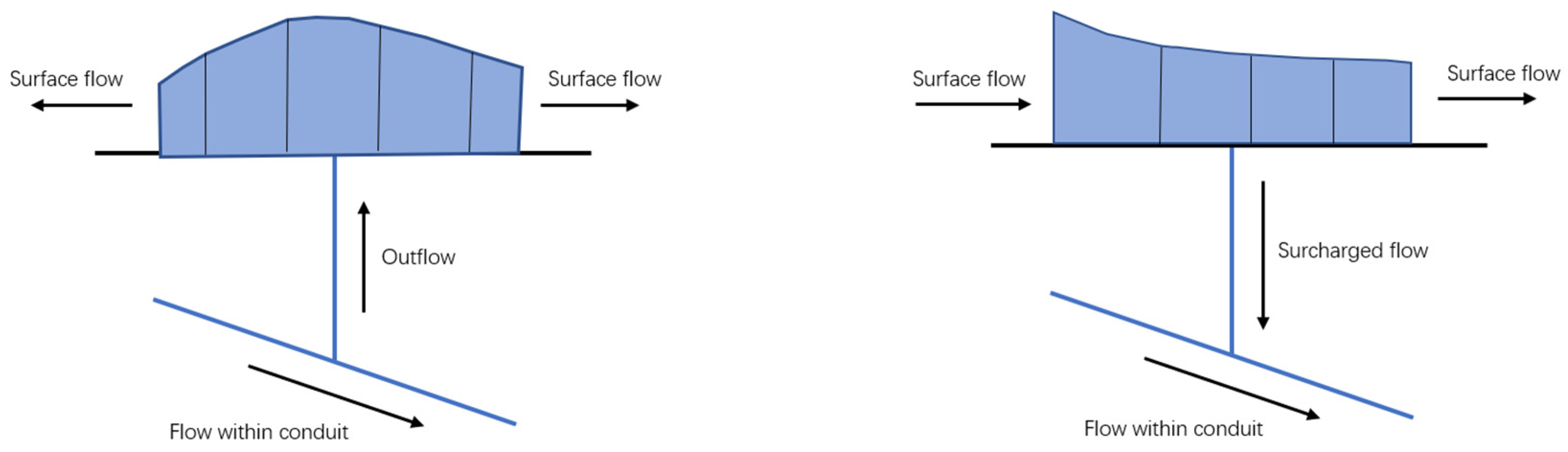
- (1)
- Junction outflow
- (2)
- Surcharged flow
2.2.3. SVR
2.2.4. Integrating Model of Mechanism and Machine Learning Models
3. Model Construction
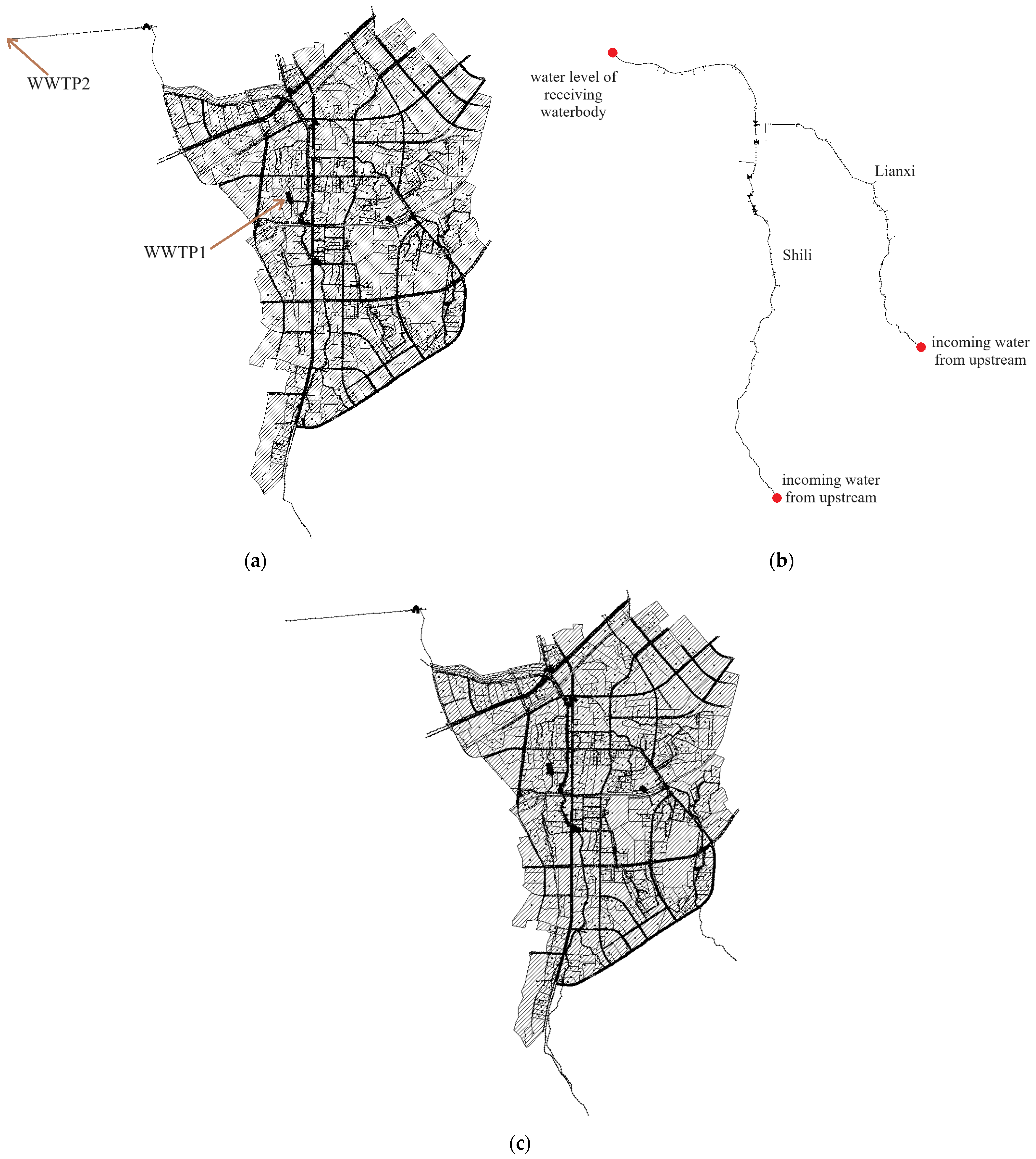
3.1. Coupling Model Construction
3.1.1. 1D Drainage System and River Model
3.1.2. Coupling of 1D and 2D Model
3.1.3. Calibration and Verification
3.2. ML Flooding Model Construction
3.2.1. Data Collection and Processing
3.2.2. Feature Engineering
3.2.3. Hyperparameters Selection
3.2.4. Training and Validating
3.2.5. Model Evaluation
4. Data
4.1. Monitor Data for Model Calibration and Validation
- (1)
- The rainfall was considered to end if there was no rain for the following 6 h.
- (2)
- The accumulated rainfall volume of a single rainfall event was assumed to be more than 1 mm.
- (3)
- Since there were multiple rain gauges in function, the analysis was conducted individually for each gauge, and the amalgamation of periods was the eventual outcome for single rainfall event division.
4.2. Simulation Data for SVR Model Training
5. Results and Discussion
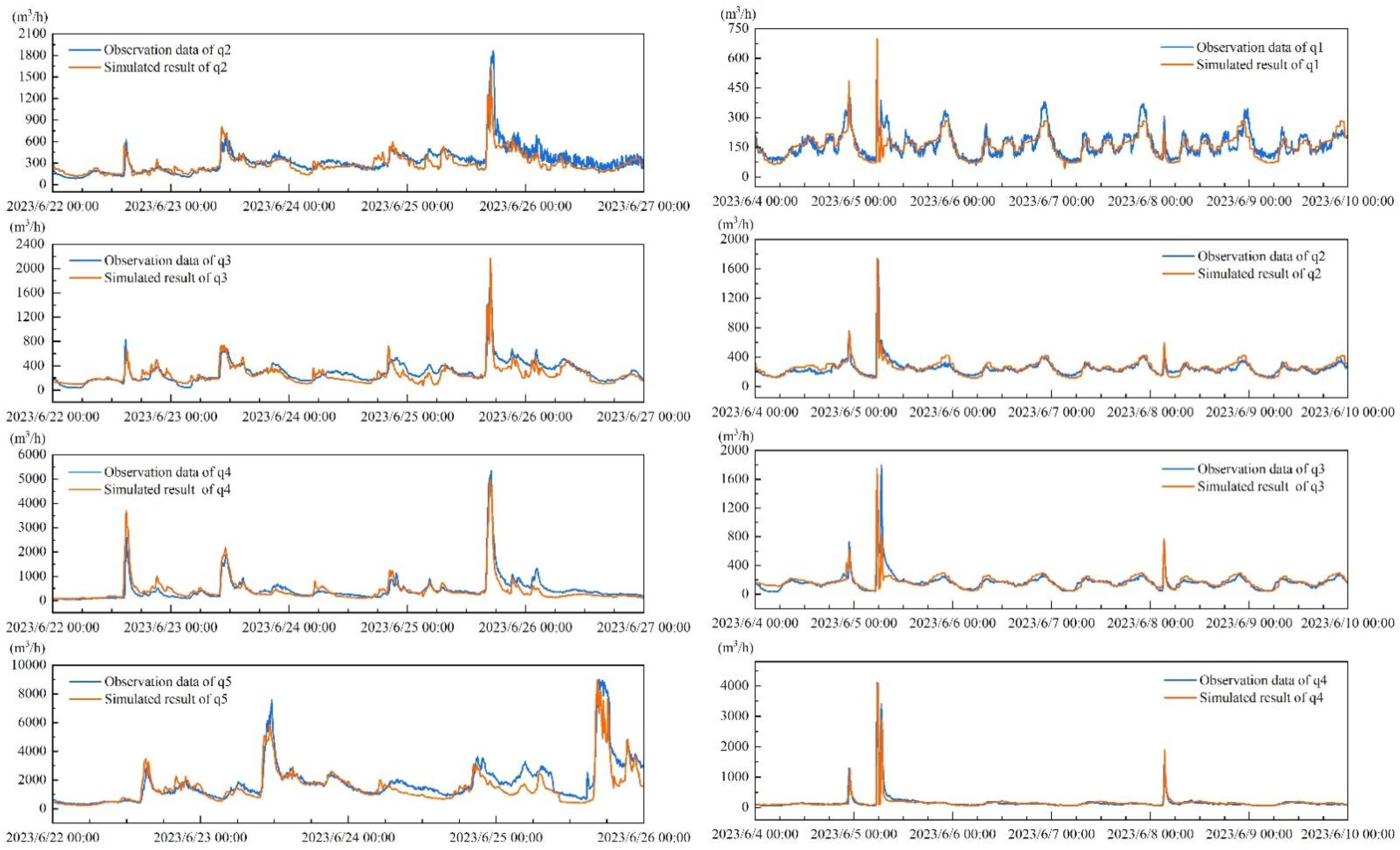
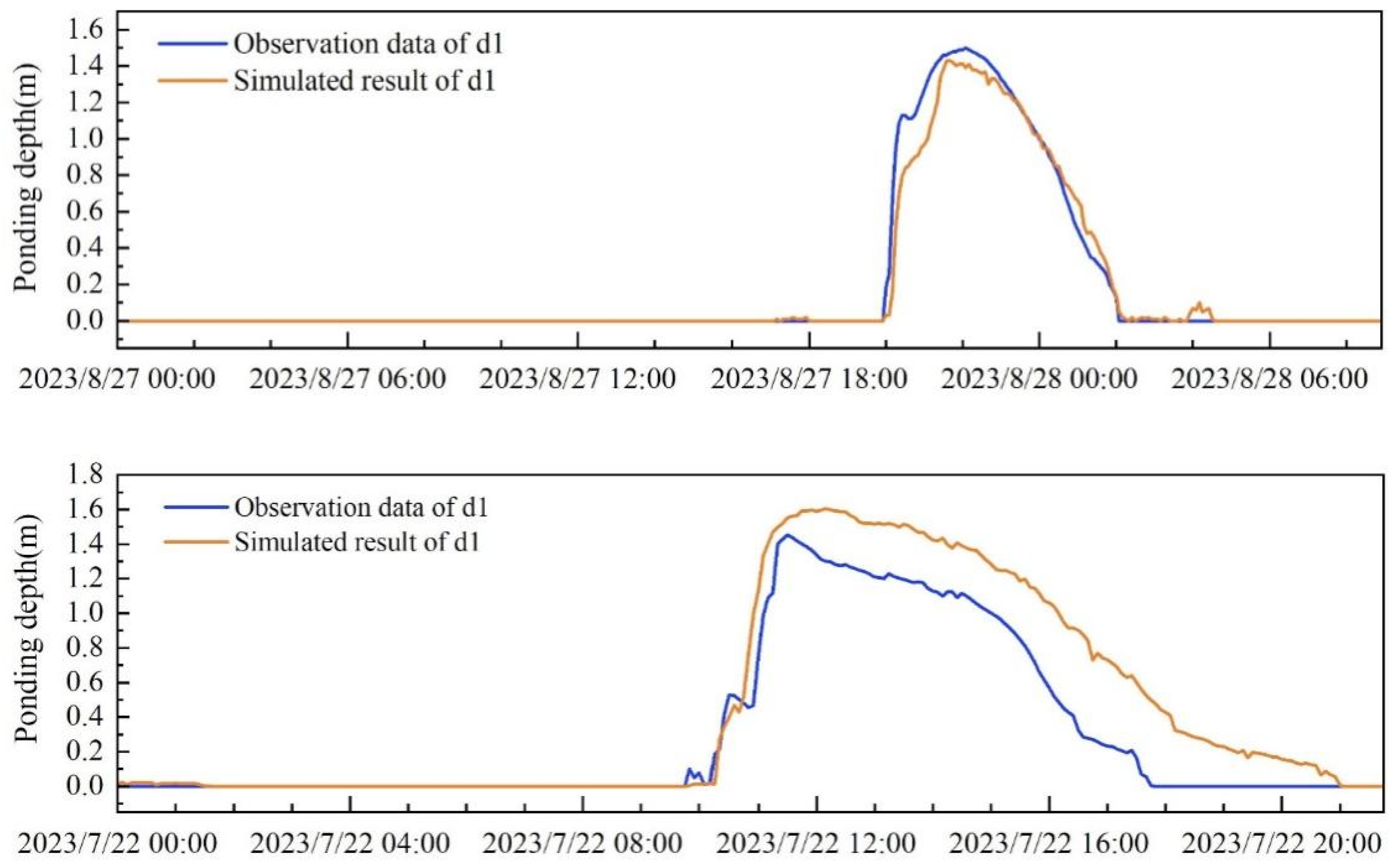
5.1. Calibration and Validation Results of the Coupled Model
5.2. Calibration and Validation Results of SVR Model
5.3. Comparison between the Mechanism Model and SVR Model
5.4. Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Han, D. Big Data and Hydroinformatics. J. Hydroinform. 2016, 18, 599–614. [Google Scholar] [CrossRef]
- Akter, S.; Wamba, S.F. Big Data and Disaster Management: A Systematic Review and Agenda for Future Research. Ann. Oper. Res. 2019, 283, 939–959. [Google Scholar] [CrossRef]
- Zhou, L.; Huang, H.; Muthu, B.A.; Sivaparthipan, C.B. Design of Internet of Things and Big Data Analytics-Based Disaster Risk Management. Soft Comput. 2021, 25, 12415–12427. [Google Scholar] [CrossRef]
- Martínez–Álvarez, F.; Morales–Esteban, A. Big Data and Natural Disasters: New Approaches for Spatial and Temporal Massive Data Analysis. Comput. Geosci. 2019, 129, 38–39. [Google Scholar] [CrossRef]
- Pedrozo-Acuña, A.; Moreno, G.; Mejía-Estrada, P.; Paredes-Victoria, P.; Breña-Naranjo, J.A.; Meza, C. Integrated Approach to Determine Highway Flooding and Critical Points of Drainage. Transp. Res. Part. D Transp. Environ. 2017, 50, 182–191. [Google Scholar] [CrossRef]
- Mignot, E.; Paquier, A.; Haider, S. Modeling Floods in a Dense Urban Area Using 2D Shallow Water Equations. J. Hydrol. 2006, 327, 186–199. [Google Scholar] [CrossRef]
- Douinot, A.; Roux, H.; Garambois, P.-A.; Larnier, K.; Labat, D.; Dartus, D. Accounting for Rainfall Systematic Spatial Variability in Flash Flood Forecasting. J. Hydrol. 2016, 541, 359–370. [Google Scholar] [CrossRef]
- Payande, A.R.; Niksokhan, M.H.; Naserian, H. Tsunami Hazard Assessment of Chabahar Bay Related to Megathrust Seismogenic Potential of the Makran Subduction Zone. Nat. Hazards 2015, 76, 161–176. [Google Scholar] [CrossRef]
- Papaioannou, G.; Loukas, A.; Vasiliades, L.; Aronica, G.T. Flood Inundation Mapping Sensitivity to Riverine Spatial Resolution and Modelling Approach. Nat. Hazards 2016, 83, 117–132. [Google Scholar] [CrossRef]
- Chang, X.; Xu, Z.; Zhao, G.; Du, L. Urban rainfall-runoff simulations and assessment of low impact development facilities using SWMM model-A case study of Qinghe catchment in Beijing. J. Hydroelectr. Eng. 2016, 35, 84–93. [Google Scholar] [CrossRef]
- Huang, G.; Huang, W.; Zhang, L.; Chen, W.; Feng, J. Simulation of rainstorm waterlogging in urban areas based on GIS and SWMM model. J. Water Resour. Water Eng. 2015, 26, 1–6. [Google Scholar] [CrossRef]
- Ma, R.; Bai, T.; Huang, Q.; Yang, W. MIKE 21 model and its application on urban waterlogging simulation. J. Nat. Disasters 2017, 26, 172–179. [Google Scholar] [CrossRef]
- Guo, F.; Qu, H.; Zeng, H.; Cong, S.; Geng, X. Flood Routing Numerical Simulation of Flood Storage Area Based on MIKE21 FM Model. Water Resour. Power 2013, 31, 34–37. [Google Scholar]
- Wei, K.; Liang, Z.; Wang, J. Flood Routing Simulation of MengWa Detention Basin based on MIKE21. South-North Water Transf. Water Sci. Technol. 2013, 11, 16–19. [Google Scholar] [CrossRef]
- Wang, X.; Han, H.; Li, H. Flood Risk and Duration Analysis of Ningjinbo and Daluze Flood Storage.detention District. Water Resour. Power 2013, 31, 59–62. [Google Scholar]
- Zheng, S.; Wan, Q.; Jia, M. Short-term forecasting of waterlogging at urban storm-waterlogging monitoring sites based on STARMA model. Prog. Geogr. 2014, 33, 949–957. [Google Scholar] [CrossRef]
- Li, X.-L.; Lü, H.; Horton, R.; An, T.; Yu, Z. Real-Time Flood Forecast Using the Coupling Support Vector Machine and Data Assimilation Method. J. Hydroinform. 2013, 16, 973–988. [Google Scholar] [CrossRef]
- Abou Rjeily, Y.; Abbas, O.; Sadek, M.; Shahrour, I.; Hage Chehade, F. Flood Forecasting within Urban Drainage Systems Using NARX Neural Network. Water Sci. Technol. 2017, 76, 2401–2412. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Jin, J.; Chen, F.; Yu, G.; Yin, H.; Wang, W. Urban Flash Flood Forecast Using Support Vector Machine and Numerical Simulation. J. Hydroinform. 2017, 20, 221–231. [Google Scholar] [CrossRef]
- Chen, W. Urban Flood Hydrological and Hydrodynamic ModelConstruction and Flood Management Key Issues Exploration; South China University of Technology: Guangzhou, China, 2020. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the Use of “Goodness-of-Fit” Measures in Hydrologic and Hydroclimatic Model Validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]



| Time | Total Rainfall Amount at Station 1 (mm) | Total Rainfall Amount at Station 2 (mm) | Available Monitors | Usage | Rain Event | Rainfall Duration (h) | |
|---|---|---|---|---|---|---|---|
| 1# | 5 June 2023 5:15–5 June 2023 6:25 | 31 | 24 | q1, q2, q3, q4 * | SWMM model verification, SVR model training | 1# | 2.1 |
| 2# | 22 June 2023 14:35–26 June 2023 7:55 | 100 | 99 | q2, q3, q4, q5 ** | SWMM model calibration, SVR model training | 2#1 | 42 |
| 2#2 | 15 | ||||||
| 2#3 | 18 | ||||||
| 3# | 22 July 2023 9:30–22 July 2023 14:30 | 34 | 21 | d1 | Coupled model verification, SVR model validation | 3# | 4.7 |
| 4# | 21 August 2023 19: 30–28 August 2023 4:20 | 44 | 37 | d1 | Coupled model calibration, SVR model validation | 4# | 8.8 |
| Type | Duration (h) | Return Period (a) | Accumulated Rainfall (mm) | Number |
|---|---|---|---|---|
| 1 | 1 | 15 * | 1 | |
| 2 | 2 | 15 * | 20, 30, 50, 100 | 5 |
| 3 | 3 | 0.05, 0.1, 0.2, 0.3, 0.5, 1, 2, 3, 5, 10, 15 *, 20, 30, 50, 100 | 15 | |
| 4 | 24 | 30, 50, 100, 150, 160 * | 6 |
| Number | Events | Observed/Coupled Model Result Max Ponding Depth at d1 (m) | SVR Result Max Ponding Depth at d1 (m) | Percentage Error |
|---|---|---|---|---|
| 1 | Design rainfall, 1 h, 15a (74 mm) | 1.2 | 1.2 | <0.01% |
| 2 | Design rainfall, 2 h, 15a (92 mm) | 1.2 | 1.2 | <0.01% |
| 3 | Design rainfall, 3 h, 15a (105 mm) | 1.2 | 1.2 | <0.01% |
| 4 | Design rainfall, 24 h, 160 mm | 1.1 | 1.1 | <0.01% |
| 5 | Observed rainfall, 4.67 h, 34 mm (Rain1) (event #3) | 1.4 | 1.7 | 16% |
| 6 | Observed rainfall, 8.75 h, 43.5 mm (Rain1) (event #4) | 1.6 | 1.6 | <0.01% |
| Model | Simulation Time for Event #3 (8 h) | Simulation Time for Event #4 (5 h) |
|---|---|---|
| The coupled mechanism model | 38 min | 24 min |
| The SVR model | 1.0 min | 1.0 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Lu, X.; Chen, R.; Guo, M.; Wang, X. Constructing a Machine Learning Model for Rapid Urban Flooding Forecast in Sloping Cities along the Yangtze River: A Case Study in Jiujiang. Water 2024, 16, 1694. https://doi.org/10.3390/w16121694
Gao Z, Lu X, Chen R, Guo M, Wang X. Constructing a Machine Learning Model for Rapid Urban Flooding Forecast in Sloping Cities along the Yangtze River: A Case Study in Jiujiang. Water. 2024; 16(12):1694. https://doi.org/10.3390/w16121694
Chicago/Turabian StyleGao, Zhong, Xiaoping Lu, Ruihong Chen, Minrui Guo, and Xiaoxuan Wang. 2024. "Constructing a Machine Learning Model for Rapid Urban Flooding Forecast in Sloping Cities along the Yangtze River: A Case Study in Jiujiang" Water 16, no. 12: 1694. https://doi.org/10.3390/w16121694
APA StyleGao, Z., Lu, X., Chen, R., Guo, M., & Wang, X. (2024). Constructing a Machine Learning Model for Rapid Urban Flooding Forecast in Sloping Cities along the Yangtze River: A Case Study in Jiujiang. Water, 16(12), 1694. https://doi.org/10.3390/w16121694






