Modeling and Data Mining Analysis for Long-Term Temperature-Stress-Strain Monitoring Data of a Concrete Gravity Dam
Abstract
1. Introduction
2. Methodology
2.1. K-Means Algorithm
2.2. Inverse Distance Weight
2.3. D-AHP Method
3. Case Study
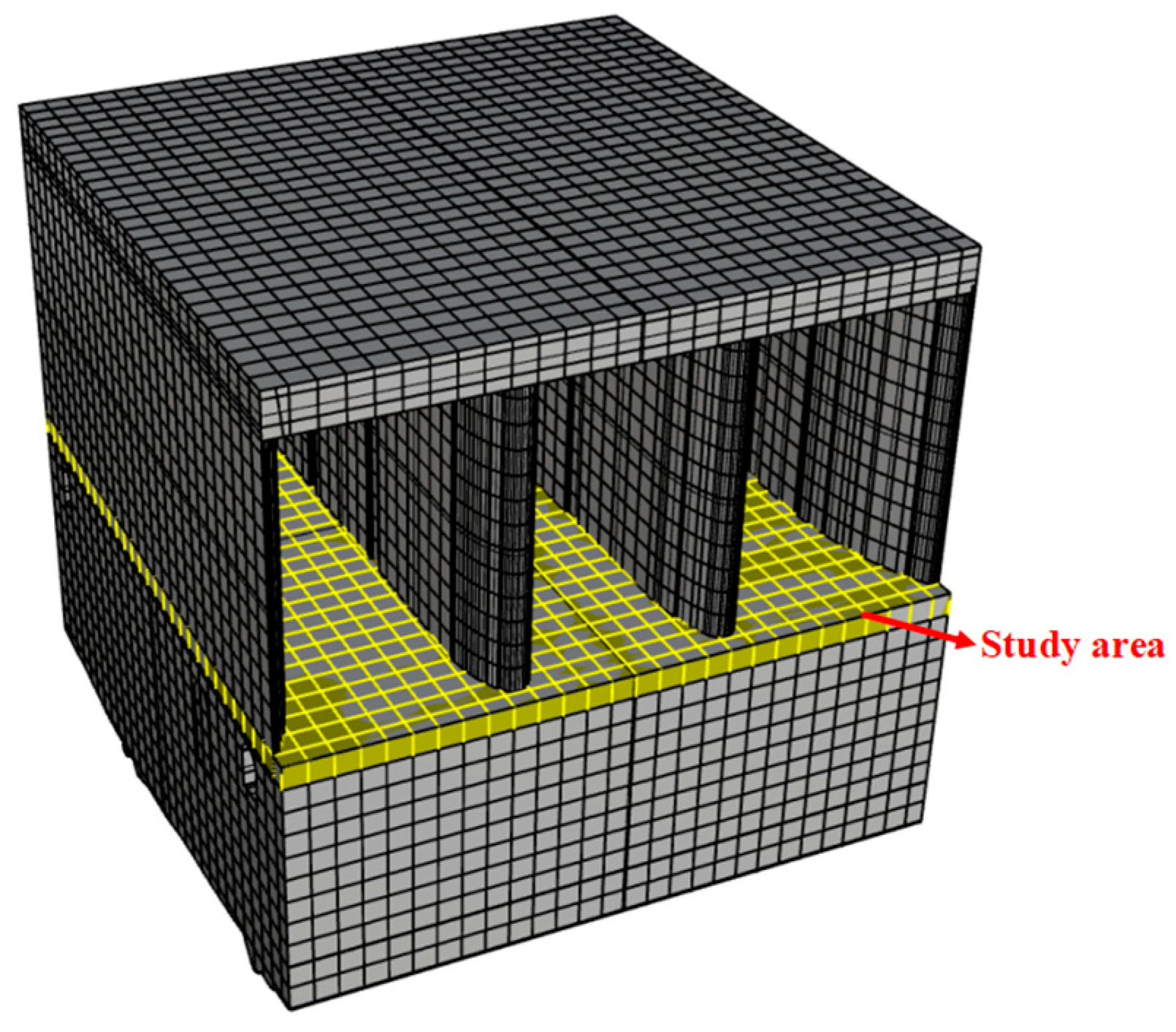
3.1. The Dam and Monitoring System
3.2. Data Mining by Long-Term Monitoring Records
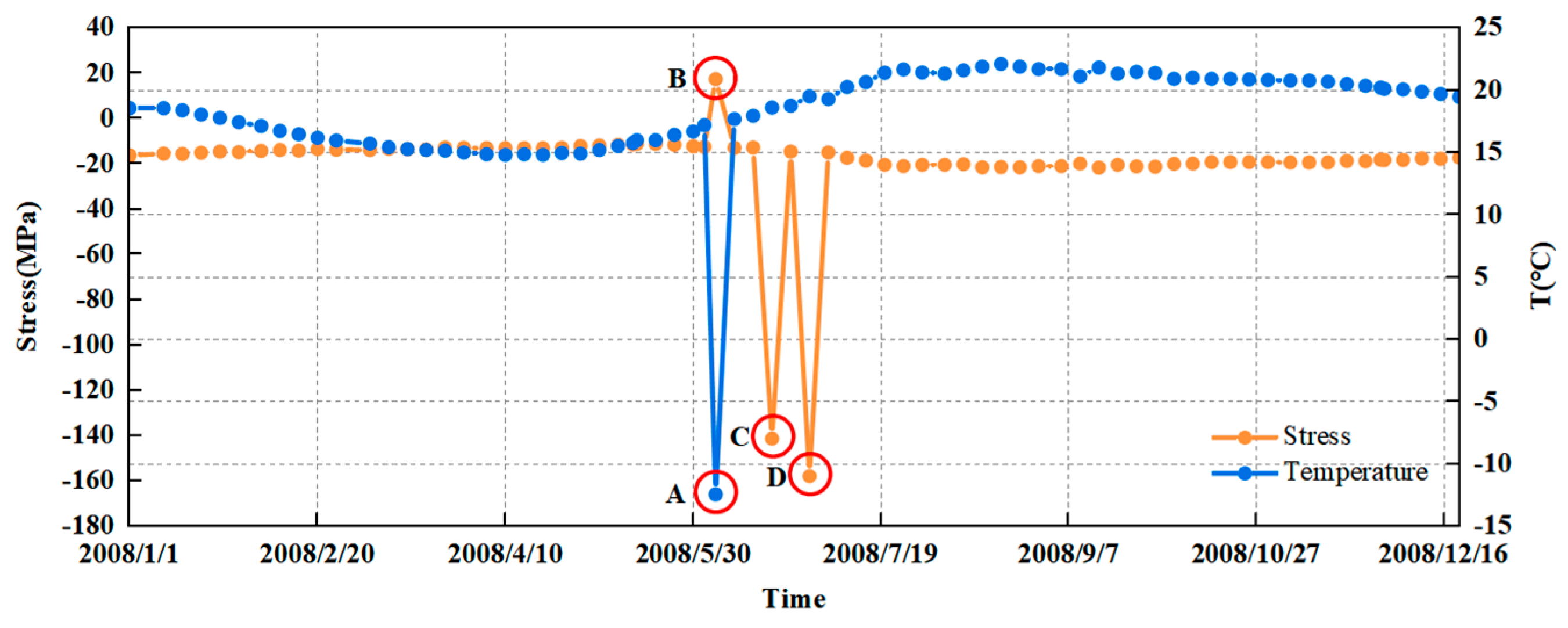
3.2.1. Data Cleaning
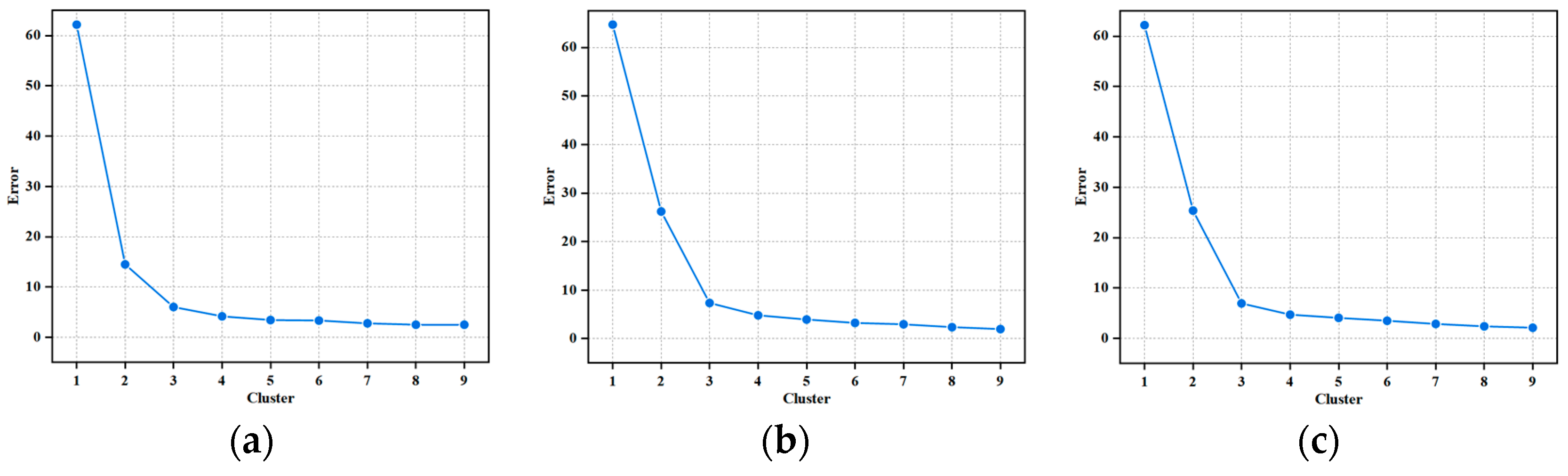
3.2.2. Evaluation Grade Classification Results
3.3. IDW Modeling of Temperature-Stress-Strain Field
4. Comprehensive Evaluation by the D-AHP Method
4.1. Calculating Weights of Indicators
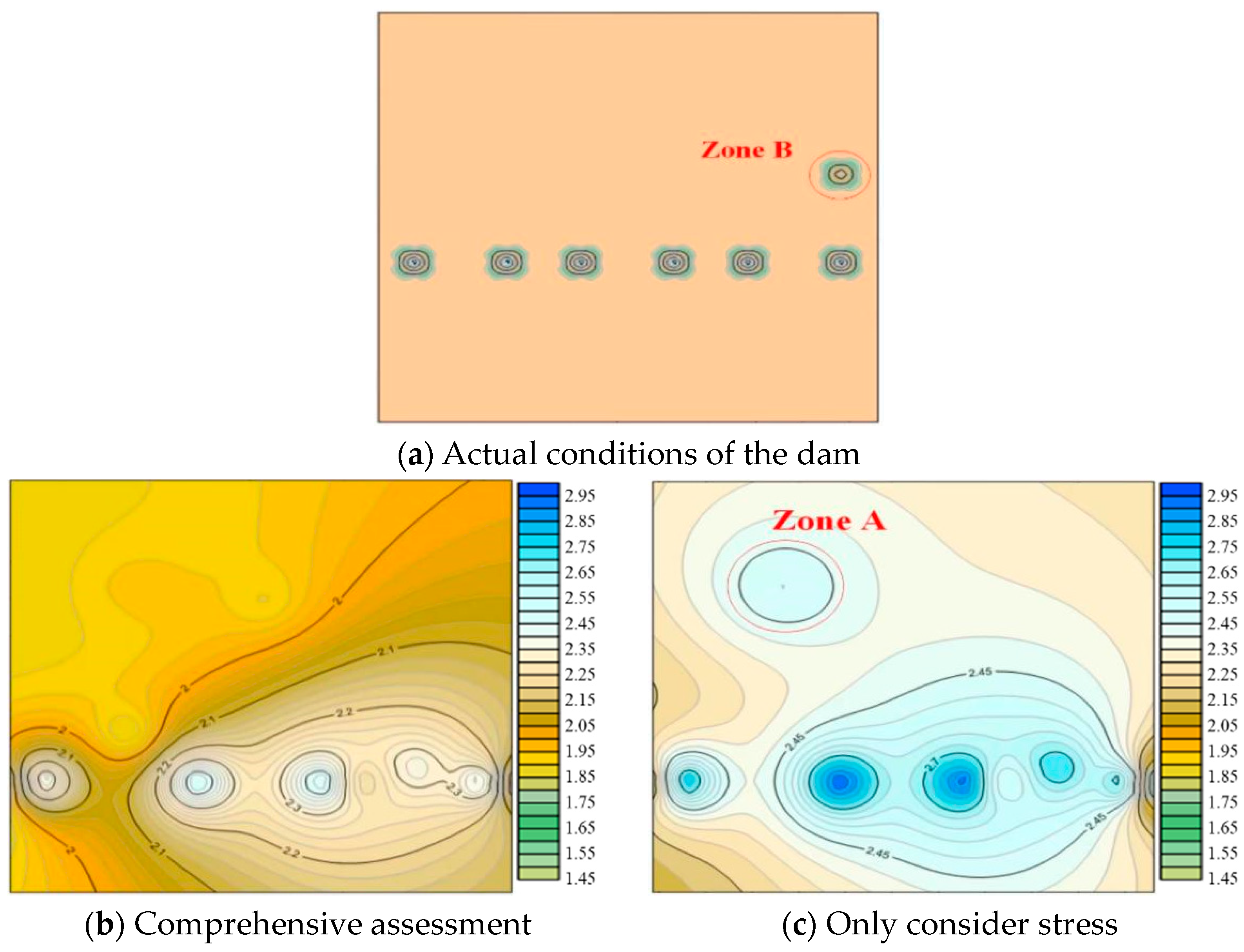
4.2. Comprehensive Evaluation Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Banerjee, A.; Paul, D.K.; Acharyya, A. Optimization and safety evaluation of concrete gravity dam section. KSCE J. Civ. Eng. 2015, 19, 1612–1619. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Li, H.; Shen, Y. A novel deep learning prediction model for concrete dam displacements using interpretable mixed attention mechanism. Adv. Eng. Inform. 2021, 50, 101407. [Google Scholar] [CrossRef]
- Gu, C.; Li, B.; Xu, G.; Yu, H. Back analysis of mechanical parameters of roller compacted concrete dam. Sci. China Technol. Sci. 2010, 53, 848–853. [Google Scholar] [CrossRef]
- Yu, H.; Wu, Z.; Bao, T.; Zhang, L. Multivariate analysis in dam monitoring data with PCA. Sci. China Technol. Sci. 2010, 53, 1088–1097. [Google Scholar] [CrossRef]
- Aly, T.; Sanjayan, J.G.; Collins, F. Effect of polypropylene fibers on shrinkage and cracking of concretes. Mater. Struct. 2008, 41, 1741–1753. [Google Scholar] [CrossRef]
- Castilho, E.; Schclar, N.; Tiago, C.; Farinha, M.L.B. FEA model for the simulation of the hydration process and temperature evolution during the concreting of an arch dam. Eng. Struct. 2018, 174, 165–177. [Google Scholar] [CrossRef]
- Qiang, S.; Xie, Z.; Zhong, R. A p-version embedded model for simulation of concrete temperature fields with cooling pipes. Water Sci. Eng. 2015, 8, 248–256. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Li, B.; Zhang, G.; Zhang, S. Study on real-time simulation analysis and inverse analysis system for temperature and stress of concrete dam. Math. Probl. Eng. 2015, 2015, 306165. [Google Scholar] [CrossRef]
- Zhong, R.; Hou, G.; Qiang, S. An improved composite element method for the simulation of temperature field in massive concrete with embedded cooling pipe. Appl. Therm. Eng. 2017, 124, 1409–1417. [Google Scholar] [CrossRef]
- Li, M.; Si, W.; Du, S.; Zhang, M.; Ren, Q.; Shen, Y. Thermal deformation coordination analysis of CC-RCC combined dam structure during construction and operation periods. Eng. Struct. 2020, 213, 110587. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhong, W.; Li, Y.; Wen, L. A deep learning prediction model of DenseNet-LSTM for concrete gravity dam deformation based on feature selection. Eng. Struct. 2023, 295, 116827. [Google Scholar] [CrossRef]
- Rakić, D.; Bojović, M.; Vulovic, S.; Zivkovic, M.; Divac, D.; Milivojević, N. Stability Analysis of Concrete Gravity Dam Using FEM; University of Kragujevac: Kragujevac, Serbia, 2017. [Google Scholar]
- Li, B.; Zhang, Z.; Liu, Y.; Yang, S. Evaluation standard for safety coefficient of roller compacted concrete dam based on finite element method. Math. Probl. Eng. 2014, 2014, 601418. [Google Scholar] [CrossRef]
- Zhang, S.; Zheng, D.; Liu, Y. Deformation prediction system of concrete dam based on IVM-SCSO-RF. Water 2022, 14, 3739. [Google Scholar] [CrossRef]
- Xing, Y.; Chen, Y.; Huang, S.; Wang, P.; Xiang, Y. Research on dam deformation prediction model based on optimized SVM. Processes 2022, 10, 1842. [Google Scholar] [CrossRef]
- Dai, B.; Gu, C.; Zhao, E.; Qin, X. Statistical model optimized random forest regression model for concrete dam deformation mon-itoring. Struct. Control. Health Monit. 2018, 25, e2170. [Google Scholar] [CrossRef]
- Su, H.; Li, X.; Yang, B.; Wen, Z. Wavelet support vector machine-based prediction model of dam deformation. Mech. Syst. Signal Process. 2018, 110, 412–427. [Google Scholar] [CrossRef]
- Kang, F.; Liu, J.; Li, J.; Li, S. Concrete dam deformation prediction model for health monitoring based on extreme learning machine. Struct. Control. Health Monit. 2017, 24, e1997. [Google Scholar] [CrossRef]
- Han, P.; Wang, W.; Shi, Q.; Yue, J. A combined online-learning model with K-means clustering and GRU neural networks for trajectory prediction. Ad Hoc Netw. 2021, 117, 102476. [Google Scholar] [CrossRef]
- Franke, R. Scattered data interpolation: Tests of some methods. Math. Comput. 1982, 38, 181–200. [Google Scholar]
- Shi, Y.; He, W.; Zhao, J.; Hu, A.; Pan, J.; Wang, H.; Zhu, H. Expected output calculation based on inverse distance weighting and its application in anomaly detection of distributed photovoltaic power stations. J. Clean. Prod. 2020, 253, 119965. [Google Scholar] [CrossRef]
- Tan, J.; Xie, X.; Zuo, J.; Xing, X.; Liu, B.; Xia, Q.; Zhang, Y. Coupling random forest and inverse distance weighting to generate climate surfaces of precipitation and temperature with multiple-covariates. J. Hydrol. 2021, 598, 126270. [Google Scholar] [CrossRef]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychology. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Burayu, D.G.; Karuppannan, S.; Shuniye, G. Identifying flood vulnerable and risk areas using the integration of analytical hierarchy process (AHP), GIS, and remote sensing: A case study of southern Oromia region. Urban Clim. 2023, 51, 101640. [Google Scholar] [CrossRef]
- Ahadi, P.; Fakhrabadi, F.; Pourshaghaghy, A.; Kowsary, F. Optimal site selection for a solar power plant in Iran via the Analytic Hierarchy Process (AHP). Renew. Energy 2023, 215, 118944. [Google Scholar] [CrossRef]
- Deng, X.; Hu, Y.; Deng, Y.; Mahadevan, S. Supplier selection using AHP methodology extended by D numbers. Expert Syst. Appl. 2014, 41, 156–167. [Google Scholar] [CrossRef]
- Fan, G.; Zhong, D.; Yan, F.; Yue, P. A hybrid fuzzy evaluation method for curtain grouting efficiency assessment based on an AHP method extended by D numbers. Expert Syst. Appl. 2016, 44, 289–303. [Google Scholar] [CrossRef]
- Zong, F.; Wang, L. Evaluation of university scientific research ability based on the output of sci-tech papers: A D-AHP approach. PLoS ONE 2017, 12, e0171437. [Google Scholar] [CrossRef]





| Item | Value |
|---|---|
| Maximum height | 47 m |
| Crest elevation | 70 m |
| Crest length | 2595 m |
| Operational water level | 51 m |
| Reservoir volume | 15.8 km3 |
| Number of generators | 22 |
| Installed capacity | 2710 MW |
| Annual energy generation | 157 × 109 kw·h |
| Assessment Level | I (Good) | II (Ordinary) | III (Poor) |
|---|---|---|---|
| Stress (MPa) | 23.88 | 126.28 | −19.28 |
| Strain (με) | −31.92 | 33.76 | 135.83 |
| Temperature (°C) | (17.82, 0.25) | (18.02, 3.93) | (27.93, 1.99) |
| Evaluation-value | 1 | 2 | 3 |
| Recorder | E-Value | Recorder | E-Value | Recorder | E-Value |
|---|---|---|---|---|---|
| R80−2 | 3 | R80−10 | 3 | R81−7 | 3 |
| R80−3 | 1 | R80−12 | 3 | R82−2 | 3 |
| R80−4 | 3 | R81−1 | 3 | R82−4 | 1 |
| R80−5 | 3 | R81−2 | 3 | R82−8 | 2 |
| R80−6 | 3 | R81−4 | 1 | E082−1 | 2 |
| R80−8 | 3 | R81−5 | 3 | E082−3 | 3 |
| Recorder | E-Value | Recorder | E-Value | Recorder | E-Value |
|---|---|---|---|---|---|
| E82−1 | 1 | E82−4 | 1 | E82−8 | 1 |
| E82−2 | 1 | E82−6 | 1 | E82−9 | 3 |
| E82−3 | 2 | E82−7 | 1 | E82−10 | 1 |
| Recorder | E-Value | Recorder | E-Value | Recorder | E-Value | Recorder | E-Value |
|---|---|---|---|---|---|---|---|
| R80−2 | 2 | R81−1 | 2 | R82−6 | 2 | E82−3 | 1 |
| R80−3 | 3 | R81−2 | 2 | R82−7 | 2 | E82−4 | 1 |
| R80−4 | 2 | R81−3 | 2 | R82−8 | 2 | E82−5 | 1 |
| R80−5 | 2 | R81−5 | 2 | J81−2 | 1 | E82−6 | 1 |
| R80−6 | 2 | R81−7 | 2 | J82−1 | 1 | E82−7 | 1 |
| R80−8 | 2 | R82−2 | 2 | E082−1 | 1 | E82−8 | 1 |
| R80−9 | 2 | R82−3 | 2 | E082−2 | 1 | E82−9 | 1 |
| R80−10 | 2 | R82−4 | 2 | E082−3 | 1 | E82−10 | 1 |
| R80−12 | 2 | R82−5 | 2 | E082−4 | 1 | E82−11 | 1 |
| Criteria | C1 (Displacement) 0.6 | C2 (Crack) 0.4 | Weight |
|---|---|---|---|
| I1 (Stress) | 0.51 | 0.50 | 0.506 |
| I2 (Temperature) | 0.31 | 0.40 | 0.346 |
| I3 (Strain) | 0.18 | 0.10 | 0.148 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, T.; Ma, N.; Su, X.; Wu, Z.; Zhong, W.; Zhang, Y. Modeling and Data Mining Analysis for Long-Term Temperature-Stress-Strain Monitoring Data of a Concrete Gravity Dam. Water 2024, 16, 1646. https://doi.org/10.3390/w16121646
Zhou T, Ma N, Su X, Wu Z, Zhong W, Zhang Y. Modeling and Data Mining Analysis for Long-Term Temperature-Stress-Strain Monitoring Data of a Concrete Gravity Dam. Water. 2024; 16(12):1646. https://doi.org/10.3390/w16121646
Chicago/Turabian StyleZhou, Tao, Ning Ma, Xiaojun Su, Zhigang Wu, Wen Zhong, and Ye Zhang. 2024. "Modeling and Data Mining Analysis for Long-Term Temperature-Stress-Strain Monitoring Data of a Concrete Gravity Dam" Water 16, no. 12: 1646. https://doi.org/10.3390/w16121646
APA StyleZhou, T., Ma, N., Su, X., Wu, Z., Zhong, W., & Zhang, Y. (2024). Modeling and Data Mining Analysis for Long-Term Temperature-Stress-Strain Monitoring Data of a Concrete Gravity Dam. Water, 16(12), 1646. https://doi.org/10.3390/w16121646






