Durability Analysis of Concrete Cutoff Wall of Earth-Rock Dams Considering Seepage and Dissolution Coupling Effect

Abstract

In this paper, a novel numerical model for characterizing the seepage and dissolution coupling effect on the durability of anti-seepage walls of earth-rock dams is proposed. The model considers the influence of hydraulic gradient-driven seepage on the non-equilibrium decomposition of the calcium dissolution in concrete, as well as the effects of seepage dissolution on pore structure, permeability, and diffusivity. The reasonableness of the model is validated by experimental and literature data, which is then applied to analyze the deterioration and failure processes of a concrete cutoff wall of an earth-rock dam in Zhejiang Province, China. On this basis, the seepage dissolution durability control indices of anti-seepage walls are identified. The findings demonstrate that the suggested method accurately explains the calcium leaching process in concrete. Under the seepage and dissolution coupling effect, calcium in the wall continuously decomposes and precipitates, leading to varying degrees of increases in structural performance parameters, which weaken the seepage control performance of the walls and consequently result in an increase in seepage discharge and hydraulic gradient. By proposing the critical hydraulic gradient as a criterion, the service life of the wall is projected to be 42.8 years. Additionally, the upstream hydraulic head, the initial permeability coefficient, and the calcium hydroxide (CH) content are three crucial indices affecting the durability of walls, and these indices should be reasonably controlled during the engineering design, construction, and operational phases.

1. Introduction

Earth-rock dams, known for their safety and cost-effectiveness, are widely utilized in hydraulic engineering worldwide [1,2,3]. Concrete cutoff walls, serving as critical reinforcement and anti-seepage structures within these dams, play a pivotal role in safeguarding against potential risks. However, the durability of these walls is a growing concern due to their exposure to high hydraulic heads and susceptibility to erosion from soft water [4,5,6]. The combined impact of hydraulic gradient-driven seepage and dissolution poses a significant threat, potentially leading to structural degradation and the failure of the dam’s anti-seepage system and the foundation [7,8]. As a result, it is imperative to thoroughly investigate the long-term behavior of concrete cutoff walls in earth-rock dams to ensure their durability and overall safety.

Seepage dissolution is an intrinsic issue affecting concrete impermeable structures, representing a time-dependent and irreversible process that leads to the degradation of structural performance [9,10,11]. During the dissolution process, the primary hydration products in concrete (i.e., calcium hydroxide (CH) and hydrated calcium silicate (C-S-H) gel) undergo decomposition and precipitation [12,13], resulting in an increase in material porosity, permeability, and diffusivity [14,15,16,17]. In contrast to traditional contact dissolution, the driving force for the leaching of calcium in concrete impermeable structures includes not only concentration gradients but also hydraulic gradients, and the seepage driven by hydraulic gradients can accelerate the dissolution of hydration products [18]. Numerous hydraulic concrete structures worldwide are currently experiencing damage from seepage dissolution. The Fengman Concrete Gravity Dam in Jilin Province, China, has been in service for 70 years and exhibits an average annual leaching of calcium from its concrete cutoff wall of approximately 6.5 tons, with localized leakage points at the Fengman Concrete Gravity Dam experiencing a concrete strength loss of up to 20% [9,19]. After 40 years of operation, the anti-seepage panels of certain sections of the Gutianxi Buttress Dam in Fujian Province, China, have essentially lost their anti-seepage capability due to the effects of seepage dissolution [20]. The Itaipu Hydroelectric Plant, built in 1979, observed the presence of seepage dissolution phenomena within a year of its operation, which led to chemical and mineralogical alterations in certain areas of the backfill concrete [18]. Moreover, the Drum Queen Pond Arch Dam and Colorado Arch Dam were decommissioned due to the severe and long-term effects of seepage dissolution [21,22].

At present, numerous scholars have conducted experiments and numerical simulations regarding the durability issues associated with concrete calcium leaching [23,24,25,26,27,28,29]. These studies not only reveal the response mechanisms of concrete calcium leaching degradation processes to various factors but also provide numerous solutions for the management of concrete calcium leaching degradation. Due to the relatively slow natural calcium leaching process of the concrete, current experiments often utilize accelerated dissolution methods to assess the long-term performance of concrete [23,24,30]. However, this approach is limited to the material scale and cannot reflect the real conditions of the entire engineering structure during actual service. Therefore, the development of engineering-scale simulation models for the analysis of concrete structural calcium leaching degradation becomes essential. Unfortunately, existing models primarily focus on contact dissolution simulations without considering seepage effects [24,25,26,31], failing to reflect the long-term dissolution degradation characteristics of concrete impermeable structures. Furthermore, the majority of the developed seepage dissolution degradation analysis models did not account for the impact of non-equilibrium decomposition of solid-phase calcium induced by seepage flow [32], which is not consistent with reality. As a result, the evolutionary process of seepage dissolution in concrete impermeable walls of earth-rock dams has yet to be truly revealed, and its seepage dissolution durability control indices remain unclear.

The purpose of this study is to provide a novel method for analyzing the impact of seepage dissolution on the durability of anti-seepage walls of earth-rock dams to compensate for the deficiencies of existing approaches in characterizing the calcium dissolution degradation of concrete impermeable structures. As a result, a seepage and dissolution coupling model is proposed that not only considers the influence of seepage and the non-equilibrium decomposition of calcium dissolution process in concrete, but also the impact on the pore structure, diffusivity, and permeability of the concrete. The validity of the suggested method was confirmed through laboratory tests and literature data. Then, the method was used to analyze the degradation and failure processes of an anti-seepage wall in an actual dam project. Finally, an orthogonal test-based sensitivity analysis method was employed to identify the durability control indices of the concrete cutoff wall. The methods and findings of this paper can not only offer a theoretical foundation and technical support for assessing the durability and safety evaluation of the concrete cutoff walls in earth-rock dams but also serve as valuable references for the design, construction, and operation of concrete cutoff walls.

2. Methodology

2.1. Coupling Model for Seepage and Calcium Leaching

The process of leaching in the dam’s anti-seepage wall involves two distinct physical processes: seepage and the calcium leaching and migration. Among these processes, convection and diffusion play dominant roles. Assuming that the flow of pore water inside the concrete cutoff wall obeys Darcy’s law, the seepage continuity equation can be employed to describe changes in the seepage field induced by calcium leaching [33]:

$$\left\{\begin{array}{c}\frac{\partial \left(\phi \rho \right)}{\partial t}+\nabla \cdot \left(\rho u\right)=Q_{\mathrm{m}}\\ u=-\frac{k\left(\phi \right)}{\mu }\nabla p \end{array}\right.,$$

(1)

where ρ represents the density of water (kg/m³); φ indicates the porosity; t is the time (s); ∇ denotes the Laplace operator; u represents the Darcy flow velocity vector (m/s); Q_m indicates the source and sink term of seepage field (kg/(m·s)); k(φ) is the permeability coefficient (m/s), which is related to the porosity; µ denotes the dynamic viscosity of water (Pa·s); and p denotes the pressure (Pa).

During the calcium leaching process, calcium ions in the concrete pore solution and calcium in the matrix follow the mass conservation equation. The flux of calcium ions is determined by characteristics such as porosity, diffusion rate, Darcy velocity, and calcium ion concentration. According to Fick’s second law, the decomposition of calcium and the migration of liquid-phase calcium ions in the structures can be described by the following equation [19]:

$$\left\{\frac{\partial C_{\mathrm{ion}}}{\partial t}+\frac{\partial C_{\mathrm{solid}}}{\partial t}=\mathrm{div}\left[D_{\mathrm{e}}\left(\phi \right)\cdot \nabla C_{\mathrm{ion}}-u{C}_{\mathrm{ion}}\right]\right.,$$

(2)

where C_ion and C_solid are the concentrations of liquid-phase Ca²⁺ and solid-phase calcium in the concrete, respectively (mol/m³); D_e(φ) represents the effective diffusion coefficient of dissolved concrete (m²/s), which is related to the porosity φ; and div denotes the divergence.

The coupled variables between Equations (1) and (2) are the porosity φ and Darcy velocity u, i.e., when solid-phase calcium dissolves, increasing porosity of the concrete, it also enlarges the diffusion coefficient and permeability. This, in turn, results in an increase in the value of u in Equation (1), indicating a change in the internal seepage field of the concrete impermeable structure. Conversely, increasing the flow velocity within the structure influences the decomposition and precipitation of calcium in Equation (2), thereby achieving the coupling between the two fields.

2.2. Non-Equilibrium Decomposition Model of Calcium

In contact dissolution, without considering the seepage effect driven by hydraulic gradients, the time required for the decomposition of CH and C-S-H is almost negligible compared to the diffusion time. Under these conditions, a thermodynamic equilibrium is maintained between liquid- and solid-phase calcium, as expressed as follows [34]:

$$C_{\mathrm{solid}}=\left\{\begin{array}{c}{C}_{\mathrm{CSH}}{\left(\frac{C_{\mathrm{ion}}}{C_{\mathrm{satu}}}\right)}^{\frac{1}{3}}\left(\frac{-2}{x_1^3}{C}_{\mathrm{ion}}^3+\frac{3}{x_1^2}{C}_{\mathrm{ion}}^2\right) 0\le C_{\mathrm{ion}}\le x_1\\ C_{\mathrm{CSH}}{\left(\frac{C_{\mathrm{ion}}}{C_{\mathrm{satu}}}\right)}^{\frac{1}{3}} x_1\le C_{\mathrm{ion}}\le x_2 \\ C_{\mathrm{CSH}}{\left(\frac{C_{\mathrm{ion}}}{C_{\mathrm{satu}}}\right)}^{\frac{1}{3}}+\frac{C_{\mathrm{CH}}}{{\left(C_{\mathrm{satu}}-x_2\right)}^3}{\left(C_{\mathrm{ion}}-x_2\right)}^3 x_2\le C_{\mathrm{ion}}\le C_{\mathrm{satu}}\end{array}\right.,$$

(3)

where C_CH and C_CSH represents the initial concentrations of CH and C-S-H gel in the concrete, respectively (mol/m³); C_satu is the saturated calcium concentration in concrete, typically taken as 22.1 mol/m³ [35]; x₁ and x₂ are the critical concentrations of the segmented functions in the solid–liquid equilibrium equation, usually taken as 2 mol/m³ and 19 mol/m³, respectively [34].

For contact dissolution, the decomposition rate of calcium in concrete can be directly obtained by taking the partial derivative of Equation (3) with respect to time t. However, concrete cutoff wall of earth-rock dams inevitably undergo seepage driven by hydraulic gradient during their service life. This leads to the time required for the dissolution of solid-phase calcium within the concrete being significantly longer than the diffusion time of liquid-phase calcium ions, i.e., the solid- and liquid-phase calcium concentrations are in a thermodynamically unbalanced state [36]. Hence, the traditional solid–liquid equilibrium equation cannot adequately express the decomposition rate of calcium in concrete impermeable structures. Ulm et al. [36] started from the thermodynamically unbalanced state between the solid and liquid calcium concentrations in the concrete materials. They introduced the chemical affinity potential (A_s) to measure the decomposition rate of calcium in concrete dissolution processes, considering the “distance” deviating from the equilibrium state. Then, they proposed an approach for describing the unbalanced decomposition of calcium. Subsequently, Gawin et al. [37] reformulated the Ulm model into a form that is easier for integration. The revised equation for the decomposition rate of calcium is as follows:

$$\frac{\partial C_{\mathrm{solid}}}{\partial t}=\frac{1}{\eta }{A}_{\mathrm{s}}=\frac{1}{\eta }\left[{{\displaystyle \int }}_{C_{\mathrm{solid}}^0}^{C_{\mathrm{solid}}^{\mathrm{eq}}}\kappa (C_{\mathrm{solid}})\mathrm{d}{C}_{\mathrm{solid}}-{{\displaystyle \int }}_{C_{\mathrm{solid}}^0}^{C_{\mathrm{solid}}^{\mathrm{de}}}\kappa (C_{\mathrm{solid}})\mathrm{d}{C}_{\mathrm{solid}}\right],$$

(4)

$$\kappa (C_{\mathrm{solid}})=\frac{R{T}_{\mathrm{ref}}}{C_{\mathrm{ion}}}{\left(\frac{\mathrm{d}{C}_{\mathrm{solid}}}{\mathrm{d}{C}_{\mathrm{ion}}}\right)}^{-1},$$

(5)

where η is a coefficient related to the calcium concentration; $C_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{d}}^{\mathrm{e}\mathrm{q}}$ and $C_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{d}}^{\mathrm{d}\mathrm{e}}$, respectively, represent the solid-phase calcium concentration and liquid calcium concentration at equilibrium and non-equilibrium states (mol/m³); $C_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{d}}^0$ is the initial calcium concentration (mol/m³); κ(C_solid) is the solid–liquid equilibrium constant; T_ref denotes the temperature, which is considered as 298.15 K; R represents the idea gas constant. The values of 1/η and dC_solid/dC_ion can be found in the literature [37].

2.3. Porosity Evolution

The dissolution of calcium in concrete will inevitably increase structural porosity. Carde et al. [38], through experiment, discovered that the rise in porosity caused by dissolution is essentially equivalent to the volume occupied by CH in cement paste. However, the dissolution of C-S-H gel only generates fine pores, causing a relatively small impact on porosity. To simplify calculating of porosity increase, C-S-H gel dissolution can be equated to CH dissolution. The variation in porosity during seepage dissolution can then be expressed as follows:

$$\phi ={\phi }_0+\Delta \phi ,$$

(6)

$$\Delta \phi =\frac{M_{\mathrm{CH}}}{{\rho }_{\mathrm{CH}}}\left(C_{\mathrm{solid}}^0-C_{\mathrm{solid}}\right),$$

(7)

where φ₀ denotes the initial porosity of the structures; ∆φ represents the porosity increment induced by dissolution. The molar mass (M_CH) and density (ρ_CH) of CH are taken as 7.41 × 10⁻² kg/mol and 2.24 × 10³ kg/m³, respectively [24].

The internal pores of cementitious materials are classified as capillary pore and gel pore, and the volume of these two pores can be estimated based on the hydration degree. Assuming that the initial pores in cementitious materials are uniformly distributed and are equivalent to the total of the initial capillary and gel porosity, the initial porosity can be expressed as follows [24,39]:

$${\phi }_0={\phi }_{\mathrm{cap},0}+{\phi }_{\mathrm{gel},0},$$

(8)

where φ_cap,0 and φ_gel,0 denote the initial capillary and gel porosity, respectively, which can be expressed as follows:

$${\phi }_{\mathrm{cap},0}=\frac{\mathrm{w}/\mathrm{c}-0.36{\alpha }_{\mathrm{m}}}{\mathrm{w}/\mathrm{c}+0.32}{V}_{\mathrm{vol}},$$

(9)

$${\phi }_{\mathrm{gel},0}=\frac{0.19{\alpha }_{\mathrm{m}}}{\mathrm{w}/\mathrm{c}+0.32}{V}_{\mathrm{vol}},$$

(10)

where w/c denotes the water-cement ratio; V_vol represents the volume percentage of cement in concrete; and α_m denotes the maximum hydration degree of the cement, which can be determined as follows [40]:

$${\alpha }_{\mathrm{m}}=0.239+0.745\tanh \left[3.62\left(\mathrm{w}/\mathrm{c}-0.095\right)\right],$$

(11)

The initial solid-phase calcium concentration, $C_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{d}}^0$, in cementitious materials can be approximately the same as the total amount from the initial calcium hydroxide and calcium silicate hydrate gel (i.e., $C_{\mathrm{C}\mathrm{H}}^0$ and $C_{\mathrm{C}\mathrm{S}\mathrm{H}}^0$). Subsequently, the Bogue method can be utilized to calculate $C_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{d}}^0$ by the content of oxides in cement [24,41]:

$$\left\{\begin{array}{c}{C}_{\mathrm{solid}}^0=C_{\mathrm{CH}}^0+C_{\mathrm{CSH}}^0 \\ C_{\mathrm{CH}}^0=\left(\frac{1.3f_{{\mathrm{C}}_3\mathrm{S}}}{M_{{\mathrm{C}}_3\mathrm{S}}}+\frac{0.3f_{{\mathrm{C}}_2\mathrm{S}}}{M_{{\mathrm{C}}_2\mathrm{S}}}\right)\times {\rho }_{\mathrm{cp}}\times {\alpha }_{\mathrm{m}}\times {10}^6 (\mathrm{mmol}/\mathrm{L}) \\ C_{\mathrm{CSH}}^0=1.7\times \left(\frac{f_{{\mathrm{C}}_3\mathrm{S}}}{M_{{\mathrm{C}}_3\mathrm{S}}}+\frac{f_{{\mathrm{C}}_2\mathrm{S}}}{M_{{\mathrm{C}}_2\mathrm{S}}}\right)\times {\rho }_{\mathrm{cp}}\times {\alpha }_{\mathrm{m}}\times {10}^6 (\mathrm{mmol}/\mathrm{L}) \end{array}\right.,$$

(12)

where ρ_cp is the density of the cement paste, which can be determined according to literature [24]; f_C3S and f_C2S are the volume fraction of C₃S and C₂S in the cement, respectively, which can be obtained by converting the mass fraction of C₃S and C₂S calculated using the Bogue method [42,43]:

$$\left\{\begin{array}{c}{m}_{{\mathrm{C}}_3\mathrm{S}}=4.07m_{\mathrm{CaO}}-7.60m_{{\mathrm{SiO}}_2}-6.72m_{{\mathrm{Al}}_2{\mathrm{O}}_3}-2.86m_{{\mathrm{SO}}_3} \\ m_{{\mathrm{C}}_2\mathrm{S}}=-3.07m_{\mathrm{CaO}}+8.60m_{{\mathrm{SiO}}_2}+5.07m_{{\mathrm{Al}}_2{\mathrm{O}}_3}+2.15m_{{\mathrm{SO}}_3}\end{array}\right.,$$

(13)

where m_CaO, m_SiO2, m_Al2O3, and m_SO3 are the content of CaO, SiO₂, Al₂O₃, and SO₃, respectively.

2.4. Diffusivity Evolution

The leaching of calcium from concrete inevitably increases the diffusivity of calcium ions within structures. To characterize this process, the modified equation suggested by van Eijk and Brouwers [44], which is based on the Garboczi model [45], was employed for modeling:

$$\begin{array}{c}{D}_{\mathrm{e}}/D_0=0.0025-0.07{\phi }_0^2-1.8{\left({\phi }_0-0.18\right)}^2\mathrm{H}\left(\phi -0.18\right)+0.14{\phi }^2\\ +3.6{\left(\phi -0.16\right)}^2\mathrm{H}\left(\phi -0.16\right)\end{array},$$

(14)

where D₀ and D_e are the initial and effective diffusion coefficients of calcium ions in concrete, respectively, (m²/s); H(x) denotes the Heaviside function, which equals 0 when x < 0 and 1 otherwise.

2.5. Permeability Evolution

The dissolution of solid-phase calcium in concrete during the dissolution process leads to an enlargement of the pore structure, resulting in changes to the permeability coefficient. Consequently, considering the evolution of permeability is critical in the seepage dissolution process of concrete impermeable structures. In this work, the Kozeny–Carman equation is applied to characterize the variation in permeability coefficient in concrete during seepage dissolution, as its effectiveness has been validated by Phung et al. [33] using laboratory leaching tests:

$$k=k_0{\left(\frac{\phi }{{\phi }_0}\right)}^3{\left(\frac{1-{\phi }_0}{1-\phi }\right)}^2,$$

(15)

where k₀ is the initial permeability coefficient (m/s).

2.6. Numerical Implementation

In this study, COMSOL software (Version 6.0) is employed to develop and apply the proposed model. The Subsurface Flow Module and the Porous Media Dilution Material Transfer Module, both integrated within COMSOL, are used to simulate the seepage and dissolution fields, respectively. Furthermore, MATLAB 2014a programming is utilized on this basis to calculate the non-equilibrium decomposition rate of calcium. MATLAB and COMSOL interact for the secondary development of the proposed model. It is important to note that when performing multi-field coupling calculations, the solution methods can be classified as strong coupling or weak coupling. Strong coupling refers to a high level of interaction between physical fields, which necessitates simultaneous solutions to the governing equation sets. As a result, strong coupling can obtain the desired variables for each physical field precisely. However, for a nonlinear system of equations, strong coupling calculations often lead to convergence difficulties and high computational costs [46]. To avoid issues with poor model convergence, the model can be decoupled using a weakly coupled computation method. Weak coupling is accomplished by solving the governing equations for individual physical fields alternately within each incremental step. This entails using the calculated results of one physical field as the known conditions or boundary conditions for the next physical field’s calculation. The effects of multi-field coupling are not considered within individual incremental steps in the weak coupling calculation process, which improves computational efficiency [47]. As a result, this paper adopts a weakly coupled approach to establish a connection between two physical fields, thereby achieving the coupled calculation of the seepage and dissolution fields in the anti-seepage wall of the dam. Figure 1 shows the calculation process for the concrete cutoff wall of an earth-rock dam. The particular steps are summarized as below:

Step 1: Create a geometric model and specify the initial parameters, as well as the initial and boundary conditions for seepage calculation.

Step 2: Calculate the seepage field within the structure using the Subsurface Flow Module, and output the distribution of flow velocities within the structure at time t.

Step 3: Setup the initial and boundary conditions, in addition to the model parameters for the dissolution field, and compute the dissolution field based on the flow velocities output from Step 2 to obtain the distribution of parameters, such as calcium ion concentration, porosity, and permeability and diffusion coefficients, within the structures at time t.

Step 4: Calculate non-equilibrium decomposition model based on the concentration of the solid and liquid phase calcium output from Step 3, so as to obtain the calcium decomposition rate within the structure at time t.

Step 5: Determine if the set dissolution calculation time has been reached. If not, update the computation time to t = t + Δt, continue the calculation. Then, calculate the distribution of calcium within the structure at time t based on the obtained decomposition rate of calcium from Step 4, as well as the distribution of porosity, permeability coefficients, and diffusion coefficients.

Step 6: Update the seepage parameters based on the results of Step 5 and repeat the above steps until reaching the final time step. Finally, output the ultimate values of calcium concentration, permeability coefficients, porosity, diffusion coefficients, and seepage discharge.

It should be noted that the transient segregated solver is used in the multi-field coupling model. When solving with the model, the solver employs a backward difference method, and the nonlinear method employs a constant Newton method. Additionally, the maximum iteration count is set at 40 to guarantee model convergence. The Anderson acceleration method is utilized to enhance stability and accelerate convergence, and the spatial dimension for iterations is set at 100.

2.7. Orthogonal Test-Based Sensitivity Analysis Method

The orthogonal test method is a scientifically designed and analyzed approach for experiments involving multiple factors, levels, and criteria [48]. It selects representative levels from combinations of various factor test levels using suitable orthogonal arrays for combined experiments. It determines the impact of each factor on the evaluation results by processing and analyzing experimental results. Based on this, it identifies model sensitive parameters, providing references for model parameter selection, calibration, and application. Additionally, it can provide guidance for engineering design.

The orthogonal test design employs orthogonal tables to orchestrate tests, analyzing the data within these tables to assess the influence of various factors on test results. This fundamentally differs from the Taguchi method, which utilizes robust design principles to evaluate system stability by analyzing the responsiveness of the system. Therefore, the foundation of the orthogonal test method is the orthogonal table, which has the following features: Each column factor’s various levels appear an equal number of times during the test, reflecting balance, and any two column factor’s various level combinations appear an equal number of times during the test, demonstrating the uniform distribution of experimental points. The orthogonal table is represented as L_d(r^c), where L is the orthogonal table’s designation; d is the test number; r is the number of levels for each component; c is the number columns, indicating the maximum number of factors that can be organized. An example of a designed orthogonal table for a six-factor, three-level scenario is provided in

Table 1. L₁₈(3⁶) orthogonal test.

Test Number	Column Number
	1	2	3	4	5	6
1	1	1	1	1	1	1
2	1	1	2	2	3	3
3	1	2	1	3	3	2
4	1	2	3	1	2	3
5	1	3	2	3	2	1
6	1	3	3	2	1	2
7	2	1	1	3	2	3
8	2	1	3	1	3	2
9	2	2	2	2	2	2
10	2	2	3	3	1	1
11	2	3	1	2	3	1
12	2	3	2	1	1	3
13	3	1	2	3	1	2
14	3	1	3	2	2	1
15	3	2	1	2	1	3
16	3	2	2	1	3	1
17	3	3	1	1	2	2
18	3	3	3	3	3	3

.

The range analysis method and the analysis of variance (ANOVA) method are two commonly used approaches to analyze the results of orthogonal tests. In comparison to the ANOVA method, the range analysis method has difficulty distinguishing factors influencing test result variation. It is limited to stating the factors’ respective orders of influence and is unable to evaluate each factor’s sensitivity quantitatively [48,49]. However, the ANOVA approach can measure how sensitive the model’s output is to different factors and is more accurate in estimating test errors. The following are the fundamental ideas behind the ANOVA method:

Taking the L_n(r^c) test as an example, let Y_k (k = 1, 2, ···, n) represent the k_th test result. Let T_ij represent the total number of the test results Y_k for the i_th level of the jth column factor, T represent the sum of all test results, and p_ij denote the number of tests for factor j at level i. The relationships are as follows:

$$T_{ij}={\displaystyle \sum _{k=1}^{p_{ij}}{Y}_k}; T={\displaystyle \sum _{k=1}^n{Y}_k}; \overline{Y}=\frac{T^2}{n}; p_{ij}=\frac{n}{r},$$

(16)

Let S_T denote the total variation among the n test results, representing the overall degree of variance across all test results. The sum of squares of variations for the jth column is represented as S_j, indicating the degree of difference between the different levels of the factor arranged in the jth column. The total sum is denoted as S_e, representing the degree of difference in test conditions during the test. The following is an expression for the calculating formulas:

$$S_T={\displaystyle \sum _{k=1}^n{Y}_k^2}-\overline{Y}; S_j=\frac{{\displaystyle \sum _{k=1}^r{T}_{ij}}}{p_{ij}}-\overline{Y}; S_e=S_T-{\displaystyle \sum _{j=1}^c{S}_j},$$

(17)

Supposing that the freedom degrees for S_T, S_j, and S_e are denoted as f_T, f_j, and f_e, respectively. Then, the following relationships can be obtained:

$$f_T=n-1; f_j=r-1; f_e=f_T-{\displaystyle \sum _{j=1}^c{f}_j},$$

(18)

During the calculation process, each test result (Y₁, Y₂, ···, Y_n) is taken to be independent and to have a normal distribution with the homoscedasticity σ². As a result, a statistical quantity for constructing an F-test can be formulated:

$$F_j=\frac{S_j/f_j}{S_e/f_e}~F\left(f_j,f_e\right)$$

(19)

By comparing the calculated F_j value with the critical value F(f_j, f_e) derived from the F-distribution table, one may ascertain how sensitive the model’s output is to variations in each factor.

3. Experimental Validations

To validate the efficacy of the suggested model, an experimental calcium dissolution test was conducted, as illustrated in Figure 2. The experimental cement used for casting concrete specimens was P·O 42.5 ordinary Portland cement (OPC), with its chemical composition listed in

Table 2. Chemical composition of cement (%).

CaO	SiO2	Fe2O3	Al2O3	MgO	Na2O	SO3	MnO	K2O	TiO2	P2O5	SrO	LOI
56.13	21.05	3.95	6.52	2.00	0.15	1.98	0.14	0.87	0.31	0.18	0.08	0.70

. Natural river sand with a fineness modulus of 2.77 was utilized for fine aggregate, while crushed stones with a maximum particle size of 20 mm were employed for coarse aggregate. The mass ratio of water, cement, sand, and stone in the concrete was 1:2.5:4.77:8.33 (i.e., w/c = 0.4). Additionally, 0.5% water reducer and 0.006% air-entraining agent were added during the experimental process to reduce the mixing water content and increase the workability, ease of placement, water retention, and cohesiveness of the concrete mix. More information on specimen materials and preparation can be found in the literature [22,30,50].

As depicted in Figure 2, the experiment employed a commonly used 6 mol/L ammonium chloride solution to speed up the calcium dissolution [15,51]. The specimens were cut with a rock cutter after accelerated dissolution for 0, 10, 30, 60, 90, and 120 days. Subsequently, 0.5% phenolphthalein reagent was sprayed on the cut surfaces to obtain the variation in dissolution depth during the dissolution process. Following this, a numerical method for simulating the dissolution of concrete specimens was constructed using the proposed model. The rationality of the proposed approach was demonstrated by comparing the simulated and measured dissolution depths of the specimens, as shown in Figure 3. The quantitative comparison results between the simulated and measured dissolution depths are provided in Figure 4. It is evident that, for the most part, the simulation results obtained using the suggested method agree with the experimental findings. Furthermore, several model evaluation metrics introduced (i.e., RMSE, R², MAE, and MRE) [52] have exhibited good performance, which quantitatively reflect the rationality of the proposed model and simulation methodology.

Considering the relatively low hydraulic head experienced by the concrete specimens in the dissolution process of this study, it is possible that the seepage effects driven by hydraulic gradients may not be prominent enough, leading to less rigorous conclusions from the established model. To dispel this concern, the accelerated seepage dissolution tests from Zhang’s thesis [53] were selected for further validation of the suggested approach. In Zhang’s experiment, multiple cylindrical cementitious specimens with diameters of 50 mm and heights of 100 mm were used as test samples. The cement used in the test was Conch brand P·O 42.5 ordinary silicate cement, and its chemical composition is shown in

Table 3. Chemical composition of cement used in Zhang’s tests (%) [53].

CaO	SiO2	Fe2O3	Al2O3	MgO	Na2O	SO3	Cl−	LOI
67.58	13.57	3.64	5.05	1.79	0.04	2.63	0.021	0.37

. During the experiment, epoxy resin was applied to all of the cylindrical specimens’ faces except the upper and lower circular parts. The specimens were put in a dissolution room, and the top circular section was subjected to a 200 kPa permeating water pressure. The acceleration solution was 6 mol/L ammonium chloride solution. In addition, the dissolution depths were measured on the 7th, 14th, 21st, and 28th days of the experiment, as shown in Figure 5.

Comparing Figure 4 and Figure 5, it is clear that the specimens’ dissolution depths show an exponential function relationship rather than a liner relationship with the square root of the dissolution period when high water pressure is applied. This indicates that high water pressure accelerates the calcium leaching process in concrete. Furthermore, it suggests that considering the seepage effects driven by high hydraulic gradients is crucial when simulating the dissolution of concrete impermeable structures. The constructed model aligns well with the literature results, affirming the rationality of the suggested approach. This implies that the method can be employed in real-word engineering situations to simulate the seepage dissolution of concrete impermeable structures.

4. Case Study

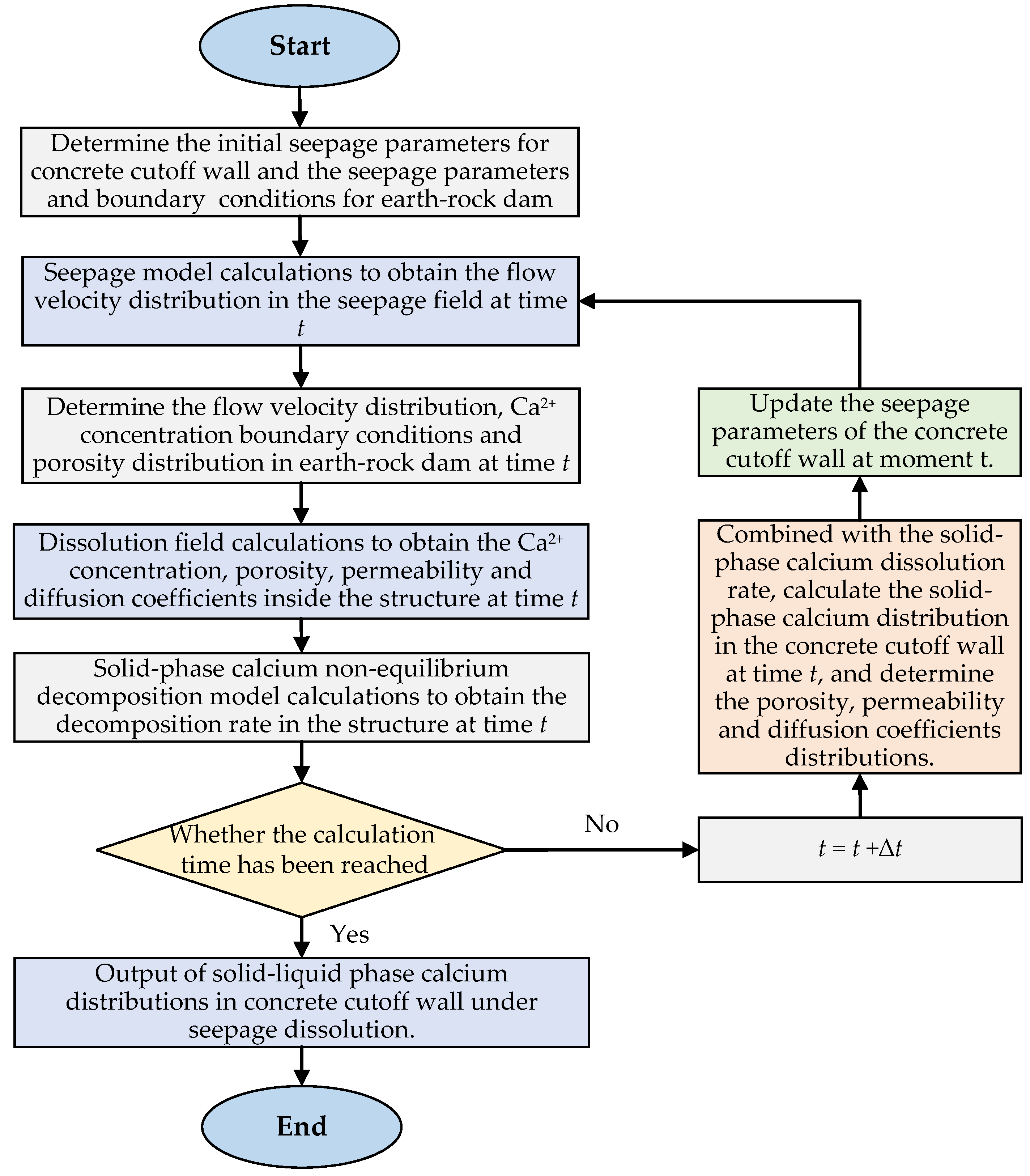
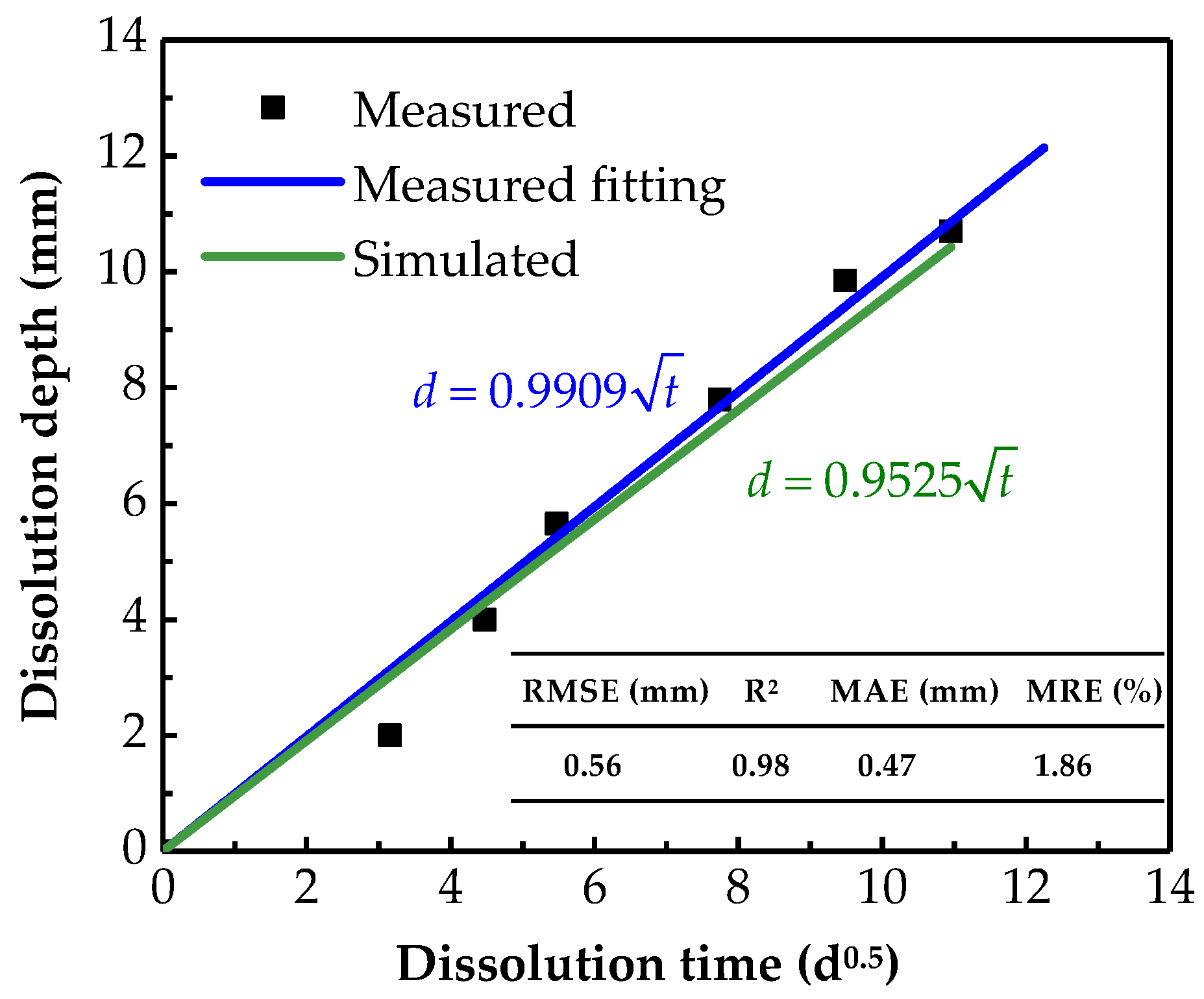
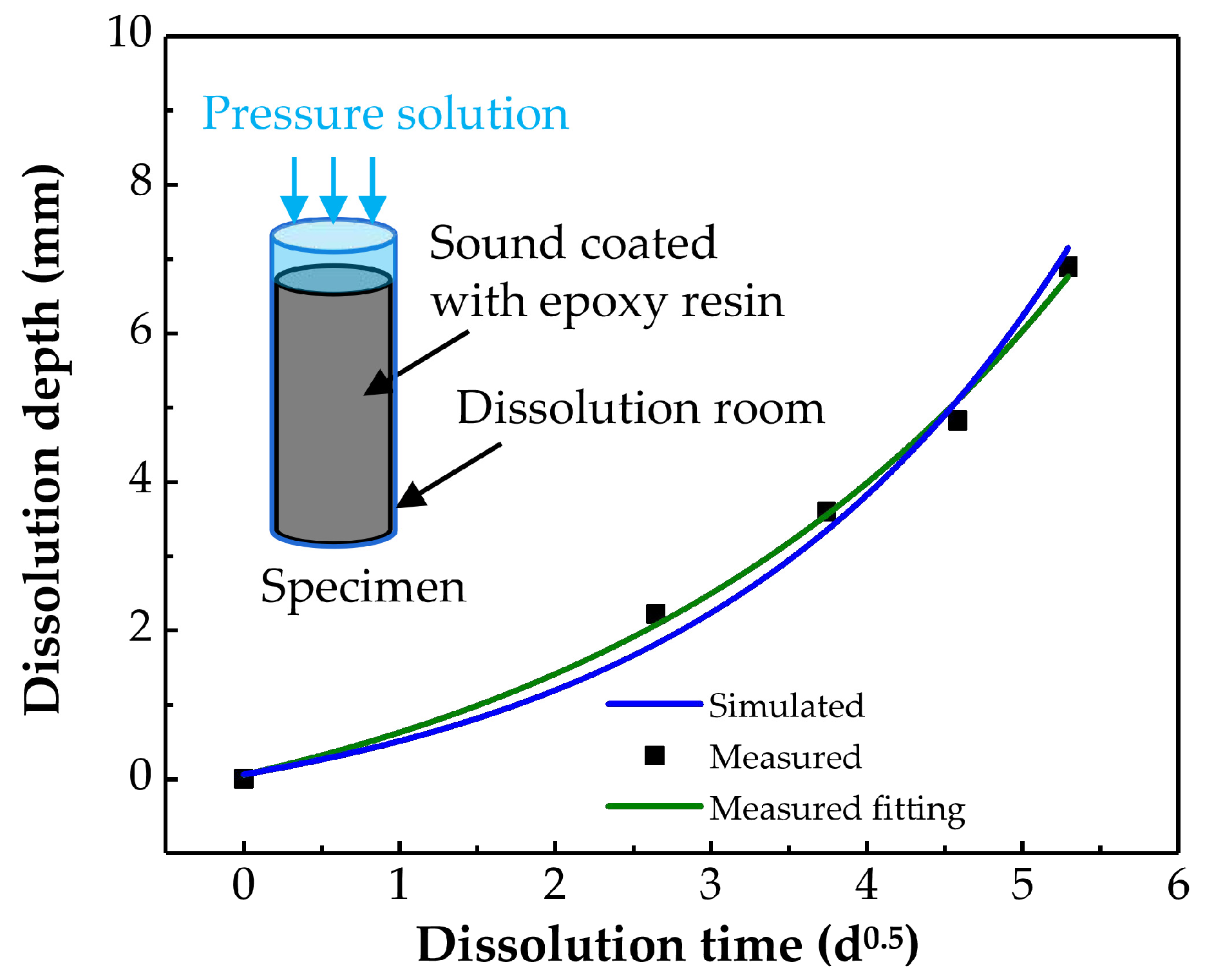
4.1. Project Overview

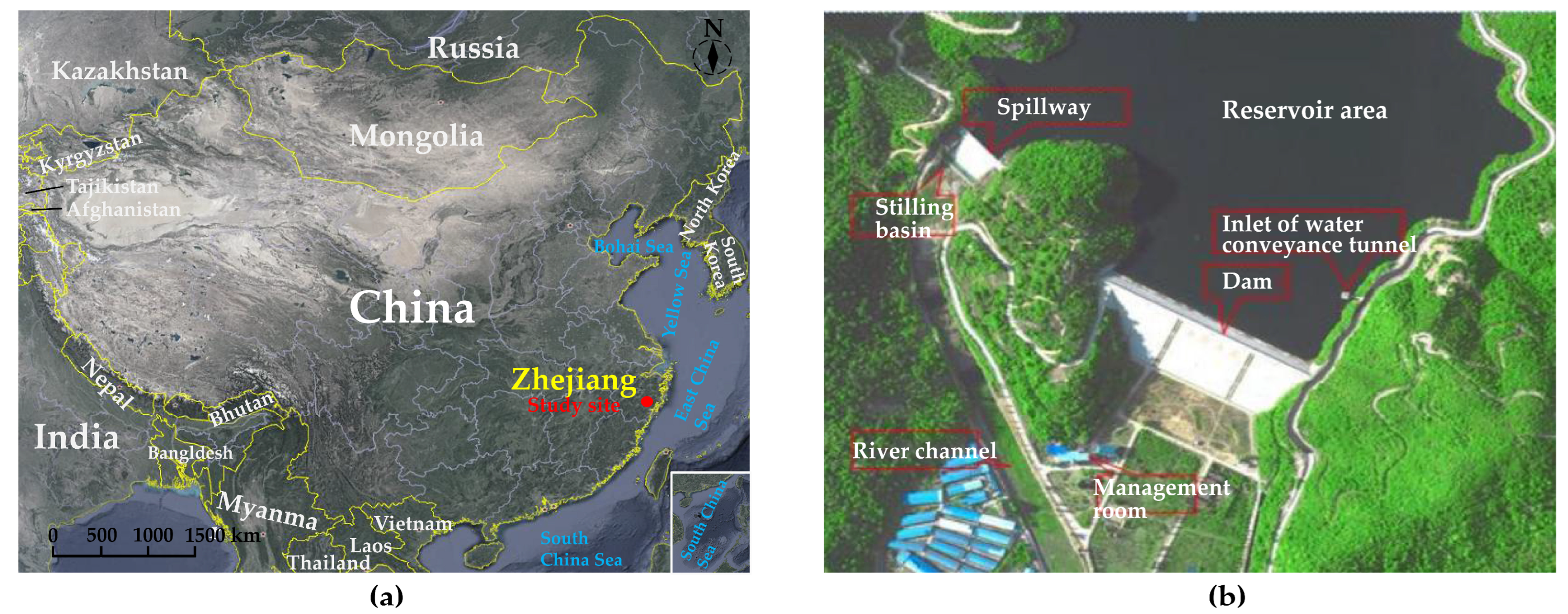
To investigate the leaching behavior of concrete cutoff walls in earth-rock dams, the Liyang Reservoir, located in Ningbo City, Zhejiang Province, China, was selected as a case study (Figure 6a). The reservoir, primarily designed for water supply and flood control, integrating various uses such as irrigation. Its main structure comprises the dam body, spillway, and water conveyance tunnels (Figure 6b). Due to the varied requirements of different sections, the main project of the reservoir is categorized as Class III. Among these, the spillway, water conveyance tunnels, and other components of the dam body are classified as Level 3, while the downstream river channel and the roads surrounding the reservoir are classified as Level 4. Phase I construction of the dam, completed in 1979, utilized a clay core wall with a dam crest elevation of 42.0 m. However, permeable pathways within the dam body and foundation due to the dispersive nature and poor compaction of the clay core used in the Phase I construction, leading to a higher permeability coefficient for the anti-seepage structure. Consequently, the local government launched a reservoir continuation and reinforcement project in 2004, incorporating a plastic concrete cutoff wall for reinforcement based on the Phase I structure.

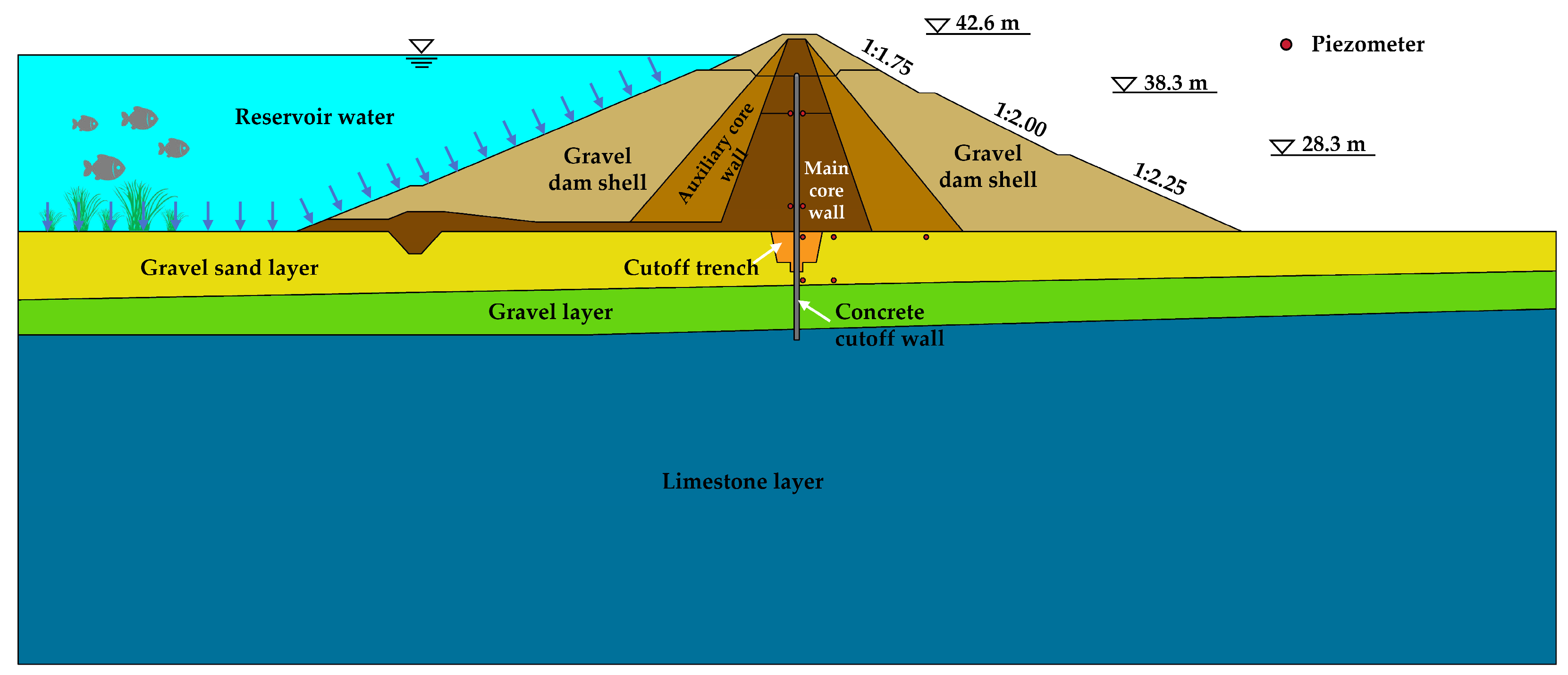
The reinforced concrete cutoff wall’s axis coincides with the crest axis of the Phase I construction and has a thickness of 0.8 m. The upper end of the anti-seepage wall is buried at an elevation of 41.5 m, and the lower portion of the concrete cutoff wall extends 0.6 m into the dam foundation’s weakly weathered layer. Additionally, the anti-seepage wall has a maximum depth of 60.85 m. A clay core wall is used for dam heightening and anti-seepage reinforcement. After the concrete cutoff wall has been built, clay core material is directly placed on its top surface to raise the dam height by 5.80 m. The Phase II reinforcement project of the dam was completed in 2008, resulting in an elevated crest elevation of 47.80 m. The dam crest is 5 m wide, its overall length is 266 m, and the maximum dam height is 31.9 m, classifying it as a medium-sized dam.

The upstream slopes of the dam are protected by dry masonry with a thickness of 30 cm. Roads, 2.0 m wide, are located at elevations of 42.6 m and 23.4 m on the upstream dam slope. Therefore, the upstream dam slope can be divided into three levels, with slope ratios of 1:1.8 (i.e., above 42.6 m elevation), 1:2.25 (i.e., between 42.6 m and 23.4 m elevation), and 1:2.5 (i.e., below 23.4 m elevation). The downstream dam slope likewise employs dry masonry with the same thickness as the upstream dam slope, and its slope ratios are also categorized into three levels. The downstream dam slope has a slope ratios of 1:1.75 (i.e., above the elevation of 38.3 m), 1:2.0 (i.e., between 38.3 m and 28.3 m elevation), and 1:2.25 (i.e., below the elevation of 28.3 m). After the reinforcement construction, the reservoir’s dead water level, normal storage level, design flood level, and checked flood level are 23.50 m, 44.50 m, 45.86 m, and 46.81 m, respectively. The corresponding reservoir capacities are approximately 300,000 m³, 11.02 million m³, 12.38 million m³, and 13.28 million m³. Figure 7 depicts a typical cross-section of the Liyang earth-rock dam.

4.2. Monitoring Data

As illustrated in Figure 7, eight piezometers are installed in the dam body and foundation of a typical dam cross-section to monitor the variation in seepage pressure during reservoir operation.

Table 4. Statistics on the location of piezometers and the relationship between their water levels and the reservoir water level.

Piezometer	UP2-1	UP2-2	UP2-3	UP2-4	UP2-5	UP2-6	UP2-7	UP2-8
Distance from dam axis (m)	−1.0	−1.0	1.0	1.0	1.0	6.0	6.0	21.1
Buried elevation (m)	35.0	20.0	20.0	15.0	8.0	15.0	8.0	15.0
Correlation coefficient	0.982	0.940	0.614	0.030	0.132	0.306	0.364	0.124

provides the specific embedded locations of each piezometer within the dam foundation and body. It is important to note that the distance of monitoring points from the dam axis is considered negative when directed towards the upstream face and positive when directed towards the downstream. Figure 8 depicts the observed temporal variations from August 2006 to July 2016 for both reservoir water levels and each piezometer at different monitoring points. Additionally, the correlation coefficients between reservoir water levels and the respective monitoring point levels are detailed in Table 4.

4.3. Model Setup and Verification

Based on the Liyang Reservoir Dam’s topographical and geological data, as well as the aforementioned proposed method, a numerical model considering the seepage and dissolution coupling effect of the anti-seepage wall at the dam’s typical cross-section is established.

Table 5. Parameters for numerical simulation.

Material	φ0	k0 (m/s)	D0 (m2/s)	${\mathit{C}}_{\mathbf{CH}}^0$ (mol/m3)	${\mathit{C}}_{\mathbf{CSH}}^0$ (mol/m3)
Gravel dam shell	0.60	3.00 × 10−5	1.06 × 10−9	−	−
Main core wall	0.38	7.84 × 10−7	1.06 × 10−9	−	−
Auxiliary core wall	0.40	7.53 × 10−7	1.06 × 10−9	−	−
Cutoff trench	0.53	1.45 × 10−6	1.06 × 10−9	−	−
Gravel sand layer	0.22	4.90 × 10−6	1.06 × 10−9	−	−
Gravel layer	0.22	4.90 × 10−6	1.06 × 10−9	−	−
Limestone layer	0.30	2.00 × 10−7	1.06 × 10−9	−	−
Concrete cutoff wall	0.05	3.80 × 10−12	4.50 × 10−10	3379	5561

shows the computational parameters of the model, which are collected from laboratory and field tests, as well as engineering design data.

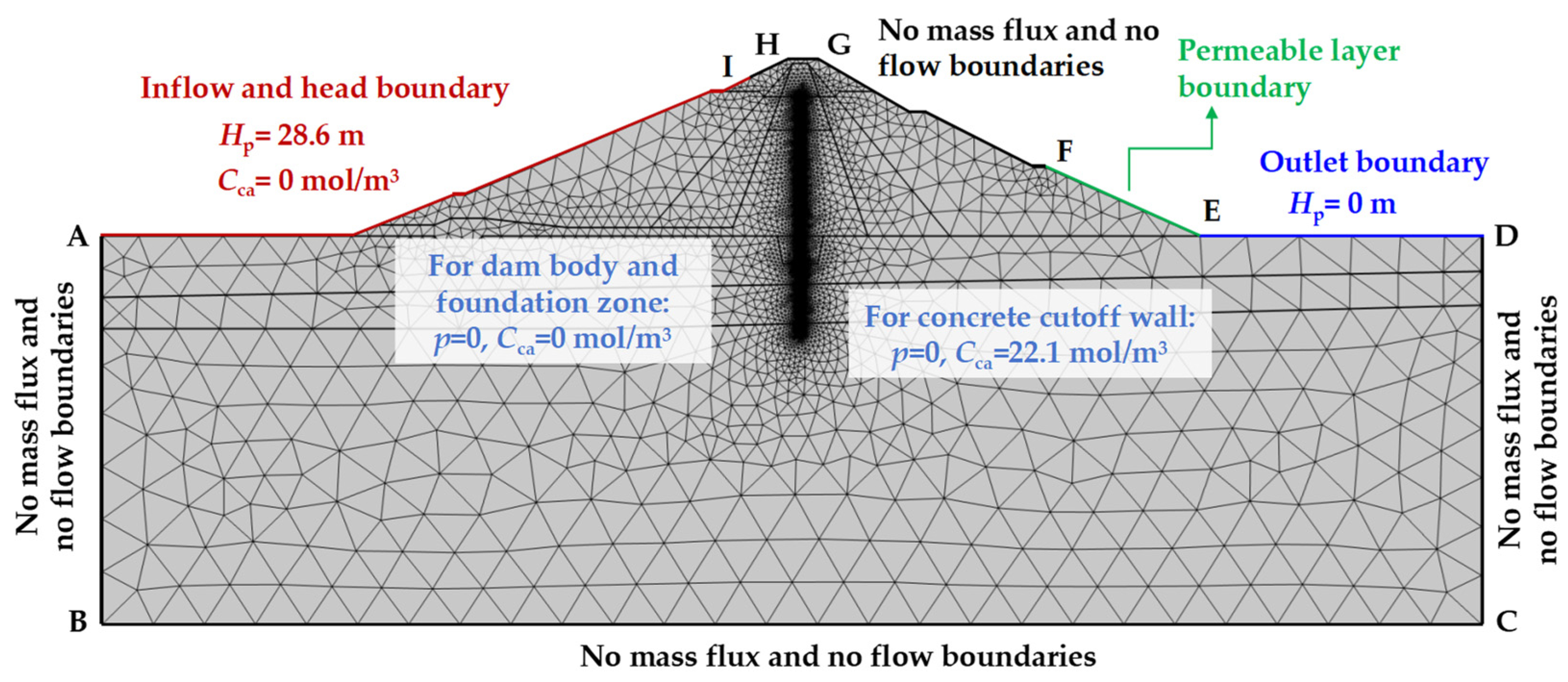
The established computational model’s boundary numbering and meshing are shown in Figure 9. The boundary under the water level (AI) was designated as the head boundary for seepage field. This boundary can be a constant head or variable head, depending on the actual monitoring data. Permeable layer boundaries, a kind of hybrid boundary, were used to establish the EF boundary at the downstream slope [54]. All other boundaries were designated as no flow boundaries, and the seepage field’s initial conditions were set to zero pressure. The upstream reservoir water’s calcium ion concentration is taken to be 0 mol/m³ for the dissolution field, with the upstream boundary (i.e., AI) serving as the inflow boundary. The remaining boundaries were set to no mass boundaries except for the DE boundary, which was defined as the outlet boundary. The computation zone’s remaining concentration is set at 0 mol/m³, with the initial calcium ion concentration of the anti-seepage wall considered to be saturation concentration (i.e., C_ca = 22.1 mol/m³). A triangular mesh was employed to discretize the computation zone. This resulted in 88,697 domain cells and 2761 boundary cells. It should be mentioned, as Figure 9 illustrates, that the anti-seepage wall’s mesh was refined to guarantee computation correctness.

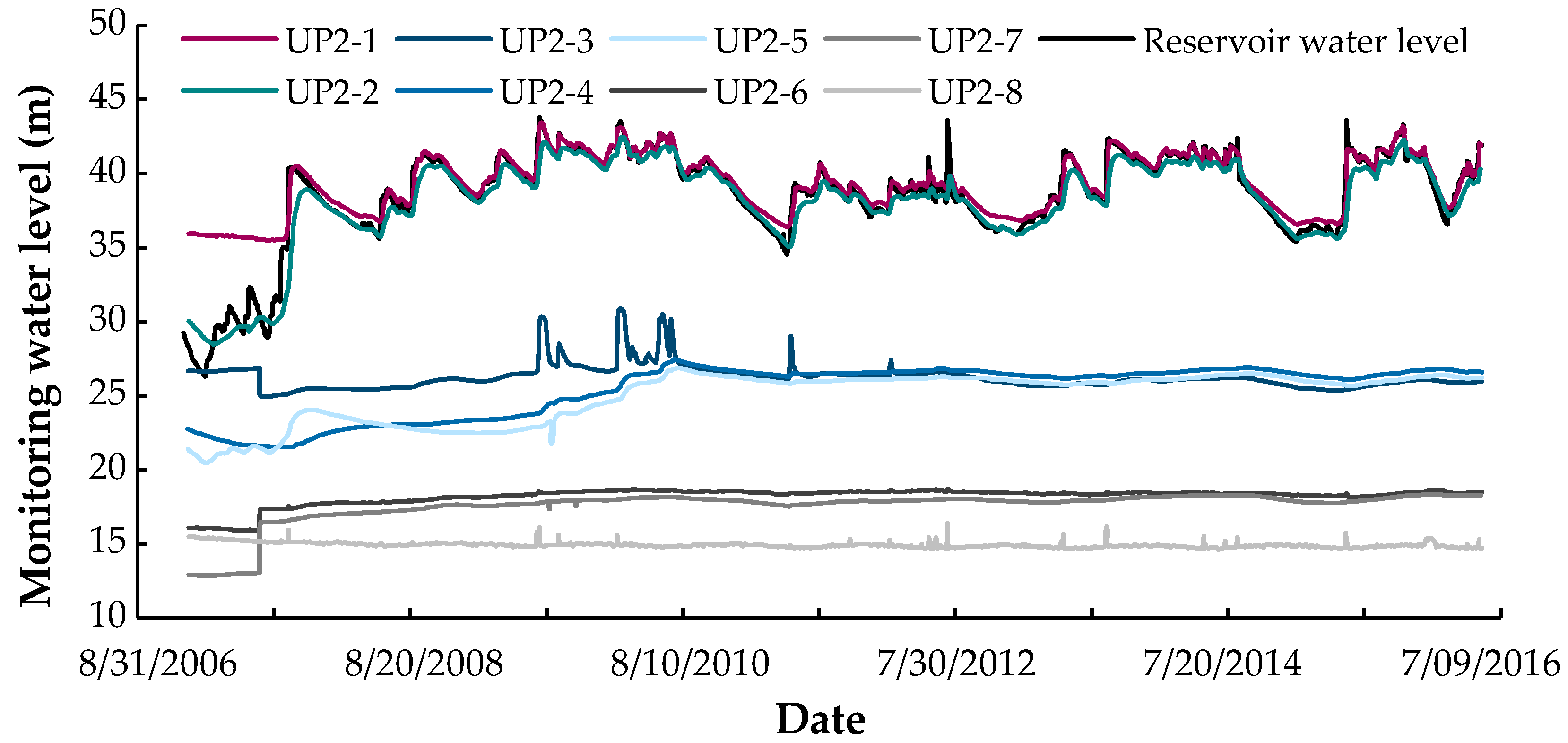
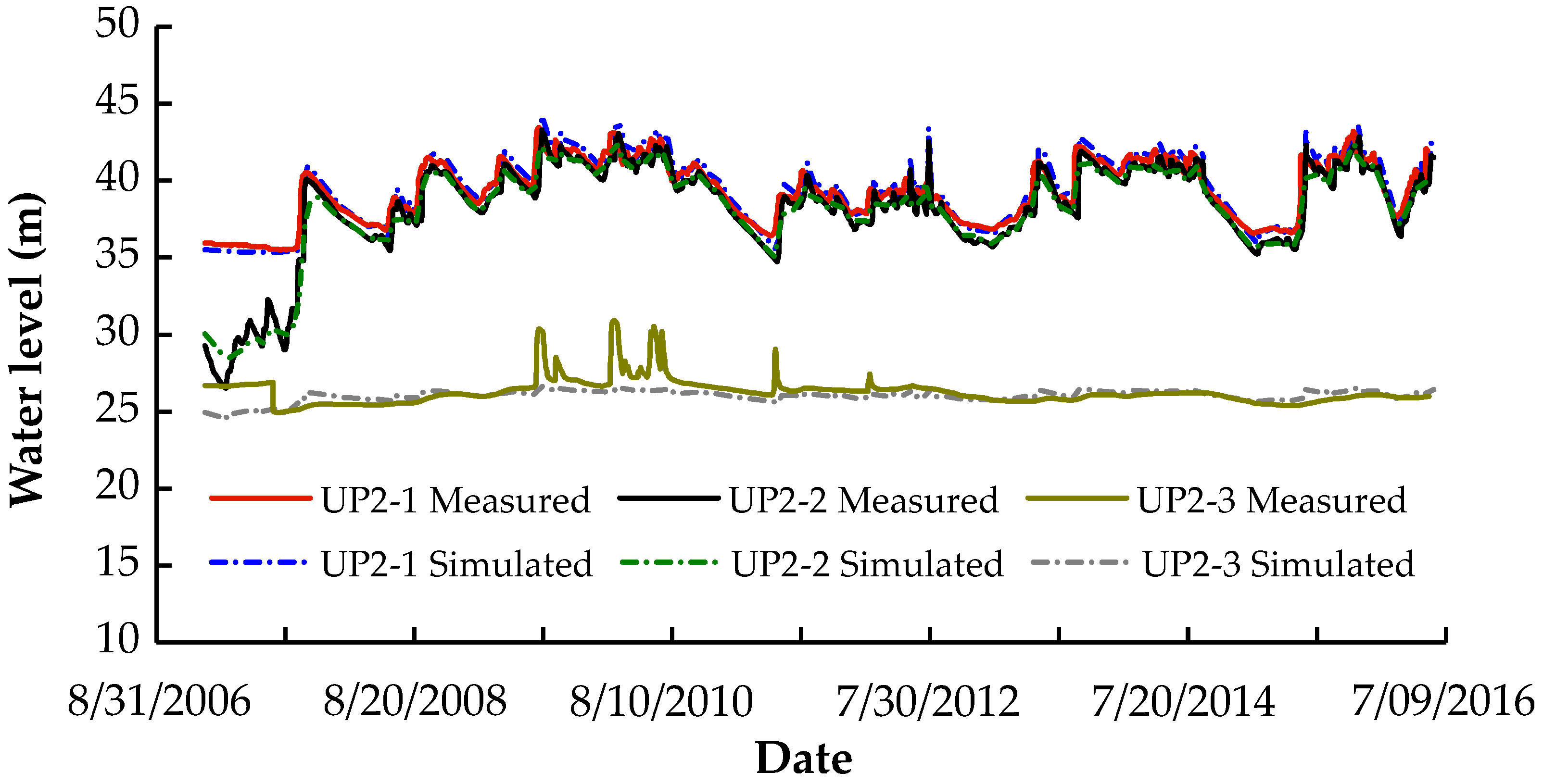
According to the established numerical model, the temporal variation data of reservoir water levels shown in Figure 8 are used as the upstream water level boundary for simulating the operation of the reservoir. By setting piezometers into the numerical model, simulated water level changes at various monitoring points are obtained. Subsequently, the simulated water level variations are compared with the actual measurements in Figure 8 to further validate the reasonableness of the model. A comparison of the measured and simulated water levels at various monitoring points is shown in Figure 10. Due to the relatively low correlation between water levels at monitoring points UP2-4 to UP2-8 and changes in reservoir water levels, they are considered anomalous monitoring points and therefore are excluded from the validation process. As shown in Figure 10, it is evident that the water level variations simulated by the suggested approach is mostly in line with the findings of the measurements. This result further demonstrates the effectiveness of the proposed model, indicating its suitability for analyzing the seepage dissolution evolution process of the concrete cutoff walls of earth-rock dams.

4.4. Seepage and Dissolution of Concrete Cutoff Wall

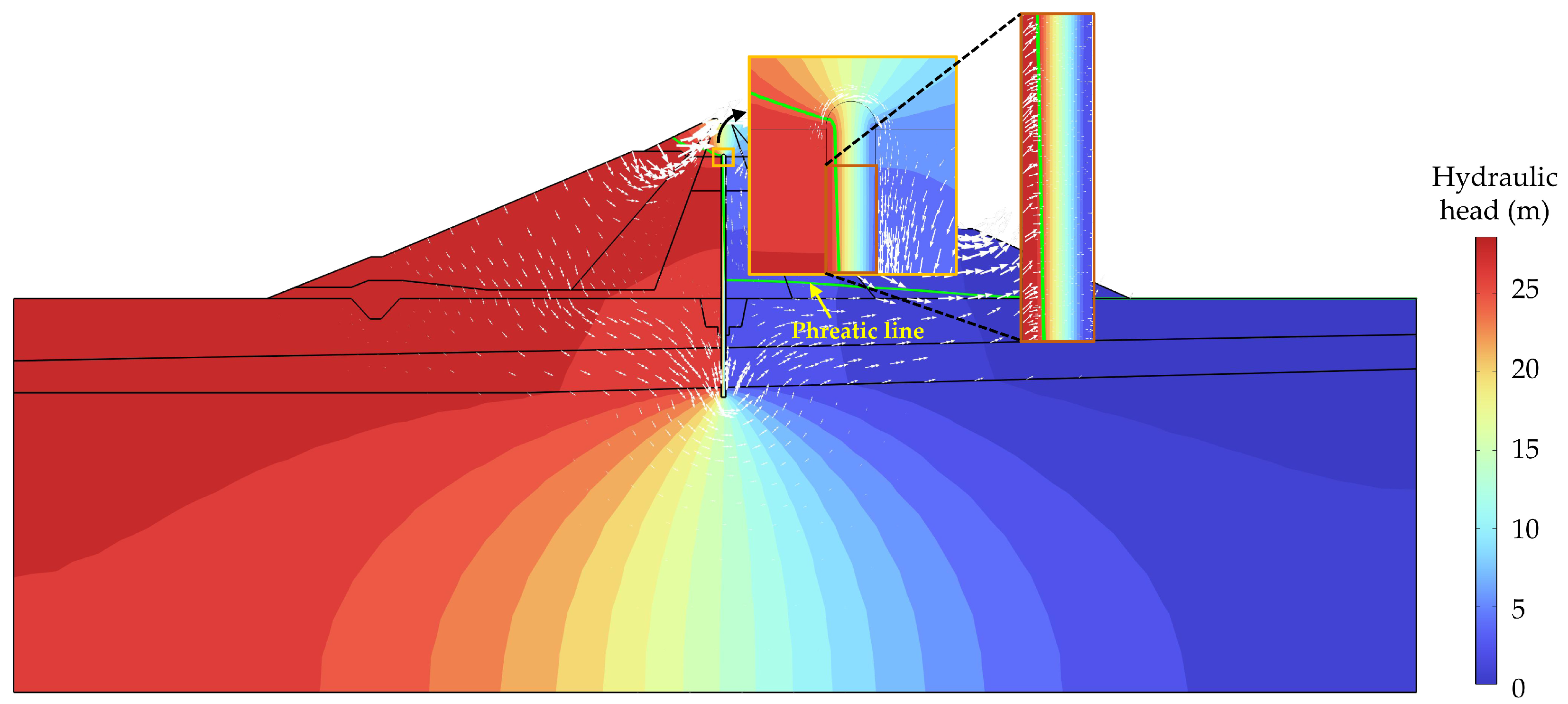
Figure 11 presents the seepage field after the completion of the Phase II reinforcement project, following the initial filling of the dam to its normal water level. The contour map of hydraulic head distribution reveals that the hydraulic head is approximately 27.81 m on the upstream side of the anti-seepage wall, significantly higher than that on its downstream side, which is only about 3.97 m. This indicates that the reinforced concrete cutoff wall has reduced the hydraulic head by 23.84 m, achieving an 85.72% reduction rate. Furthermore, the variation in the phreatic line within the dam body shows a distinct abrupt change (i.e., a sharp drop) at the location of the anti-seepage wall, indicating its effective impermeability within the dam foundation and body. The impermeable qualities of the concrete cutoff wall and the clay core wall result in a significant differential in hydraulic head between their upstream and downstream sides, creating a driving force for seepage within the dam foundation and body.

The direction of the water flow is shown by the white arrows in Figure 11, which are sized according to the flow velocity. It can be observed that there is a significant bypass seepage phenomenon occurring at the top and bottom of the anti-seepage wall, resulting in relatively higher flow velocities at the bottom of the anti-seepage wall. In contrast, the flow velocity at the top of the concrete cutoff wall is notably lower, mainly due to its location within the lower-permeability clay core wall, which impedes most of the water flow.

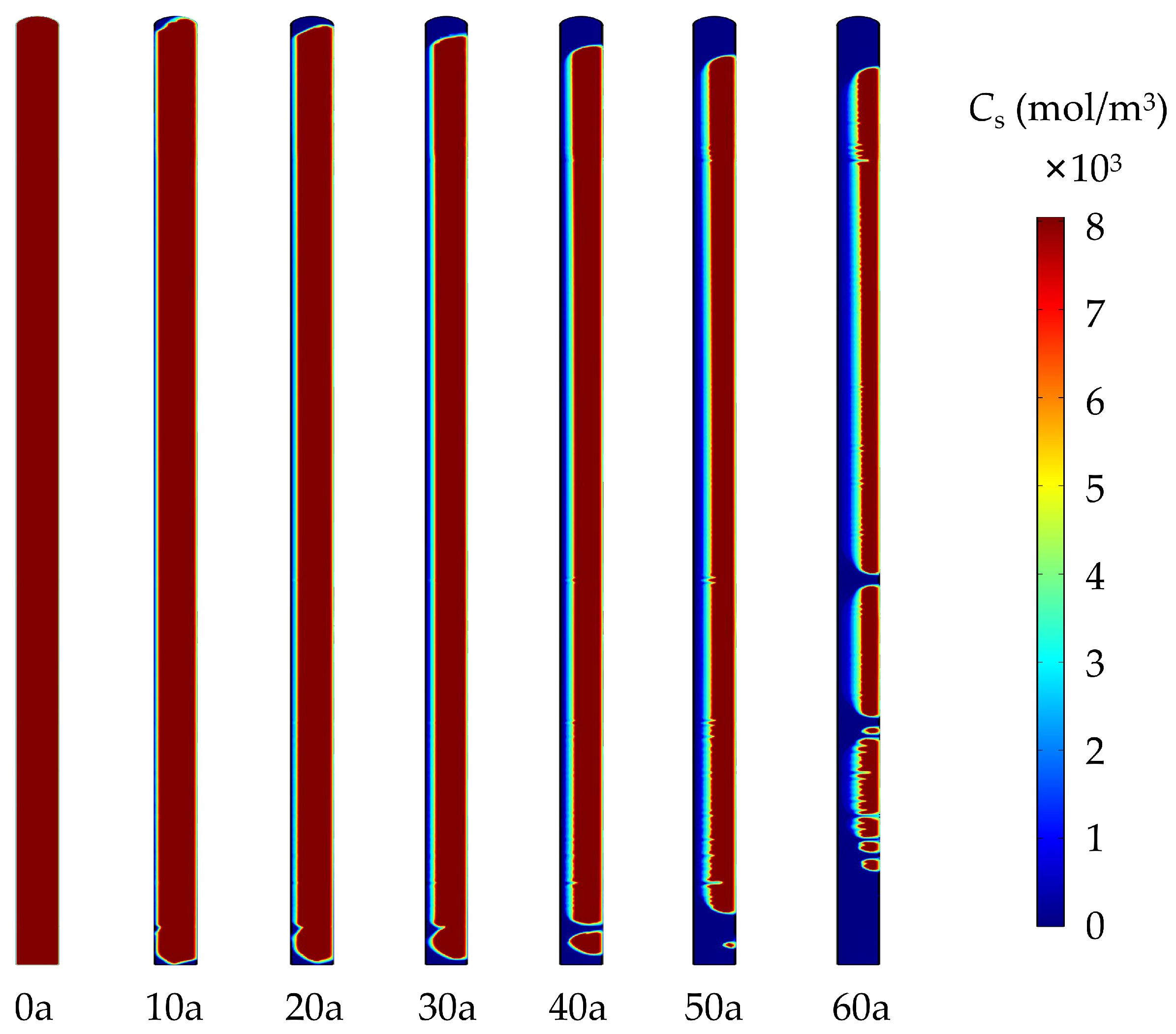
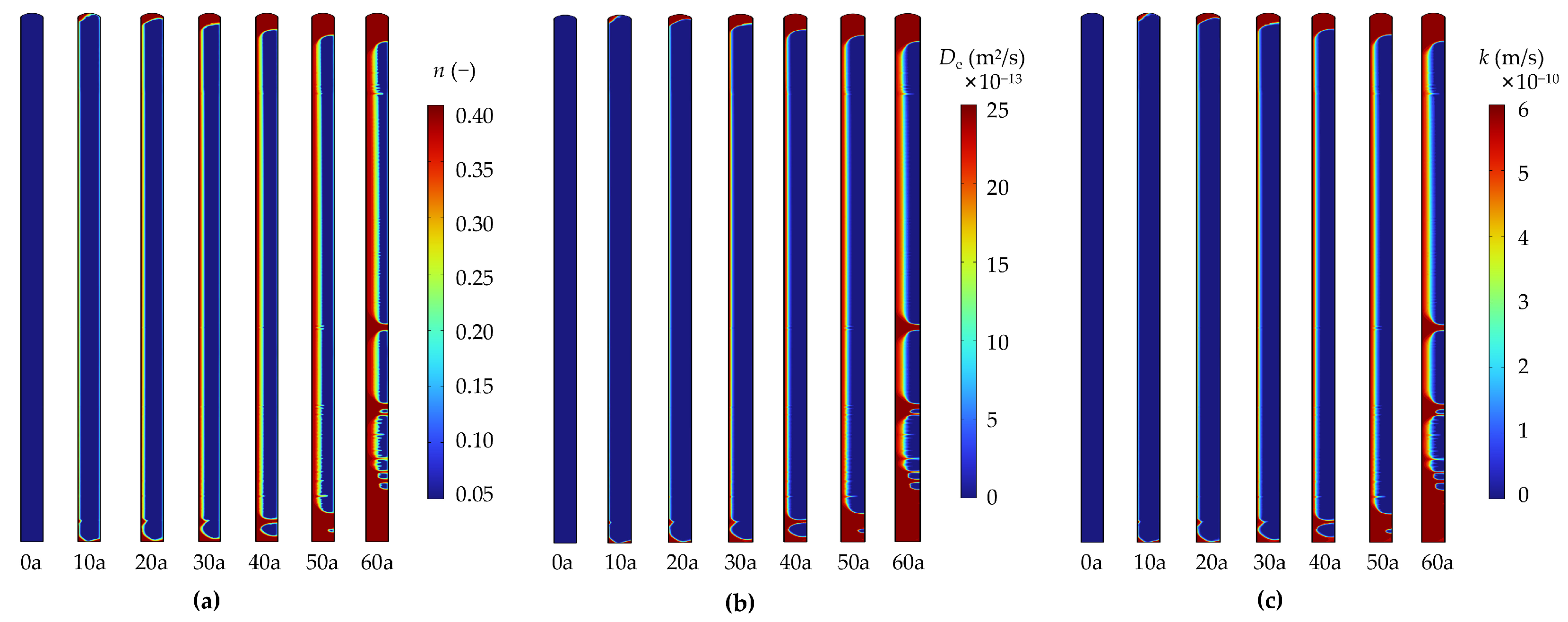
Figure 12 displays the spatial distribution of calcium within the wall during its service life. It is evident that the calcium leaching in the wall primarily occurs at the upstream water-facing surface, as well as its top and bottom sections, with the leached area gradually expanding with increasing years of service. In contrast, the downstream side of the wall exhibits negligible calcium leaching behavior, practically approaching insignificance.

For the upstream side of the anti-seepage wall, it experiences a relatively higher hydraulic head during its service life, creating a noticeable hydraulic head differential with the downstream face. Despite the obstruction of the majority of water flow within the dam foundation and body by the anti-seepage wall, the hydraulic gradient drives an inevitable internal flow within the concrete cutoff wall from upstream to downstream (Figure 11). Due to the significantly higher flow velocity in the high hydraulic head region on the upstream face of the concrete cutoff wall compared to the low hydraulic head region on its downstream side, the leaching of calcium is accelerated in this region. Consequently, the upstream water-facing surface of the anti-seepage wall emerges as the primary area for calcium leaching. The dissolution at the top and bottom of the anti-seepage wall is predominantly induced by bypass seepage, as the flow velocity in these regions is notably higher than in other parts of the anti-seepage wall, resulting in relatively significant severe calcium leaching in these specific locations.

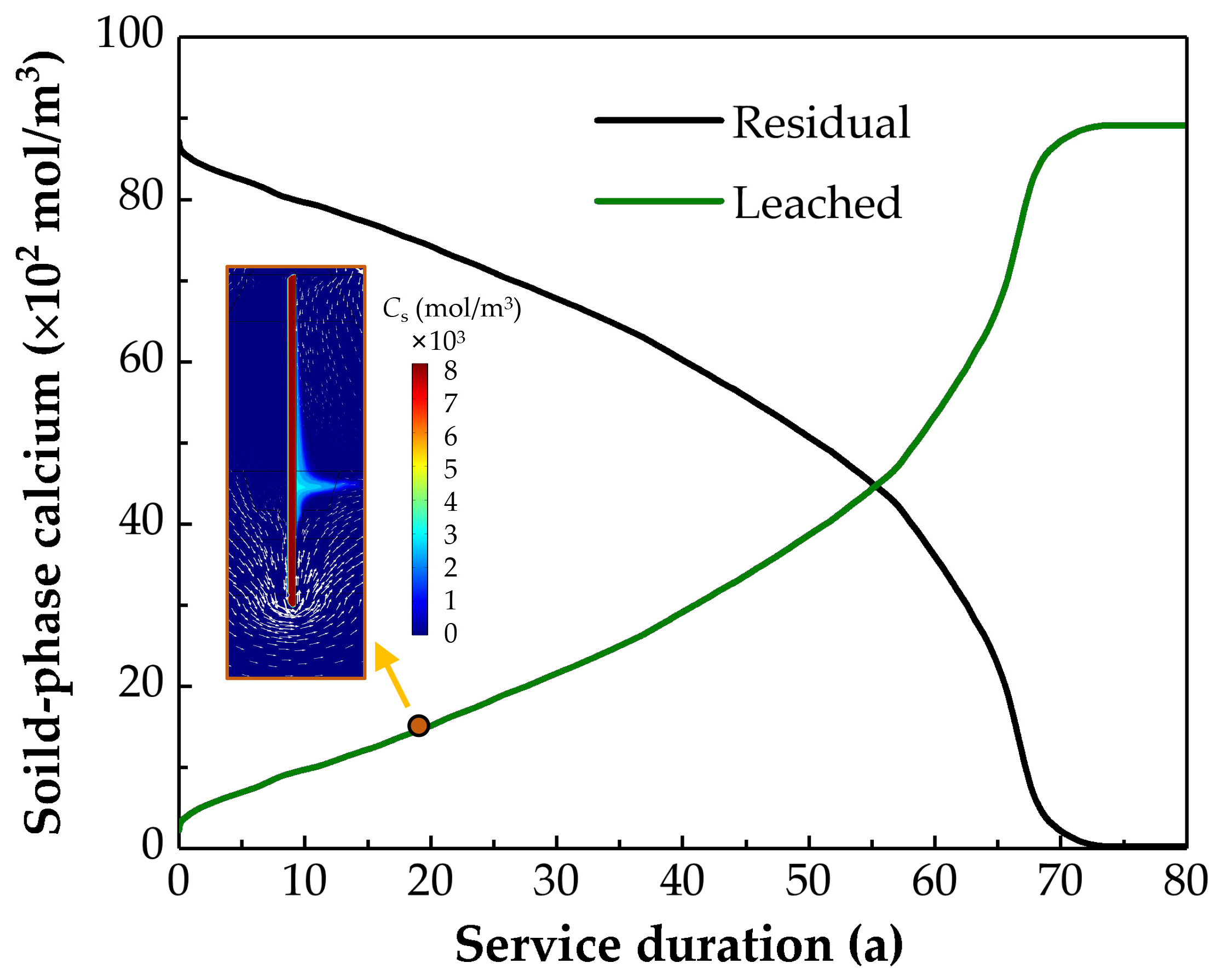
Figure 13 presents the changes in leached and residual calcium content during the service of the anti-seepage wall. It is evident that the calcium within the anti-seepage wall continuously leaches with the increase in years of service. Consequently, the amount of calcium that remains in the concrete cutoff wall steadily reduces. At approximately 73.5 years of service, the calcium within the anti-seepage wall undergoes complete dissolution. In the preceding 68 years of service, the leached calcium within the anti-seepage wall exhibits a trend of exponential growth concerning the service time, i.e., as the service time increases, the dissolution rate of calcium accelerates. Such behavior notably differs from the power–law relationship observed in traditional contact dissolution studies, where the dissolution rate of solid-phase calcium decreases gradually with time and eventually reaches a plateau [12,17]. The disparity primarily arises from the driving force for calcium leaching in contact dissolution, which is solely governed by concentration gradients. The calcium concentration in the external water environment progressively rises over the course of the dissolution time, which reduces the concentration difference between the ions in the external water environment and the concrete pore solution and slows down the dissolution process.

In contrast to contact dissolution, the seepage dissolution mechanism in the concrete cutoff wall involves not only concentration gradients but also hydraulic gradients. The seepage driven by the hydraulic gradient maintains relatively low ion concentrations in the external water environment, ensuring a constant concentration gradient between the inside and outside of the structure. Furthermore, under the combined influence of concentration and hydraulic gradients, the pore structure within the anti-seepage wall continuously enlarges, enhancing permeability, and the flow velocity of the internal pore fluid gradually increases. This, in turn, promotes the calcium leaching behavior of the anti-seepage wall. Therefore, for anti-seepage walls subjected to seepage dissolution, when there is a sufficient supply of calcium available for dissolution within the interior, the dissolution rate of calcium exhibits a gradual increase. When the calcium within the anti-seepage wall is nearly completely dissolved and leached, the reduction in concentration gradients both internally and externally, coupled with the predominance of slow-degrading C-S-H gel in the remaining calcium, causes the rate of calcium leaching to gradually decline until it becomes zero upon complete dissolution.

4.5. Influence of Calcium Dissolution on the Performance of Concrete Cutoff Wall

Figure 14 depicts the distribution of performance parameters, such as porosity, diffusion coefficient, and permeability coefficient, in the concrete cutoff wall at different durations. As can be seen, these three performance parameters at the upstream-facing surface, as well as the top and bottom of the anti-seepage wall, progressively increase with increasing service duration. Furthermore, their distribution patterns closely match the distribution pattern of calcium presented in Figure 12, i.e., these three performance parameters of the calcium-dissolved area become larger, while those of the non-dissolved area remain basically unchanged.

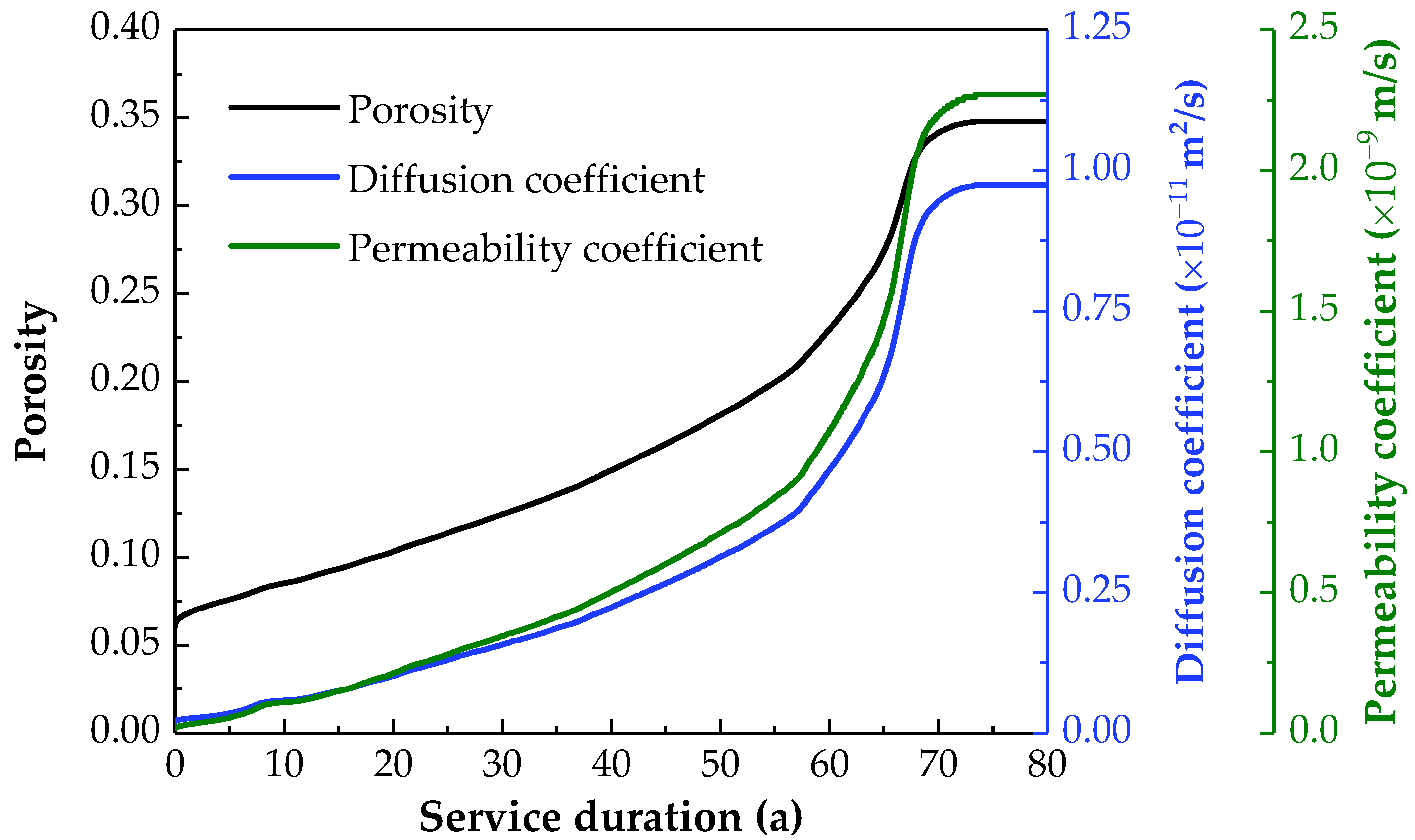
For further elucidation, the changes in the mean value of three performance parameters (i.e., porosity, diffusion, and permeability coefficients) in anti-seepage walls during service are presented in Figure 15. It is observable that these three performance parameters exhibit a trend consistent with the leaching of calcium, i.e., an exponential growth in the initial 68 years of service, followed by a gradual slowdown and eventual cessation of growth due to the near-complete dissolution of solid-phase calcium. Consequently, the rise in these three performance parameters in the relevant regions is directly attributed to the leaching of calcium in the anti-seepage wall. Moreover, Figure 15 provides quantitative evidence that completely dissolved wall’s typical porosity is about 0.35, which is approximately seven times larger than its initial porosity. Due to the rise in porosity, the diffusion coefficient and permeability coefficient of the anti-seepage wall increased by about two to three orders of magnitude, leading to an extremely negative impact on the impermeability of the anti-seepage wall.

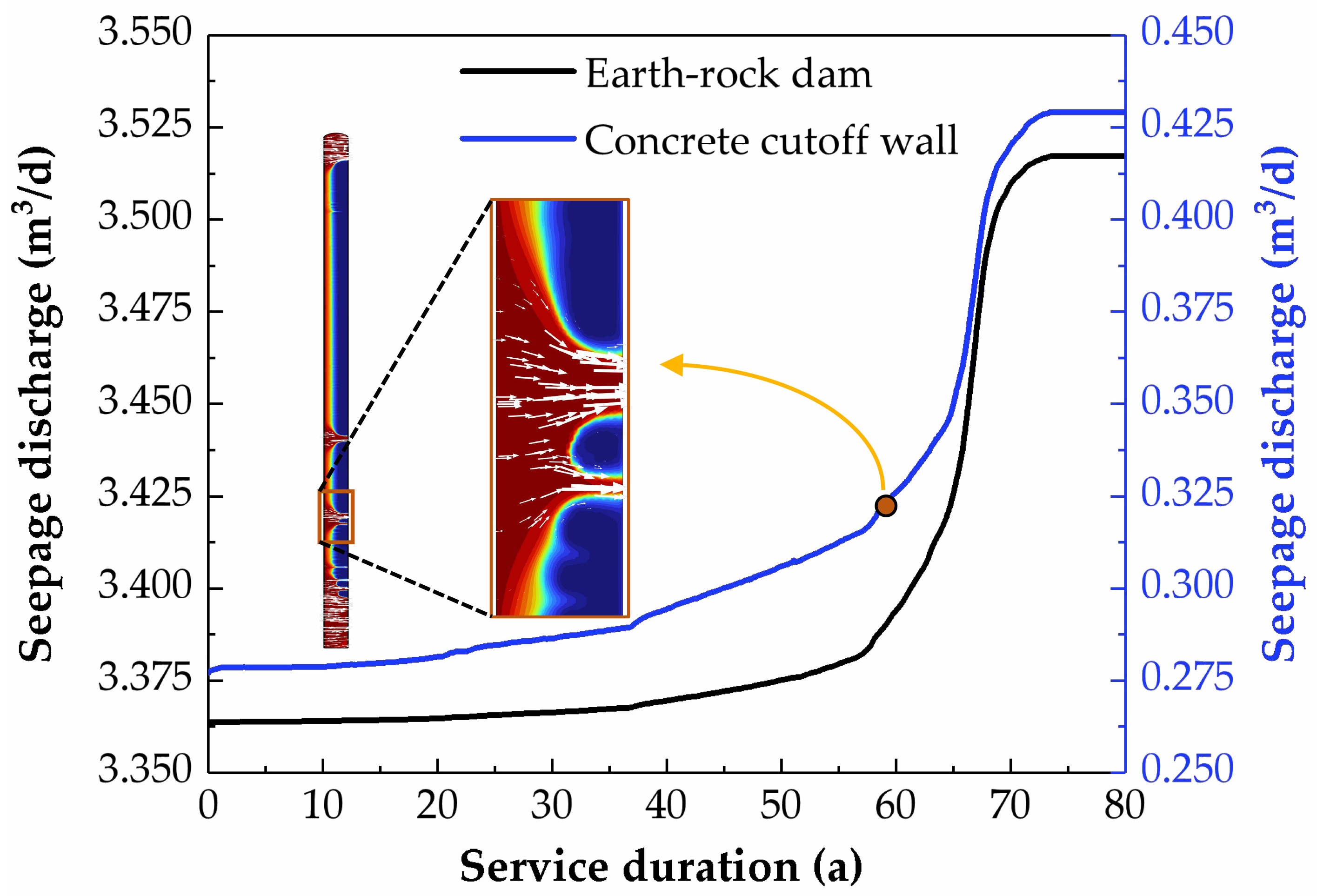
To further investigate the performance characteristics during the service life of the concrete cutoff wall, Figure 16 presents the variation in single-width seepage discharge for the dam throughout its service duration. It is evident that the seepage discharge curves of the anti-seepage wall and the dam exhibit a relatively consistent trend. In the initial 40 years of dam operation, both the dam and the anti-seepage wall demonstrated minimal growth in seepage discharge, maintaining a relatively low level. However, both structures exhibit an abrupt rise in seepage discharge around the 60-year mark of operation. This primary cause of this phenomenon is attributed to the dissolution of the anti-seepage wall, resulting in the formation of a calcium-free zone that penetrates through the wall, as depicted in Figure 12. The formation of the calcium-free zone increases porosity, diffusion coefficient, and permeability coefficient in the corresponding regions (as shown in Figure 14), providing a pathway for downward seepage of groundwater enriched on the upstream face of the anti-seepage wall, as illustrated in Figure 16. Therefore, the formation of a permeable zone devoid of calcium in the anti-seepage wall is identified as the primary cause for the abrupt increase in seepage discharge.

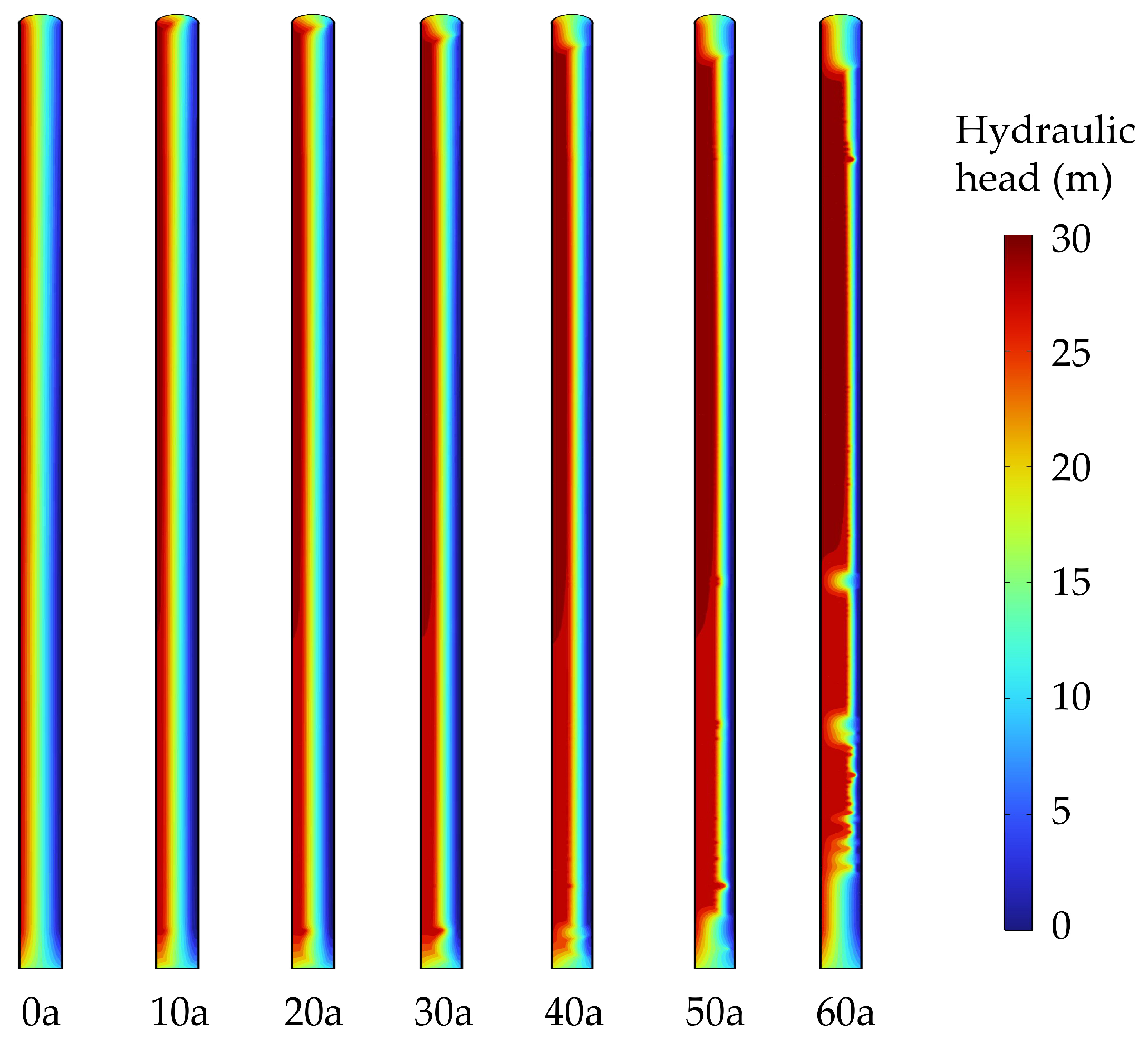
The distribution of hydraulic head within the anti-seepage wall undergoing seepage dissolution at various stages of its service duration is illustrated in Figure 17. It can be observed that, with the increase in service time, the high hydraulic head zone within the anti-seepage wall gradually expands, while the low hydraulic head zone diminishes. This indicates that the effective area of the concrete cutoff wall capable of withstanding the influence of high hydraulic heads progressively decreases. The front of the high hydraulic head in the anti-seepage wall gradually advances towards the downstream side with the increase in service time, which means that the seepage path gradually shortens. Therefore, the hydraulic gradient of the anti-seepage wall will increase.

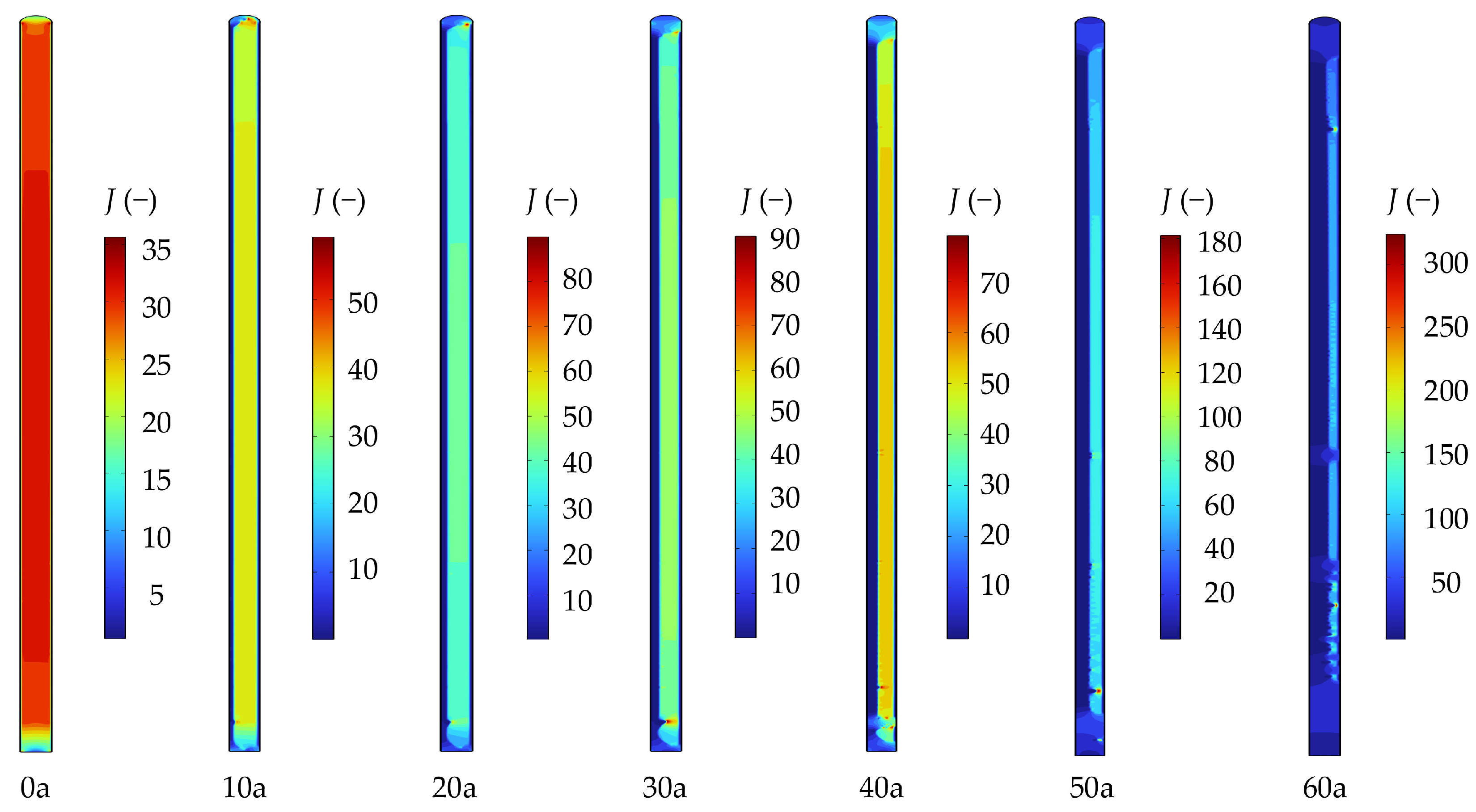
Figure 18 illustrates the hydraulic head distribution within the anti-seepage wall during its service life. In the absence of seepage dissolution, the anti-seepage wall maintains a maximum hydraulic gradient of approximately 35.6. As service time increases, the internal hydraulic gradient progressively increases. According to the relevant literature and standards [55], the allowable hydraulic gradient for a plastic concrete cutoff wall is approximately 60 (i.e., J_c = 60). This means that if the hydraulic gradient at a specific location within the concrete cutoff wall exceeds J_c, hydraulic failure is likely to occur. Upon examining the results depicted in Figure 18, when the concrete cutoff wall has been in service for around 10 years, the maximum hydraulic gradient in the localized area at its top reaches 59, approaching the critical hydraulic gradient. Furthermore, the contours of hydraulic gradient distribution for the 20-, 30-, and 40-year service intervals reveal that localized regions at the top and bottom of the anti-seepage wall exceed the critical hydraulic gradient, although overall they remain below the critical threshold.

Combining the aforementioned observation with Figure 16, it is evident that both the anti-seepage wall and the dam exhibit a minor increase in seepage discharges during the initial 40 years of service. This suggests that hydraulic damage to localized areas of the anti-seepage wall has a negligible influence on its overall performance during this period. However, by the 50th year of service, the hydraulic gradients in the non-dissolved region of the concrete cutoff wall had generally exceeded the critical hydraulic gradient, with the maximum hydraulic gradient reaching 181. This implies that the entire concrete cutoff wall experiences hydraulic failure at this point. Therefore, utilizing the critical hydraulic gradient as the criterion for determining the service life of the anti-seepage wall suggests that its service life falls within a range of 40 to 50 years. 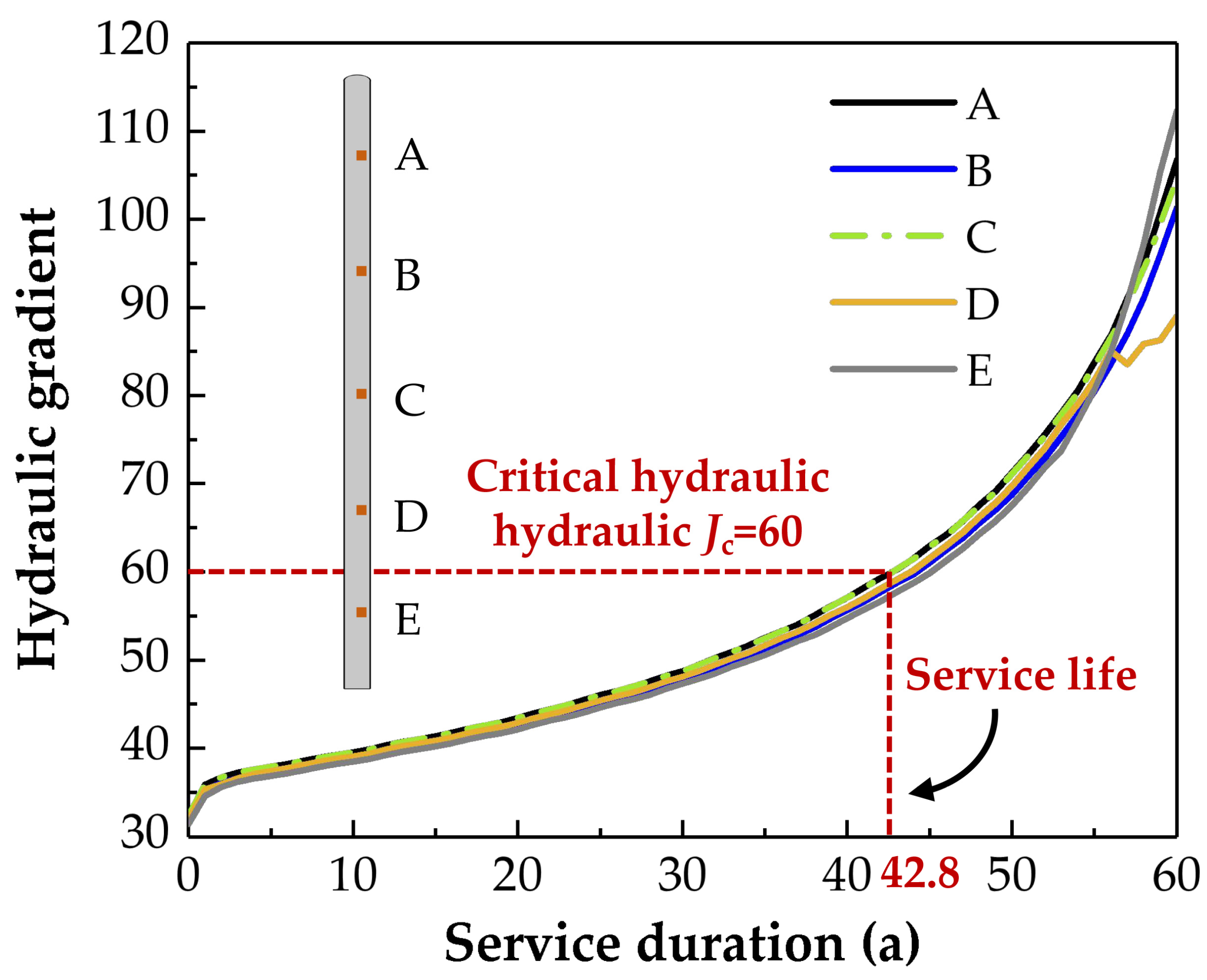Figure 19 provides the temporal variation in hydraulic gradients at five different elevations within the concrete cutoff wall. It is evident that these points exhibit exponential growth in hydraulic gradients with increasing service time. Based on a critical hydraulic gradient of 60 as the criterion, the anticipated service life of the anti-seepage wall is about 42.8 years. At this juncture, the cumulative leaching of calcium in the single-width anti-seepage wall amounts to 1.16 × 10⁵ mol, accounting for 37.7% of the total solid-phase calcium content.

4.6. Identification of Seepage Dissolution Durability Control Indices

Based on the aforementioned analytical results, the degradation of the anti-seepage wall and the subsequent increase in leakage can be attributed to calcium leaching during the dissolution process. To identify the key control indices for the seepage dissolution durability of concrete cutoff walls, a sensitivity analysis of the model parameters impacting the output results of solid-phase calcium leaching (C_sout) was conducted using the constructed numerical model. The involved model parameters include the initial permeability coefficient (k₀), initial diffusion coefficient (D₀), initial percentage of CH content in solid-phase calcium ($C_{\mathrm{CH}}^0$/$C_{\mathrm{solid}}^0$), water/cement (w/c) ratio, upstream hydraulic head (H), and volume fraction of cement matrix in concrete (V_vol). During numerical computations, each parameter is investigated at three levels, with each level representing the reference value, a 10% increase, and a 10% decrease from the reference value, respectively. The levels of each factor in the parameter sensitivity analysis are listed in

Table 6. Factor levels for orthogonal test.

Factor Levels	k0 (m/s)	D0 (m2/s)	${\mathit{C}}_{\mathbf{CH}}^0$/${\mathit{C}}_{\mathbf{soild}}^0$ (%)	w/c	H (m)	Vvol
1	3.42 × 10−12	4.05 × 10−10	34.02	0.36	25.74	0.1332
2	3.80 × 10−12	4.50 × 10−10	37.80	0.40	28.60	0.1480
3	4.18 × 10−12	4.95 × 10−10	41.58	0.44	31.46	0.1628

. It is essential to point out that the adjustments to the aforementioned parameters apply only to the concrete cutoff wall, while the material parameters for other regions within the earth-rock dam remain consistent with those shown in Table 5. Additionally, the output variable C_sout represents the solid-phase calcium content corresponding to a service duration of 42.8 years under various scenarios.

Following the principles of orthogonal test design, an L₁₈(3⁶) orthogonal table was selected to design the orthogonal test. This table randomly allocated test factors, and the corresponding design parameter values were substituted for each element based on the associated factor and level. The orthogonal test table for the sensitivity analysis of the parameters in the suggested model was generated using this procedure, as indicated in

Table 7. Factor levels for orthogonal test.

Scenario	k0 (m/s)	D0 (m2/s)	${\mathit{C}}_{\mathbf{CH}}^0$/${\mathit{C}}_{\mathbf{soild}}^0$ (%)	w/c	H (m)	Vvol	Csout (mol/m3)
1	3.42 × 10−12	4.05 × 10−10	34.02	0.36	25.74	0.1332	2528.769
2	3.42 × 10−12	4.05 × 10−10	37.80	0.40	31.46	0.1628	3145.648
3	3.42 × 10−12	4.50 × 10−10	34.02	0.44	31.46	0.1480	2867.699
4	3.42 × 10−12	4.50 × 10−10	41.58	0.36	28.60	0.1628	2944.168
5	3.42 × 10−12	4.95 × 10−10	37.80	0.44	28.60	0.1332	2825.907
6	3.42 × 10−12	4.95 × 10−10	41.58	0.40	25.74	0.1480	2620.043
7	3.80 × 10−12	4.05 × 10−10	34.02	0.44	28.60	0.1628	2859.115
8	3.80 × 10−12	4.05 × 10−10	41.58	0.36	31.46	0.1480	3966.561
9	3.80 × 10−12	4.50 × 10−10	37.80	0.40	28.60	0.1480	3207.139
10	3.80 × 10−12	4.50 × 10−10	41.58	0.44	25.74	0.1332	3005.924
11	3.80 × 10−12	4.95 × 10−10	34.02	0.40	31.46	0.1332	3513.074
12	3.80 × 10−12	4.95 × 10−10	37.80	0.36	25.74	0.1628	2786.374
13	4.18 × 10−12	4.05 × 10−10	37.80	0.44	25.74	0.1480	3050.079
14	4.18 × 10−12	4.05 × 10−10	41.58	0.40	28.60	0.1332	3917.417
15	4.18 × 10−12	4.50 × 10−10	34.02	0.40	25.74	0.1628	2887.259
16	4.18 × 10−12	4.50 × 10−10	37.80	0.36	31.46	0.1332	4369.345
17	4.18 × 10−12	4.95 × 10−10	34.02	0.36	28.60	0.1480	3513.630
18	4.18 × 10−12	4.95 × 10−10	41.58	0.44	31.46	0.1628	3896.514

. Each row in Table 7 represents a test design, correlating to a combination of factor levels. For each test scenario, the test index C_sout was computed using the designs displayed in Table 6 and entered into the final column of the table. Finally, the sensitivity of the test indices to each parameter was assessed using the ANOVA approach, depending on the outcomes of the several test designs.

The significance of each factor on the model’s output findings was computed following the principles of analysis of variance, as depicted in

Table 8. ANOVA for the factors affecting the test index C_sout.

Source of Variance	Sum of Squares of Deviations Sj	Degree of Freedom fj	Statistics Fj	Significance
k0	1,842,743.646	2	205.22	Significant
D0	8214.654	2	0.91	Insignificant
$C_{\mathrm{CH}}^0$/$C_{\mathrm{solid}}^0$	398,145.831	2	44.34	Significant
w/c	214,326.931	2	23.87	Moderately significant
H	1,985,145.037	2	221.08	Significant
Vvol	225,964.066	2	25.17	Moderately significant
Random error	22,448.238	5	\	\

. The calculated statistic F_j was compared to the F-values corresponding to the two selected significance testing levels, α = 0.001 and α = 0.005. This procedure enable the evaluation of each factor’s importance. Three categories were established for the significance levels: (a) when F_j > F_0.001 (2, 5), it indicates high sensitivity of the factor with a significant impact; (b) when F_0.001 (2, 5) > F_j > F_0.005 (2, 5), it suggests moderate sensitivity of the factor with a moderately significant impact; (c) when F_j < F_0.005 (2, 5), it signifies low sensitivity of the factor with an insignificant impact. It is noted that F_0.001 (2, 5) = 37.12 and F_0.005 (2, 5) = 18.31, according to the probability statistics F distribution table. This allows for the assessment of each parameter’s relative importance the test index C_sout.

The sensitivity ranking of the calcium leaching in anti-seepage walls to various parameters is displayed in Table 8 in descending order: H, k₀, $C_{\mathrm{CH}}^0$/$C_{\mathrm{solid}}^0$, V_vol, w/c, and D₀. The upstream hydraulic head (H) and the initial permeability coefficient of the anti-seepage wall (k₀) exhibit substantial influences on the leaching of solid-phase calcium, with respective statistical values F_j reaching as high as 221.08 and 205.22. The statistical values for the other parameters are notably lower than the F_j values for H and k₀, which also significantly surpass F_0.001 (2, 5). Although the statistical value for the $C_{\mathrm{CH}}^0$/$C_{\mathrm{solid}}^0$ is not as substantial as the first two, its F_j value surpasses F_0.001 (2, 5), indicating it is a sensitive parameter affecting the calcium leaching in anti-seepage walls and, consequently, influencing their seepage dissolution durability. In comparison, the F_j values for the V_vol and the w/c are relatively smaller, falling between F_0.001 (2, 5) and F_0.005 (2, 5). Hence, these parameters are moderately significant in influencing the durability of concrete against seepage dissolution. During the seepage dissolution process, the D₀ has minimal impact on the leaching of solid-phase calcium, with its F_j value being merely 0.91, significantly lower than F_0.005 (2, 5). Consequently, it stands as the least sensitive parameter.

According to the aforementioned analysis, the seepage dissolution durability of anti-seepage walls in earth-rock dams is primarily associated with the H, k₀, and $C_{\mathrm{CH}}^0$/$C_{\mathrm{solid}}^0$. Therefore, to enhance the service durability of anti-seepage walls in earth-rock dams, it is imperative, during the design and construction phases of these walls, to elevate their resistance to permeation by either increasing their impermeability grade. While the influence of the w/c and appears moderately significant, it may stem from a limitation of the model in this study. Due to the absence of a functional relationship between the initial permeability coefficient and concrete parameters such as the w/c in existing research, the model fails to establish a connection between these two factors, potentially underestimating the impact of the w/c ratio on the results during sensitivity analysis. It is well-known that altering the w/c ratio can enhance the concrete’s impermeability (i.e., the initial permeability coefficient of concrete is closely related to concrete parameters such as the w/c ratio), with lower w/c ratio generally considered advantageous for reducing the initial permeability coefficient of concrete. The actual w/c ratio of concrete may exert a larger influence on the model’s output than anticipated. Therefore, the sensitivity of concrete parameters such as w/c ratio on the dissolution durability of concrete cutoff walls needs to be further discussed in future studies.

In addition, measures such as increasing the admixture of silica fume, fly ash, and similar additives are necessary to reduce the CH content in the cement slurry of concrete cutoff walls. From an engineering maintenance perspective, it is essential to judiciously control the reservoir’s water storage level, avoiding indiscriminate pursuit of economic benefits from high-head water storage for power generation. While these measures may initially increase project costs, they will significantly extend the service life and performance of concrete cutoff walls, making them economically justifiable in the long term.

5. Conclusions

This study developed a novel modeling approach to evaluate the effects of seepage dissolution on the durability of anti-seepage walls. The numerical implementation was conduct using the COMSOL Multiphysics software (Version 6.0) package with a weak coupling method. The model’s effectiveness was carefully assessed and compared with laboratory and field observations. Additionally, the deterioration and failure processes of an anti-seepage wall in a dam case study were numerically investigated. Durability control indices for anti-seepage wall, considering the seepage and dissolution coupling effect, were identified through sensitivity analysis. The primary conclusions are as follows:

(1)

The suggested model accurately replicates the temporal variation in calcium dissolution depth during contact dissolution and performs well in experimental validation of seepage dissolution. Compared to contact dissolution without considering seepage effects, concrete subjected to seepage dissolution exhibits a greater dissolution depth at the same time duration.

(2)

The seepage dissolution of anti-seepage walls is a surface-to-inward process, primarily occurring at the upstream-facing surface of the wall, as well as at the bottom and top bypass seepage areas. The dissolution process is significantly influenced by the seepage field within the dam. Continuous leaching of solid-phase calcium, driven by concentration and hydraulic gradients, occurs during the concrete seepage dissolution of anti-seepage walls, exhibiting an exponential growth trend with service time. As the calcium inside the wall is nearly completely leached, the dissolution rate slows until there is no further leaching.

(3)

Due to calcium leaching during the concrete seepage dissolution process, the porosity of the corresponding regions within the anti-seepage wall has increased approximately sevenfold. The diffusion and permeability coefficients have increased by two to three orders of magnitude. Additionally, their mean values show a temporal variation pattern highly consistent with the increase in solid-phase calcium over the service life. As these performance parameters deteriorate, seepage flow within the dam and the anti-seepage wall increases, leading to a gradual decrease in the effective region capable of withstanding high hydraulic heads within the anti-seepage wall. Consequently, the hydraulic gradient within the anti-seepage wall increases, and based on the critical hydraulic gradient, the estimated service life of the anti-seepage wall in the presented case study is 42.8 years.

(4)

The orthogonal test sensitivity analysis method revealed that the upstream hydraulic head, the initial permeability coefficient of the anti-seepage wall, and the initial percentage of CH content in solid-phase calcium are three important indices affecting the long-term seepage dissolution durability of the anti-seepage wall. Controlling these factors judiciously during the design, construction, and operation phases of the anti-seepage wall is crucial to ensuring its sustained and secure operation over the long term.