Employing Tank Constraints to Present Total Cost and Water Age Trade-Offs in Optimal Operation of Water Distribution Systems
Abstract
1. Introduction
2. Methodology
2.1. Water Distribution System Optimal Operation Problem Formulation
2.2. Modification of Tank Operation Constraint
2.3. Conceptual Definition of Water Age
3. Results
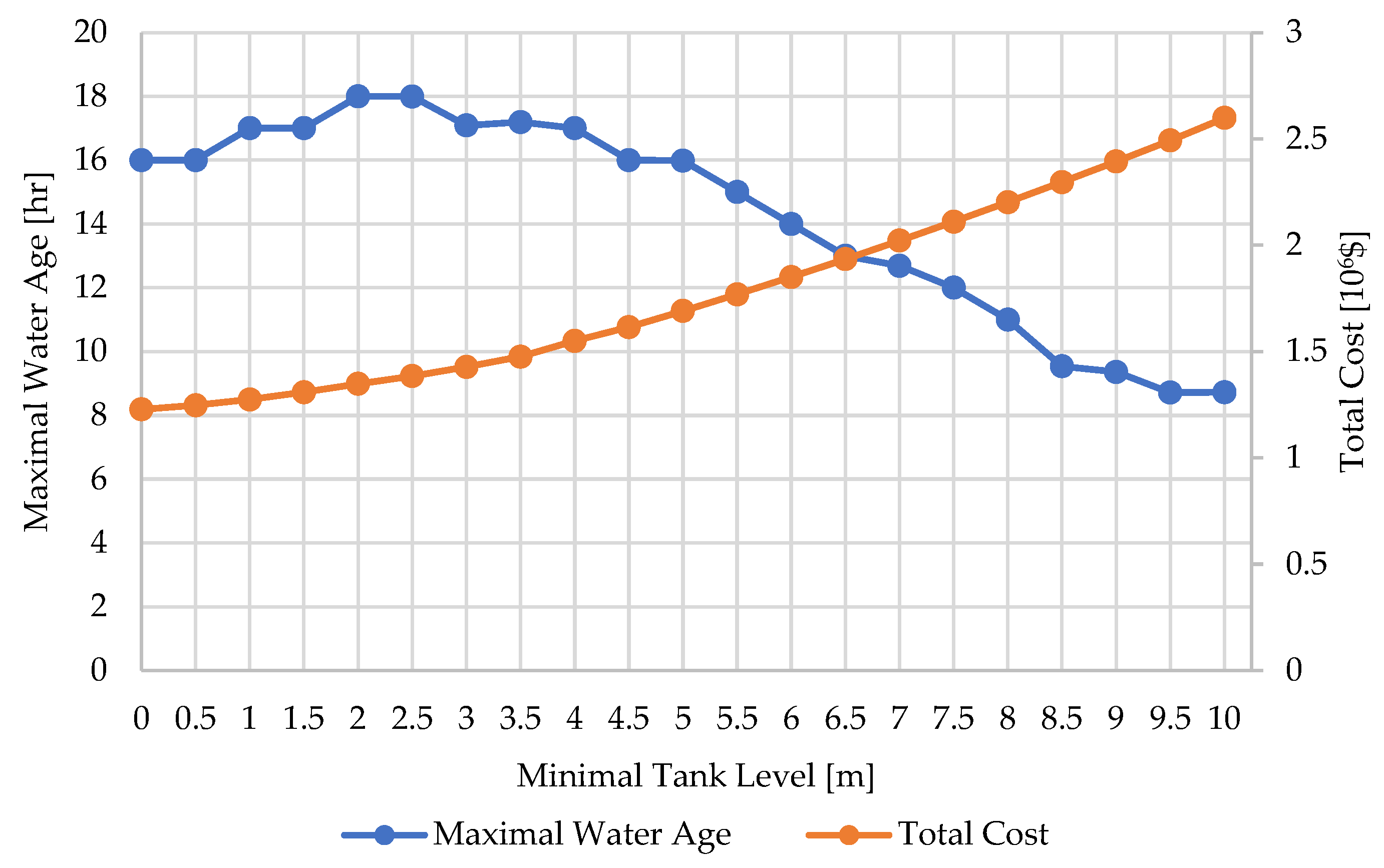
3.1. Case Study 1
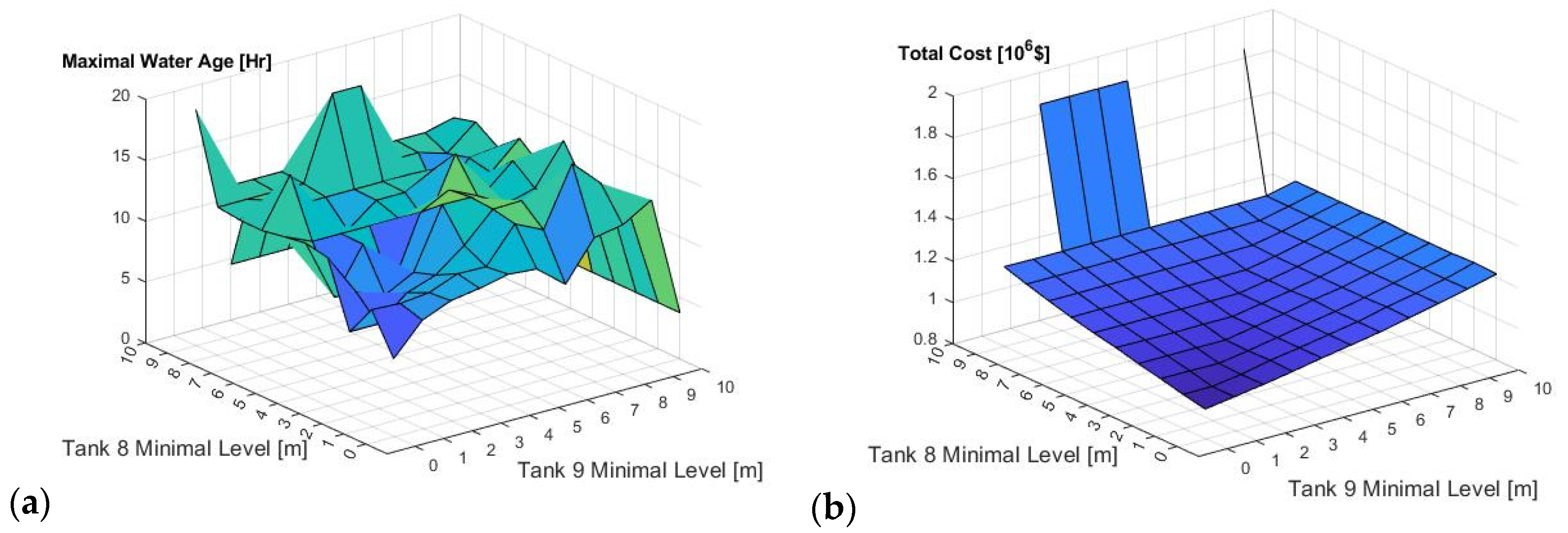
3.2. Case Study 2
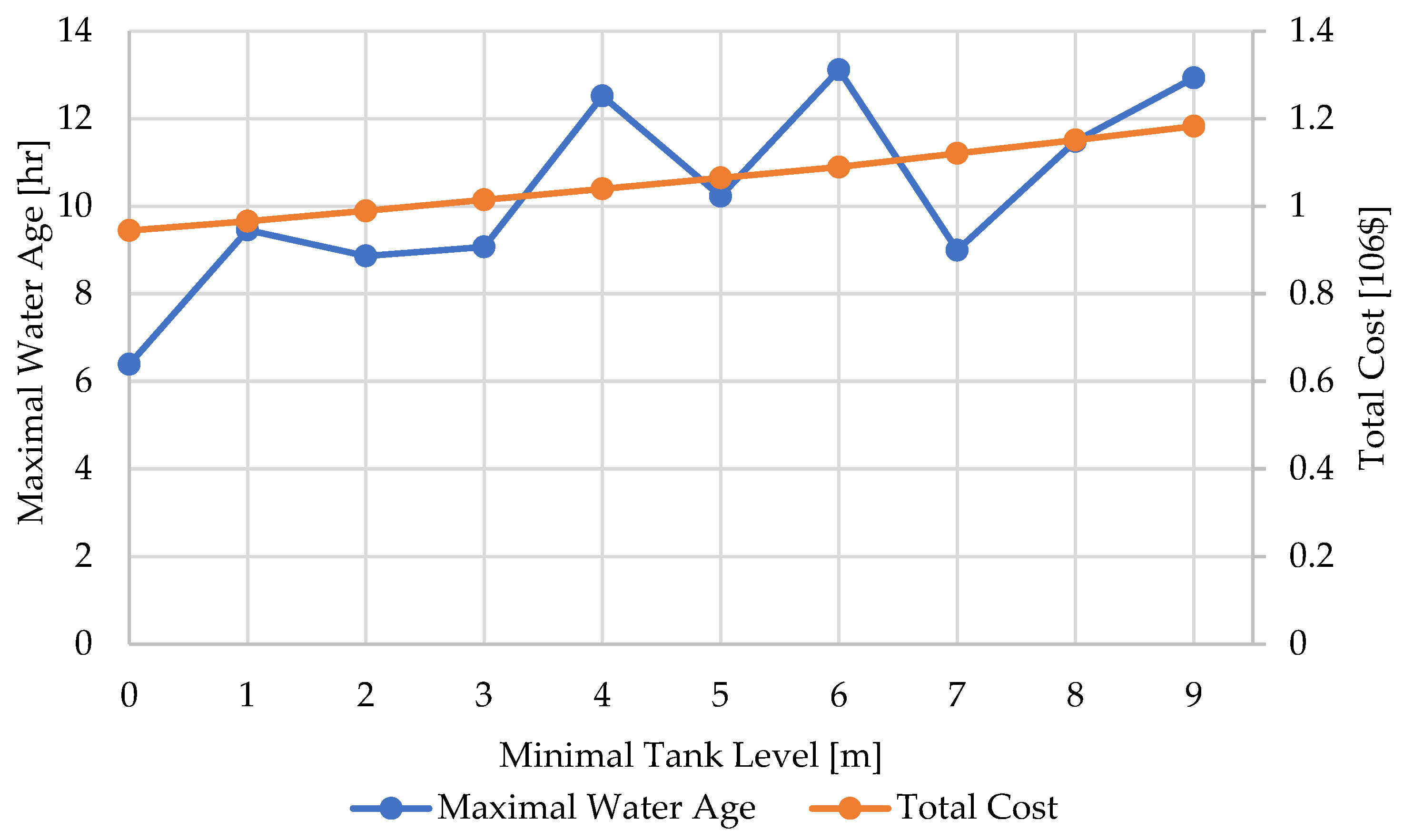
3.3. Case Study 3
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Besner, M.; Gauthier, V.; Barbeau, B.; Millette, R.; Chapleau, R.; Prévost, M. Understanding distribution system water quality. J. AWWA 2001, 93, 101–114. [Google Scholar] [CrossRef]
- Kim, J.H.; Tran, T.V.; Chung, G. Optimization of water quality sensor locations in water distribution systems considering imperfect mixing. In Water Distribution Systems Analysis; ASCE: Reston, VA, USA, 2010. [Google Scholar] [CrossRef]
- Boorman, G.A. Drinking water disinfection byproducts: Review and approach to toxicity evaluation. Environ. Health Perspect. 1999, 107 (Suppl. S1), 207–217. [Google Scholar] [CrossRef]
- Helbling, D.E.; VanBriesen, J.M. Modeling residual chlorine response to a microbial contamination event in drinking water distribution systems. J. Environ. Eng. 2009, 135, 918–927. [Google Scholar] [CrossRef]
- Ostfeld, A. A review of modeling water quality in Distribution Systems. Urban Water J. 2005, 2, 107–114. [Google Scholar] [CrossRef]
- Kurek, W.; Ostfeld, A. Multi-objective optimization of water quality, pumps operation, and storage sizing of water distribution systems. J. Environ. Manag. 2013, 115, 189–197. [Google Scholar] [CrossRef] [PubMed]
- Shokoohi, M.; Tabesh, M.; Nazif, S.; Dini, M. Water quality based multi-objective optimal design of Water Distribution Systems. Water Resour. Manag. 2016, 31, 93–108. [Google Scholar] [CrossRef]
- Tu, M.-Y.; Tsai, F.T.-C.; Yeh, W.W.-G. Optimization of water distribution and water quality by hybrid genetic algorithm. J. Water Resour. Plan. Manag. 2005, 131, 431–440. [Google Scholar] [CrossRef]
- Yang, S.; Sun, Y.-H.; Yeh, W.W.-G. Optimization of regional water distribution system with blending requirements. J. Water Resour. Plan. Manag. 2000, 126, 229–235. [Google Scholar] [CrossRef]
- Sakarya, A.B.; Mays, L.W. Optimal operation of water distribution pumps considering water quality. J. Water Resour. Plan. Manag. 2000, 126, 210–220. [Google Scholar] [CrossRef]
- Islam, N.; Sadiq, R.; Rodriguez, M.J. Optimizing booster chlorination in water distribution networks: A water quality index approach. Environ. Monit. Assess. 2013, 185, 8035–8050. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E. Conjunctive optimal scheduling of pumping and booster chlorine injections in water distribution systems. Eng. Optim. 2006, 38, 337–352. [Google Scholar] [CrossRef]
- Mulholland, M.; Latifi, M.A.; Purdon, A.; Buckley, C.; Brouckaert, C. Multi-objective optimisation of the operation of a water distribution network. J. Water Supply Res. Technol. -Aqua 2014, 64, 235–249. [Google Scholar] [CrossRef]
- EPA. 2023. Available online: https://www.epa.gov/sciencematters/epanet-220-epa-and-water-community-collaboration (accessed on 9 May 2024).
- EPA. Available online: https://www.epa.gov/dwreginfo/drinking-water-distribution-system-tools-and-resources (accessed on 9 May 2024).
- Caldarola, F.; Maiolo, M. A mathematical investigation on the invariance problem of some hydraulic indices. Appl. Math. Comput. 2021, 409, 125726. [Google Scholar] [CrossRef]
- Analysis Algorithms—EPANET 2.2 Documentation. Available online: https://epanet22.readthedocs.io/en/latest/12_analysis_algorithms.html#water-quality (accessed on 30 May 2024).
- Download and Install MATLAB. Available online: https://www.mathworks.com/help/install/ug/install-products-with-internet-connection.html (accessed on 1 February 2024).
- Getting Started, YALMIP. 2016. Available online: https://yalmip.github.io/tutorial/basics/ (accessed on 2 March 2024).
- Ostfeld, A. Optimal design and operation of multiquality networks under unsteady conditions. J. Water Resour. Plan. Manag. 2005, 131, 116–124. [Google Scholar] [CrossRef]







| Component | Attribute | Value |
|---|---|---|
| Source | Elevation [m] | 0 |
| Pipes | Diameter [mm] | 600 |
| Length [km] | 3 | |
| Roughness [-] | 110 | |
| Nodes | Base demand [CMH] | 475 |
| Elevation [m] | 0 | |
| Service pressure [m] | 30 | |
| Pump | Efficiency [%] | 85 |
| Curve coefficients | [1 × 10−5, 200] | |
| Rotation speed range [rpm] | [0, 50] | |
| Tank | Pipe length [km] | 0.5 |
| Elevation [m] | 35 | |
| Cross-section area [m2] | 1000 | |
| Level range [m] | [0, 7] | |
| Initial level [m] | 7 |
| Component | Attribute | Value |
|---|---|---|
| Source | Elevation [m] | 0 |
| Pipes | Diameter [mm] | 600 |
| Roughness [-] | 120 | |
| Pipes 3, 4, 5, 6, 7, 9 | Length [km] | 2 |
| Pipe 8 | 4 | |
| Nodes | Elevation [m] | 0 |
| Service pressure [m] | 30 | |
| Nodes 4, 5 | Base demand [CMH] | 150 |
| Node 6 | 300 | |
| Node 7 | 400 | |
| Pumps | Efficiency [%] | 85 |
| Curve coefficients | [1 × 10−5, 200] | |
| Rotation speed range [rpm] | [0, 50] | |
| Tanks | Pipe length [km] | 0.4 |
| Pipe diameter [mm] | 750 | |
| Elevation [m] | 30 | |
| Cross-section area [m2] | 490.87 | |
| Level range [m] | [0, 10] | |
| Initial level [m] | 10 |
| Link ID | Diameter [mm] | Length [m] | Link ID | Diameter [mm] | Length [m] |
|---|---|---|---|---|---|
| 1 | 132.7600 | 204 | 21 | 83.9600 | 368 |
| 2 | 374.6800 | 80 | 22 | 49.8200 | 511 |
| 3 | 119.7400 | 80 | 23 | 78.5000 | 450 |
| 4 | 312.7200 | 80 | 24 | 99.2700 | 368 |
| 5 | 289.0900 | 130 | 25 | 82.2900 | 307 |
| 6 | 336.3300 | 80 | 26 | 147.4900 | 163 |
| 7 | 135.8100 | 80 | 27 | 197.3200 | 204 |
| 8 | 201.2600 | 80 | 28 | 83.3000 | 511 |
| 9 | 132.5300 | 80 | 29 | 113.8000 | 450 |
| 10 | 144.6600 | 80 | 30 | 80.8200 | 307 |
| 11 | 175.7200 | 102 | 31 | 340.9700 | 130 |
| 12 | 112.1700 | 163 | 32 | 77.3900 | 80 |
| 13 | 210.7400 | 257 | 33 | 112.3700 | 80 |
| 14 | 75.4100 | 102 | 34 | 37.3400 | 204 |
| 15 | 181.4200 | 92 | 35 | 108.8500 | 257 |
| 16 | 146.9600 | 736 | 36 | 182.8200 | 80 |
| 17 | 162.6900 | 450 | 37 | 136.0200 | 80 |
| 18 | 99.6400 | 368 | 38 | 56.7000 | 80 |
| 19 | 52.9800 | 204 | 39 | 124.0800 | 80 |
| 20 | 162.9700 | 204 | 40 | 234.6000 | 80 |
| 41 | 203.8300 | 204 | 51 | 215.0500 | 163 |
| 42 | 248.0500 | 80 | 52 | 144.4400 | 80 |
| 43 | 65.1900 | 163 | 53 | 34.7400 | 257 |
| 44 | 210.0900 | 163 | 54 | 59.9300 | 368 |
| 45 | 147.5700 | 204 | 55 | 165.6700 | 163 |
| 46 | 103.8000 | 80 | 56 | 119.9700 | 102 |
| 47 | 210.9500 | 163 | 57 | 83.1700 | 163 |
| 48 | 75.0800 | 257 | 59 | 100.0000 | 80 |
| 49 | 180.2900 | 80 | 60 | 100.0000 | 80 |
| 50 | 149.0500 | 80 |
| Node ID | Base Demand [CMH] | Node ID | Base Demand [CMH] |
|---|---|---|---|
| 1 | 7.055916 | 19 | 27.071680 |
| 2 | 14.975824 | 20 | 13.391844 |
| 3 | 14.687828 | 21 | 13.823836 |
| 4 | 11.663864 | 22 | 13.967836 |
| 5 | 9.071892 | 23 | 12.383856 |
| 6 | 11.375868 | 24 | 9.647888 |
| 7 | 3.743956 | 25 | 11.087868 |
| 8 | 8.351900 | 26 | 24.335712 |
| 9 | 7.775908 | 27 | 20.447760 |
| 10 | 15.983812 | 28 | 4.319948 |
| 11 | 25.199703 | 29 | 8.927896 |
| 12 | 13.103844 | 30 | 7.775908 |
| 13 | 16.703804 | 31 | 12.959848 |
| 14 | 7.775908 | 32 | 14.831824 |
| 15 | 15.839812 | 33 | 11.087868 |
| 16 | 17.423796 | 34 | 10.655876 |
| 17 | 18.287785 | 35 | 16.703804 |
| 18 | 29.087656 | 36 | 6.767920 |
| Component | Attribute | Value |
|---|---|---|
| Sources | Elevation [m] | 0 |
| Nodes | Elevation [m] | 0 |
| Service pressure [m] | 30 | |
| Pumps | Efficiency [%] | 85 |
| Curve coefficients | [1 × 10−5, 200] | |
| Rotation speed range [rpm] | [0, 50] | |
| Elevation [m] | 40 | |
| Cross-section area [m2] | 19.635 | |
| Level range [m] | [0, 10] | |
| Initial level [m] | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shmaya, T.; Ostfeld, A. Employing Tank Constraints to Present Total Cost and Water Age Trade-Offs in Optimal Operation of Water Distribution Systems. Water 2024, 16, 1637. https://doi.org/10.3390/w16121637
Shmaya T, Ostfeld A. Employing Tank Constraints to Present Total Cost and Water Age Trade-Offs in Optimal Operation of Water Distribution Systems. Water. 2024; 16(12):1637. https://doi.org/10.3390/w16121637
Chicago/Turabian StyleShmaya, Tomer, and Avi Ostfeld. 2024. "Employing Tank Constraints to Present Total Cost and Water Age Trade-Offs in Optimal Operation of Water Distribution Systems" Water 16, no. 12: 1637. https://doi.org/10.3390/w16121637
APA StyleShmaya, T., & Ostfeld, A. (2024). Employing Tank Constraints to Present Total Cost and Water Age Trade-Offs in Optimal Operation of Water Distribution Systems. Water, 16(12), 1637. https://doi.org/10.3390/w16121637







