Runoff Prediction in Different Forecast Periods via a Hybrid Machine Learning Model for Ganjiang River Basin, China
Abstract
1. Introduction
2. Methodology
2.1. Variational Mode Decomposition
2.2. Principal Component Analysis
2.3. Long Short-Term Memory Network
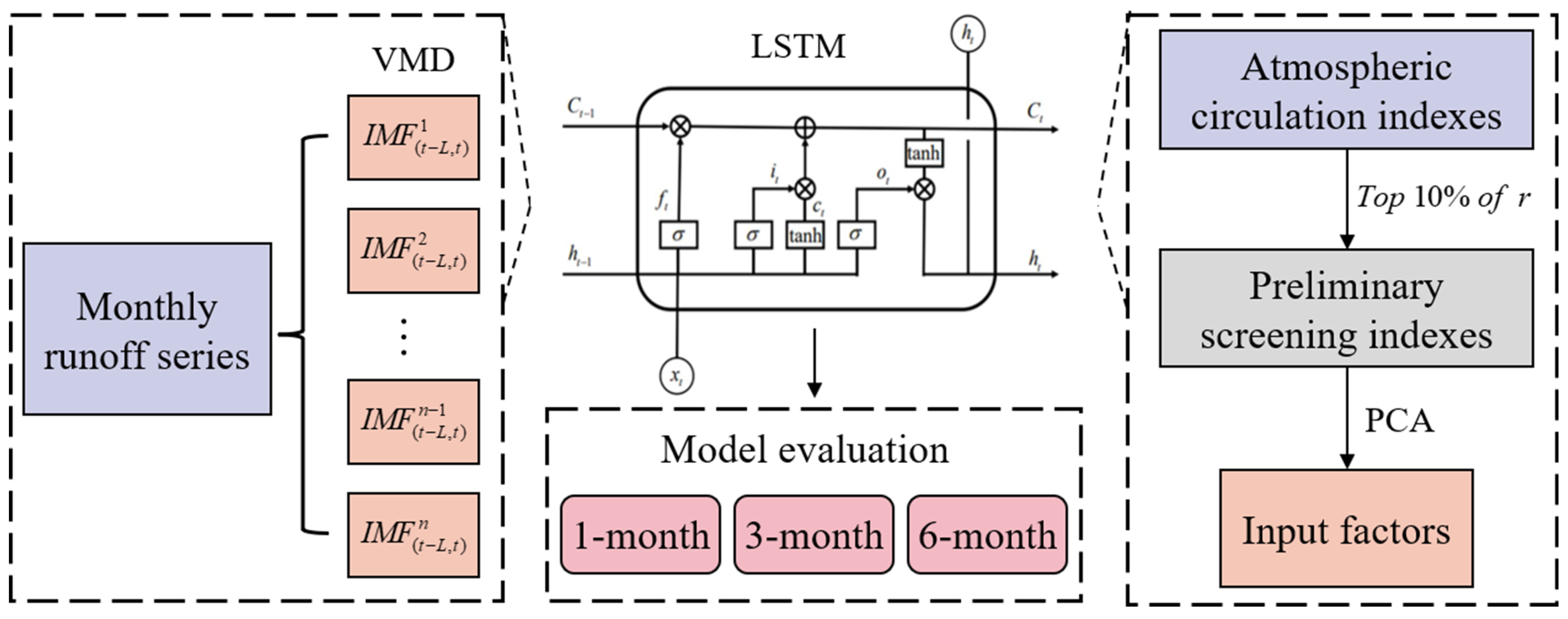
2.4. VMD-PCA-LSTM
- (1)
- Multiple stationary intrinsic modal components (IMF) and a residual component (residual) were obtained by decomposing the runoff series according to the VMD method;
- (2)
- The PCA method was used to reduce the dimension of the atmospheric circulation indexes, and then principal components with a cumulative contribution rate greater than 90% were selected as forecasting factors;
- (3)
- Normalized processing and determinations of the inputs and outputs of the LSTM model were carried out.
2.5. Evaluation Metrics
3. Study Area and Data Preprocessing
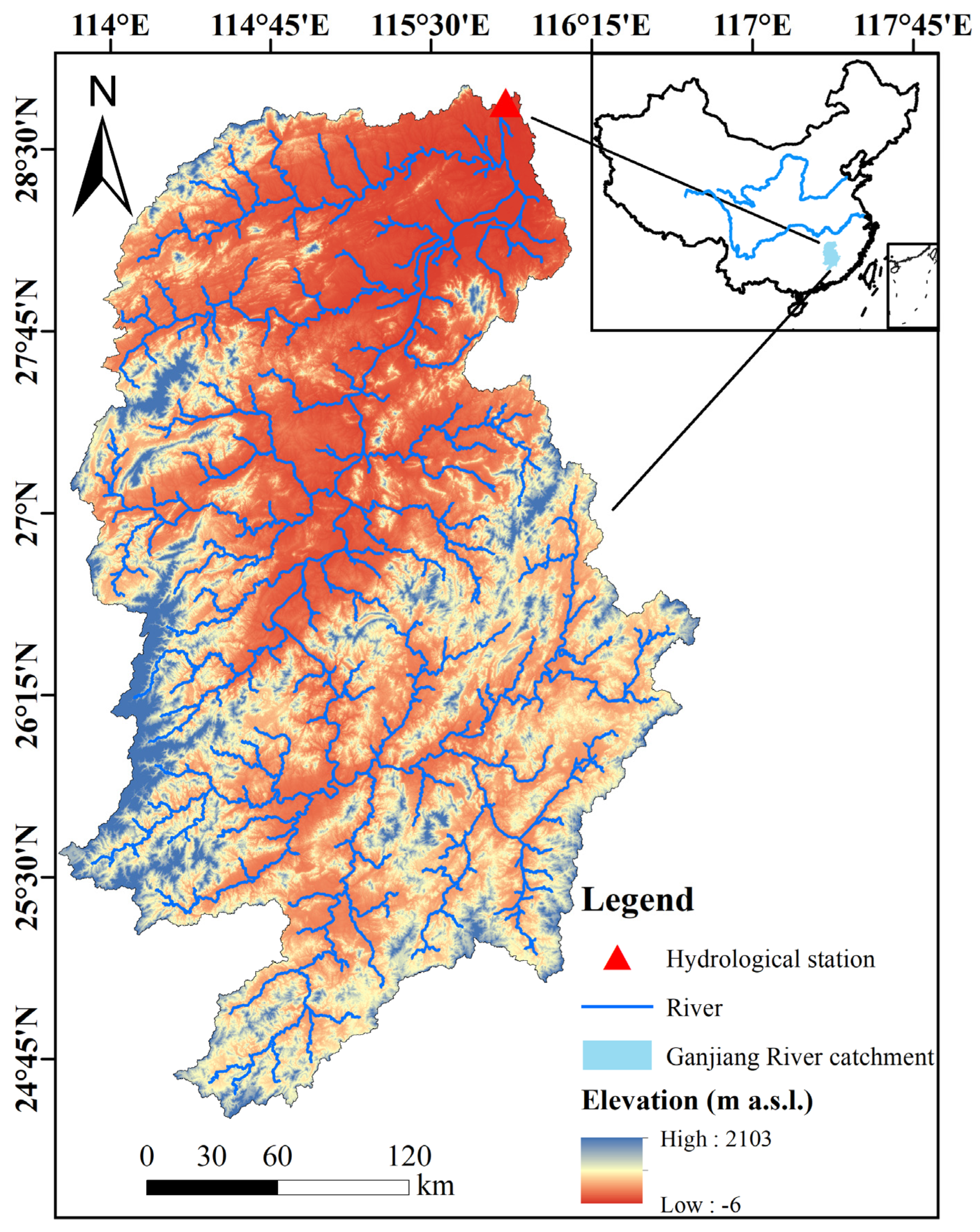
3.1. Gangjiang River Basin
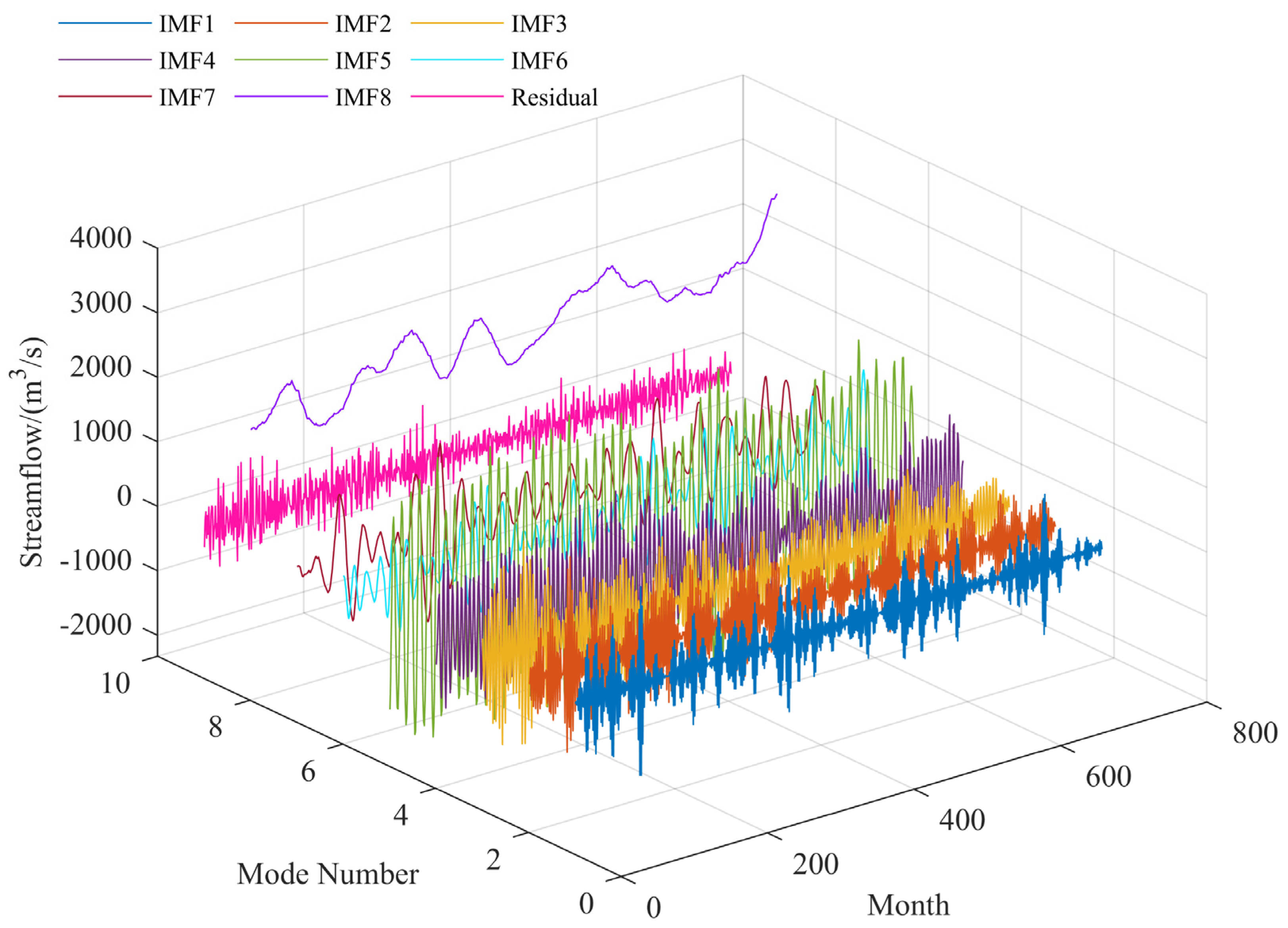
3.2. Monthly Runoff from the VMD Decomposition
4. Results and Discussion
4.1. Determining Forecasting Factors and Model Parameter
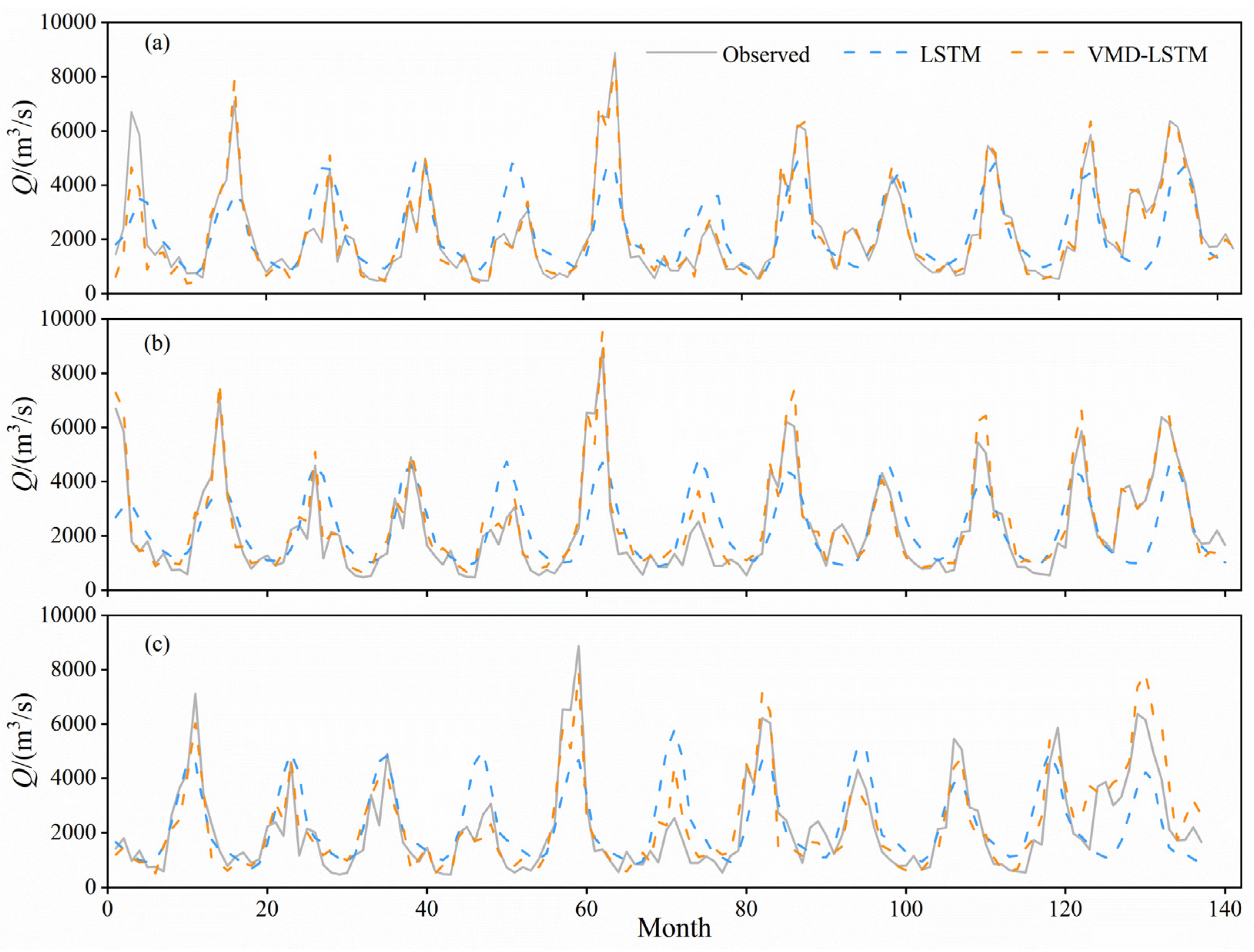
4.2. Effect of VMD Decomposition on Runoff Prediction of LSTM Model
4.3. Effect of Considering Atmospheric Circulation on Runoff Prediction of LSTM Model
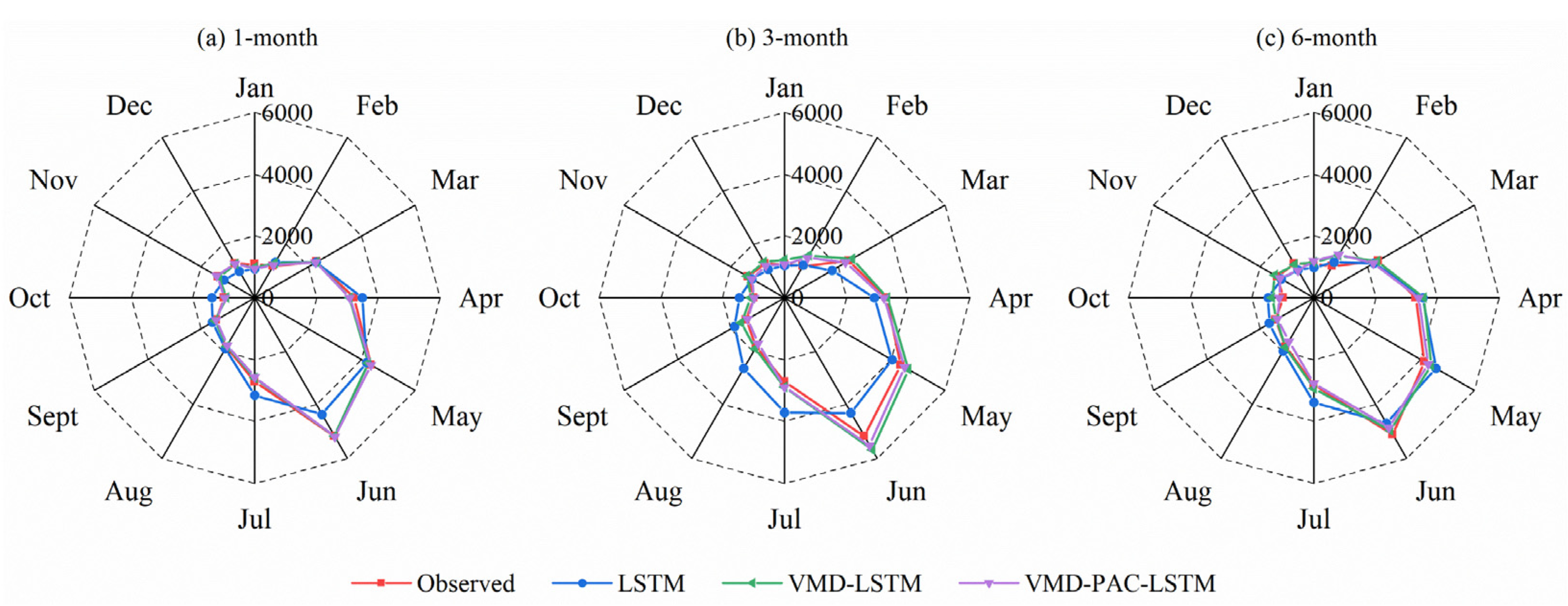
4.4. Performance of Runoff Prediction in Flood and Non-Flood Season
4.5. Discussion
5. Conclusions
- (1)
- For Waizhou station, the number of mode decomposition K is 8, with lag time (L) equaling 1 month. The L of atmospheric circulation indexes is mainly equal to 7 and 8, and the r of North African Subtropical High Ridge Position Indexes, Indian Subtropical High Ridge Position Indexes, and Western Pacific Subtropical High Ridge Position Indexes separately are the top three. The first two principal components are selected as the forecasting factors from the above atmospheric circulation indexes by the PCA method.
- (2)
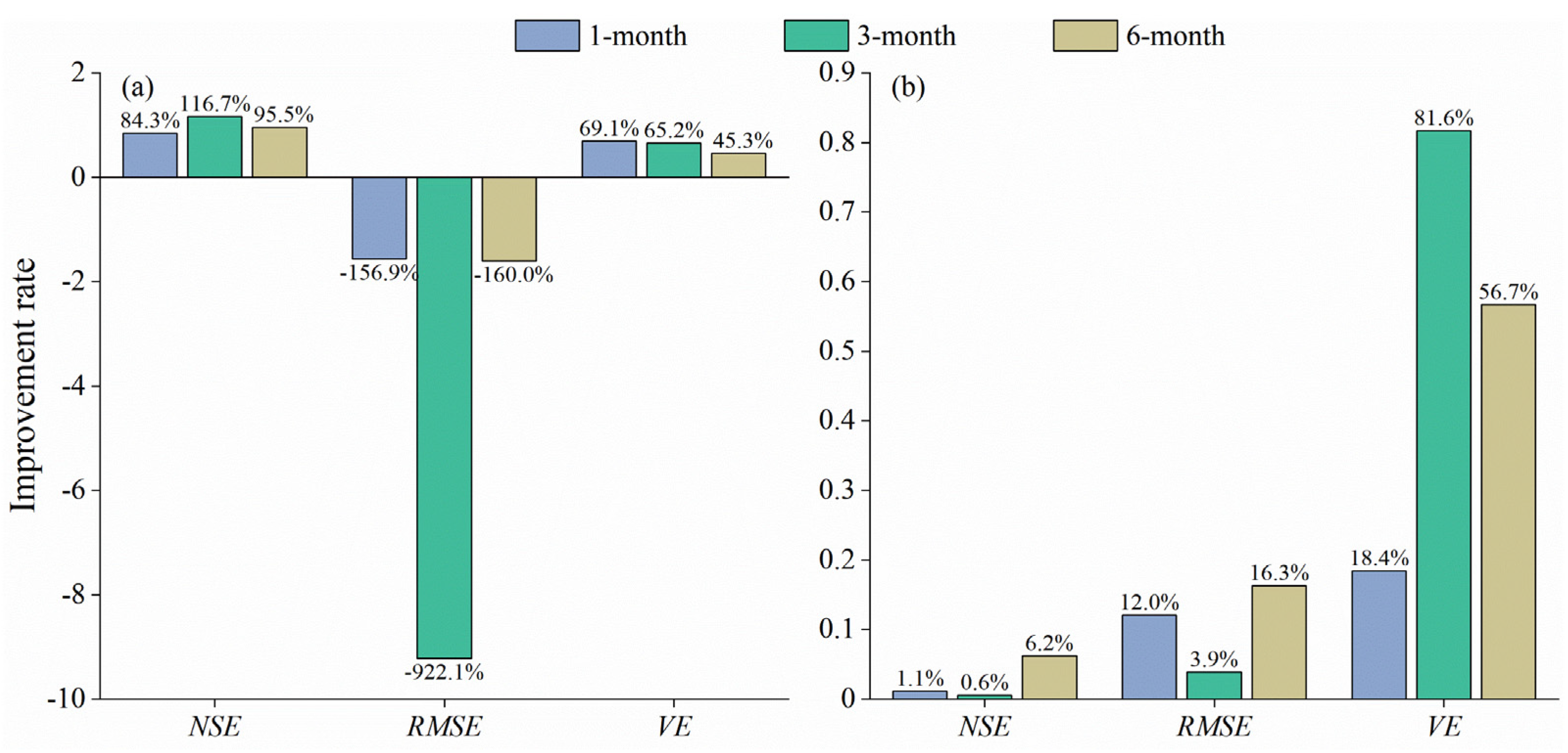
- The VMD decomposition method can significantly improve the prediction accuracy of the single LSTM model, especially concentrating on the prediction of high flow during the flood and non-flood seasons, and the improvement rate of NSE and RMSE are 84.3–116.7% and 156.9–922.1% except the VE. Additionally, as the forecast period increases, the prediction accuracy of the VMD-LSTM model degenerates less, indicating that the VMD-LSTM model has good robustness. Only considering VMD decomposition can improve the LSTM model accuracy of other monthly runoff predictions except from November to February, which is not significantly different from the VMD-PCA-LSTM model.
- (3)
- Considering the atmospheric circulation indexes as the forecasting factors, compared to the VMD-LSTM model, significantly enhances prediction accuracy in high flow caused by a small number of samples, especially the decrease in VE of up to 81.6%. With the increase in the forecast period, the improvement after integrating atmospheric circulation indexes becomes more significant, especially when the forecast period is 6 months. The NSE and RMSE have the most significant improvement increasing by 6.2% and 16.3%. However, it is worth noting that the VMD-PCA-LSTM model does not offer a comprehensive enhancement over the VMD-LSTM model in all periods, but rather focuses only on the flood season, particularly for high flows.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Niu, W.-J.; Feng, Z.-K. Evaluating the performances of several artificial intelligence methods in forecasting daily streamflow time series for sustainable water resources management. Sustain. Cities Soc. 2021, 64, 102562. [Google Scholar] [CrossRef]
- Feng, Z.-K.; Niu, W.-J.; Tang, Z.-Y.; Jiang, Z.-Q.; Xu, Y.; Liu, Y.; Zhang, H.-R. Monthly runoff time series prediction by variational mode decomposition and support vector machine based on quantum-behaved particle swarm optimization. J. Hydrol. 2020, 583, 124627. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Souag-Gamane, D.; Ahmed, A.N.; Sammen, S.S.; Kisi, O.; Huang, Y.F.; El-Shafie, A. Rainfall-runoff modelling using improved machine learning methods: Harris hawks optimizer vs. particle swarm optimization. J. Hydrol. 2020, 589, 125133. [Google Scholar] [CrossRef]
- Akbarian, M.; Saghafian, B.; Golian, S. Monthly streamflow forecasting by machine learning methods using dynamic weather prediction model outputs over Iran. J. Hydrol. 2023, 620, 129480. [Google Scholar] [CrossRef]
- Dung, N.B.; Long, N.Q.; Goyal, R.; An, D.T.; Minh, D.T. The Role of Factors Affecting Flood Hazard Zoning Using Analytical Hierarchy Process: A Review. Earth Syst. Environ. 2022, 6, 697–713. [Google Scholar] [CrossRef]
- Stergiadi, M.; Di Marco, N.; Avesani, D.; Righetti, M.; Borga, M. Impact of Geology on Seasonal Hydrological Predictability in Alpine Regions by a Sensitivity Analysis Framework. Water 2020, 12, 2255. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, H.; Wang, G.; Luo, S.; Chen, D.; Peng, W.; Shao, J. Dynamic runoff simulation in a changing environment: A data stream approach. Environ. Model. Softw. 2019, 112, 157–165. [Google Scholar] [CrossRef]
- Deng, C.; Wang, W. Runoff Predicting and Variation Analysis in Upper Ganjiang Basin under Projected Climate Changes. Sustainability 2019, 11, 5885. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, K.; Luo, Y.; Zhang, Q.; Zhou, J.; Fan, Y.; Huang, P.; Yao, C.; Chao, L.; Bao, H. A distributed hydrological model for semi-humid watersheds with a thick unsaturated zone under strong anthropogenic impacts: A case study in Haihe River Basin. J. Hydrol. 2023, 623, 129765. [Google Scholar] [CrossRef]
- Kirsta, Y.B.; Troshkova, I.A. High-Performance Forecasting of Spring Flood in Mountain River Basins with Complex Landscape Structure. Water 2023, 15, 1080. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, C.; Wu, Q.; Jian, S.; Li, Z.; Chen, Y.; Zhang, G.; Zhang, Z.; Wang, S. Research on particle swarm optimization in LSTM neural networks for rainfall-runoff simulation. J. Hydrol. 2022, 608, 127553. [Google Scholar] [CrossRef]
- Meng, J.; Dong, Z.; Shao, Y.; Zhu, S.; Wu, S. Monthly Runoff Forecasting Based on Interval Sliding Window and Ensemble Learning. Sustainability 2023, 15, 100. [Google Scholar] [CrossRef]
- Han, D.Y.; Liu, P.; Xie, K.; Li, H.; Xia, Q.; Cheng, Q.; Wang, Y.B.; Yang, Z.K.; Zhang, Y.J.; Xia, J. An attention-based LSTM model for long-term runoff forecasting and factor recognition. Environ. Res. Lett. 2023, 18, 13. [Google Scholar] [CrossRef]
- Kim, T.; Yang, T.; Gao, S.; Zhang, L.; Ding, Z.; Wen, X.; Gourley, J.J.; Hong, Y. Can artificial intelligence and data-driven machine learning models match or even replace process-driven hydrologic models for streamflow simulation?: A case study of four watersheds with different hydro-climatic regions across the CONUS. J. Hydrol. 2021, 598, 126423. [Google Scholar] [CrossRef]
- Zhang, S.; Gan, T.Y.; Bush, A.B.G.; Zhang, G. Evaluation of the impact of climate change on the streamflow of major pan-Arctic river basins through machine learning models. J. Hydrol. 2023, 619, 129295. [Google Scholar] [CrossRef]
- Zang, S.; Li, Z.; Zhang, K.; Yao, C.; Liu, Z.; Wang, J.; Huang, Y.; Wang, S. Improving the flood prediction capability of the Xin’anjiang model by formulating a new physics-based routing framework and a key routing parameter estimation method. J. Hydrol. 2021, 603, 126867. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Behrangi, A.; Khakbaz, B.; Jaw, T.C.; AghaKouchak, A.; Hsu, K.; Sorooshian, S. Hydrologic evaluation of satellite precipitation products over a mid-size basin. J. Hydrol. 2011, 397, 225–237. [Google Scholar] [CrossRef]
- Avesani, D.; Galletti, A.; Piccolroaz, S.; Bellin, A.; Majone, B. A dual-layer MPI continuous large-scale hydrological model including Human Systems. Environ. Model. Softw. 2021, 139, 105003. [Google Scholar] [CrossRef]
- Nazemi, A.; Wheater, H.S. On inclusion of water resource management in Earth system models—Part 1: Problem definition and representation of water demand. Hydrol. Earth Syst. Sci. 2015, 19, 33–61. [Google Scholar] [CrossRef]
- Bozorg-Haddad, O.; Zarezadeh-Mehrizi, M.; Abdi-Dehkordi, M.; Loáiciga, H.A.; Mariño, M.A. A self-tuning ANN model for simulation and forecasting of surface flows. Water Resour. Manag. 2016, 30, 2907–2929. [Google Scholar] [CrossRef]
- Hagen, J.S.; Leblois, E.; Lawrence, D.; Solomatine, D.; Sorteberg, A. Identifying major drivers of daily streamflow from large-scale atmospheric circulation with machine learning. J. Hydrol. 2021, 596, 126086. [Google Scholar] [CrossRef]
- Liu, P.; Wang, J.; Sangaiah, A.K.; Xie, Y.; Yin, X. Analysis and Prediction of Water Quality Using LSTM Deep Neural Networks in IoT Environment. Sustainability 2019, 11, 2058. [Google Scholar] [CrossRef]
- Yu, Q.; Jiang, L.; Wang, Y.; Liu, J. Enhancing streamflow simulation using hybridized machine learning models in a semi-arid basin of the Chinese loess Plateau. J. Hydrol. 2023, 617, 129115. [Google Scholar] [CrossRef]
- Wang, X.; Sun, W.; Lu, F.; Zuo, R. Combining Satellite Optical and Radar Image Data for Streamflow Estimation Using a Machine Learning Method. Remote Sens. 2023, 15, 5184. [Google Scholar] [CrossRef]
- Kim, T.; Shin, J.Y.; Kim, H.; Heo, J.H. Ensemble-Based Neural Network Modeling for Hydrologic Forecasts: Addressing Uncertainty in the Model Structure and Input Variable Selection. Water Resour. Res. 2020, 56, 19. [Google Scholar] [CrossRef]
- Bedi, J. Transfer learning augmented enhanced memory network models for reference evapotranspiration estimation. Knowl.-Based Syst. 2022, 237, 107717. [Google Scholar] [CrossRef]
- Xu, L.; Yu, H.; Chen, Z.; Du, W.; Chen, N.; Huang, M. Hybrid Deep Learning and S2S Model for Improved Sub-Seasonal Surface and Root-Zone Soil Moisture Forecasting. Remote Sens. 2023, 15, 3410. [Google Scholar] [CrossRef]
- Castangia, M.; Grajales, L.M.M.; Aliberti, A.; Rossi, C.; Macii, A.; Macii, E.; Patti, E. Transformer neural networks for interpretable flood forecasting. Environ. Model. Softw. 2023, 160, 105581. [Google Scholar] [CrossRef]
- Yao, Z.; Wang, Z.; Wang, D.; Wu, J.; Chen, L. An ensemble CNN-LSTM and GRU adaptive weighting model based improved sparrow search algorithm for predicting runoff using historical meteorological and runoff data as input. J. Hydrol. 2023, 625, 129977. [Google Scholar] [CrossRef]
- Song, P.; Liu, W.; Sun, J.; Wang, C.; Kong, L.; Nong, Z.; Lei, X.; Wang, H. Annual Runoff Forecasting Based on Multi-Model Information Fusion and Residual Error Correction in the Ganjiang River Basin. Water 2020, 12, 2086. [Google Scholar] [CrossRef]
- Zhao, X.; Lv, H.; Lv, S.; Sang, Y.; Wei, Y.; Zhu, X. Enhancing robustness of monthly streamflow forecasting model using gated recurrent unit based on improved grey wolf optimizer. J. Hydrol. 2021, 601, 126607. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.; Ren, K.; Huang, Q.; Huang, G.; Cheng, G.; Li, K. Examining the applicability of different sampling techniques in the development of decomposition-based streamflow forecasting models. J. Hydrol. 2019, 568, 534–550. [Google Scholar] [CrossRef]
- Zuo, G.G.; Luo, J.G.; Wang, N.; Lian, Y.N.; He, X.X. Two-stage variational mode decomposition and support vector regression for streamflow forecasting. Hydrol. Earth Syst. Sci. 2020, 24, 5491–5518. [Google Scholar] [CrossRef]
- Wang, W.-C.; Chau, K.-W.; Xu, D.-M.; Chen, X.-Y. Improving Forecasting Accuracy of Annual Runoff Time Series Using ARIMA Based on EEMD Decomposition. Water Resour. Manag. 2015, 29, 2655–2675. [Google Scholar] [CrossRef]
- Zuo, G.; Luo, J.; Wang, N.; Lian, Y.; He, X. Decomposition ensemble model based on variational mode decomposition and long short-term memory for streamflow forecasting. J. Hydrol. 2020, 585, 124776. [Google Scholar] [CrossRef]
- Kirono, D.G.C.; Chiew, F.H.S.; Kent, D.M. Identification of best predictors for forecasting seasonal rainfall and runoff in Australia. Hydrol. Process. 2010, 24, 1237–1247. [Google Scholar] [CrossRef]
- Chavasse, D.I.; Seoane, R.S. Assessing and predicting the impact of El Nino southern oscillation (ENSO) events on runoff from the Chopim River basin, Brazil. Hydrol. Process. 2009, 23, 3261–3266. [Google Scholar] [CrossRef]
- Champagne, O.; Arain, M.A.; Coulibaly, P. Atmospheric circulation amplifies shift of winter streamflow in southern Ontario. J. Hydrol. 2019, 578, 124051. [Google Scholar] [CrossRef]
- Yan, X.; Chang, Y.; Yang, Y.; Liu, X. Monthly runoff prediction using modified CEEMD-based weighted integrated model. J. Water Clim. Change 2020, 12, 1744–1760. [Google Scholar] [CrossRef]
- Mostaghimzadeh, E.; Ashrafi, S.M.; Adib, A.; Geem, Z.W. A long lead time forecast model applying an ensemble approach for managing the great Karun multi-reservoir system. Appl. Water Sci. 2023, 13, 124. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, F.; Yin, Q.; Qi, Y.; Sun, S. A runoff prediction method based on hyperparameter optimisation of a kernel extreme learning machine with multi-step decomposition. Sci. Rep. 2023, 13, 19341. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2016, 374, 16. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Thiemann, M.; Trosset, M.; Gupta, H.; Sorooshian, S. Bayesian recursive parameter estimation for hydrologic models. Water Resour. Res. 2001, 37, 2521–2535. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall-runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Ling, H.; Xu, H.; Shi, W.; Zhang, Q. Regional climate change and its effects on the runoff of Manas River, Xinjiang, China. Environ. Earth Sci. 2011, 64, 2203–2213. [Google Scholar] [CrossRef]
- Mo, R.; Xu, B.; Zhong, P.-A.; Dong, Y.; Wang, H.; Yue, H.; Zhu, J.; Wang, H.; Wang, G.; Zhang, J. Long-term probabilistic streamflow forecast model with “inputs–structure–parameters” hierarchical optimization framework. J. Hydrol. 2023, 622, 129736. [Google Scholar] [CrossRef]
- Deng, C.; Yin, X.; Zou, J.; Wang, M.; Hou, Y. Assessment of the impact of climate change on streamflow of Ganjiang River catchment via LSTM-based models. J. Hydrol. Reg. Stud. 2024, 52, 101716. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, D.; Chang, H.; Li, H. Deep learning of subsurface flow via theory-guided neural network. J. Hydrol. 2020, 584, 124700. [Google Scholar] [CrossRef]
- Tong, X.; Yan, Z.; Xia, J.; Lou, X. Decisive Atmospheric Circulation Indices for July–August Precipitation in North China Based on Tree Models. J. Hydrometeorol. 2019, 20, 1707–1720. [Google Scholar] [CrossRef]
- Amini, A.; Dolatshahi, M.; Kerachian, R. Real-time rainfall and runoff prediction by integrating BC-MODWT and automatically-tuned DNNs: Comparing different deep learning models. J. Hydrol. 2024, 631, 130804. [Google Scholar] [CrossRef]
- Ma, K.; He, D.; Liu, S.; Ji, X.; Li, Y.; Jiang, H. Novel time-lag informed deep learning framework for enhanced streamflow prediction and flood early warning in large-scale catchments. J. Hydrol. 2024, 631, 130841. [Google Scholar] [CrossRef]
- Li, B.-J.; Sun, G.-L.; Liu, Y.; Wang, W.-C.; Huang, X.-D. Monthly Runoff Forecasting Using Variational Mode Decomposition Coupled with Gray Wolf Optimizer-Based Long Short-term Memory Neural Networks. Water Resour. Manag. 2022, 36, 2095–2115. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, S.; Kisi, O.; Singh, V.P.; Parasuraman, K. River Stage Forecasting Using Wavelet Packet Decomposition and Machine Learning Models. Water Resour. Manag. 2016, 30, 4011–4035. [Google Scholar] [CrossRef]
- Yang, C.; Jiang, Y.; Liu, Y.; Liu, S.; Liu, F. A novel model for runoff prediction based on the ICEEMDAN-NGO-LSTM coupling. Environ. Sci. Pollut. Res. 2023, 30, 82179–82188. [Google Scholar] [CrossRef]
- Wang, W.-C.; Du, Y.-J.; Chau, K.-W.; Cheng, C.-T.; Xu, D.-M.; Zhuang, W.-T. Evaluating the Performance of Several Data Preprocessing Methods Based on GRU in Forecasting Monthly Runoff Time Series. Water Resour. Manag. 2024. [Google Scholar] [CrossRef]
- Li, H.Y.; Xie, M.; Jiang, S. Recognition method for mid- to long-term runoff forecasting factors based on global sensitivity analysis in the Nenjiang River Basin. Hydrol. Process. 2012, 26, 2827–2837. [Google Scholar] [CrossRef]
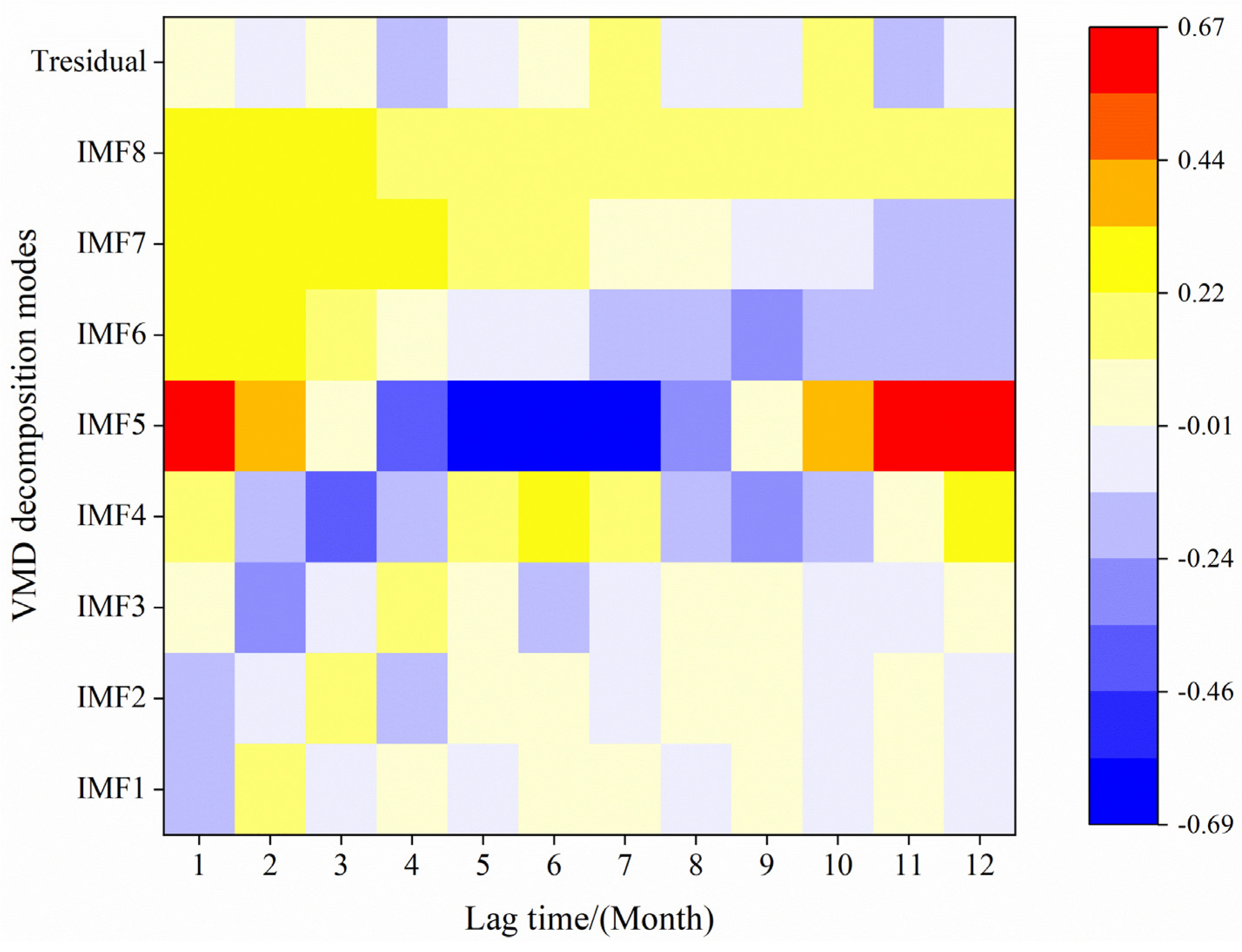


| K | r1–2 | r2–3 | r3–4 | r4–5 | r5–6 | r6–7 | r7–8 | r8–9 |
|---|---|---|---|---|---|---|---|---|
| 2 | 0.128 | - | - | - | - | - | - | - |
| 3 | 0.011 | 0.113 | - | - | - | - | - | - |
| 4 | 0.009 | 0.071 | 0.203 | - | - | - | - | - |
| 5 | 0.031 | 0.035 | 0.050 | 0.184 | - | - | - | - |
| 6 | 0.044 | 0.029 | 0.050 | 0.174 | 0.170 | - | - | - |
| 7 | 0.076 | 0.082 | 0.024 | 0.045 | 0.170 | 0.169 | - | - |
| 8 | 0.092 | 0.075 | 0.081 | 0.018 | 0.042 | 0.168 | 0.169 | - |
| 9 | 0.085 | 0.089 | 0.051 | 0.153 | 0.026 | 0.035 | 0.166 | 0.169 |
| Rank of r | Factor Type | Lag Time /(Month) |
|---|---|---|
| 6 | Northern Hemisphere Subtropical High Ridge Position Indexes | 7 |
| 3 | Western Pacific Subtropical High Ridge Position Indexes | |
| 10 | South China Sea Subtropical High Ridge Position Indexes | |
| 5 | Pacific Subtropical High Ridge Position Indexes | |
| 11 | North African-North Atlantic-North American Subtropical High Area Indexes | 8 |
| 13 | North American Subtropical High Area Indexes | |
| 9 | Atlantic Subtropical High Area Indexes | |
| 8 | North American-Atlantic Subtropical High Area Indexes | |
| 1 | North African Subtropical High Ridge Position Indexes | |
| 12 | North African-North Atlantic-North American Subtropical High Ridge Position Indexes | |
| 2 | Indian Subtropical High Ridge Position Indexes | |
| 7 | Northern Hemisphere Polar Vortex Central Intensity Indexes | |
| 4 | East Asian Trough Intensity Indexes |
| Component | Total | Variance/(%) | Cumulative Variance/(%) |
|---|---|---|---|
| 1 | 11.10 | 85.42 | 85.42 |
| 2 | 0.90 | 6.94 | 92.36 |
| 3 | 0.35 | 2.68 | 95.04 |
| 4 | 0.17 | 1.34 | 96.38 |
| 5 | 0.11 | 0.83 | 97.21 |
| 6 | 0.098 | 0.75 | 97.96 |
| Forecast Period | Model | NSE | RMSE/(m3/s) | VE/(%) |
|---|---|---|---|---|
| 1 month | LSTM | 0.518 | 1185 | −0.77 |
| VMD-LSTM | 0.954 | 366 | −1.97 | |
| 3 months | LSTM | 0.430 | 1292 | 0.76 |
| VMD-LSTM | 0.931 | 450 | 7.81 | |
| 6 months | LSTM | 0.424 | 1299 | 1.62 |
| VMD-LSTM | 0.828 | 710 | 4.21 |
| Forecast Period | NSE | RMSE/(m3/s) | VE/(%) |
|---|---|---|---|
| 1 month | 0.954→0.964 | 366→322 | −1.97→−1.61 |
| 3 months | 0.931→0.936 | 450→432 | 7.81→1.43 |
| 6 months | 0.828→0.879 | 710→595 | 4.21→−1.82 |
| Season | Forecast Period | r | RMSE/(m3/s) |
|---|---|---|---|
| non-flood season | 1 month | 0.974→0.957 | 215→269 |
| 3 months | 0.940→0.923 | 343→359 | |
| 6 months | 0.846→0.797 | 564→568 | |
| flood season | 1 month | 0.978→0.982 | 469→366 |
| 3 months | 0.966→0.966 | 532→491 | |
| 6 months | 0.907→0.941 | 833→589 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Tang, S.; Zou, J.; Li, D.; Ge, X.; Huang, J.; Yin, X. Runoff Prediction in Different Forecast Periods via a Hybrid Machine Learning Model for Ganjiang River Basin, China. Water 2024, 16, 1589. https://doi.org/10.3390/w16111589
Wang W, Tang S, Zou J, Li D, Ge X, Huang J, Yin X. Runoff Prediction in Different Forecast Periods via a Hybrid Machine Learning Model for Ganjiang River Basin, China. Water. 2024; 16(11):1589. https://doi.org/10.3390/w16111589
Chicago/Turabian StyleWang, Wei, Shinan Tang, Jiacheng Zou, Dong Li, Xiaobin Ge, Jianchu Huang, and Xin Yin. 2024. "Runoff Prediction in Different Forecast Periods via a Hybrid Machine Learning Model for Ganjiang River Basin, China" Water 16, no. 11: 1589. https://doi.org/10.3390/w16111589
APA StyleWang, W., Tang, S., Zou, J., Li, D., Ge, X., Huang, J., & Yin, X. (2024). Runoff Prediction in Different Forecast Periods via a Hybrid Machine Learning Model for Ganjiang River Basin, China. Water, 16(11), 1589. https://doi.org/10.3390/w16111589







