Analysis of the Effectiveness of Water Hammer Protection Programs for Complex Long-Distance and High-Head Water Supply Projects
Abstract
1. Introduction
2. Materials and Methods
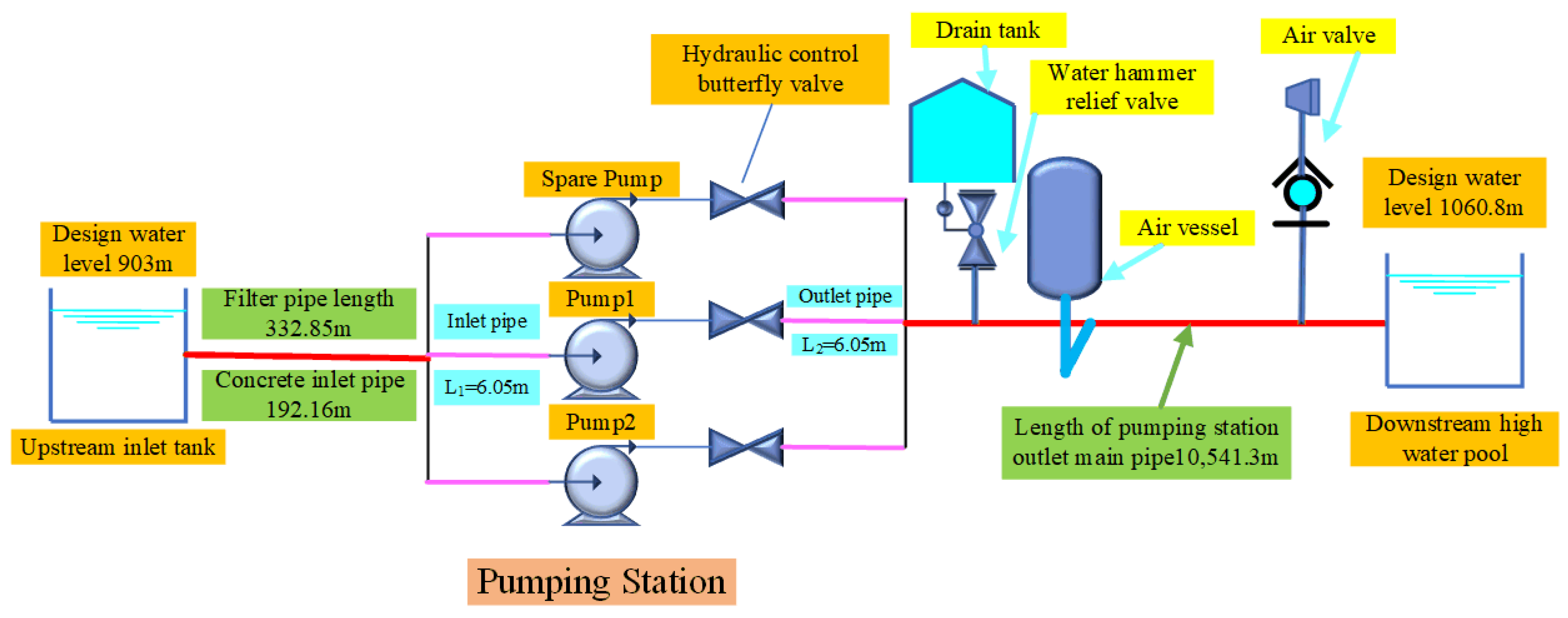
2.1. Study Area and Selection of Protective Measures
2.2. Governing Equations and Calculation Methods
2.2.1. Basic Equations of Hydraulic Transition Process
- (1)
- The differential equation of motion is as follows:
- (2)
- The continuous differential equation is as follows:
2.2.2. Characteristic Equation of Hydraulic Transition Process
2.2.3. Boundary Conditions of Hydraulic-Control Butterfly Valve
2.2.4. Boundary Conditions of Air Valve and Vacuum Break Valve
2.2.5. Boundary Conditions of Air Vessel
2.2.6. Boundary Conditions of Water Hammer Relief Valve
2.2.7. Basic Equations of Rotational Inertia
2.3. Effectiveness Analysis Methodology
3. Results and Discussion
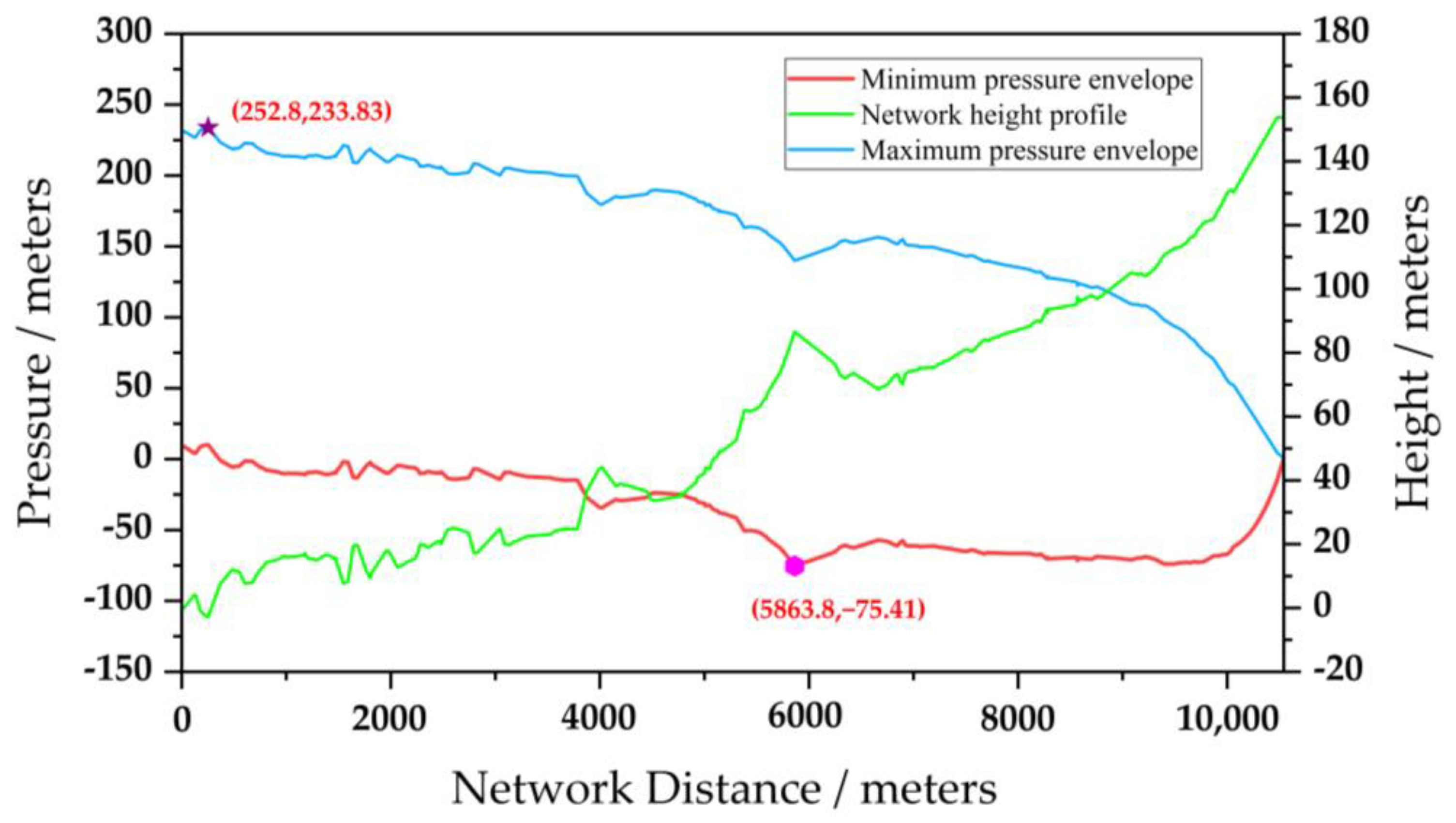
3.1. Numerical Simulation of Hydraulic Transition without Valve Protection Measures
3.2. Numerical Simulation of Hydraulic Transition of Two-Stage Hydraulic-Control Butterfly Valve Protection
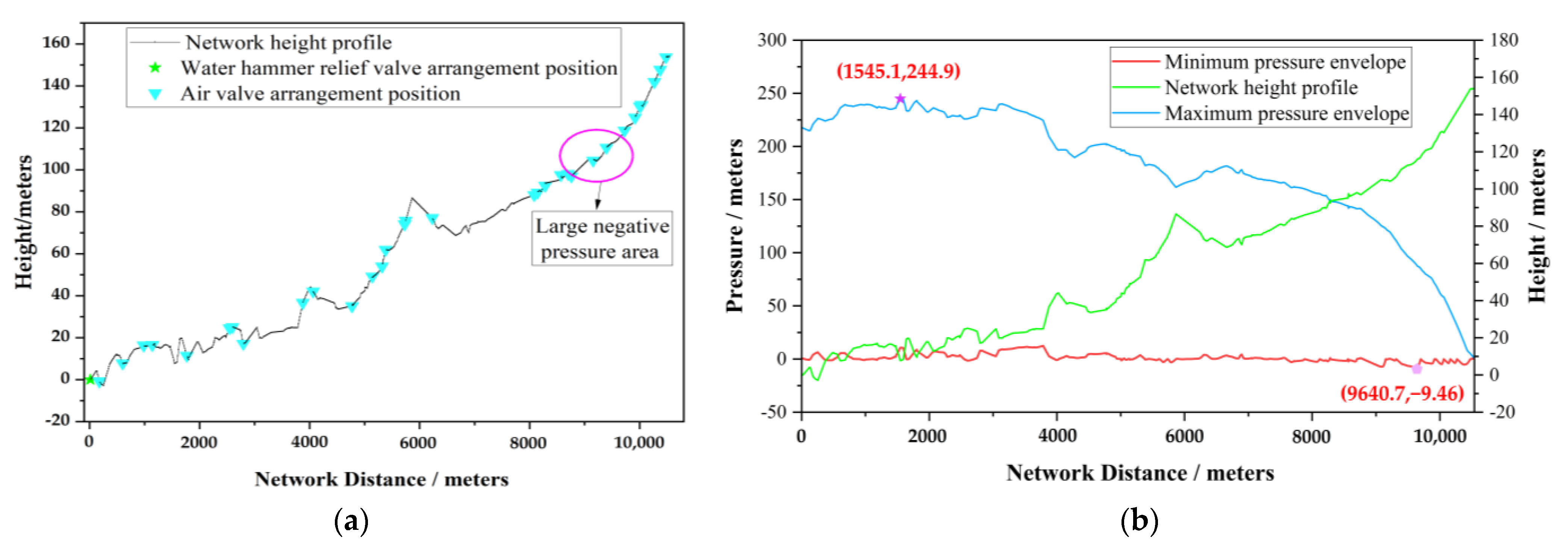
3.3. Numerical Simulation of Butterfly Valve–Air Valve–Water Hammer Relief Valve Joint Protection Hydraulic Transition
3.4. Two-Stage Numerical Simulation of Joint Protection of Hydraulic-Control Butterfly Valve, Air Valve, and Increased Motor Moment of Inertia
3.5. Numerical Simulation of Two-Stage Hydraulic Butterfly Valve, Air Valve, Plus Vacuum Break Valve Joint Protection
3.6. Numerical Simulation of One-Phase, Two-Phase, and Three-Phase Hydraulic-Control Butterfly Valve Plus Air Valve and Air Vessel Joint Protection
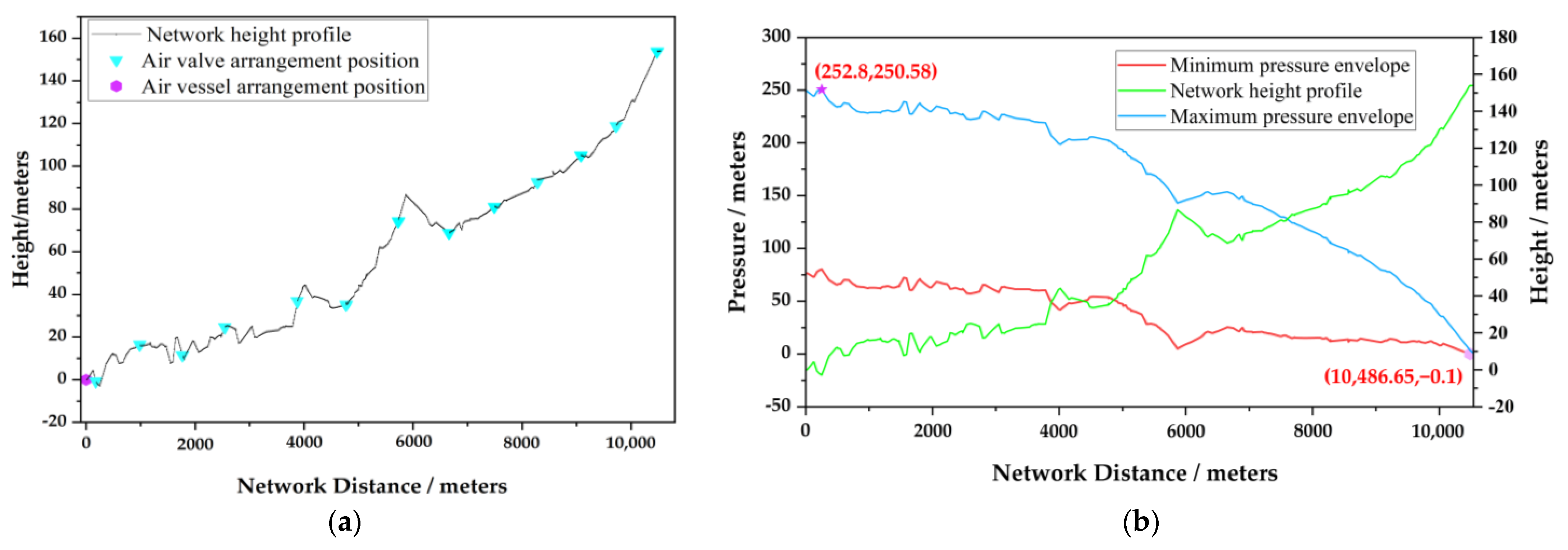
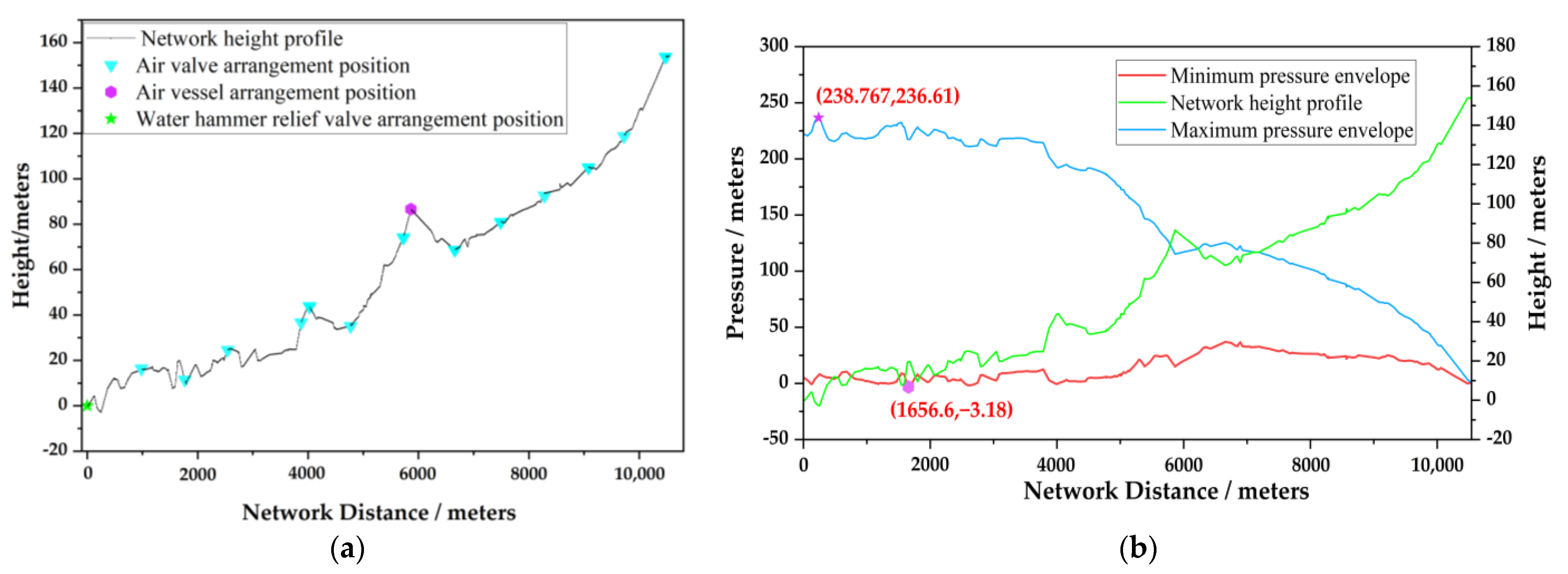
3.7. Numerical Simulation of One-Stage Joint Protection of Hydraulic-Control Butterfly Valve Plus Air Valve, Air Vessel, and Water Hammer Relief Valve
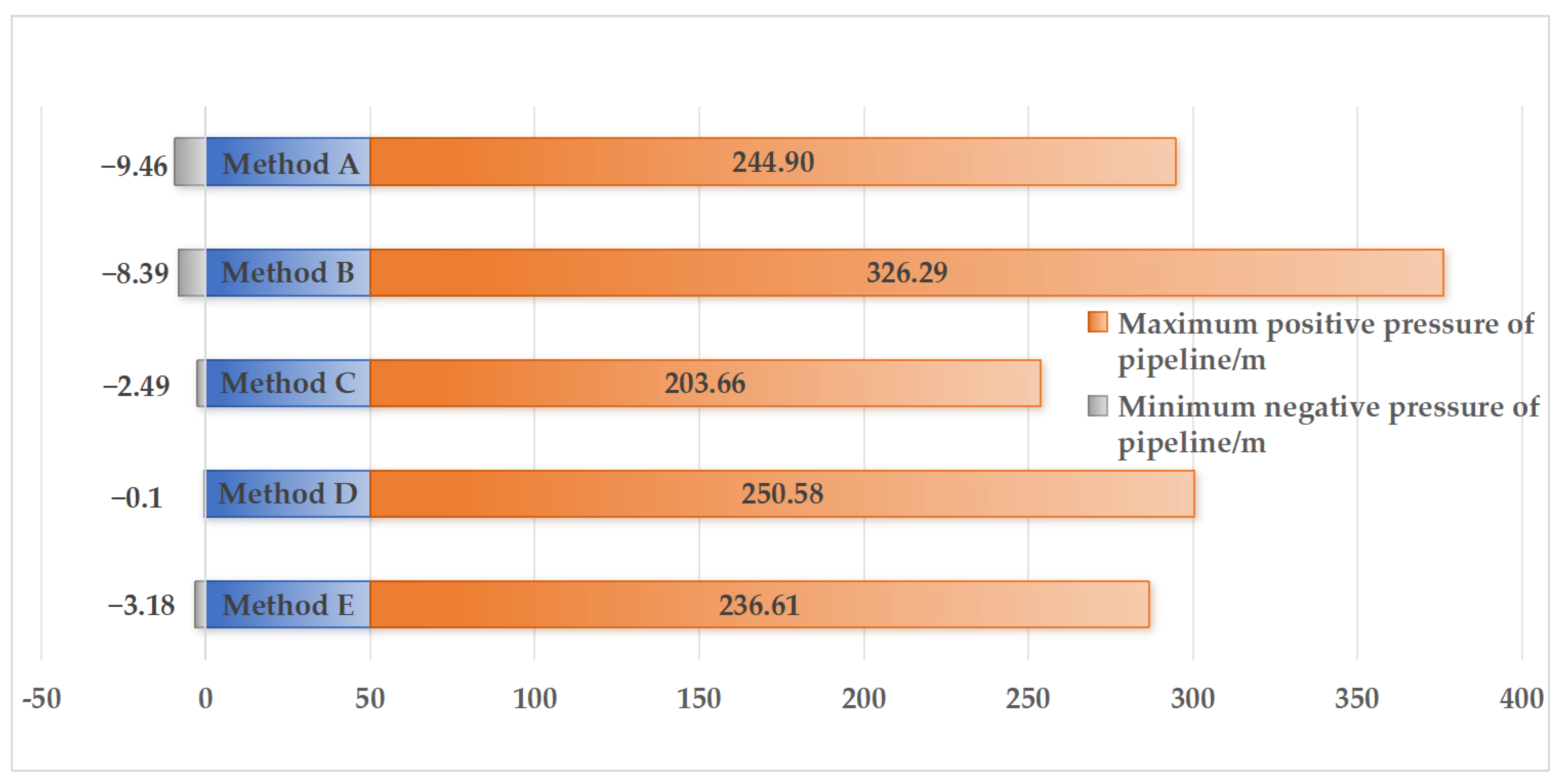
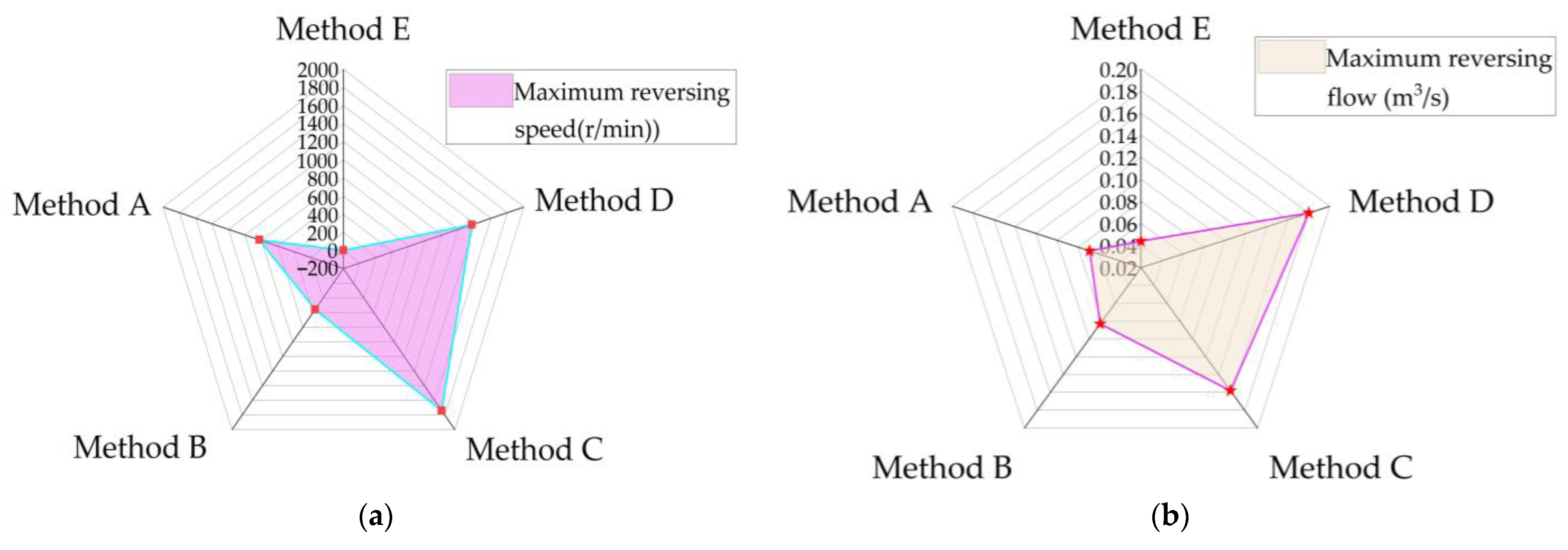
3.8. Effectiveness Analysis
4. Conclusions
- In the example of a long-distance and high-lift water supply project, the comparison of the results of various comprehensive protection measures for water hammer shows that the combined protection scheme of one-stage hydraulic-control butterfly valve plus air valve, water hammer elimination tank, and water hammer relief valve is the most effective and economical scheme.
- The simulation results have important reference value for the design of long-distance high-lift water supply projects with obvious characteristics, the calculation of hydraulic transition processes, and safe and economical operation. Most of the previous research work was aimed at a single water hammer protection combination, and there are few studies on the comprehensive protection measures of various water hammers and the application of water hammer elimination tanks, which do not address the reality that the pipeline distance of water hammer design is becoming longer and the head and flow are becoming larger. In this paper, the results of various water hammer comprehensive protection measures are compared, and the optimal protection measures are selected. In the design and operation of the project, the closing time, pipe diameter, and flow of each valve should be strictly controlled to ensure the safety of the project.
- The main factors affecting the water hammer protection effect in the two-stage shut-off parameters of the hydraulic butterfly valve are the fast-shut-off angle and the slow-shut-off time.
- There are many factors affecting the performance of waterproof hammers in long-distance water pumping stations. By comparing the calculation results of various comprehensive protection measures for water hammers and multiple sets of orthogonal experimental designs, the optimal solution can be quickly obtained, which addresses the optimization problems in previous engineering projects. By combining the protection of the water hammer elimination tank and the water hammer discharge valve, the volume of the water hammer elimination tank and the performance of the water hammer of the pipeline can be greatly optimized, which can greatly reduce the cost of the project.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| h | pressure head (m) |
| x | propagation distance (m) |
| v | flow velocity (m/s) |
| t | time (s) |
| λ | resistance coefficient of the pipeline |
| D | diameter of the pipeline (m) |
| θ | the angle between the pipeline and the ground (°) |
| c | propagation speed of the water hammer wave (m/s) |
| g | the acceleration of gravity (m2/s) |
| HP | head of Point P at intersection of two lines in Figure 2 (m) |
| HA | the head of point A at which location x and time t are specified in Figure 2 (m) |
| HB | the head of point B at which location x and time t are specified in Figure 2 (m) |
| QP | the flow rate of point P at the intersection of two lines in Figure 2 (m3/s) |
| QA | the flow rate of point A at the given time of location x and time t in Figure 2 (m3/s) |
| QB | the flow rate of point B at the given time of location x and time t in Figure 2 (m3/s) |
| ∆x | the length of a pipeline divided into N spaced steps (m) |
| ∆H | head loss (m) |
| Cv, Cd | flow coefficient |
| Q | rate of flow (m3/s) |
| ξ | resistance coefficient of the corresponding opening |
| Av | opening area of the butterfly valve (m2) |
| air mass flow rate (m3/s) | |
| valve inlet flow coefficient | |
| valve outlet flow coefficient | |
| A | inlet and exhaust valve circulation area (m2) |
| P0 | absolute pressure of the gas outside the tube (Pa) |
| P | absolute pressure of the gas inside the tube (Pa) |
| k | adiabatic index |
| R | gas constants |
| T0 | absolute temperature of the ambient atmosphere outside the tube (K) |
| T | absolute temperature of the gas in the tube (K) |
| p | absolute pressure of gas in tank (Pa) |
| V | tank gas volume (m3) |
| C | gas state constant |
| Qp1, Qp2 | tank upstream and downstream flow respectively (m3/s) |
| Qst | flow through the tank (m3/s) |
| Zst | tank level (m) |
| p0 | atmospheric pressure outside the tank (Pa) |
| γ | unit weight of water (N/m3) |
| k1 | hydraulic loss coefficient |
| Ast | tank cross-sectional area (m2) |
| HP | pressure at the connection between the tank and the pipeline (m) |
| flow upstream, downstream, and in front of the water hammer relief valve (m3/s) | |
| pressure head upstream, downstream and in front of the water hammer relief valve (m) | |
| AG | cross-sectional area of overflow after opening of water hammer relief valve (m2) |
| Ho | external pressure head after water hammer relief valve (m) |
| J | rigid body moment of inertia (kg∙m2) |
| D1 | diameter of the rigid body (m) |
| G | total weight of rigid body (N) |
| Mr | deceleration resistance moment (N∙m) |
| angular acceleration of rotor (rad/s2) | |
| R1 | range |
| u | the maximum or minimum values of the different parameters of method A |
| t1 | maximum or minimum value of valveless protection |
| Acronyms | |
| MOC | method of characteristics |
References
- Ammar, H.T.; Al-Zahrani, M.A. Water Hammer Analysis for Khobar-Dammam Water Transmission Ring Line. Arab. J. Sci. Eng. 2015, 40, 2183–2199. [Google Scholar] [CrossRef]
- Iyanda, F.; Ayodele, I. Numerical solution for the pipe diameters and wall thickness of water hammer model using crank-nicolson algorithm. Trans. Niger. Assoc. Math. Phys. 2021, 15, 19–28. [Google Scholar]
- Zhang, J.; Yu, X.; An, J.; Hazrati, A. Polyline closure law design and realization in long-distance water-supply project. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Vancouver, BC, Canada, 12–18 November 2010; pp. 129–134. [Google Scholar]
- Li, N.; Zhang, J.; Shi, L.; Chen, X.; Zhang, X. Water hammer protection characteristic of combined air vessel and overpressure relief valve. J. Drain. Irrig. Mach. Eng. 2020, 38, 254–260. (In Chinese) [Google Scholar]
- Bergant, A.; Simpson, A.R.; Tijsseling, A.S. Water hammer with column separation: A historical review. J. Fluids Struct. 2006, 22, 135–171. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, H.; Liu, D.; Ma, J.; Wang, P.; Xia, L. A second-order finite volume method for pipe flow with water column separation. J. Hydro-Environ. Res. 2017, 17, 47–55. [Google Scholar] [CrossRef]
- Albahrani, H.S.M. Analysis of water hammer for al-kut water supply project using the method of characteristics. Al-Qadisiya J. Eng. Sci. 2009, 2, 33–45. [Google Scholar]
- Wu, L.; Wang, H.; Li, X.; Sang, Z.; Chen, Z. Ultimate bearing capacity analysis of pipelines under water hammer. J. Pipeline Syst. Eng. Pract. 2024, 15, 04023063. [Google Scholar] [CrossRef]
- Miao, D.; Zhang, J.; Chen, S.; Yu, X. Water hammer suppression for long distance water supply systems by combining the air vessel and valve. J. Water Supply Res. Technol.-Aqua 2017, 66, 319–326. [Google Scholar] [CrossRef]
- Arefi, M.H.; Ghaeini-Hessaroeyeh, M.; Memarzadeh, R. Numerical modeling of water hammer in long water transmission pipeline. Appl. Water Sci. 2021, 11, 140. [Google Scholar] [CrossRef]
- Wang, L.; Wang, F.; Karney, B.W.; Malekpour, A.; Wang, Z. Influence of velocity head on filling transients in a branched pipeline. Eng. Comput. 2018, 35, 2502–2513. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, H.T.; Wu, Z.Y.; Wu, X.; Kim, H.D.; Lin, Z. Experimental studies of cavitation evolution through a butterfly valve at different regulation conditions. Exp. Fluids 2024, 65, 4. [Google Scholar] [CrossRef]
- Besharat, M.; Teresa Viseu, M.; Ramos, H.M. Experimental Study of Air Vessel Behavior for Energy Storage or System Protection in Water Hammer Events. Water 2017, 9, 63. [Google Scholar] [CrossRef]
- Sun, Q.; Wu, Y.B.; Xu, Y.; Jang, T.U. Optimal sizing of an air vessel in a long-distance water-supply pumping system using the SQP method. J. Pipeline Syst. Eng. Pract. 2016, 7, 05016001. [Google Scholar] [CrossRef]
- Miao, D.; Zhang, J.; Chen, S.; Li, D. An approximate analytical method to size an air vessel in a water supply system. Water 2017, 17 (Suppl. S1), 1016–1021. [Google Scholar] [CrossRef]
- Rezaei, V.; Calamak, M.; Bozkus, Z. Performance of a pumped discharge line with combined application of protection devices against water hammer. KSCE J. Civ. Eng. 2017, 21, 1493–1500. [Google Scholar] [CrossRef]
- Zeng, M.; Xie, J.; Huang, W.; Zu, Z.H.; Liao, C.X.; Cheng, J.C. Discussion on hydraulic control mode of long-distance negative-lift pump station. J. Chang. River Sci. Res. Inst. 2023, 40, 1–6. (In Chinese) [Google Scholar]
- Abdeldayem, O.M.; Ferràs, D.; van der Zwan, S.; Kennedy, M. Analysis of Unsteady Friction Models Used in Engineering Software for Water Hammer Analysis: Implementation Case in WANDA. Water 2021, 13, 495. [Google Scholar] [CrossRef]
- Liu, J.; Wu, J.; Zhang, Y.; Wu, X. Sensitivity Analysis of Hydraulic Transient Simulations Based on the MOC in the Gravity Flow. Water 2021, 13, 3464. [Google Scholar] [CrossRef]
- Zhou, L.; Feng, R.L.; Pan, T.; Li, Y.; Liu, D.; Che, T.C. Coupled Second-Order GTS-MOC Scheme for Transient Pipe Flows with an Entrapped Air Pocket. J. Hydraul. Eng. 2023, 149, 04023030. [Google Scholar] [CrossRef]
- Wu, D.; Yang, S.; Wu, P.; Wang, L. MOC-CFD Coupled Approach for the Analysis of the Fluid Dynamic Interaction between Water Hammer and Pump. J. Hydraul. Eng. 2015, 141, 06015003. [Google Scholar] [CrossRef]
- Gong, J.; Lambert, M.F.; Simpson, A.R.; Zecchin, A.C. Detection of Localized Deterioration Distributed along Single Pipelines by Reconstructive MOC Analysis. J. Hydraul. Eng. 2014, 140, 190–198. [Google Scholar] [CrossRef]
- Liu, J.Y.; Dou, S.Q.; Abdellahi, E.H.H. Cost-effectiveness analysis of different types of payments for ecosystem services: A case in the urban wetland ecosystem. J. Clean. Prod. 2020, 249, 119325. [Google Scholar]
- Chen, S.G.; Zhang, Y.; Lin, X.K.; Lu, X.C. Spatiotemporal characteristics analysis of water saving potential and economic effectiveness of rainwater harvesting system in China. Water 2022, 22 (Suppl. S1), 4606–4623. [Google Scholar]
- Kyriakopoulos, G.L.; Aminpour, Y.; Yamini, O.A.; Movahedi, A.; Mousavi, S.H.; Kavianpour, M.R. Hydraulic Performance of Howell–Bunger and Butterfly Valves Used for Bottom Outlet in Large Dams under Flood Hazards. Appl. Sci. 2022, 12, 10971. [Google Scholar] [CrossRef]
- Arab, M.A.; Gamil, A.I.; Syam, T.; Umer, M.; Ghani, S. Air Expulsion Analysis of an Industrial Air Valve Using CFD. In Proceedings of the 2021 12th International Conference on Mechanical and Aerospace Engineering (ICMAE), Athens, Greece, 16–19 July 2021; pp. 552–557. [Google Scholar]
- Zhang, X.-Y.; Fan, C.-Y.; Yu, X.-D.; Zhang, J.; Lv, J.-W.; Xu, T.-Y. Study on the Mathematical Model of Vacuum break valve for Large Air Mass Conditions. Water 2019, 11, 1358. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, J.; Yu, X.; Chen, S.; Shi, L. Study on Joint Protection of Air vessel and Air Valve in Long-Distance Water Supply System. ASME J. Press. Vessel Technol. 2022, 144, 061701. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.W. Effect of combination vacuum relief and air release valve on hydraulic transients during pipeline filling process. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 052032. [Google Scholar] [CrossRef]
- Wan, W.; Zhang, B.; Chen, X. Investigation on Water Hammer Control of Centrifugal Pumps in Water Supply Pipeline Systems. Energies 2019, 12, 108. [Google Scholar] [CrossRef]




| Flow (m3/s) | Head (m) | Efficiency (%) | NPSH (m) | Rotational Speed (r/min) |
|---|---|---|---|---|
| 0.0467 | 205.0 | 58.3 | 2.61 | 1480 |
| 0.0834 | 186.0 | 74.0 | 4.17 | |
| 0.0972 | 178.0 | 74.3 | 5.5 |
| Maximum Pressure (m) | Minimum Pressure (m) | Maximum Reversing Flow (m3/s) | Maximum Reversing Speed (r/min) | Moment of Zero Flow (s) | Moment of Zero Rotation Speed (s) |
|---|---|---|---|---|---|
| 233.83 | −75.41 | −0.148 | −1900 | 1.2 | 6.5 |
| Valve-Closing Method | The Highest Pressure Point | The Smallest Pressure Point | Maximum Reversing Speed (r/min) | |||
|---|---|---|---|---|---|---|
| Hmax/m | Network Distance/m | Hmin/m | Network Distance/m | |||
| plan 1 | Phase 1:3 s off 50%; Phase 2:100 s off 50% | 233.84 | 252.8 | −75.41 | 5863.8 | 1900.2 |
| plan 2 | Phase 1:3 s off 70%; Phase 2:100 s off 30% | 233.85 | 252.8 | −75.41 | 5863.8 | 1899.9 |
| plan 3 | Phase 1:3 s off 90%; Phase 2:100 s off 10% | 233.42 | 252.8 | −75.29 | 5863.8 | 1893.6 |
| plan 4 | Phase 1:3 s off 50%; Phase 2:50 s off 50% | 256.16 | 252.8 | −75.41 | 5863.8 | 1900.2 |
| plan 5 | Phase 1:3 s off 70%; Phase 2:50 s off 30% | 255.08 | 252.8 | −75.40 | 5863.8 | 1899.2 |
| plan 6 | Phase 1:3 s off 90%; Phase 2:50 s off 10% | 249.59 | 252.8 | −75.28 | 5863.8 | 1887.4 |
| plan 7 | Phase 1:3 s off 50%; Phase 2:10 s off 50% | 317.27 | 252.8 | −75.41 | 5863.8 | 506.82 |
| plan 8 | Phase 1:3 s off 70%; Phase 2:10 s off 30% | 317.24 | 252.8 | −75.38 | 5863.8 | 502.02 |
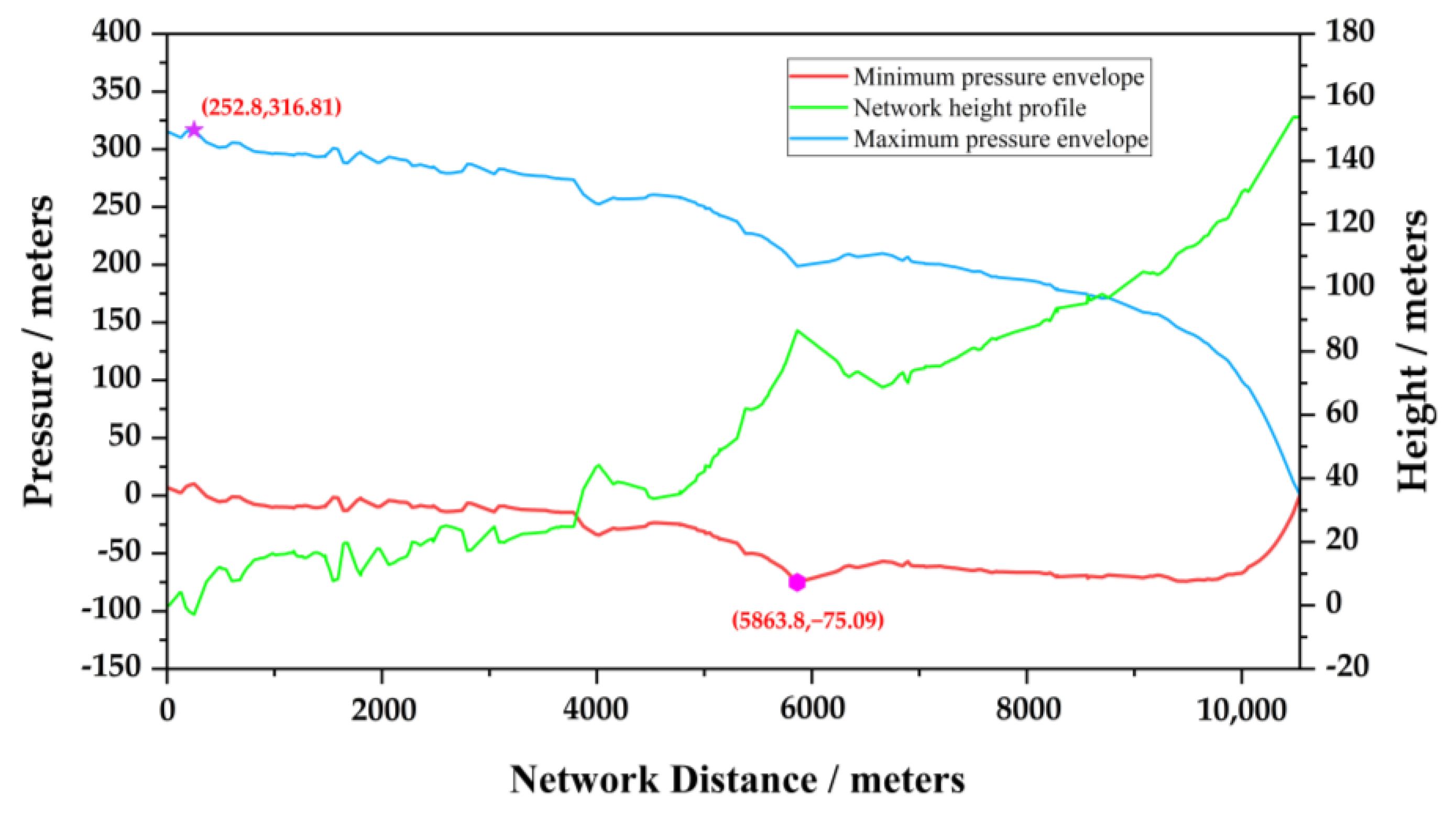
| plan 9 | Phase 1:3 s off 90%; Phase 2:10 s off 10% | 316.81 | 252.8 | −75.09 | 5863.8 | 466.32 |
| plan 10 | Phase 1:10 s off 50%; Phase 2:100 s off 50% | 233.84 | 252.8 | −75.42 | 5863.8 | 1900.4 |
| plan 11 | Phase 1:10 s off 70%; Phase 2:100 s off 30% | 233.86 | 252.8 | −75.41 | 5863.8 | 1900.1 |
| plan 12 | Phase 1:10 s off 90%; Phase 2:100 s off 10% | 233.45 | 252.8 | −75.41 | 5863.8 | 1895.2 |
| plan 13 | Phase 1:10 s off 50%; Phase 2:50 s off 50% | 252.71 | 252.8 | −75.42 | 5863.8 | 1900.3 |
| plan 14 | Phase 1:10 s off 70%; Phase 2:50 s off 30% | 252.11 | 252.8 | −75.41 | 5863.8 | 1899.8 |
| plan 15 | Phase 1:10 s off 90%; Phase 2:50 s off 10% | 250.76 | 252.8 | −75.41 | 5863.8 | 1892.5 |
| plan 16 | Phase 1:10 s off 50%; Phase 2:10 s off 50% | 311.87 | 252.8 | −75.42 | 5863.8 | 1660.9 |
| plan 17 | Phase 1:10 s off 70%; Phase 2:10 s off 30% | 311.02 | 252.8 | −75.41 | 5863.8 | 1612.0 |
| plan 18 | Phase 1:10 s off 90%; Phase 2:10 s off 10% | 310.73 | 252.8 | −75.41 | 5863.8 | 1303.5 |
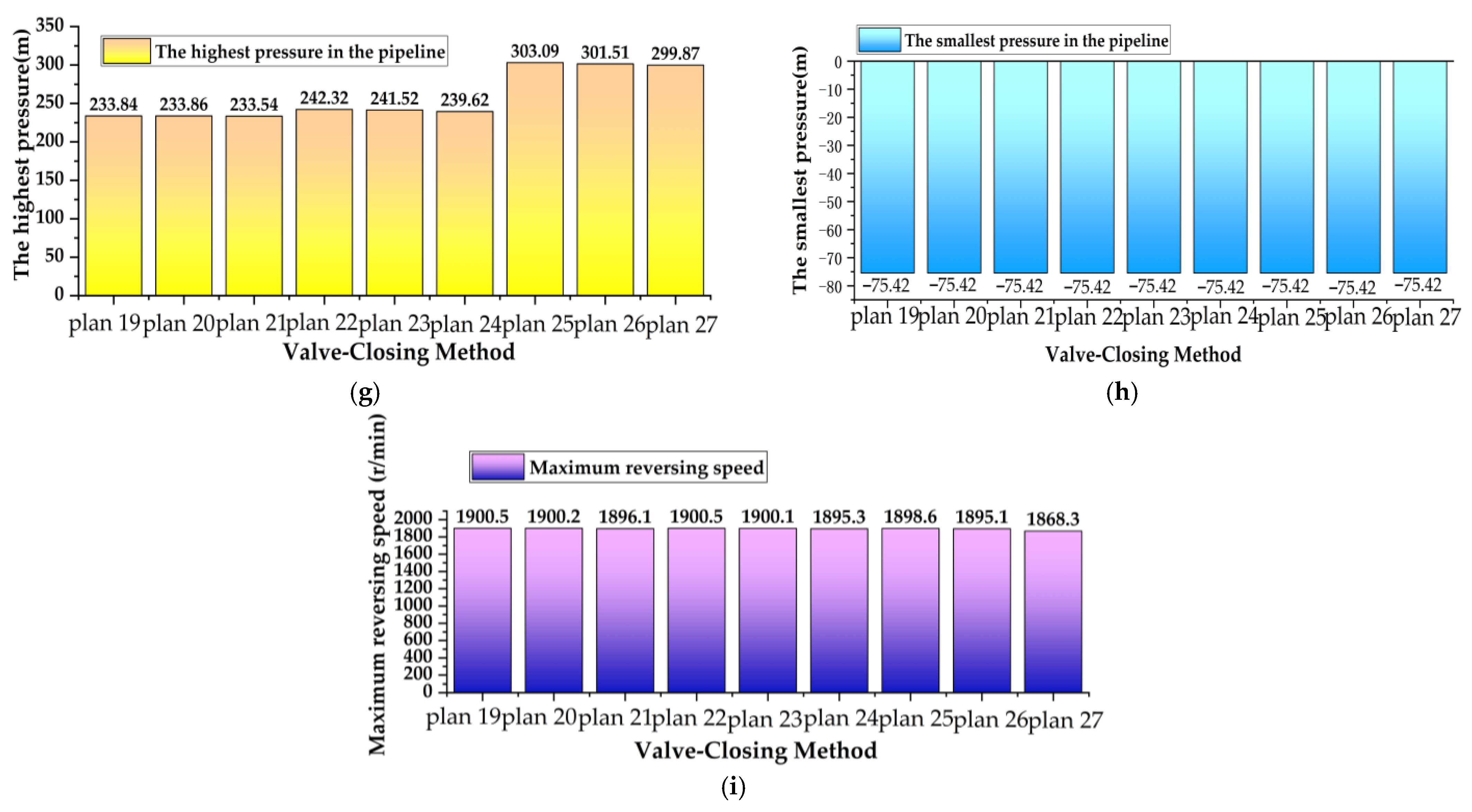
| plan 19 | Phase 1:18 s off 50%; Phase 2:100 s off 50% | 233.84 | 252.8 | −75.42 | 5863.8 | 1900.5 |
| plan 20 | Phase 1:18 s off 70%; Phase 2:100 s off 30% | 233.86 | 252.8 | −75.42 | 5863.8 | 1900.2 |
| plan 21 | Phase 1:18 s off 90%; Phase 2:100 s off 10% | 233.54 | 252.8 | −75.42 | 5863.8 | 1896.1 |
| plan 22 | Phase 1:18 s off 50%; Phase 2:50 s off 50% | 242.32 | 252.8 | −75.42 | 5863.8 | 1900.5 |
| plan 23 | Phase 1:18 s off 70%; Phase 2:50 s off 30% | 241.52 | 252.8 | −75.42 | 5863.8 | 1900.1 |
| plan 24 | Phase 1:18 s off 90%; Phase 2:50 s off 10% | 239.62 | 252.8 | −75.42 | 5863.8 | 1895.3 |
| plan 25 | Phase 1:18 s off 50%; Phase 2:10 s off 50% | 303.09 | 252.8 | −75.42 | 5863.8 | 1898.6 |
| plan 26 | Phase 1:18 s off 70%; Phase 2:10 s off 30% | 301.51 | 252.8 | −75.42 | 5863.8 | 1895.1 |
| plan 27 | Phase 1:18 s off 90%; Phase 2:10 s off 10% | 299.87 | 252.8 | −75.42 | 5863.8 | 1868.3 |
| Valve-Closing Method | Maximum Pressure /m | Minimum Pressure /m | Maximum Reversing Flow (m3/s) | Maximum Reversing Speed (r/min) | Moment of Zero Flow (s) | Moment of Zero Rotation Speed (s) |
|---|---|---|---|---|---|---|
| Fast-closing phase: closing time 3 s, closing angle 90%; Slow-closing phase: closing time 10 s, closing angle 10% | 316.81 | −75.09 | −0.053 | −466.32 | 1.2 | 6.5 |
| Valve-Closing Method | Increase in Moment of Inertia/(kg∙m2) | Maximum Positive Pressure of Pipeline/m | Ratio of Maximum Positive Pressure to Rated Pressure in Pipeline | Minimum Negative Pressure in Pipeline/m | Maximum Reversing Flow (m3/s) | Maximum Reversing Speed (r/min) | Ratio of Maximum Reverse Speed to Rated Speed of Water Pump |
|---|---|---|---|---|---|---|---|
| Fast-closing phase: closing time 3 s, closing angle 90%; Slow-closing phase: closing time 10 s, closing angle 10% | 0 (8.5) | 330.32 | 1.78 | −9.46 | −0.069 | −826.07 | 0.558 |
| +10% (9.4) | 330.12 | 1.77 | −9.32 | −0.071 | −794.58 | 0.537 | |
| +30% (11.1) | 329.73 | 1.77 | −8.91 | −0.079 | −686.04 | 0.464 | |
| +50% (12.8) | 328.51 | 1.76 | −8.71 | −0.083 | −533.32 | 0.360 | |
| +70% (14.5) | 326.29 | 1.75 | −8.39 | −0.083 | −360.20 | 0.243 |
| Air Vessel | Water Depth of Air Vessel/m | Air Chamber Height /m | Total Height /m | Tank Diameter/m | Total Tank Volume (m3) | Connection Tube Diameter /m |
|---|---|---|---|---|---|---|
| A | 1.2 | 0.8 | 2 | 3 | 15 | 0.1 |
| B | 1.4 | 0.6 | 2 | 3 | 15 | 0.1 |
| C | 1.6 | 0.4 | 2 | 3 | 15 | 0.1 |
| D | 0.7 | 0.3 | 1 | 3 | 7 | 0.1 |
| E | 2.1 | 0.9 | 3 | 3 | 21 | 0.1 |
| Valve-Closing Method | Air Vessel | Maximum Positive Pressure of Pipeline/m | Ratio of Maximum Positive Pressure to Rated Pressure in Pipeline | Minimum Negative Pressure in Pipeline/m | Maximum Reversing Flow (m3/s) | Maximum Reversing Speed (r/min) | Ratio of Maximum Reverse Speed to Rated Speed of Water Pump |
|---|---|---|---|---|---|---|---|
| Stage 1: 3 s off 90% Stage 2: 10 s off 10% | A | 253.14 | 1.36 | −0.1 | −0.183 | −1411.2 | 0.954 |
| B | 269.94 | 1.45 | −1.04 | −0.180 | −1363.64 | 0.921 | |
| C | 300.47 | 1.61 | −12.55 | −0.174 | −1283.81 | 0.867 | |
| D | 318.46 | 1.71 | −12.53 | −0.167 | −1214.27 | 0.821 | |
| E | 250.87 | 1.35 | −0.1 | −0.185 | −1430.23 | 0.966 | |
| 5 s off 100% | A | 243.14 | 1.31 | −0.1 | −0.183 | −1412.58 | 0.954 |
| B | 250.58 | 1.35 | −0.1 | −0.180 | −1364.89 | 0.922 | |
| C | 282.05 | 1.51 | −7.05 | −0.174 | −1284.99 | 0.868 | |
| D | 303.95 | 1.63 | −12.51 | −0.167 | −1215.54 | 0.821 | |
| E | 240.45 | 1.29 | −0.1 | −0.185 | −1431.63 | 0.967 | |
| Stage 1: 3 s off 50% Stage 2: 10 s off 30% Stage 3: 20 s off 20% | A | 294.43 | 1.58 | −0.1 | −0.184 | −1412.64 | 0.954 |
| B | 300.28 | 1.61 | −1.11 | −0.180 | −1364.95 | 0.922 | |
| C | 321.41 | 1.73 | −12.55 | −0.174 | −1285.06 | 0.868 | |
| D | 338.23 | 1.82 | −12.53 | −0.167 | −1302.57 | 0.88 | |
| E | 287.49 | 1.54 | −0.1 | −0.184 | −1431.69 | 0.967 |
| Air Vessel Location | Air Vessel | Maximum Positive Pressure of Pipeline/m | Ratio of Maximum Positive Pressure to Rated Pressure in Pipeline | Minimum Negative Pressure in Pipeline/m | Maximum Reversing Flow (m3/s) | Maximum Reversing Speed (r/min) | Ratio of Maximum Reverse Speed to Rated Speed of Water Pump |
|---|---|---|---|---|---|---|---|
| Method 1: Pile No. 0 + 013 | D | 232.85 | 1.25 | −6.14 | −0.166 | −1197.99 | 0.809 |
| Method 2: Pile No. 5 + 863.8 | D | 236.61 | 1.27 | −3.18 | −0.044 | no inversion | - |
| Method 3: Pile No. 9 + 820 | D | 230.45 | 1.24 | −15.38 | −0.044 | no inversion | - |
| Evaluation Indicators | Different Combinations of Water Hammer Protection Measures | Range | ||||||
|---|---|---|---|---|---|---|---|---|
| K | A | B | C | D | E | R1 | ||
| k1 | Maximum positive pressure of pipeline/m | 233.83 | 244.9 | 326.29 | 203.66 | 250.58 | 236.61 | −30.17 |
| k2 | Minimum negative pressure in pipeline/m | −75.41 | −9.46 | −8.39 | −2.49 | −0.1 | −3.18 | 75.31 |
| k3 | Maximum reversing speed (r/min) | −1900 | −826.08 | −360.20 | −1737.9 | −1364.89 | 0 | 1900 |
| k4 | Maximum reversing flow (m3/s) | −0.148 | −0.069 | −0.083 | −0.158 | −0.18 | −0.044 | 0.104 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Cheng, Y.; Shen, L.; Wu, J.; Zhang, Y.; Li, Q.; Yuan, L. Analysis of the Effectiveness of Water Hammer Protection Programs for Complex Long-Distance and High-Head Water Supply Projects. Water 2024, 16, 1582. https://doi.org/10.3390/w16111582
Tang Y, Cheng Y, Shen L, Wu J, Zhang Y, Li Q, Yuan L. Analysis of the Effectiveness of Water Hammer Protection Programs for Complex Long-Distance and High-Head Water Supply Projects. Water. 2024; 16(11):1582. https://doi.org/10.3390/w16111582
Chicago/Turabian StyleTang, Yuan, Yixiong Cheng, Lixia Shen, Jianhua Wu, Yusheng Zhang, Qianxi Li, and Lixian Yuan. 2024. "Analysis of the Effectiveness of Water Hammer Protection Programs for Complex Long-Distance and High-Head Water Supply Projects" Water 16, no. 11: 1582. https://doi.org/10.3390/w16111582
APA StyleTang, Y., Cheng, Y., Shen, L., Wu, J., Zhang, Y., Li, Q., & Yuan, L. (2024). Analysis of the Effectiveness of Water Hammer Protection Programs for Complex Long-Distance and High-Head Water Supply Projects. Water, 16(11), 1582. https://doi.org/10.3390/w16111582






