A Study of Precipitation Forecasting for the Pre-Summer Rainy Season in South China Based on a Back-Propagation Neural Network
Abstract
1. Introduction
2. Data and Methods
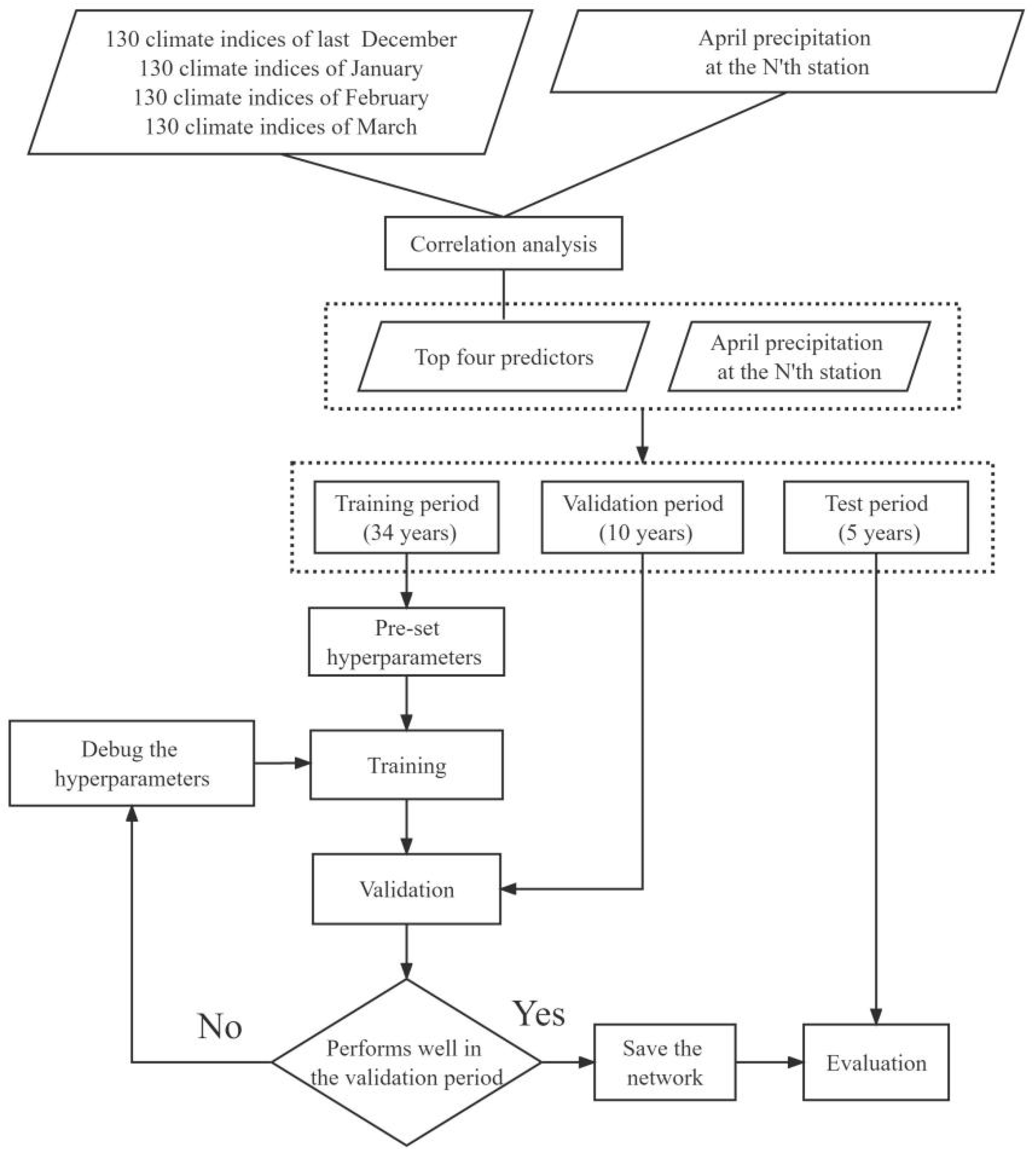
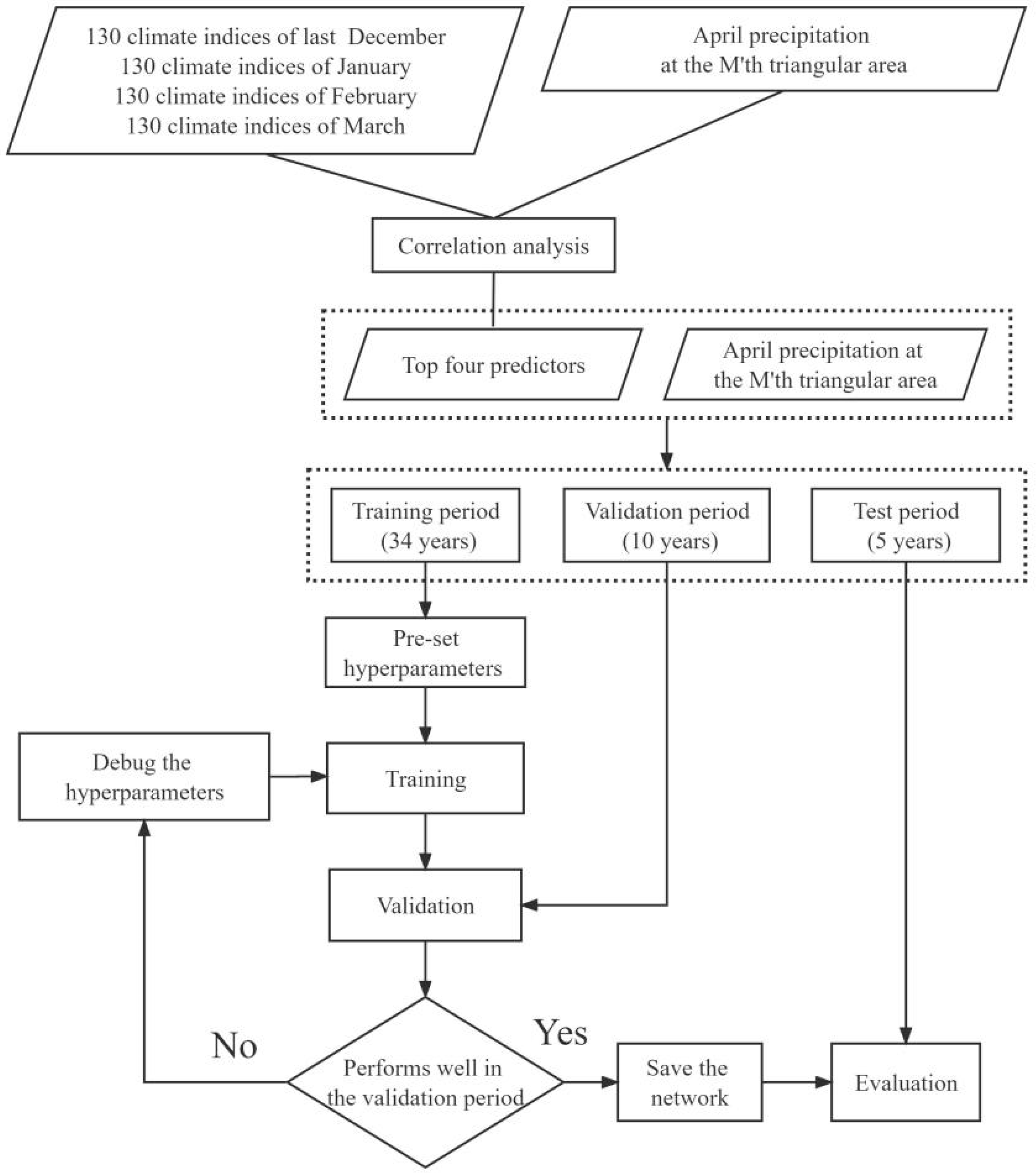
2.1. Overview of the Experiments
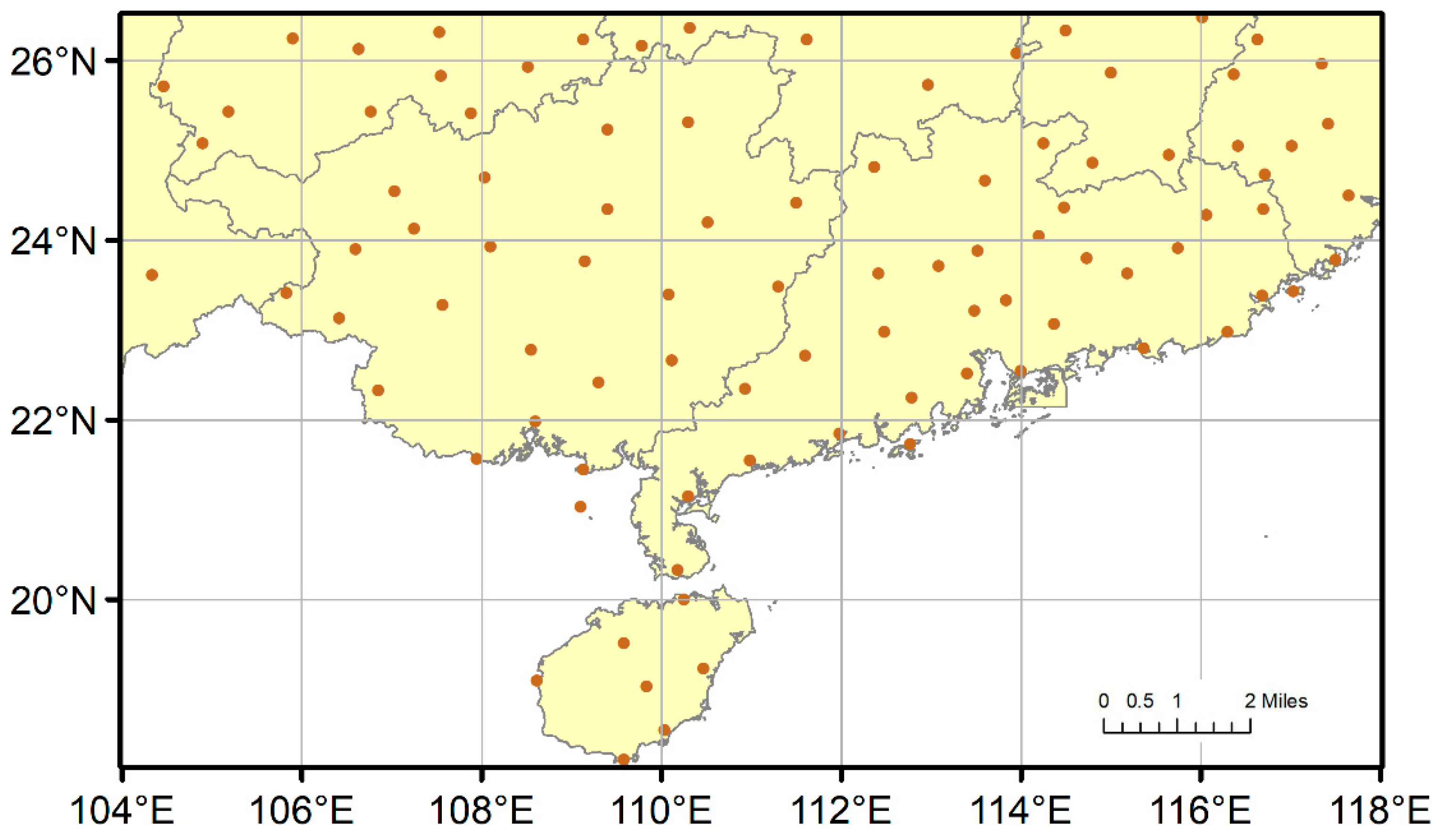
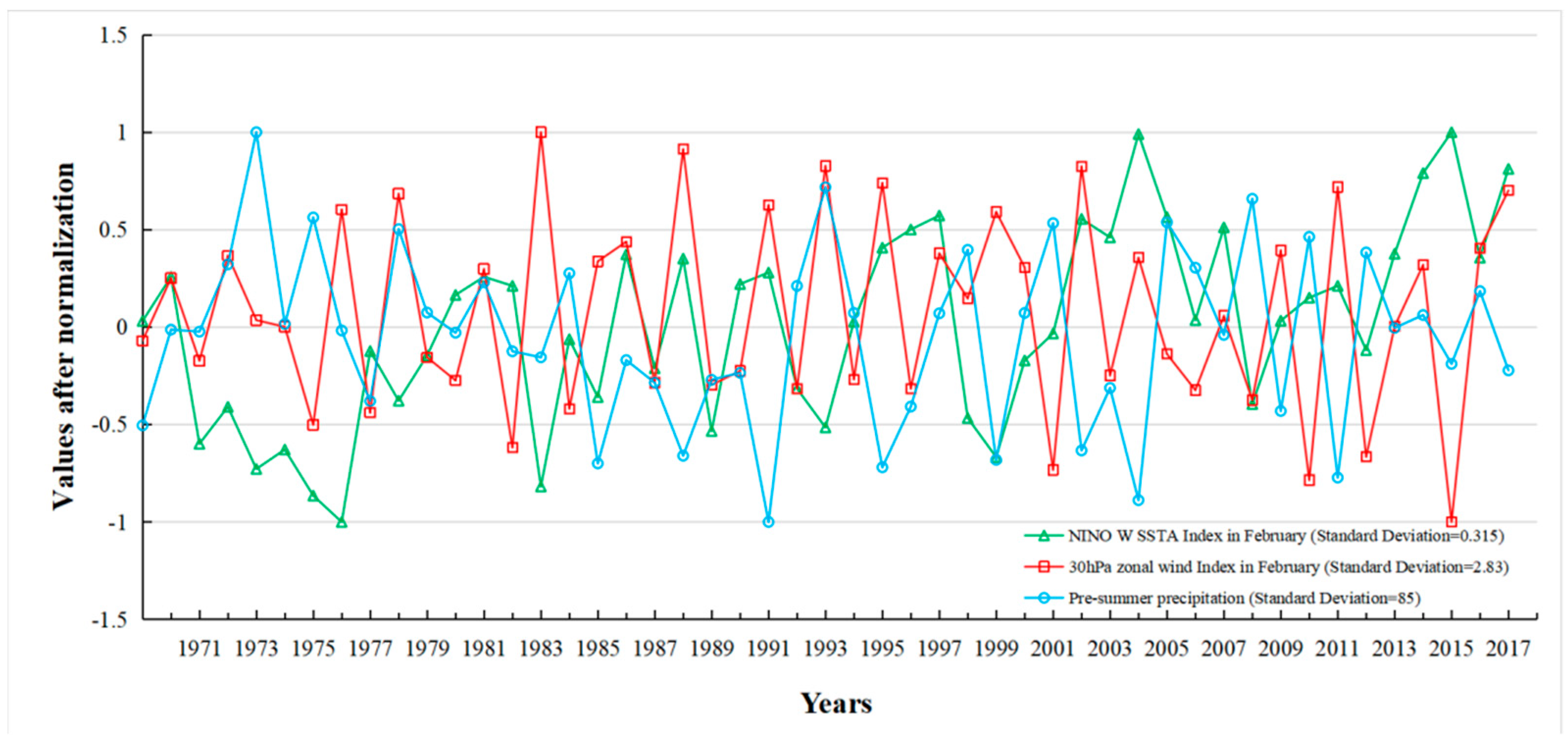
2.2. Data Sources and Processing
2.3. Methods
2.3.1. Correlation Analysis
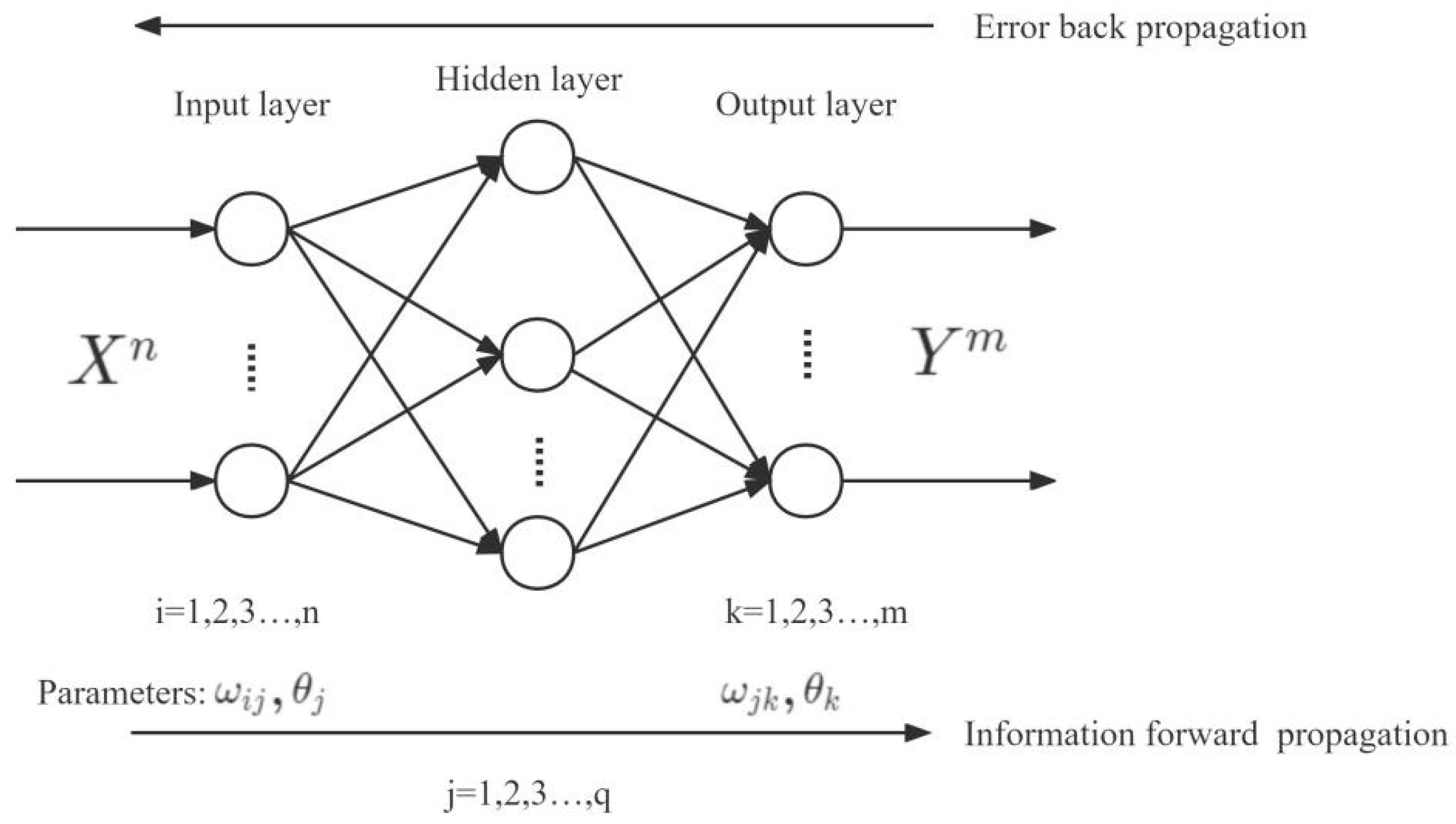
2.3.2. Back-Propagation Neural Network (BPNN)
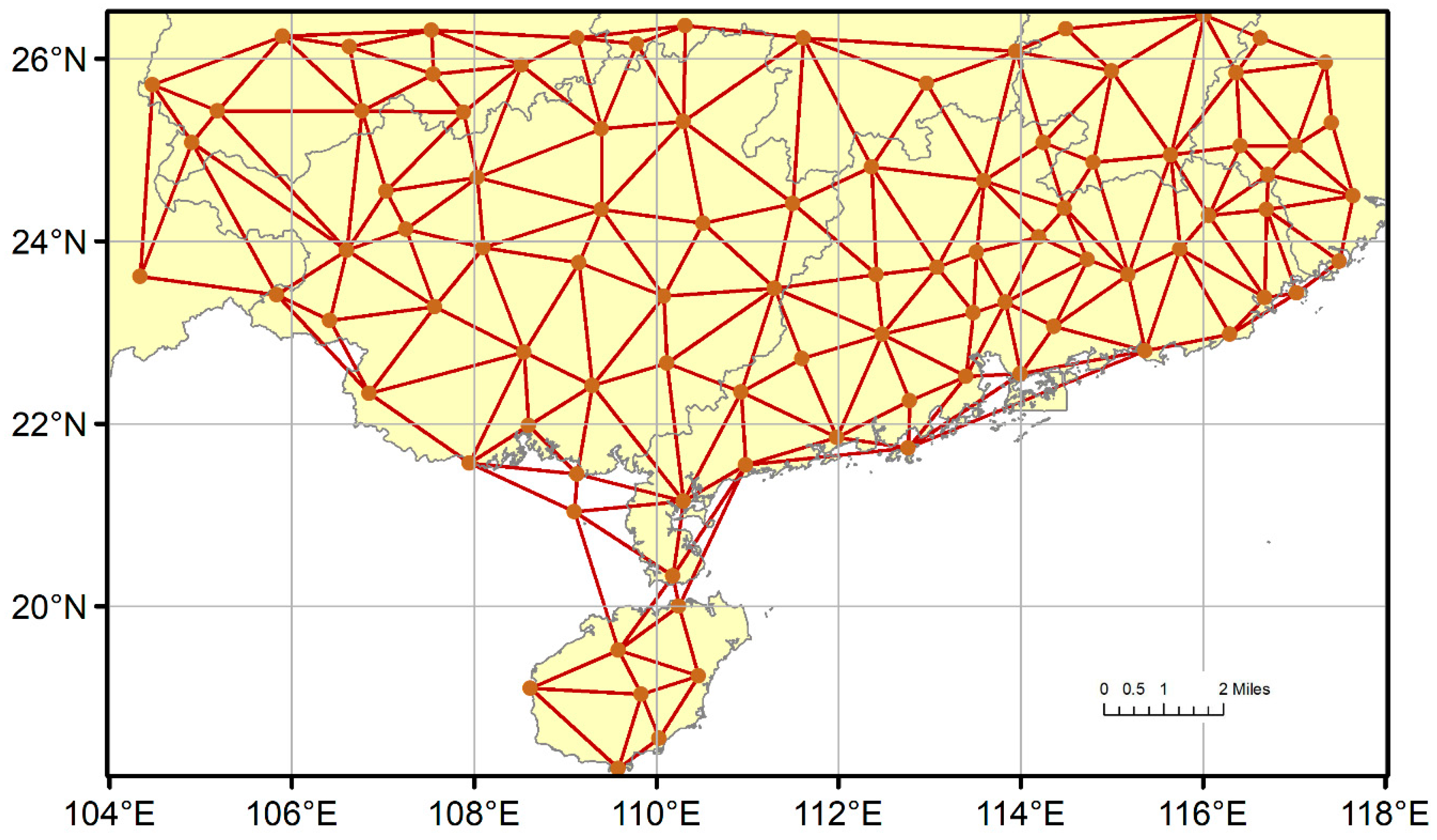
2.3.3. Triangular Irregular Network (TIN)
2.3.4. Genetic Algorithm (GA)
2.3.5. Evaluation Indices
3. Results
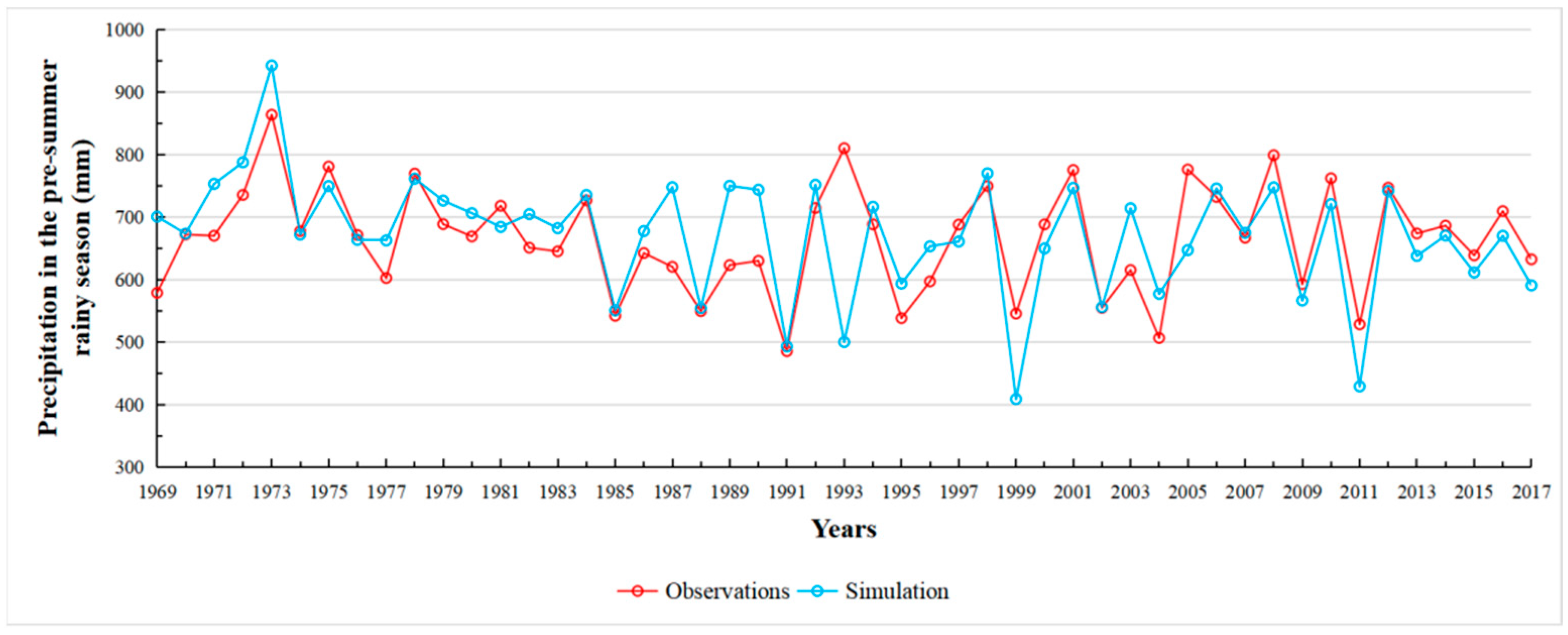
3.1. Comparison of Simulation for Different Schemes
3.2. Hindcast and Model Evaluation
3.2.1. Judgment of Overfitting
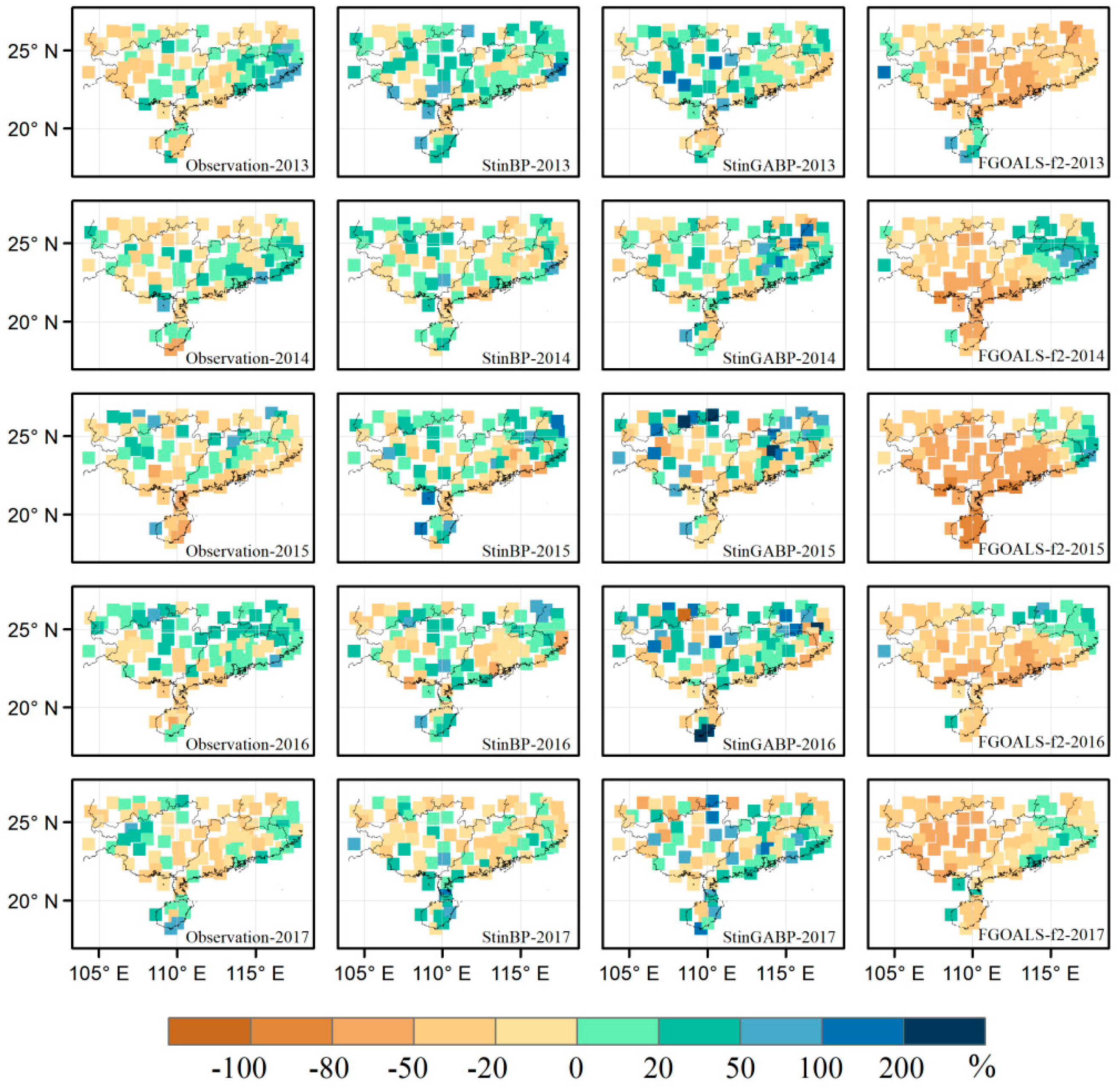
3.2.2. Evaluation of Forecasting Capability
4. Discussion
5. Summary
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ding, Y.H. Monsoons over China; Springer: Dordrecht, The Netherland, 1994; pp. 135–136. [Google Scholar]
- Hu, Y.M.; Zhai, P.M.; Luo, X.L.; Lv, J.M.; Qin, Z.N.; Hao, Q.C. Large scale circulation and low frequency signal characteristics for the persistent extreme precipitation in the first rainy season over South China in 2013. Acta Meteorol. Sin. 2014, 72, 465–477. (In Chinese) [Google Scholar]
- Zhao, Y.C.; Wang, Y.H. A review of studies on torrential rain during pre-summer flood season in South China since the 1980’s. Torrential Rain Disasters 2009, 28, 3–38. (In Chinese) [Google Scholar]
- Lin, A.L.; Ji, Z.P.; Gu, D.J.; Li, C.H.; Zheng, B.; He, C. Application of atmospheric intraseasonal oscillation in precipitation forecast over South China. J. Trop. Meteorol. 2016, 32, 878–889. (In Chinese) [Google Scholar]
- Qiang, X.M.; Yang, X.Q. Onset and end of the first rainy season in south China. Chin. J. Geophys. 2008, 51, 1333–1345. (In Chinese) [Google Scholar]
- Li, Z.H.; Luo, Y.L.; Du, Y.; Chan, C.L. Statistical characteristics of pre-summer rainfall over South China and associated synoptic conditions. J. Meteorol. Soc. Jpn. Ser. II 2020, 98, 213–233. [Google Scholar] [CrossRef]
- Chen, Y.M.; Qian, Y.F. Numerical study of influence of the SSTA in Western Pacific warm pool on precipitation in the first flood period in South China. J. Trop. Meteorol. 2005, 21, 13–23. (In Chinese) [Google Scholar]
- Yang, H.; Sun, S.Q. The characteristics of longitudinal movement of the subtropical high in the Western Pacific in the pre-rainy season in South China. Adv. Atmos. Sci. 2005, 22, 392–400. [Google Scholar]
- Zhou, X.Y.; Cheng, Z.Q.; Li, H.W.; Hu, D.M. Comparison between the roles of low-level jets in two heavy rainfall events over South China. J. Meteorol. Res. 2022, 36, 326–341. [Google Scholar] [CrossRef]
- Hussain, A.; Hussain, I.; Ali, S. Assessment of precipitation extremes and their association with NDVI, monsoon and oceanic indices over Pakistan. Atmos. Res. 2023, 292, 106873. [Google Scholar] [CrossRef]
- Wu, H.Q.; Zhang, A.H.; Jiang, B.R.; Qin, W. Relationship between the variation of Antarctic sea ice and the pre-flood season rainfall in South China. J. Nanjing Inst. Meteorol. 1998, 21, 266–273. (In Chinese) [Google Scholar]
- Yao, S.X.; Huang, Q.; Zhao, C. Variation characteristics of rainfall in the pre-flood season of South China and its correlation with sea surface temperature of Pacific. Atmosphere 2016, 7, 5. [Google Scholar] [CrossRef]
- Cai, X.Z. The influence of abnormal snow cover over Qinghai-Xizang Plateau and East Asian monsoon on early rainy season rainfall over South China. J. Appl. Meteorol. Sci. 2001, 12, 358–367. (In Chinese) [Google Scholar]
- Wu, X.S.; Guo, S.L.; Ba, H.H.; He, S.K.; Xiong, F. Long-range precipitation forecasting based on multi-pole sea surface temperature. J. Hydraul. Eng. 2018, 49, 1276–1283. (In Chinese) [Google Scholar]
- Singhrattna, N.; Rajagopalan, B.; Clark, M.; Krishna Kumar, K. Seasonal forecasting of Thailand summer monsoon rainfall. Int. J. Climatol. A J. R. Meteorol. Soc. 2005, 25, 649–664. [Google Scholar] [CrossRef]
- Zeng, X.M.; Xi, C.L. Study of the effects of reducing systematic errors on monthly regional climate dynamical forecast. J. Trop. Meteorol. 2009, 15, 102–105. [Google Scholar]
- Zhao, S.Y.; Yang, S.; Deng, Y.; Li, Q.P. Skills of yearly prediction of the early-season rainfall over southern China by the NCEP climate forecast system. Theor. Appl. Climatol. 2015, 122, 743–754. [Google Scholar] [CrossRef]
- Wang, D.H.; Zhao, Y.F. Effective approaches to extending medium-term forecasting of persistent severe precipitation in regional models. Atmos. Ocean. Sci. Lett. 2018, 11, 150–156. [Google Scholar] [CrossRef]
- Chen, J.; Pang, B.; Wu, Z.Q.; Chen, F.J.; Chen, Y.X.; Liu, X.; Ma, Y.N. Evaluation of fine-scale precipitation forecast of GRAPES_Meso 3 km convective-scale model in early summer rainy season in South China under complex topographical conditions. Trans. Atmos. Sci. 2022, 45, 99–111. (In Chinese) [Google Scholar]
- Xie, J.G.; Qin, B.B.; Wang, J.Y. The application of singular value decomposition analysis in the prediction of seasonal rainfall. Acta Meteorol. Sin. 1997, 117–123. (In Chinese) [Google Scholar] [CrossRef]
- Huang, Y.; Jin, L. Prediction model for annually first rainy season precipitation in South China and prediction tests. J. Trop. Meteorol. 2011, 27, 753–757. (In Chinese) [Google Scholar]
- Lu, Z.; Guo, Y.; Zhu, J.S.; Kang, N. Seasonal forecast of early summer rainfall at stations in South China using a statistical downscaling model. Weather. Forecast. 2020, 35, 1633–1643. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, K.; Wang, H.J. Statistical downscaling prediction of summer precipitation in Southeastern China. Atmos. Ocean. Sci. Lett. 2011, 4, 173–180. [Google Scholar]
- Guo, Y.; Li, J.P.; Li, Y. Seasonal forecasting of North China summer rainfall using a statistical downscaling model. J. Appl. Meteorol. Climatol. 2014, 53, 1739–1749. [Google Scholar] [CrossRef]
- Li, J.; Cheng, J.H.; Shi, J.Y.; Huang, F. Brief introduction of back propagation (BP) neural network algorithm and its improvement. In Advances in Computer Science and Information Engineering. Advances in Intelligent and Soft Computing; Jin, D., Lin, S., Eds.; Springer: Berlin, Germany, 2012; Volume 169. [Google Scholar]
- Danandeh Mehr, A. Seasonal rainfall hindcasting using ensemble multi-stage genetic programming. Theor. Appl. Climatol. 2021, 143, 461–472. [Google Scholar] [CrossRef]
- Shang, S.H. System Analysis of Water Resources: Methods and Applications; Tsinghua University Press: Beijing, China, 2006; p. 192. (In Chinese) [Google Scholar]
- David, S.; John, A.D. Artificial neural network and long-range precipitation in California. J. Appl. Meteorol. Climatol. 2000, 39, 57–66. [Google Scholar]
- Min, J.J.; Sun, J.R.; Liu, H.Z.; Wang, S.G.; Cao, X.Z. An improved BP algorithm and its application to precipitation forecast. J. Appl. Meteorol. Sci. 2010, 21, 55–62. (In Chinese) [Google Scholar]
- Moustris, K.P.; Larissi, I.K.; Nastos, P.T.; Paliatsos, A.G. Precipitation forecast using artificial neural networks in specific regions of Greece. Water Resour. Manag. 2011, 25, 1979–1993. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Zeng, X.M.; Li, G.; Lu, B.; Xiao, M.Z.; Wang, B.Z. Summer precipitation forecast using an optimized artificial neural network with a genetic algorithm for Yangtze-Huaihe River basin, China. Atmosphere 2022, 13, 929. [Google Scholar] [CrossRef]
- Valipour, M.; Khoshkam, H.; Bateni, S.M.; Jun, C. Machine-learning-based short-term forecasting of daily precipitation in different climate regions across the contiguous United States. Expert Syst. Appl. 2024, 238, 121907. [Google Scholar] [CrossRef]
- Gupta, B.; Negi, S.S. Image denoising with linear and non-linear filters: A review. Int. J. Comput. Sci. Issues 2013, 10, 149–154. [Google Scholar]
- Thomas, R.K.; Kevin, E.T. Modern global climate change. Science 2003, 302, 1719–1723. [Google Scholar]
- Zhang, L.R.; Wang, X.Z.; Wang, G.Q.; Liu, J.F.; Li, S.M. Consistency and reliability analysis of hydrological sequence in environment change. J. China Hydrol. 2015, 35, 39–43. (In Chinese) [Google Scholar]
- Zhou, T.; Chen, Z.; Zou, L.; Chen, X.; Yu, Y.; Wang, B.; Bao, Q.; Bao, Y.; Cao, J.; He, B.; et al. Development of climate and earth system models in China: Past achievements and new CMIP6 results. J. Meteorol. Res. 2020, 34, 1–19. [Google Scholar] [CrossRef]
- Ren, H.L.; Wu, Y.; Bao, Q.; Ma, J.; Liu, C.; Wan, J.; Li, Q.; Wu, X.; Liu, Y.; Tian, B.; et al. The China Multi-Model Ensemble prediction system and its application to flood-season prediction in 2018. J. Meteorol. Res. 2019, 33, 540–552. [Google Scholar] [CrossRef]
- Liu, J.T.; Chang, H.B.; Hsu, T.Y.; Ruan, X.Y. Prediction of the flow stress of high-speed steel during hot deformation using a BP artificial neural network. J. Mater. Process. Technol. 2000, 103, 200–205. [Google Scholar] [CrossRef]
- Safari, M.J.S.; Arashloo, S.R.; Vaheddoost, B. Multiple kernel fusion: A novel approach for lake water depth modeling. Environ. Res. 2023, 217, 114856. [Google Scholar] [CrossRef]
- Tsai, V.J.D. Delaunay triangulations in TIN creation: An overview and a linear-time algorithm. Int. J. Geogr. Inf. Syst. 1993, 7, 501–524. [Google Scholar] [CrossRef]
- Pratibha, P.S.; Sumit, S.K. Review on digital elevation model. Int. J. Mod. Eng. Res. 2013, 3, 2412–2418. [Google Scholar]
- Ding, S.F.; Su, C.Y.; Yu, J.Z. An optimizing BP neural network algorithm based on genetic algorithm. Artif. Intell. Rev. 2011, 36, 153–162. [Google Scholar] [CrossRef]
- Zhu, C.H.; Zhang, J.J.; Liu, Y.; Ma, D.H.; Li, M.F.; Xiang, B. Comparison of GA-BP and PSO-BP neural network models with initial BP model for rainfall-induced landslides risk assessment in regional scale: A case study in Sichuan, China. Nat. Hazards 2020, 100, 173–204. [Google Scholar] [CrossRef]
- Chen, G.Y.; Zhao, Z.G. Assessment methods of short range climate prediction and their operational application. J. Appl. Meteorol. Sci. 1998, 9, 178–185. (In Chinese) [Google Scholar]
- Li, T.; Chen, J.; Wang, F.; Han, R. A correction algorithm of summer precipitation prediction based on neural network in China. J. Arid. Meteorol. 2022, 40, 308–316. (In Chinese) [Google Scholar]
- Thomas, M. Machine Learning; McGraw-Hill Education: New York, NY, USA, 1997. [Google Scholar]
- Ma, H.; Chen, Z.H.; Jiang, L.P.; Wang, Q.Q.; Lin, Z.J. SVD analysis between the annually first raining period precipitation in South China and the SST over offshore waters in China. J. Trop. Meteorol. 2009, 25, 241–245. (In Chinese) [Google Scholar]
- Hu, Y.H.; Rong, Y.S.; Wei, J.; Li, C.H.; Tang, H.B.; Li, S.S. Relationship between pre-flood season precipitation in South China and Indian Ocean SST at earlier stages. Water Resour. Prot. 2017, 33, 106–116. (In Chinese) [Google Scholar]
- Chen, Z.; Zhou, L.; Yang, X.; Wang, Z.; Ding, Z. A GABP based method to improved software defect prediction. In Proceedings of the 12th International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE 2022), Emeishan, China, 27–30 July 2022; Volume 2022, pp. 1556–1563. [Google Scholar]
- Zhao, M.; Zhang, C.; Weng, Y. Improved artificial neural networks (ANNs) for predicting the gas separation performance of polyimides. J. Membr. Sci. 2023, 681, 121765. [Google Scholar] [CrossRef]
- Araghi, A.; Jaghargh, M.R.; Maghrebi, M.; Martinez, C.J.; Fraisse, C.W.; Olesen, J.E.; Hoogenboom, G. Investigation of satellite-related precipitation products for modeling of rainfed wheat production systems. Agric. Water Manag. 2021, 258, 107222. [Google Scholar] [CrossRef]
- Zheng, B.; Gu, D.J.; Li, C.H.; Lin, A.L.; Liang, J.Y. Frontal rain and summer monsoon rain during pre-rainy season in South China. Part II: Spatial patterns. Chin. J. Atmos. Sci. 2007, 31, 495–504. (In Chinese) [Google Scholar]
- Kawatani, Y.; Hamilton, K. Weakened stratospheric quasibiennial oscillation driven by increased tropical mean upwelling. Nature 2013, 497, 478–481. [Google Scholar] [CrossRef] [PubMed]
- Gu, S.N.; Yang, X.Q. Variability of the northern circumpolar vortex and its association with climate anomaly in China. Sci. Meteorol. Sin. 2006, 26, 135–142. (In Chinese) [Google Scholar]
- Luo, Y.Y.; Lu, J.; Liu, F.K.; Wan, X.Q. The positive Indian Ocean Dipole-like response in the tropical Indian Ocean to global warming. Adv. Atmos. Sci. 2016, 33, 476–488. [Google Scholar] [CrossRef]
- Jia, X.J.; Zhang, C.; Wu, R.G.; Qian, Q.F. Changes in the relationship between spring precipitation in southern China and tropical Pacific-South Indian Ocean SST. J. Clim. 2021, 34, 6267–6279. [Google Scholar] [CrossRef]
- Zhang, H.D.; Gao, S.T.; Zhang, Y.S. The interdecadal variation of north polar vortex and its relationships with spring precipitation in China. Clim. Environ. Res. 2006, 11, 593–604. (In Chinese) [Google Scholar]
- Zheng, B.; Gu, D.; Lin, A.; Li, C. Dynamical mechanism of the stratospheric quasi-biennial oscillation impact on the South China Sea Summer Monsoon. Sci. China Ser. D Earth Sci. 2007, 50, 1424–1432. [Google Scholar] [CrossRef]
- Li, C.X.; Zhao, T.B. Seasonal responses of precipitation in china to El Niño and positive Indian Ocean Dipole modes. Atmosphere 2019, 10, 372. [Google Scholar] [CrossRef]
- Gao, T.; Wang, H.J.; Zhou, T.J. Changes of extreme precipitation and nonlinear influence of climate variables over monsoon region in China. Atmos. Res. 2017, 197, 379–389. [Google Scholar] [CrossRef]



| Schemes | Inputs | Expected Output | Initial Weights and Biases | Other Hyperparameters | Training Period | Validation Period | Test Period |
|---|---|---|---|---|---|---|---|
| SregBP | Predictors correlated with the regional precipitation | Station precipitation | Random | Manual debugging | 1969–2002 | 2003–2012 | 2013–2017 |
| SstnBP | Predictors correlated with the station precipitation | As in SregBP | As in SregBP | As in SregBP | As in SregBP | As in SregBP | As in SregBP |
| StinBP | As in SstnBP | TIN precipitation | As in SregBP | As in SregBP | As in SregBP | As in SregBP | As in SregBP |
| StinGABP | As in SstnBP | As in StinBP | GA optimization | As in SregBP | As in SregBP | As in SregBP | As in SregBP |
| Grades of Precipitation Anomalies | Basis |
|---|---|
| Extreme | |
| First grade | |
| Second grade | |
| Normal |
| Months | Modeling Schemes | Training Period | Validation Period | Training and Validation Periods | |||
|---|---|---|---|---|---|---|---|
| RMSE (mm) | MAPE (%) | RMSE (mm) | MAPE (%) | RMSE (mm) | MAPE (%) | ||
| April | SregBP | 77.9 | 96.2 | 118.7 | 152.9 | 90.2 | 109.1 |
| SstnBP | 80.8 | 99.6 | 110.1 | 133.3 | 90.3 | 107.2 | |
| StinBP | 69.2 | 57.9 | 93.7 | 86.0 | 75.2 | 64.3 | |
| StinGABP | 121.7 | 61.7 | 61.7 | 47.5 | 111.0 | 58.5 | |
| May | SregBP | 116.8 | 52.5 | 144.3 | 74.9 | 125.2 | 57.6 |
| SstnBP | 103.1 | 47.4 | 131.3 | 74.6 | 111.9 | 53.6 | |
| StinBP | 89.3 | 32.4 | 112.1 | 46.3 | 95.0 | 35.6 | |
| StinGABP | 130.3 | 34.1 | 58.0 | 22.7 | 117.9 | 31.5 | |
| June | SregBP | 128.4 | 53.7 | 183.9 | 66.8 | 144.7 | 56.7 |
| SstnBP | 108.7 | 46.2 | 170.4 | 67.4 | 127.8 | 51.1 | |
| StinBP | 95.6 | 33.9 | 149.4 | 43.1 | 110.1 | 36.0 | |
| StinGABP | 157.3 | 36.9 | 108.6 | 31.5 | 147.7 | 35.7 | |
| Months | Schemes | Training and Validation Periods | Hindcast Period | ||
|---|---|---|---|---|---|
| RMSE (mm) | MAPE (%) | RMSE (mm) | MAPE (%) | ||
| April | StinBP | 75.2 | 64.3 | 97.5 | 78.9 |
| StinGABP | 111.0 | 58.5 | 137.0 | 87.9 | |
| May | StinBP | 95.0 | 35.6 | 136.2 | 44.4 |
| StinGABP | 117.9 | 31.5 | 220.2 | 55.1 | |
| June | StinBP | 110.1 | 36.0 | 120.9 | 46.4 |
| StinGABP | 147.7 | 35.7 | 241.5 | 66.8 | |
| Years | AR(%) | ACC | Ps | ||||||
|---|---|---|---|---|---|---|---|---|---|
| StinBP | StinGABP | FGOALS-f2 | StinBP | StinGABP | FGOALS-f2 | StinBP | StinGABP | FGOALS-f2 | |
| 2013 | 39.8 | 38.7 | 47.3 | −0.050 | −0.205 | −0.169 | 43.4 | 40.6 | 50.0 |
| 2014 | 63.4 | 53.8 | 54.8 | 0.172 | 0.134 | 0.205 | 64.9 | 57.0 | 57.1 |
| 2015 | 55.9 | 60.2 | 55.9 | 0.097 | 0.199 | 0.124 | 60.2 | 66.1 | 61.0 |
| 2016 | 54.8 | 64.5 | 52.7 | 0.028 | 0.076 | 0.250 | 57.6 | 68.3 | 56.9 |
| 2017 | 49.5 | 55.9 | 53.8 | −0.027 | 0.243 | −0.026 | 52.5 | 61.0 | 59.8 |
| Mean | 52.7 | 54.6 | 52.9 | 0.044 | 0.089 | 0.077 | 55.7 | 58.6 | 57.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.-Z.; Liu, S.-J.; Zeng, X.-M.; Lu, B.; Zhang, Z.-X.; Zhu, J.; Ullah, I. A Study of Precipitation Forecasting for the Pre-Summer Rainy Season in South China Based on a Back-Propagation Neural Network. Water 2024, 16, 1423. https://doi.org/10.3390/w16101423
Wang B-Z, Liu S-J, Zeng X-M, Lu B, Zhang Z-X, Zhu J, Ullah I. A Study of Precipitation Forecasting for the Pre-Summer Rainy Season in South China Based on a Back-Propagation Neural Network. Water. 2024; 16(10):1423. https://doi.org/10.3390/w16101423
Chicago/Turabian StyleWang, Bing-Zeng, Si-Jie Liu, Xin-Min Zeng, Bo Lu, Zeng-Xin Zhang, Jian Zhu, and Irfan Ullah. 2024. "A Study of Precipitation Forecasting for the Pre-Summer Rainy Season in South China Based on a Back-Propagation Neural Network" Water 16, no. 10: 1423. https://doi.org/10.3390/w16101423
APA StyleWang, B.-Z., Liu, S.-J., Zeng, X.-M., Lu, B., Zhang, Z.-X., Zhu, J., & Ullah, I. (2024). A Study of Precipitation Forecasting for the Pre-Summer Rainy Season in South China Based on a Back-Propagation Neural Network. Water, 16(10), 1423. https://doi.org/10.3390/w16101423










