Abstract
Rain gardens are used to solve urban problems related to the negative impact of stormwater. (1) Scientific contributions from different countries provide general guidelines for the design and operation of rain gardens in different geographical areas. Given the small spatial scale of rain gardens, the use of existing infiltration models often leads to design errors. (2) The purpose of this paper is to develop a hydrological model by introducing a system of equations that extends the ability to calculate the rate, flow rate and time of saturation of layers with moisture and rainwater leakage from the rain garden system. (3) The results obtained allow us to describe the dynamic processes of passage and saturation of layers of the rain garden at a certain point in time, which extends the ability to calculate the flow rate. It was established that the smaller the area of the rain garden compared to the area of the catchment basin, the faster it reaches its full saturation. Increasing the thickness of the rain garden layers allows for an increase in the efficiency of water retention at a lower value of the area ratio. (4) The practical significance of the results obtained is especially important for the correct description of hydrodynamics in the system and determining the optimal conditions for the effective functioning and management of the rain garden structure for any climatic region.
1. Introduction
Progressing urbanization process in the modern world, inadequate planning of sewerage networks, extreme climate change, and outdated drainage systems pose numerous challenges for scientists, architects, politicians, and administrators, among which the biggest problem is the increase in the area of impervious areas in settlements, which leads to urban flooding [1,2]. The sewerage system, which has a lifespan of only 20–30 years, is unable to effectively discharge sufficient stormwater due to the increase in runoff, and increasing its capacity is an extremely uneconomic solution [3,4]. In addition, stormwater runoff from roofs, roads, and car parks is often contaminated with bacteria, organic compounds, and heavy metals, which negatively impact the aquatic environment and require special treatment [5,6].
As a result, conventional stormwater management is criticized and characterized as an unsustainable solution. Promoting sustainable stormwater management (SSM) is an important issue that requires developing and implementing effective strategies [7].
We focus on a specific type of green infrastructure—rain gardens—which are implemented in residential areas and allow localized management of stormwater runoff from surrounding sidewalks, car parks, and roofs, directing rainwater from impermeable surfaces into multilayered structures with vegetation cover, where water is filtered, retained, and slowly discharged into groundwater, local drainage systems, or reservoirs [8,9].
A typical rain garden design consists of three main functional blocks: (1) a topsoil layer for planting, (2) a transitional infiltration layer, and (3) a gravel layer for water drainage [10]. There can be a different number of such layers. The topsoil layer, which is a mixture of soil, sand, sandy loam, or loam, is a growing medium for plants and partially determines the infiltration rate, pollutant removal potential, and stability of rain gardens [11]. The infiltration layer is designed to increase the permeability of the upper soil layer and usually consists of fine gravel or coarse sand; in addition to being well drained, it must also be strong enough to support the weight of the upper layers [12]. A gravel layer is a layer of medium or coarse gravel designed to drain infiltration water to the drainage system or water table [13].
Thus, the introduction of rain gardens allows for solving such important problems as reducing the volume of rainwater runoff from the catchment area, reducing the speed and delaying the peak flow of water in the sewerage system, recharging groundwater through infiltration and removing pollutants from water before it enters local streams [14].
Rain gardens require less documentation, do not require specialized expertise or complex design, unlike green roofs, and do not necessarily require the use of heavy machinery [15].
One of the main weaknesses of rain garden designs is the relatively high need for land, the area of which depends on the type of soil environment. Thus, the garden area should be equal to 20 to 30% of the catchment area for sandy soil and about 60% for clay soil [16]. The optimal size of the rain garden design area is considered to be 4–7% of the area from which runoff will be collected (catchment area) [17]. Similar recommendations are proposed in [18], according to which the design of a rain garden should be from 5 to 10% of the catchment area.
When designing rain gardens, the most important aspect is to take into account their main parameters and the hydrological processes that take place in them. The main factors that determine the hydrological performance of rain gardens are soil composition and thickness of the layers of the structure, their water-holding capacity, choice of plants, consideration of the height of the water column on the surface of the structure, choice of the structure area and effective volume for water retention [19,20].
Scientific contributions from different countries provide general guidelines for the design and operation of rain gardens in different geographical areas, as shown in Table 1.

Table 1.
Classifications of rain garden systems according to recommendations from around the world.
Recommendations that do not take local climatic conditions into account often lead to malfunctioning of systems. For example, Wang et al. [29] noted that the low efficiency of rain garden designs installed in tropical countries is because the systems were designed based on recommendations from temperate zones.
Modeling plays an important role in rain garden research as it allows for the prediction and evaluation of the hydrological characteristics of systems operating under different climatic conditions [30]. In addition, modeling provides an opportunity to take into account different operating parameters and obtain relevant data for designing rain gardens in real-world conditions, which is not always possible to achieve through experiments.
Infiltration is the main hydrological process in rain garden structures, which determines the productivity and efficiency of rainwater management [31]. Models designed to describe the infiltration process aim to provide a reliable tool for estimating the design parameters of specific rain garden designs rather than focusing on estimating catchment-level capacities.
The first models of infiltration water flow in soil layers were based on the Richards equation [32,33,34], which describes a single-phase incompressible flow through the soil layer, taking into account thermal effects and the absence of air resistance. One of these numerical models is called Recharge, which allows us to describe the hydrological behavior of rain gardens to design and evaluate their efficiency [35]. According to the authors’ theory, the flow of water through the soil layer of a rain garden is simulated at three levels: the root zone, the middle layer with high water conductivity, and the lower soil layer. The developed model assumes a single-phase vertical matrix flow under isothermal conditions and no air influence. The Recharge model was further developed in 2009 as part of a research study [36], leading to the creation of the R2D model to model infiltration in rain gardens. However, it was noted that this infiltration model was very difficult to apply, so models based on other equations were developed. To improve the accuracy of the Recharge model, Roy-Poiret et al. [37] developed a one-dimensional hydrological model of water retention by rain gardens. This model can accurately reproduce the hydrological behavior of rain gardens throughout a low-to-medium-intensity rain event. Later, the authors of [38] applied the Recharge model to analyze the hydrological performance of rain gardens in the tropical climate of Singapore. Models based on the Richards equations allow for the quantification of the average efficiency of rain gardens in managing rainwater, provided they operate in a continuous simulation mode. However, there is a question of obtaining the parameters used to model the detailed infiltration/saturation processes.
An alternative version of the Recharge model is the Recarga model, which uses the less complex Green-Ampth equation instead of the Richards equation to describe the infiltration process. It was developed and discussed by Dussaillant et al. [39]. It showed that it can produce results similar to the Recharge model and was recommended for use in sizing rain gardens by the state of Wisconsin. However, some authors [40] noted that the water retention efficiency of rain garden systems cannot be simply described using equations based on the constant permeability of water to the soil medium, such as the Green-Ampt equation [41], which does not allow for a description of the infiltration process in rain gardens in the field.
The next stage in the development of infiltration modeling was the use of the Hydrologic Engineering Centre–Hydrologic Modelling System (HEC–HMS), developed by the authors [42] in 2006 to assess hydrological modifications of rain gardens. This model introduces the concept of a «sub-basin» to describe the drainage area of a rain garden. Using the characteristics of the sub-basin, incoming rainfall is converted into runoff. The model also includes drainage elements that simulate hydrological conditions and the effect of changes in soil moisture on infiltration rates. The model uses a «stage-flow» relationship to control runoff, and the rain garden in this model is represented by a reservoir covered by a dam. This model has been used to monitor data from rain gardens located at Villanova University to predict water levels in the gardens [43,44].
Considering that the HEC-HMS model is one-dimensional and does not take into account horizontal exfiltration into surrounding soils, the authors of [45] proposed a two-dimensional mechanical model to analyze the influence of the surrounding soil and the initial water content of the substrate. This model allows taking into account different types of substrate, lateral and bottom exfiltration into surrounding soils, as well as the size of the rain garden structure.
In 2013, the authors of [40] proposed the use of the Drainmod model to predict the hydrological response of rain gardens to runoff fluctuations in a continuous and long-term observation mode. Some of the advantages offered by the Drainmod model include the ability to account for substrate characteristics, pre-saturation of the system, and the ability to model the drainage configuration of the internal water storage area. Recently, the Drainmod model has been used for modeling the evaluation of rain garden systems by [46], which allowed for the continuous modeling of a detailed water balance and a region that represents the volume of water stored in the system. Infiltration in the Drainmod model is described using the Green-Ampt equation and requires the user to specify a characteristic curve at the soil–water interface and saturated hydraulic conductivity.
A more recent model that allows describing infiltration processes is Hydrus. This is a finite element variable saturation model that uses the Richard equation to describe the movement of saturated and unsaturated water and is widely used in research to model infiltration systems [47,48,49]. In [46], the authors used the Hydrus-1D model to analyze hydrological processes in different scenarios and optimized key parameters that affect the control effect. Both software products provided comparable modeling results; however, there were no field data to verify the results.
One approach to simulating the hydrological operation of rain gardens is the use of analytical equations that take the influence of local climatic conditions into account [50]. In [51], an analytical probabilistic approach was used to study the hydrological performance of rain gardens. The authors developed analytical equations that can be used in different locations to design the critical dimensions of rain gardens to ensure the desired stormwater retention efficiency. The effectiveness of the analytical equations was tested by comparing them with the results of a series of continuous simulations using long-term rainfall data from Atlanta, Georgia. However, the resulting models developed based on the analytical approach do not allow for the current position of water in the layers, treating each layer as a separate capacitive object that holds a certain amount of water. In particular, the models do not take into account the degree of saturation of each layer of the system and the processes that occur during the drying of the layers after precipitation. These limitations can affect the accuracy and realism of hydrological process simulations.
Recently, modern computer technologies have been used to model hydrological processes, in particular, infiltration processes [52,53,54]. The authors of [55] proposed the use of computer simulation to predict the rate of infiltration through various soil media. The study [56] compared the performance of several machine learning models, Support Vector Machine (SVM), artificial neural network (ANN), and Adaptive Logical Inference System (ANFIS), to estimate the infiltration rate through the soil. Study [57] compared the performance of an artificial neural network with other artificial intelligence tools, such as the Gaussian Process (GP), Gene Expression Programming (GEP), and General Regression Neural Network (GRNN), to estimate the rate of soil infiltration.
Despite the large number of existing models that can describe hydrological processes in rain gardens, an important aspect that remains insufficiently studied is the consideration of key dynamic processes, such as the passage and saturation of water through the layers of the rain garden system at a certain point in time and the loss of vertical filtration flow head concerning the filtration coefficient. This is especially important for the correct description of hydrodynamics in the system and the determination of optimal conditions for the rain garden.
The purpose of this study is to develop a universal hydrological model based on Darcy’s law and Bernoulli’s equation, which allows for the description of dynamic processes and hydrological features in the rain garden design. The model requires knowledge of one of the main indicators of the quality and productivity of soil materials—water retention capacity. This parameter should be determined by experimentation in experimental filter columns.
The scientific novelty of this study is the creation and verification of the efficiency of the model of the passage and saturation of the layers of the rain garden system with water at a certain point in time and the loss of head of the vertical filtration flow, taking into account the filtration coefficient. Assessment of the infiltration efficiency of a rain garden, calculation of its area about the corresponding area of the catchment surface, and selection of the optimal thickness of the layers are important tasks in the decision-making process to solve the problems of urban rainwater management. The practical significance of the study is to expand the possibilities for calculating rainwater flow and its outflow from the system when designing rain gardens, which, in turn, will increase the efficiency of their operation.
2. Materials and Methods
2.1. Rain Event
A rain garden is designed for a large or intense number of rain events, so conventional methods developed for average rainfall events are not suitable for rain garden design. It is recommended that extreme rainfall events should be considered for the dynamic analysis of the parameters to be considered in the design phase of rain gardens, and the structure should be sized to retain at least 80% of the local distribution of rainfall depth [58].
The rain event used to test the developed model was simulated based on the data obtained from the meteorological station of the Borys Sreznevsky Central Geophysical Observatory. For example, on 22 July 2023, a record rainfall of 36 mm/h or 0.00001 m/s was recorded in Kyiv (Ukraine), a record for the last 16 years. Specific data for this rainfall event are not available. Typically, intense rains in the temperate climate of Ukraine do not last more than an hour, so we assumed the duration of the rain event to be 3600 s. It was necessary to model the non-stationary mode of the infiltration process from the beginning to the end of the rain, including the full rise–peak–decline process over time. At the input to the mathematical model, the inflow of rainwater, which is variable in time, is set by Figure 1.
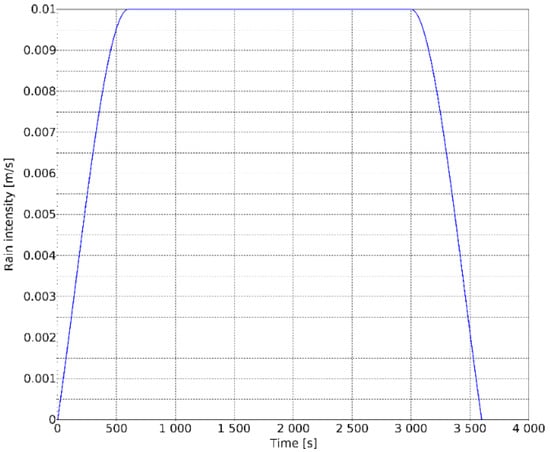
Figure 1.
The curve of rain intensity changes over time.
The onset and cessation of rain were assumed to ensure a smooth curve within 5 min. The nodal points were (0;0), (600;0.01), (3000;0.01) and (3600;0). A Hermite spline was applied to these nodal points using the monotone algorithm in Scilab software. This is an open-source numerical algebra system that has been successfully used to solve most mathematical problems related to matrices, numerical methods, etc. [59]. It ensures that there are no additional oscillations and provides a straight horizontal line if two points have the same ordinate. The resulting spline is smooth.
Using the example of an experimental setup that simulates the design of rain gardens in the laboratory (Figure 2), we determined the value of the water retention capacity, which is important for planning, designing, and simulating rain garden structures.
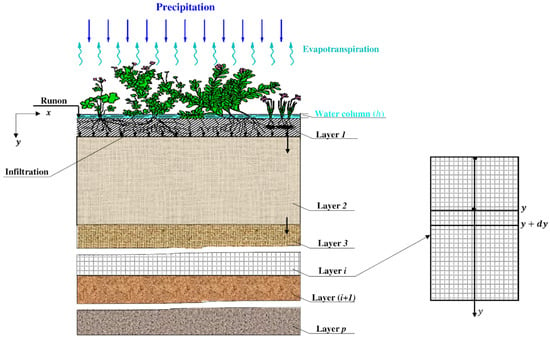
Figure 2.
Conceptual diagram of the rain garden and associated water flows.
2.2. Hydrological Model
Infiltration laws are effective in saturated layers of a structure, while diffusion laws are manifested in unsaturated layers [60]. Therefore, when simulating the hydrological process of the upper layer, it is important to take into account diffusion processes, particularly saturation processes.
To write the differential equations, an infinitely thin layer of soil or substrate (Figure 2) was identified between the levels and . Rainwater flows from the catchment basin, with area , m2, to the upper surface of the rain garden structure, with an average flow rate , m/s.
For simplicity, we assume that the water is immediately evenly distributed over the entire area of the rain garden, as a sponge, , m2. Otherwise, you will have to use computational fluid dynamics programs to calculate flows in two phases.
Between the soil layers, first, there is saturation with water at the level of , m, with an increase in moisture content , m3/m3 to the saturated state , m3/m3 without flow advancement, and then the flow transits through the saturated layers without changing the velocity, according to the continuity equation. Thus, the problem is simplified to a one-dimensional one.
According to Darcy’s law [61], the head loss of the vertical infiltration flow is described using the filtration coefficient , which varies along in a stepwise manner, according to the layers:
The process of passage-saturation of the soil layer with water is described by the following equation:
The physical meaning of the equation is as follows: the rate of water flow through already saturated soil layers is equal to the rate of water flow through the soil surface. The first equation of the system is equal to the rate of water inflow to the area of the rain garden structure, taking into account both the rainfall and runoff from the entire catchment area. Saturation occurs in an infinitesimally thin layer, with a thickness , so it is almost instantaneous. This means that the front between the saturated and unsaturated parts of the soil moves at a speed , as described in the second equation of the system. In the unsaturated part, there is no water movement, i.e., = 0.
From Formulas (1) and (2) we have the following:
We integrate the transmission–saturation equation from the outer surface to the level :
or
Hence, we determine the position of at the moment of time :
Any multilayer structure can be represented as a single-layer structure with a variable saturation function , in which case the sum loses its meaning, and Equation (6) takes on the following form:
Formula (7) is simplified compared to (6) if we accept a spatial grid according to the layers of the structure without dividing them, which is convenient for engineering problems of calculating the time of filling the structure with water but subject to the approximation of the rain rate function, for example, by the Hermite spline [62]. In this case, it is necessary to plot this spline and make sure that there are no additional oscillations. Such an approximation avoids the numerical integration of tabular data, which greatly simplifies the implementation of the program. The disadvantage of the polynomial and polynomial–spline approximations is the possibility of oscillations, i.e., fluctuations in the approximation curve that do not correspond to the physical content and occur as artifacts. This problem can be avoided only by reducing the degree of smoothness of the approximation (the «monotone» algorithm) or by increasing the degree with the selection of additional unknowns, which, in both cases, complicates the problem. Therefore, it is advisable to plot the spline and make sure that there are no additional oscillations. Additionally, only if they are present can the above methods be applied.
Integrate Darcy’s law from level in layer to level in layer :
After the transformation and integration of the pressure loss between the levels and , we obtain the following:
To integrate from the free surface = 0 to the current level = in the current layer :
Bernoulli equation between levels and for the zero level at :
where is the excess static pressure head, which characterizes the specific potential pressure energy at a given point (at a given level); the sum of is the total hydrostatic or simply static head, which expresses the total specific potential energy at a given point (at a given level); and is the velocity or dynamic head, which characterizes the kinetic energy at a given point (at a given level).
We move on to the excess static pressure , Pa, above atmospheric pressure by subtracting the atmospheric pressure , Pa, divided by , from both parts of the equation. We have the following:
At the level , there is complete absorption of water with no downward movement, and at an infinitesimal downward distance, there is no water. Therefore, = 0. The static pressure at = 0 is found from the Bernoulli equation for the layer below the top layer of the water column and for y with zero level. At this level, there is no static pressure and no head loss in the free column, so it can be written as follows:
Bernoulli’s equation for the rain garden structure from the upper boundary to the current coordinate after removing the same dynamic head on both sides:
After the transformations with the substitution of Equation (10), we have the following:
If , then the excess static pressure in section y is zero, due to the absence of water under this section. We have the following:
If all layers are saturated, the rate of water infiltration into the soil or drainage, , m/s, is determined accordingly:
The value of can be changed until the rain event is completely over.
The water flow rate (m3/s) will be defined as follows:
When a rainfall event occurs, some of the water becomes surface runoff and flows toward the rain garden structure, penetrating the layers. Provided that the rate of inflow exceeds the infiltration capacity of the rain garden layers, a water column level appears in the depression on the surface of the rain garden. During an intense rainfall event, the surface depression can be filled with water, and the excess water is discharged as an overflow. Infiltration occurs whenever there is an inflow or water column level in the rain garden structure.
If the rain intensity during a rain event can be well approximated by a function, then the grid spacing is not essential. Otherwise, the grid spacing should correspond to the meteorological data recording spacing. Additionally, the smaller the grid step, the more accurate the result will be.
For each grid step (between nodes), we used Equation (7) in the following form:
Provided that is in the next layer, the sum of the thicknesses of the layers from the soil level to the current layer inclusive is substituted into Equations (2) and (18) instead of , and the equation is solved concerning .
Thus, we obtain the time at which the saturation depth crosses the layer boundary, and then Equation (7) takes the following form:
The process continues until the entire thickness of the layers is covered. If exceeds the thickness of the rain garden structure, then at time the structure will be filled with water. The depth of filling will be determined by the total thickness of all layers, and the velocity will be determined by Formula (8).
2.3. Algorithm and Software
Using Equations (1)–(20), an algorithm for the simulation of water retention and transmission by sponge facilities has been developed. After the beginning of the algorithm (block 1) in Figure A1 Appendix A, the data are entered according to the list and description in block 2. Next, the results and service variables are initialized in block 3. By default, time TauFil is assumed to be insufficient to fill the entire structure. We start from the top level of the structure (y = 0). Thus, we should assign the number of the current layer j = 1 for the first layer from which the filling started. The number of layers is accepted to correspond to the number of rows in the Layers matrix. The Ab_As_wsat parameter is calculated by dividing the ratio of the areas (in the program, the Ab_As variable) by the water holding capacity wsati. The last is selected from the Layers matrix as the first row of the second column. The total thickness is taken as the thickness of the first layer since it is the only one used at the beginning. Next, we start the loop (block 4) through the nodes of the time grid. Since the state is assumed to be dry at the beginning of time, the first node already contains the correct depth value y = 0. Therefore, we start the loop from the second node. The depth value at the current time step y(i) is calculated (block 6) based on the known value at the previous time step y(i−1) and the increment of this depth using Formula (7). It is necessary to check (block 6) whether the layer boundary has been crossed. If the boundary has not been crossed (“−”), then it is possible to continue the loop to the next time grid node.
If the boundary has been crossed (“+”), the equation by the water saturation depth (y) of the layer boundary structure (TotalTh) should be solved (block 7). The equation is solved relative to the time taucr. As an initial approximation, we take the arithmetic mean between the time of the given node (taus(i)) and the previous one (taus(i−1)). The equation can be solved using various numerical methods. In this paper, the solve function in the Scilab system. To do this, a subroutine is created—blocks A–E—which will be discussed below.
After that, the next layer, j+1, should be accepted as the current one j (block 8). Now, it is necessary to check (block 9) whether we have not gone beyond the structure. If the structure is filled (“+”), then all subsequent mesh nodes should be filled with the total depth of the structure, which automatically appears in the TotalTh variable as the sum of the thicknesses of all layers. The time of filling is taken as the critical time of crossing the boundary of the last layer. Finally, the algorithm returns the data, as described in block 11, and finishes (block 12).
If the entire depth of the structure (“−”) is not reached in block 9, then the algorithm determines a new value of the Ab_As_wsat parameter (block 13) by dividing the ratio of the areas (in the program, the Ab_As variable) by the water-holding capacity wsati, which is selected from the Layers matrix as the j-th row, second column. The structure’s water saturation depth at the current time node should be determined (block 14). The depth of immersion at time taucr corresponds to the value of the TotalTh variable, so this depth is defined as the sum of the value of the TotalTh variable and the increment of this depth from time taucr to the current time node using Formula (7).
After that, the total thickness of the layers involved is changed by adding the thickness of the new current layer j to it (block 15). After that, the loop (block 4) should be continued. If all the nodes are calculated, then the program jumps to the data output in block 11.
The equation in block 7 is written as a separate subroutine. After it is run at block A, the program takes all data described in block B as arguments. Next, the deviation of the equation is calculated as the difference between the water saturation depth of the structure if the current layer is continued without restrictions, and the total thickness of the involved layers (Block C). As the equations are solved, this deviation will decrease to a negligible value close to zero. The function returns (block D) this deviation and the execution returns (block E) to the point of the function call. The algorithms of the functions that perform the numerical solution are not given in this paper nor are they give in the integration algorithm because computer algebra systems have such built-in functions.
2.4. Water Retention Capacity of Soil Materials
The hydraulic characteristics of soil materials used in multilayer rain gardens are important indicators of their rainwater retention efficiency. One of the key parameters of the developed hydrological infiltration model is the water-holding capacity of the soil. This parameter determines how much water a soil material can hold per unit mass before water begins to infiltrate or leak out of the system. The value of the soil’s water-holding capacity has a direct impact on the ability of the rain garden to control water flows and reduce the risk of overflow or flooding. To verify the correctness of the proposed model, it was necessary to know the value of the water retention capacity for each layer of the structure. This parameter is not a constant physical quantity, so models that use a fixed value may describe hydrological processes incorrectly. Using the example of experimental columns that simulate the design of rain gardens in the laboratory (Figure 3), the value of the water-holding capacity of soil materials was determined.

Figure 3.
Laboratory samples of rain garden design.
The experimental setup was constructed in the form of cylindrical columns using transparent PVC materials, 100 mm in diameter, to create economical and compact samples with a diameter that would limit the potential edge effect and dispersion in the columns [63]. Typical rain garden designs typically use a mixture of 10–15% gravel by volume, 50% construction or river sand, 20–30% topsoil, and 20–30% mulch [64]. The bulk layers in our samples (in the sequence from top to bottom) were as follows: 330 mm of soil, 330 mm of sand, and 180 mm of gravel. Since the main functions of the mulch layer in rain garden designs are to inhibit weed growth, increase the moisture supply to plants, and reduce the risk of waterlogging of the soil environment [10], we decided to neglect this layer in the laboratory.
The water holding capacity was determined using the method proposed by Bernard [65] and validated by Nelson [66] using a funnel and filter paper after 2 h of gravity drainage from a saturated sample. This method is sometimes referred to as «gravity-drained» or «container capacity» [67]. In this method, soil samples were placed in a 100 cm3 funnel with filter paper placed at the bottom. The funnel was placed on top of a 500 cm3 graduated cylinder. To each sample, 100 cm3 of water was added and left for 72 h to allow the water to drain. The water retention capacity () was determined as the difference between the amount of water added to the funnel and the amount of water collected in the cylinder after 72 h.
3. Results and Discussion
The experimentally determined values of water holding capacity were as follows: topsoil: = 0.33 m3/m3; intermediate/infiltration sand layer: = 0.31 m3/m3; and bottom gravel layer: = 0.1 m3/m3.
Similar soil materials were chosen by the authors for the implementation of the urban rain garden in Taipei (Taiwan) [68]. According to the results of the study and taking into account climatic conditions, the authors established the value of the water-holding capacity of the layers of the structure, which ranges from 28.2% to 41.0%. In another study [69], the water-holding capacity of environments similar to ours was measured at 24.3% to 40.5%, which correlates with our values, depending on the type of soil mixtures.
Using the developed model, the selected rain event, and the Scilab software, at the given values of the water-holding capacity of the loose layers of the rain garden (0.33/0.33/0.1 m3/m3), the hydrological efficiency of the structure was calculated, depending on the change in the thickness of the layers, and the optimal ratio of areas was proposed, at which the rain garden structure completely retains water runoff at a given rainfall intensity.
Table 2 shows the critical values of the ratio of areas , at which there is a complete saturation of all layers of the structure with water for the corresponding time with a change in the value of and constant values of , , , and , which allows us to predict the degree of water retention efficiency of a rain garden.

Table 2.
Dependence of the rainwater retention efficiency of the rain garden structure on changes in the thickness of the top layer for planting , m.
The topsoil for planting is a mixture of soil, sand, sandy loam, or loam, with a thickness in the average range of 10–60 cm. The results show that an increase in the thickness of the top layer by 10 cm allows for achieving the optimal value of the area ratio, and therefore, the area of the rain garden structure, which, according to recommendations [17], should be within 4–7% of the area of the territory from which runoff will be collected (catchment area). For example, if the catchment area is 100 m2, the optimal value of the rain garden construction area will be 7 m2, which can be achieved for a given intensity of the rain event with a layer thickness of 0.6/0.7/0.3 m. In this case, the rain garden will be filled with water in 3511.9 s without overflowing the structure (Figure 4). Each curve consists of four segments. The first segment corresponds to the saturation of the upper soil layer (the segment is curved and starts from 0). The second segment corresponds to the saturation of the second layer of the structure. Due to the small difference in water retention capacity, the fracture is almost invisible. The third segment corresponds to the saturation of the lowest layer. Due to the significant difference in water-holding capacity, the fracture is visible. The fourth segment is horizontal and corresponds to the complete saturation of all layers. Since the ratio of areas was taken in increments of 0.1, it is impossible to accurately guess this ratio because the structure is filled at the last second. Therefore, a ratio was assumed at which the rain garden still leaks water, and when one-tenth is added, it is underfilled. This leads to an error of up to 1% in the value of the area ratio, and the water loss is no more than 0.82% of the total water loss of the rain event.
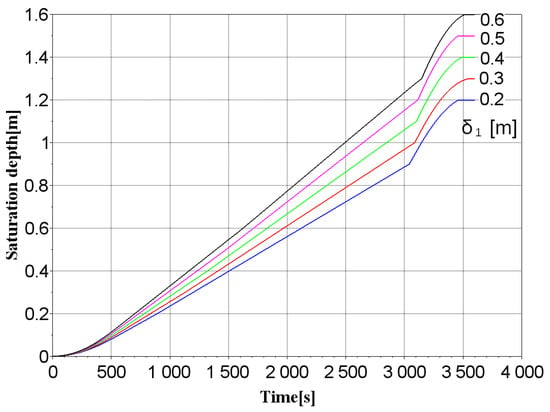
Figure 4.
Curves of changes in the depth of saturation of the layers of the rain garden structure over time depending on the thickness of the top layer for planting , m.
It is worth emphasizing that this is a calculation of the stormwater retention efficiency of a rain garden for the extreme case when the rain intensity is 36 mm/h or 0.00001 m/h. Typically, precipitation of this intensity, which lasts for almost a day, causes localized flooding in cities. In the case of this rain event, this phenomenon was not observed, as the precipitation, despite its high intensity, was not of a significant duration. Usually, the intensity of a rain event in Kyiv is 5–10 mm/h; therefore, the calculated parameters of the rain garden design can be even more effective.
The parameters describing the dependence of the rainwater retention efficiency of the rain garden structure on the thickness of the infiltration layer are given in Table 3. The infiltration layer is designed to increase the permeability of the upper soil layer and usually consists of fine gravel or coarse sand; in addition to being well drained, it must be strong enough to support the weight of the upper layers. The porosity should be, on average, 20–40% [70] and the layer depth should be 20–120 cm [10].

Table 3.
Dependence of the rainwater retention efficiency of a rain garden structure on changes in the thickness of the infiltration layer , m.
We increased the thickness of the infiltration layer in 10 cm increments. As can be seen from the simulation results, by increasing the value of , it is possible to adjust the optimal values of the area ratio and select the appropriate area of the rain garden structure. For example, for variant 5, with a layer thickness of 0.4/0.7/0.3 m, the complete saturation of the structure occurs within a time of τ = 3487 s (Figure 5). In this case, the size of the structure’s area is 8.2% of the catchment area, which can also be considered an effective indicator, according to the recommendations of [18], which suggest a range of 5–10%.
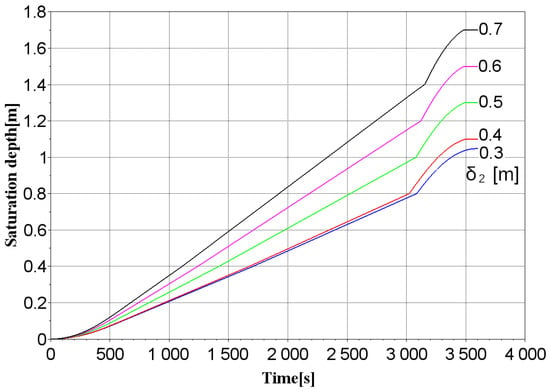
Figure 5.
Curves of changes in the depth of saturation of the layers of the rain garden structure in time depending on the thickness of the infiltration layer , m.
The developed model was also used to test the dependence of the rainwater retention efficiency of the rain garden structure on changes in the thickness of the gravel layer (Table 4).

Table 4.
Dependence of rainwater retention efficiency of a rain garden structure on changes in the thickness of the gravel layer , m.
The bottom gravel layer consists of medium or coarse gravel and is designed to retain and temporarily store water with subsequent discharge either to groundwater or to the drainage system. The thickness of the gravel layer is calculated by the density of the infiltration layer but is not less than 30 cm [71]. Therefore, similarly to the previous results, we changed the thickness of by 10 cm with the given values of = 0.4 m and = 0.7 m. As can be seen from the parameters shown in Table 3, the change in the value of the area ratio with the increase in occurs in small increments compared to the cases when we adjusted the values of and . Thus, for variant 5, the complete water saturation of a structure with an area of 7.8 m2 and a catchment area of 100 m2 occurs within 3547.8 s (Figure 6).
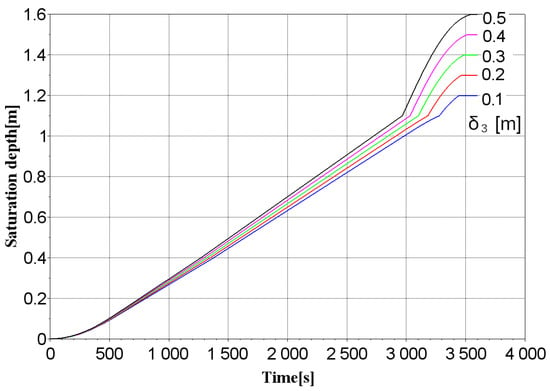
Figure 6.
Curves of changes in the depth of saturation of the layers of the rain garden structure in time depending on the thickness of the gravel layer , m.
This allows us to conclude that adjusting the thickness of the gravel layer is not an effective method of achieving the required level of rainwater retention efficiency in terms of the rain garden structure. This can be explained by the fact that the value of the water-holding capacity of gravel ( = 0.1 m3/m3) is negligible compared to the values of and , and it is intended primarily for temporary water storage. The gravel layer can contain drainage pipes and tanks for accumulating water diverted from the system, which can be used as technical water for domestic needs (if the rain garden is located near residential buildings), for washing cars (if the rain garden is located near service stations and petrol stations), for irrigation and irrigation of areas with green spaces on main streets where water supply is limited (if the rain garden is located along highways).
Therefore, a critical function of rain garden design is the ability to increase the rate of water infiltration underground. As can be seen from the results obtained, the design of each layer and the properties of the materials are important parameters that directly affect the hydrological performance of the rain garden and, consequently, the degree of effectiveness of stormwater management. Various designs have been described in the literature; for example, Australian guidelines [72] recommend the following layer sizes: topsoil for planting 0.3 m, transition layer 0.1 m, gravel layer 0.3–0.4 m. Two variants of a rain garden for rainwater management in Chiang Mai (Thailand) were developed in [10]: (1) topsoil for planting 0.6 m, transition layer 0.3 m, gravel layer 0.4 m; (2) topsoil for planting 0.4 m, transition layer 0.7 m, gravel layer 0.2 m. The materials for the structures are soil mixed with sandy loam (top layer), sand (infiltration layer), and gravel (storage layer). Therefore, we assumed the water-holding capacity of each layer to be similar to our calculations.
Using the hydrological model developed within the framework of the study, the effectiveness of rain garden designs proposed in the literature was tested, and the results obtained were compared with the authors’ conclusions. The parameters of the structures calculated by the simulation method, depending on the main values of the layers proposed in the literature, are shown in Table 5.

Table 5.
Dependence of the rainwater retention efficiency of rain gardens with the characteristics proposed in the literature.
The simulation results showed that the full saturation of the first rain garden structure begins with a threshold value corresponding to an area ratio of 5.2 for a time of τ = 3399.9 s. If, with a catchment area of 100 m2, a rain garden structure with an area of 19.2 m2 and a depth of 0.7 m is arranged, this will allow to completely retain rainfall of a given intensity while avoiding overflow of the structure. Therefore, the simulation results are consistent with the recommendations given in [72], except for the percentage of the rain garden structure area (19.2%) about the catchment area, which goes beyond the recommended values [17,18].
The height of rain garden structure 1 is 0.7 m. The ratio between the area of the catchment basin and the area of the rain garden structure as a sponge was assumed to be 1, 3, and 5, and a critical value corresponding to an area ratio of 5.2 (Figure 7).
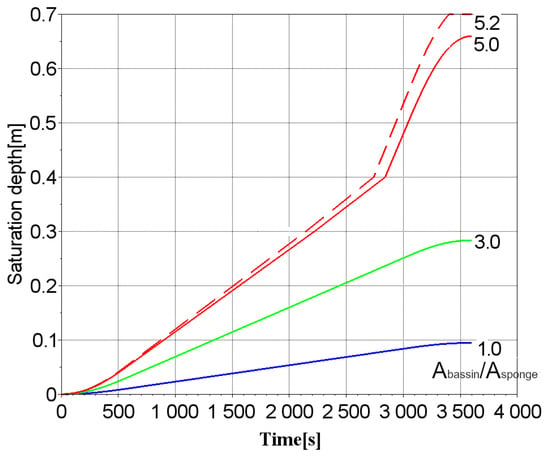
Figure 7.
Curves of changes in the depth of saturation of the layers of Design one over time depending on the ratio of areas .
The height of rain garden structures 2 and 3 is 1.3 m in each case, but with different layer thicknesses. The area ratio of the second rain garden structure was assumed to be 1, 3, 5, 7, and 10, and a critical value corresponding to the area ratio value of 10.7 (Figure 8).
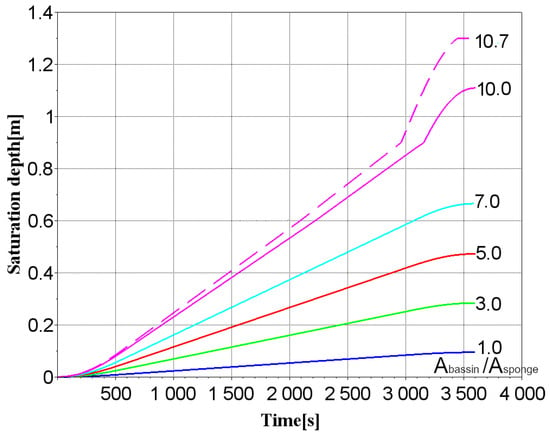
Figure 8.
Curves of changes in the depth of saturation of the layers of Design two over time depending on the ratio of areas .
According to the simulation results, the full saturation of the second rain garden structure occurs within a time of τ = 3442.3 s with an area ratio of 10.7. For example, if you install a rain garden with an area of 9.7 m2 and a depth of 1.3 m on a catchment area of 100 m2, it will effectively retain rainfall of a given intensity, preventing the structure from overflowing.
According to the simulation results, the full water saturation of the third structure occurs in 3465.6 s with an area ratio of 11.9 (Figure 9). Effective rainwater retention without overflowing the structure can be achieved by constructing a rain garden with an area of 8.4 m2 and a depth of 1.3 m.
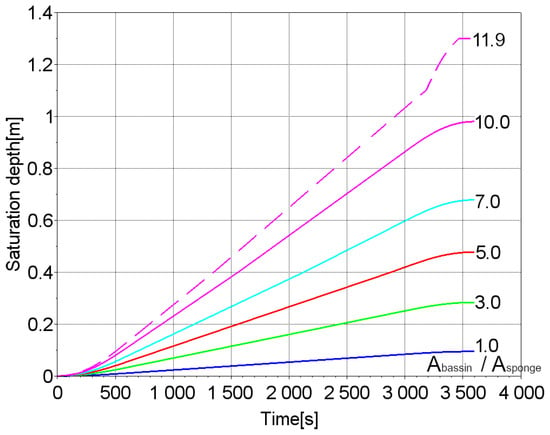
Figure 9.
Curves of changes in the depth of saturation of the layers of Design three over time depending on the ratio of areas .
As can be seen from the results obtained, with the same depth used in structures 2 and 3, complete water saturation occurs for different areas, which can be explained by the different depths of the infiltration layers, which are the main ones in the process of infiltration penetration. That is, the depth of the infiltration substrate directly affects the hydrological characteristics of rain garden systems. This conclusion is consistent with the results obtained by Li [73], who studied the effect of the depth of the infiltration substrate on the hydrological performance of rain gardens and determined that a greater substrate depth (1.2 m) corresponds to a water retention volume of 80%, while a smaller media depth (0.5–0.6 m) is only 44% effective. The results obtained in [10] showed that the efficiency of rainwater harvesting in variant 2 was high, but variant 3 was more efficient, which also fully coincides with our findings.
A similar study was carried out by Makbul and Desi [74], who devoted their work to the development of a rain garden model for the treatment of greywater in residential areas of Makassar. According to the authors’ research, the time required to fill layers of a rain garden structure that is 0.8 m wide and 1.2 m deep was 105 s at a flow rate of = 0.3 m3/s, while the infiltration rate was set to 0.009142857 m3/s. These results are comparable to those obtained in our work if we recalculate the water flow rate from 0.3 m/s to 0.00001 m/s.
The simulation results of the hydrological processes in rain garden structures with different layer thicknesses show that the ratio of areas and the thickness of the structure’s layers directly affect the rate and time of full saturation, demonstrating the different efficiencies of the rain garden structures.
This is due to the fact that by increasing the thickness of the rain garden layers, the value of the ratio of the areas () increases accordingly. The intensity of water flow through the system increases, which leads to a reduction in the time required to completely fill the structure. Thus, changes in the main parameters of the model directly affect the hydrological behavior of the rain garden structure. This is confirmed by the results of the calculations within this work and those presented in the literature.
In a study [38], the numerical model Recharge was used to simulate the hydrological characteristics of a rain garden in the tropical climate of Singapore for six months, which covered 80 rain events. The simulation results, compared to field studies, showed that the performance of the design increases with increasing system depth (above 0.4 m), decreasing area ratio (below 20), or increasing hydraulic conductivity (above 10 cm/h). The modeling error in the study was 5.1 ± 7.5% for each rain event and 0.3% in general.
Other authors [75] investigated the effectiveness of rain gardens with different area ratios (10, 15, and 20). The study was conducted on the campus of the University of Padua in Italy. The test results showed that even in rain gardens with the smallest area ratio (10), almost the entire volume of runoff from the catchment successfully penetrates the soil.
These studies, as well as the results of the simulation in this article, confirm that during high-intensity rainfall, a column of water is formed in the rain garden structure, which causes active passage and saturation of the layers with water, starting from the top down and the center to the perimeter zone. On the other hand, the authors of [76] showed that rain gardens can support the operation of insufficient sewerage infrastructure, especially during medium-intensity rain events (15–20 mm/h).
Similar to our model, the authors of [77] developed a simplified hydrological infiltration model for a rain garden based on the Darcy equation. The model takes into account such factors as evaporation, overflow, infiltration in the system, exfiltration into the surrounding soil, and water removal through drainage. Field data from a controlled rain garden design in Melbourne, Australia, were used to test the model’s performance. The test results were based on 22 rain events: two events were used for calibration and twenty for validation. The modeled runoff infiltration rates and their temporal dynamics were well reproduced. However, there was some discrepancy between the modeled and measured water levels. In addition, the model did not allow for a description of the dynamics of water levels in the rain garden structure. The authors concluded that to improve the model, it is necessary to take into account additional hydrodynamic parameters of the soil (e.g., water holding capacity) that allow for a more accurate description of the infiltration process, which was achieved within our model.
Our research, as well as the research of other authors, confirms that the study of the functional features of a rain garden is an important aspect of engineering practice, allowing us to identify key factors in determining the size of the structure, as well as the physical and chemical properties of the bulk layers. The results of this study provide valuable information for urban planners and policymakers looking to implement rain gardens as part of an urban stormwater management strategy.
4. Conclusions
In this study, a universal hydrological model based on Darcy’s law was developed to describe the dynamic processes in a rain garden structure at a particular point in time. The proposed system of equations expands the possibilities for calculating rainwater flow and outflow from the system when designing rain garden structures. All rain garden structures are designed for frequent small rain events. In this study, the correctness of the developed model was verified by calculating the main hydrological parameters of rain garden structures based on a real rain event, taken as an extreme case with a maximum rainfall of 36 mm/h or 0.00001 m/s. An experiment with columns simulating rain garden structures was designed to determine the water retention capacity of the embankments used in the development of the model and its validation for a real rainfall event. The simulation results show that the time of complete saturation of rain garden structures depends on the specified parameters of structural layers and the value of the area ratio. It was found that the smaller the area of the rain garden structure compared to the area of the catchment basin, the faster it reaches its full saturation. Increasing the thickness of the layers of the rain garden structure allows for an increase in the efficiency of water retention at a lower area ratio. The main layer of the rain garden structure in the process of infiltration penetration is an intermediate infiltration layer, the adjustment of the depth of which allows for an increase in the efficiency of the entire structure. The calculations established by the developed simulation method confirm that rain gardens can help reduce stormwater runoff in urban areas by retaining water inside the layers of the rain garden, which act as reservoirs and allow water to penetrate the soil instead of flowing to the surface. The right choice of rain garden parameters allows them to retain and infiltrate almost 100% of precipitation even in extreme conditions. The proposed model is a valuable tool for understanding the hydrological processes occurring in a rain garden structure and designing efficient systems based on local climatic conditions. The results of the work will be used as a basis for the development of rain gardens, which are planned to be tested in field studies. The proposed model enables the calculation and evaluation of the impact of the main operating parameters of the rain garden design on the hydrological features of the systems. This will provide data for the design of rain gardens in real-world conditions to avoid water overflows in the structure. Further research will focus on the development of a numerical model to determine the height of the water column above the surface of the rain garden, taking into account the filtration coefficient of each layer, which is important when the area available for sponge tools is small compared to the area of the catchment. In addition, it will be necessary to investigate a series of rain events, taking into account the drying process of the upper layers, and to conduct a more in-depth study of the hydrological behavior of rain gardens, taking into account the process of evapotranspiration, which is an essential component of the water balance, as well as the influence of vegetation and the physical and chemical properties of the materials used in the construction layers.
Author Contributions
Conceptualization, M.K, T.T. and V.M.; methodology, M.K., Y.T. and V.M.; software, R.T. and V.M.; validation, T.T. and V.M.; formal analysis, Y.T. and R.T.; investigation, M.K., T.T. and V.M.; re-sources, Y.T. and R.T.; data curation, M.K., T.T. and V.M.; writing—original draft preparation, M.K., Y.T. and R.T.; writing—review and editing, Y.T. and R.T.; visualization, M.K., T.T. and V.M.; supervision, Y.T. and R.T.; project administration, M.K., Y.T. and R.T.; funding acquisition, M.K., Y.T. and R.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research is performed in the framework of the Erasmus + Programme “Multilevel Local, Nation- and Regionwide Education and Training in Climate Services, Climate Change Adaptation and Mitigation–Claimed” 619285-EPP-1-2020-1-FI-EPPKA2-CBHE-JP and the State Grant of Ministry of Education and Science of Ukraine “Creating perspective technologies of forming the safe building environment combining “green structures”, phytodesign, and engineering systems”, reg. no. 0122U001197.
Data Availability Statement
The experimental research does not have data to publicly archive yet.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
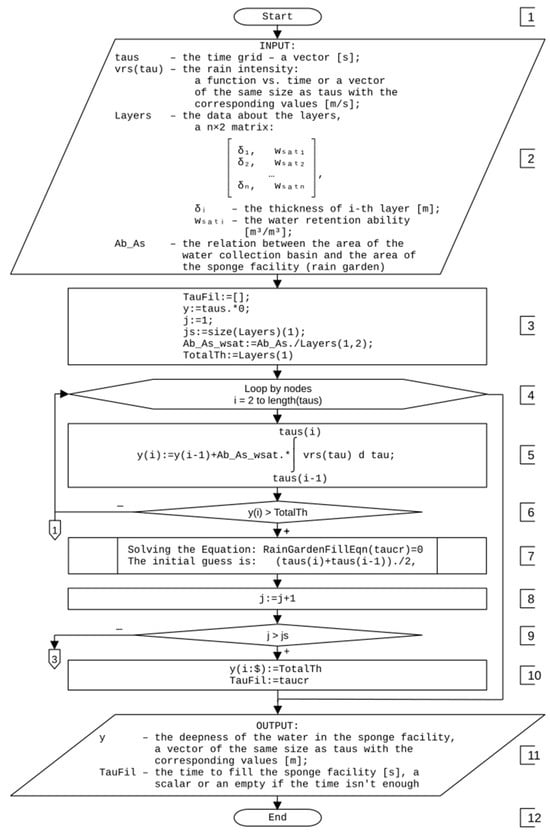
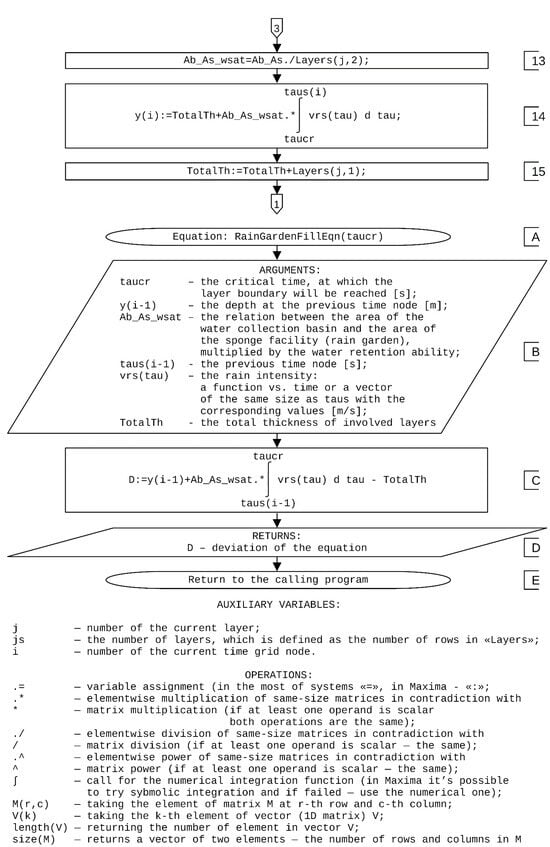
Figure A1.
Flowchart of the methodology.
References
- Coates, R. Infrastructural events? Flood disaster, narratives and framing under hazardous urbanisation. Int. J. Disaster Risk Reduct. 2022, 74, 102918. [Google Scholar] [CrossRef]
- Hlushchenko, R.; Tkachenko, T.; Mileikovskyi, V.; Kravets, V.; Tkachenko, O. “Green structures” for effective rainwater management on roads. Prod. Eng. Arch. 2022, 28, 295–299. [Google Scholar] [CrossRef]
- Katsifarakis, K.L.; Vafeiadis, M.; Theodossiou, N. Sustainable Drainage and Urban Landscape Upgrading Using Rain Gardens. Site Selection in Thessaloniki, Greece. Agric. Agric. Sci. Procedia 2015, 4, 338–347. [Google Scholar] [CrossRef][Green Version]
- Trach, R.; Lendo-Siwicka, M.; Pawluk, K.; Połoński, M. Analysis of direct rework costs in Ukrainian construction. Arch. Civ. Eng. 2021, 67, 397–411. [Google Scholar] [CrossRef]
- Martin, A.R.; Ahiablame, L.M.; Engel, B.A. Modeling low impact development in two Chicago communities. Environ. Sci. Water Res. Technol. 2015, 1, 855–864. [Google Scholar] [CrossRef]
- Qiao, X.-J.; Liao, K.-H.; Randrup, T.B. Sustainable stormwater management: A qualitative case study of the Sponge Cities initiative in China. Sustain. Cities Soc. 2020, 53, 101963. [Google Scholar] [CrossRef]
- Zhang, K.; Chui, T.F.M. A comprehensive review of spatial allocation of LID-BMP-GI practices: Strategies and optimization tools. Sci. Total Environ. 2018, 621, 915–929. [Google Scholar] [CrossRef]
- Kravchenko, M.V.; Tkachenko, T.M. Problems of Improving the Terminology and Modern Classification of “Green” Constructions for the Creation of Ukrainian “Green” Standards. Collect. Sci. Publ. NUS 2023, 493, 194–204. [Google Scholar] [CrossRef]
- Abu Deeb, S.; Tkachenko, T.; Mileikovskyi, V. Environmental Assessment of Relationships and Mutual Influences in the System “Protective Forest Plantations—Anthropogenic Landscapes. ” IOP Conf. Ser. Earth Environ. Sci. 2021, 940, 012083. [Google Scholar] [CrossRef]
- Wanitchayapaisit, C.; Suppakittpaisarn, P.; Charoenlertthanakit, N.; Surinseng, V.; Yaipimol, E.; Rinchumphu, D. Rain garden design for stormwater management in Chiang Mai, Thailand: A Research-through-Design Study. Nakhara J. Environ. Des. Plan. 2022, 21, 222. [Google Scholar] [CrossRef]
- Fassman-Beck, E.; Wang, S.; Simcock, R.; Liu, R. Assessing the Effects of Bioretention’s Engineered Media Composition and Compaction on Hydraulic Conductivity and Water Holding Capacity. J. Sustain. Water Built Environ. 2015, 1, 04015003. [Google Scholar] [CrossRef]
- Vijayaraghavan, K.; Biswal, B.K.; Adam, M.G.; Soh, S.H.; Tsen-Tieng, D.L.; Davis, A.P.; Chew, S.H.; Tan, P.Y.; Babovic, V.; Balasubramanian, R. Bioretention systems for stormwater management: Recent advances and future prospects. J. Environ. Manag. 2021, 292, 112766. [Google Scholar] [CrossRef] [PubMed]
- Sharma, R.; Malaviya, P. Management of stormwater pollution using green infrastructure: The role of rain gardens. WIREs Water 2021, 8, e1507. [Google Scholar] [CrossRef]
- Morash, J.; Wright, A.; LeBleu, C.; Meder, A.; Kessler, R.; Brantley, E.; Howe, J. Increasing Sustainability of Residential Areas Using Rain Gardens to Improve Pollutant Capture, Biodiversity and Ecosystem Resilience. Sustainability 2019, 11, 3269. [Google Scholar] [CrossRef]
- Bąk, J.; Barjenbruch, M. Benefits, Inconveniences, and Facilities of the Application of Rain Gardens in Urban Spaces from the Perspective of Climate Change—A Review. Water 2022, 14, 1153. [Google Scholar] [CrossRef]
- Home|Natural Resources Conservation Service. Available online: https://www.nrcs.usda.gov/ (accessed on 12 March 2024).
- Rinchumphu, D.; Suriyanon, N.; Phichetkunbodee, N.; Munlikawong, S.; Wanitchayapaisit, C.; Sitthikankun, S. Economics and cost effectiveness of a rain garden for flood-resistant urban design. Glob. J. Environ. Sci. Manag. 2023, 10, 1–12. [Google Scholar] [CrossRef]
- Rain Gardens. Available online: https://www.susdrain.org/delivering-suds/using-suds/suds-components/infiltration/rain-gardens.html (accessed on 12 March 2024).
- Zhou, Z.; Guo, Q. Drainage Alternatives for Rain Gardens on Subsoil of Low Permeability: Balance among Ponding Time, Soil Moisture, and Runoff Reduction. J. Sustain. Water Built Environ. 2022, 8, 05022002. [Google Scholar] [CrossRef]
- Jackisch, N.; Weiler, M. The hydrologic outcome of a Low Impact Development (LID) site including superposition with streamflow peaks. Urban Water J. 2017, 14, 143–159. [Google Scholar] [CrossRef]
- Adoption Guidelines for Stormwater Biofiltration Systems: Cities as Water Supply Catchments—Sustainable Technologies—CRC for Water Sensitive Cities. Available online: https://watersensitivecities.org.au/content/stormwater-biofilter-design/ (accessed on 18 April 2024).
- MD: Prince George’s County: Bioretention Manual|PDF. Available online: https://www.slideshare.net/Sotirakou964/md-prince-georges-county-bioretention-manual (accessed on 18 April 2024).
- NJDEP|Stormwater|NJ Stormwater Best Management Practices Manual NJ Stormwater Best Management Practices Manual. Available online: https://dep.nj.gov/stormwater/bmp-manual/ (accessed on 18 April 2024).
- DOVER TOWNSHIP—Building Futures and Creating Memories. Available online: https://www.dovertownship.org/ (accessed on 18 April 2024).
- Design Criteria for Bioretention—Minnesota Stormwater Manual. Available online: https://stormwater.pca.state.mn.us/index.php/Design_criteria_for_bioretention (accessed on 18 April 2024).
- Wisconsin Department of Natural Resources. Available online: https://dnr.wisconsin.gov/ (accessed on 18 April 2024).
- Department of Irrigation and Drainage. Available online: https://www.water.gov.my/ (accessed on 18 April 2024).
- Home|PUB, Singapore’s National Water Agency. Available online: https://www.pub.gov.sg/ (accessed on 18 April 2024).
- Wang, J.; Chua, L.H.C.; Shanahan, P. Evaluation of pollutant removal efficiency of a bioretention basin and implications for stormwater management in tropical cities. Environ. Sci. Water Res. Technol. 2017, 3, 78–91. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Babovic, V.; Gin, K.Y.H. A comprehensive integrated catchment-scale monitoring and modelling approach for facilitating management of water quality. Environ. Model. Softw. 2019, 120, 104489. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, K.K. Rain garden infiltration rate modeling using gradient boosting machine and deep learning techniques. Water Sci. Technol. 2021, 84, 2366–2379. [Google Scholar] [CrossRef]
- Miller, C.T.; Williams, G.A.; Kelley, C.T.; Tocci, M.D. Robust solution of Richards’ equation for nonuniform porous media. Water Resour. Res. 1998, 34, 2599–2610. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary Conduction of Liquids Through Porous Mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Kavetski, D.; Binning, P.; Sloan, S.W. Adaptive time stepping and error control in a mass conservative numerical solution of the mixed form of Richards equation. Adv. Water Resour. 2001, 24, 595–605. [Google Scholar] [CrossRef]
- Dussaillant, A.R.; Wu, C.H.; Potter, K.W. Richards Equation Model of a Rain Garden. J. Hydrol. Eng. 2004, 9, 219–225. [Google Scholar] [CrossRef]
- Aravena, J.E.; Dussaillant, A. Storm-Water Infiltration and Focused Recharge Modeling with Finite-Volume Two-Dimensional Richards Equation: Application to an Experimental Rain Garden. J. Hydraul. Eng. 2009, 135, 1073–1080. [Google Scholar] [CrossRef]
- Roy-Poirier, A.; Filion, Y.; Champagne, P. An event-based hydrologic simulation model for bioretention systems. Water Sci. Technol. 2015, 72, 1524–1533. [Google Scholar] [CrossRef]
- Wang, J.; Chua, L.H.C.; Shanahan, P. Hydrological modeling and field validation of a bioretention basin. J. Environ. Manag. 2019, 240, 149–159. [Google Scholar] [CrossRef]
- Dussaillant, A.; Cozzetto, K.; Brander, K.; Potter, K. Green-Ampt Model of a Rain Garden and Comparison to Richards Equation Model. WIT Trans. Ecol. Environ. 2003, 67, 10. [Google Scholar] [CrossRef]
- Brown, R.A.; Skaggs, R.W.; Hunt, W.F. Calibration and validation of DRAINMOD to model bioretention hydrology. J. Hydrol. 2013, 486, 430–442. [Google Scholar] [CrossRef]
- Mein, R.G.; Larson, C.L. Modeling infiltration during a steady rain. Water Resour. Res. 1973, 9, 384–394. [Google Scholar] [CrossRef]
- Heasom, W.; Traver, R.G.; Welker, A. Hydrologic Modeling of A Bioinfiltration Best Management PracticE. J. Am. Water Resour. Assoc. 2006, 42, 1329–1347. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Li, Y. SWMM-based evaluation of the effect of rain gardens on urbanized areas. Environ. Earth Sci. 2016, 75, 17. [Google Scholar] [CrossRef]
- Poresky, A.L.; Allen, V.P.; Reynolds, S.K.; Orr, A. Biofiltration Equivalency: Assessing Relative Performance of Innovative and Conventional Designs. Proc. Water Environ. Fed. 2016, 2016, 4406–4415. [Google Scholar] [CrossRef]
- He, Z.; Davis, A.P. Process Modeling of Storm-Water Flow in a Bioretention Cell. J. Irrig. Drain. Eng. 2011, 137, 121–131. [Google Scholar] [CrossRef]
- Li, J.; Liu, F.; Li, Y. Simulation and design optimization of rain gardens via DRAINMOD and response surface methodology. J. Hydrol. 2020, 585, 124788. [Google Scholar] [CrossRef]
- Jiang, C.; Li, J.; Li, H.; Li, Y. Experiment and simulation of layered bioretention system for hydrological performance. J. Water Reuse Desalination 2019, 9, 319–329. [Google Scholar] [CrossRef]
- Li, J.; Liu, Z.; Jiang, C.; Li, Y.; Li, H.; Xia, J. Optimization design of key parameters for bioretention cells with mixed filter media via HYDRUS-1D model and regression analysis. Ecol. Eng. 2021, 164, 106206. [Google Scholar] [CrossRef]
- Stewart, R.D.; Lee, J.G.; Shuster, W.D.; Darner, R.A. Modelling hydrological response to a fully-monitored urban bioretention cell. Hydrol. Process. 2017, 31, 4626–4638. [Google Scholar] [CrossRef]
- Guo, Y.; Baetz, B.W. Sizing of Rainwater Storage Units for Green Building Applications. J. Hydrol. Eng. 2007, 12, 197–205. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, Y. Analytical Probabilistic Model for Evaluating the Hydrologic Performance of Green Roofs. J. Hydrol. Eng. 2013, 18, 19–28. [Google Scholar] [CrossRef]
- Trach, R.; Khomenko, O.; Trach, Y.; Kulikov, O.; Druzhynin, M.; Kishchak, N.; Ryzhakova, G.; Petrenko, H.; Prykhodko, D.; Obodianska, O. Application of Fuzzy Logic and SNA Tools to Assessment of Communication Quality between Construction Project Participants. Sustainability 2023, 15, 5653. [Google Scholar] [CrossRef]
- Trach, R.; Moshynskyi, V.; Chernyshev, D.; Borysyuk, O.; Trach, Y.; Striletskyi, P.; Tyvoniuk, V. Modeling the Quantitative Assessment of the Condition of Bridge Components Made of Reinforced Concrete Using ANN. Sustainability 2022, 14, 15779. [Google Scholar] [CrossRef]
- Trach, R.; Ryzhakova, G.; Trach, Y.; Shpakov, A.; Tyvoniuk, V. Modeling the Cause-and-Effect Relationships between the Causes of Damage and External Indicators of RC Elements Using ML Tools. Sustainability 2023, 15, 5250. [Google Scholar] [CrossRef]
- Kumar, M.; Sihag, P. Assessment of Infiltration Rate of Soil Using Empirical and Machine Learning-Based Models. Irrig. Drain. 2019, 68, 588–601. [Google Scholar] [CrossRef]
- Angelaki, A.; Singh Nain, S.; Singh, V.; Sihag, P. Estimation of models for cumulative infiltration of soil using machine learning methods. ISH J. Hydraul. Eng. 2021, 27, 162–169. [Google Scholar] [CrossRef]
- Sihag, P.; Singh, B.; Sepah Vand, A.; Mehdipour, V. Modeling the infiltration process with soft computing techniques. ISH J. Hydraul. Eng. 2020, 26, 138–152. [Google Scholar] [CrossRef]
- Guo, J.C.Y.; Luu, T.M. Hydrologic Model Developed for Stormwater Infiltration Practices. J. Hydrol. Eng. 2015, 20, 06015001. [Google Scholar] [CrossRef]
- Azure, I.; Wiredu, J.K.; Musah, A.; Akolgo, E. AI-Enhanced Performance Evaluation of Python, MATLAB, and Scilab for Solving Nonlinear Systems of Equations: A Comparative Study Using the Broyden Method. AJCM 2023, 13, 644–677. [Google Scholar] [CrossRef]
- Philip, J.R. Theory of Infiltration. In Advances in Hydroscience; Elsevier: Amsterdam, The Netherlands, 1969; Volume 5, pp. 215–296. ISBN 978-1-4831-9936-8. [Google Scholar] [CrossRef]
- O’Sullivan, C.; Arson, C.; Coasne, B. A Perspective on Darcy’s Law across the Scales: From Physical Foundations to Particulate Mechanics. J. Eng. Mech. 2022, 148, 04022064. [Google Scholar] [CrossRef]
- Fageot, J.; Aziznejad, S.; Unser, M.; Uhlmann, V. Support and approximation properties of Hermite splines. J. Comput. Appl. Math. 2020, 368, 112503. [Google Scholar] [CrossRef]
- Brown, R.A.; Hunt, W.F. Impacts of Media Depth on Effluent Water Quality and Hydrologic Performance of Undersized Bioretention Cells. J. Irrig. Drain. Eng. 2011, 137, 132–143. [Google Scholar] [CrossRef]
- Stormwater Management for Smart Growth; Springer-Verlag: New York, NY, USA, 2005; ISBN 978-0-387-26048-8. [CrossRef]
- Bernard, J.M. Forest Floor Moisture Capacity of the New Jersey Pine Barrens. Ecology 1963, 44, 574–576. [Google Scholar] [CrossRef]
- Nelson, J.T.; Adjuik, T.A.; Moore, E.B.; VanLoocke, A.D.; Ramirez Reyes, A.; McDaniel, M.D. A Simple, Affordable, Do-It-Yourself Method for Measuring Soil Maximum Water Holding Capacity. Commun. Soil Sci. Plant Anal. 2024, 55, 1190–1204. [Google Scholar] [CrossRef]
- Govindasamy, P.; Mahawer, S.K.; Mowrer, J.; Bagavathiannan, M.; Prasad, M.; Ramakrishnan, S.; Halli, H.M.; Kumar, S.; Chandra, A. Comparison of Low-Cost Methods for Soil Water Holding Capacity. Commun. Soil Sci. Plant Anal. 2023, 54, 287–296. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Chen, Z.-A. Water retention capacity and runoff peak flow duration of the urban food garden: A city-based model and field experiment. Ecol. Eng. 2021, 159, 106073. [Google Scholar] [CrossRef]
- Jiang, C.; Li, J.; Li, H.; Li, Y. Nitrogen retention and purification efficiency from rainfall runoff via retrofitted bioretention cells. Sep. Purif. Technol. 2019, 220, 25–32. [Google Scholar] [CrossRef]
- (PDF) The Determination of Soil Infiltration Rate of Urban Bioretention Design Process in Chiang Mai, Thailand|Damrongsak Rinchumphu—Academia.edu. Available online: https://www.academia.edu/101619693/The_Determination_of_Soil_Infiltration_Rate_of_Urban_Bioretention_Design_Process_in_Chiang_Mai_Thailand (accessed on 14 March 2024).
- Dunnett, N.; Clayden, A. Rain Gardens: Managing Water Sustainably in the Garden and Designed Landscape; Third printed; Timber Press: Portland, OR, USA, 2008; ISBN 978-0-88192-826-6. [Google Scholar]
- Request Unavailable—Melbourne Water. Available online: https://www.melbournewater.com.au/media/446/download (accessed on 12 March 2024).
- Li, H.; Sharkey, L.J.; Hunt, W.F.; Davis, A.P. Mitigation of Impervious Surface Hydrology Using Bioretention in North Carolina and Maryland. J. Hydrol. Eng. 2009, 14, 407–415. [Google Scholar] [CrossRef]
- Makbul, R.; Desi, N. Sudirman Reduction of Gray Water and Run-off in a Residential Environment with Rain Garden Model (Case Study “Settlements in Makassar City”). IOP Conf. Ser. Earth Environ. Sci. 2021, 921, 012021. [Google Scholar] [CrossRef]
- Bortolini, L.; Zanin, G. Hydrological behaviour of rain gardens and plant suitability: A study in the Veneto plain (north-eastern Italy) conditions. Urban For. Urban Green. 2018, 34, 121–133. [Google Scholar] [CrossRef]
- Basdeki, A.; Katsifarakis, L.; Katsifarakis, K.L. Rain Gardens as Integral Parts of Urban Sewage Systems-a Case Study in Thessaloniki, Greece. Procedia Eng. 2016, 162, 426–432. [Google Scholar] [CrossRef]
- Bonneau, J.; Lipeme Kouyi, G.; Lassabatere, L.; Fletcher, T.D. Field validation of a physically-based model for bioretention systems. J. Clean. Prod. 2021, 312, 127636. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).