Modeling Plant Height and Biomass Production of Cluster Bean and Sesbania across Diverse Irrigation Qualities in Pakistan’s Thar Desert
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Field Conditions
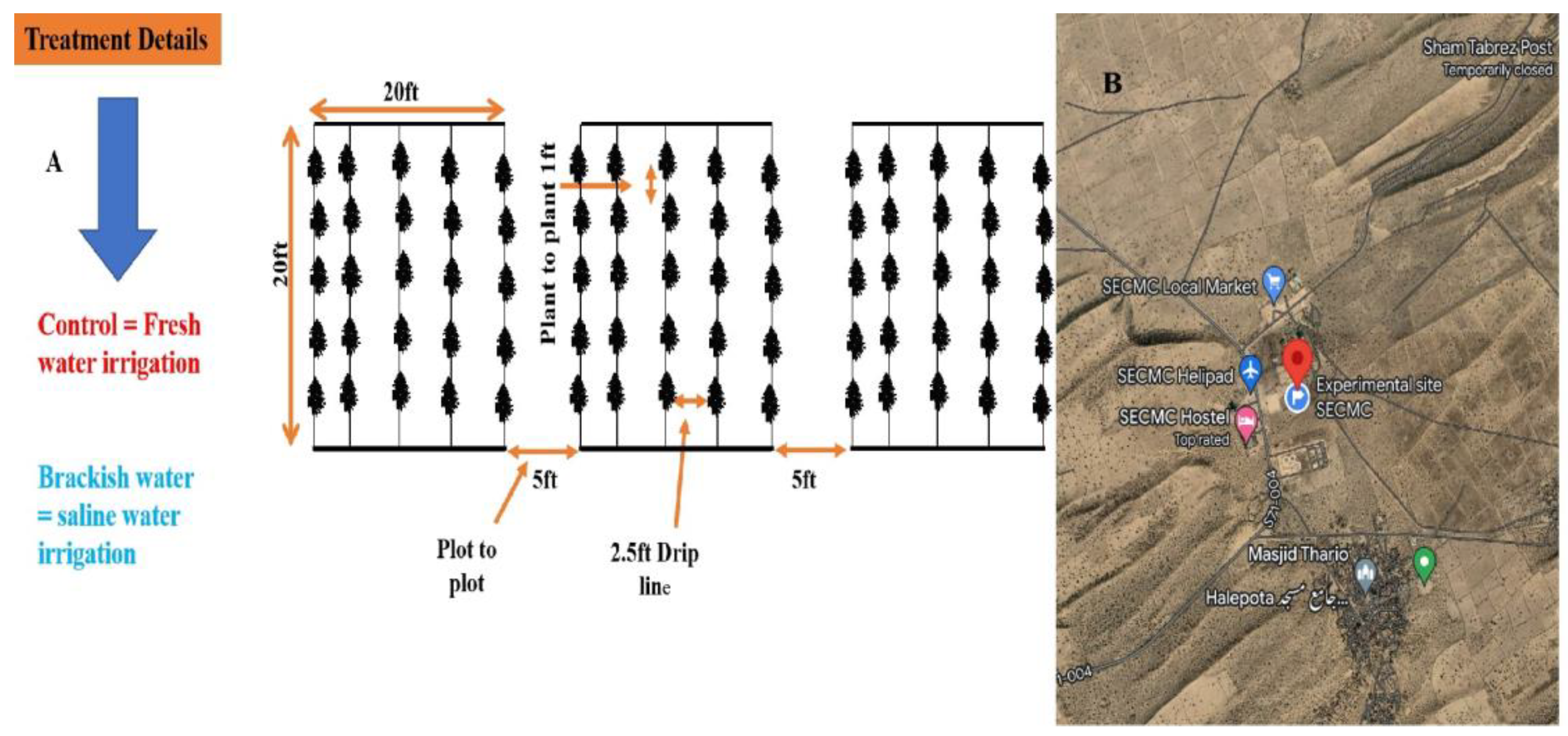
2.2. Experimental Design
2.3. Growth Trails
Calculation of GDD
2.4. Plant Height Growth Models
2.5. Statistical Analysis
3. Results and Discussion
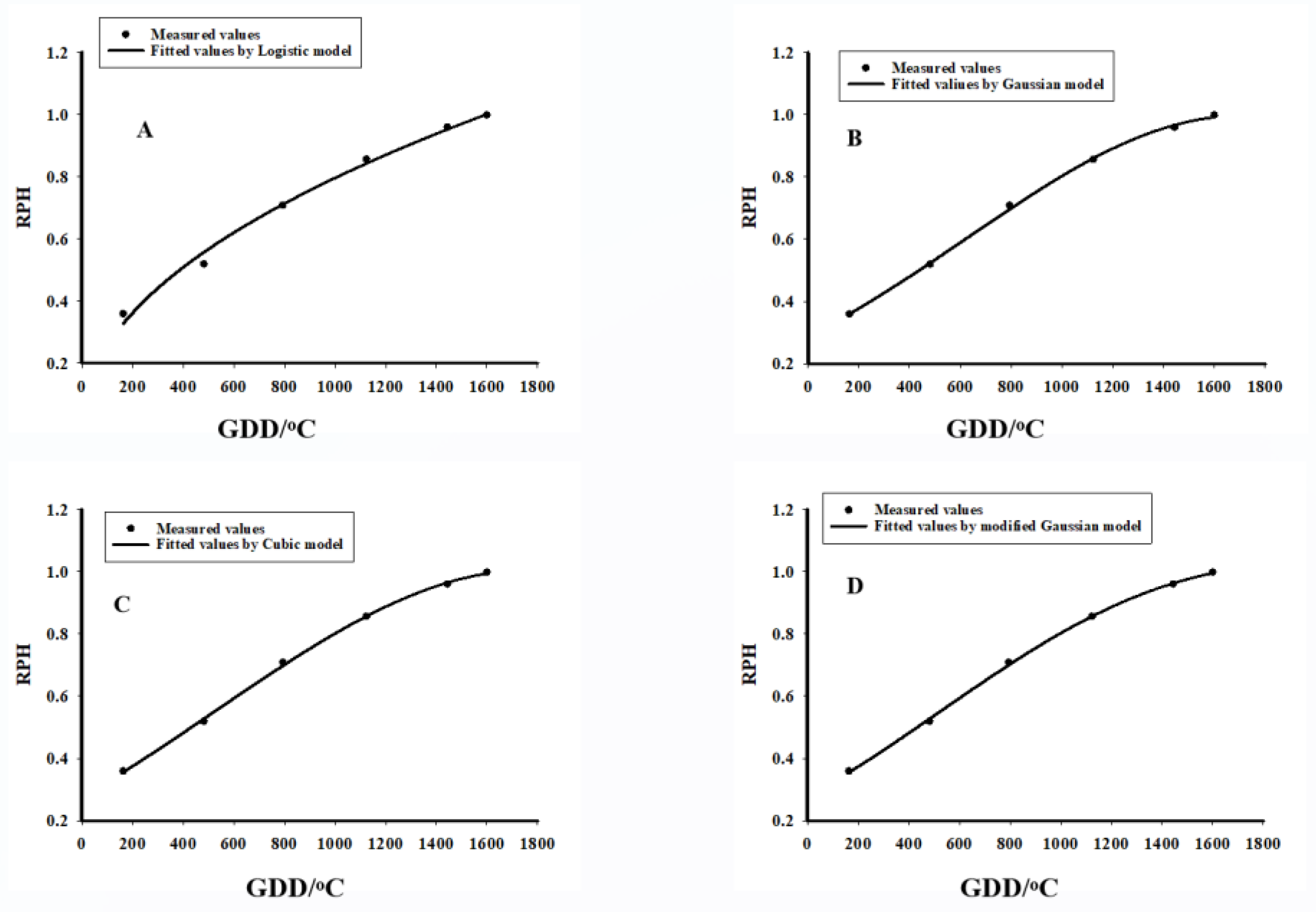
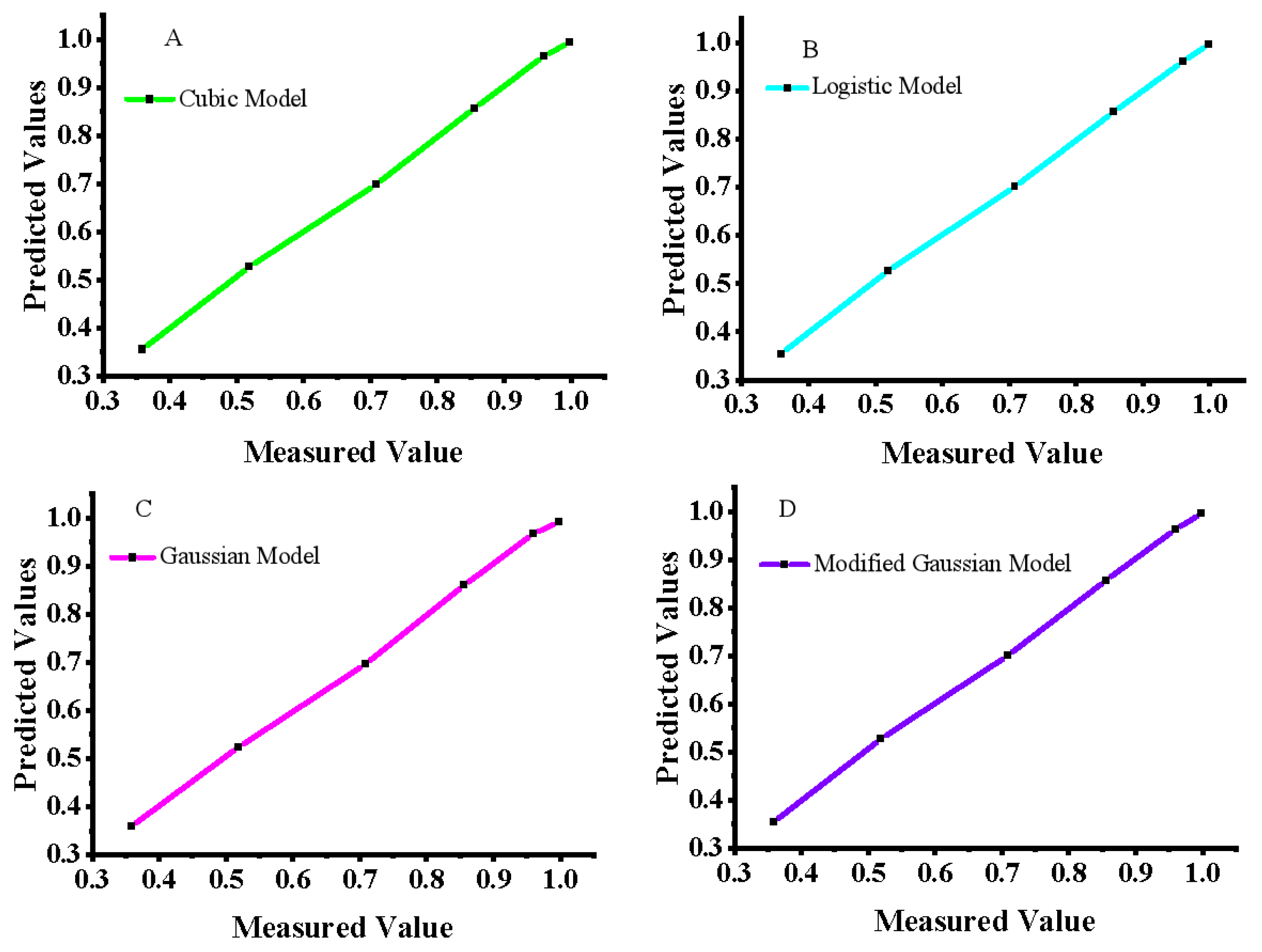
3.1. Plant Height Simulation Models
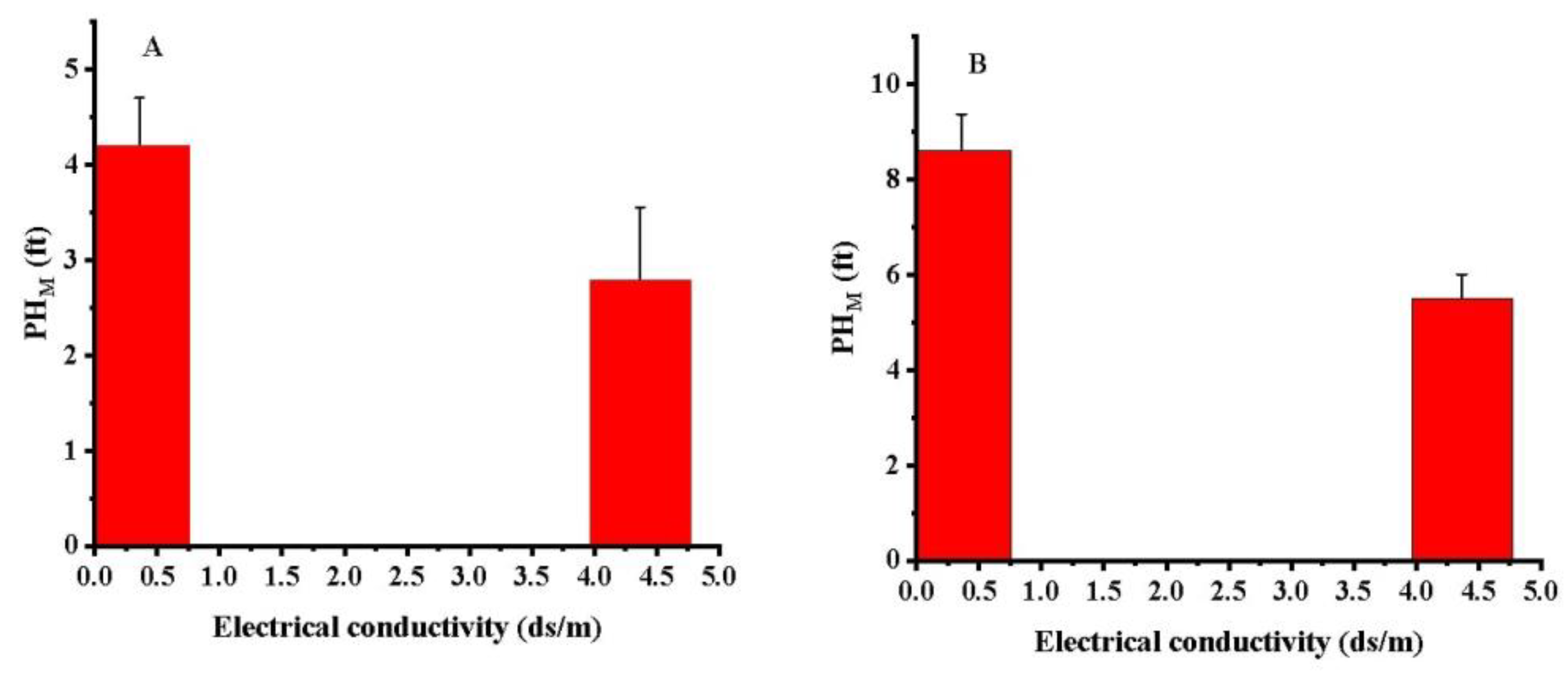
3.2. Relationship between Plant Height and Water Quality
3.3. Mathematical Models for Biomass per Plant Production
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qureshi, A.S.; Perry, C. Managing water and salt for sustainable agriculture in the Indus Basin of Pakistan. Sustainability 2021, 13, 5303. [Google Scholar] [CrossRef]
- Chandio, A.A.; Jiang, Y.; Magsi, H. Agricultural sub-sectors performance: An analysis of sector-wise share in agriculture GDP of Pakistan. Int. J. Econ. Finance 2016, 8, 156. [Google Scholar] [CrossRef]
- Rahman, S.U.; Basit, A.; Ara, N.; Ullah, I.; Rehman, A.U. Morpho-physiological responses of tomato genotypes under saline conditions. Gesunde Pflanz. 2021, 73, 541–553. [Google Scholar] [CrossRef]
- Upreti, P.; Narayan, S.; Khan, F.; Tewari, L.M.; Shirke, P.A. Drought-induced responses on physiological performance in cluster bean [Cyamopsis tetragonoloba (L.) Taub.]. Plant Physiol. Rep. 2021, 26, 49–63. [Google Scholar] [CrossRef]
- Yadav, G.; Meena, M. Bioprospecting of endophytes in medicinal plants of Thar Desert: An attractive resource for biopharmaceuticals. Biotechnol. Rep. 2021, 30, e00629. [Google Scholar] [CrossRef] [PubMed]
- Blinkhorn, J.; Achyuthan, H.; Jaiswal, M.; Singh, A.K. The first dated evidence for Middle-Late Pleistocene fluvial activity in the central Thar Desert. Quat. Sci. Rev. 2020, 250, 106656. [Google Scholar] [CrossRef]
- Samtio, M.S.; Jahangir, T.M.; Mastoi, A.S.; Lanjwani, M.F.; Rajper, R.H.; Lashari, R.A.; Agheem, M.H.; Noonari, M.W. Impact of rock-water interaction on hydrogeochemical characteristics of groundwater: Using multivariate statistical, water quality index and irrigation indices of chachro sub-district, thar desert, sindh, Pakistan. Groundw. Sustain. Dev. 2023, 20, 100878. [Google Scholar] [CrossRef]
- Azeem, A.; Javed, Q.; Sun, J.; Ullah, I.; Kama, R.; DU, D. Adaptation of singapore daisy (wedelia trilobata) to different environmental conditions; water stress, soil type and temperature. Appl. Ecol. Environ. Res. 2020, 18, 5247–5261. [Google Scholar] [CrossRef]
- Javed, Q.; Wu, Y.; Xing, D.; Ullah, I.; Azeem, A.; Rasool, G. Salt-induced effects on growth and photosynthetic traits of Orychophragmus violaceus and its restoration through re-watering. Braz. J. Bot. 2018, 41, 29–41. [Google Scholar] [CrossRef]
- Soltani, M.D.; Meftahizadeh, H.; Barani, M.; Rahdar, A.; Hosseinikhah, S.M.; Hatami, M.; Ghorbanpour, M. Guar (Cyamopsis tetragonoloba L.) plant gum: From biological applications to advanced nanomedicine. Int. J. Biol. Macromol. 2021, 193, 1972–1985. [Google Scholar] [CrossRef]
- Guo, X.; Zhu, G.; Jiao, X.; Zhou, G. Effects of nitrogen application and planting density on growth and yield of Sesbania pea grown in saline soil. Curr. Sci. 2019, 116, 758–764. [Google Scholar] [CrossRef]
- Hussain, I.; Ali, M.; Ghoneim, A.M.; Shahzad, K.; Farooq, O.; Iqbal, S.; Nawaz, F.; Ahmad, S.; Bárek, V.; Brestic, M.; et al. Improvement in growth and yield attributes of cluster bean through optimization of sowing time and plant spacing under climate change scenario. Saudi J. Biol. Sci. 2022, 29, 781–792. [Google Scholar] [CrossRef] [PubMed]
- Bunma, S.; Balslev, H. A review of the economic botany of Sesbania (Leguminosae). Bot. Rev. 2019, 85, 185–251. [Google Scholar] [CrossRef]
- Acharya, B.R.; Sandhu, D.; Dueñas, C.; Ferreira, J.F.; Grover, K.K. Deciphering molecular mechanisms involved in salinity tolerance in guar (Cyamopsis tetragonoloba (L.) Taub.) using transcriptome analyses. Plants 2022, 11, 291. [Google Scholar] [CrossRef] [PubMed]
- Garcia, A.; Grover, K.; VanLeeuwen, D.; Stringam, B.; Schutte, B. Growth and Performance of Guar (Cyamopsis tetragonoloba (L.) Taub.) Genotypes under Various Irrigation Regimes with and without Biogenic Silica Amendment in Arid Southwest US. Plants 2023, 12, 2486. [Google Scholar] [CrossRef] [PubMed]
- Uslu, O.S.; Babur, E.; Alma, M.H.; Solaiman, Z.M. Walnut shell biochar increases seed germination and early growth of seedlings of fodder crops. Agriculture 2020, 10, 427. [Google Scholar] [CrossRef]
- Amanullah; Khalid, S.; Imran; Khan, H.A.; Arif, M.; Altawaha, A.R.; Adnan, M.; Fahad, S.; Shah, A.; Parmar, B. Effects of climate change on irrigation water quality. In Environment, Climate, Plant and Vegetation Growth; Springer Nature: Cham, Switzerland, 2020; pp. 123–132. [Google Scholar] [CrossRef]
- Zhou, B.; Liang, C.; Chen, X.; Ye, S.; Peng, Y.; Yang, L.; Duan, M.; Wang, X. Magnetically-treated brackish water affects soil water-salt distribution and the growth of cotton with film mulch drip irrigation in Xinjiang, China. Agric. Water Manag. 2022, 263, 107487. [Google Scholar] [CrossRef]
- Sob, M.E. Response of okra based on electrophysiological modeling under salt stress and re-watering. Growth 2017, 1, 9. [Google Scholar]
- Azeem, A.; Javed, Q.; Sun, J.; Nawaz, M.I.; Ullah, I.; Kama, R.; Du, D. Functional traits of okra cultivars (Chinese green and Chinese red) under salt stress. Folia Hortic. 2020, 32, 159–170. [Google Scholar] [CrossRef]
- Su, L.; Tao, W.; Sun, Y.; Shan, Y.; Wang, Q. Mathematical Models of Leaf Area Index and Yield for Grapevines Grown in the Turpan Area, Xinjiang, China. Agronomy 2022, 12, 988. [Google Scholar] [CrossRef]
- Wang, K.; Su, L.; Wang, Q. Cotton growth model under drip irrigation with film mulching: A case study of Xinjiang, China. Agron. J. 2021, 113, 2417–2436. [Google Scholar] [CrossRef]
- Li, L.; Chen, S.W.; Yang, C.F.; Meng, F.J.; Sigrimis, N. Prediction of plant transpiration from environmental parameters and relative leaf area index using the random forest regression algorithm. J. Clean. Prod. 2020, 261, 121136. [Google Scholar] [CrossRef]
- Hasegawa, K.; Matsuyama, H.; Tsuzuki, H.; Sweda, T. Improving the estimation of leaf area index by using remotely sensed NDVI with BRDF signatures. Remote Sens. Environ. 2010, 114, 514–519. [Google Scholar] [CrossRef]
- Wang, H.; Sánchez-Molina, J.; Li, M.; Berenguel, M.; Yang, X.; Bienvenido, J. Leaf area index estimation for a greenhouse transpiration model using external climate conditions based on genetics algorithms, back-propagation neural networks and nonlinear autoregressive exogenous models. Agric. Water Manag. 2017, 183, 107–115. [Google Scholar] [CrossRef]
- Ishihara, M.I.; Hiura, T. Modeling leaf area index from litter collection and tree data in a deciduous broadleaf forest. Agric. For. Meteorol. 2011, 151, 1016–1022. [Google Scholar] [CrossRef]
- Liu, J.-H.; Yan, Y.; Ali, A.; Yu, M.-F.; Xu, Q.-J.; Shi, P.-J.; Chen, L. Simulation of crop growth, time to maturity and yield by an improved sigmoidal model. Sci. Rep. 2018, 8, 7030. [Google Scholar] [CrossRef] [PubMed]
- Bouras, E.H.; Olsson, P.-O.; Thapa, S.; Díaz, J.M.; Albertsson, J.; Eklundh, L. Wheat Yield Estimation at High Spatial Resolution through the Assimilation of Sentinel-2 Data into a Crop Growth Model. Remote Sens. 2023, 15, 4425. [Google Scholar] [CrossRef]
- Dong, T.; Liu, J.; Shang, J.; Qian, B.; Ma, B.; Kovacs, J.M.; Walters, D.; Jiao, X.; Geng, X.; Shi, Y. Assessment of red-edge vegetation indices for crop leaf area index estimation. Remote Sens. Environ. 2019, 222, 133–143. [Google Scholar] [CrossRef]
- Döring, J.; Stoll, M.; Kauer, R.; Frisch, M.; Tittmann, S. Indirect estimation of leaf area index in VSP-trained grapevines using plant area index. Am. J. Enol. Vitic. 2014, 65, 153–158. [Google Scholar] [CrossRef]
- Su, L.; Wang, Q.; Wang, C.; Shan, Y. Simulation models of leaf area index and yield for cotton grown with different soil conditioners. PLoS ONE 2015, 10, e0141835. [Google Scholar] [CrossRef]
- Liu, Y.; Su, L.; Wang, Q.; Zhang, J.; Shan, Y.; Deng, M. Comprehensive and quantitative analysis of growth characteristics of winter wheat in China based on growing degree days. Adv. Agron. 2020, 159, 237–273. [Google Scholar]
- Xiangxiang, W.; Quanjiu, W.; Jun, F.; Lijun, S.; Xinlei, S. Logistic model analysis of winter wheat growth on China’s Loess Plateau. Can. J. Plant Sci. 2014, 94, 1471–1479. [Google Scholar] [CrossRef]
- Fujikawa, H.; Kai, A.; Morozumi, S. A new logistic model for Escherichia coli growth at constant and dynamic temperatures. Food Microbiol. 2004, 21, 501–509. [Google Scholar] [CrossRef]
- Sharma, A.; Deepa, R.; Sankar, S.; Pryor, M.; Stewart, B.; Johnson, E.; Anandhi, A. Use of growing degree indicator for developing adaptive responses: A case study of cotton in Florida. Ecol. Indic. 2021, 124, 107383. [Google Scholar] [CrossRef]
- Wypych, A.; Sulikowska, A.; Ustrnul, Z.; Czekierda, D. Variability of growing degree days in Poland in response to ongoing climate changes in Europe. Int. J. Biometeorol. 2017, 61, 49–59. [Google Scholar] [CrossRef] [PubMed]
- Boschetti, M.; Stroppiana, D.; Brivio, P.A.; Bocchi, S. Multi-year monitoring of rice crop phenology through time series analysis of MODIS images. Int. J. Remote Sens. 2009, 30, 4643–4662. [Google Scholar] [CrossRef]
- Liu, F.; Liu, Y.; Su, L.; Tao, W.; Wang, Q.; Deng, M. Integrated growth model of typical crops in China with regional parameters. Water 2022, 14, 1139. [Google Scholar] [CrossRef]
- Overman, A.R. Rational basis for the logistic model for forage grasses. J. Plant Nutr. 1995, 18, 995–1012. [Google Scholar] [CrossRef]
- Overman, A.R.; Wilkinson, S.R. Extended logistic model of forage grass response to applied nitrogen as affected by soil erosion. Trans. ASAE 2003, 46, 1375. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, L.; Bai, Y.; Lu, Y.; Ni, L.; Wang, Y.; Xu, M. Quantitative relationship between effective accumulated temperature and plant height & leaf area index of summer maize under different nitrogen, phosphorus and potassium levels. Phosphorus and Potassium Levels. Sci. Agric. Sin. 2021, 54, 4761–4777. [Google Scholar]
- Sui, M.; Chen, K.; Shen, F. Monitoring of wheat height based on multi-GNSS reflected signals. Remote Sens. 2022, 14, 4955. [Google Scholar] [CrossRef]
- Azeem, A.; Sun, J.; Javed, Q.; Jabran, K.; Saifullah, M.; Huang, Y.; Du, D. Water deficiency with nitrogen enrichment makes Wedelia trilobata to become weak competitor under competition. Int. J. Environ. Sci. Technol. 2021, 19, 319–326. [Google Scholar] [CrossRef]
- Azeem, A.; Wu, Y.; Xing, D.; Javed, Q.; Ullah, I. Photosynthetic response of two okra cultivars under salt stress and re-watering. J. Plant Interact. 2017, 12, 67–77. [Google Scholar] [CrossRef]
- Zhu, G.; Xu, Y.; Xu, Z.; Ahmad, I.; Nimir, N.E.A.; Zhou, G. Improving productivity of Sesbania pea in saline soils by enhancing antioxidant capacity with optimum application of nitrogen and phosphate combination. Front. Plant Sci. 2022, 13, 1027227. [Google Scholar] [CrossRef] [PubMed]
- Mai, W.; Xue, X.; Azeem, A. Growth of cotton crop (Gossypium hirsutum L.) higher under drip irrigation because of better phosphorus uptake. Appl. Ecol. Environ. Res. 2022, 20, 4865–4878. [Google Scholar] [CrossRef]
- Azeem, A.; Mai, W.; Tian, C.; Javed, Q. Dry Weight Prediction of Wedelia trilobata and Wedelia chinensis by Using Artificial Neural Network and MultipleLinear Regression Models. Water 2023, 15, 1896. [Google Scholar] [CrossRef]
- Mai, W.; Xue, X.; Azeem, A. Plant Density Differentially Influences Seed Weight in Different Portions of the Raceme of Castor. Pol. J. Environ. Stud. 2023, 32, 3247–3254. [Google Scholar] [CrossRef]
- McMaster, G.S.; Wilhelm, W. Growing degree-days: One equation, two interpretations. Agric. For. Meteorol. 1997, 87, 291–300. [Google Scholar] [CrossRef]
- Yang, L.; Wang, Y.; Kang, M.; Dong, Q. Simulation of tomato fruit individual growth rule based on revised logistic model. Trans. Chin. Soc. Agric. Mach. 2008, 39, 81–84. [Google Scholar]
- Wang, R.; Li, S.; Wang, Q.; Zheng, J.; Fan, J.; Li, S. Evaluation of simulation models of spring-maize leaf area and biomass in semiarid agro-ecosystems. Chin. J. Eco-Agric. 2008, 16, 139–144. [Google Scholar] [CrossRef]
- Javed, Q.; Azeem, A.; Sun, J.; Ullah, I.; Jabran, K.; Anandkumar, A.; Prabakaran, K.; Buttar, N.; Du, D. Impacts of salt stress on the physiology of plants and opportunity to rewater the stressed plants with diluted water: A review. Appl. Ecol. Environ. Res. 2019, 17, 12583. [Google Scholar] [CrossRef]
- Steduto, P.; Hsiao, T.C.; Fereres, E. On the conservative behavior of biomass water productivity. Irrig. Sci. 2007, 25, 189–207. [Google Scholar] [CrossRef]
- Vanuytrecht, E.; Raes, D.; Steduto, P.; Hsiao, T.C.; Fereres, E.; Heng, L.K.; Vila, M.G.; Moreno, P.M. AquaCrop: FAO’s crop water productivity and yield response model. Environ. Modell. Softw. 2014, 62, 351–360. [Google Scholar] [CrossRef]
- Azeem, A.; Sun, J.; Javed, Q.; Jabran, K.; Du, D. The effect of submergence and eutrophication on the trait’s performance of Wedelia trilobata over its congener native Wedelia chinensis. Water 2020, 12, 934. [Google Scholar] [CrossRef]
- Javed, Q.; Azeem, A.; Sun, J.; Ullah, I.; Du, D.; Imran, M.A.; Nawaz, M.I.; Chattha, H.T. Growth prediction of Alternanthera philoxeroides under salt stress by application of artificial neural networking. Plant Biosyst.—Int. J. Deal. All Asp. Plant Biol. 2022, 156, 61–67. [Google Scholar] [CrossRef]



| EC (ds/m) | Texture | Organic Carbon (%) | pH | Phosphorus (kg/ha) | Nitrogen (kg/ha) |
|---|---|---|---|---|---|
| 0.167 | Loamy Sandy | 0.30 | 6.96 | 21.07 | 238.22 |
| Water Quality | EC (ds/m) | Total Dissolved Solid (mg/L) | Nitrate (mg/L) | Nitrite (mg/L) | Chloride (mg/L) | Fluoride (mg/L) | Manganese (mg/L) |
|---|---|---|---|---|---|---|---|
| Brackish water | 4.368 | 6240 | 0.4 | 0.002 | 2231.03 | 1.15 | 0.006 |
| Fresh water | 0.357 | 510 | 0.4 | 0.015 | 196.75 | 0.35 | 0.006 |
| Treatment | Amount of Water (mm/acre) |
|---|---|
| Freshwater (control) | 450 mm |
| Brackish water | 414 mm because 7 days are rain |
| Crops | Time/Days | GDD/°C | RPH | Mean RPH | Standard Deviation | |
|---|---|---|---|---|---|---|
| Fresh | Brackish | |||||
| Cluster bean | 191 | 163.5 | 0.280 | 0.437 | 0.358 | 0.111 |
| 211 | 482 | 0.431 | 0.605 | 0.518 | 0.122 | |
| 232 | 794 | 0.610 | 0.805 | 0.708 | 0.137 | |
| 253 | 1124.5 | 0.887 | 0.824 | 0.855 | 0.044 | |
| 273 | 1444 | 0.918 | 1 | 0.959 | 0.0577 | |
| 283 | 1600.5 | 1 | 0.99 | 0.998 | 0.002 | |
| Sesbania | 191 | 163.5 | 0.1208 | 0.181 | 0.151 | 0.042 |
| 211 | 482 | 0.377 | 0.479 | 0.428 | 0.071 | |
| 232 | 794 | 0.518 | 0.634 | 0.576 | 0.082 | |
| 253 | 1124.5 | 0.855 | 0.814 | 0.834 | 0.029 | |
| 273 | 1444 | 1 | 0.976 | 0.988 | 0.016 | |
| 283 | 1600.5 | 1 | 1 | 1 | 0 | |
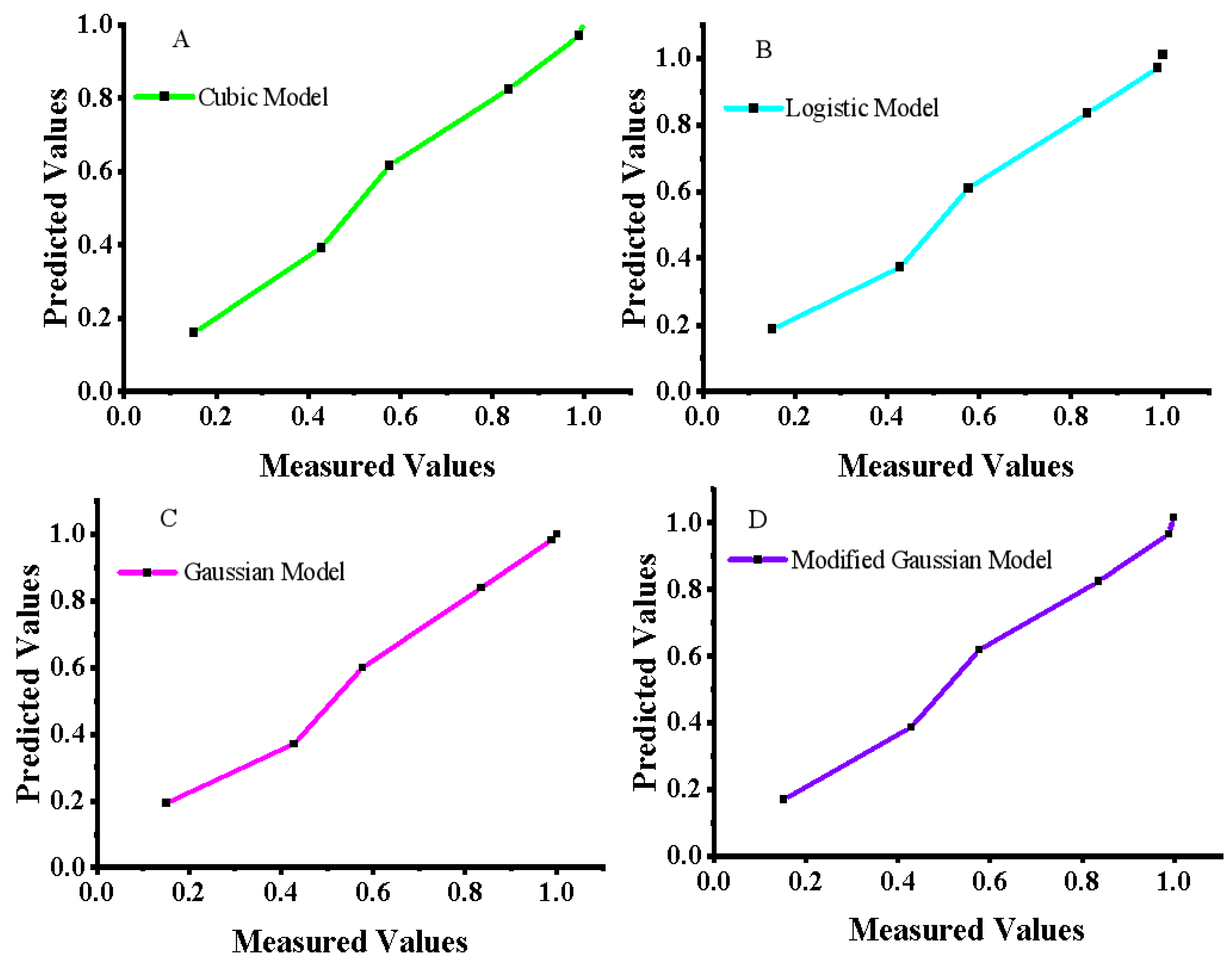
| Cluster Bean | Expression | RE% | Parameters | RMSE | R |
|---|---|---|---|---|---|
| Logistic model | 0.000072 | 3 | 0.0019 | 0.9932 | |
| Gaussian model | 0.00011 | 3 | 0.0028 | 0.9945 | |
| Modified Gaussian | 0.000032 | 4 | 0.0021 | 0.9932 | |
| Cubic model | 0.00000012 | 4 | 0.0016 | 0.9942 | |
| Sesbania | |||||
| Logistic model | 0.0019 | 3 | 0.0125 | 0.9826 | |
| Gaussian model | 0.0020 | 3 | 0.0128 | 0.9902 | |
| Modified Gaussian | 0.0007 | 4 | 0.011 | 0.9918 | |
| Cubic model | 0.00000000093 | 4 | 0.0100 | 0.9937 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azeem, A.; Mai, W.; Ali, R. Modeling Plant Height and Biomass Production of Cluster Bean and Sesbania across Diverse Irrigation Qualities in Pakistan’s Thar Desert. Water 2024, 16, 9. https://doi.org/10.3390/w16010009
Azeem A, Mai W, Ali R. Modeling Plant Height and Biomass Production of Cluster Bean and Sesbania across Diverse Irrigation Qualities in Pakistan’s Thar Desert. Water. 2024; 16(1):9. https://doi.org/10.3390/w16010009
Chicago/Turabian StyleAzeem, Ahmad, Wenxuan Mai, and Rajib Ali. 2024. "Modeling Plant Height and Biomass Production of Cluster Bean and Sesbania across Diverse Irrigation Qualities in Pakistan’s Thar Desert" Water 16, no. 1: 9. https://doi.org/10.3390/w16010009
APA StyleAzeem, A., Mai, W., & Ali, R. (2024). Modeling Plant Height and Biomass Production of Cluster Bean and Sesbania across Diverse Irrigation Qualities in Pakistan’s Thar Desert. Water, 16(1), 9. https://doi.org/10.3390/w16010009





