Comparing Deterministic and Stochastic Methods in Geospatial Analysis of Groundwater Fluoride Concentration
Abstract
:1. Introduction
2. Methodology
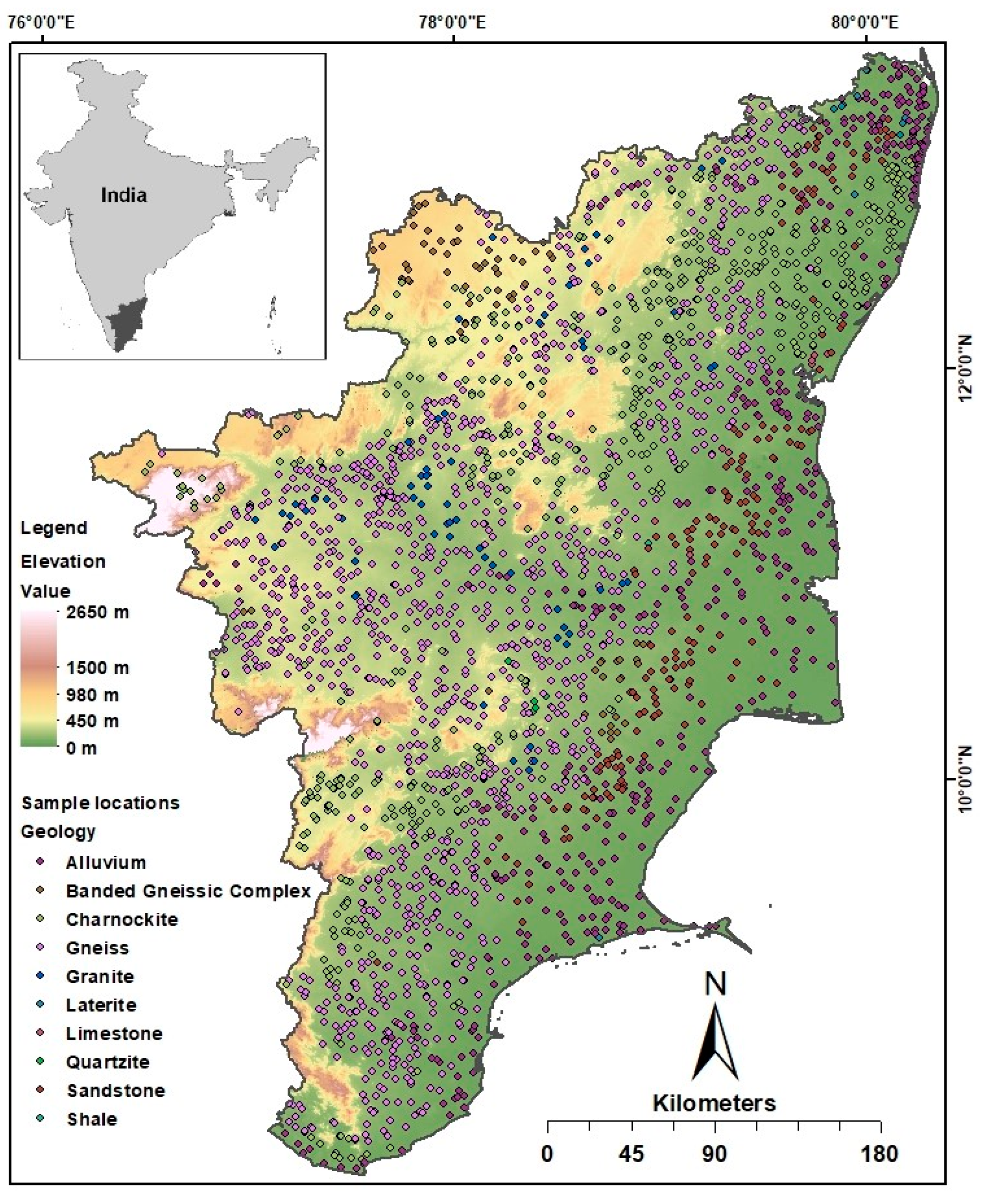
2.1. Dataset Description
2.2. Interpolation Methods
2.2.1. Inverse Distance Weighting
2.2.2. Radial Basis Functions
2.2.3. Local Polynomial Interpolation
2.2.4. Kriging Methods
2.3. Validation of the Interpolation Methods
2.3.1. Leave-One-Out Cross-Validation
2.3.2. Hold-Out Validation
2.3.3. Validation with an Independent Dataset
2.4. Comparison of the Interpolation Methods
3. Results
3.1. Measured Fluoride Concentration
3.2. Variation Based on Aquifer Type
3.3. Statistical Accuracy of Various Methods
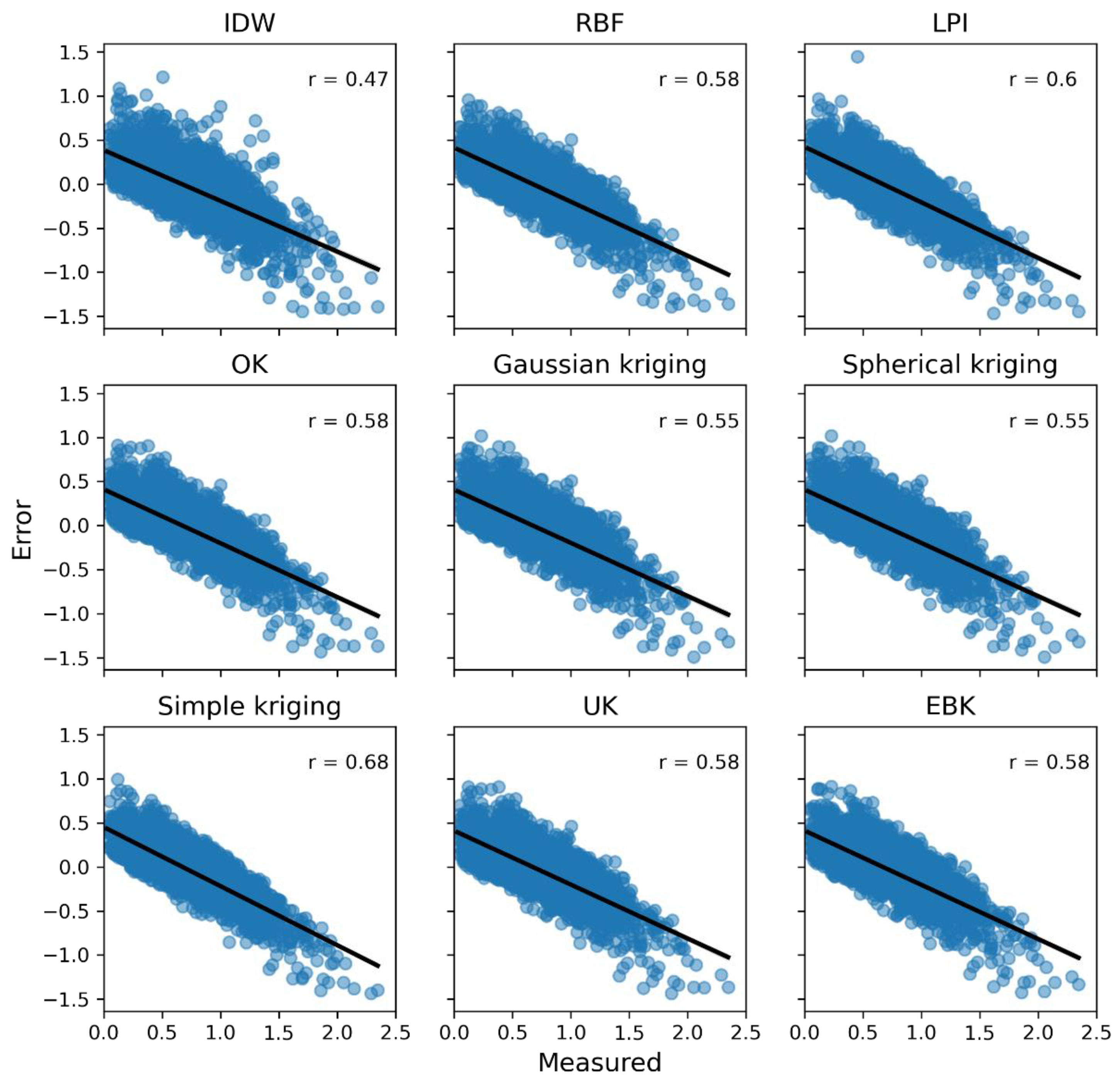
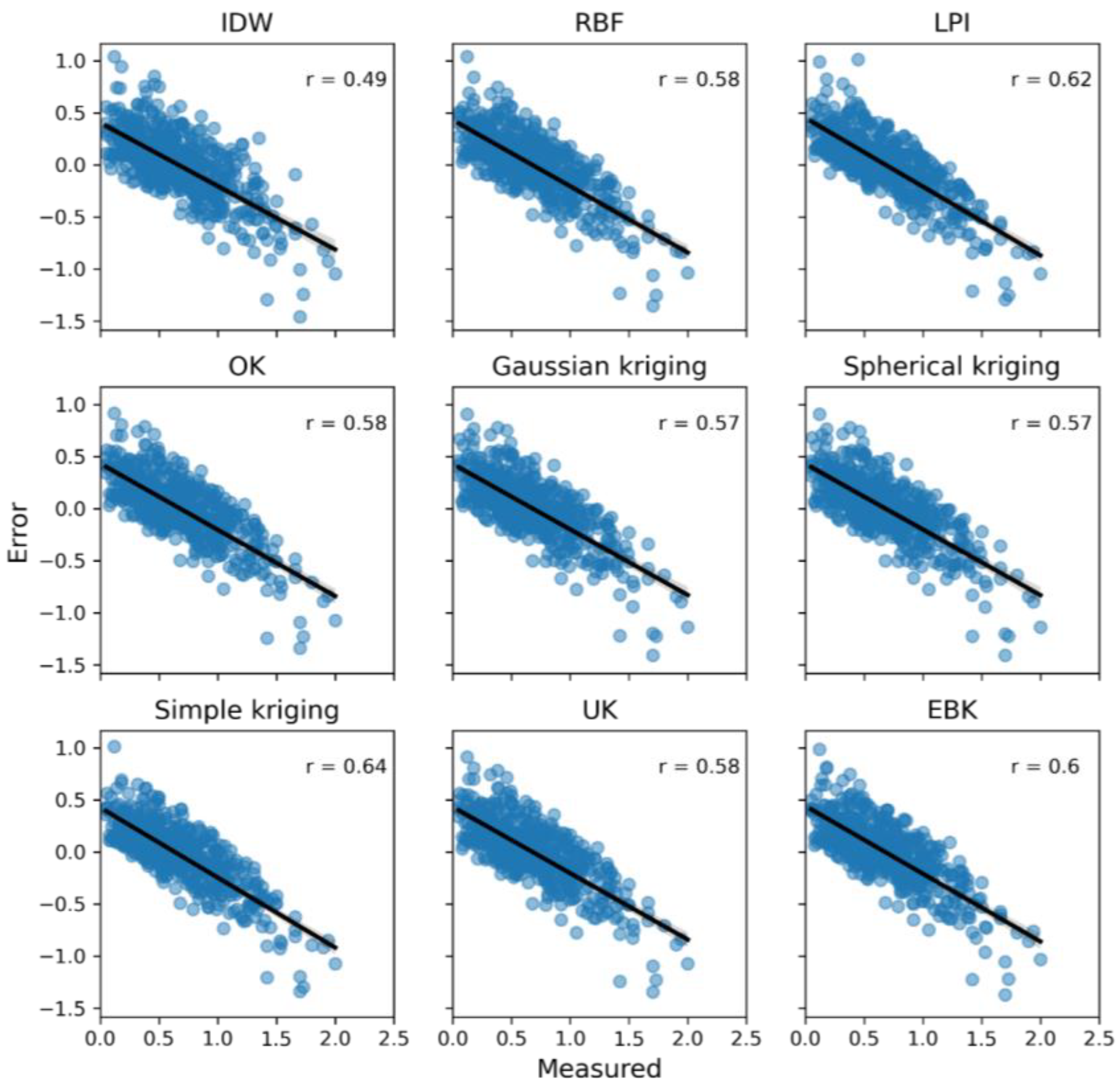
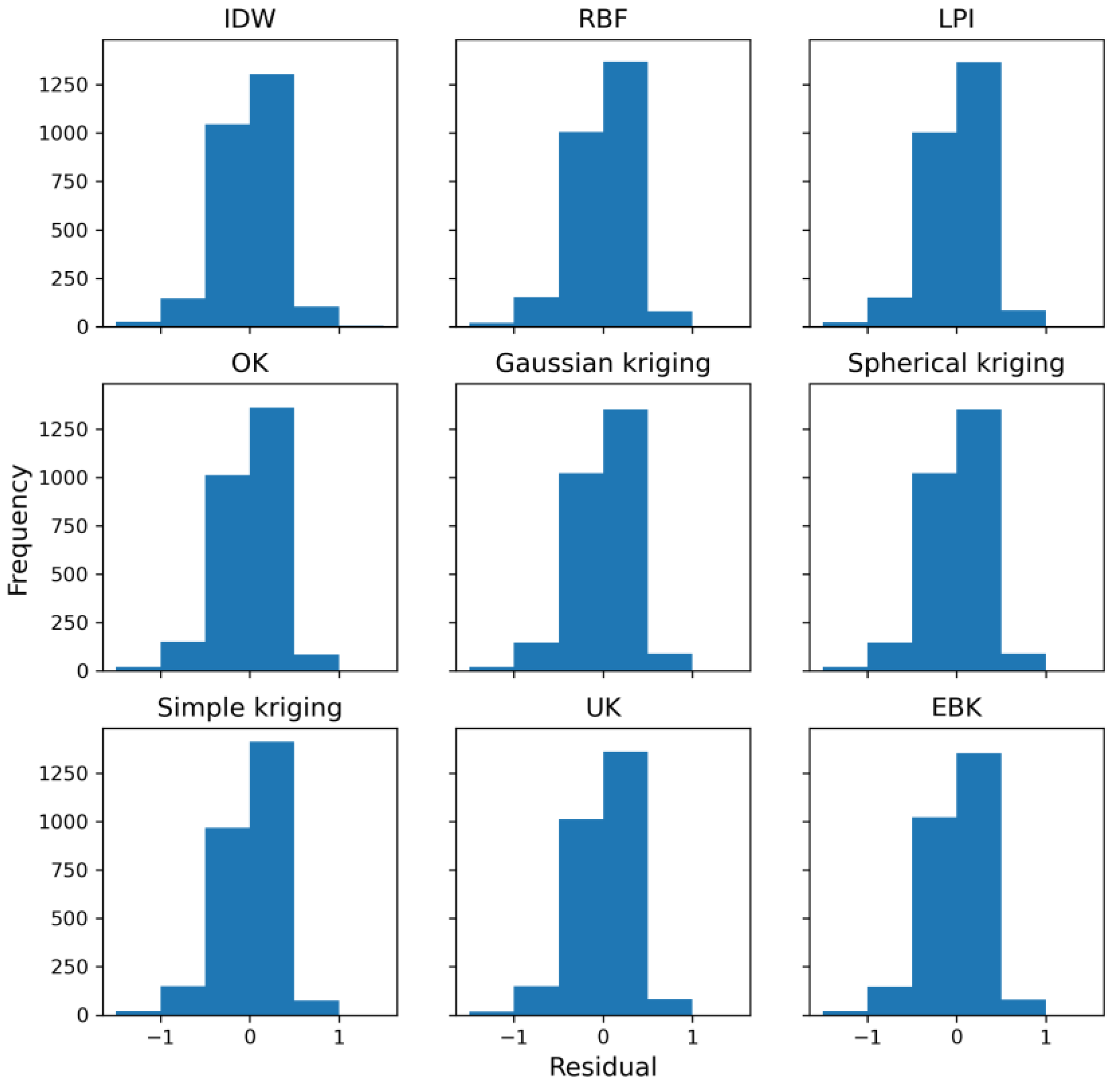
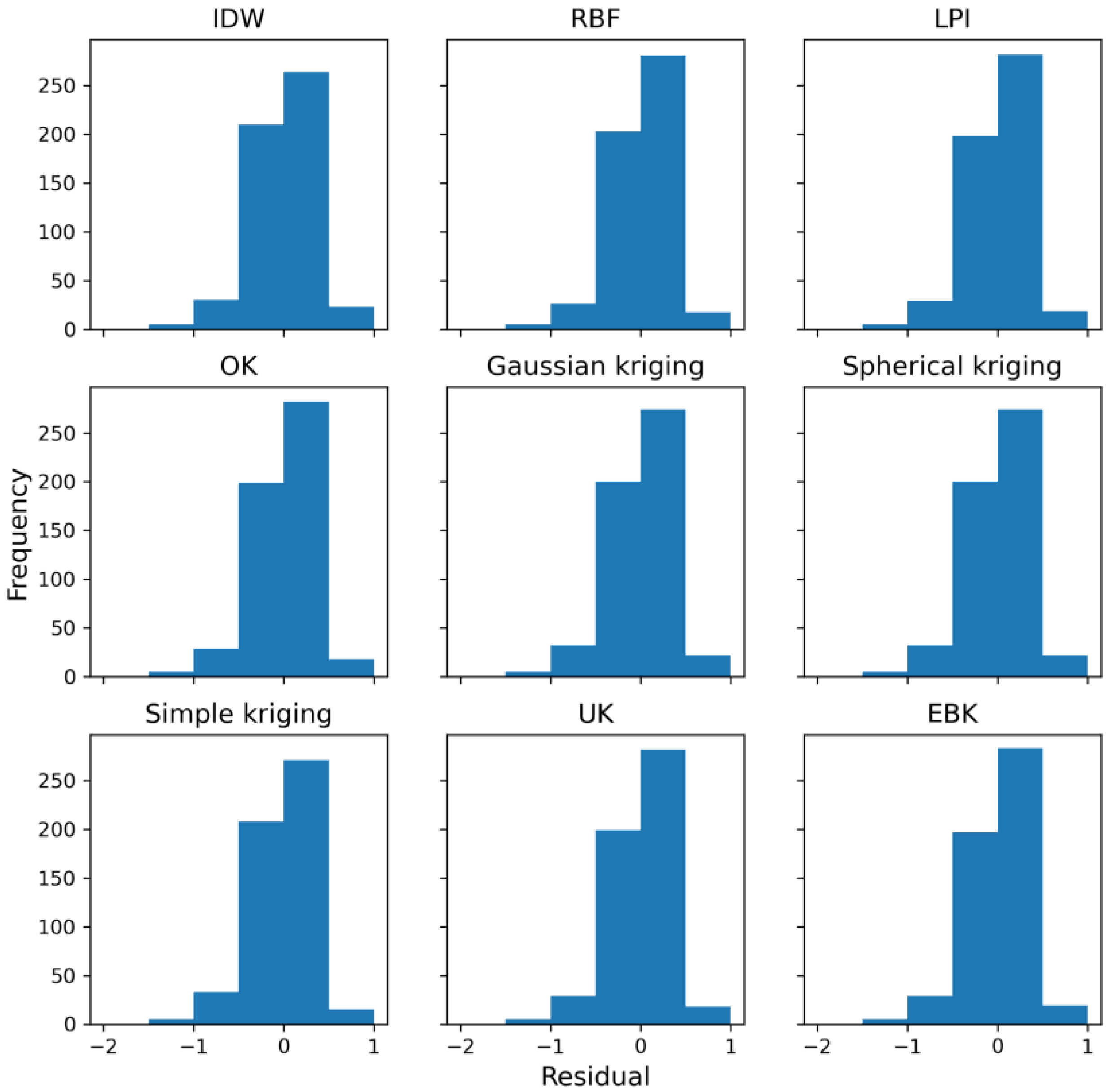
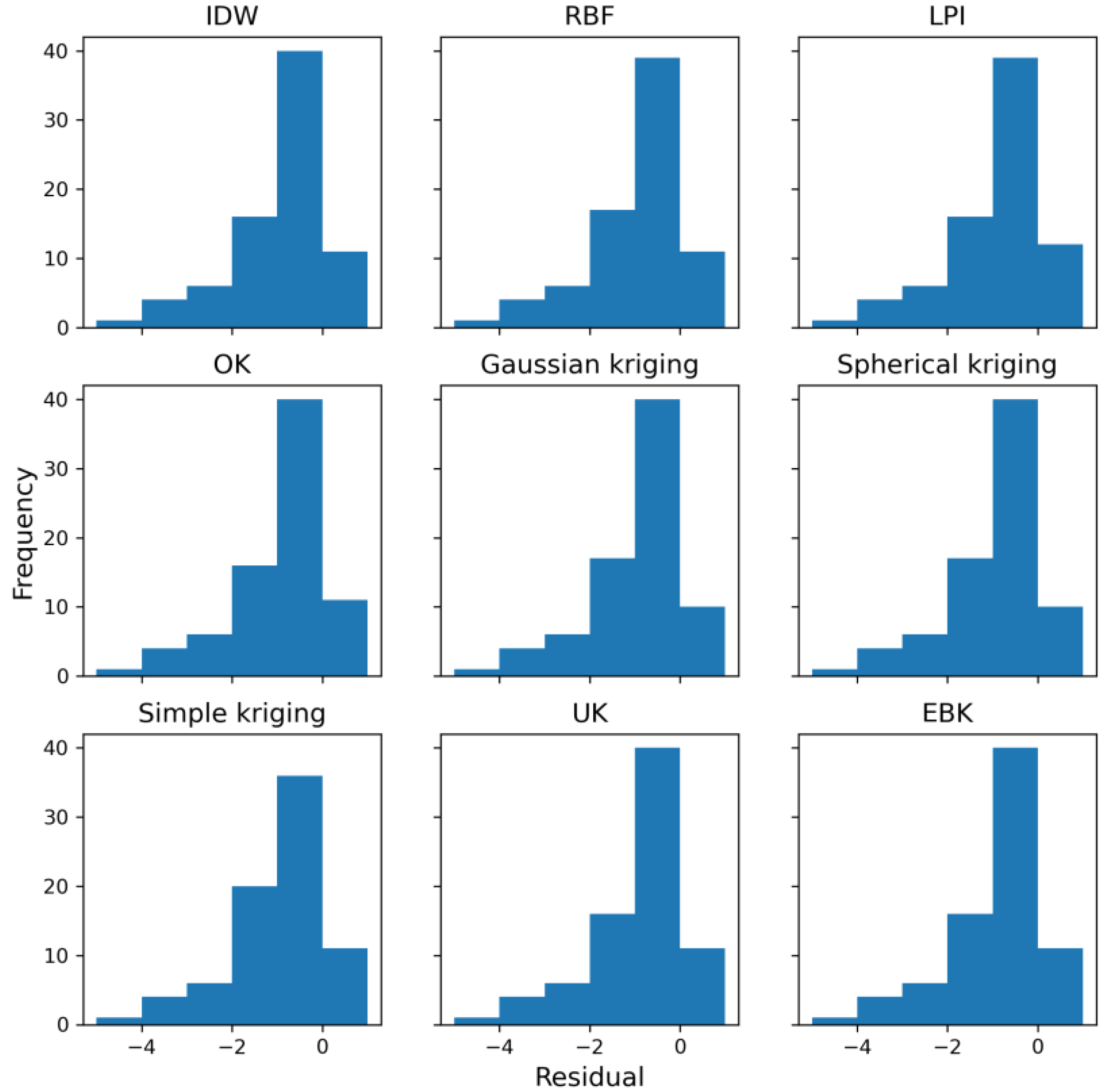
3.4. Correlation and Prediction Error
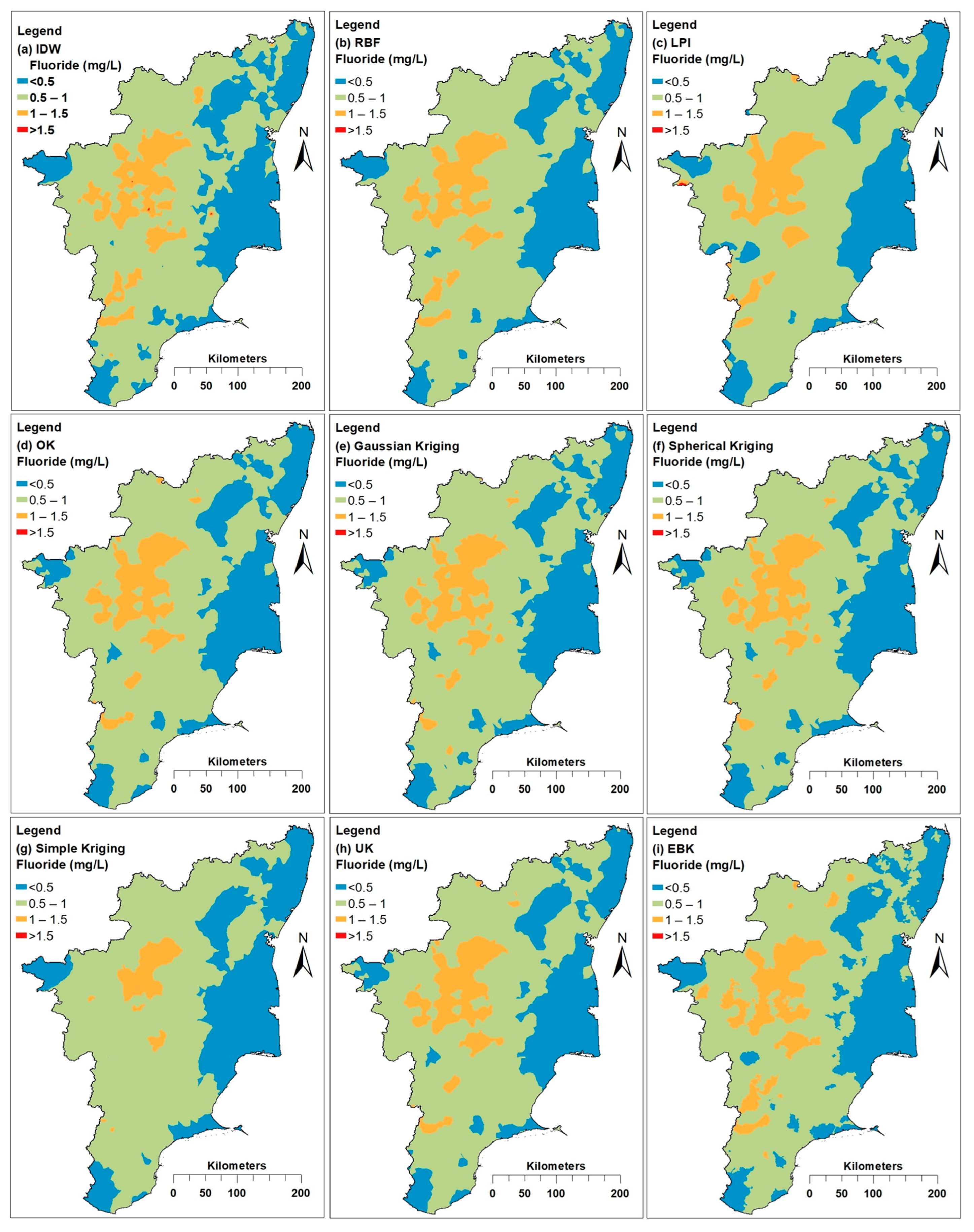
3.5. Prediction of Contaminated Areas Using Various Methods
3.6. Over- and Under-Estimation of Contaminated Areas
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amini, M.; Mueller, K.; Abbaspour, K.C.; Rosenberg, T.; Afyuni, M.; Møller, K.N.; Sarr, M.; Johnson, C.A. Statistical Modeling of Global Geogenic Fluoride Contamination in Groundwaters. Environ. Sci. Technol. 2008, 42, 3662–3668. [Google Scholar] [CrossRef] [PubMed]
- WHO. Guidelines for Drinking Water Quality, 4th ed.; World Health Organization: Geneva, Switzerland, 2011. [Google Scholar]
- Podgorski, J.E.; Labhasetwar, P.; Saha, D.; Berg, M. Prediction Modeling and Mapping of Groundwater Fluoride Contamination throughout India. Environ. Sci. Technol. 2018, 52, 9889–9898. [Google Scholar] [CrossRef] [PubMed]
- Chakraborti, D.; Rahman, M.M.; Chatterjee, A.; Das, D.; Das, B.; Nayak, B.; Pal, A.; Chowdhury, U.K.; Ahmed, S.; Biswas, B.K.; et al. Fate of over 480 million inhabitants living in arsenic and fluoride endemic Indian districts: Magnitude, health, socio-economic effects and mitigation approaches. J. Trace Elem. Med. Biol. 2016, 38, 33–45. [Google Scholar] [CrossRef]
- Raju, N.J. Prevalence of fluorosis in the fluoride enriched groundwater in semi-arid parts of eastern India: Geochemistry and health implications. Quat. Int. 2017, 443, 265–278. [Google Scholar] [CrossRef]
- Nayak, B.; Roy, M.M.; Chakraborti, D. Dental fluorosis. Clin. Toxicol. 2009, 47, 355. [Google Scholar] [CrossRef]
- Yadugiri, V.T. Fluorosis: A persistent problem. Curr. Sci. 2011, 100, 1475–1477. [Google Scholar]
- Bhowmik, A.D.; Shaw, P.; Mondal, P.; Munshi, C.; Chatterjee, S.; Bhattacharya, S.; Chattopadhyay, A. Incidence of fluorosis and urinary fluoride concentration are not always positively correlated with drinking water fluoride level. Curr. Sci. 2019, 116, 1551–1554. [Google Scholar] [CrossRef]
- Chakraborti, D.; Chanda, C.; Samanta, G.; Chowdhury, U.; Mukherjee, S.; Pal, A.; Sharma, B.; Mahanta, K.; Ahmed, H.; Sing, B. Fluorosis in Assam, India. Curr. Sci. 2000, 78, 1421–1423. [Google Scholar]
- Sahoo, P.K.; Ray, S.B.; Kerketta, A.; Behera, P.; Neogi, G.; Sahoo, H.B. Geogenic enrichment of fluoride in groundwater of hard rock aquifer in fluorosis prevalent area of Balangir district, Odisha, India. Groundw. Sustain. Dev. 2022, 19, 100830. [Google Scholar] [CrossRef]
- Jaydhar, A.K.; Chandra Pal, S.; Saha, A.; Islam, A.R.M.T.; Ruidas, D. Hydrogeochemical evaluation and corresponding health risk from elevated arsenic and fluoride contamination in recurrent coastal multi-aquifers of eastern India. J. Clean. Prod. 2022, 369, 133150. [Google Scholar] [CrossRef]
- Gotway, C.A.; Ferguson, R.B.; Hergert, G.W.; Peterson, T.A. Comparison of Kriging and Inverse-Distance Methods for Mapping Soil Parameters. Soil Sci. Soc. Am. J. 1996, 60, 1237–1247. [Google Scholar] [CrossRef]
- Liu, R.; Chen, Y.; Sun, C.; Zhang, P.; Wang, J.; Yu, W.; Shen, Z. Uncertainty analysis of total phosphorus spatial–temporal variations in the Yangtze River Estuary using different interpolation methods. Mar. Pollut. Bull. 2014, 86, 68–75. [Google Scholar] [CrossRef]
- Adhikary, P.P.; Dash, C.J. Comparison of deterministic and stochastic methods to predict spatial variation of groundwater depth. Appl. Water Sci. 2017, 7, 339–348. [Google Scholar] [CrossRef]
- Amini, M.A.; Torkan, G.; Eslamian, S.; Zareian, M.J.; Adamowski, J.F. Analysis of deterministic and geostatistical interpolation techniques for mapping meteorological variables at large watershed scales. Acta Geophys. 2019, 67, 191–203. [Google Scholar] [CrossRef]
- Ahmad, A.Y.; Saleh, I.A.; Balakrishnan, P.; Al-Ghouti, M.A. Comparison GIS-Based interpolation methods for mapping groundwater quality in the state of Qatar. Groundw. Sustain. Dev. 2021, 13, 100573. [Google Scholar] [CrossRef]
- Bronowicka-Mielniczuk, U.; Mielniczuk, J.; Obroślak, R.; Przystupa, W. A Comparison of Some Interpolation Techniques for Determining Spatial Distribution of Nitrogen Compounds in Groundwater. Int. J. Environ. Res. 2019, 13, 679–687. [Google Scholar] [CrossRef]
- Wameling, A. Accuracy of geostatistical prediction of yearly precipitation in Lower Saxony. Environmetrics 2003, 14, 699–709. [Google Scholar] [CrossRef]
- Shahmohammadi-Kalalagh, S.; Taran, F. Evaluation of the classical statistical, deterministic and geostatistical interpolation methods for estimating the groundwater level. Int. J. Energy Water Resour. 2021, 5, 33–42. [Google Scholar] [CrossRef]
- Adhikary, P.P.; Dash, C.J.; Bej, R.; Chandrasekharan, H. Indicator and probability kriging methods for delineating Cu, Fe, and Mn contamination in groundwater of Najafgarh Block, Delhi, India. Environ. Monit. Assess. 2011, 176, 663–676. [Google Scholar] [CrossRef]
- Murphy, R.R.; Curriero, F.C.; Ball, W.P. Comparison of Spatial Interpolation Methods for Water Quality Evaluation in the Chesapeake Bay. J. Environ. Eng. 2010, 136, 160–171. [Google Scholar] [CrossRef]
- Farzaneh, G.; Khorasani, N.; Ghodousi, J.; Panahi, M. Application of geostatistical models to identify spatial distribution of groundwater quality parameters. Environ. Sci. Pollut. Res. 2022, 29, 36512–36532. [Google Scholar] [CrossRef] [PubMed]
- Elumalai, V.; Brindha, K.; Sithole, B.; Lakshmanan, E. Spatial interpolation methods and geostatistics for mapping groundwater contamination in a coastal area. Environ. Sci. Pollut. Res. 2017, 24, 11601–11617. [Google Scholar] [CrossRef] [PubMed]
- Gong, G.; Mattevada, S.; O’Bryant, S.E. Comparison of the accuracy of kriging and IDW interpolations in estimating groundwater arsenic concentrations in Texas. Environ. Res. 2014, 130, 59–69. [Google Scholar] [CrossRef]
- Magesh, N.S.; Elango, L. Spatio-Temporal Variations of Fluoride in the Groundwater of Dindigul District, Tamil Nadu, India: A Comparative Assessment Using Two Interpolation Techniques. In GIS and Geostatistical Techniques for Groundwater Science; Senapathi, V., Viswanathan, P.M., Chung, S.Y., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 283–296. [Google Scholar]
- CGWB. Aquifer Systems of Tamilnadu and Puducherry, Central Ground Water Board, South Eastern Coastaö Region, Chennai; Ministry of Water Resources, Government of India: New Delhi, India, 2012.
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 1968 ACM National Conference, New York, NY, USA, 27–29 August 1968; pp. 517–524. [Google Scholar]
- Aguilar, F.; Agüera, F.; Aguilar, M.; Carvajal, F. Effects of Terrain Morphology, Sampling Density, and Interpolation Methods on Grid DEM Accuracy. Photogramm. Eng. Remote Sens. 2005, 71, 805–816. [Google Scholar] [CrossRef]
- Mitášová, H.; Mitáš, L. Interpolation by regularized spline with tension: I. Theory and implementation. Math. Geol. 1993, 25, 641–655. [Google Scholar] [CrossRef]
- Xie, Y.; Chen, T.-B.; Lei, M.; Yang, J.; Guo, Q.-J.; Song, B.; Zhou, X.-Y. Spatial distribution of soil heavy metal pollution estimated by different interpolation methods: Accuracy and uncertainty analysis. Chemosphere 2011, 82, 468–476. [Google Scholar] [CrossRef] [PubMed]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists, 2nd ed.; Statistics in Practice; John Wiley & Sons, Ltd.: Chichester, UK, 2007. [Google Scholar]
- Ryu, J.-S.; Kim, M.; Cha, K.-J.; Lee, T.H.; Choi, D. Kriging interpolation methods in geostatistics and DACE model. KSME Int. J. 2002, 16, 619–632. [Google Scholar] [CrossRef]
- Lichtenstern, A. Kriging Methods in Spatial Statistics. Bachelor’s Thesis, Technische Universität Müunchen, Munich, Germany, 2013; p. 97. [Google Scholar]
- Krivoruchko, K. Empirical Bayesian Kriging; ArcUser Fall; Esri Press: Redlands, CA, USA, 2012; pp. 6–10. [Google Scholar]
- Kalpana, L.; Brindha, K.; Elango, L. FIMAR: A new Fluoride Index to mitigate geogenic contamination by Managed Aquifer Recharge. Chemosphere 2018, 220, 381–390. [Google Scholar] [CrossRef]
- Brindha, K.; Jagadeshan, G.; Kalpana, L.; Elango, L. Fluoride in weathered rock aquifers of southern India: Managed Aquifer Recharge for mitigation. Environ. Sci. Pollut. Res. Int. 2016, 23, 8302–8316. [Google Scholar] [CrossRef]
- Kalpana, L. Groundwater Quality with Special Reference to Fluoride and Groundwater Modelling for Simulating the Effect of Managed Aquifer Recharge in Pambar Basin, India. Unpublished. Ph.D. Thesis, Anna University, Chennai, India, 2014. [Google Scholar]
- Jagadeshan, G. Geochemical Reactions Responsible for Fluoride Rich Groundwater and Remediation by Induced Recharge in Vaniyar River Basin, Tamil Nadu, India. Unpublished. Ph.D. Thesis, Anna University, Chennai, India, 2015. [Google Scholar]
- IS10500; Indian Standard Drinking Water Specification. Bureau of Indian Standards (BIS): New Delhi, India, 2012.
- WHO; UNICEF. Progress on Drinking Water, Sanitation and Hygiene: 2017 Update and SDG Baselines. Geneva: World Health Organization (WHO) and the United Nations Children’s Fund (UNICEF); Licence: CC BY-NC-SA 3.0 IGO; WHO: Geneva, Switzerland, 2017; p. 108. [Google Scholar]
- Brindha, K.; Elango, L. Hydrochemical characteristics of groundwater for domestic and irrigation purposes in Madhuranthakam, Tamil Nadu, India. Earth Sci. Res. J. 2011, 15, 101–108. [Google Scholar]
- Karthikeyan, K.; Nanthakumar, K.; Velmurugan, P.; Tamilarasi, S.; Lakshmanaperumalsamy, P. Prevalence of certain inorganic constituents in groundwater samples of Erode district, Tamilnadu, India, with special emphasis on fluoride, fluorosis and its remedial measures. Environ. Monit. Assess. 2010, 160, 141–155. [Google Scholar] [CrossRef]
- Jagadeshan, G.; Kalpana, L.; Elango, L. Hydrogeochemistry of high fluoride groundwater in hard rock aquifer in a part of Dharmapuri district, Tamil Nadu, India. Geochem. Int. 2015, 53, 554–564. [Google Scholar] [CrossRef]
- Nair, I.S.; Brindha, K.; Elango, L. Identification of salinization by bromide and fluoride concentration in coastal aquifers near Chennai, southern India. Water Sci. 2016, 30, 41–50. [Google Scholar] [CrossRef]
- Thivya, C.; Chidambaram, S.; Rao, M.S.; Thilagavathi, R.; Prasanna, M.V.; Manikandan, S. Assessment of fluoride contaminations in groundwater of hard rock aquifers in Madurai district, Tamil Nadu (India). Appl. Water Sci. 2017, 7, 1011–1023. [Google Scholar] [CrossRef]
- Falivene, O.; Cabrera, L.; Tolosana-Delgado, R.; Sáez, A. Interpolation algorithm ranking using cross-validation and the role of smoothing effect. A coal zone example. Comput. Geosci. 2010, 36, 512–519. [Google Scholar] [CrossRef]
- Falivene, O.; Cabrera, L.; Sáez, A. Optimum and robust 3D facies interpolation strategies in a heterogeneous coal zone (Tertiary As Pontes basin, NW Spain). Int. J. Coal Geol. 2007, 71, 185–208. [Google Scholar] [CrossRef]
- Mirzaei, R.; Sakizadeh, M. Comparison of interpolation methods for the estimation of groundwater contamination in Andimeshk-Shush Plain, Southwest of Iran. Environ. Sci. Pollut. Res. Int. 2016, 23, 2758–2769. [Google Scholar] [CrossRef]
- Singaraja, C.; Chidambaram, S.; Jacob, N.; Johnson Babu, G.; Selvam, S.; Anandhan, P.; Rajeevkumar, E.; Balamurugan, K.; Tamizharasan, K. Origin of high fluoride in groundwater of the Tuticorin district, Tamil Nadu, India. Appl. Water Sci. 2018, 8, 54. [Google Scholar] [CrossRef]
- Manikandan, S.; Chidambaram, S.; Ramanathan, A.L.; Prasanna, M.V.; Karmegam, U.; Singaraja, C.; Paramaguru, P.; Jainab, I. A study on the high fluoride concentration in the magnesium-rich waters of hard rock aquifer in Krishnagiri district, Tamilnadu, India. Arab. J. Geosci. 2014, 7, 273–285. [Google Scholar] [CrossRef]
- Jagadeshan, G.; Kalpana, L.; Elango, L. Major ion signatures for identification of geochemical reactions responsible for release of fluoride from geogenic sources to groundwater and associated risk in Vaniyar River basin, Dharmapuri district, Tamil Nadu, India. Environ. Earth Sci. 2015, 74, 2439–2450. [Google Scholar] [CrossRef]
- Pan, H.; Huang, W.-Q. Influence of uncertainty in delimitation of seismic statistical zone on results of PSHA. Acta Seismol. Sin. 2003, 16, 213–218. [Google Scholar] [CrossRef]


| Aquifer Type | Number of Measured Fluoride Samples | Range (mg/L) | Mean (mg/L) | SD | Number of Samples above 1.5 mg/L of Fluoride |
|---|---|---|---|---|---|
| Alluvium | 2368 | 0.01–2.77 | 0.47 | 0.38 | 48 |
| Banded Gneissic Complex | 380 | 0.05–1.77 | 0.71 | 0.35 | 8 |
| Charnockite | 2900 | 0.01–5.00 | 0.62 | 0.48 | 146 |
| Gneiss | 6479 | 0.01–5.00 | 0.77 | 0.51 | 563 |
| Granite | 307 | 0.01–2.50 | 0.88 | 0.49 | 32 |
| Laterite | 38 | 0.05–1.95 | 0.41 | 0.39 | 1 |
| Limestone | 67 | 0.05–1.50 | 0.59 | 0.36 | 0 |
| Quartzite | 27 | 0.15–1.68 | 0.93 | 0.48 | 5 |
| Sandstone | 1013 | 0.01–4.90 | 0.40 | 0.40 | 18 |
| Shale | 6 | 0.55–1.35 | 0.92 | 0.29 | 0 |
| Total | 13,585 | 0.01–5.00 | 0.66 | 0.49 | 821 |
| Measure | IDW | RBF | LPI | OK | Gaussian Kriging | Spherical Kriging | Simple Kriging | UK | EBK |
|---|---|---|---|---|---|---|---|---|---|
| LOOCV | |||||||||
| Predicted mean | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 |
| MRE | 0.53 | 0.54 | 0.54 | 0.53 | 0.53 | 0.54 | 0.56 | 0.53 | 0.54 |
| RMSE | 0.32 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 |
| CV, predicted (%) | 42 | 37 | 36 | 37 | 38 | 38 | 32 | 37 | 37 |
| r, measured vs. predicted | 0.32 | 0.35 | 0.34 | 0.35 | 0.34 | 0.34 | 0.34 | 0.35 | 0.35 |
| r, measured vs. error | 0.47 | 0.58 | 0.60 | 0.58 | 0.55 | 0.55 | 0.68 | 0.58 | 0.58 |
| Hold-out validation | |||||||||
| Predicted mean | 0.67 | 0.67 | 0.68 | 0.67 | 0.68 | 0.68 | 0.65 | 0.67 | 0.68 |
| MRE | 0.56 | 0.58 | 0.58 | 0.58 | 0.57 | 0.57 | 0.55 | 0.58 | 0.58 |
| RMSE | 0.32 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 |
| CV, predicted (%) | 41 | 36 | 34 | 36 | 37 | 37 | 34 | 36 | 35 |
| r, measured vs. predicted | 0.28 | 0.31 | 0.30 | 0.31 | 0.31 | 0.31 | 0.30 | 0.31 | 0.30 |
| r, measured vs. error | 0.49 | 0.58 | 0.62 | 0.58 | 0.57 | 0.57 | 0.64 | 0.58 | 0.60 |
| Validation with an independent dataset | |||||||||
| Predicted mean | 0.86 | 0.86 | 0.87 | 0.86 | 0.86 | 0.85 | 0.82 | 0.86 | 0.86 |
| MRE | 0.50 | 0.51 | 0.50 | 0.50 | 0.50 | 0.50 | 0.53 | 0.50 | 0.50 |
| RMSE | 1.48 | 1.48 | 1.48 | 1.48 | 1.48 | 1.48 | 1.52 | 1.48 | 1.49 |
| CV, predicted (%) | 8 | 9 | 5 | 8 | 11 | 11 | 6 | 8 | 8 |
| r, measured vs. predicted | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.07 | 0.00 | 0.02 |
| r, measured vs. error | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 |
| Method | Fluoride Range and Area in % | |||
|---|---|---|---|---|
| <0.5 | 0.5 to 1 | 1 to 1.5 | >1.5 | |
| Very Low Fluoride | Low Fluoride | Suitable Range | Unsuitable | |
| IDW | 28.0 | 61.2 | 10.6 | 0.2 |
| RBF | 25.4 | 64.4 | 10.2 | - |
| LPI | 26.0 | 63.2 | 10.6 | 0.2 |
| OK | 26.5 | 63.6 | 9.9 | - |
| Gaussian kriging | 26.6 | 63.2 | 10.2 | - |
| Spherical kriging | 26.5 | 63.2 | 10.3 | - |
| Simple kriging | 29.6 | 65.9 | 4.5 | - |
| UK | 26.5 | 63.6 | 9.9 | - |
| EBK | 27.1 | 61.5 | 11.4 | - |
| Comparison | Under-Estimated | Equal | Over-Estimated |
| IDW minus OK | 11.2 | 77.9 | 10.9 |
| IDW minus Gaussian Kriging | 12.9 | 74.4 | 12.7 |
| IDW minus Spherical Kriging | 13.2 | 73.9 | 12.9 |
| IDW minus Simple Kriging | 11.5 | 63.3 | 25.2 |
| IDW minus UK | 11.2 | 77.9 | 10.9 |
| IDW minus EBK | 11 | 78.2 | 10.8 |
| IDW minus RBF | 7.2 | 85.1 | 7.7 |
| IDW minus LPI | 12.3 | 74.8 | 12.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brindha, K.; Taie Semiromi, M.; Boumaiza, L.; Mukherjee, S. Comparing Deterministic and Stochastic Methods in Geospatial Analysis of Groundwater Fluoride Concentration. Water 2023, 15, 1707. https://doi.org/10.3390/w15091707
Brindha K, Taie Semiromi M, Boumaiza L, Mukherjee S. Comparing Deterministic and Stochastic Methods in Geospatial Analysis of Groundwater Fluoride Concentration. Water. 2023; 15(9):1707. https://doi.org/10.3390/w15091707
Chicago/Turabian StyleBrindha, K., Majid Taie Semiromi, Lamine Boumaiza, and Subham Mukherjee. 2023. "Comparing Deterministic and Stochastic Methods in Geospatial Analysis of Groundwater Fluoride Concentration" Water 15, no. 9: 1707. https://doi.org/10.3390/w15091707






