A Robust Regime Shift Change Detection Algorithm for Water-Flow Dynamics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Region
2.2. Streamflow Data
2.3. Methods
2.3.1. Seasonal Modeling and Gap Filling of Hydrometric Data Time Series
- : Seasonal Autoregressive Parameter,
- : Autoregressive Parameter,
- : the difference operator where d specifies the order of differencing,
- : the seasonal difference operator where D is the order of seasonal differencing,
- : Moving Average Parameter,
- : Seasonal Moving Average Parameter.
2.3.2. Regime Shift Change Detection (RSCD)
- and are average values of a subset of ,
- n = n(X) is the number of elements of set X,
- is the number of elements of set ,
- for ,
- for .
2.3.3. RSCD Thresholds
| Algorithm 1 Regime Shift Change Detection (RSCD) algorithm, * Refine Method (RM). This parameter determines the two specializations of this method. ** xr is a point right after point c(j+1) |
| Input: , μ, σ, ε, and RM * Output: Periods P ← potential change point candidates through with 1 ≤ j ≤ n − 1; if n(Y) ≥ 2 then ← consecutive potential change point candidates; while n(C) ≥ 2 do for () do if there is a period after then if > then Remove from C else Remove from C end else if GR(, ) > GR(, ) ** then Remove from C else Remove from C end end end Update C end Update Y end if n(Y) ≥ 1 then ← periods defined using m change points; while n(P) ≥ 2 do for do if RM = Relative-Difference then if RD() < ε then Merge periods and end end if RM = Growth Rate then if GR() < ε then Merge periods and end end end Update P end else There is no regime shift. End |
2.3.4. RSCD for Newly Observed Data
3. Results
3.1. Seasonal Modeling and Gap Filling of Hydrometric Data Time Series
3.2. Regime Shift Change Detection (RSCD)
3.3. RSCD Algorithm for the Test Set
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ARB | Athabasca River Basin |
| ARIMA | Autoregressive Integrated Moving Average |
| GR | Growth Rate |
| MA | Moving-Average |
| RFR | Random Forest Regressor |
| RSCD | Regime Shift Change Detection |
| RD | Relative Difference |
| RSCD-GR | RSCD with Growth Rate |
| RSCD-RD | RSCD with Relative Difference |
| SARIMA | Seasonal Autoregressive Integrated Moving Average |
| SRTM | Shuttle Radar Topography Mission |
| RAMP | The Regional Aquatics Monitoring Program |
| WSC | Water Survey of Canada |
References
- Myronidis, D.; Fotakis, D.; Ioannou, K.; Sgouropoulou, K. Comparison of ten notable meteorological drought indices on tracking the effect of drought on streamflow. Hydrol. Sci. J. 2018, 63, 2005–2019. [Google Scholar] [CrossRef]
- Zaghloul, M.S.; Ghaderpour, E.; Dastour, H.; Farjad, B.; Gupta, A.; Eum, H.; Achari, G.; Hassan, Q.K. Long Term Trend Analysis of River Flow and Climate in Northern Canada. Hydrology 2022, 9, 197. [Google Scholar] [CrossRef]
- Jiongxin, X. The water fluxes of the Yellow River to the sea in the past 50 years, in response to climate change and human activities. Environ. Manag. 2005, 35, 620–631. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.; Li, E.; Mu, X.; Wen, Z.; Rayburg, S.; Tian, P. Changing trends and regime shift of streamflow in the Yellow River basin. Stoch. Environ. Res. Risk Assess. 2015, 29, 1331–1343. [Google Scholar] [CrossRef]
- Burke, A.R.; Kasahara, T. Subsurface lateral flow generation in aspen and conifer-dominated hillslopes of a first order catchment in northern Utah. Hydrol. Process. 2011, 25, 1407–1417. [Google Scholar] [CrossRef]
- Godsey, S.E.; Kirchner, J.W.; Tague, C.L. Effects of changes in winter snowpacks on summer low flows: Case studies in the Sierra Nevada, California, USA. Hydrol. Process. 2014, 28, 5048–5064. [Google Scholar] [CrossRef]
- Tang, G.; Li, S.; Yang, M.; Xu, Z.; Liu, Y.; Gu, H. Streamflow response to snow regime shift associated with climate variability in four mountain watersheds in the US Great Basin. J. Hydrol. 2019, 573, 255–266. [Google Scholar] [CrossRef]
- Rostami, S.; He, J.; Hassan, Q.K. Water quality response to river flow regime at three major rivers in Alberta. Water Qual. Res. J. 2020, 55, 79–92. [Google Scholar] [CrossRef]
- Aminikhanghahi, S.; Cook, D.J. A survey of methods for time series change point detection. Knowl. Inf. Syst. 2017, 51, 339–367. [Google Scholar] [CrossRef]
- Zhu, Z. Change detection using landsat time series: A review of frequencies, preprocessing, algorithms, and applications. ISPRS J. Photogramm. Remote Sens. 2017, 130, 370–384. [Google Scholar] [CrossRef]
- Rodionov, S. A brief overview of the regime shift detection methods, Large-Scale Disturbances (Regime Shifts) and Recovery in Aquatic ecosystems: Challenges for Management Toward Sustainability. In Proceedings of the UNESCO-ROSTE/BAS Workshop on Regime Shifts, Varna, Bulgaria, 14–16 June 2005; pp. 17–24. [Google Scholar]
- Goossens, C.; Berger, A. How to recognize an abrupt climatic change? In Abrupt Climatic Change; Springer: Berlin/Heidelberg, Germany, 1987; pp. 31–45. [Google Scholar]
- Pettitt, A.N. A non-parametric approach to the change-point problem. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Chu, P.S.; Zhao, X. Bayesian change-point analysis of tropical cyclone activity: The central North Pacific case. J. Clim. 2004, 17, 4893–4901. [Google Scholar] [CrossRef]
- Karl, T.R.; Williams, C.N. An Approach to Adjusting Climatological Time Series for Discontinuous Inhomogeneities. J. Appl. Meteorol. 1987, 26, 1744–1763. [Google Scholar] [CrossRef]
- Basseville, M.; Nikiforov, I.V. Detection of Abrupt Changes: Theory and Application; Prentice Hall: Englewood Cliffs, NJ, USA, 1993; Volume 104. [Google Scholar]
- Solow, A.R. Testing for climate change: An application of the two-phase regression model. J. Appl. Meteorol. Climatol. 1987, 26, 1401–1405. [Google Scholar] [CrossRef]
- Storch, H.v. Misuses of statistical analysis in climate research. In Analysis of Climate Variability; Springer: Berlin/Heidelberg, Germany, 1999; pp. 11–26. [Google Scholar]
- Wang, F.; Zhao, G.; Mu, X.; Gao, P.; Sun, W. Regime shift identification of runoff and sediment loads in the Yellow River Basin, China. Water 2014, 6, 3012–3032. [Google Scholar] [CrossRef]
- Khan, M.; Dahal, V.; Jeong, H.; Markus, M.; Bhattarai, R. Relative Contribution of Climate Change and Anthropogenic Activities to Streamflow Alterations in Illinois. Water 2021, 13, 3226. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Taylor, W. A Pattern Test for Distinguishing between Autoregressive and Mean-Shift Data; Taylor Enterprises: Libertyville, IL, USA, 2000; pp. 1–14. [Google Scholar]
- Rodionov, S. A sequential method of detecting abrupt changes in the correlation coefficient and its application to Bering Sea climate. Climate 2015, 3, 474–491. [Google Scholar] [CrossRef]
- Rodionov, S.N. A comparison of two methods for detecting abrupt changes in the variance of climatic time series. Adv. Stat. Climatol. Meteorol. Oceanogr. 2016, 2, 63–78. [Google Scholar] [CrossRef]
- Afrin, S.; Gupta, A.; Farjad, B.; Ahmed, M.R.; Achari, G.; Hassan, Q.K. Development of land-use/land-cover maps using Landsat-8 and MODIS data, and their integration for hydro-ecological applications. Sensors 2019, 19, 4891. [Google Scholar] [CrossRef]
- Meshesha, T.W.; Wang, J.; Melaku, N.D.; McClain, C.N. Modelling groundwater quality of the Athabasca River Basin in the subarctic region using a modified SWAT model. Sci. Rep. 2021, 11, 13574. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Wang, J. Current and future hot-spots and hot-moments of nitrous oxide emission in a cold climate river basin. Environ. Pollut. 2018, 239, 648–660. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Du, X.; Wang, J. Assessing climate change impacts on fresh water resources of the Athabasca River Basin, Canada. Sci. Total Environ. 2017, 601, 425–440. [Google Scholar] [CrossRef] [PubMed]
- Hatfield Consultants; Kilgour & Associates Ltd.; Klohn Crippen Berger Ltd.; Western Resource Solutions. RAMP: Technical design and Rationale. 2009. Available online: ramp-alberta.org (accessed on 2 February 2023).
- Box, G.E.P.; Jenkins, G.M.; Bacon, D.W. Models for Forecasting Seasonal and Non-Seasonal Time Series; University of Wisconsin Madison—Department of Statistics: Madison, WI, USA, 1967. [Google Scholar]
- Box, G.E.P.; Pierce, D.A. Distribution of Residual Autocorrelations in Autoregressive-Integrated Moving Average Time Series Models. J. Am. Stat. Assoc. 1970, 65, 1509–1526. [Google Scholar] [CrossRef]
- Breiman, L. Rejoinder: Arcing classifiers. Ann. Stat. 1998, 26, 841–849. [Google Scholar] [CrossRef]
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API design for machine learning software: Experiences from the scikit-learn project. In ECML PKDD Workshop: Languages for Data Mining and Machine Learning; MIT Press: Cambridge, MA, USA, 2013; pp. 108–122. [Google Scholar]
- Brockwell, P.J.; Davis, R.A. Time Series: Theory and Methods; Springer: New York, NY, USA, 1991. [Google Scholar]
- Hipel, K.W.; McLeod, A.I. Time Series Modelling of Water Resources and Environmental Systems; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Dabral, P.; Murry, M.Z. Modelling and Forecasting of Rainfall Time Series Using SARIMA. Environ. Process. 2017, 4, 399–419. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Good, R.; Fletcher, H.J. Reporting explained variance. J. Res. Sci. Teach. 1981, 18, 1–7. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Prasad, N.N.; Rao, J.N. The estimation of the mean squared error of small-area estimators. J. Am. Stat. Assoc. 1990, 85, 163–171. [Google Scholar] [CrossRef]
- Steel, R.G.D.; Torrie, J.H. Principles and procedures of statistics. In Principles and Procedures of Statistics; McGraw-Hill Book Company, Inc.: New York, NY, USA; Toronto, ON, Canada; London, UK, 1960. [Google Scholar]
- Carter, T.; Parry, M.; Harasawa, H.; Nishioka, S. IPCC technical guidelines for assessing climate change impacts and adaptations. In Part of the IPCC Special Report to the First Session of the Conference of the Parties to the UN Framework Convention on Climate Change, Intergovernmental Panel on Climate Change. Department of Geography, University College London, UK and Center for Global Environmental Research, National Institute for Environmental Studies, Tsukuba, Japan; Publications of the Natural Resources Institute Finland: Helsinki, Finland, 1994; Volume 59. [Google Scholar]
- Dastour, H.; Ghaderpour, E.; Hassan, Q.K. A Combined Approach for Monitoring Monthly Surface Water/Ice Dynamics of Lesser Slave Lake Via Earth Observation Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6402–6417. [Google Scholar] [CrossRef]
- Terrell, G.R.; Scott, D.W. Variable kernel density estimation. Ann. Stat. 1992, 20, 1236–1265. [Google Scholar] [CrossRef]
- Epanechnikov, V.A. Non-parametric estimation of a multivariate probability density. Theory Probab. Its Appl. 1969, 14, 153–158. [Google Scholar]
- Scott, D.W. Scott’s rule. Computational Statistics. Wiley Interdiscip. Rev. 2010, 2, 497–502. [Google Scholar] [CrossRef]
- Kozak, R.; Kozak, A.; Staudhammer, C.; Watts, S. Introductory Probability and Statistics, Revised Edition: Applications for Forestry and the Natural Sciences; CABI: Wallingford, UK, 2019. [Google Scholar]
- Han, J.; Kamber, M.; Pei, J. Getting to know your data. In Data Mining; Morgan Kaufmann: Boston, MA, USA, 2012; Volume 2, pp. 39–82. [Google Scholar]
- Shao, J. Linear model selection by cross-validation. J. Am. Stat. Assoc. 1993, 88, 486–494. [Google Scholar] [CrossRef]
- Schumacher, M.; Holländer, N.; Sauerbrei, W. Resampling and cross-validation techniques: A tool to reduce bias caused by model building? Stat. Med. 1997, 16, 2813–2827. [Google Scholar] [CrossRef]

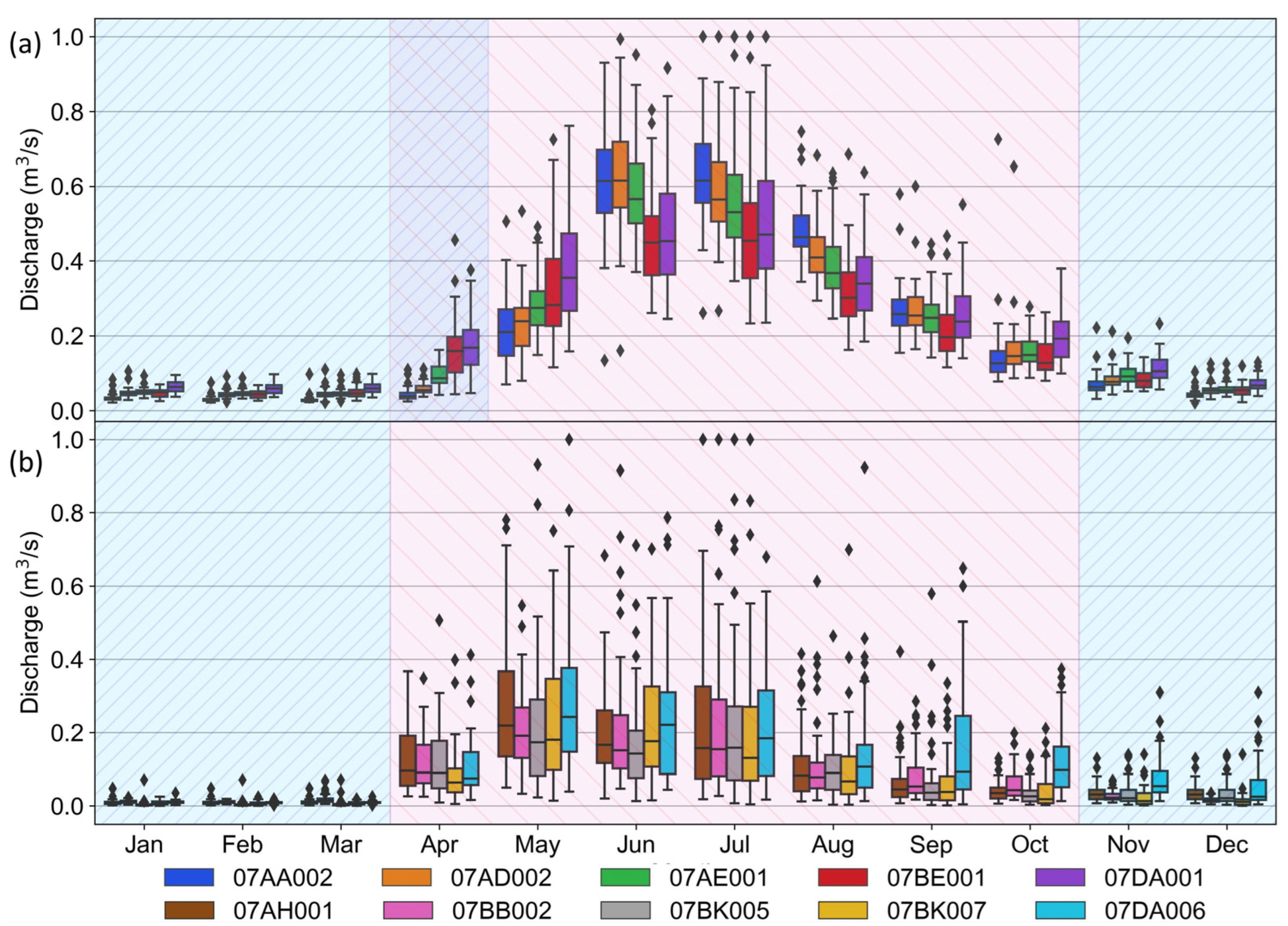

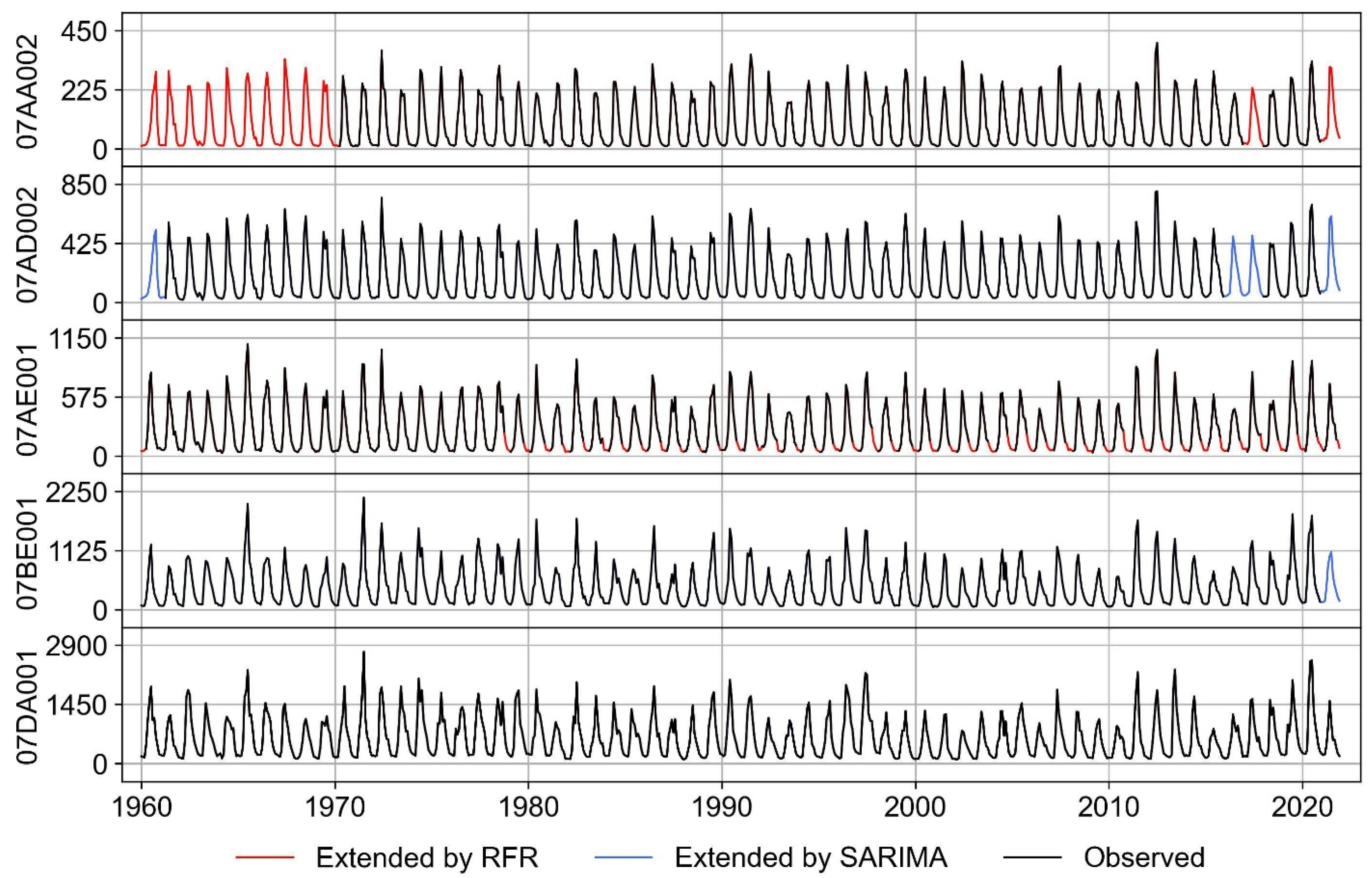
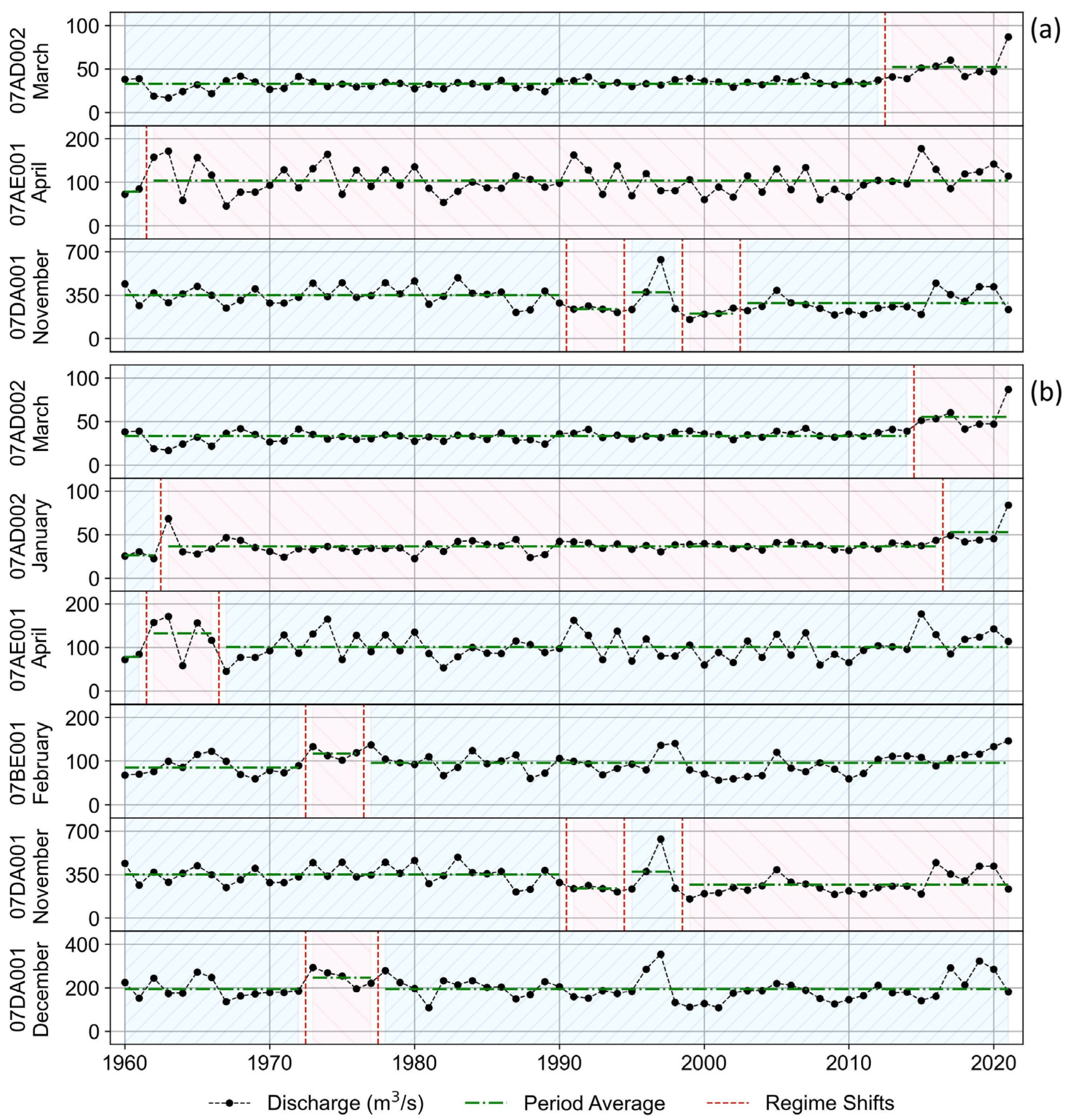
| Set | ID | Name | Considered Period for This Study | Gross Drainage Area (km2) | Elevation (m) |
|---|---|---|---|---|---|
| 07AA002 | Athabasca River near Jasper | 1960–2021 | 3870 | 1041 | |
| 07AD002 | Athabasca River at Hinton | 1960–2021 | 9760 | 963 | |
| Train | 07AE001 | Athabasca River near Windfall | 1960–2021 | 19,600 | 735 |
| 07BE001 | Athabasca River at Athabasca | 1960–2021 | 74,600 | 513 | |
| 07DA001 | Athabasca River below Fort McMurray | 1960–2021 | 133,000 | 246 | |
| 07AH001 | Freeman River near Fort Assiniboine | 1965–2020 | 1660 | 661 | |
| 07BB002 | Pembina River near Entwistle | 1960–2015 | 4400 | 727 | |
| Test | 07BK005 | Saulteaux River near Spurfield | 1969–2015 | 2600 | 585 |
| 07BK007 | Driftwood River near the Mouth | 1968–2020 | 2100 | 569 | |
| 07DA006/S38 1 | Steepbank River near Fort McMurray | 1972–2021 | 1320 | 277 |
| ID | Season | Growth Rate ε | Relative Difference ε |
|---|---|---|---|
| 07AA002 | Cold | 0.322 | 0.130 |
| 07AA002 | Warm | 0.215 | 0.135 |
| 07AD002 | Cold | 0.231 | 0.160 |
| 07AD002 | Warm | 0.257 | 0.202 |
| 07AE001 | Cold | 0.293 | 0.197 |
| 07AE001 | Warm | 0.193 | 0.174 |
| 07BE001 | Cold | 0.288 | 0.202 |
| 07BE001 | Warm | 0.285 | 0.174 |
| 07DA001 | Cold | 0.271 | 0.200 |
| 07DA001 | Warm | 0.350 | 0.230 |
| General | Cold | 0.288 | 0.197 |
| General | Warm | 0.257 | 0.174 |
| Metrics | 07AA002 | 07AD002 | 07AE001 | 07BE001 |
|---|---|---|---|---|
| Train: EVS | 1.00 ± 2.32 × 10−4 | 0.901 | 0.99 ± 1.50 × 10−3 | 0.789 |
| Test: EVS | 0.98 ± 2.20 × 10−3 | 0.96 ± 4.15 × 10−2 | ||
| Train: MAE | 2.89 ± 9.64 × 10−2 | 30.692 | 9.74 ± 1.01 × 100 | 104.842 |
| Test: MAE | 7.60 ± 6.00 × 10−1 | 27.83 ± 8.83 × 100 | ||
| Train: MSE | 23.16 ± 2.01 × 100 | 2982.181 | 294.80 ± 8.40 × 101 | 30,943.826 |
| Test: MSE | 159.69 ± 2.07 × 101 | 2563.86 ± 2.70 × 103 | ||
| Train: R2 | 1.00 ± 2.32 × 10−4 | 0.901 | 0.99 ± 1.50 × 10−3 | 0.788 |
| Test: R2 | 0.98 ± 2.21 × 10−3 | 0.95 ± 4.31 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dastour, H.; Gupta, A.; Achari, G.; Hassan, Q.K. A Robust Regime Shift Change Detection Algorithm for Water-Flow Dynamics. Water 2023, 15, 1571. https://doi.org/10.3390/w15081571
Dastour H, Gupta A, Achari G, Hassan QK. A Robust Regime Shift Change Detection Algorithm for Water-Flow Dynamics. Water. 2023; 15(8):1571. https://doi.org/10.3390/w15081571
Chicago/Turabian StyleDastour, Hatef, Anil Gupta, Gopal Achari, and Quazi K. Hassan. 2023. "A Robust Regime Shift Change Detection Algorithm for Water-Flow Dynamics" Water 15, no. 8: 1571. https://doi.org/10.3390/w15081571







