A Model for Assessing the Importance of Runoff Forecasts in Periodic Climate on Hydropower Production
Abstract
:1. Introduction
2. Model Framework
2.1. Assessment Model
2.2. Ensemble Forecasting with Biennial Periodicity
2.3. Optimisation Model for Cascade Hydropower Stations
2.4. Performance Indicators
3. Case Study
4. Results
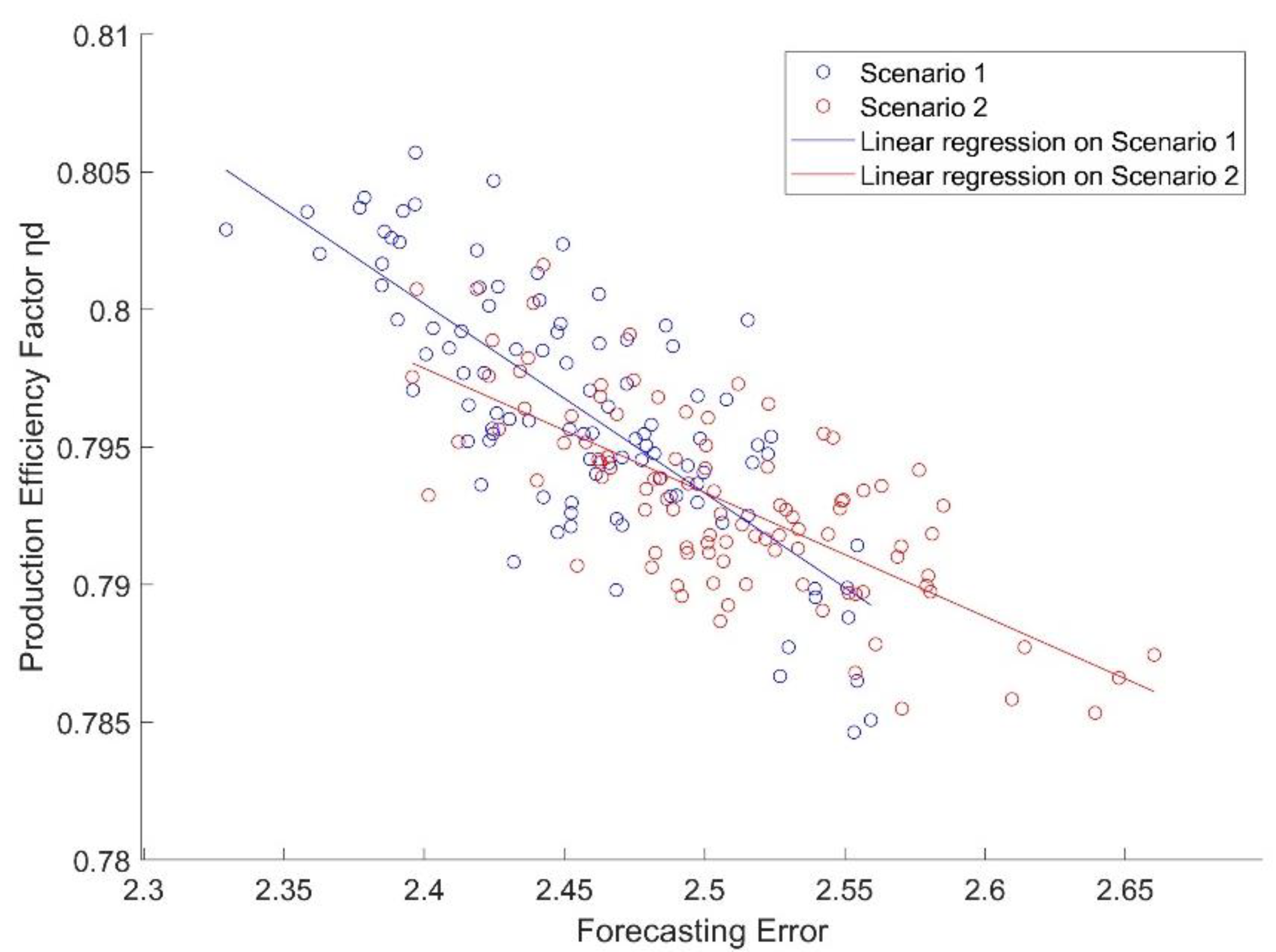
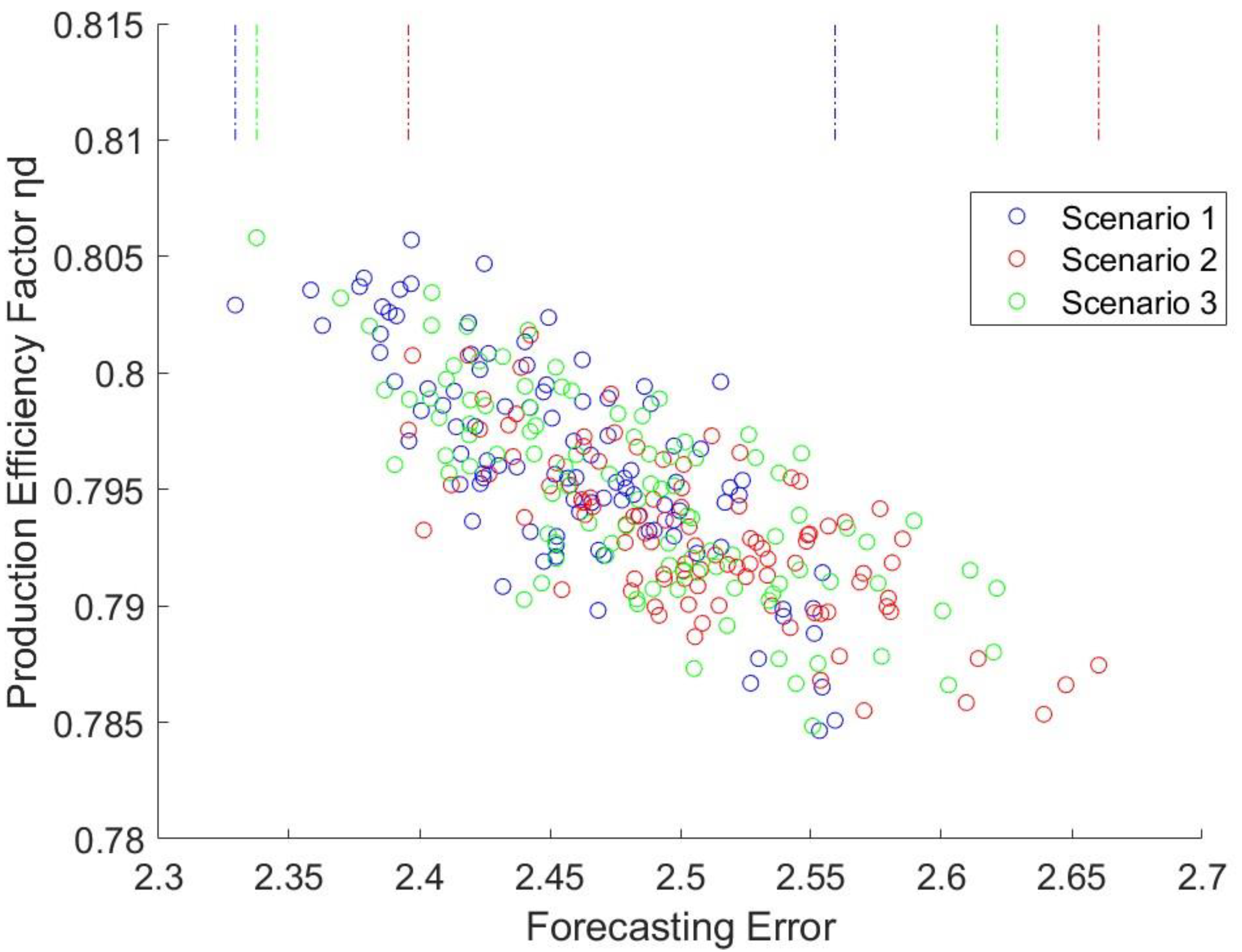
4.1. Assessment of the Effects of Forecast Error on Production Efficiency in the Dalälven River Basin
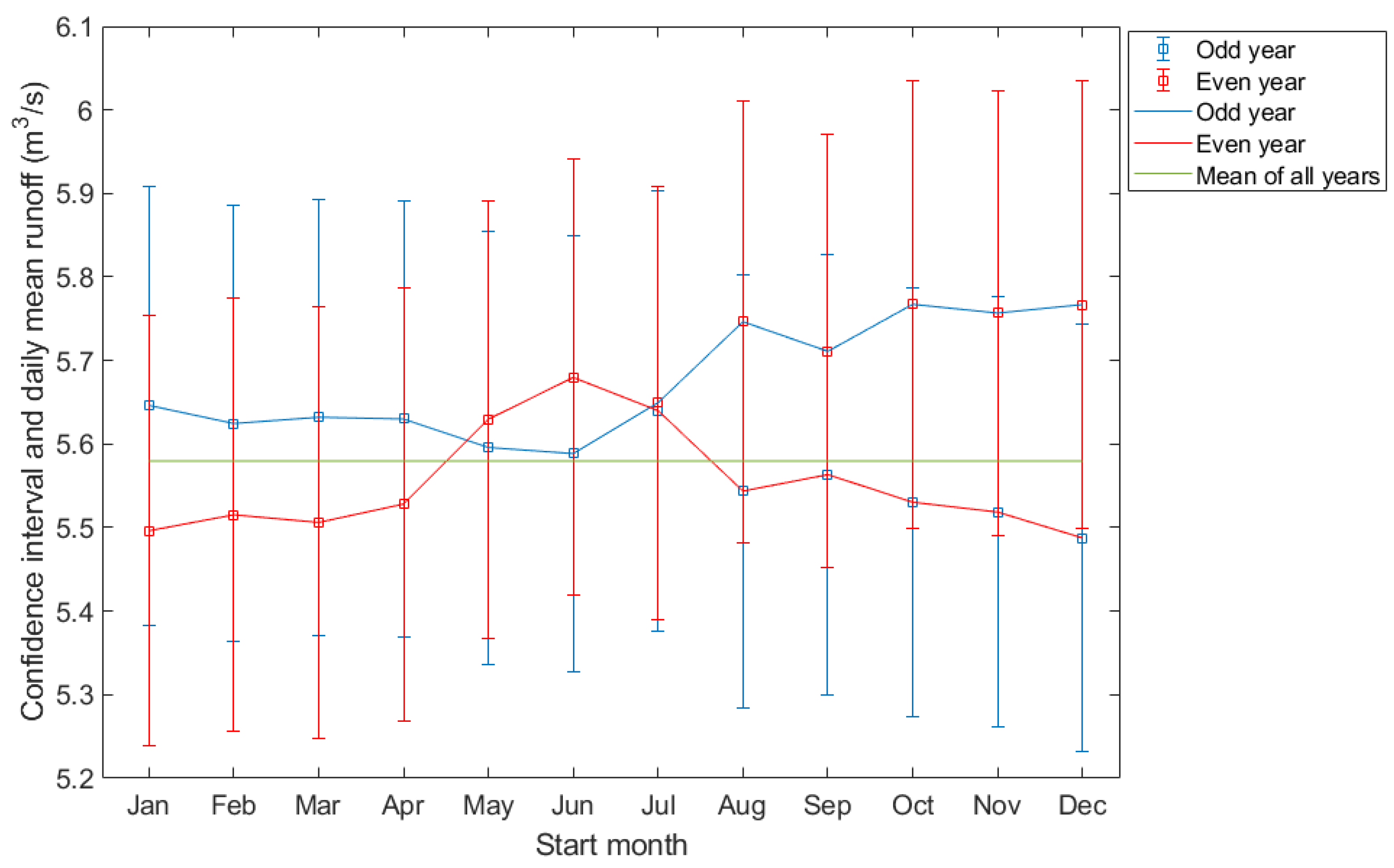
4.2. Start-Month Impact on the Biennial Periodicity
5. Conclusions and Discussions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, J.; Wang, X.; Li, Y.; Wang, Y.; Zhang, H. Hydropower plant operation rules optimization response to climate change. Energy 2018, 160, 886–897. [Google Scholar] [CrossRef]
- Haguma, D.; Leconte, R.; Côté, P.; Krau, S.; Brissette, F. Optimal Hydropower Generation Under Climate Change Conditions for a Northern Water Resources System. Water Resour. Manag. 2014, 28, 4631–4644. [Google Scholar] [CrossRef]
- Tarroja, B.; AghaKouchak, A.; Samuelsen, S. Quantifying climate change impacts on hydropower generation and implications on electric grid greenhouse gas emissions and operation. Energy 2016, 111, 295–305. [Google Scholar] [CrossRef]
- de Queiroz, A.R.; Faria, V.A.D.; Lima, L.M.M.; Lima, J.W.M. Hydropower revenues under the threat of climate change in Brazil. Renew. Energy 2019, 133, 873–882. [Google Scholar] [CrossRef]
- Anghileri, D.; Botter, M.; Castelletti, A.; Weigt, H.; Burlando, P. A Comparative Assessment of the Impact of Climate Change and Energy Policies on Alpine Hydropower. Water Resour. Res. 2018, 54, 9144–9161. [Google Scholar] [CrossRef]
- Forrest, K.; Tarroja, B.; Chiang, F.; AghaKouchak, A.; Samuelsen, S. Assessing climate change impacts on California hydropower generation and ancillary services provision. Clim. Change 2018, 151, 395–412. [Google Scholar] [CrossRef]
- van Vliet, M.T.H.; Wiberg, D.; Leduc, S.; Riahi, K. Power-generation system vulnerability and adaptation to changes in climate and water resources. Nat. Clim. Chang. 2016, 6, 375–380. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013—The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Foster, K. Hydrological Seasonal Forecasting; Lund University: Lund, Sweden, 2019. [Google Scholar]
- Uvo, C.B.; Foster, K.; Olsson, J. The spatio-temporal influence of atmospheric teleconnection patterns on hydrology in Sweden. J. Hydrol. Reg. Stud. 2021, 34, 100782. [Google Scholar] [CrossRef]
- Wörman, A.; Lindström, G.; Riml, J. The power of runoff. J. Hydrol. 2017, 548, 784–793. [Google Scholar] [CrossRef]
- Schmidt, R.; Petrovic, S.; Güntner, A.; Barthelmes, F.; Wünsch, J.; Kusche, J. Periodic components of water storage changes from GRACE and global hydrology models. J. Geophys. Res. Solid Earth 2008, 113, 1–14. [Google Scholar] [CrossRef]
- Poveda, G.; Mesa, O.J. Feedbacks between Hydrological Processes in Tropical South America and Large-Scale Ocean–Atmospheric Phenomena. J. Clim. 1997, 10, 2690–2702. [Google Scholar] [CrossRef]
- Rajagopalan, B.; Lall, U. Interannual variability in western US precipitation. J. Hydrol. 1998, 210, 51–67. [Google Scholar] [CrossRef]
- Krokhin, V.; Luxemburg, W.M.J. Temperatures and precipitation totals over the Russian Far East and Eastern Siberia: Long-term variability and its links to teleconnection indices. Hydrol. Earth Syst. Sci. 2007, 11, 1831–1841. [Google Scholar] [CrossRef]
- Lopez, M.G.; Crochemore, L.; Pechlivanidis, I.G. Benchmarking an operational hydrological model for providing seasonal forecasts in Sweden. Hydrol. Earth Syst. Sci. 2021, 25, 1189–1209. [Google Scholar] [CrossRef]
- Voisin, N.; Dyreson, A.; Fu, T.; O’Connell, M.; Turner, S.W.; Zhou, T.; Macknick, J. Impact of climate change on water availability and its propagation through the Western U.S. power grid. Appl. Energy 2020, 276, 115467. [Google Scholar] [CrossRef]
- Chowdhury, A.F.M.K.; Dang, T.D.; Nguyen, H.T.T.; Koh, R.; Galelli, S. The Greater Mekong’s Climate-Water-Energy Nexus: How ENSO-Triggered Regional Droughts Affect Power Supply and CO2 Emissions. Earth’s Futur. 2021, 9, 1–19. [Google Scholar] [CrossRef]
- Siala, K.; Chowdhury, A.K.; Dang, T.D.; Galelli, S. Solar energy and regional coordination as a feasible alternative to large hydropower in Southeast Asia. Nat. Commun. 2021, 12, 4159. [Google Scholar] [CrossRef]
- Marco, J.B.; Harboe, R.; Salas, J.D. Stochastic Hydrology and its Use in Water Resources Systems Simulation and Optimization; Springer: Dordrecht, The Netherlands, 1993. [Google Scholar] [CrossRef]
- Feiring, B.R.; Sastri, T.; Sim, L.S.M. A stochastic programming model for water resource planning. Math. Comput. Model. 1998, 27, 1–7. [Google Scholar] [CrossRef]
- Yevjevich, V. Stochastic models in hydrology. Stoch. Hydrol. Hydraul. 1987, 1, 17–36. [Google Scholar] [CrossRef]
- Tiberi-Wadier, A.L.; Goutal, N.; Ricci, S.; Sergent, P.; Taillardat, M.; Bouttier, F.; Monteil, C. Strategies for hydrologic ensemble generation and calibration: On the merits of using model-based predictors. J. Hydrol. 2021, 599, 126233. [Google Scholar] [CrossRef]
- Wu, L.; Seo, D.-J.; Demargne, J.; Brown, J.D.; Cong, S.; Schaake, J. Generation of ensemble precipitation forecast from single-valued quantitative precipitation forecast for hydrologic ensemble prediction. J. Hydrol. 2011, 399, 281–298. [Google Scholar] [CrossRef]
- Yuan, F.; Berndtsson, R.; Zhang, L.; Uvo, C.B.; Hao, Z.; Wang, X.; Yasuda, H. Hydro Climatic Trend and Periodicity for the Source Region of the Yellow River. J. Hydrol. Eng. 2015, 20, 05015003. [Google Scholar] [CrossRef]
- Engström, J.; Uvo, C.B. Effect of Northern Hemisphere Teleconnections on the Hydropower Production in Southern Sweden. J. Water Resour. Plan. Manag. 2016, 142, 5015008. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Prestwich, S.; Rossi, R.; Tarim, S.A.; Hnich, B. Mean-based error measures for intermittent demand forecasting. Int. J. Prod. Res. 2014, 52, 6782–6791. [Google Scholar] [CrossRef]
- Kokko, V.; Hjerthén, P.; Ingfält, H.; Löwen, K.E.; Sjögren, A. Development of Dalälven hydro power scheme in Sweden. Houille Blanche 2015, 6368, 5–14. [Google Scholar] [CrossRef]
- Lindström, G.; Pers, C.; Rosberg, J.; Strömqvist, J.; Arheimer, B. Development and testing of the HYPE (Hydrological Predictions for the Environment) water quality model for different spatial scales. Hydrol. Res. 2010, 41, 295–319. [Google Scholar] [CrossRef]



| Parameter | Definition | Parameter Value in the Example Application |
|---|---|---|
| Time horizon of optimisation: the duration of the forecasted time series placed into one optimisation procedure. | = 90 (days) | |
| Period of simulation: the maximum shift in time of the horizon in the receding horizon approach; . | = 90 (days) | |
| Updating period: the time during which the decided turbine discharges are applied, whereafter the reservoir levels are updated and new decisions are taken; . | = 2 (days) | |
| Numerical time step used to represent the watershed dynamics and to move between the states used in the optimization. | = 0.5 (days) | |
| . Index for the numerical time step for water dynamics; . | = 180 | |
| Index for the reservoirs. | = 49 | |
| . Index for the repetition number of one updating period simulation with different stochastic runoff forecasts, which was used to make the average decision. | = 10 | |
| . Index for the simulation time step in order to progress over the simulation period . The number of updating time steps is . | = 45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, S.; Wörman, A.; Riml, J.; Bottacin-Busolin, A. A Model for Assessing the Importance of Runoff Forecasts in Periodic Climate on Hydropower Production. Water 2023, 15, 1559. https://doi.org/10.3390/w15081559
Hao S, Wörman A, Riml J, Bottacin-Busolin A. A Model for Assessing the Importance of Runoff Forecasts in Periodic Climate on Hydropower Production. Water. 2023; 15(8):1559. https://doi.org/10.3390/w15081559
Chicago/Turabian StyleHao, Shuang, Anders Wörman, Joakim Riml, and Andrea Bottacin-Busolin. 2023. "A Model for Assessing the Importance of Runoff Forecasts in Periodic Climate on Hydropower Production" Water 15, no. 8: 1559. https://doi.org/10.3390/w15081559
APA StyleHao, S., Wörman, A., Riml, J., & Bottacin-Busolin, A. (2023). A Model for Assessing the Importance of Runoff Forecasts in Periodic Climate on Hydropower Production. Water, 15(8), 1559. https://doi.org/10.3390/w15081559






