Analytical Solution of the One-Dimensional Transport of Ionic Contaminants in Porous Media with Time-Varying Velocity
Abstract
:1. Introduction
2. Basic Assumptions and Calculation Model
2.1. Basic Assumptions
2.2. Governing Equations and Solution Conditions
2.3. Solution of the Model
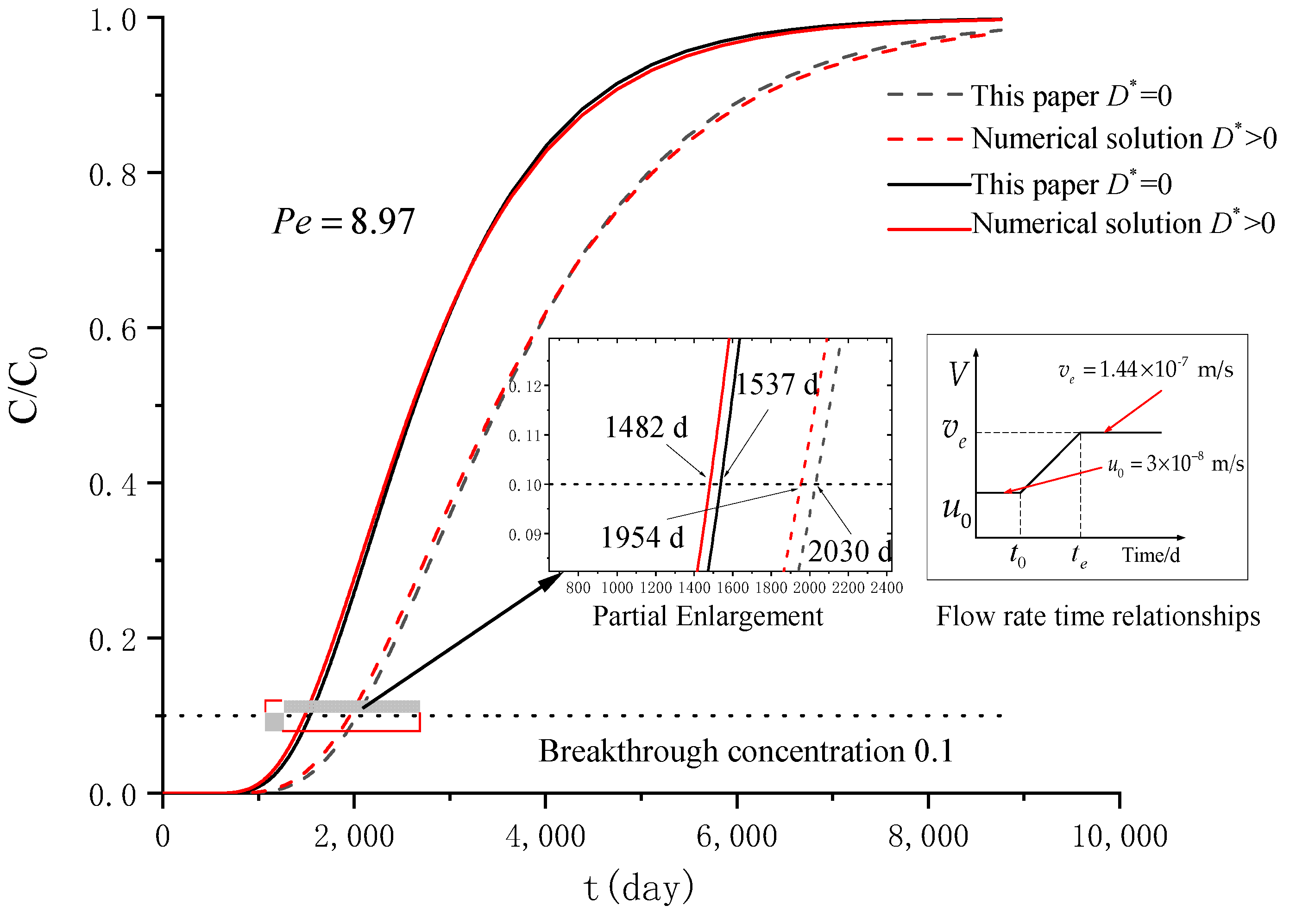
3. Verification
4. Parameter Impact Analysis
- (1)
- Influence coefficient varies, maximum velocity varies, and the time to maximum velocity is constant.
- (2)
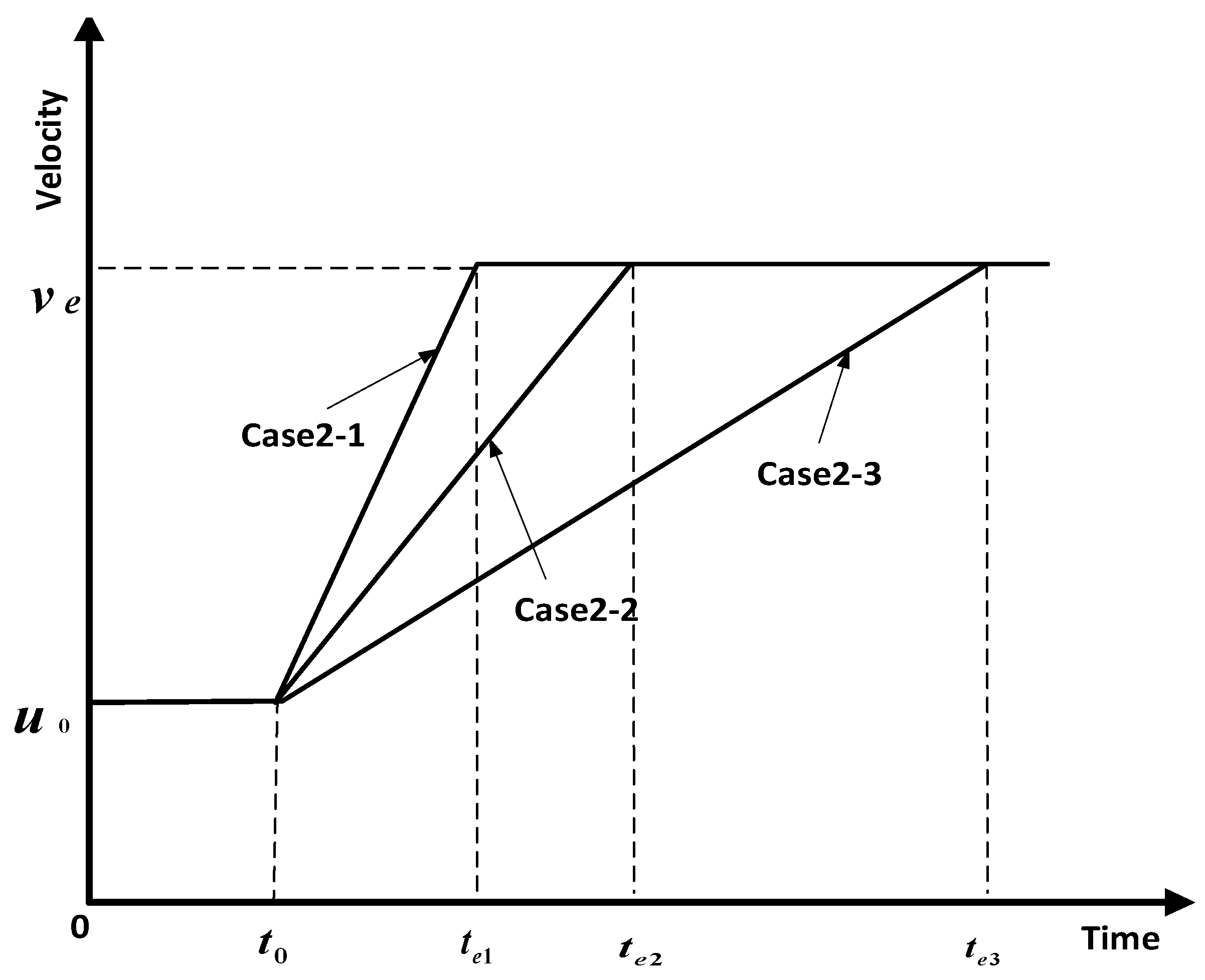
- Influence coefficient varies, maximum velocity is constant, and the time to maximum velocity varies.
- (3)
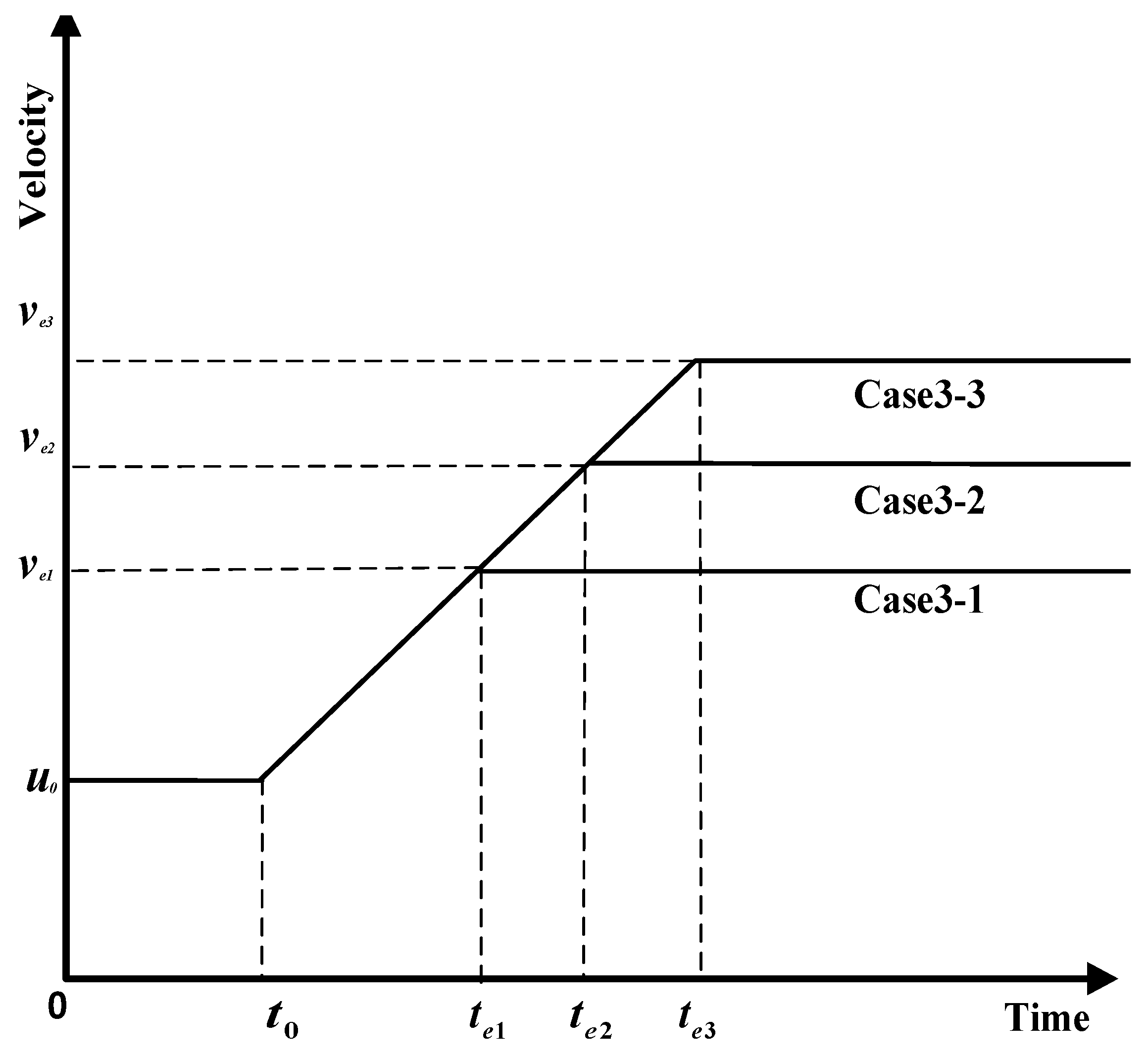
- Influence coefficient is constant, maximum velocity varies, and the time to maximum velocity varies.
4.1. Analysis of Parameter Influence in Group 1
4.2. Analysis of Parameter Influence in Group 2
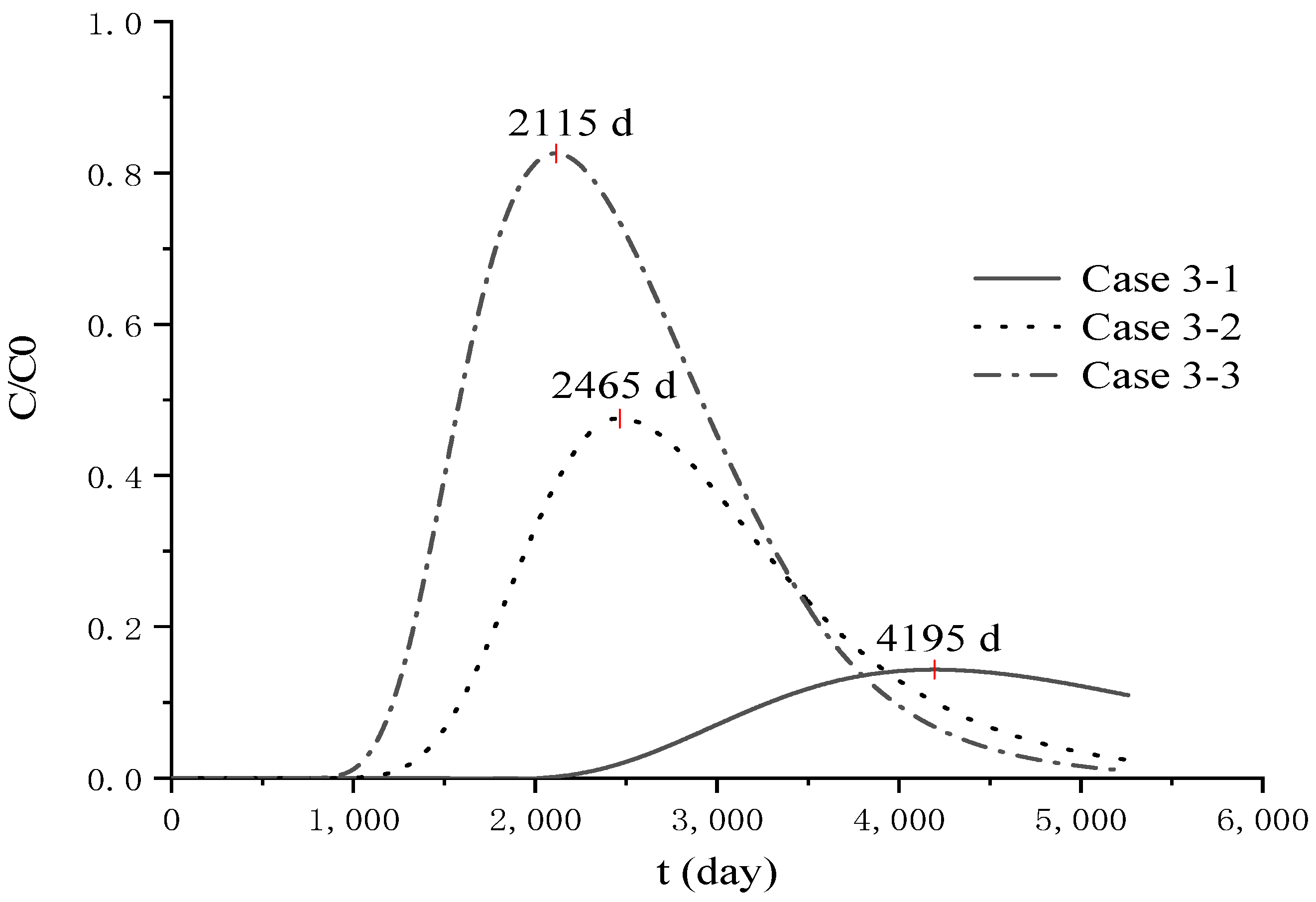
4.3. Analysis of Parameter Influence in Group 3
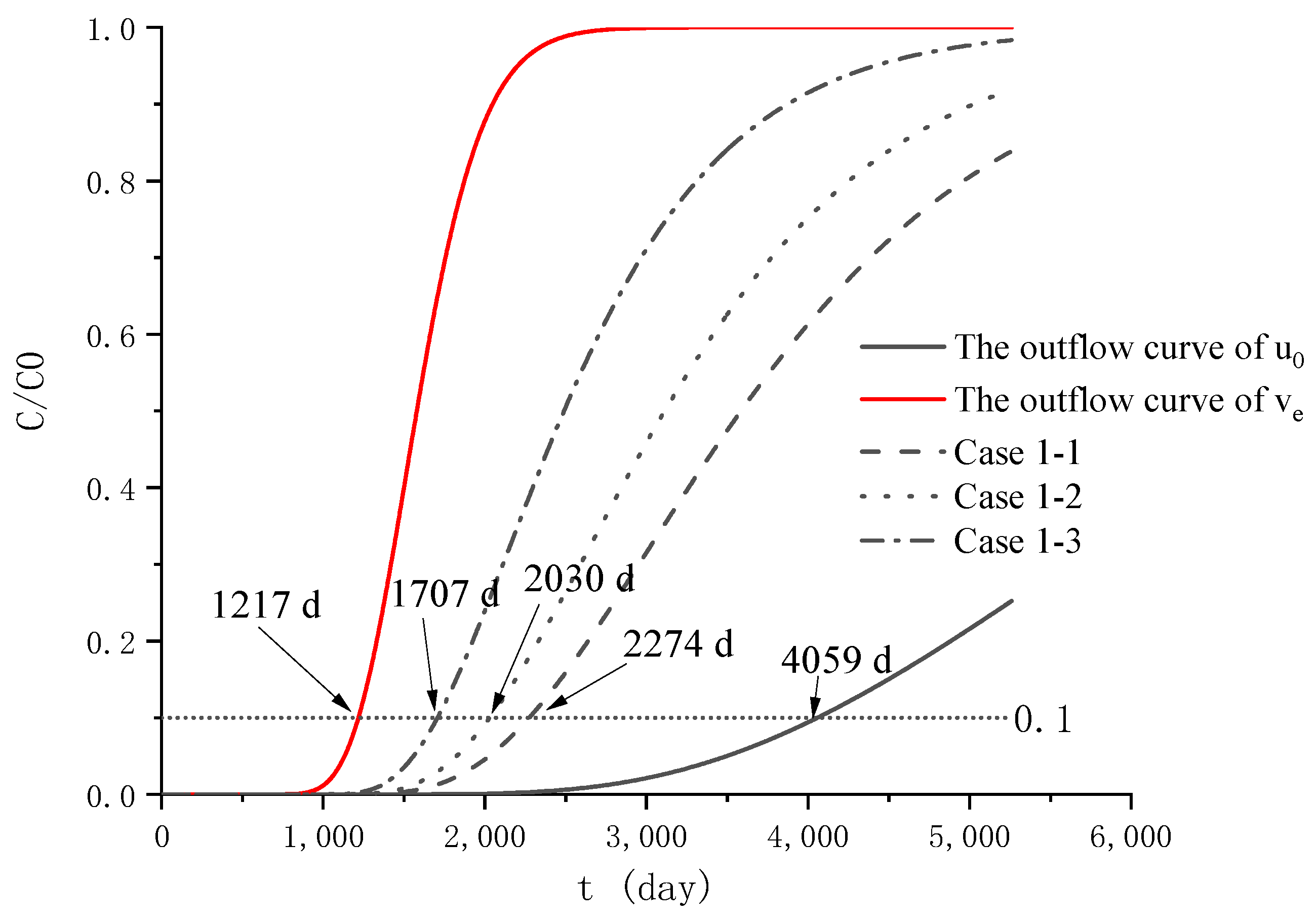
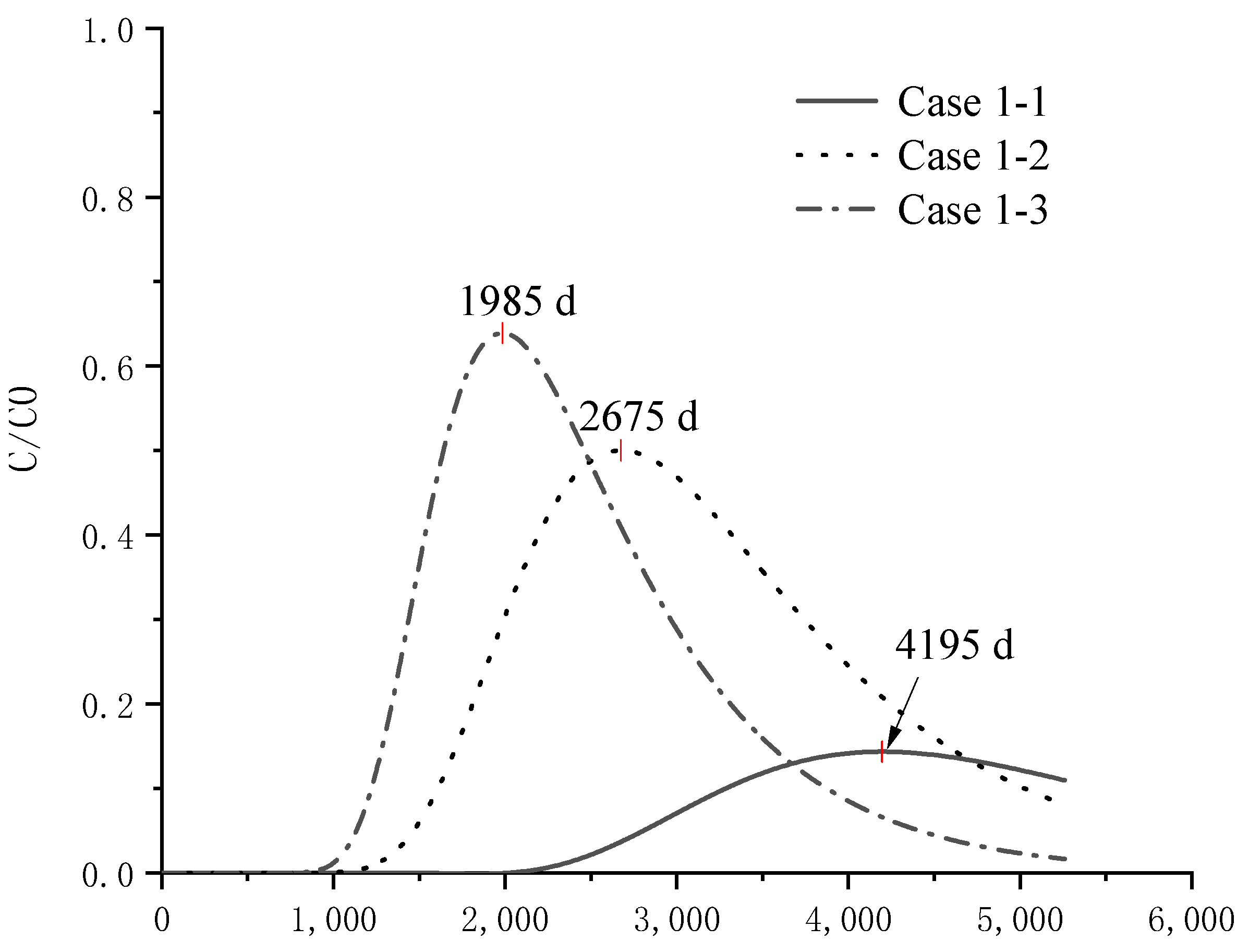
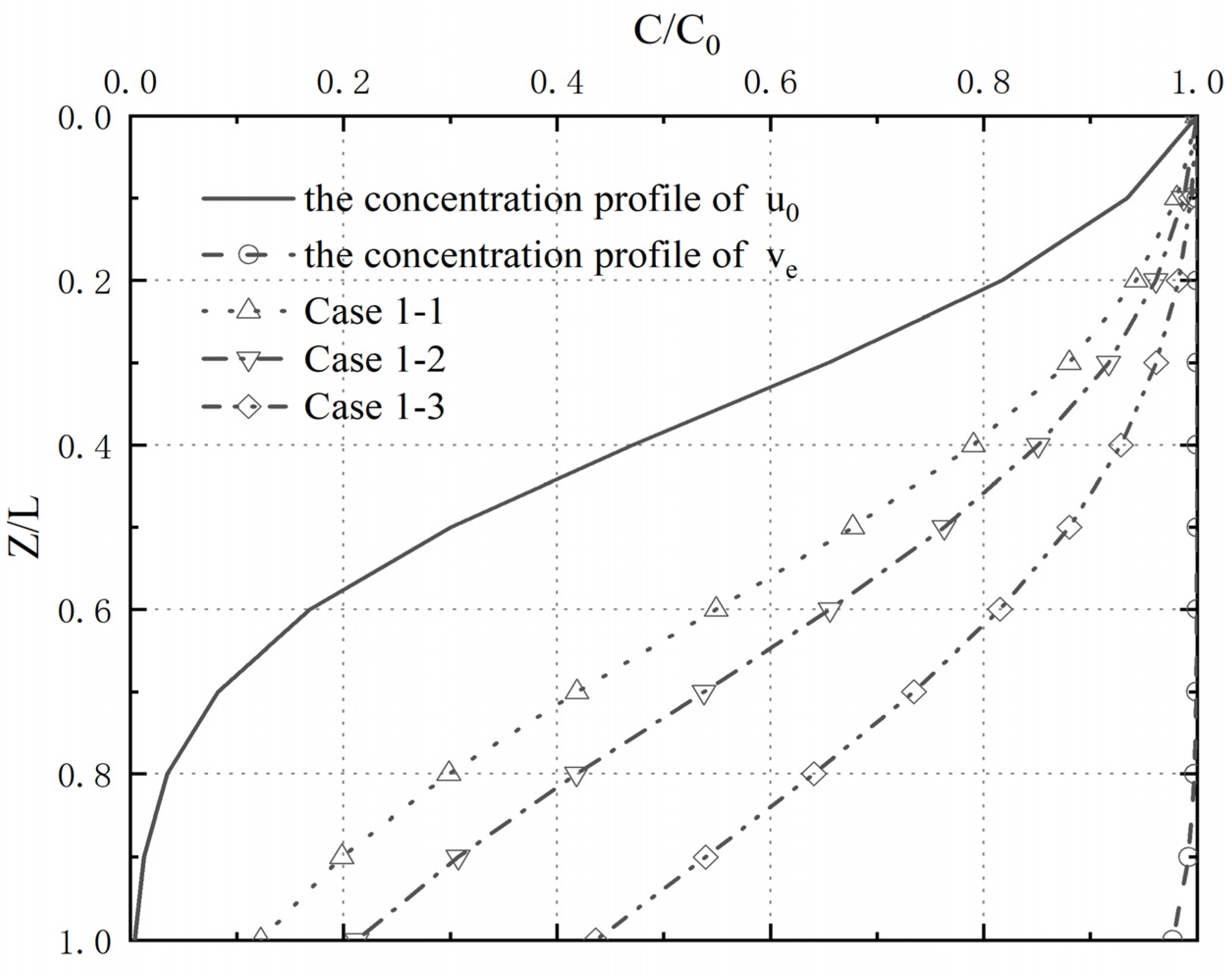
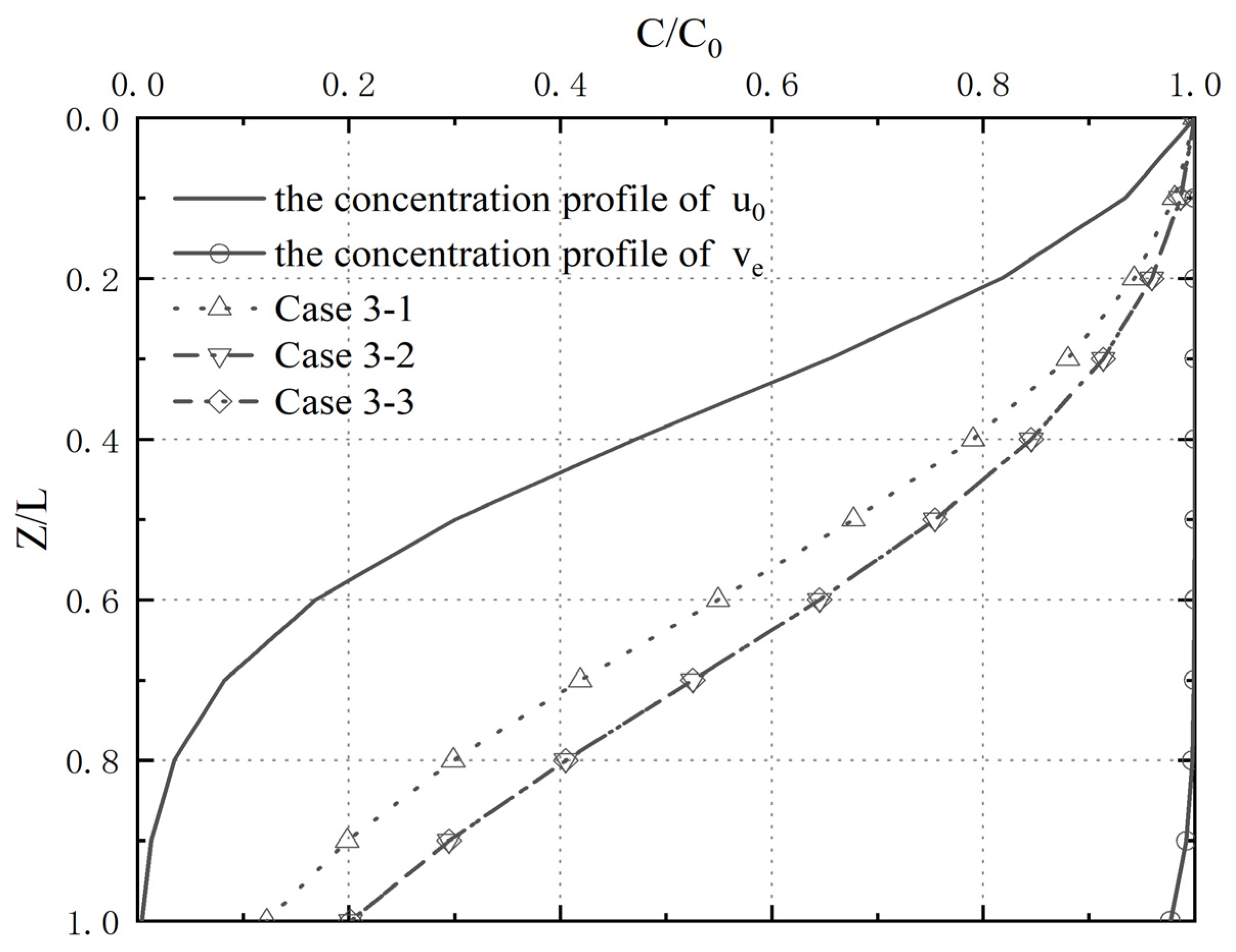
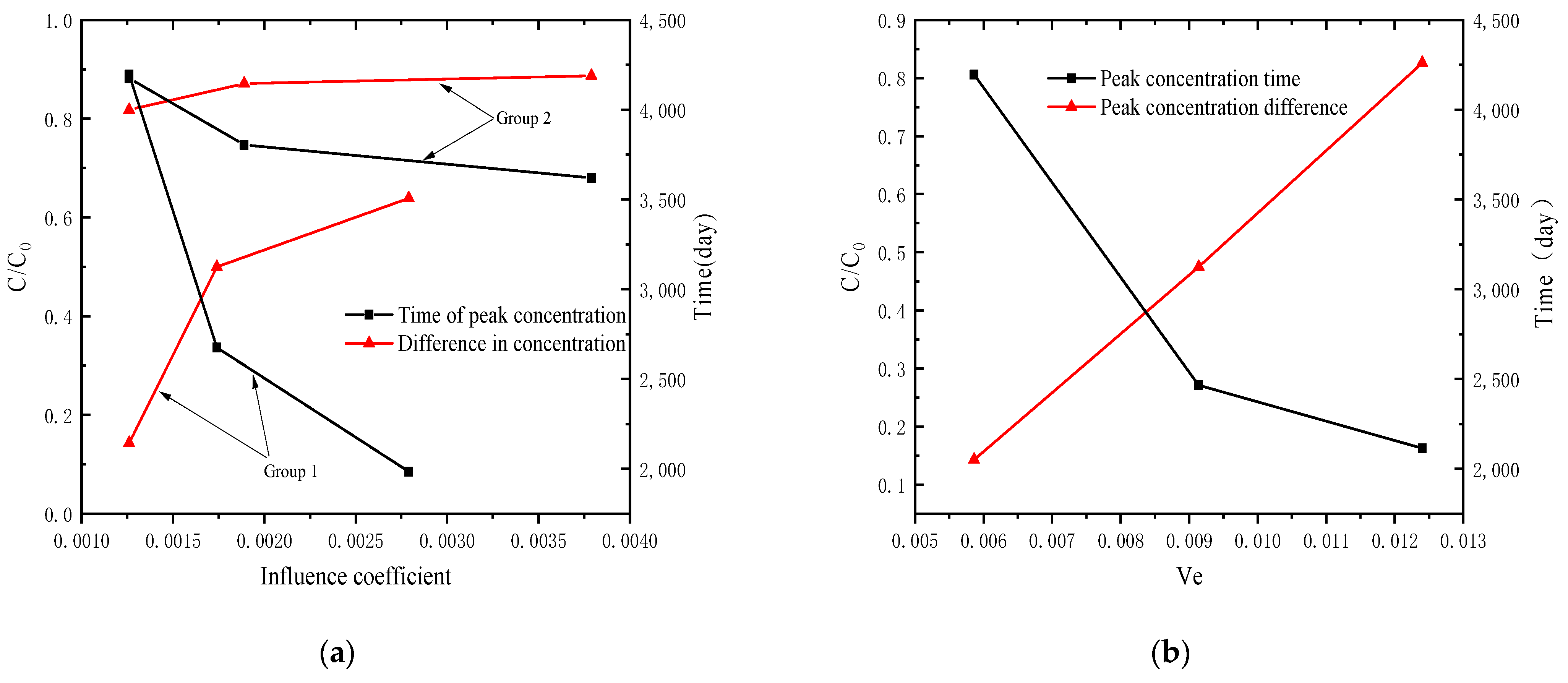
4.4. Analysis of Pollutant Concentration Differences
5. Example Analysis
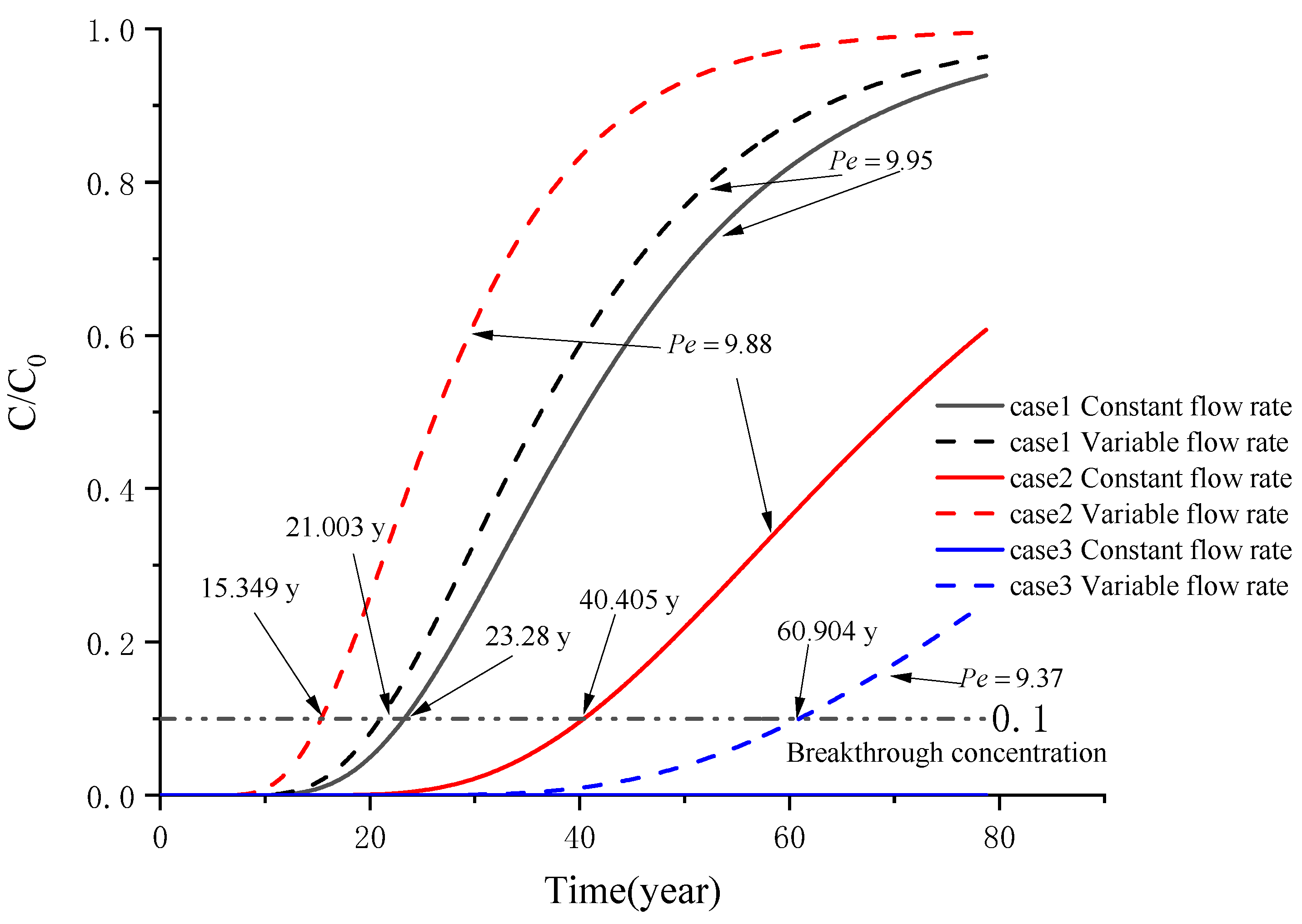
5.1. Analysis of a Soil–Attapulgite Barrier
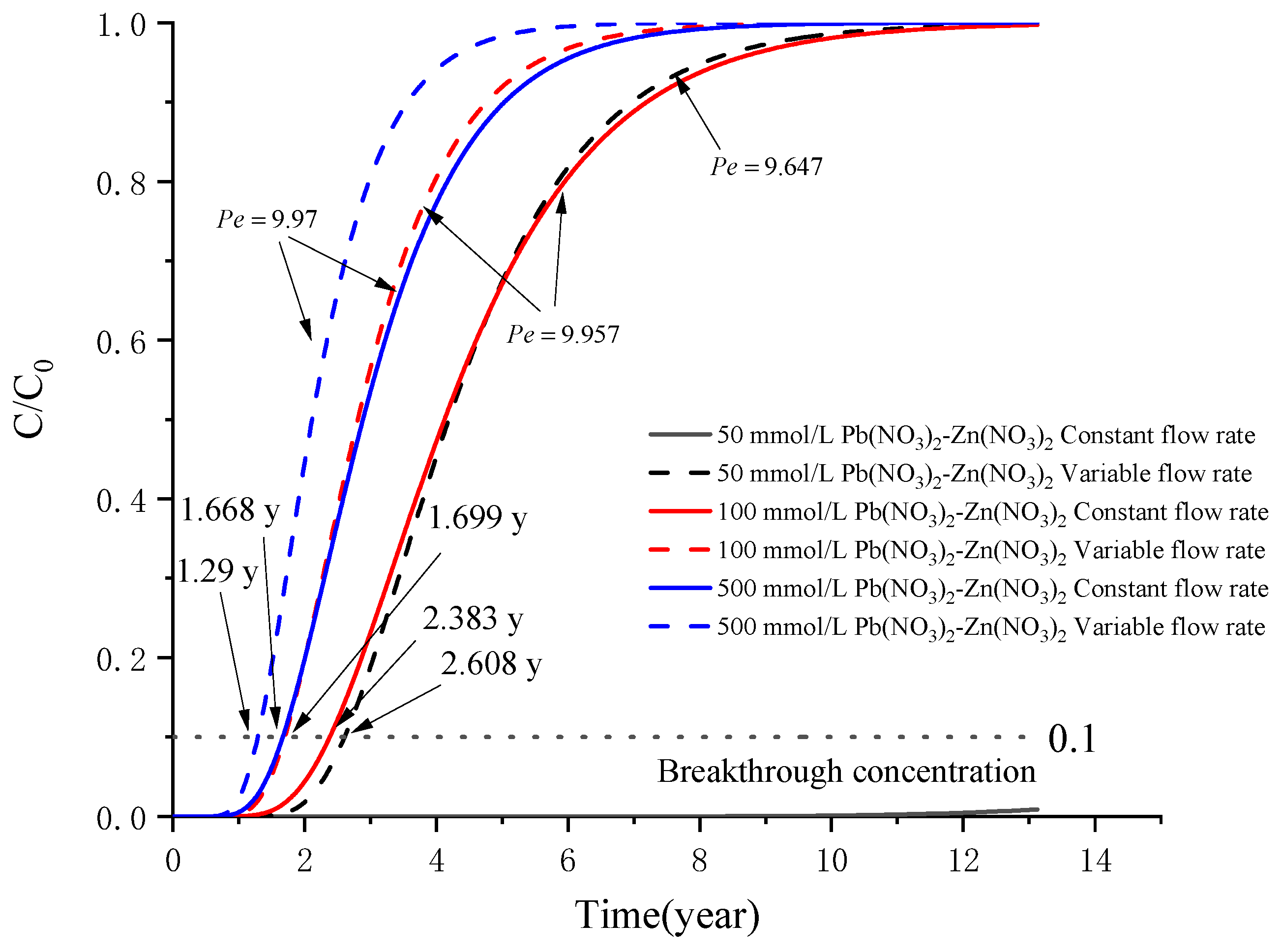
5.2. Analysis of a Sand–Bentonite Mixture (SBM) Barrier
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Xiang, Y.; Chen, W. Heavy metal content in the bark of camphora tree in Xiangtan and its environmental significance. Appl. Ecol. Environ. Res. 2019, 17, 9827–9835. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, J.; Zhang, W.; Liu, M.; Shi, Z. Research progress of remediation technology for heavy metal chromium(VI) contamination in soils. Soil Bull. 2022, 53, 1220–1227. [Google Scholar]
- Zeng, X.; Su, J.; Wang, H.; Gao, T. Centrifuge Modeling of Chloride Ions Completely Breakthrough Kaolin Clay Liner. Sustainability 2022, 14, 6976. [Google Scholar] [CrossRef]
- Du, Y.-J.; Jin, F.; Liu, S.-Y.; Chen, L.; Zhang, F. Review of stabilization/solidification technique for remediation of heavy metals contaminated lands. Yantu Lixue = Rock Soil Mech. 2011, 32, 116–124. [Google Scholar]
- Liu, S. Geotechnical investigation and remediation for industrial contaminated sites. Chin. J. Geotech. Eng. 2018, 40, 1–37. [Google Scholar]
- Liu, Y.; Bouazza, A.; Gates, W.; Rowe, R. Hydraulic performance of geosynthetic clay liners to sulfuric acid solutions. Geotext. Geomembr. 2015, 43, 14–23. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, J.; Jiang, W.; Huang, Z.; Xiang, Y.; Zeng, F. Study on the Heavy Metal Pollution Evaluation and Countermeasures of Middle Size and Small Cities in Typical Drainage Area-Taking Xiangtan Reach of Xiangjiang River as an Example. Res. J. Chem. Environ. 2012, 16, 172–179. [Google Scholar]
- Zhang, Y.; Xiang, Y.; Yu, G.; Yuan, K.; Wang, X.; Mo, H. Classification of environmental disaster in Hunan Province. Disaster. Adv. 2012, 5, 1756–1759. [Google Scholar]
- Zhang, Y.; Huang, F. Indicative significance of the magnetic susceptibility of substrate sludge to heavy metal pollution of urban lakes. ScienceAsia 2021, 47, 374. [Google Scholar] [CrossRef]
- Fetter, C.W.; Boving, T.; Kreamer, D. Contaminant Hydrogeology; Waveland Press: Long Grove, IL, USA, 2017. [Google Scholar]
- Zeng, X.; Li, Y.; Liu, X.; Yao, J.; Lin, Z. Relationship between the Shear Strength and the Depth of Cone Penetration in Fall Cone Tests. Adv. Civ. Eng. 2020, 2020, 8850430. [Google Scholar] [CrossRef]
- Zeng, X.; Liu, X.; Li, Y.-H. The breakthrough time analyses of lead ions in CCL considering different adsorption isotherms. Adv. Civ. Eng. 2020, 2020, 8861866. [Google Scholar] [CrossRef]
- Li, Y.; Zeng, X.; Lin, Z.; Su, J.; Gao, T.; Deng, R.; Liu, X. Experimental study on phosphate rock modified soil-bentonite as a cut-off wall material. Water Supply 2022, 22, 1676–1690. [Google Scholar] [CrossRef]
- Gao, G.; Feng, S.; Ma, Y.; Zhan, H.; Huang, G. Kinetic model and semi-analytical solution for reactive solute transport considering dispersive scale effects and immobile water bodies. Hydrodyn. Res. Prog. A Ser. 2010, 25, 206–216. [Google Scholar]
- Xie, H.; Tang, X.; Chen, y. One-dimensional model for contaminant diffusion through layered media. J.-Zhejiang Univ. Eng. Sci. 2006, 40, 2191. [Google Scholar]
- Selim, H. Transport of Reactive Solutes during Transient, Unsaturated Water Flow in Multilayered SOILS1. Soil Sci. 1978, 126, 127–135. [Google Scholar] [CrossRef]
- Foose, G.J. Transit-time design for diffusion through composite liners. J. Geotech. Geoenviron. Eng. 2002, 128, 590–601. [Google Scholar] [CrossRef]
- Chen, Y.-M.; Xie, H.-J.; Ke, H.; Tang, X.-W. Analytical solution of one-dimensional diffusion of volatileorganic compounds (VOCs) through composite liners. Yantu Gongcheng Xuebao 2006, 28, 1076–1080. [Google Scholar]
- Rowe, R.; Booker, J.R. The analysis of pollutant migration in a non-homogeneous soil. Geotechnique 1984, 34, 601–612. [Google Scholar] [CrossRef]
- Yu, C.; Wang, H.; Fang, D.; Ma, J.; Cai, X.; Yu, X. Semi-analytical solution to one-dimensional advective-dispersive-reactive transport equation using homotopy analysis method. J. Hydrol. 2018, 565, 422–428. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, H.; Yao, J.; Li, Y. Analysis of Factors for Compacted Clay Liner Performance Considering Isothermal Adsorption. Appl. Sci. 2021, 11, 9735. [Google Scholar] [CrossRef]
- Zhan, L.-T.; Zeng, X.; Li, Y.; Chen, Y. Analytical solution for one-dimensional diffusion of organic pollutants in a geomembrane–bentonite composite barrier and parametric analyses. J. Environ. Eng. 2014, 140, 57–68. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Y.; Zhang, W.; Chi, Y.; Guo, Z.; Xiao, J.; Hu, J. Effects of pH, ionic strength, time and temperature on the sorption of Cd (II) to illite. J. Nucl. Radiochem. 2012, 34, 358–363. [Google Scholar]
- Zhang, J. Thermodynamic and Mechanistic Study on the Adsorption of Concave Barite Clay for the Treatment of Lead Containing Wastewater and Highly Fluorinated Water. Master’s Thesis, Peking University, Beijing, China, 2008. [Google Scholar]
- Rao, S.N.; Mathew, P.K. Effects of exchangeable cations on hydraulic conductivity of a marine clay. Clays Clay Miner. 1995, 43, 433–437. [Google Scholar] [CrossRef]
- Zhu, W.; Xu, H.-Q.; Wang, S.-W.; Fan, X.-H. Influence of CaCl2 solution on the permeability of different clay-based cutoff walls. Rock Soil Mech. 2016, 37, 1224–1230. [Google Scholar]
- Malusis, M.A.; McKeehan, M.D. Chemical compatibility of model soil-bentonite backfill containing multiswellable bentonite. J. Geotech. Geoenviron. Eng. 2013, 139, 189–198. [Google Scholar] [CrossRef] [Green Version]
- Bohnhoff, G.L.; Shackelford, C.D. Hydraulic conductivity of polymerized bentonite-amended backfills. J. Geotech. Geoenviron. Eng. 2014, 140, 04013028. [Google Scholar] [CrossRef]
- Xu, H.; Shu, S.; Wang, S.; Zhou, A.; Jiang, P.; Zhu, W.; Fan, X.; Chen, L. Studies on the chemical compatibility of soil-bentonite cut-off walls for landfills. J. Environ. Manag. 2019, 237, 155–162. [Google Scholar] [CrossRef]
- Pickens, J.F.; Grisak, G.E. Modeling of scale-dependent dispersion in hydrogeologic systems. Water Resour. Res. 1981, 17, 1701–1711. [Google Scholar] [CrossRef]
- Singh, M.K.; Mahato, N.K.; Kumar, N. Pollutant’s horizontal dispersion along and against sinusoidally varying velocity from a pulse type point source. Acta. Geophys. 2015, 63, 214–231. [Google Scholar] [CrossRef] [Green Version]
- Barry, D.; Sposito, G. Analytical solution of a convection-dispersion model with time-dependent transport coefficients. Water Resour. Res. 1989, 25, 2407–2416. [Google Scholar] [CrossRef]
- Zamani, K.; Bombardelli, F.A. Analytical solutions of nonlinear and variable-parameter transport equations for verification of numerical solvers. Environ. Fluid Mech. 2014, 14, 711–742. [Google Scholar] [CrossRef]
- Guerrero, J.P.; Pontedeiro, E.; van Genuchten, M.T.; Skaggs, T. Analytical solutions of the one-dimensional advection–dispersion solute transport equation subject to time-dependent boundary conditions. Chem. Eng. J. 2013, 221, 487–491. [Google Scholar] [CrossRef]
- Basha, H.; El-Habel, F. Analytical solution of the one-dimensional time-dependent transport equation. Water Resour. Res. 1993, 29, 3209–3214. [Google Scholar] [CrossRef]
- Singh, M.K.; Ahamad, S.; Singh, V.P. Analytical solution for one-dimensional solute dispersion with time-dependent source concentration along uniform groundwater flow in a homogeneous porous formation. J. Eng. Mech. 2012, 138, 1045–1056. [Google Scholar] [CrossRef]
- Yates, S. An analytical solution for one-dimensional transport in heterogeneous porous media. Water Resour. Res. 1990, 26, 2331–2338. [Google Scholar] [CrossRef]
- Kumar, A.; Jaiswal, D.K.; Kumar, N. Analytical solutions to one-dimensional advection–diffusion equation with variable coefficients in semi-infinite media. J. Hydrol. 2010, 380, 330–337. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1979. [Google Scholar]
- Ogata, A.; Banks, R.B. A Solution of the Differential Equation of Longitudinal Dispersion in Porous Media; US Government Printing Office: Washington, DC, USA, 1961.
- Li, Y.C.; Cleall, P.J. Analytical solutions for advective–dispersive solute transport in double-layered finite porous media. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 438–460. [Google Scholar] [CrossRef]
- Chen, Z.; Luo, B.; Wang, Z.; Huang, Z. Effect of temperature on the impermeability of landfill impermeable layers. Environ. Eng. 2015, 33, 133–136. [Google Scholar]
- Dong, J.; Wang, C.-L.; Yin, Y.; Lou, Q.-Z.; Wang, X.-S.; Yang, Z. Influences of the freezing and thawing action on the performance of landfill liners. J. Jilin Univ. 2011, 41, 541–544. [Google Scholar]
- Chi, Y. Study on the Modification of Albite and Its Adsorption of Heavy Metal Ions. Master’s Thesis, Qinghai Normal University, Xining, China, 2013. [Google Scholar]
- Huang, R. Study on the Adsorption Characteristics and Soil Remediation Efficacy of Modified Bumpy Clay for Heavy Metals. Master’s Thesis, Guangdong University of Technology, Guangzhou, China, 2020. [Google Scholar]
- Lei, H.; Shi, J.Y.; Wu, X. Prediction of landfill temperature considering biodegradation. Henan Sci. 2018, 36, 584–592. [Google Scholar]
- Guo, T. Experimental Study on the Influence of Temperature on the Permeability of Anti-Seepage Walls of Sand-Attapulgite Soil. Master’s Thesis, Yangzhou University, Yangzhou, China, 2022. [Google Scholar]
- Fan, R.; Du, Y.; Liu, S.; Yang, Y. Experimental study on the chemical compatibility of sand-bentonite vertical barrier materials under the action of inorganic salt solutions. Geotechnics 2020, 41, 736–746. [Google Scholar] [CrossRef]






| Group | Case | |||
|---|---|---|---|---|
| 1 | 1-1 | 1365 | ||
| 1-2 | 1365 | |||
| 1-3 | 1365 | |||
| 2 | 2-1 | 1365 | ||
| 2-2 | 2365 | |||
| 2-3 | 3365 | |||
| 3 | 3-1 | 1365 | ||
| 3-2 | 2365 | |||
| 3-3 | 3365 |
| Parameter Value | |
|---|---|
| 7.5 mL/g | |
| 1 m | |
| 5 | |
| 0.1 m | |
| 0.5 | |
| 365/d | |
| 20 | |
| Case | Ratio % | Porosity | Permeability Coefficient m/s | |||
|---|---|---|---|---|---|---|
| 30 °C | 60 °C | |||||
| 1 | A10S90 | 0.286 | 0.0036 | 81 | ||
| 2 | A30S70 | 0.405 | 0.0056 | 61 | ||
| 3 | A60S40 | 0.5 | 0.0068 | 49 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, X.; Gao, T.; Xie, L.; He, Z. Analytical Solution of the One-Dimensional Transport of Ionic Contaminants in Porous Media with Time-Varying Velocity. Water 2023, 15, 1530. https://doi.org/10.3390/w15081530
Zeng X, Gao T, Xie L, He Z. Analytical Solution of the One-Dimensional Transport of Ionic Contaminants in Porous Media with Time-Varying Velocity. Water. 2023; 15(8):1530. https://doi.org/10.3390/w15081530
Chicago/Turabian StyleZeng, Xing, Tong Gao, Linhui Xie, and Zijian He. 2023. "Analytical Solution of the One-Dimensional Transport of Ionic Contaminants in Porous Media with Time-Varying Velocity" Water 15, no. 8: 1530. https://doi.org/10.3390/w15081530






