Optimization of Key Hydraulic Structure Parameters of a New Type of Water–Pesticide Integrated Sprinkler Based on Response Surface Experiment
Abstract
:1. Introduction
2. Materials and Methods
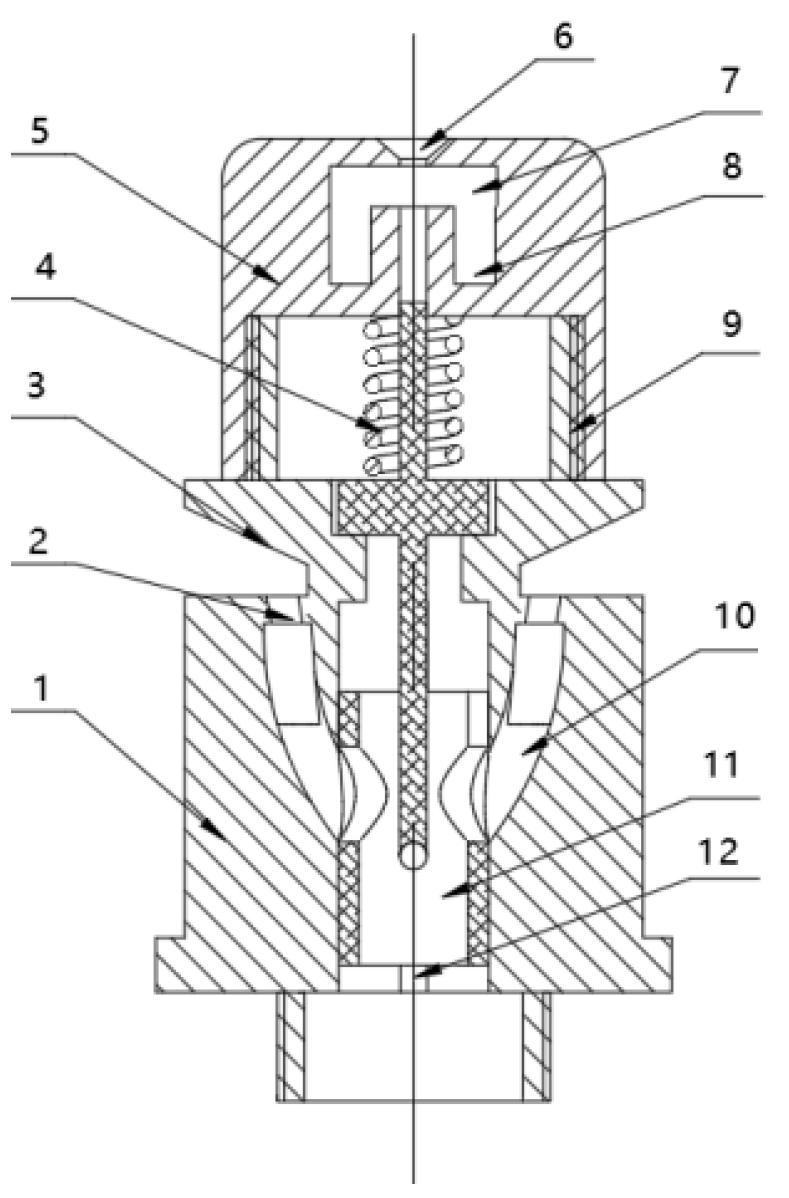
2.1. Structural Design and Working Principle
2.2. Experimental Setup
3. Results and Discussion
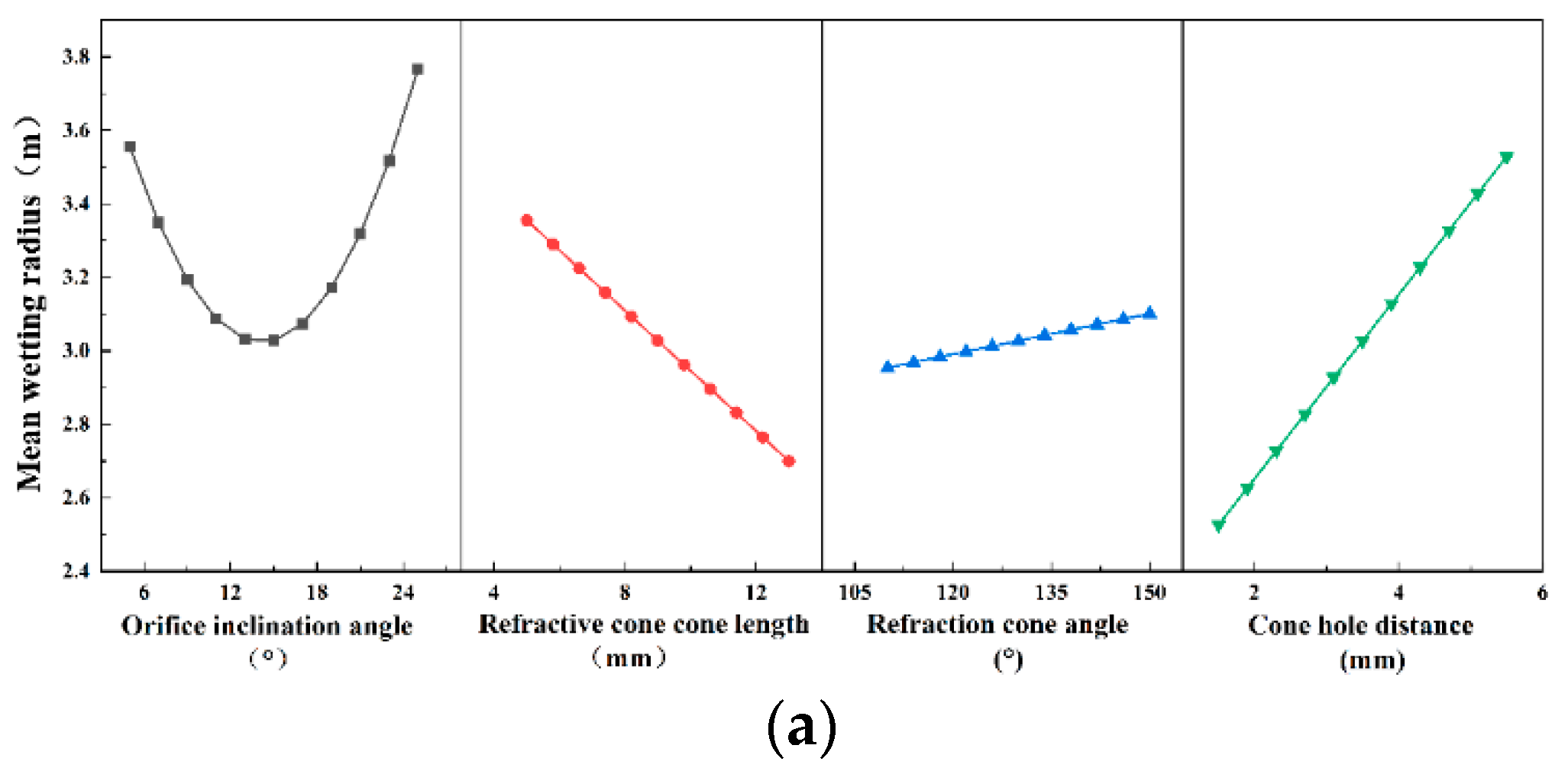
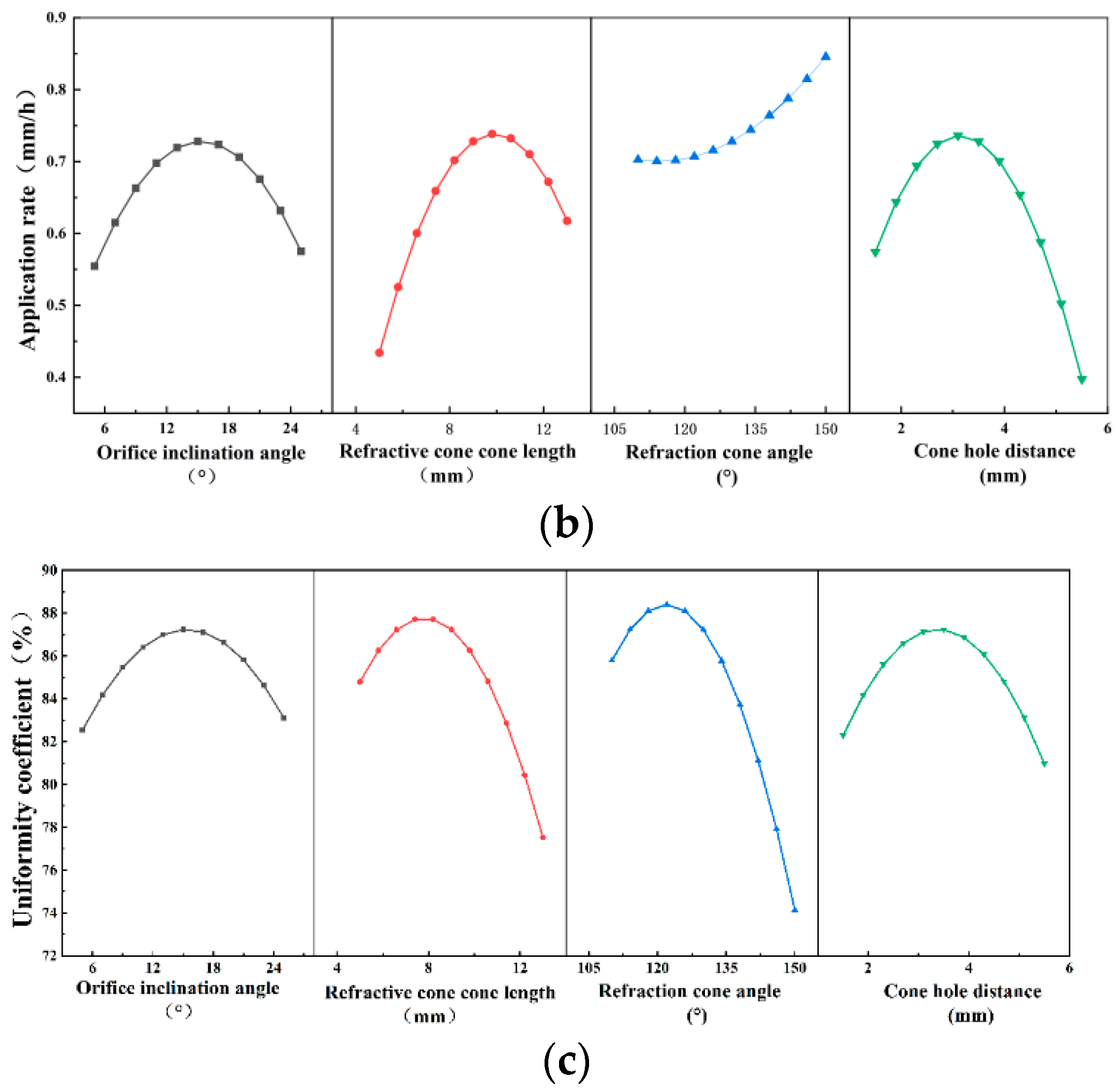
3.1. Influence of Different Structural Parameters on Irrigation Performance
3.1.1. The Response Surface of Variance and the Regression Analysis
3.1.2. Analysis of Main Effect and the Interaction Effect
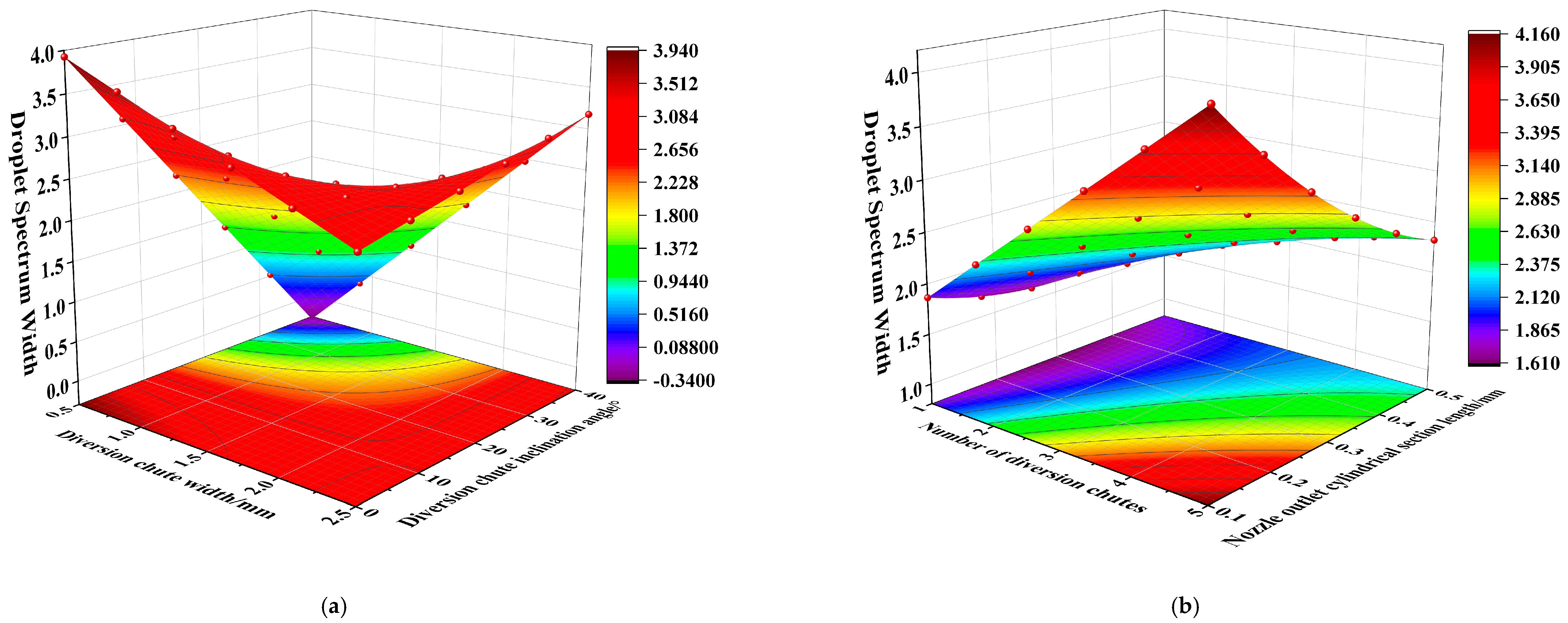
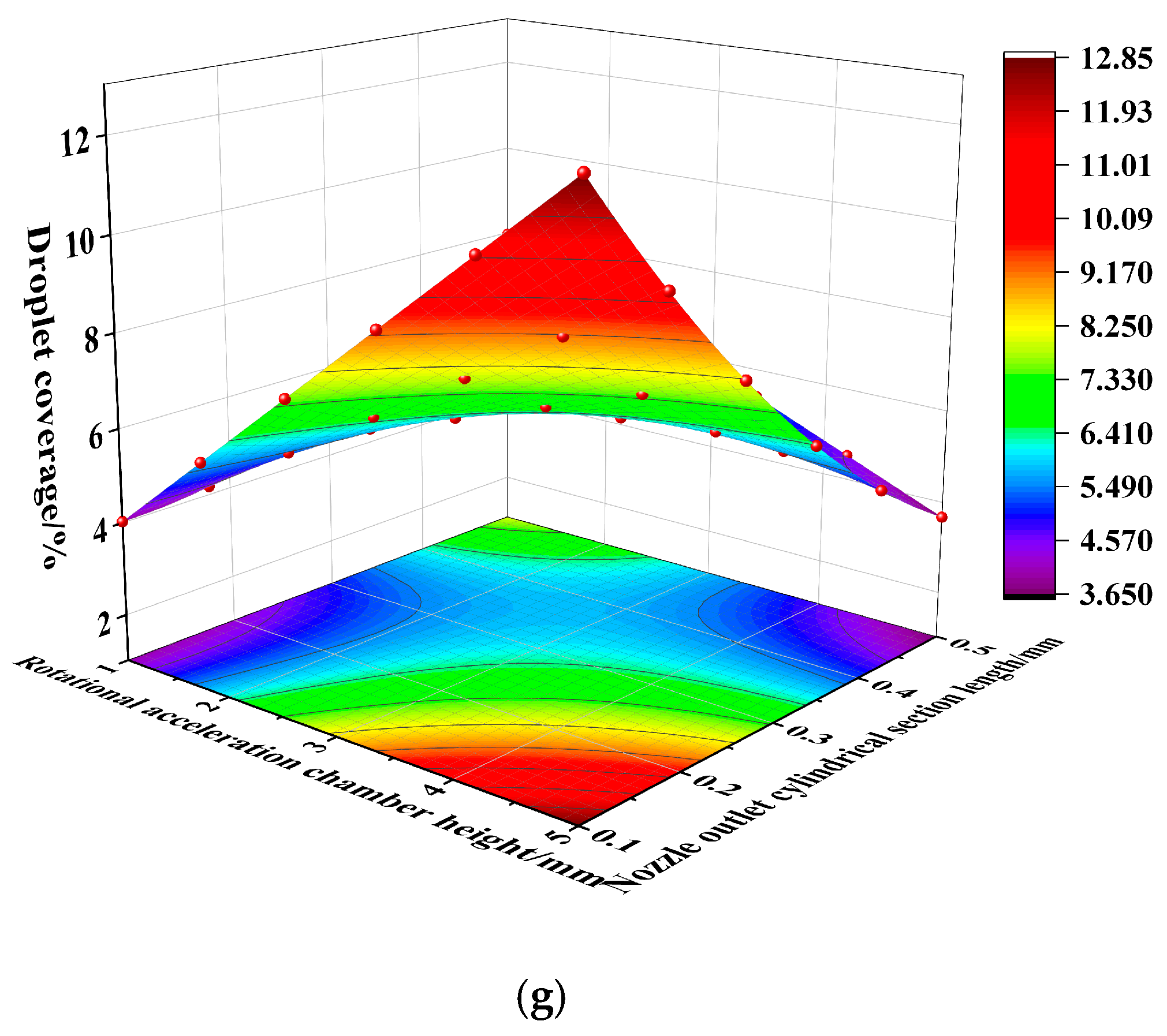
3.2. Influence of Different Structural Parameters on Spraying Pesticide Performance
3.2.1. The Response Surface of Variance and the Regression Analysis
3.2.2. Analysis of Main Effect and the Interaction Effect
4. Conclusions
- (1)
- The influences of key structural parameters, such as the diversion hole inclination angle, the refractive cone angle, the refractive cone length, and the cone hole distance on sprinkler irrigation performance were revealed. The influence laws of key structural parameters of different diversion chute widths, the number of diversion chutes, the diversion chute inclination angle, the rotary acceleration chamber height, and the nozzle outlet cylindrical section length on sprinkler spraying pesticide performance were revealed, respectively.
- (2)
- Taking the wetted radius, average irrigation application rate, and uniformity coefficient as the parameters of irrigation performance and droplet volume mid-diameter, droplet spectral width, and droplet coverage as the parameters of spraying pesticide performance, the proposed design values of key structural parameters with better performance are obtained: the diversion hole inclination angle was 20.8°, the refractive cone angle was 123.7°, the refractive cone length was 8.8 mm, the cone hole distance was 3.6 mm, the diversion chute width was 2.5 mm, the number of diversion chutes was 2, the diversion chute inclination angle was 10°, the rotary acceleration chamber height was 1.3 mm, and the nozzle outlet cylindrical section length was 0.7 mm. The performance parameters of the sprinkler can meet the needs of grape irrigation and pesticide spraying, thereby improving the utilization rate of water and pesticides in the agricultural production process.
Author Contributions
Funding
Conflicts of Interest
References
- Song, Y.; Zhang, Z.; Fan, Q.; Gao, D.; Zhang, H.; Zhang, X. Research status and development trend of ditching fertilization machinery in orchards in China. Chin. J. Agric. Mech. 2019, 40, 7–12. [Google Scholar]
- China National Data Center. Available online: https://data.stats.gov.cn/easyquery.htm?cn=C01&zb=A0D0H&sj=2022 (accessed on 27 February 2023).
- Deng, W.; Meng, Z.; Chen, L.; Wang, X.; Guo, J.; Chen, T.; Xu, G.; Zhang, R. Measurement method of droplet size and velocity of pesticide spray. Agric. Mech. Res. 2011, 33, 26–30. [Google Scholar]
- Gil, Y.; Sinfort, C. Emission of pesticides to the air during sprayer application: A bibliographic review. Atmos. Environ. 2005, 39, 5183–5193. [Google Scholar] [CrossRef]
- Brice, K.N.; Patricia, A.F.; Norbert, N.T.; Mpoame, M. Environmental and human health assessment in relation to pesticide use by local farmers and the Cameroon Development Corporation (CDC), Fako Division, South-West Cameroon. Eur. Sci. J. 2017, 13, 454–473. [Google Scholar] [CrossRef]
- Matthews, G. Pesticides: Health, Safety and the Environment; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Zheng, Y.J.; Chen, B.T.; Lyu, H.T.; Kang, F.; Jiang, S.J. Research progress of orchard plant protection mechanization technology and equipment in China. Trans. Chin. Soc. Agric. Eng. 2020, 36, 110–124. [Google Scholar]
- Baolong, Y. Development of 3WZG-500 self-propelled grape sprayer. Trans. Chin. Soc. Agric. Mach. 2018, 8, 102–104. [Google Scholar]
- Li, Y.; Yang, N.; Sun, Z.; Feng, L.; Wang, Y.; Wang, P. Progress on researching and application of chemigation. Chin. J. Pestic. Sci. 2019, 58, 553–560. [Google Scholar]
- Zhou, R.; Zhang, H.; Zhou, H.; Zheng, J.; Hu, H. Interaction effects of spray parameters on pesticide spray droplet drift. J. Drain. Irrig. Mach. Eng. 2019, 37, 612–617+638. [Google Scholar]
- Watson, T.T.; Desaeger, J.A. Evaluation of non-fumigant chemical and biological nematicides for strawberry production in Florida. Crop. Prot. 2019, 117, 100–107. [Google Scholar] [CrossRef]
- Mao, L.G.; Wang, Q.X.; Yan, D.D.; Liu, P.F.; Jin, S.H.; Fang, W.S.; Hu, X.M.; Yuan, L.I.; Ouyang, C.B.; Guo, M.X.; et al. Application of the combination of 1, 3-dichloropropene and dimethyl disulfide by soil injection or chemigation: Effects against soilborne pests in cucumber in China. J. Integr. Agric. 2016, 15, 145–152. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z. Grape Disease and Pest Control Technology in China; China Agriculture Press: Beijing, China, 2009. (In Chinese) [Google Scholar]
- Zhang, Q.; Liu, J.; Yuan, S.; Li, Y.; Li, H. Structure design and hydraulic performance test of water and pesticide integrated sprinkler. J. Drain. Irrig. Mach. Eng. 2022, 40, 102–108. [Google Scholar]
- Xie, C.; He, X.; Song, J.; Herbst, A. Comparative study on atomization process of two types of fan fog heads. Trans. Chin. Soc. Agric. Eng. 2013, 29, 25–30. [Google Scholar]
- Yang, F.; Xue, X.; Cai, C.; Zhou, Q.; Sun, Z. Study on atomization performance test and influence factors of aviation special centrifugal nozzle. Trans. Chin. Soc. Agric. Mach. 2019, 50, 96–104. [Google Scholar]
- Liu, J.; Zhu, X.; Yuan, S.; Li, H.; Tang, Y. Research progress and development trend of agricultural water-saving micro-irrigation equipment in China. J. Drain. Irrig. Mach. Eng. 2022, 40, 87–96. [Google Scholar]
- Box, G.E.P.; Wilson, K.B. On the experimental attainment of optimum conditions. J. R. Stat. Soc. 1951, 13, 1–45. [Google Scholar] [CrossRef]
- Wang, X.; Liu, J.; Zhang, Q. Water–Pesticide Integrated micro-sprinkler design and influence of key structural parameters on performance. Agriculture 2022, 12, 1532. [Google Scholar] [CrossRef]
- Liu, J.; Li, T.; Zhang, Q. Experimental study on influence of flow channel structure on hydraulic performance of low pressure rotary sprinkler. J. Drain. Irrig. Mach. Eng. 2013, 9, 312–317. [Google Scholar]
- Liu, J.; Zhu, X.; Yuan, S.; Liu, X. Droplet motion model and simulation of a complete fluidic sprinkler. Trans. ASABE 2018, 61, 1297–1306. [Google Scholar]
- Liu, J.; Zhu, X.; Yuan, S.; Wan, J.; Chikangaise, P. Hydraulic performance assessment of sprinkler irrigation with rotating spray plate sprinklers in indoor experiments. J. Irrig. Drain. Eng. 2018, 144, 06018005. [Google Scholar] [CrossRef]
- Fengzhi, L. Current situation and development trend of viticulture in China. Deciduous Fruit Trees 2017, 49, 1–4. [Google Scholar]
- Wang, G.; Li, X.; Andaloro, J.; Chen, S.; Han, X.; Wang, J.; Shan, C.; Lan, Y. Field pesticide droplet accurate sampling technology and development trend. Agric. Eng. J. 2021, 37, 1–12. [Google Scholar]
- Tang, Q.; Chen, L.; Zhang, R.; Zhang, B.; Yin, T.; Xu, W.; Xu, G. Atomization characteristics of standard fan-shaped nozzle and air-induced nozzle under high-speed air flow. J. Agric. Eng. 2016, 32, 121–128. [Google Scholar]
- Bolat, A.; Özlüoymak, Ö.B. Evaluation of performances of different types of spray nozzles in site-specific pesticide spraying. Semin. Ciências Agrárias 2020, 41, 1199–1212. [Google Scholar] [CrossRef]
- Sinha, R.; Ranjan, R.; Khot, L.R.; Hoheisel, G.A.; Grieshop, M.J. Drift potential from a solid set canopy delivery system and an axial-fan air-assisted sprayer during applications in grapevines. Biosyst. Eng. 2019, 188, 207–216. [Google Scholar] [CrossRef]
- Matsukawa-Nakata, M.; Nguyen, H.T.; Bui, T.T.B.; Van Le, H.; Nguyen, C.H.; Kobori, Y. Spatial evaluation of the pesticide application method by farmers in a paddy field in the northern part of Vietnam. Appl. Entomol. Zool. 2019, 54, 451–457. [Google Scholar] [CrossRef]
- Xiao, L.; Zhu, H.; Wallhead, M.; Horst, L.; Ling, P.; Krause, C.R. Characterization of biological pesticide deliveries through hydraulic nozzles. Trans. ASABE 2018, 61, 897–908. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, Y.; Wen, C.; Tang, J. Research on orthogonal experimental design and analysis method. Exp. Technol. Manag. 2010, 27, 52–55. [Google Scholar]
- Hafeez, K.; Rowlands, H.; Kanji, G.; Iqbal, S. Design optimization using ANOVA. J. Appl. Stat. 2002, 29, 895–906. [Google Scholar] [CrossRef]
- Qiu, T.; Liu, H.; Dai, Y.; Xu, Y. Multi-objective optimization experiment of lens injection compression molding process parameters based on orthogonal experiment and response surface method. Plast. Ind. 2021, 49, 70–73. [Google Scholar]

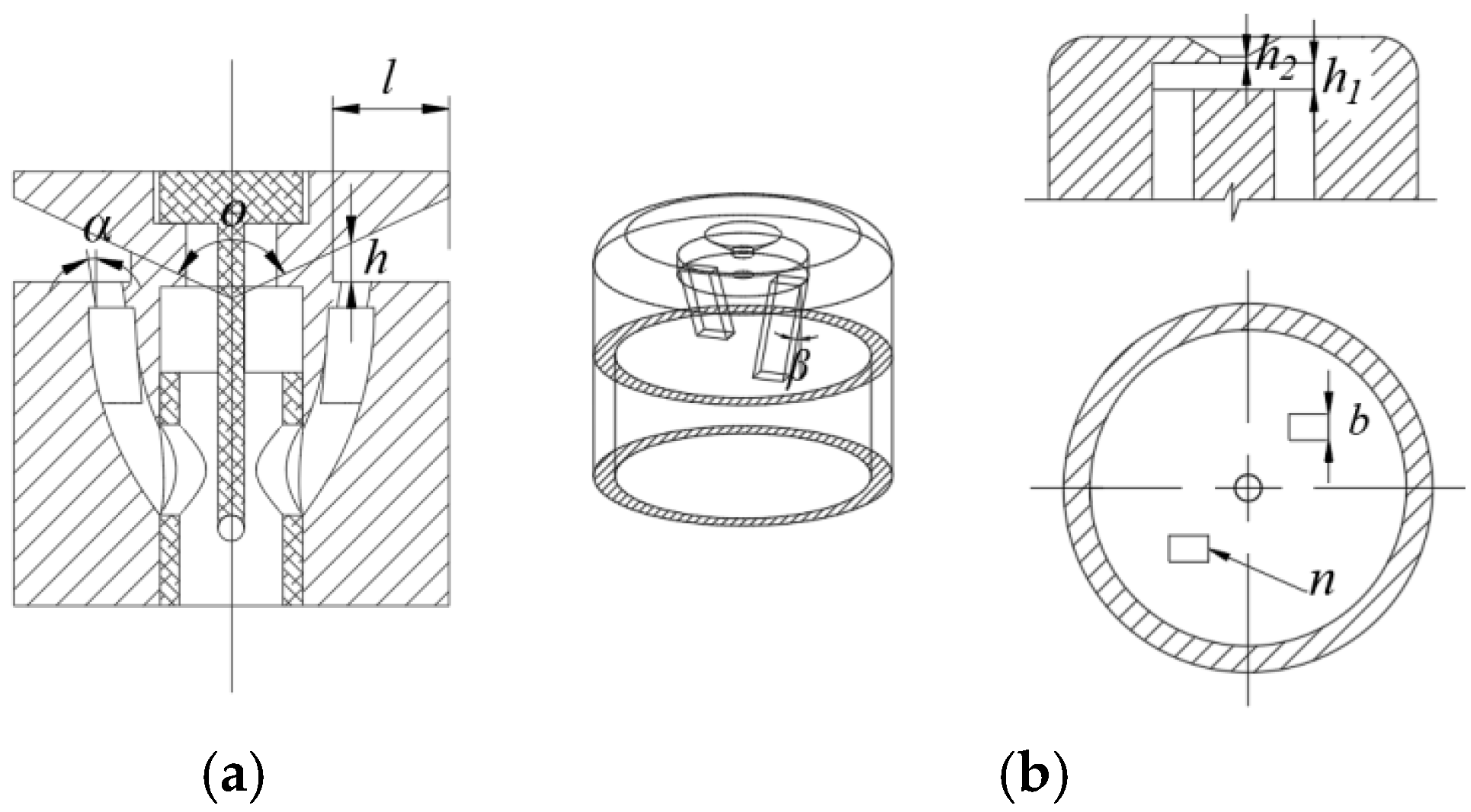


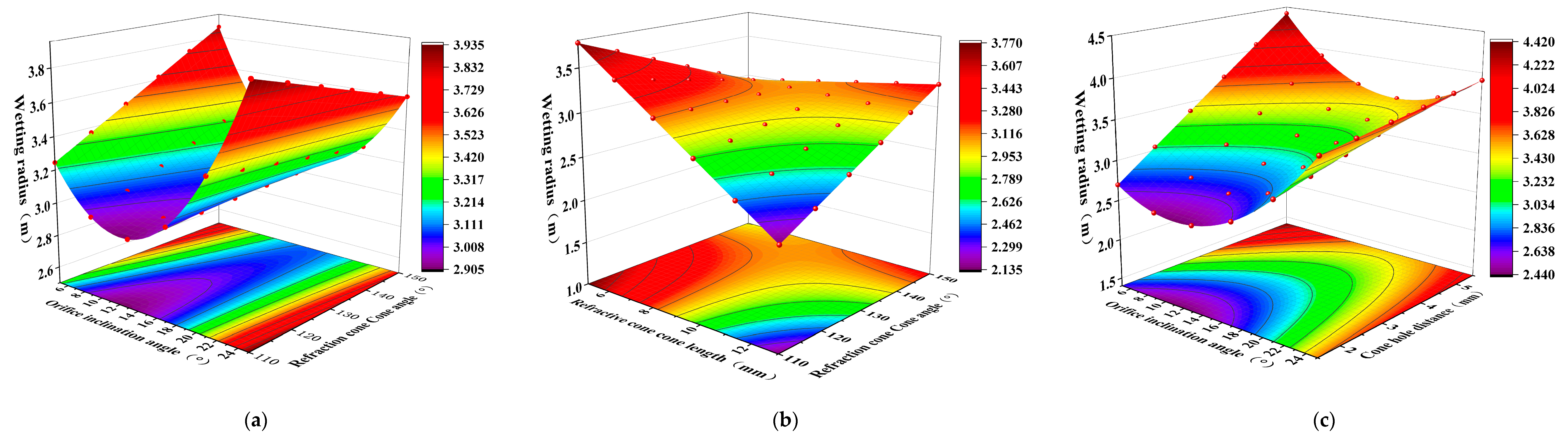
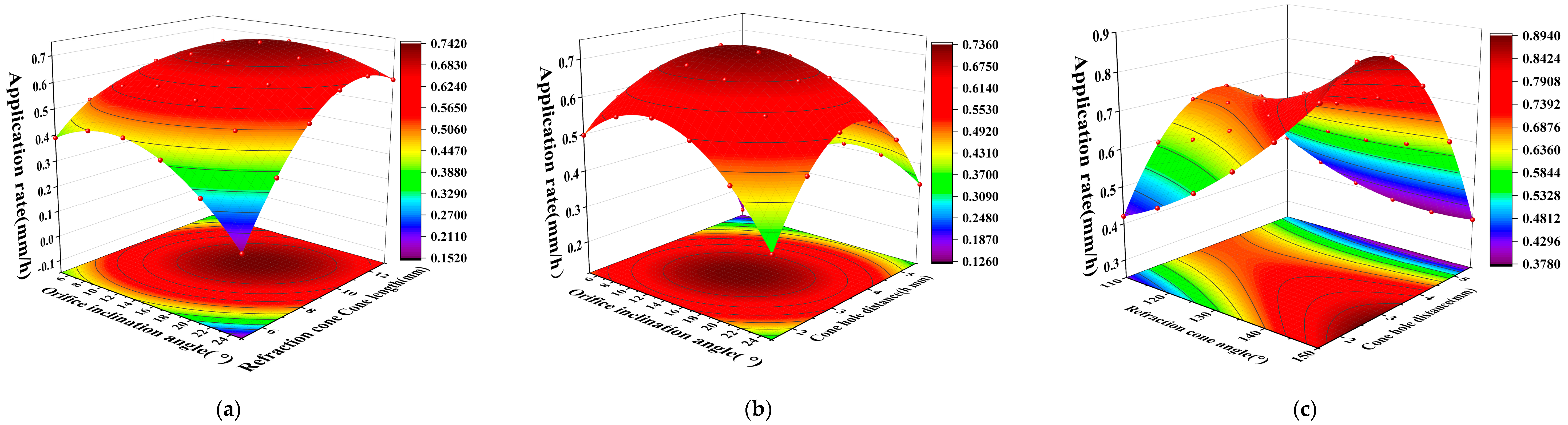
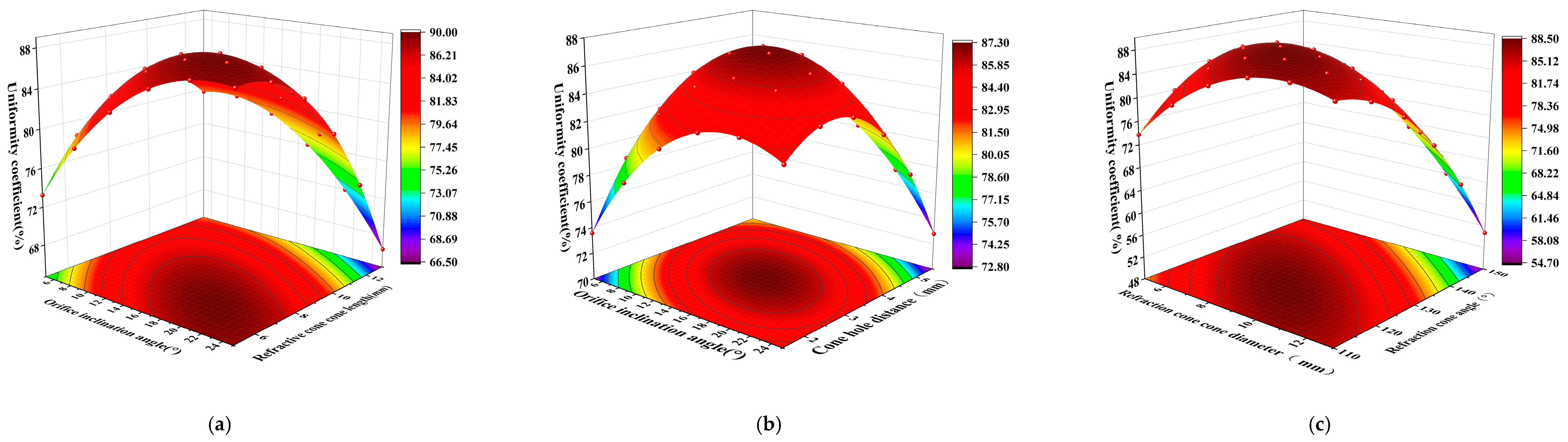

| Serial Number | Diversion Hole Inclination Angle α/° | Refractive Cone Length l/mm | Refraction Cone Angle θ/° | Cone Hole Distance/mm | Wetted Radius/m | Average Irrigation Application Rate/(mm/h) | Uniformity Coefficient/% |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 7 | 120 | 2.5 | 2.93 | 0.56 | 83.10 |
| 2 | 20 | 7 | 120 | 2.5 | 3.54 | 0.50 | 86.28 |
| 3 | 10 | 11 | 120 | 2.5 | 2.53 | 0.61 | 87.13 |
| 4 | 20 | 11 | 120 | 2.5 | 2.85 | 0.60 | 85.58 |
| 5 | 10 | 7 | 140 | 2.5 | 3.13 | 0.69 | 80.45 |
| 6 | 20 | 7 | 140 | 2.5 | 3.18 | 0.58 | 86.76 |
| 7 | 10 | 11 | 140 | 2.5 | 3.03 | 0.73 | 75.87 |
| 8 | 20 | 11 | 140 | 2.5 | 3.10 | 0.78 | 74.93 |
| 9 | 10 | 7 | 120 | 4.5 | 3.80 | 0.49 | 83.99 |
| 10 | 20 | 7 | 120 | 4.5 | 3.70 | 0.48 | 85.26 |
| 11 | 10 | 11 | 120 | 4.5 | 3.28 | 0.55 | 89.91 |
| 12 | 20 | 11 | 120 | 4.5 | 3.26 | 0.65 | 82.02 |
| 13 | 10 | 7 | 140 | 4.5 | 3.60 | 0.49 | 82.26 |
| 14 | 20 | 7 | 140 | 4.5 | 3.50 | 0.47 | 84.16 |
| 15 | 10 | 11 | 140 | 4.5 | 3.68 | 0.51 | 77.37 |
| 16 | 20 | 11 | 140 | 4.5 | 3.52 | 0.70 | 72.99 |
| 17 | 5 | 9 | 130 | 3.5 | 3.53 | 0.57 | 82.50 |
| 18 | 25 | 9 | 130 | 3.5 | 3.83 | 0.56 | 85.26 |
| 19 | 15 | 5 | 130 | 3.5 | 3.30 | 0.47 | 84.08 |
| 20 | 15 | 13 | 130 | 3.5 | 2.58 | 0.59 | 80.72 |
| 21 | 15 | 9 | 110 | 3.5 | 3.13 | 0.68 | 86.39 |
| 22 | 15 | 9 | 150 | 3.5 | 3.21 | 0.87 | 75.64 |
| 23 | 15 | 9 | 130 | 1.5 | 2.55 | 0.58 | 84.13 |
| 24 | 15 | 9 | 130 | 5.5 | 3.53 | 0.40 | 81.25 |
| 25 | 15 | 9 | 130 | 3.5 | 3.10 | 0.72 | 88.21 |
| 26 | 15 | 9 | 130 | 3.5 | 3.10 | 0.72 | 88.21 |
| 27 | 15 | 9 | 130 | 3.5 | 3.10 | 0.72 | 88.21 |
| 28 | 15 | 9 | 130 | 3.5 | 3.10 | 0.72 | 88.21 |
| 29 | 15 | 9 | 130 | 3.5 | 3.10 | 0.72 | 88.21 |
| 30 | 15 | 9 | 130 | 3.5 | 3.10 | 0.72 | 88.21 |
| 31 | 15 | 9 | 130 | 3.5 | 3.10 | 0.72 | 88.21 |
| Project | Freedom | Adj SS | Adj MS | F | p |
|---|---|---|---|---|---|
| Model | 14 | 601.618 | 42.973 | 65.21 | 0.000 |
| Linear | 4 | 258.748 | 64.687 | 98.15 | 0.000 |
| α | 1 | 1.307 | 1.307 | 1.98 | 0.178 |
| l | 1 | 39.117 | 39.117 | 59.35 | 0.000 |
| θ | 1 | 216.961 | 216.961 | 329.21 | 0.000 |
| h | 1 | 1.363 | 1.363 | 2.07 | 0.170 |
| Suqare | 4 | 184.974 | 46.243 | 70.17 | 0.000 |
| α | 1 | 33.084 | 33.084 | 50.20 | 0.000 |
| l | 1 | 61.635 | 61.635 | 93.52 | 0.000 |
| θ | 1 | 91.816 | 91.816 | 139.32 | 0.000 |
| h | 1 | 53.916 | 53.916 | 81.81 | 0.000 |
| Two-factor interaction | 6 | 157.896 | 26.316 | 39.93 | 0.000 |
| α × l | 1 | 39.816 | 39.816 | 60.42 | 0.000 |
| α × θ | 1 | 2.031 | 2.031 | 3.08 | 0.098 |
| α × h | 1 | 12.110 | 12.110 | 18.38 | 0.001 |
| l × θ | 1 | 103.327 | 103.327 | 156.79 | 0.000 |
| l × h | 1 | 0.221 | 0.221 | 0.34 | 0.571 |
| θ × h | 1 | 0.391 | 0.391 | 0.59 | 0.453 |
| Error | 16 | 10.545 | 0.659 |
| Test Number | Diversion Chute Width b/mm | Number of Diversion Chutes n | Diversion Chute Inclination Angle /° | Rotational Acceleration Chamber Height h1/mm | Length of Cylindrical Section at Nozzle Outlet h2/mm | Droplet Volume Mid-Diameter/μm | Droplet Spectral Width | Droplet Coverage/% |
|---|---|---|---|---|---|---|---|---|
| 1 | 1.0 | 2 | 10 | 2 | 0.5 | 289.36 | 1.93 | 7.49 |
| 2 | 2.0 | 2 | 10 | 2 | 0.1 | 307.11 | 2.52 | 7.03 |
| 3 | 1.0 | 4 | 10 | 2 | 0.1 | 289.3 | 4.13 | 6.40 |
| 4 | 2.0 | 4 | 10 | 2 | 0.5 | 127.17 | 1.94 | 2.97 |
| 5 | 1.0 | 2 | 30 | 2 | 0.1 | 240.17 | 1.44 | 2.21 |
| 6 | 2.0 | 2 | 30 | 2 | 0.5 | 315.22 | 1.96 | 7.66 |
| 7 | 1.0 | 4 | 30 | 2 | 0.5 | 309.03 | 1.41 | 6.78 |
| 8 | 2.0 | 4 | 30 | 2 | 0.1 | 231.57 | 3.59 | 6.78 |
| 9 | 1.0 | 2 | 10 | 4 | 0.1 | 245.78 | 3.30 | 7.91 |
| 10 | 2.0 | 2 | 10 | 4 | 0.5 | 172.76 | 2.85 | 4.71 |
| 11 | 1.0 | 4 | 10 | 4 | 0.5 | 300.52 | 2.87 | 6.01 |
| 12 | 2.0 | 4 | 10 | 4 | 0.1 | 241.11 | 4.08 | 11.77 |
| 13 | 1.0 | 2 | 30 | 4 | 0.5 | 227.72 | 1.57 | 1.89 |
| 14 | 2.0 | 2 | 30 | 4 | 0.1 | 295.92 | 2.83 | 8.87 |
| 15 | 1.0 | 4 | 30 | 4 | 0.1 | 250.56 | 2.36 | 11.81 |
| 16 | 2.0 | 4 | 30 | 4 | 0.5 | 188.98 | 2.54 | 4.01 |
| 17 | 0.5 | 3 | 20 | 3 | 0.3 | 248.49 | 1.24 | 3.22 |
| 18 | 2.5 | 3 | 20 | 3 | 0.3 | 157.81 | 2.65 | 3.03 |
| 19 | 1.5 | 1 | 20 | 3 | 0.3 | 272.51 | 1.32 | 6.19 |
| 20 | 1.5 | 5 | 20 | 3 | 0.3 | 201.30 | 3.23 | 6.15 |
| 21 | 1.5 | 3 | 0 | 3 | 0.3 | 229.30 | 3.48 | 7.55 |
| 22 | 1.5 | 3 | 40 | 3 | 0.3 | 251.64 | 1.12 | 4.86 |
| 23 | 1.5 | 3 | 20 | 1 | 0.3 | 284.64 | 1.62 | 5.24 |
| 24 | 1.5 | 3 | 20 | 5 | 0.3 | 240.93 | 2.20 | 7.19 |
| 25 | 1.5 | 3 | 20 | 3 | 0.1 | 266.32 | 3.06 | 7.87 |
| 26 | 1.5 | 3 | 20 | 3 | 0.7 | 322.12 | 2.19 | 7.33 |
| 27 | 1.5 | 3 | 20 | 3 | 0.3 | 175.51 | 2.50 | 6.01 |
| 28 | 1.5 | 3 | 20 | 3 | 0.3 | 175.51 | 2.50 | 6.01 |
| 29 | 1.5 | 3 | 20 | 3 | 0.3 | 175.51 | 2.5 | 6.01 |
| 30 | 1.5 | 3 | 20 | 3 | 0.3 | 175.51 | 2.5 | 6.01 |
| 31 | 1.5 | 3 | 20 | 3 | 0.3 | 175.51 | 2.5 | 6.01 |
| Project | Freedom | Adj SS | Adj MS | F | p |
|---|---|---|---|---|---|
| Model | 20 | 86,113.0 | 4305.6 | 11.12 | 0.000 |
| Linear | 5 | 16,156.0 | 3652.1 | 9.43 | 0.001 |
| b | 1 | 8587.4 | 8587.4 | 22.18 | 0.001 |
| n | 1 | 3706.4 | 3706.4 | 9.57 | 0.010 |
| β | 1 | 712.2 | 712.2 | 1.84 | 0.202 |
| h1 | 1 | 3105.3 | 3105.3 | 8.02 | 0.016 |
| h2 | 1 | 44.7 | 2149.3 | 5.55 | 0.038 |
| Suqare | 5 | 36,060.3 | 7212.1 | 18.63 | 0.000 |
| b × b | 1 | 6.4 | 77.2 | 0.20 | 0.664 |
| n × n | 1 | 2182.9 | 2982.6 | 7.70 | 0.018 |
| β × β | 1 | 3077.9 | 3535.6 | 9.13 | 0.012 |
| h1 × h1 | 1 | 8622.0 | 8055.2 | 20.81 | 0.001 |
| h2 × h2 | 1 | 22,171.1 | 22,171.1 | 57.27 | 0.000 |
| Two-factor interaction | 10 | 33,896.7 | 3389.7 | 8.76 | 0.001 |
| b × n | 1 | 12,574.9 | 12,574.9 | 32.48 | 0.000 |
| b × β | 1 | 4935.8 | 4935.8 | 12.75 | 0.004 |
| b × h1 | 1 | 27.5 | 27.5 | 0.07 | 0.795 |
| b × h2 | 1 | 8668.1 | 8668.1 | 22.39 | 0.001 |
| n × β | 1 | 110.1 | 110.1 | 0.28 | 0.604 |
| n × h1 | 1 | 3415.6 | 3415.6 | 8.82 | 0.013 |
| n × h2 | 1 | 0.5 | 0.5 | 0.00 | 0.971 |
| β × h1 | 1 | 400.4 | 400.4 | 1.03 | 0.331 |
| β × h2 | 1 | 2922.3 | 2922.3 | 7.55 | 0.019 |
| h1 × h2 | 1 | 841.4 | 841.4 | 2.17 | 0.168 |
| Error | 11 | 4258.4 | 387.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Wang, X.; Liu, Q.; Hussain, Z.; Zhao, Y. Optimization of Key Hydraulic Structure Parameters of a New Type of Water–Pesticide Integrated Sprinkler Based on Response Surface Experiment. Water 2023, 15, 1486. https://doi.org/10.3390/w15081486
Liu J, Wang X, Liu Q, Hussain Z, Zhao Y. Optimization of Key Hydraulic Structure Parameters of a New Type of Water–Pesticide Integrated Sprinkler Based on Response Surface Experiment. Water. 2023; 15(8):1486. https://doi.org/10.3390/w15081486
Chicago/Turabian StyleLiu, Junping, Xinjian Wang, Qingsong Liu, Zawar Hussain, and Yuxia Zhao. 2023. "Optimization of Key Hydraulic Structure Parameters of a New Type of Water–Pesticide Integrated Sprinkler Based on Response Surface Experiment" Water 15, no. 8: 1486. https://doi.org/10.3390/w15081486






