Migration of DNAPL in Saturated Porous Media: Validation of High-Resolution Shock-Capturing Numerical Simulations through a Sandbox Experiment
Abstract
:1. Introduction
2. Materials and Methods
2.1. Governing Equations
2.2. Experimental Equipment
2.2.1. Tracer
2.2.2. Experimental Setup for DNAPL Migration in a Column
2.2.3. Experimental Setup for DNAPL Migration in a Sandbox
2.2.4. Data Acquisition
3. Results
3.1. Numerical Setup of a DNAPL Migration
3.1.1. Numerical Setup of a DNAPL Migration in a Column
3.1.2. Numerical Setup of a DNAPL Migration in a Sandbox
3.2. Comparison of DNAPL Migration between Experiment and Numerical Simulations in a Column
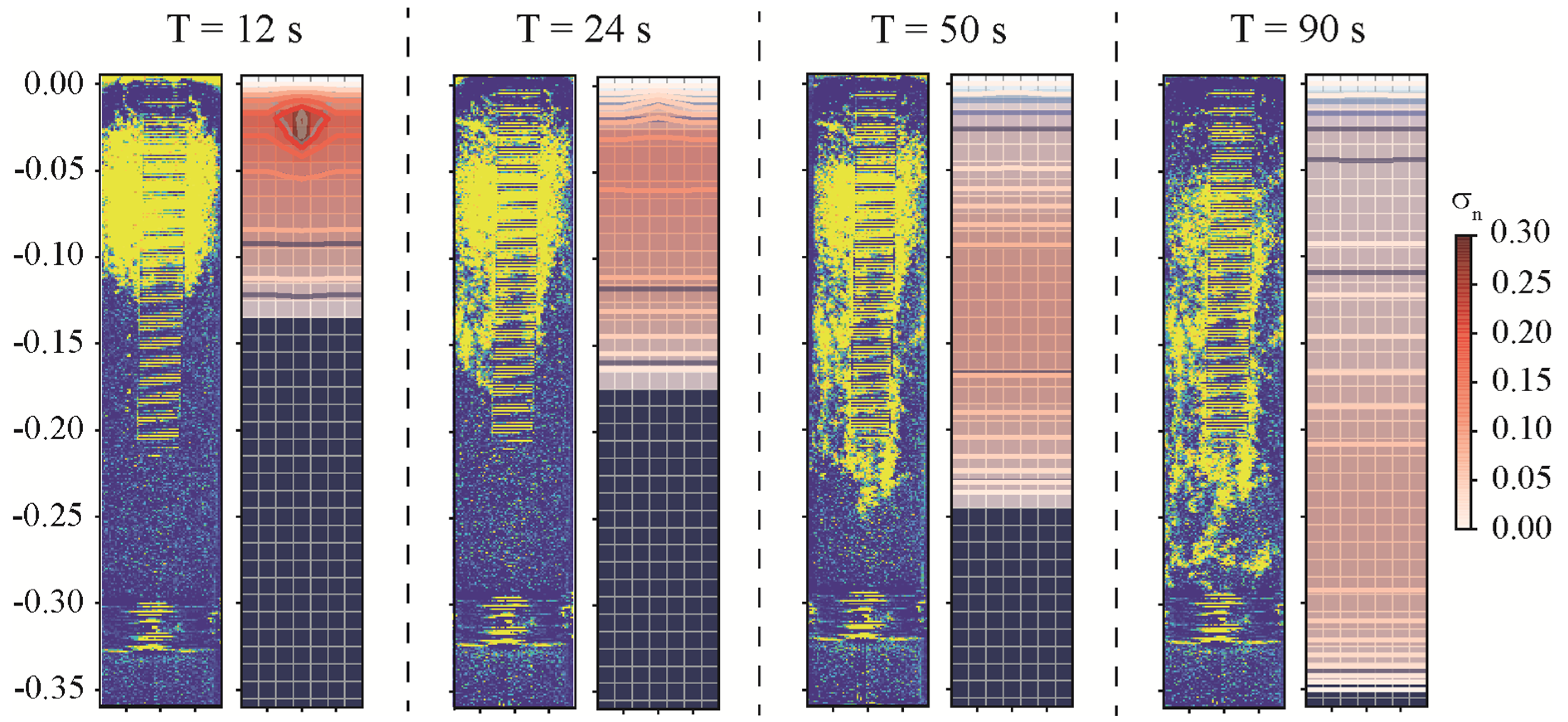
3.3. Comparison of DNAPL Migration between Experiment and Numerical Simulations in a Sandbox
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goswami, R.R.; Clement, T.P. Laboratory-scale investigation of saltwater intrusion dynamics. Water Resour. 2007, 43, W04418. [Google Scholar] [CrossRef]
- Silliman, S.E.; Zheng, L. Comparison of observations from a laboratory model with stochastic theory: Initial analysis of hydraulic and tracer experiments. Transp. Porous Media 2001, 42, 85–107. [Google Scholar] [CrossRef]
- Rathfelder, K.M.; Abriola, L.M.; Taylor, T.P.; Pennell, K.D. Surfactant enhanced recovery of tetrachloroethylene from a porous medium containing low permeability lenses 2. Numerical simulation. J. Contam. Hydrol. 2001, 48, 351–374. [Google Scholar] [CrossRef]
- Luciano, A.; Viotti, P.; Papini, M.P. Laboratory investigation of DNAPL migration in porous media. J. Hazard. Mater. 2010, 176, 1006–1017. [Google Scholar] [CrossRef] [PubMed]
- Luciano, A.; Mancini, G.; Torretta, V.; Viotti, P. An empirical model for the evaluation of the dissolution rate from a DNAPL-contaminated area. Environ. Sci. Pollut. Res. 2018, 25, 33992–34004. [Google Scholar] [CrossRef]
- Citarella, D.; Cupola, F.; Tanda, M.G.; Zanini, A. Evaluation of dispersivity coefficients by means of a laboratory image analysis. J. Contam. Hydrol. 2015, 172, 10–23. [Google Scholar] [CrossRef] [PubMed]
- Seyedpour, S.M.; Valizadeh, I.; Kirmizakis, P.; Doherty, R.; Ricken, T. Optimization of the Groundwater Remediation Process Using a Coupled Genetic Algorithm-Finite Difference Method. Water 2021, 13, 383. [Google Scholar] [CrossRef]
- Aksoy, A.; Guney, M.S. Experimental determination of three-dimensional dispersivities in homogeneous porous medium. Environ. Earth Sci. 2010, 60, 383–393. [Google Scholar] [CrossRef]
- Castro-Alcala, E.; Fernàndez-Garcia, D.; Carrera, J.; Bolster, D. Visualization of mixing processes in a heterogeneous sand box aquifer. Environ. Sci. Technol. 2012, 46, 3228–3235. [Google Scholar] [CrossRef]
- Praseeja, A.V.; Sajikumar, N. A review on the study of immiscible fluid flow in unsaturated porous media: Modeling and remediation. J. Porous Media 2019, 22, 889–922. [Google Scholar] [CrossRef]
- Soga, K.; Page, J.W.E.; Illangasekare, T.H. A review of NAPL source zone remediation efficiency and the mass flux approach. J. Hazard. Mater. 2004, 110, 13–27. [Google Scholar] [CrossRef]
- Engelmann, C.; Lari, K.S.; Schmidt, L.; Werth, C.J.; Walther, M. Towards predicting DNAPL source zone formation to improve plume assessment: Using robust laboratory and numerical experiments to evaluate the relevance of retention curve characteristics. J. Hazard. Mater. 2021, 407, 124741. [Google Scholar] [CrossRef] [PubMed]
- Zheng, F.; Gao, Y.; Sun, Y.; Shi, X.; Xu, H.; Wu, J. Influence of flow velocity and spatial heterogeneity on DNAPL migration in porous media: Insights from laboratory experiments and numerical modelling. Hydrogeol. J. 2015, 23, 1703–1718. [Google Scholar] [CrossRef]
- Parker, B.L.; Cherry, J.A.; Chapman, S.W. Field study of TCE diffusion profiles below DNAPL to assess aquitard integrity. J. Contam. Hydrol. 2004, 74, 197–230. [Google Scholar] [CrossRef]
- Harbaugh, A.W.; Banta, E.W.; Hill, M.C.; McDonald, M.G. MODFLOW-2000, the U.S. Geological Survey Modular Ground-Water Model—User Guide to Modularization Concepts and the Ground-Water Flow Process; Open File Report 00-92; United States Geological Survey: Reston, VA, USA, 2000.
- Zheng, C.; Wang, P.P. MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems; Documentation and User’s Guide No. SERDP-99-1; U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 1999.
- Feo, A.; Celico, F. High-resolution shock-capturing numerical simulations of three-phase immiscible fluids from the unsaturated to the saturated zone. Sci. Rep. 2021, 11, 5212. [Google Scholar] [CrossRef]
- Feo, A.; Celico, F. Investigating the migration of immiscible contaminant fluid flow in homogeneous and heterogeneous aquifers with high-precision numerical simulations. PLoS ONE 2022, 17, e0266486. [Google Scholar] [CrossRef] [PubMed]
- Kurganov, A.; Tadmor, E. New high-resolution central scheme for non-linear conservation laws and convection-diffusion equations. J. Comput. Phys. 2000, 160, 241–282. [Google Scholar] [CrossRef] [Green Version]
- Lax, P.; Wendroff, B. Systems of conservation laws. Commun. Pure Appl. Math. 1960, 3, 217–237. [Google Scholar] [CrossRef] [Green Version]
- Hou, T.Y.; LeFloch, P.G. Why nonconservative schemes converge to wrong solutions: Error analysis. Math. Comp. 1994, 62, 497–530. [Google Scholar] [CrossRef]
- Allen, G.; Goodale, T.; Lanfermann, G.; Radke, T.; Rideout, D.; Thornburg, J. Cactus Users’ Guide. 2011. Available online: http://www.cactuscode.org/documentation/UsersGuide.pdf (accessed on 1 January 2023).
- Cactus Developers. Cactus Computational Toolkit. Available online: http://www.cactuscode.org/ (accessed on 1 January 2023).
- Goodale, T.; Allen, G.; Lanfermann, G.; Massó, J.; Radke, T.; Seidel, E.; Shalf, J. The Cactus Framework and Toolkit: Design and Applications. In Vector and Parallel Processing—VECPAR’2002, Proceedings of the 5th International Converence, Porto, Portugal, 26–28 June 2002; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Schnetter, E.; Hawley, S.H.; Hawke, I. Evolutions in 3D numerical relativity using fixed mesh refinement. Class. Quantum Gravity 2004, 21, 1465–1488. [Google Scholar] [CrossRef] [Green Version]
- Schnetter, E.; Diener, P.; Dorband, E.N.; Tiglio, M. A multi-block infrastructure for three-dimensional time-dependent numerical relativity. Class. Quantum Gravity 2006, 23, S553. [Google Scholar] [CrossRef] [Green Version]
- Faust, C.R. Transport of immiscible fluids within and below the unsaturated zone: A numerical model. Water Resour. Res. 1985, 21, 587–596. [Google Scholar] [CrossRef]
- Faust, C.R.; Guswa, J.H.; Mercer, J.W. Simulations of three-dimensional flow of immiscible fluids within and below the unsaturated zone. Water Resour. Res. 1989, 25, 2449–2464. [Google Scholar] [CrossRef]
- Parker, J.C.; Lenhard, R.J.; Kuppusamy, T. A parametric model for constitutive properties governing multi-phase flow in porous media. Water Resour. Res. 1987, 23, 618–624. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A closed form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Chiapponi, L. Water retention curves of multicomponent mixtures of spherical particles. Powder Technol. 2017, 320, 646–655. [Google Scholar] [CrossRef]
- Hu, X.; Meng, X.; Wei, K.; Li, W.; Wu, J. Compressed Liquid Viscosity Measurements of HFE-7000, HFE-7100, HFE-7200, and HFE-7500 at temperatures from (253 to 373) K and pressures up to 30 Mpa. J. Chem Eng. Data 2015, 60, 3562–3570. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, J.A. Groundwater Book; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Carsel, R.F.; Parrish, R.S. Developing Joint Probability Distributions of Soil Water Retention Characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef] [Green Version]




| Parameter | Symbol | Value |
|---|---|---|
| Absolute permeability, | ||
| Rock compressibility, | ||
| Porosity | ||
| Water viscosity, | ||
| Water density, | ||
| DNAPL HFE-7100 dynamic viscosity, | ||
| DNAPL HFE-7100 density, | ||
| Air viscosity, | ||
| Air density, | ||
| Van Genuchten parameter | ||
| Irreducible wetting phase saturation | ||
| Surface tension DNAPL, | ||
| Interfacial tension DNAPL, | ||
| Surface tension water, | ||
| Capillary pressure air-water at zero saturation, | ||
| Capillary pressure DNAPL-water at zero saturation, | ||
| Capillary pressure air-nonaqueous at zero saturation, | ||
| Resolution, |
| Time (s) | Position of the Contaminant in the Experimental Column (m) | Position of the Contaminant in the Numerical Model (m) |
|---|---|---|
| 12 | ||
| 24 | ||
| 50 | ||
| 90 |
| Time (s) | Position of the Contaminant in the Experimental Sandbox (m) | Position of the Contaminant in the Numerical Model (m) |
|---|---|---|
| 5 | ||
| 25 | ||
| 50 | ||
| 75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feo, A.; Celico, F.; Zanini, A. Migration of DNAPL in Saturated Porous Media: Validation of High-Resolution Shock-Capturing Numerical Simulations through a Sandbox Experiment. Water 2023, 15, 1471. https://doi.org/10.3390/w15081471
Feo A, Celico F, Zanini A. Migration of DNAPL in Saturated Porous Media: Validation of High-Resolution Shock-Capturing Numerical Simulations through a Sandbox Experiment. Water. 2023; 15(8):1471. https://doi.org/10.3390/w15081471
Chicago/Turabian StyleFeo, Alessandra, Fulvio Celico, and Andrea Zanini. 2023. "Migration of DNAPL in Saturated Porous Media: Validation of High-Resolution Shock-Capturing Numerical Simulations through a Sandbox Experiment" Water 15, no. 8: 1471. https://doi.org/10.3390/w15081471
APA StyleFeo, A., Celico, F., & Zanini, A. (2023). Migration of DNAPL in Saturated Porous Media: Validation of High-Resolution Shock-Capturing Numerical Simulations through a Sandbox Experiment. Water, 15(8), 1471. https://doi.org/10.3390/w15081471








