An Empirical Model for Aeolian Sandy Soil Wetting Front Estimation with Subsurface Drip Irrigation
Abstract
:1. Introduction
| Category | Applied Soil | Irrigation Method | Equation | Basis for Establishment |
|---|---|---|---|---|
| Mathematical Model | Silt | Surface point source [27] | Derivation of Richards’ equation | |
| Numerical Model | All soil types [28,29,30,31] | - | Inversion of soil parameters | |
| Empirical Model | Sandy clay loam | Surface point source [32] | Test fitting | |
| All soil types | Surface point source [33] | |||
| Loam, sandy loam | Point source [34] | |||
| All soil types | Surface [35] | |||
| All soil types | Surface [38] | |||
| Loam, silty and sandy loam | Subsurface line source [22] |
2. Materials and Methods
2.1. Infiltration Experiment of Aeolian Sand
2.1.1. Experimental Soil Characteristics
2.1.2. Experimental Setup
2.1.3. Experimental Trials
2.2. Model Establishment Method
2.2.1. Wetting Front Distance Model
2.2.2. Wetting Body Elliptical Model
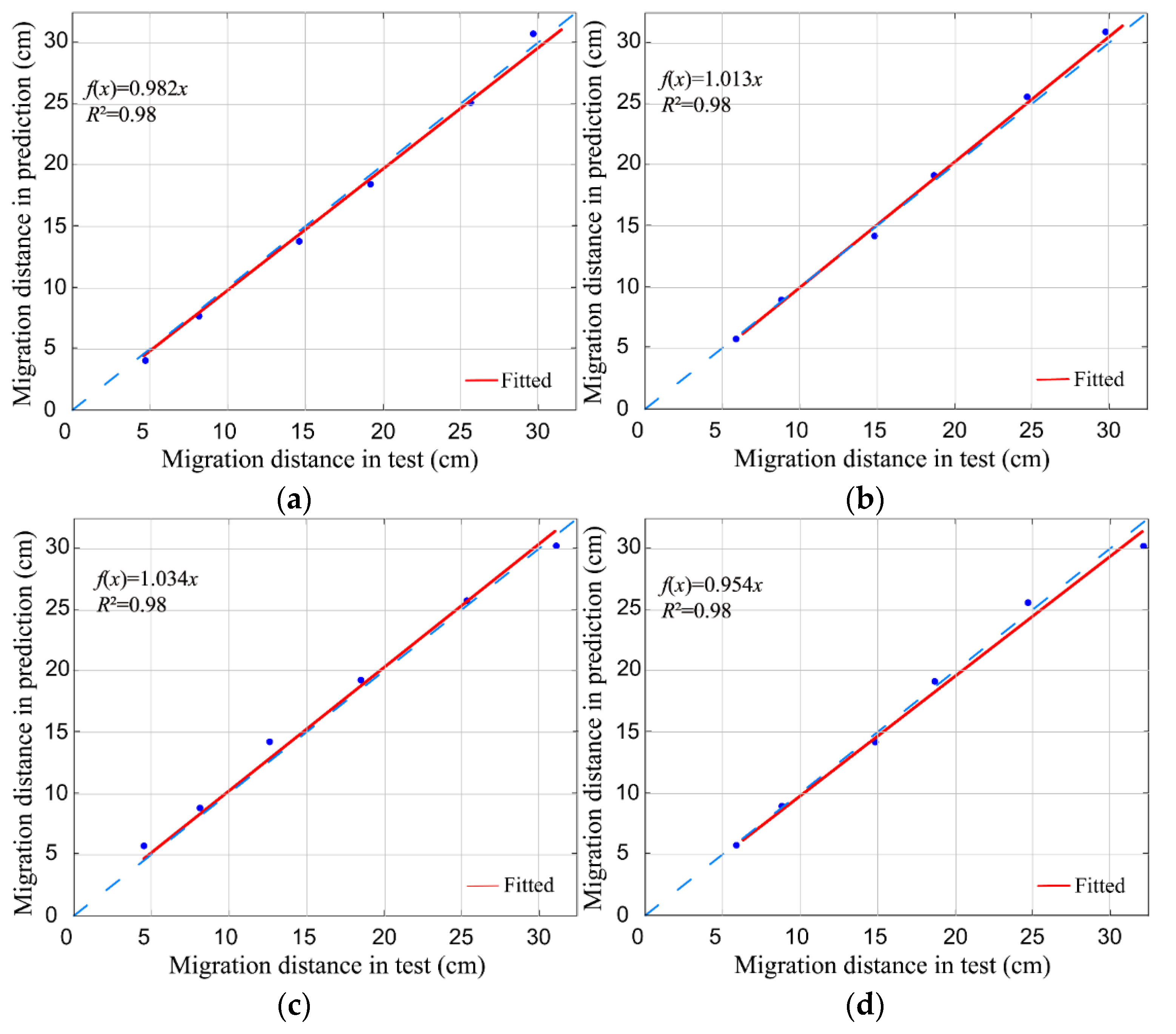
2.2.3. Model Evaluation
2.2.4. Numerical Model
3. Results
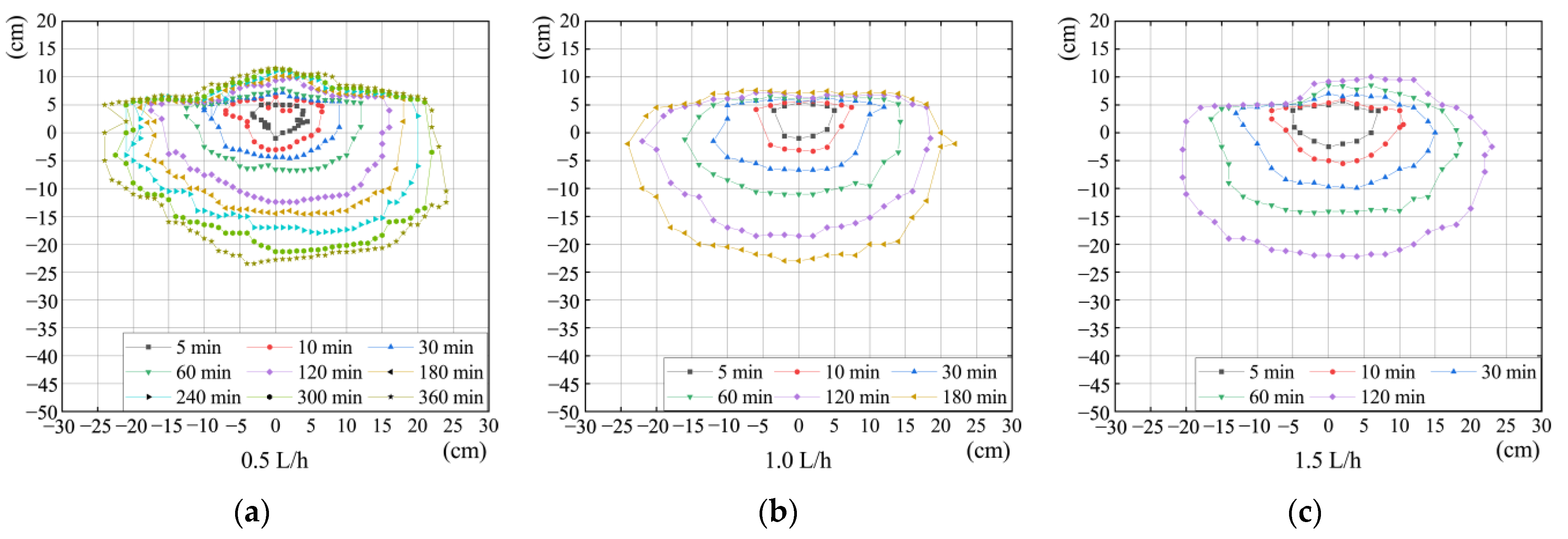
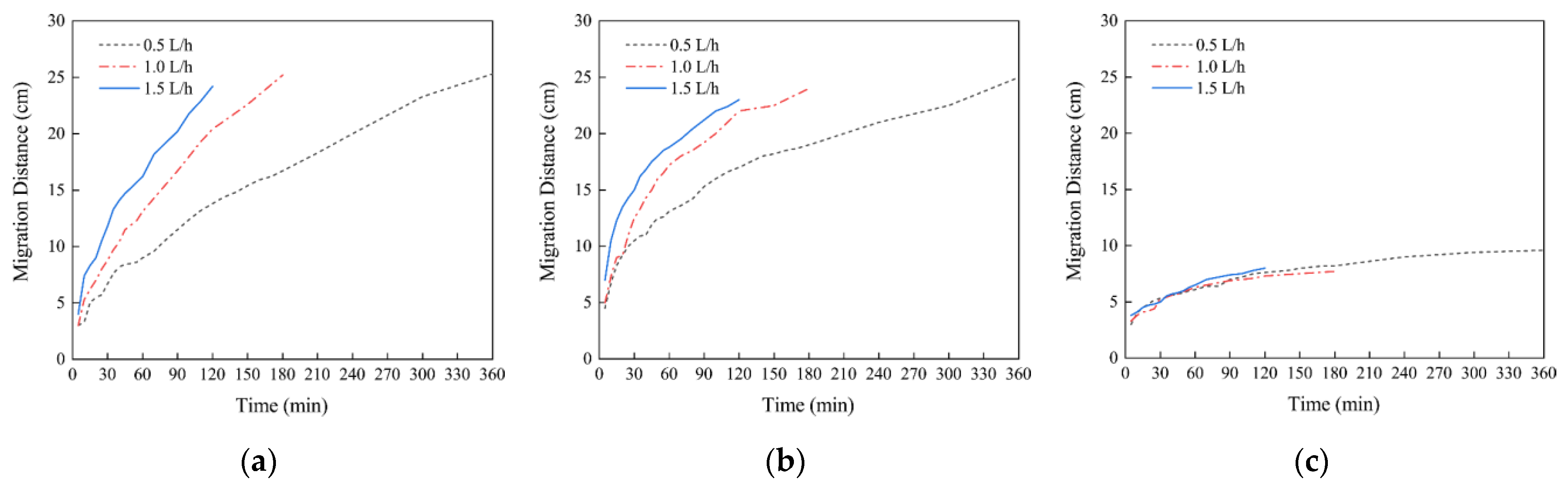
3.1. Wetting Front Distribution
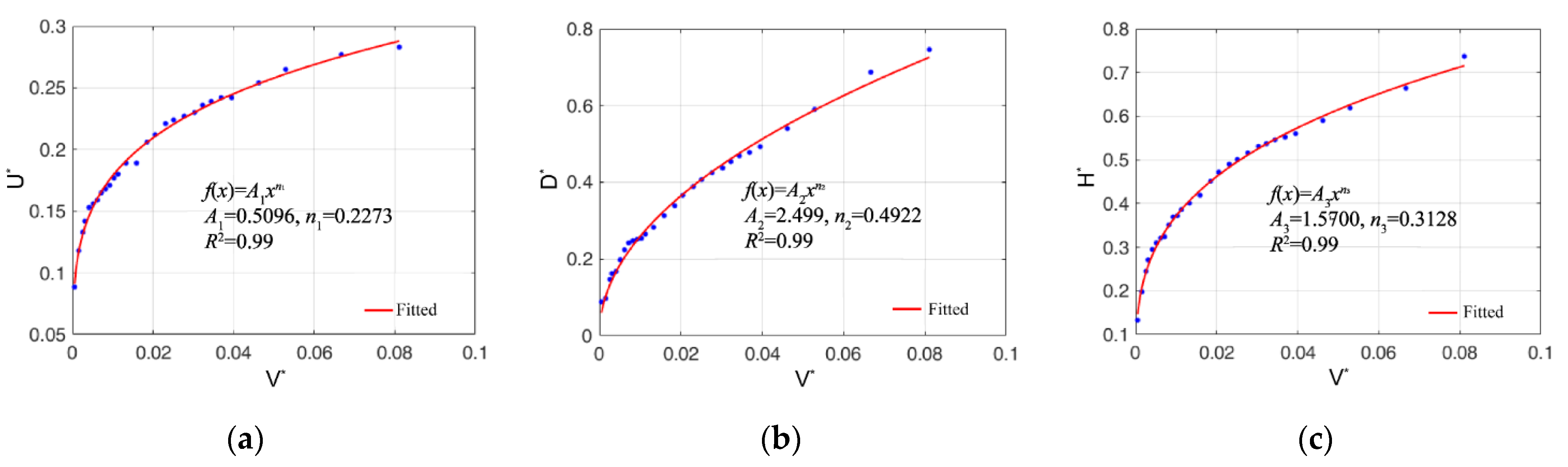
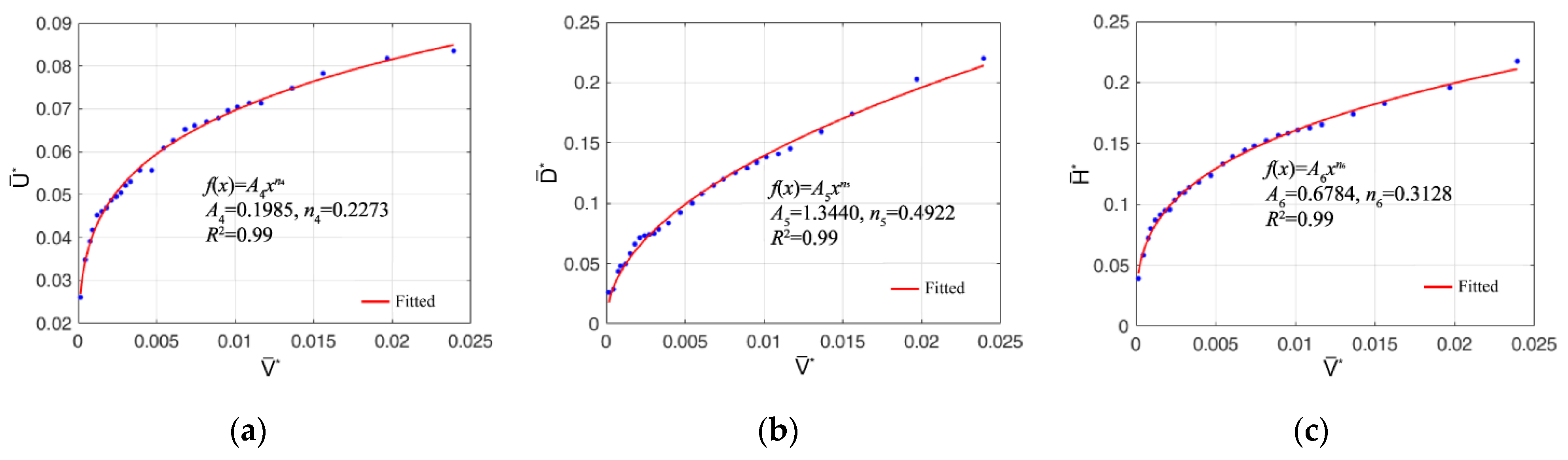
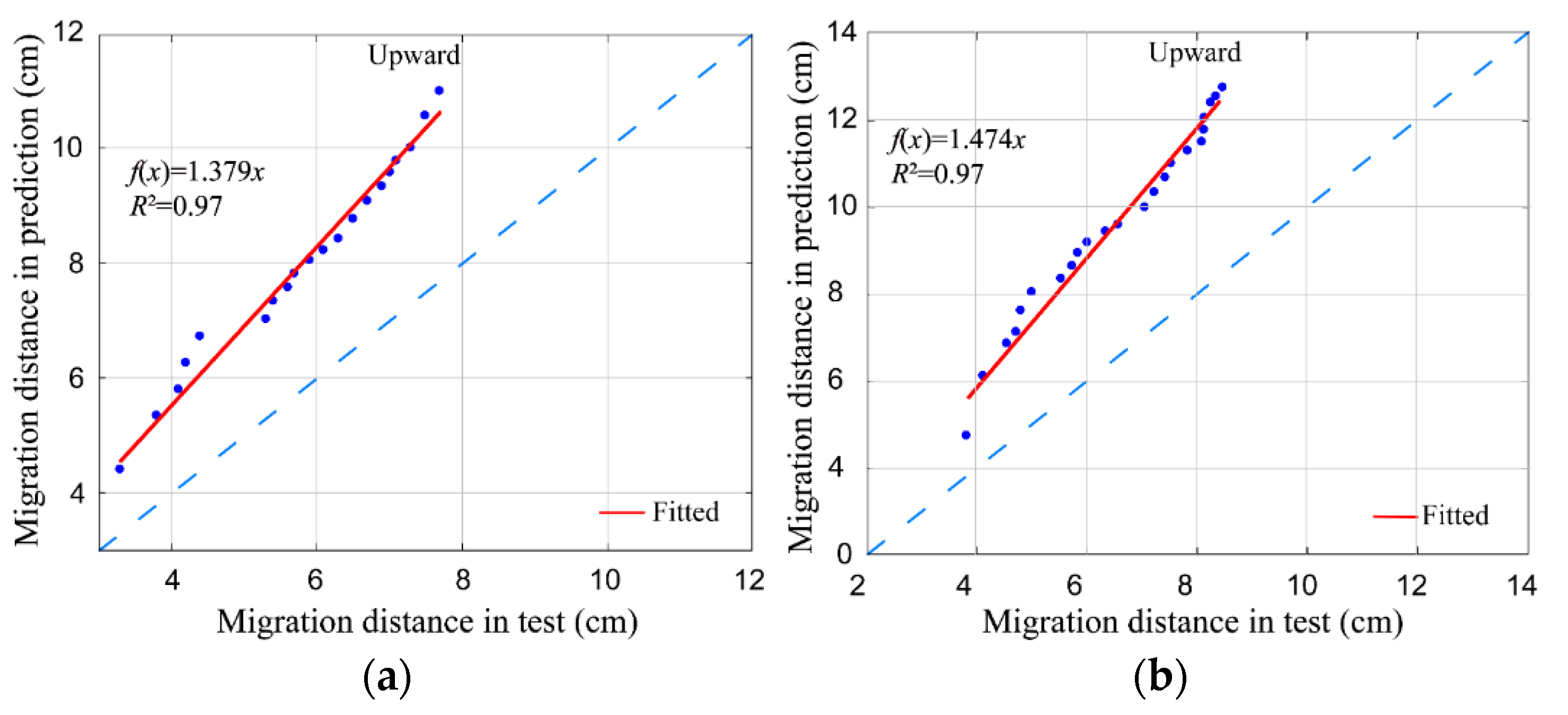
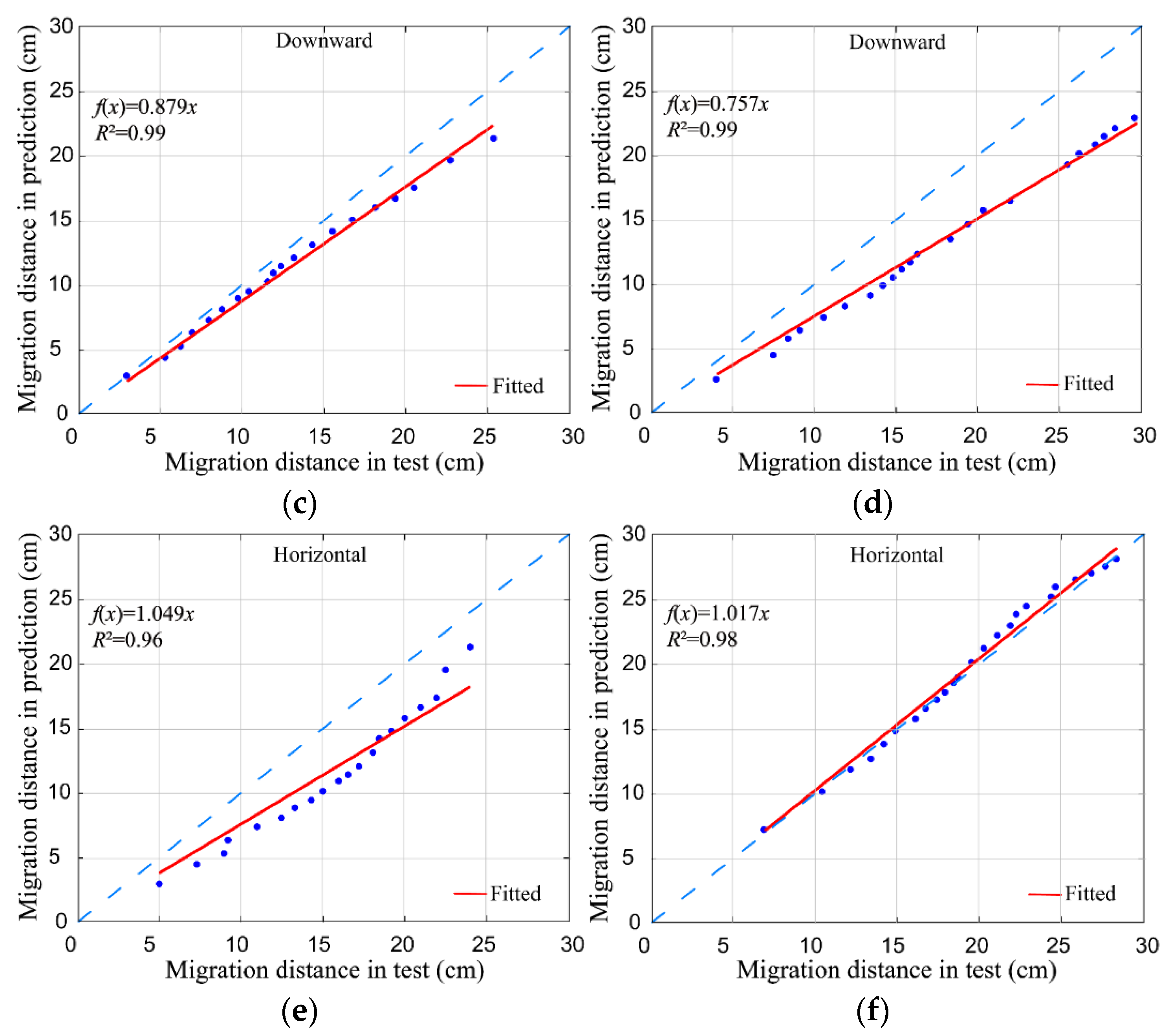
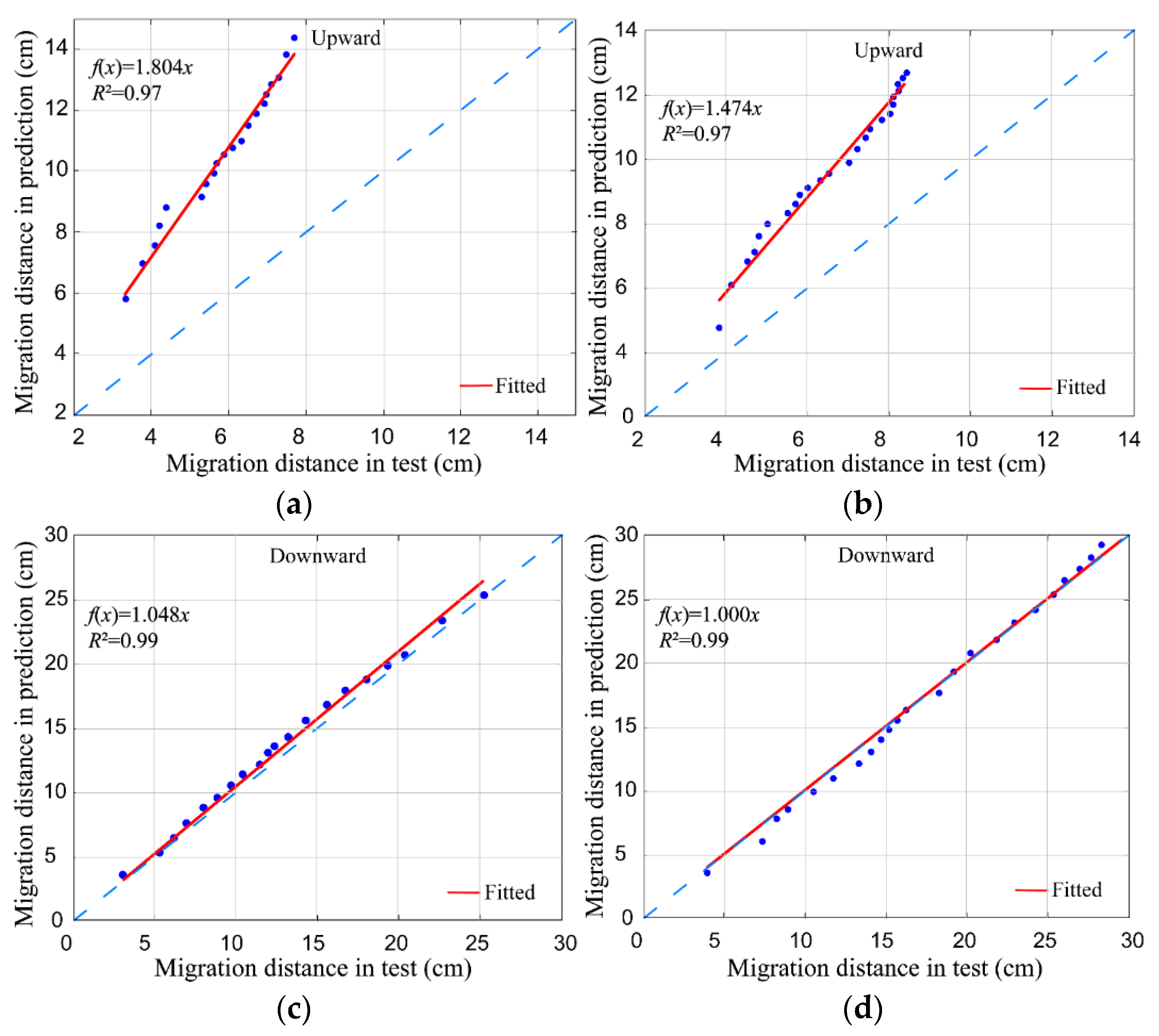
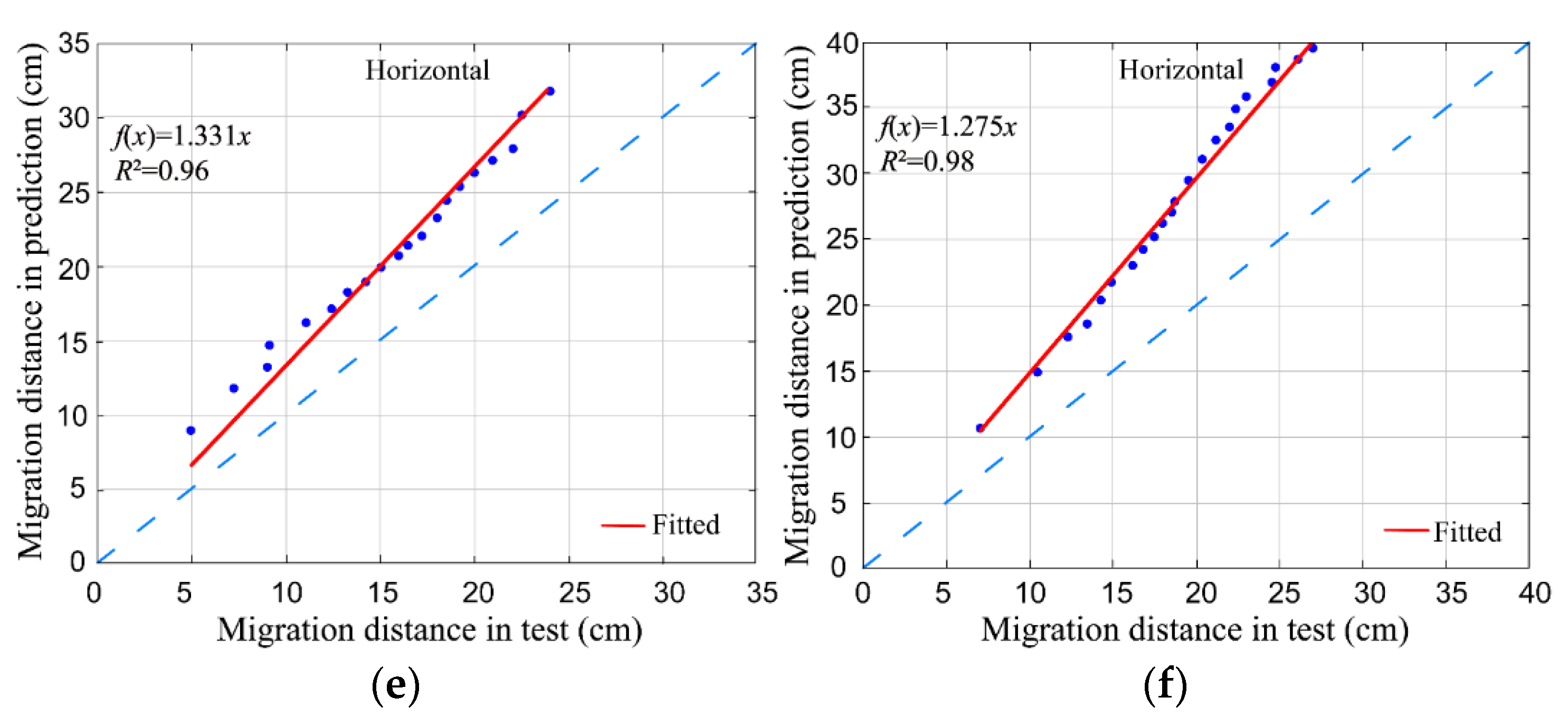
3.2. Proposed Model
3.2.1. Wetting Front Distance Model
3.2.2. Wetting Body Elliptical Model
4. Discussion
4.1. Wetting Front Distribution
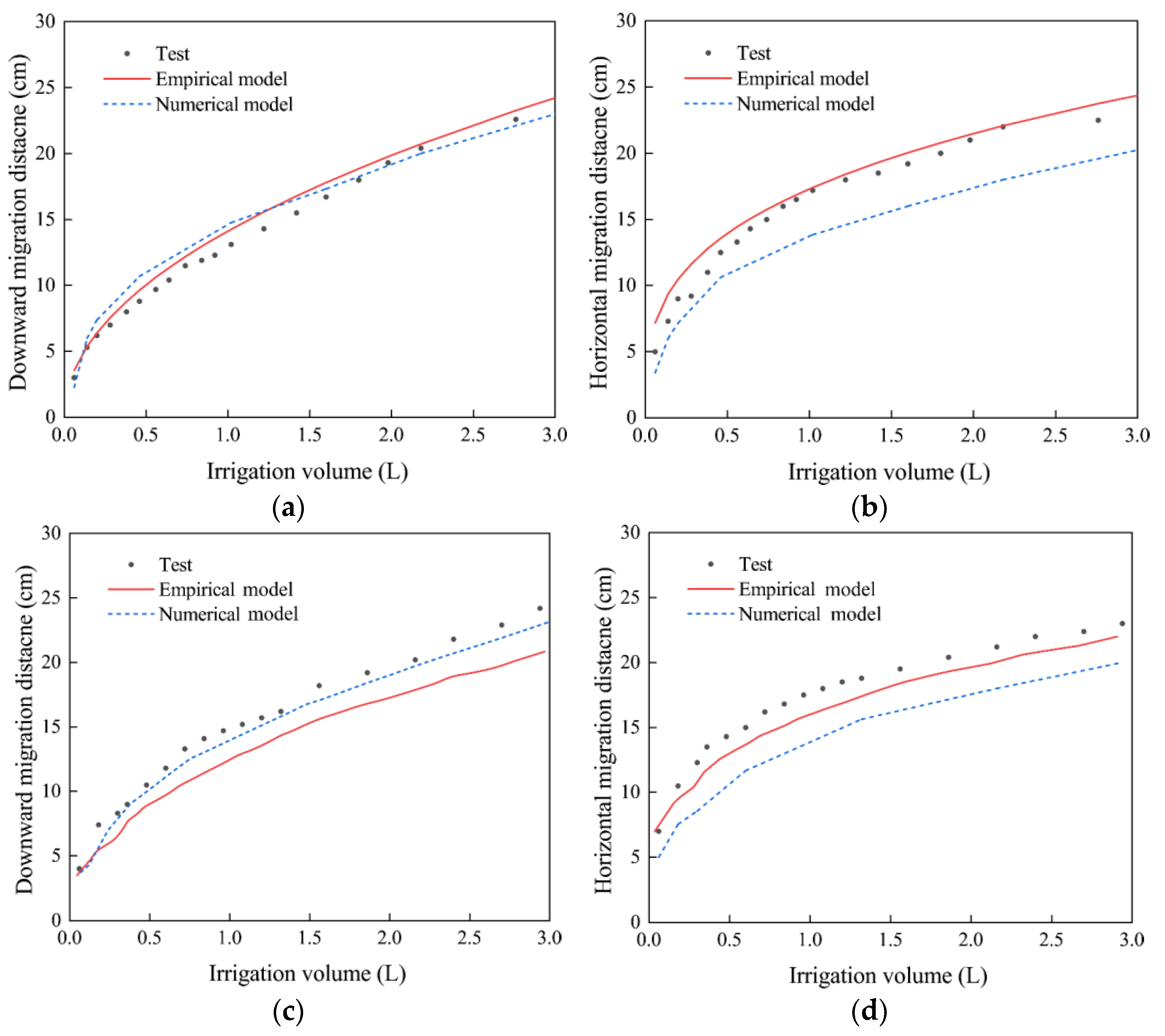
4.2. Comparison with a Numerical Model
5. Conclusions
- (1)
- The aeolian sandy soil wetting front shape resembles a “bowl”. At the same irrigation volume, the wetting front shape is more significant when the flow rate is low, while at the same irrigation time, the wetting front shape is more prominent when the flow rate is significant. As the time increases, the wetting front transport distance increment first increases and then decreases, and the transport direction is mainly horizontal and then vertical.
- (2)
- The point source infiltration model (Equation (12)) is more suitable for calculating the wetting front transport distance in the horizontal direction. The line source infiltration model (Equation (13)) is more suitable for calculating the wetting front transport distances in the vertical direction. The model proposed in this study (Equation (14)) can accurately calculate the wetting front transport pattern of aeolian sandy soil with subsurface drip irrigation.
- (3)
- The prediction degree of the model is consistent with that of HYDRUS-2D/3D and shows a better fit than HYDRUS-2D/3D in the horizontal direction. In practical applications, the model parameters are easy to obtain and use.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, J.; Lei, J.; Wang, Y.; Zhao, Y.; Xu, X. Survival and growth of three afforestation species under high saline drip irrigation in the Taklimakan Desert, China. Ecosphere 2016, 7, e01285. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zhao, Y.; Li, S.; Shen, F.; Jia, M.; Zhang, J.; Xu, X.; Lei, J. Soil aggregation formation in relation to planting time, water salinity, and species in the Taklimakan Desert Highway shelterbelt. J. Soil Sediment 2018, 18, 1466–1477. [Google Scholar] [CrossRef]
- Camp, C.R. Subaurface Drip Irrigation: A Review. Trans. ASAE 1998, 41, 1353. [Google Scholar] [CrossRef]
- Ayars, J.E.; Phene, C.J.; Hutmacher, R.B.; Davis, K.R.; Schoneman, R.A.; Vail, S.S.; Mead, R.M. Subsurface drip irrigation of row crops: A review of 15 years of research at the Water Management Research Laboratory. Agric. Water Manag. 1999, 42, 1–27. [Google Scholar] [CrossRef]
- Cote, C.M.; Bristow, K.L.; Charlesworth, P.B.; Cook, F.J.; Thorburn, P.J. Analysis of soil wetting and solute transport in subsurface trickle irrigation. Irrig. Sci. 2003, 22, 143–156. [Google Scholar] [CrossRef]
- Kang, Y.H.; Ma, X.Y.; Li, J.; Zhao, W.J. Research and Development on Subsurface Drip Irrigation Techni Que. J. Irrig. Drain. 2007, 6, 34–40. (In Chinese) [Google Scholar]
- Xuan, C.; Ding, R.; Shao, J.; Liu, Y. Evapotranspiration and Quantitative Partitioning of Spring Maize with Drip Irrigation under Mulch in an Arid Region of Northwestern China. Water 2021, 13, 3169. [Google Scholar] [CrossRef]
- Kalfountzos, D.; Alexiou, I.; Kotsopoulos, S.; Zavakos, G.; Vyrlas, P. Effect of Subsurface Drip Irrigation on Cotton Plantations. Water Resour. Manag. 2007, 21, 1341. [Google Scholar] [CrossRef]
- Çetin, O.; Kara, A. Assesment of water productivity using different drip irrigation systems for cotton. Agric. Water Manag. 2019, 223, 105693. [Google Scholar] [CrossRef]
- Cetin, O.; Uzen, N.; Temiz, M.G.; Altunten, H. Improving Cotton Yield, Water Use and Net Income in Different Drip Irrigation Systems Using Real-Time Crop Evapotranspiration. Pol. J. Environ. Stud. 2021, 30, 4463–4474. [Google Scholar] [CrossRef]
- Meshkat, M.; Warner, R.C.; Workman, S.R. Evaporation reduction potential in an undisturbed soil irrigated with surface drip and sand tube irrigation. Trans. ASAE 2000, 43, 79–86. [Google Scholar] [CrossRef]
- Yanni, S.; Nimah, M.N.; Bashour, I. Gravel vertical mulching for improving water use efficiency of drip irrigated orchards. Acta Horticulturae. 2004, 9, 664. [Google Scholar] [CrossRef]
- Adamsen, F.J. Irrigation Method and Water-Quality Effect on Peanut Yield and Grade. Agron. J. 1989, 81, 589–593. [Google Scholar] [CrossRef]
- Ma, X.; Sanguinet, K.A.; Jacoby, P.W. Direct root-zone irrigation outperforms surface drip irrigation for grape yield and crop water use efficiency while restricting root growth. Agric. Water Manag. 2020, 231, 105993. [Google Scholar] [CrossRef]
- Montoya, F.; Sánchez, J.M.; González-Piqueras, J.; López-Urrea, R. Is the Subsurface Drip the Most Sustainable Irrigation System for Almond Orchards in Water-Scarce Areas? Agronomy 2022, 12, 1778. [Google Scholar] [CrossRef]
- Moncef, H.; Khemaies, Z. Optimizing Emitters’ Density and Water Supplies in Trickle Irrigation Systems. Am. J. Water Sci. Eng. 2019, 5, 16–21. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.; Shuqian, W.; Dan, X. Experimental Investigations on Influence of Fracture Networks on Overland Flow and Water Infiltration in Soil. Water. 2022, 14, 3483. [Google Scholar]
- Dasberg, S.; Or, D. Practical Applications of Drip Irrigation; Springer: Berlin/Heidelberg, Germany, 1999; pp. 125–138. [Google Scholar]
- Huang, M.; Barbour, S.L.; Elshorbagy, A.; Zettl, J.D.; Si, B.C. Infiltration and drainage processes in multi-layered coarse soils. Can. J. Soil Sci. 2011, 91, 169–183. [Google Scholar] [CrossRef]
- Khoshravesh Miangoleh, M.; Kiani, A.R. Effect of magnetized water on infiltration capacity of different soil textures. Soil Use Manag. 2014, 30, 588–594. [Google Scholar] [CrossRef]
- Li, M.S.; Kang, S.Z.; Sun, H.Y. Relationships between dripper discharge and soil wetting pattern for drip irrigation. Trans. Chin. Soc. Agric. Eng. 2006, 22, 32–35. (In Chinese) [Google Scholar]
- Fan, Y.; Ma, L.; Wei, H.; Zhu, P. Numerical investigation of wetting front migration and soil water distribution under vertical line source irrigation with different influencing factors. Water Supply 2021, 21, 2233–2248. [Google Scholar] [CrossRef]
- Geng, L.; Li, L.; Li, W.; Yang, C.; Meng, F. HYDRUS-2D simulations of water movement in a drip irrigation system under soilless substrate. Int. J. Agric. Biol. Eng. 2022, 15, 210–216. [Google Scholar] [CrossRef]
- Malek, K.; Peters, R.T. Wetting Pattern Models for Drip Irrigation: New Empirical Model. J. Irrig. Drain. Eng. 2011, 137, 530–536. [Google Scholar] [CrossRef]
- Al-Ogaidi, A.A.M.; Wayayok, A.; Kamal, M.R.; Abdullah, A.F. A modified empirical model for estimating the wetted zone dimensions under drip irrigation. J. Teknol. 2015, 76, 69–73. [Google Scholar] [CrossRef] [Green Version]
- Shiri, J.; Karimi, B.; Karimi, N.; Kazemi, M.H.; Karimi, S. Simulating wetting front dimensions of drip irrigation systems: Multi criteria assessment of soft computing models. J. Hydrol. 2020, 585, 124792. [Google Scholar] [CrossRef]
- Moncef, H.; Hedi, D.; Jelloul, B.; Mohamed, M. Approach for predicting the wetting front depth beneath a surface point source: Theory and numerical aspect. Irrig. Drain. 2002, 51, 347–360. [Google Scholar] [CrossRef]
- Iacute, G.; A Morillo, J.; Iacute, R.; Iacute, G.D.; Az, J.A.; Camacho, E.; Montesinos, P. Drip Irrigation Scheduling Using Hydrus 2-D Numerical Model Application for Strawberry Production in South-West Spain. Irrig. Drain. 2017, 66, 797–807. [Google Scholar]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Development and Applications of the HYDRUS and STANMOD Software Packages and Related Codes. Vadose Zone J. 2008, 7, 587–600. [Google Scholar] [CrossRef] [Green Version]
- Zapata-Sierra, A.J.; Roldán-Cañas, J.; Reyes-Requena, R.; Moreno-Pérez, M.F. Study of the Wet Bulb in Stratified Soils (Sand-Covered Soil) in Intensive Greenhouse Agriculture under Drip Irrigation by Calibrating the Hydrus-3D Model. Water 2021, 13, 600. [Google Scholar] [CrossRef]
- Bufon, V.B.; Lascano, R.J.; Bednarz, C.; Booker, J.D.; Gitz, D.C. Soil water content on drip irrigated cotton: Comparison of measured and simulated values obtained with the Hydrus 2-D model. Irrig. Sci. 2012, 30, 259–273. [Google Scholar] [CrossRef]
- Cristóbal-Muñoz, I.; Prado-Hernández, J.V.; Martínez-Ruiz, A.; Pascual-Ramírez, F.; Cristóbal-Acevedo, D.; Cristóbal-Muñoz, D. An Improved Empirical Model for Estimating the Geometry of the Soil Wetting Front with Surface Drip Irrigation. Water 2022, 14, 1827. [Google Scholar] [CrossRef]
- Fan, Y.; Shao, X.; Gong, J.; Wang, Y. An empirical model for estimating soil wetting pattern dimensions during film hole irrigation. Arch. Agron. Soil Sci. 2020, 66, 1765–1779. [Google Scholar] [CrossRef]
- Vishwakarma, D.K.; Kumar, R.; Kumar, A.; Kushwaha, N.L.; Elbeltagi, K.S.K.A. Evaluation and development of empirical models for wetted soil fronts under drip irrigation in high-density apple crop from a point source. Irrig. Sci. 2022, 1–24. [Google Scholar] [CrossRef]
- Al-Ogaidi, A.A.M.A.; Wayayok, A.; Rowshon, M.K.; Abdullah, A.F. Wetting patterns estimation under drip irrigation systems using an enhanced empirical model. Agric. Water Manag. 2016, 176, 203–213. [Google Scholar] [CrossRef]
- Hu, B.; Cheng, W.; Han, Z.; Ma, T. Experimental study on degradation law of organic matter and ammonia nitrogen in biological aerated filter. J. Hydraul. Eng. 2010, 41, 374–378. (In Chinese) [Google Scholar]
- Subbauah, R.; Mashru, H.H. Modeling for predicting soil wetting radius under point source surface trickle irrigation. Agric. Eng. Int. CIGR J. 2013, 15, 1–10. [Google Scholar]
- Zur, B. Wetted soil volume as a design objective in trickle irrigation. Irrig. Sci. 1996, 16, 101–105. [Google Scholar] [CrossRef]
- Moncef, H.H.M.Y.; Khemaies, Z. An analytical approach to predict the moistened bulb volume beneath a surface point source. Agric. Water Manag. 2016, 166, 123–129. [Google Scholar] [CrossRef] [Green Version]
- Kandelous, M.M.; Šimůnek, J. Comparison of numerical, analytical, and empirical models to estimate wetting patterns for surface and subsurface drip irrigation. Irrig. Sci. 2010, 28, 435–444. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.F.Y.; Huang, N.H.N.; Gong, J.G.J.; Shao, X.S.X.; Zhang, J.Z.J.; Zhao, T.Z.T. A Simplified Infiltration Model for Predicting Cumulative Infiltration during Vertical Line Source Irrigation. Water 2018, 10, 89. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Wang, Q. Simulation of soil water distribution under vertical line source infiltration. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2011, 42, 51–57. [Google Scholar]
- Bingyao, W.; Wei, W.; Liu, L.; Wang, Z. Water Movement and Its Potential for Uptake by Roots under Plug-in Subsurface Drip Irrigation. J. Irrig. Drain. 2019, 38, 1–10. (In Chinese) [Google Scholar]
- Zitterell, D.B.; Frizzone, J.A.; Neto, O.R. Dimensional analysis approach to estimate local head losses in microirrigation connectors. Irrig. Sci. 2014, 32, 169–179. [Google Scholar] [CrossRef]
- Matchev, K.T.; Matcheva, K.; Roman, A. Analytical Modeling of Exoplanet Transit Spectroscopy with Dimensional Analysis and Symbolic Regression. Astrophys. J. 2022, 930, 33. [Google Scholar] [CrossRef]
- Kazemi, M.; Barati, R. Application of dimensional analysis and multi-gene genetic programming to predict the performance of tunnel boring machines. Appl. Soft Comput. 2022, 124, 108997. [Google Scholar] [CrossRef]
- Ma, J.; Yang, Z.; Yang, L.; Tang, J. A physical view of computational neurodynamics. J. Zhejiang Univ.-Sci. A 2019, 9, 639–659. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, Y.; Xu, H. Effective length factor of a non-symmetrical cross-bracing system with a discontinuous diagonal. J. Zhejiang Univ.-Sci. A 2019, 20, 590–600. [Google Scholar] [CrossRef]
- Zhang, J.Z.J.; Xu, X.X.X.; Lei, J.L.J.; Sun, S.S.S.; Fan, J.F.J.; Li, S.L.S.; Gu, F.G.F.; Qiu, Y.Q.Y.; Xu, B.X.B. The salt accumulation at the shifting aeolian sandy soil surface with high salinity groundwater drip irrigation in the hinterland of the Taklimakan Desert. Chin. Sci. Bull. 2008, 53, 63–70. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zhang, H.; Xu, X. Study on the wetting front of water infiltration and soil water redistribution in aeolian sandy soil. J. Arid. Environ. 2009, 23, 190–194. (In Chinese) [Google Scholar]
- Pan, Y.; Wang, X.; Ma, X.; Zhang, Y.; Hu, R. The stable isotopic composition variation characteristics of desert plants and water sources in an artificial revegetation ecosystem in Northwest China. Catena 2020, 189, 104499. [Google Scholar] [CrossRef]
- Buckingham, E. On Physically Similar Systems; Illustrations of the Use of Dimensional Equations. Phys. Rev. 1914, 4, 345. [Google Scholar] [CrossRef]
- Schwartzman, M.; Zur, B. Emitter Spacing and Geometry of Wetted Soil Volume. J. Irrig. Drain. Eng. 1986, 112, 242–253. [Google Scholar] [CrossRef]
- Ritter, A.; Ntilde, M.; Oz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]


| Soil | Particle Size (mm) | Saturated Water Content (%) | Saturated Hydraulic Conductivity Ks (cm/s) | Soil Bulk Density (g/cm3) | ||
|---|---|---|---|---|---|---|
| >0.075 (%) | 0.075~0.002 (%) | <0.002 (%) | ||||
| Aeolian sandy soil | 90 | 2.1 | 7.9 | 41.54 | 2.37 × 10−3 | 1.565 |
| Point source infiltration | A1 | n1 | A2 | n2 | A3 | n3 |
| 0.5096 | 0.2273 | 2.4990 | 0.4922 | 1.5700 | 0.3128 | |
| Line source infiltration | A4 | n4 | A5 | n5 | A6 | n6 |
| 0.1985 | 0.2273 | 1.3440 | 0.4922 | 0.6784 | 0.3128 |
| Model | MAE (cm) | RMSE (cm) | PBIAS (%) | NSE (−) |
|---|---|---|---|---|
| Downward | 0.50 | 0.61 | 1.007 | 0.99 |
| Horizontal | 1.16 | 1.39 | −5.89 | 0.94 |
| Model | MAE (cm) | RMSE (cm) | PBIAS (%) | NSE (−) | |
|---|---|---|---|---|---|
| 1.0 L/h | 30° | 0.70 | 0.95 | 1.28 | 0.98 |
| 60° | 0.83 | 0.95 | −3.01 | 0.98 | |
| 1.5 L/h | 30° | 0.71 | 0.95 | 1.37 | 0.98 |
| 60° | 0.88 | 0.96 | −3.47 | 0.99 | |
| Flowrate | Q = 0.5 L/h | Q = 1.0 L/h | Q = 1.5 L/h | |||
|---|---|---|---|---|---|---|
| Wetted Body Scale | Maximum Width d | Maximum Depth D | Maximum Width d | Maximum Depth D | Maximum Width d | Maximum Depth D |
| Test | 47.5 | 34.6 | 46.6 | 32.9 | 44.2 | 32.2 |
| Zur’s model | 17.5 | 34.6 | 21.6 | 32.9 | 24.5 | 32.2 |
| Soil | Saturated Water Content θs (cm3/cm3) | Residual Water Content θr (cm3/cm3) | Parameter α | Parameter n | Saturated Hydraulic Conductivity (cm/s) |
|---|---|---|---|---|---|
| Aeolian sandy soil | 0.415 | 0.025 | 0.292 | 2.428 | 3.02 × 10−3 |
| Model | Irrigation Flow (L/h) | Wetting Front Direction | MAE (cm) | RMSE (cm) | NSE (−) |
|---|---|---|---|---|---|
| Hydrus 3D | 1.0 | Horizontal | 2.53 | 2.69 | 0.84 |
| Downward | 1.05 | 1.16 | 0.98 | ||
| 1.5 | Horizontal | 3.06 | 3.10 | 0.68 | |
| Downward | 0.54 | 0.62 | 0.99 | ||
| Proposed model | 1.0 | Horizontal | 1.00 | 1.20 | 0.95 |
| Downward | 0.75 | 0.83 | 0.98 | ||
| 1.5 | Horizontal | 1.16 | 1.39 | 0.94 | |
| Downward | 0.50 | 0.61 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, W.; Luo, Z.; Lin, D.; Zhang, Z.; Wang, S. An Empirical Model for Aeolian Sandy Soil Wetting Front Estimation with Subsurface Drip Irrigation. Water 2023, 15, 1336. https://doi.org/10.3390/w15071336
Qiao W, Luo Z, Lin D, Zhang Z, Wang S. An Empirical Model for Aeolian Sandy Soil Wetting Front Estimation with Subsurface Drip Irrigation. Water. 2023; 15(7):1336. https://doi.org/10.3390/w15071336
Chicago/Turabian StyleQiao, Wei, Zhihua Luo, Daming Lin, Zhongjian Zhang, and Songjiang Wang. 2023. "An Empirical Model for Aeolian Sandy Soil Wetting Front Estimation with Subsurface Drip Irrigation" Water 15, no. 7: 1336. https://doi.org/10.3390/w15071336





