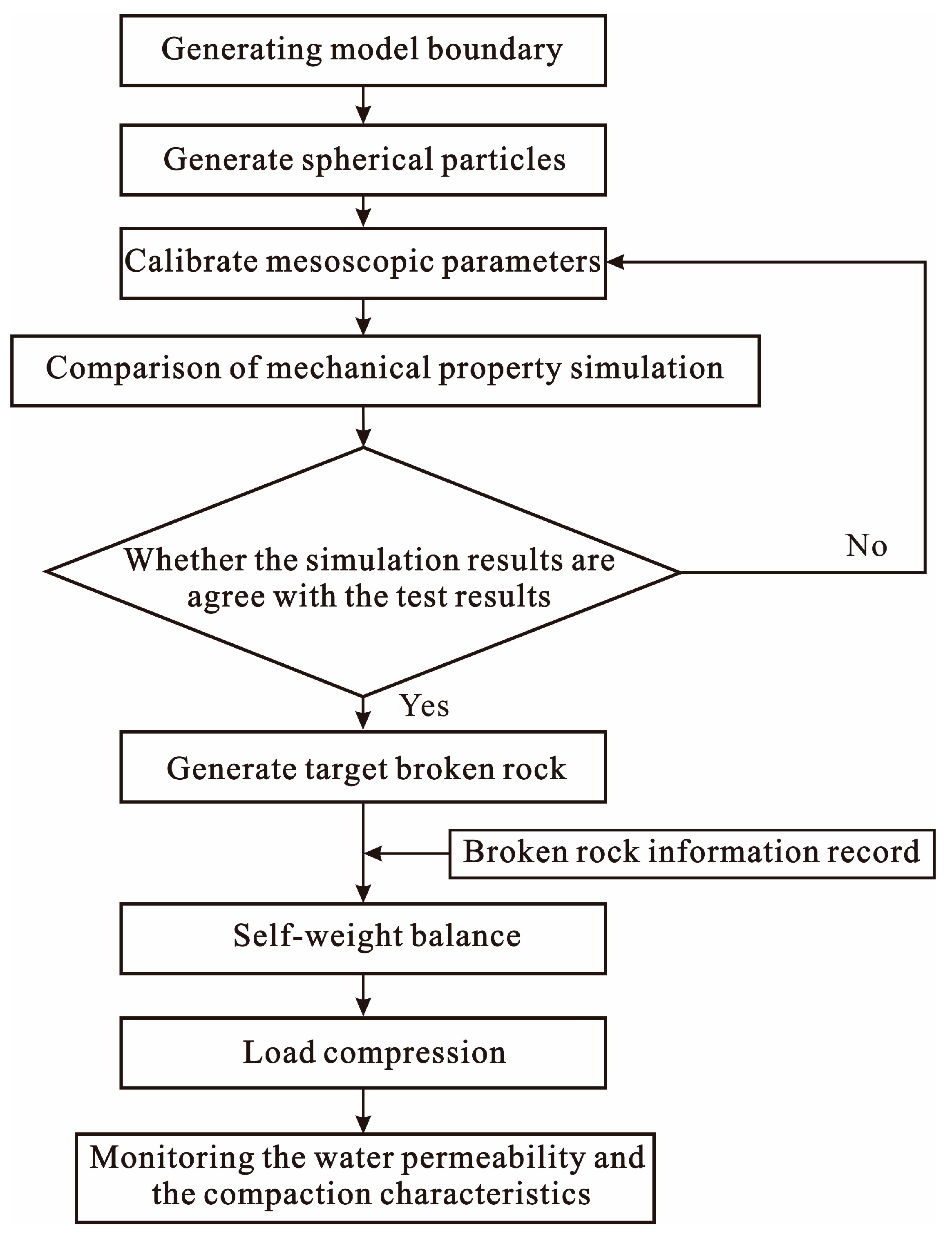
3.1. Compaction and Deformation Characteristics of Caving Rock Masses with Different Shapes
The crushed rock was gradually compacted and deformed under the pressure of the overburden rock. Five different prism-number particle clusters—tetragonal, pentagonal, hexagon, octagonal and decagonal—were obtained to establish test samples, and the numerical simulation of lateral compression was carried out. The numerical simulation results are shown in
Figure 7.
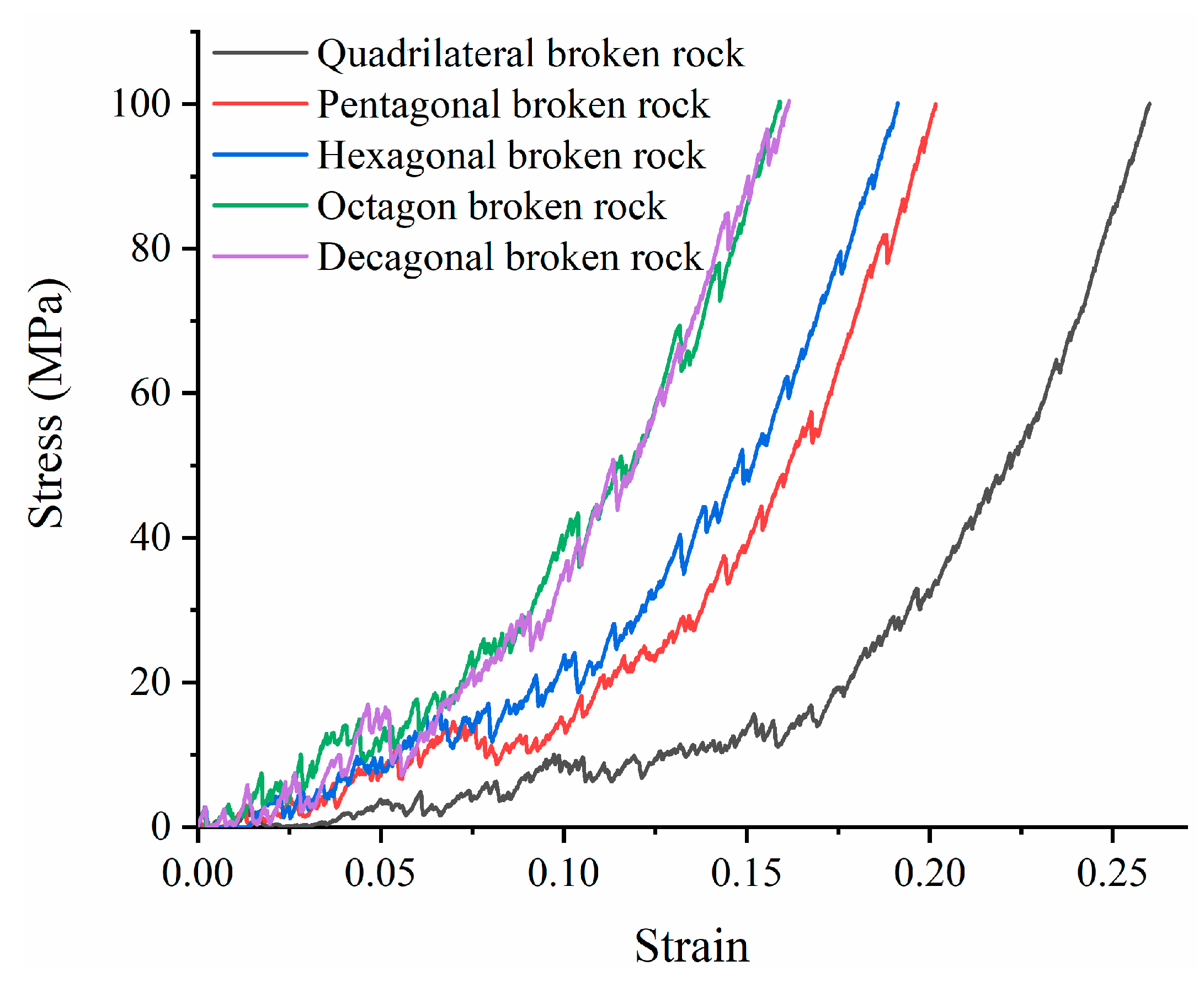
Through processing the numerical simulation results, the stress–strain curve changes of different shapes of caving rock masses were sorted out, as shown in
Figure 8. As shown in
Figure 8, the changes in the compaction stress–strain curves of the caving rock masses of different shapes are exponential, and there are both compaction stages (straight section) and nonlinear change stages. This is similar to the compaction stress–strain relationship of broken rock masses under different size and grading conditions [
7,
8]. When the stress level was low, it was mainly manifested as the compaction stage; the longest stage was for the quadrangular caving rock masses, and the shortest stage was for the decagonal caving rock masses. At this stage, the caving rock masses were loose porous media, and the strain greatly increased when the stress increment was small. With the increase in stress, when the axial strain of the tetragonal caving rocks and ten deformed caving rocks reached approximately 17% and 6%, respectively, a nonlinear stage was gradually shown, in which the stress increment was large and the strain increment was small. Under the same stress conditions, the strain produced by the quadrangular caving rock masses was the largest, and the ultimate limit strain was larger, while the limit strain of the caving rock masses with more prisms was smaller.
3.2. Stress–Strain Relationship and Deformation Modulus of Caving Rock Mass with Different Shapes
The tangent modulus and secant modulus of a broken rock mass are important indexes to measure the deformation resistance of a broken rock mass under compression.
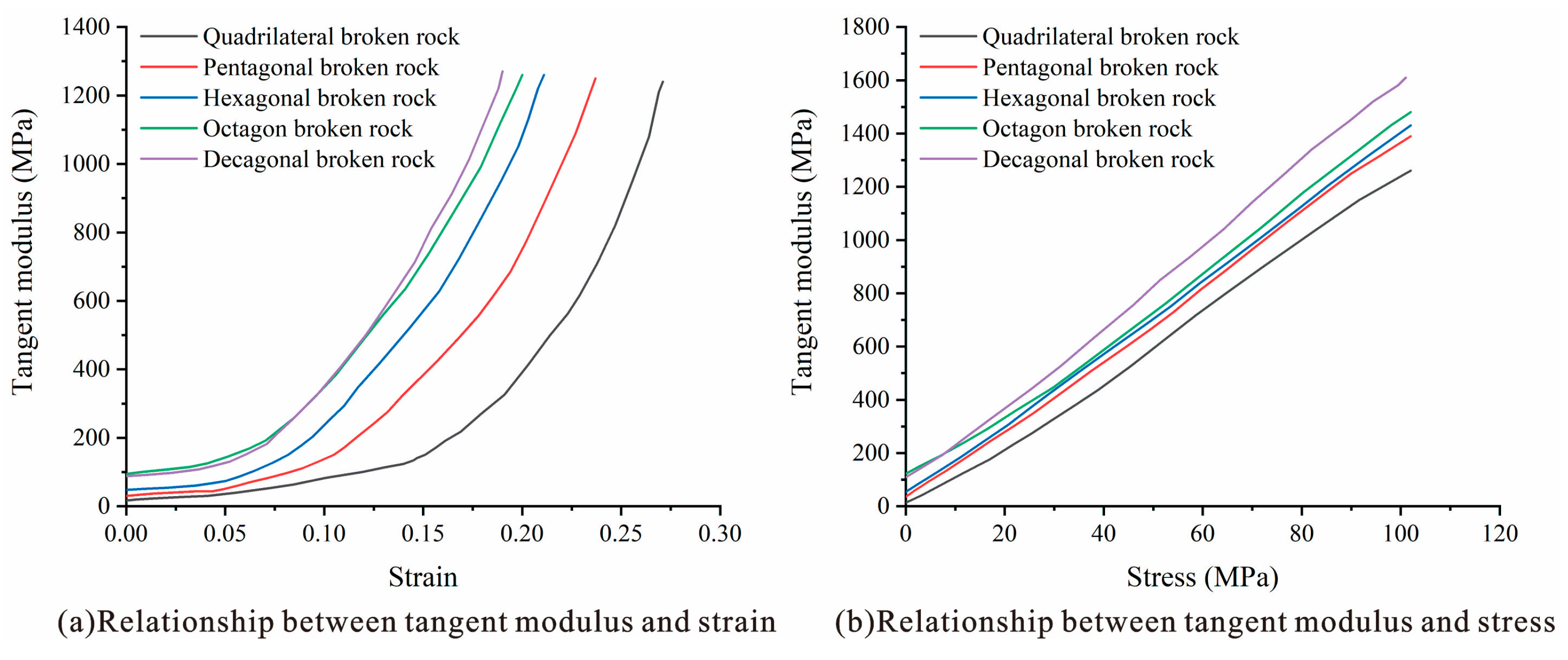
Figure 9a shows the relationship of the tangential modulus of the caving rock masses with the strain in different rock mass shapes. The tangential modulus of rock masses of different shapes is exponentially related to the strain [
18]. When the strain is small (approximately 8%), the tangential moduli of rock masses with different shapes are not significantly different. Rock masses with few edges are slightly smaller than that with more edges. With a continuous increase in strain, the tangential modulus of the octagonal and decagonal caving rock masses enters the nonlinear stage and starts to rapidly increase. Later, the caving rock masses with fewer edges enters the nonlinear stage, and when the number of edges continuously increases to a certain extent, the shape resembles a circle, and the shape has minimal influence on the tangential modulus.
Figure 9b shows the relationship of the tangential modulus of the caving rock masses with stress in different shapes of rock mass. The tangential modulus of the caving rock masses of different shapes exhibits a slight difference when the stress is small. With a continuous increase in stress, the tangential modulus gradually increases [
18]. The tangential modulus of the caving rock masses with a larger number of edges increases at a faster rate than that of the caving rock masses with fewer edges.
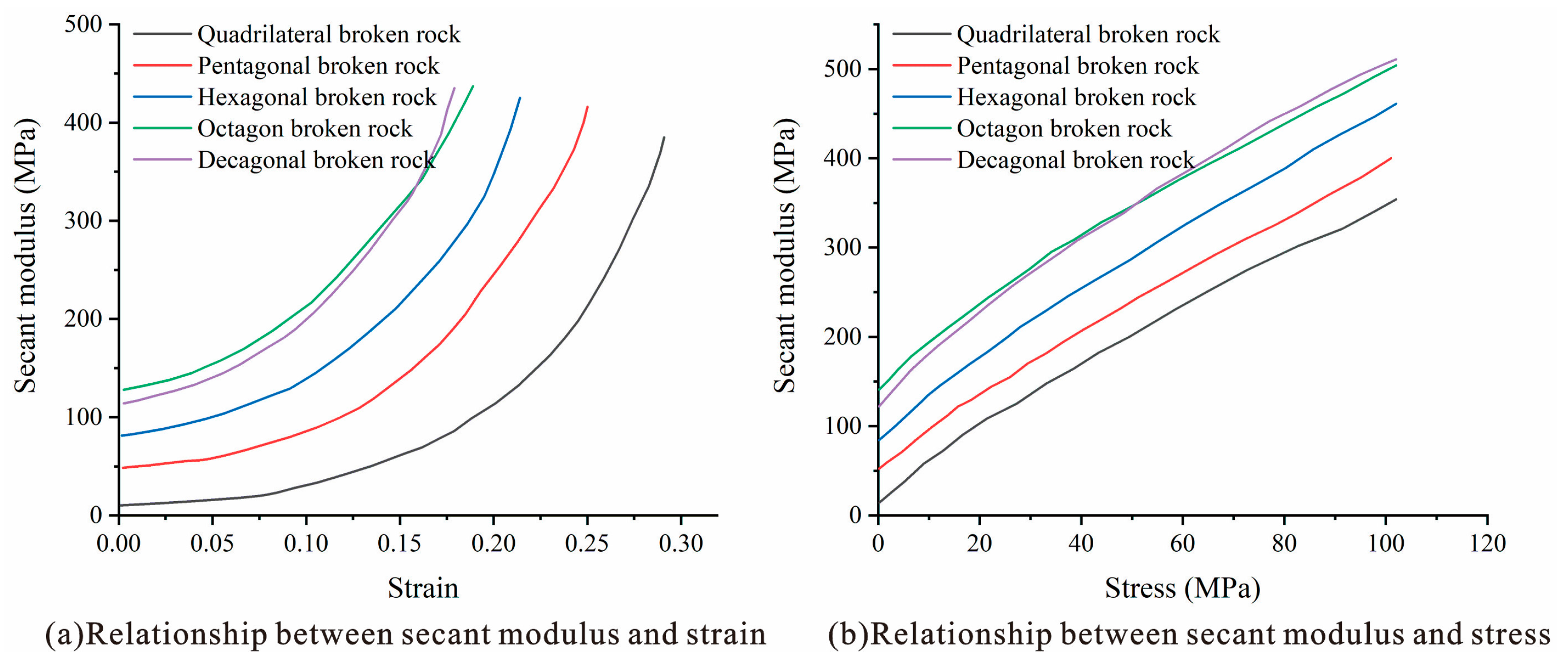
Figure 10 shows the relationship of the secant modulus of the caving rock masses with the stress–strain curve. The sectional modulus of rock masses of different shapes is exponentially related to strain [
18]. At the beginning of strain, the difference in the sectional modulus of the rock masses of different shapes was obvious, and the initial sectional modulus of rock masses with few edges was small. With a continuous increase in strain, the more edges the caving rock masses had, the earlier their secant modulus entered the acceleration stage. The secant modulus of rock masses with different shapes is linearly related to the stress, and the growth rate of the secant modulus is similar to that of the stress. Under the same stress conditions, the higher the number of edges, the larger the sectional modulus of the caving rock masses. With an increase in the number of edges, the trend gradually weakens.
3.3. Influence of Different Caving Rock Mass Shapes on the Porosity and the Coefficient of Fragmentation
- (1)
Fragmentation expansion coefficient
The fragmentation of the caving rock masses refers to the increase in the volume of the whole rock after it has been broken, which is usually expressed by the coefficient of fragmentation,
i0 [
5].
where
v1 is the volume after the collapse of the caving rock masses and
v0 is the original volume [
5].
where
m refers to the quality of the caving rock masses and
ρ is the density of the caving rock masses.
- (2)
Porosity
The caving zone of a goaf can be regarded as a porous medium composed of broken rock masses. The continuous subsidence of overlying strata compacting a goaf caving zone results in the change in porosity of the caving zone itself. The change in porosity directly affects the physical and mechanical properties and pore seepage characteristics of the caving zone. Therefore, the characteristics of porosity variation in the compaction process of broken rock masses in the caving zone of a goaf can be accurately identified. It is of great significance to study the movement of overlying strata and the mechanism of surface subsidence.
The porosity of the caving rock masses is the ratio of the pore volume to the total volume (including the pore volume), as shown in Formula (7) [
4]:
where
v1 is the volume after the collapse of the caving rock masses and
v0 is the original volume.
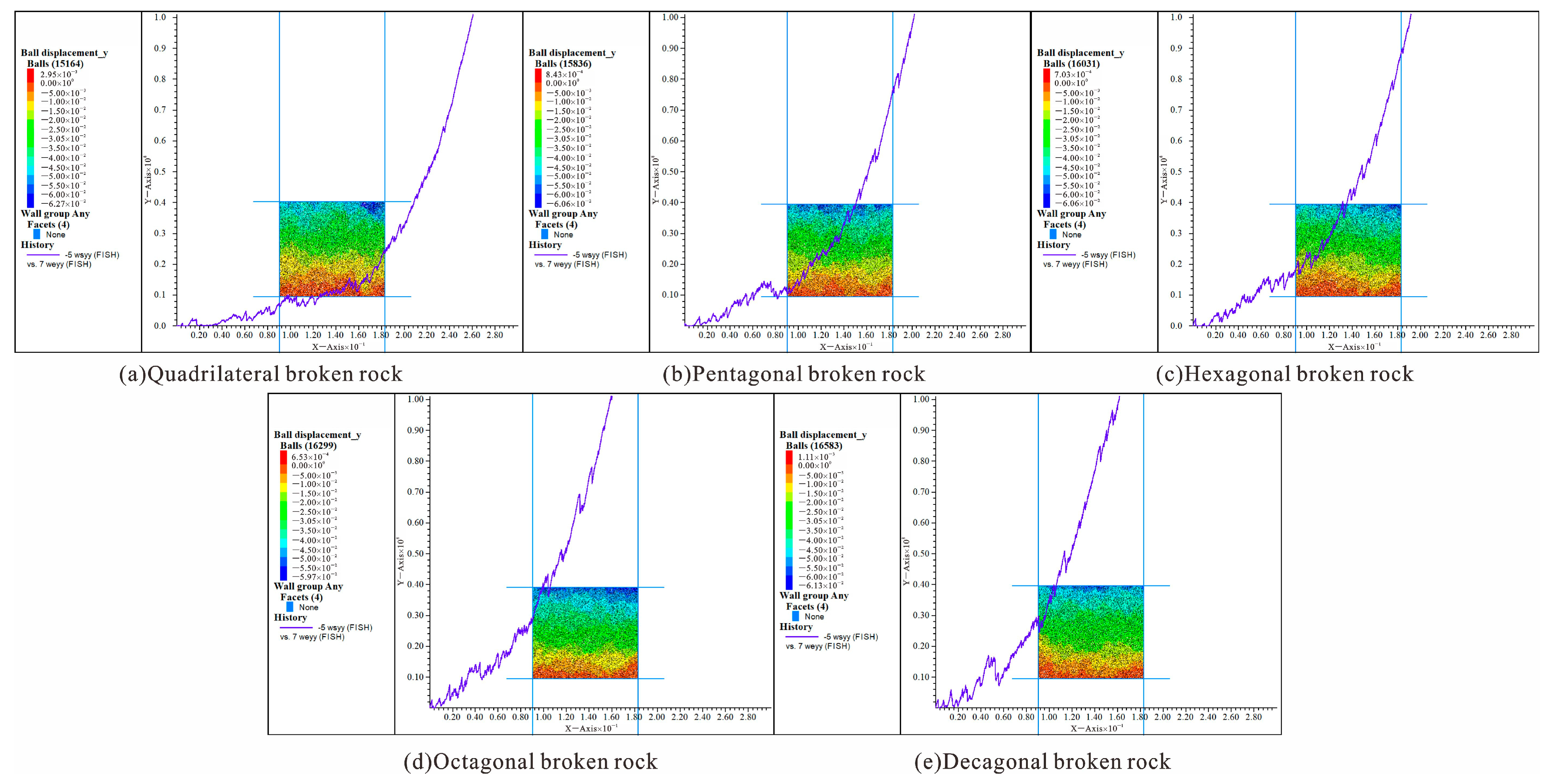
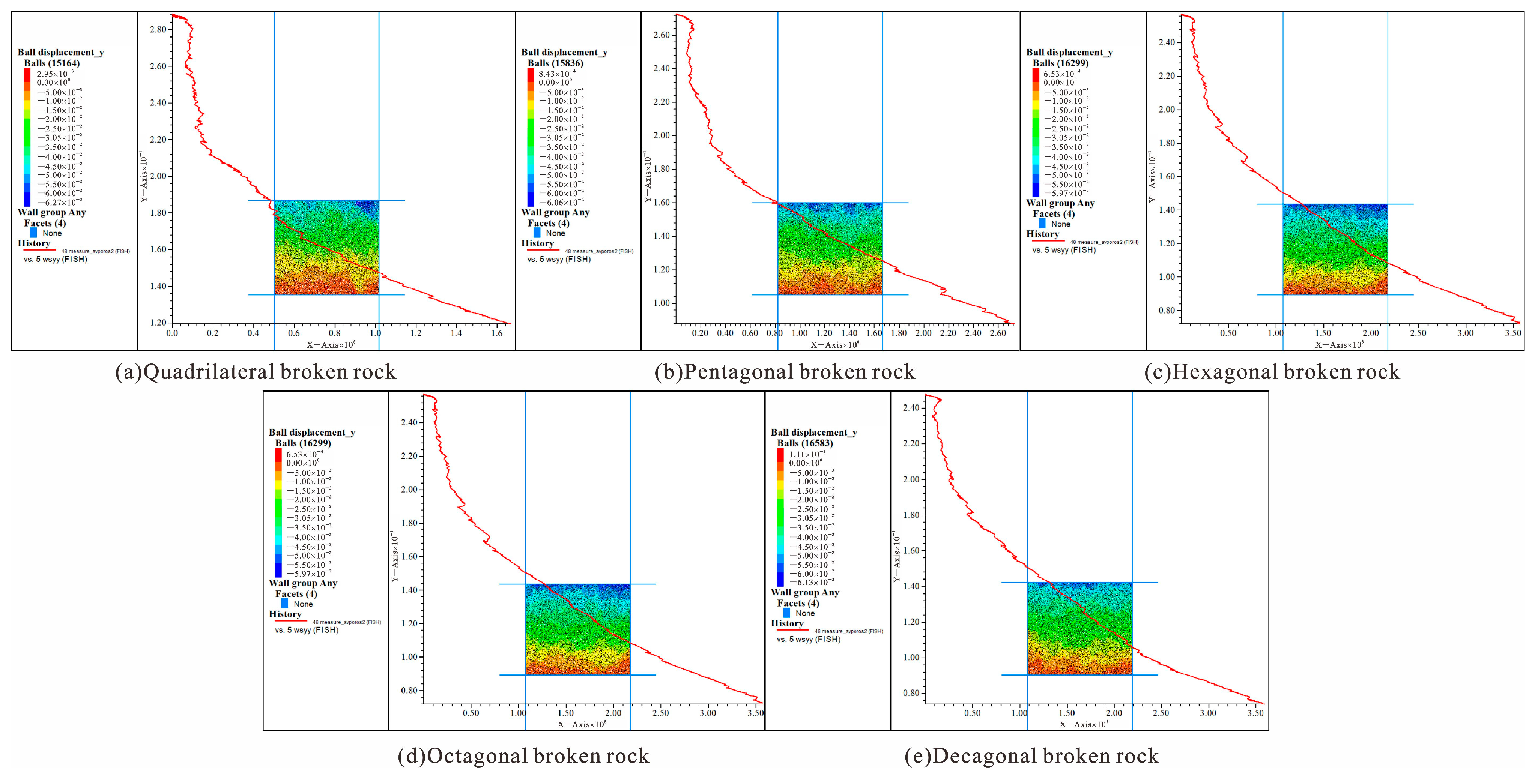
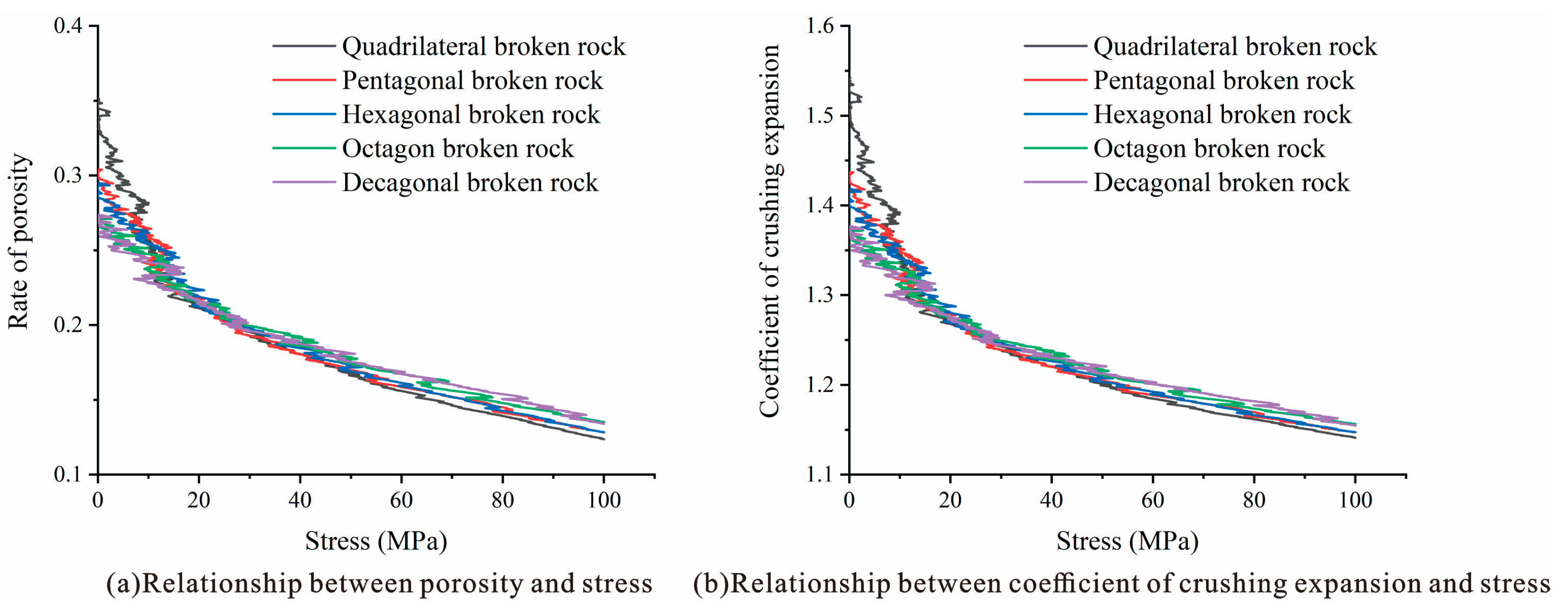
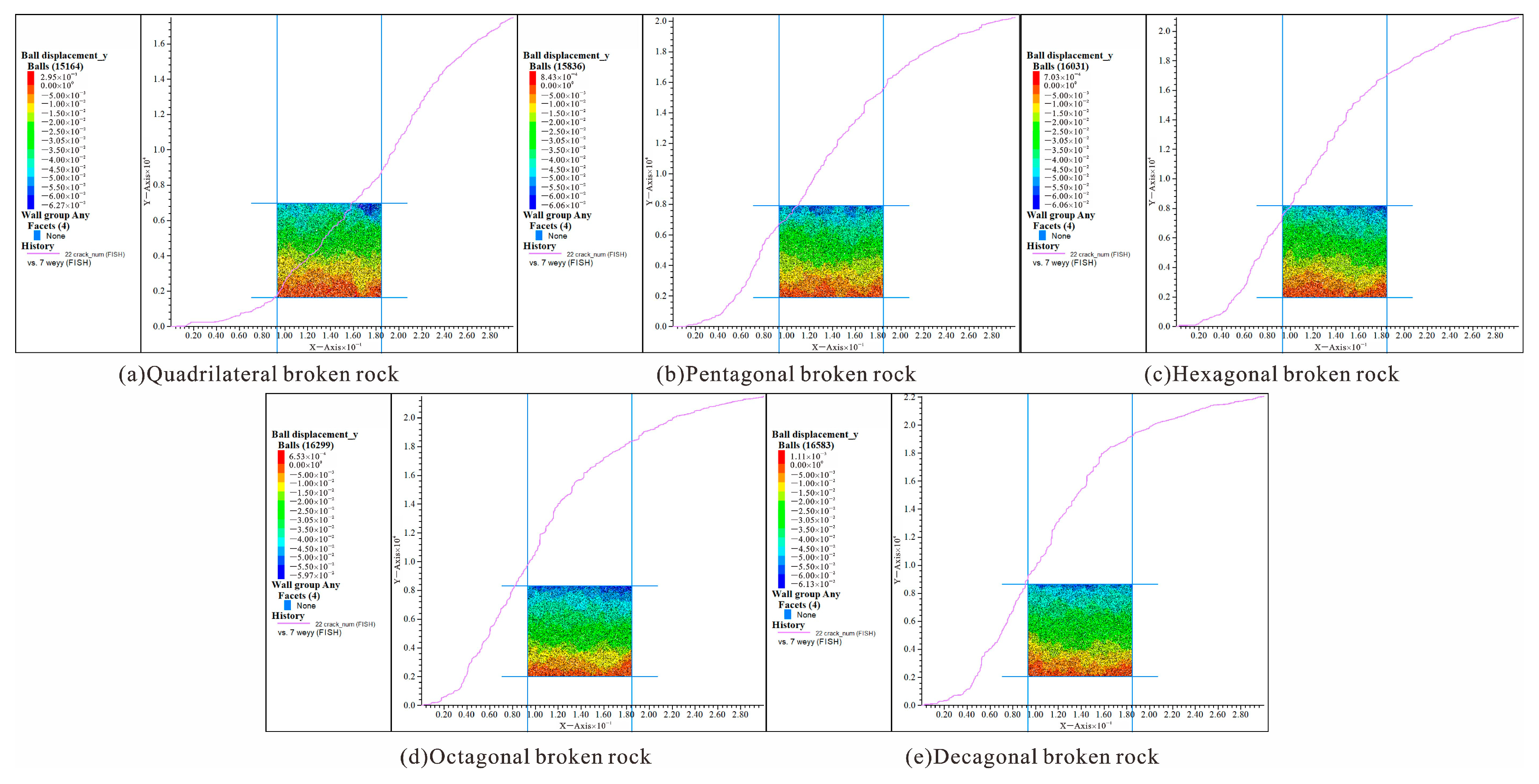
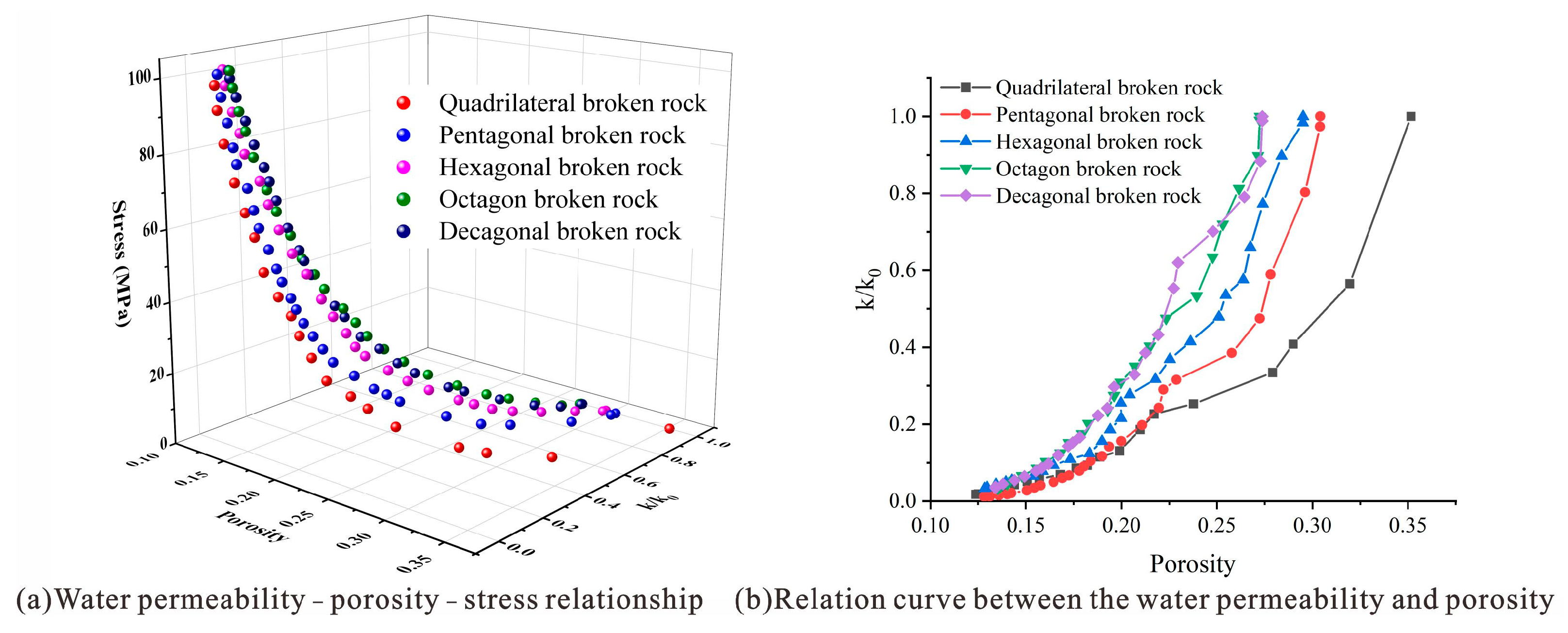
Figure 11 shows the change curve of porosity with stress and the displacement nephogram of different forms of caving broken rock masses during compaction.
Figure 12 shows the variation curves of the porosity and coefficient of the fracturing expansion of the caving rock masses with stress during compaction. By monitoring the actual volume of the caving rock masses and the dynamic volume change of the test steel, the corresponding porosity curves are obtained. The porosity of caving rock masses of different shapes decreases with increasing stress, and the decreasing trend gradually decreases [
26]. When the stress level is approximately 0–20 MPa, the porosity of the quadrangular caving rock masses most obviously decreases, which indicates that the less prismatic the caving rock masses appear, the more obvious is the whole compaction and translation process, and the more obvious is the fracturing phenomenon in the whole process. With a decrease in the gaps in the caving rock masses, the compactness increases, and the decreasing tendency of porosity gradually decreases. The porosity of caving rock masses of different shapes is not significantly different. The porosity curves fluctuate during the process of variation due to the rebreaking of the caving rock masses, which continuously occurs during compaction and recurs until a stable compacted entity is formed.
Figure 12b shows that the coefficient of the collapse and expansion of the caving rock masses of different shapes varies in the range of 1.15–1.55 as a whole with increasing stress and continuously decreases with increasing stress. The trend of overall change is the same as that of porosity. The coefficient of the initial collapse and expansion of the caving rock masses with few edges is higher than that of rock masses with many edges, but the coefficient of collapse and expansion of those is smaller at the later stage of compaction.
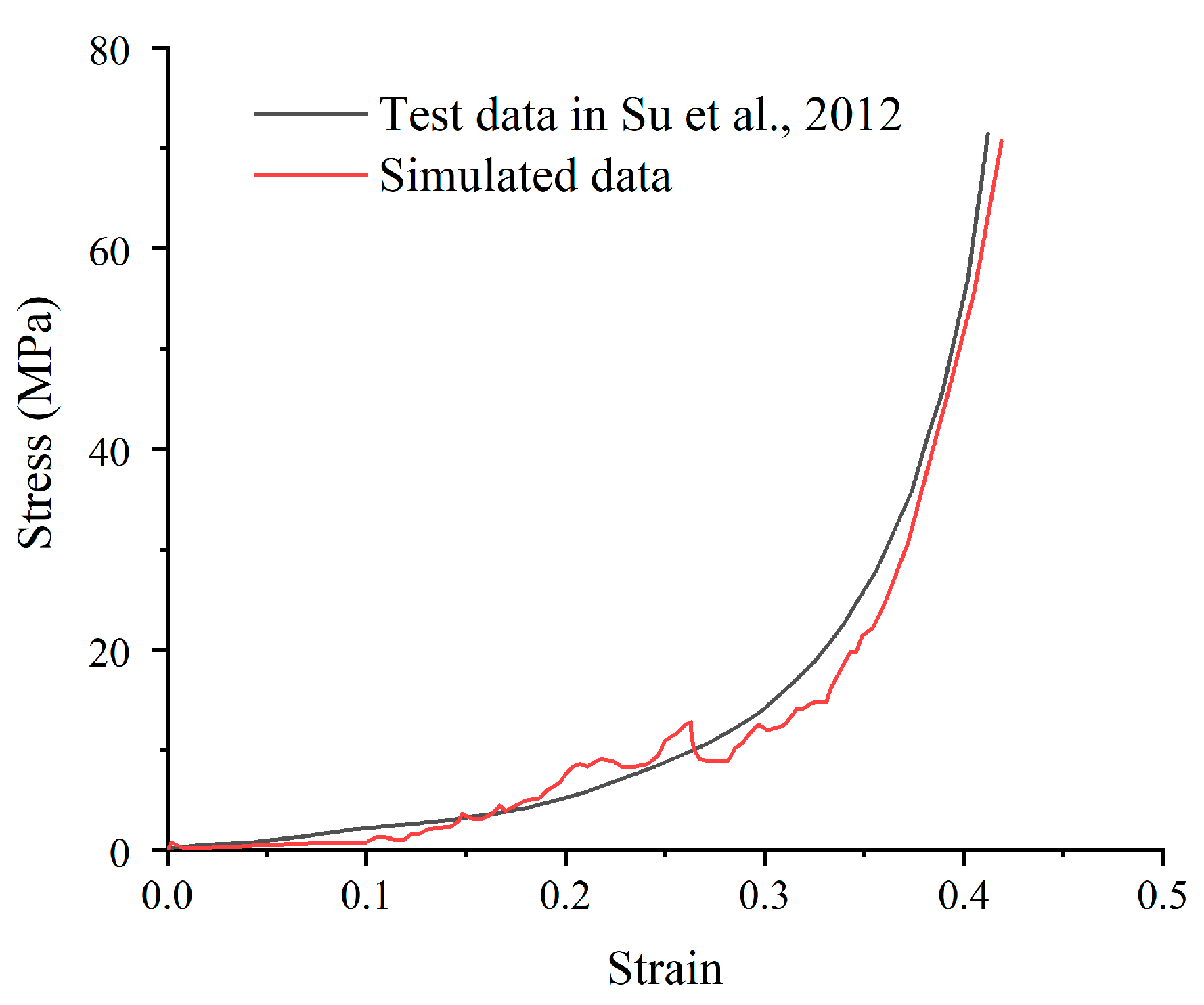
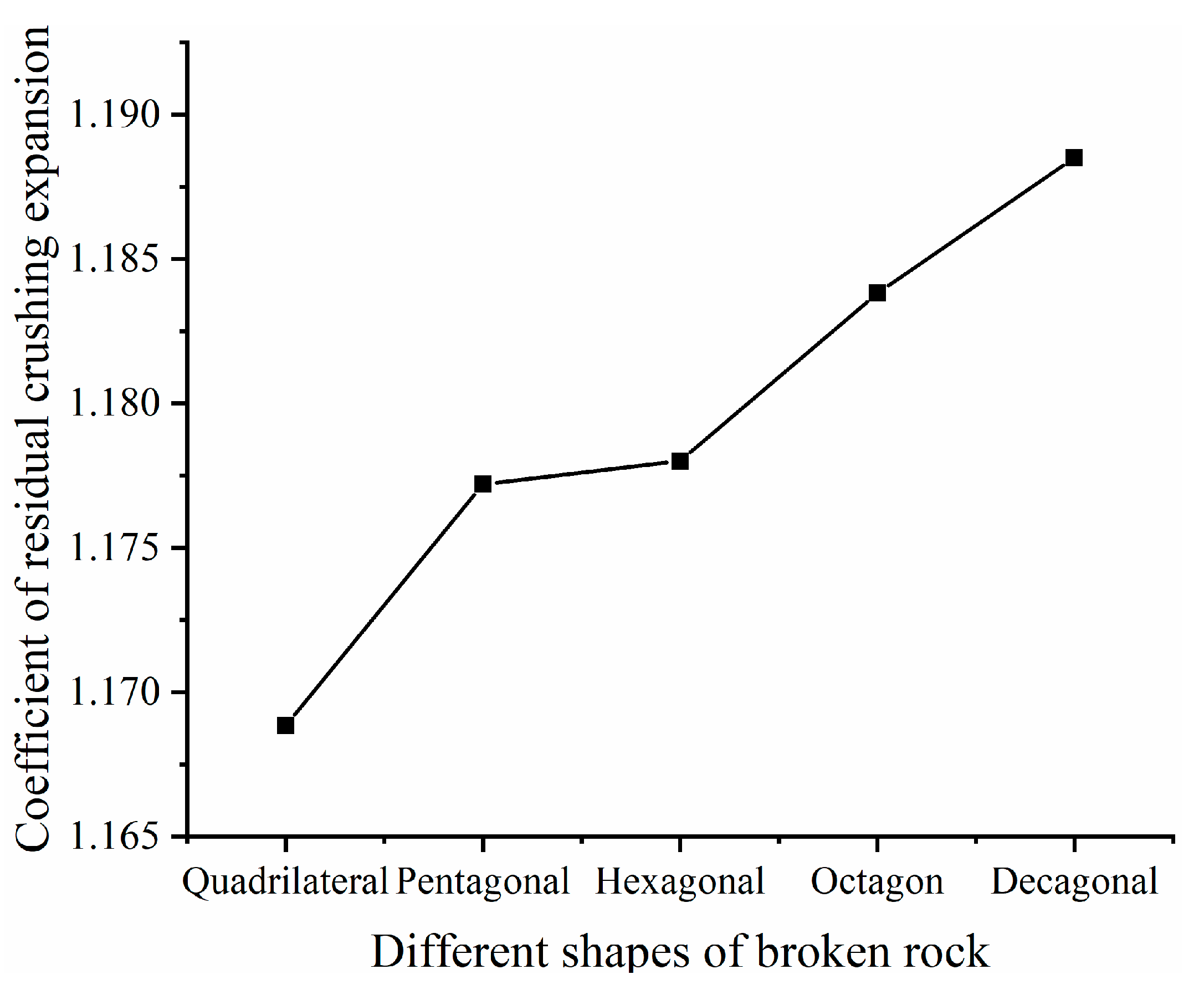
Based on the laboratory test data, the compressive strength of the sandy mudstone was selected as 71.8 MPa [
10], and the relationship between the residual fracturing expansion coefficient and the morphology of different caving rock masses was obtained, as shown in
Figure 13. The residual fracturing expansion coefficient of the caving rock masses basically remained the same, with a difference of 0.02. With an increase in the number of edges, the coefficient of residual dilation slightly increased because the initial bearing capacity of the rock masses with few edges was lower than that of the rock masses with many edges. When the stress reached the compressive strength, the failure of the rock masses was more serious, while the filling phenomenon was more obvious, resulting in a smaller coefficient of final dilation.
3.4. Influence of Different Shapes of Caving Rock Mass on the Water Permeability Characteristics
After coal mining, the broken rock masses in the caving zone of the goaf had the characteristics of irregular size and shape, and sharp edges and corners, and they were easy to break, resulting in differences in the water permeability of different shapes of broken rock masses in the goaf. The difference in the water permeability will affect the seepage of groundwater into the excavation space. On one hand, it easily causes major water inrush and well flooding accidents. On the other hand, it causes the groundwater level of the overlying aquifer to drop, the recharge and the drainage relationship of the groundwater flow system to change, and the ecological environment to be damaged.
The water permeability coefficient can better reflect the hydraulic characteristics and the water permeability of a permeable medium. For porous media, it is generally believed that the water permeability and the porosity evolution can be linked by a cubic mechanism. Therefore, the water permeability can be determined as follows [
24]:
where
is the water permeability coefficient,
is the initial water permeability coefficient,
is the porosity and
is the initial porosity.
According to the literature, the water permeability ratio is combined with the compaction constitutive mechanism of broken rock mass, and the calculation formula for the water permeability ratio is as follows [
24]:
where
is the initial volume of broken rock masses,
is the solid volume,
and
are the fitting parameters and
is the overlying load.
It can be seen from Formula (9) that the size and size distribution of broken rock particles are not directly involved in calculating the water permeability of a goaf, which makes it convenient for us to study the influence of the shape characteristics of broken rock masses on their water permeability. Therefore, the water permeability ratio equation can be used to predict the water permeability of different fractured rock masses.
Figure 14 and
Figure 15 shows the relationship curve of porosity with displacement under 10% and 25% strain, respectively. It can be seen from the figure that the porosity of caving rock masses of different shapes decreases slowly when the strain is small. When the strain is large, the decreasing trend of the porosity of caving rock masses of different shapes is approximately linear. Porosity has obvious stage characteristics in different compaction periods. According to the above-described theoretical relationship between porosity and water permeability, it can be seen that the water permeability of broken rock masses of different shapes also has obvious stage characteristics in different compaction periods.
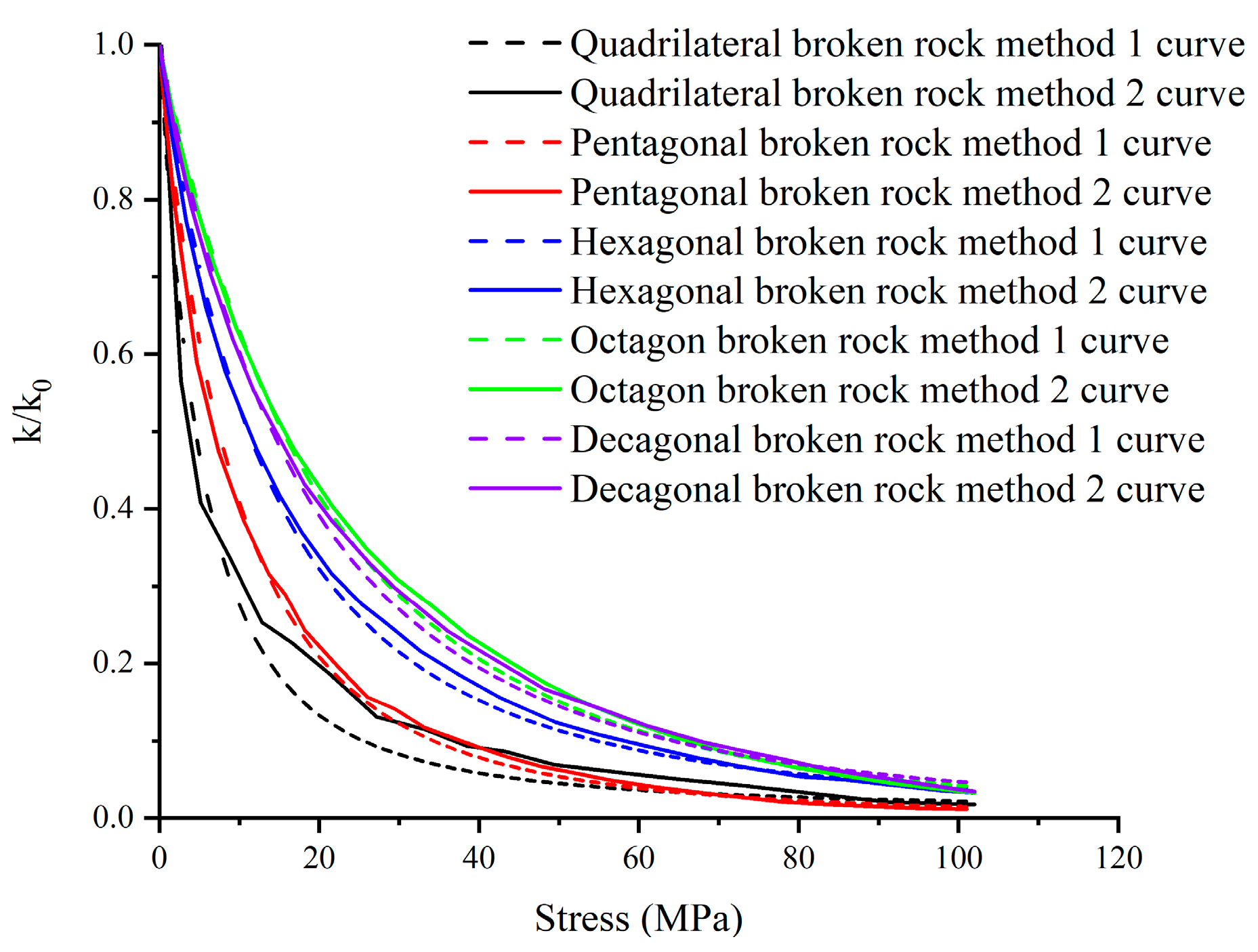
As shown in
Figure 16, the relationship curve between the water permeability coefficient ratio and the overlying load is shown. The dotted line in the figure shows the evolution trend of the water permeability coefficient ratio of broken rock masses of different shapes obtained through an empirical formula. The solid line in the figure is the change relationship between the modulus and the pressure brought into numerical simulation, and the evolution trend of the water permeability coefficient ratio of broken rock masses of different shapes is obtained. It can be seen from the figure that the evolution curve of the permeability coefficient ratio obtained by the two methods has good correspondence. The evolution trend of the water permeability coefficient ratio of the fractured rock masses of different shapes is similar, showing a logarithmic relationship. With the increase in stress, the water permeability coefficient decreases gradually. When the stress reaches 80 MPa, the water permeability coefficient ratio changes, becoming stable. The smaller the number of broken rock edges, the faster the ratio of the breaking water permeability coefficient decreases in the initial compaction stage, and the smaller the ratio of the final water permeability coefficient. This is due to the smaller sphericity and irregular shape of the broken rock masses with fewer edges, resulting in less contact points around it and poor strength. When the same normal stress is given to the broken rock masses, stress concentration easily occurs, the broken rock masses are more damaged, and the water permeability coefficient decreases faster. To sum up, the larger the number of edges on broken rock masses, the smaller the loss of the water permeability coefficient under the same compaction state.
3.5. Differential Degree of Compacted and Fractured Rocks with Different Shapes
The fracture of the caving rock masses depends on the bond strength and contact strength of the particles. When the stress reaches the critical value, tension or shear failure occurs in the caving rock masses. The maximum tensile stress and shear stress are expressed as:
where
is the normal stress,
is the tangential stress,
is the bending moment,
is the torque,
A is the cross-section area,
L and
J are the moment of inertia and extreme moment of inertia, respectively, and
R is the particle radius between contacts.
As shown in
Figure 17, the numerical simulation results of the crushing rate of caving rock masses with different shapes are shown.
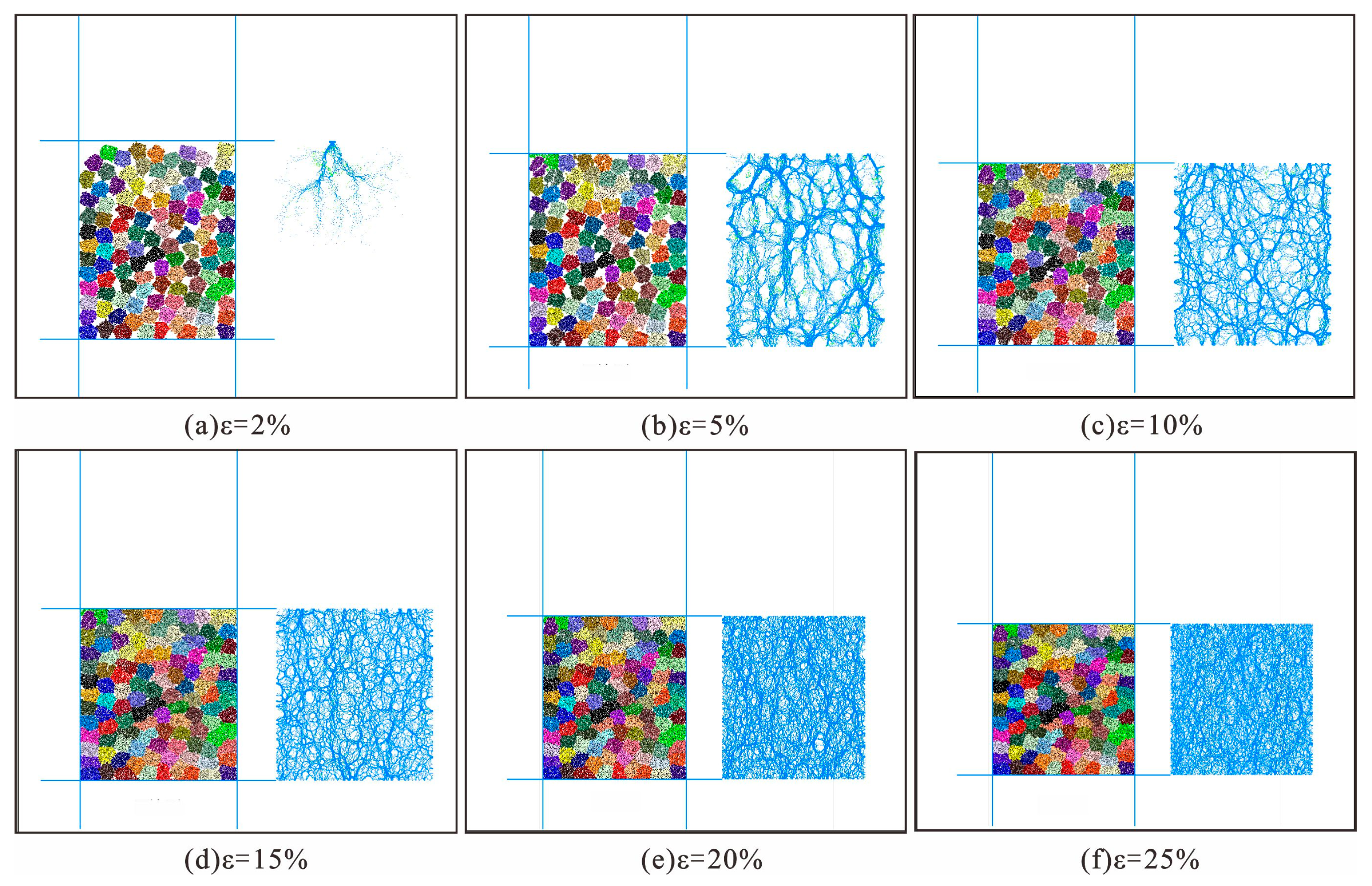
Figure 18a shows the relationship between the number of cracks and the strain in different shapes of caving rock masses. The contact between the particles in the caving rock masses is realized by parallel bonding and linear contact. Particle breakage will degrade the parallelly bonded fracture into linear contact. Therefore, the degree of fracture for the caving rock masses is indicated by monitoring the number of parallel bonded fractures. The growth of cracks in different shapes of caving rock masses presents three stages: slow-fast-slow. The more edges there are in the caving rock masses, the earlier the crack number enters the rapid growth stage and the faster the growth rate. When the rock masses are compacted to 80% of their ultimate strain, the growth in the crack number begins to slow again.
Under the same strain condition, the number of cracks in rock masses with few edges is small, but this does not mean that the breakage rate is low. The total contact number of different rock masses with few edges is inconsistent, and the number of particle clusters in rock masses with few edges is small, which results in the least contact of a single rock mass. Therefore, the concept of the breakage rate is introduced, which is expressed as the ratio of the current reduction of the number of parallel bond contacts to the initial parallel bond contact [
11]:
where
m is the number of parallel bonds and ∆
m is the reduction of parallel bonds, which can be used to visually characterize the degree of fracture of caving rock masses.
The relationship between the fracture rate and fracture strain is shown in
Figure 18b. The fracturing rate of rock masses with different shapes changes slowly rapidly slowly with strain [
25], and the final failure rate of the rock masses is in the range of 25–30%.
Figure 18 shows two inflection points on the curve. The first inflection point is mainly due to the large gap between the broken rock masses at the initial stage of compaction, and the broken rock mainly rotates and moves; at this time, the increase in the breaking rate is small. With increasing stress, broken rock masses are broken and destroyed, leading to a sharp rise in the breaking rate, and the first inflection point of the breaking rate change curve. When it comes to the late stage of compaction, the structural pores of broken rock masses are filled, it is difficult to for new displacement and filling to occur, and integrity is enhanced. Therefore, the growth trend of the breakage rate tends to be flat, and the curve of the breakage rate changes at the second inflection point. With an increase in the number of edges on caving rock masses, the fracturing rate of the caving rock masses decreases. The final fracturing rate of tetragonal rock masses reaches 30%, while the final fracturing rate of decagonal rock masses reaches 26%. The main reason is that with an increase in the number of edges on caving rock masses, the roundness continuously increases. The more contact there is between caving rock masses, the less stress concentration occurs, and the lower is the fracturing rate of the caving rock masses. The ultimate failure rate of rock masses with different shapes does not exceed 30% because the porosity of the rock mass structure is small at this time, it is difficult to displace and fill, and the integrity is enhanced. Thus, the growth trend of the failure rate tends to be flat.
Combining the change trend of porosity and fracturing rate, it can be concluded by analysis that broken rock masses with fewer edges have irregular shapes, smaller sphericity and sharper edges. When broken rocks sustain each other, large pores are formed, resulting in less contact points around them, and in their own strength being poor. When the same normal stress was applied to the rock masses, stress concentration easily occurred, and the stress spread by the single-point contact was greater. Thus, the stress at this point was more easily damaged than its own strength. Therefore, the rock masses with few edges had a higher fracturing rate than those with many edges.
3.6. Characteristics of Energy Evolution during Compaction and Fracture of Caving Rock Masses with Different Shapes
Influenced by the overlying load, many defects, such as cracks, often occur in the compaction process of caved and crushed rock masses. The existence of defects weakens the physical and mechanical properties of the caved rock masses, and the stress concentration on the tip of defects is very likely to cause the overall failure of the caved rock masses. The failure of a caving rock mass is a state destabilization phenomenon under the action of energy conversion, which is essentially an irreversible thermodynamic process in which energy dissipation and release are very important. Therefore, it is necessary to analyze the compaction and fracture mechanism of rock masses with different shapes from the angle of energy conversion.
Assuming that there is no heat exchange effect between the test environment and the outside and disregarding the kinetic energy transformed by the ejection of the caving rock masses, the total input energy
of the work performed by the external force is the total strain energy. According to the first mechanism of thermodynamics, the calculation formula of the strain energy in the process of lateral compression of the caving rock masses is obtained as follows [
8]:
where
is the elastic strain energy and
is the dissipated strain energy. The total strain energy,
, absorbed by the caving rock masses is converted to releasable elastic strain energy,
, stored in the specimen and dissipated strain energy,
, utilized for damage propagation.
Since only axial stresses work on the specimens during the whole test process, according to thermodynamic theory,
,
and
are obtained by the following formula [
8]:
where
is the axial stress,
is strain, and
is the modulus of elasticity.
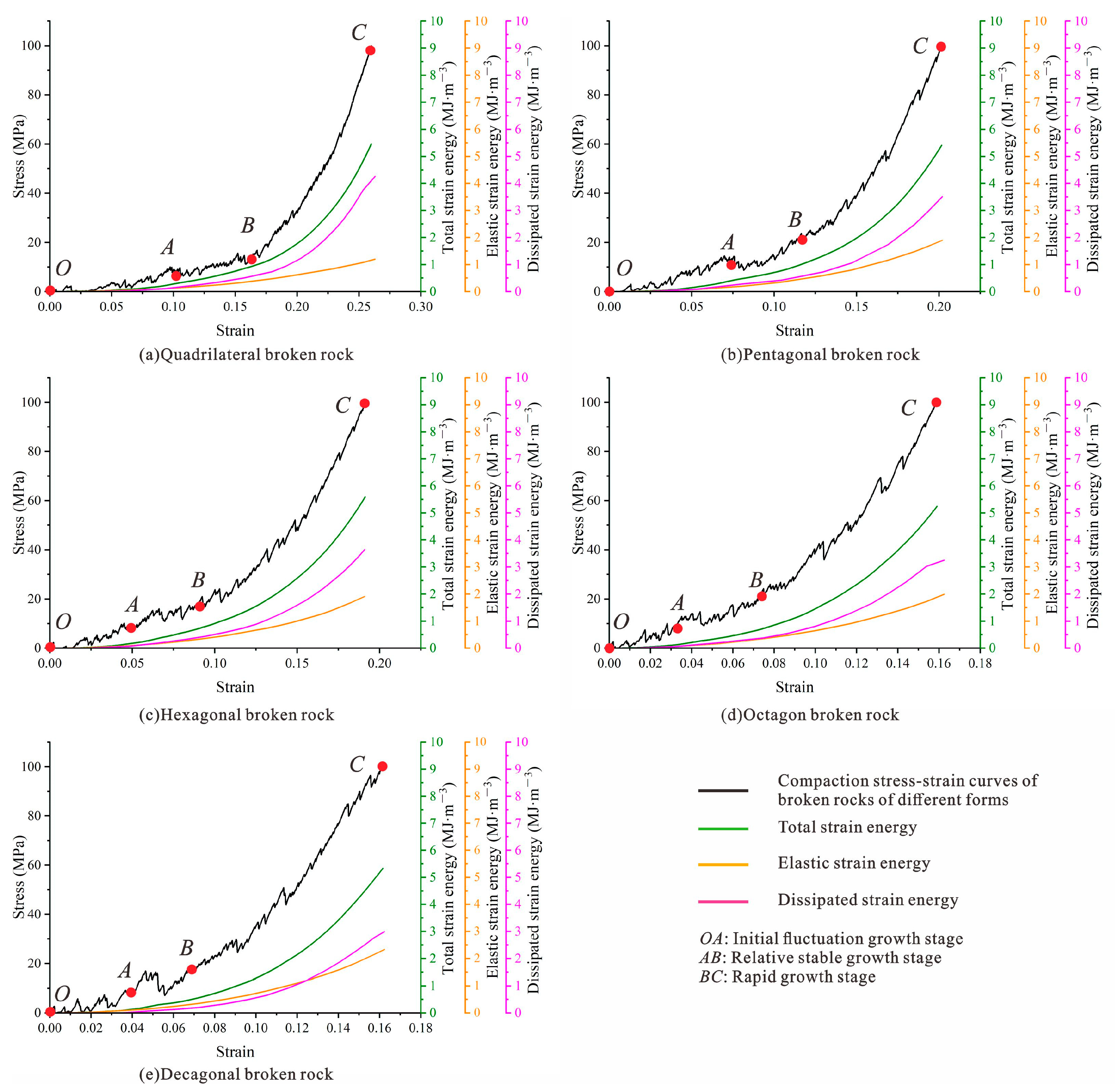
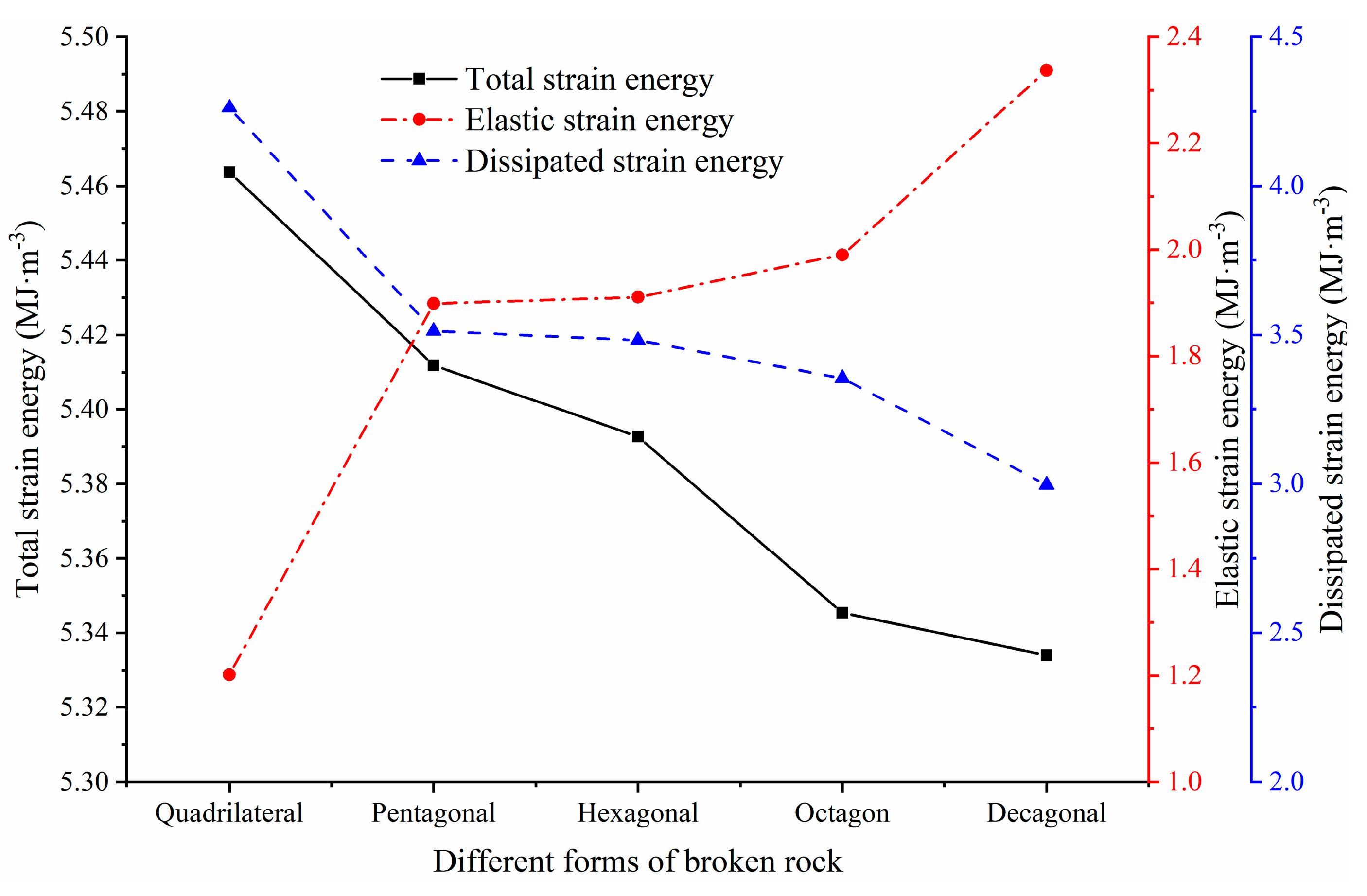
Figure 19 shows the evolution curves of the stress–strain curve, total strain energy (
), elastic strain energy (
) and dissipated strain energy (
) during the confined compression compaction of broken rocks of different shapes. According to the characteristics of stress–strain curves and crack growth rules, the energy evolution characteristics during the failure process of rock with different shapes are divided into three stages [
8]: initial fluctuation growth stage (stage I), relative stable growth stage (stage II) and rapid growth stage (stage III). In
Figure 19, three stages of compaction of broken rocks of different shapes are marked on the stress–strain curves with red dots and identified with capital letters
O~
C. Although the stresses and stored energy in different stages of compaction and failure process of broken rocks with different shapes are different, the energy variation mechanisms of the caving rocks are similar and have undergone the above three stages.
For the initial wave growth stage (OA segment), the broken rock is translated and rotated, the gap between blocks is significantly reduced, and the stress strain curve’s OA segment is concave. The external force performs work on the broken rock, and the caving rock masses gradually accumulate energy. Due to the small stress, the increase rate of total strain energy, elastic strain energy and dissipative strain energy is small, showing a nonlinear upward trend. At this stage, the strain energy of the caving rock masses is mainly stored in the form of elastic strain energy, and a small part of it is converted to dissipative strain energy, which indicates that, in the initial wave growth stage, the broken rock mainly consumes a part of its capacity by block translation, rotation and other behaviors. However, there are few broken phenomena.
For the relatively stable growth stage (AB segment), the AB segment of the stress–strain curve changes approximately linearly. With increasing axial stress, the energy stored in the broken rock continuously increases, and its growth rate is greater than that of stage I. Because the collapsed rock masses are mainly broken at this stage, the overall change in the collapsed rock masses is small, and some edges and corners are broken. The caving rock masses continuously undergoes plastic deformation at this stage, so the strain absorbed by the caving rock masses begins to change from elastic strain energy to dissipative strain energy, and the proportion of dissipative strain energy is gradually higher than that of elastic strain energy.
For the rapid growth stage (BC section), the stress strain curve of section BC shows a nonlinear change. Under the action of higher stress, the specimen still absorbs energy, the total energy curve still shows an upward trend, and its growth rate is far greater than that of stage II. As the caving rock masses mainly break and grind at this stage, the work performed by the external force is mainly consumed in the process of particle rubbing, which is manifested by the continuous expansion and connection of the internal cracks of the caving rock masses, breaking into several small particles or even powders, and an increasing amount of damage, leading to the accelerated growth trend of the dissipated strain energy and of the proportion of the dissipated strain energy.