1. Introduction
Buried pipeline networks, such as in-service waterworks pipelines, are crucial components of modern cities that support industrial and residential activities by transmitting essential resources and energy. Moreover, buried pipeline networks have become increasingly complex as cities continue to develop and the demand for resources and energy increases. Therefore, the issue of pipeline failure becomes a critical problem that must be addressed in order to maintain the functionality of cities, and it is increasingly being prioritized. As a result, the risk of pipeline failure has become a major concern for cities and is receiving increased attention from the management agencies responsible for the pipeline networks, such as water, gas, and oil companies. It has been found that corrosion, material defects, third-party interference (TPI), and ground loads were the primary causes of buried pipeline failures [
1,
2,
3]. Most problems can be prevented through proper maintenance and continuous management, but instances of TPI are not only unpreventable but also cause unexpected large-scale accidents [
4,
5]. Therefore, technology such as structural health monitoring is becoming increasingly important to ensure the reliability and integrity of buried pipeline networks, especially to prevent unexpected accidents caused by TPI.
The research on pipeline integrity was initiated with an emphasis on detecting leaks. Early-stage leak-detection methods relied on acoustical analyses by skilled experts utilizing listening rods, frequently producing incorrect results [
6]. To overcome these limitations, leak-detection methods based on a correlation analysis were proposed [
7]. As a result, while the detection range was limited to a few meters, leak detection based on a frequency-domain analysis became possible [
8]. As the propagation speed of waves was understood to be a key variable in leak detection, researchers subsequently focused on conducting theoretical-mode analyses of fluid-filled pipelines. Theoretically, it was found that most of the energy in fluid-filled pipelines is transmitted through four waves [
9]. Among them, the quasi-longitudinal wave was confirmed to be the most suitable for leak detection due to its ability to propagate over long distances [
10]. Moreover, the theoretical description of the dependence of the propagation speed of quasi-longitudinal waves on the physical properties and burial environment of pipelines allowed for more accurate estimations of the propagation speed of these waves [
11]. With consideration of the factors mentioned earlier, an algorithm for selecting the optimal frequency band for leak detection was proposed based on an analysis of the power spectral density (PSD) and coherence of the signals as obtained from sensors [
12]. The effectiveness of this algorithm was demonstrated through experiments conducted on actual buried pipelines [
8]. Thus, numerous studies are attempting to devise methods capable of detecting leaks in pipelines, from the development of theoretical models to experimental validation. Based on these research findings, various leakage detection studies have been conducted in different environments, and leakage detection technologies for monitoring the integrity of pipelines under onshore, offshore, subsea, and arctic conditions have been developed and applied [
13]. However, the research on preventing pipeline failures due to impact damage such as TPI is relatively insufficient. In relation to damage caused by TPI, some studies are underway, such as a recent study related to impact-damage detection of pipelines, with an acoustic propagation model suggested for the initial detection of impacts that induce damage in gas pipelines. The feasibility of the algorithm was verified through lab-scale experiments [
14]. In addition, the possibility of high-accuracy source location for damage detection was verified by applying the continuous wavelet transform in an environment with actual noise [
15]. This study highlights the ongoing efforts to detect and prevent impact damage in pipelines. While research in this area is still limited, the proposed acoustic propagation model and the application of the continuous wavelet transform showed promising results in terms of the development of effective impact-damage detection systems. In conclusion, in order to prevent pipeline failures due to impact damage caused, for instance, by TPI, it is necessary to detect the activities that may cause such damage before they affect the pipelines.
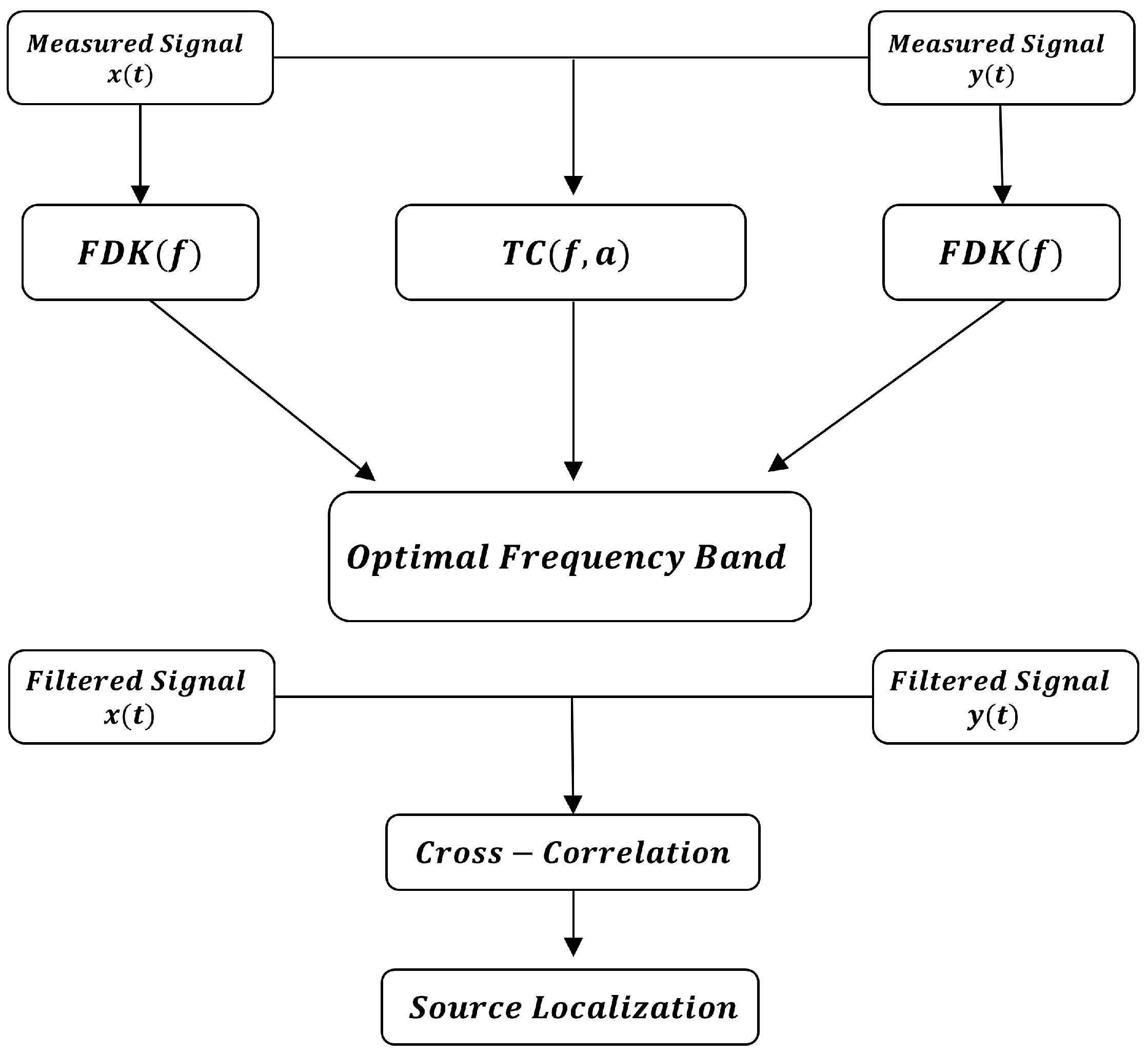
In this study, a novel algorithm is proposed for early detection of pipeline failure by detecting ground excavation activities conducted on the surface above buried pipelines. The algorithm operates by utilizing energy and similarity measurements, similar to the methodology applied in well-developed leak-detection algorithms. The proposed approach identifies suitable factors for impact detection by observing the theoretical differences between leak signals and impact signals. Frequency-domain kurtosis (FDK) is used to determine the frequency band on which the energy of the impact signals is concentrated, and a time-shift coherence function is introduced to overcome the limitation of coherence functions in measuring the similarity of impact signals. With these elements combined, the proposed algorithm aims to ensure the safety and to detect failures of buried pipelines early.
This paper is organized as follows. In
Section 2, a theoretical comparison is made between the proposed method and the conventional leak-detection method. The experimental setup for excavation using a backhoe on a surface where pipelines are buried is introduced in
Section 3. Finally, the performance and verification results of the proposed algorithm are discussed in
Section 4 based on the experimental results.
3. Experiments
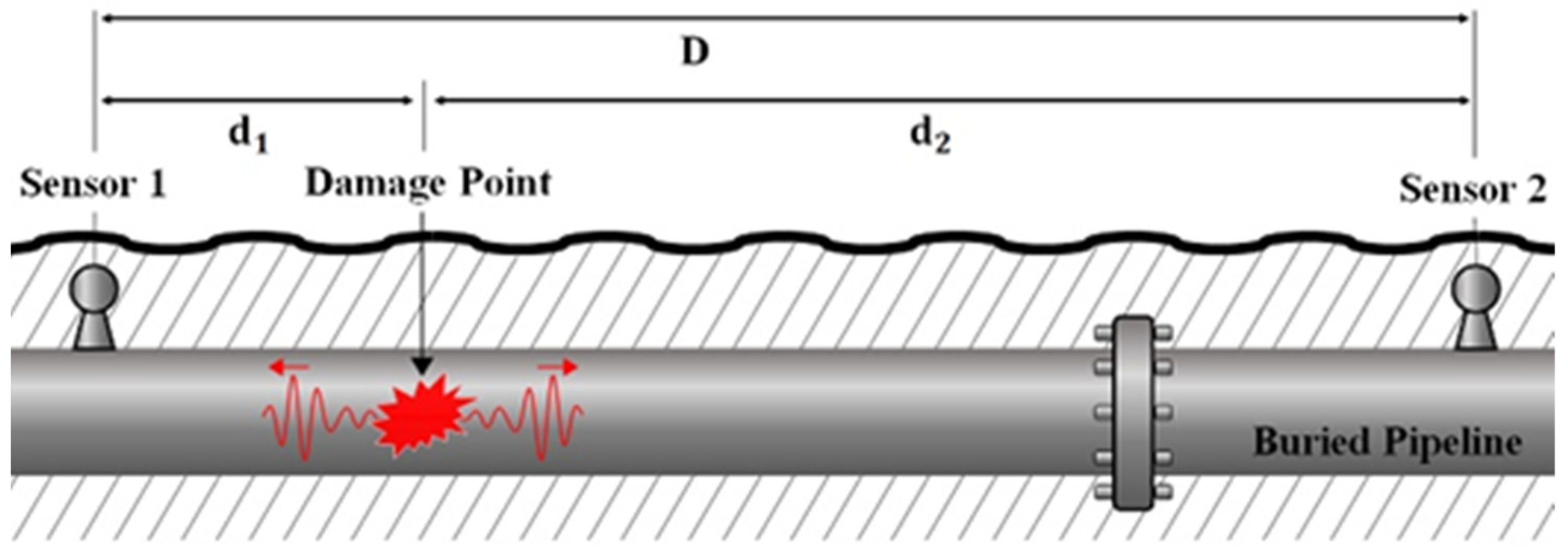
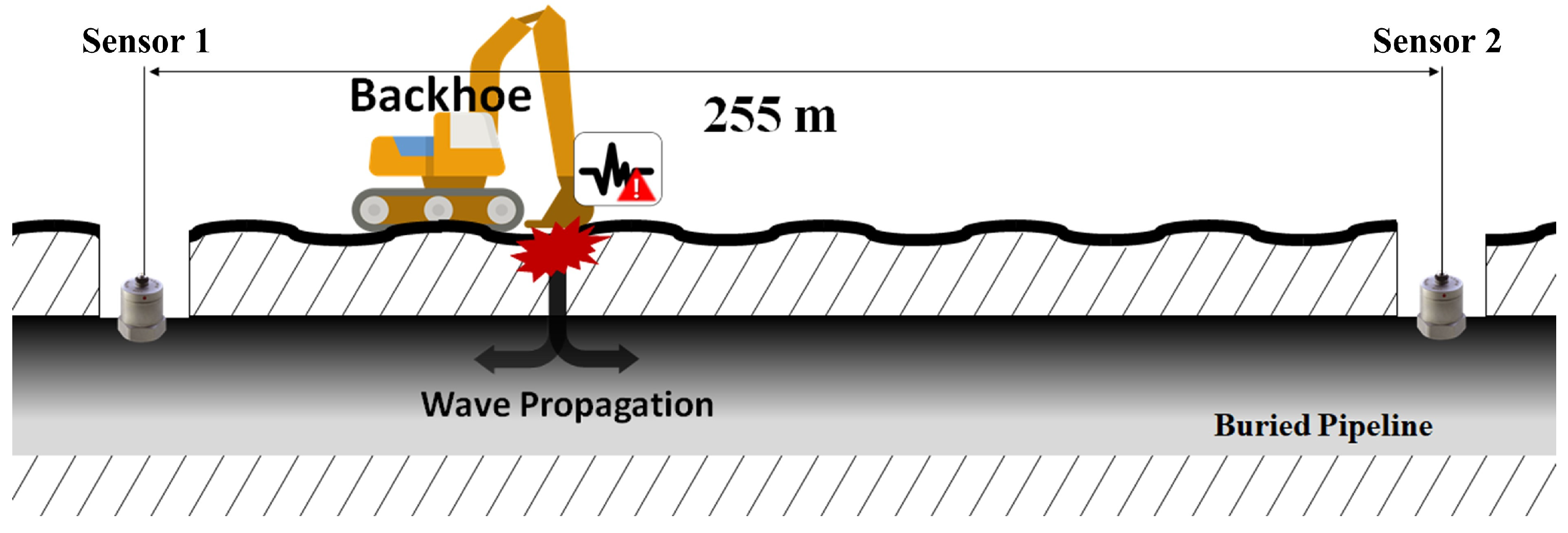
To validate the algorithm proposed for preventing pipeline damage due to TPI, experiments were conducted on in-service buried pipelines in O-Song, a city in Korea. A pipeline with a 2200 mm diameter buried approximately 3 m underground was used, with a 255 m section selected as the testbed, as shown in
Figure 12a. To test the prevention of damage caused by TPI, backhoe excavation was performed on the ground where the pipeline was buried, as shown in
Figure 12b. The impact energy applied to the ground was transmitted through the pipeline, and the aim was to detect this and prevent damage before a failure occurs, as shown in
Figure 13.
Accelerometers with a sensitivity of 10 V/g were attached to both ends of the monitoring area, and for this, the National Instruments NI-9234 model was used. The signals were measured with a sampling frequency of 5.12 kHz in an environment with various types of noise, as the target pipeline was buried under a two-way eight-lane roadway and a parking lot.
Experiments were conducted at different locations, including 60 m, 80 m, 100 m, 125 m, 150 m, and 180 m out of the total 255 m section, as shown in
Figure 12, to validate the proposed approach. The experiments were performed under different ground conditions, and the goal was to detect the actual excavation location by applying the proposed approach to the measured signals.
4. Results and Discussion
As described earlier, the optimal frequency band is selected by observing the FDK and of the measured signals for impact signal detection. Subsequently, the signals are filtered using a bandpass filter designed on the optimal frequency band, and the arrival time difference of the impact signals is estimated by applying these filtered signals to the cross-correlation.
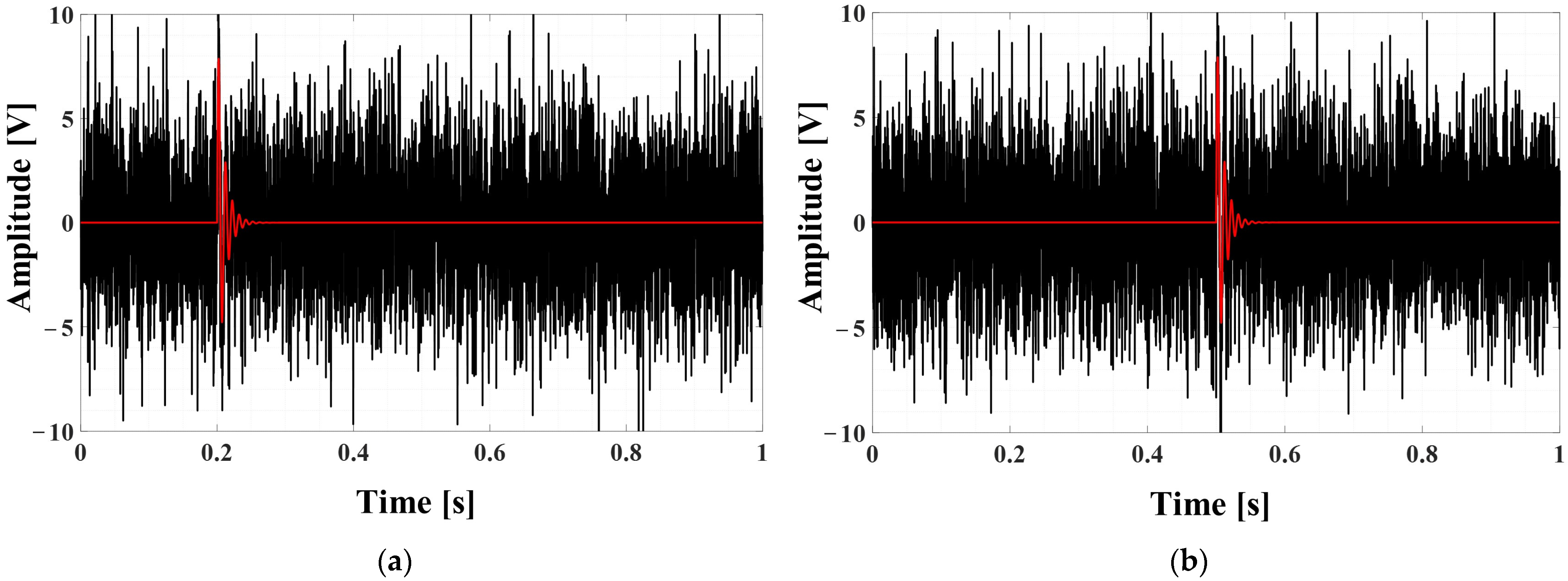
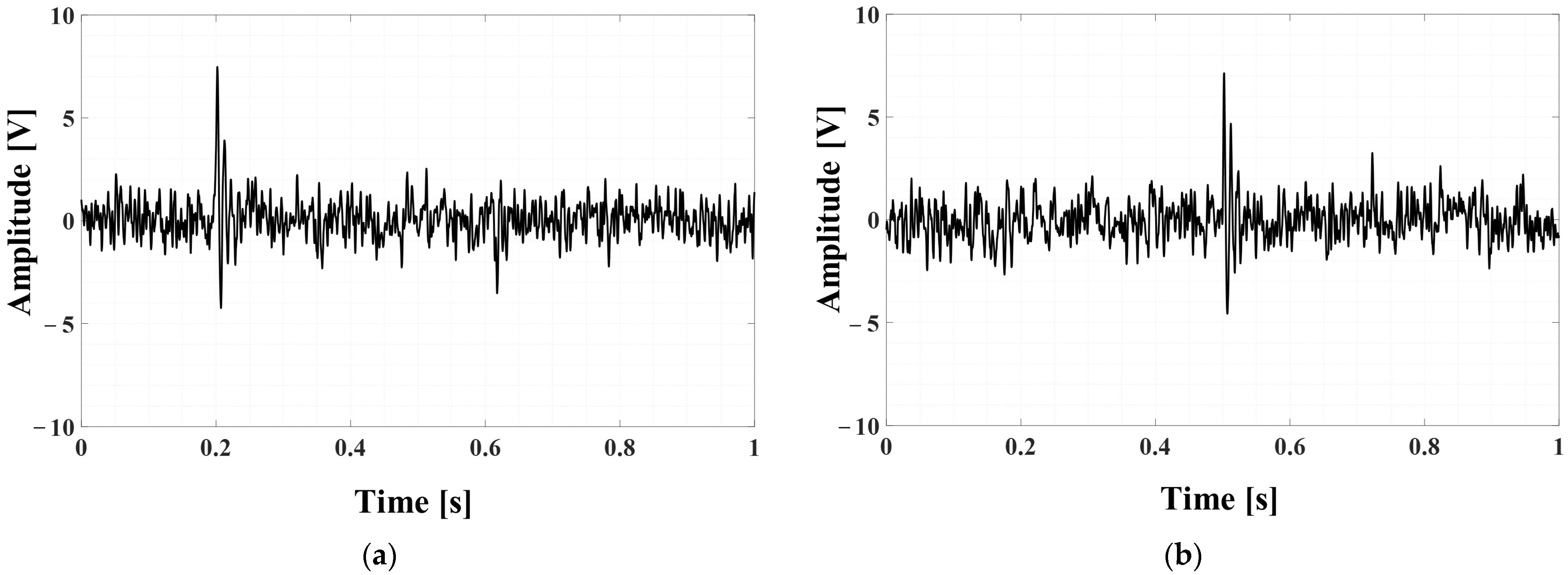
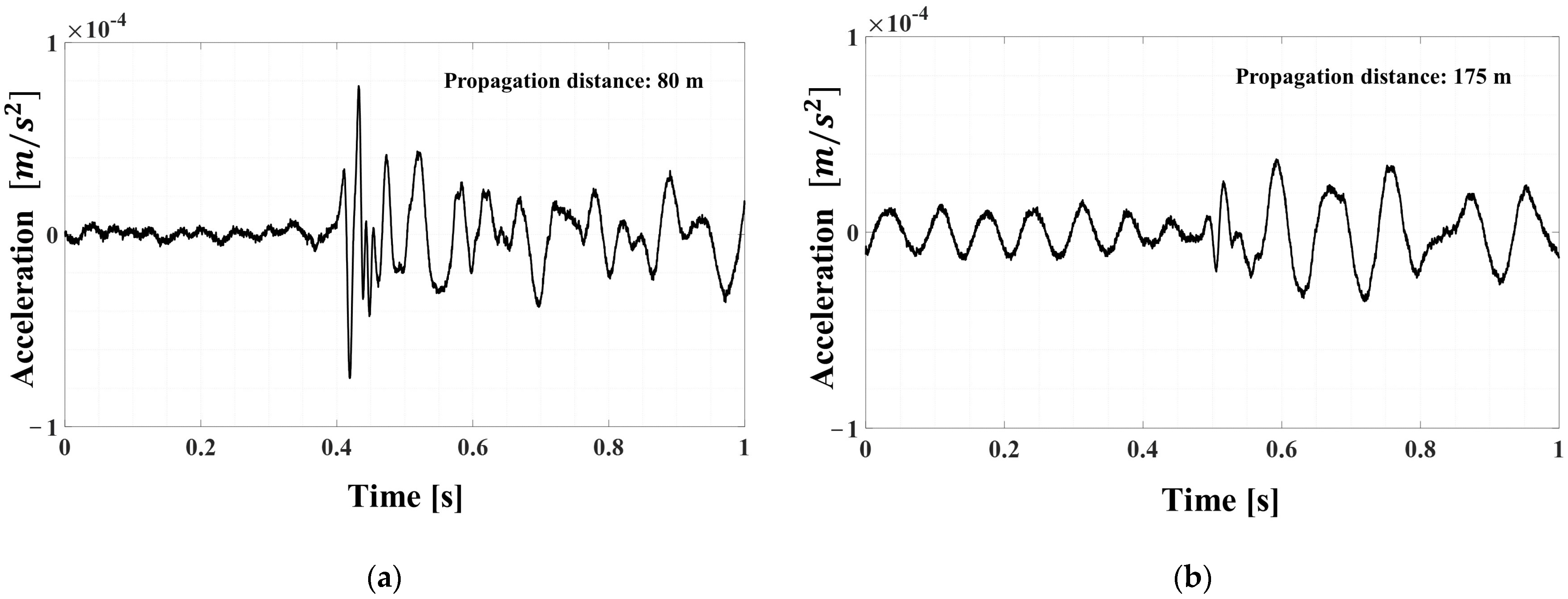
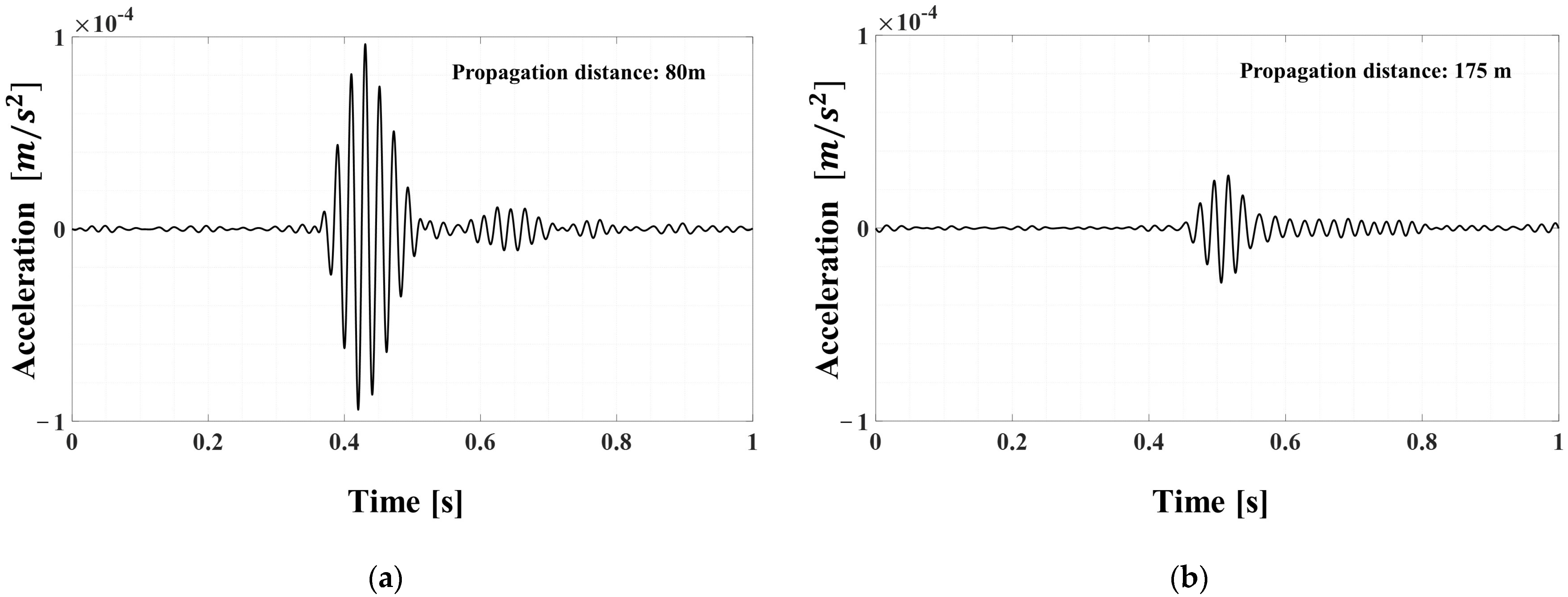
Figure 14a,b show the results of the signals generated during excavation activities at the 80 m position in the 255 m pipeline. Sensor 1 measures the signal that propagated from 80 m, as shown in
Figure 14a, while sensor 2 measures the signal that propagated from 175 m, as shown in
Figure 14b. In particular, the measurement signal of sensor 2 is exposed to various types of noise due to its proximity to the road. Therefore, as shown in
Figure 14b, it can be seen that it is difficult to distinguish the impact signal from the noise due to the low signal-to-noise ratio in the raw signal. On the other hand, the measurement signal of sensor 1 in
Figure 14a has a short propagation distance and is located in a relatively noise-free area, resulting in a high signal-to-noise ratio. This is a characteristic of typical field experiments, indicating that different conditions exist at each position, even in the same testbed.
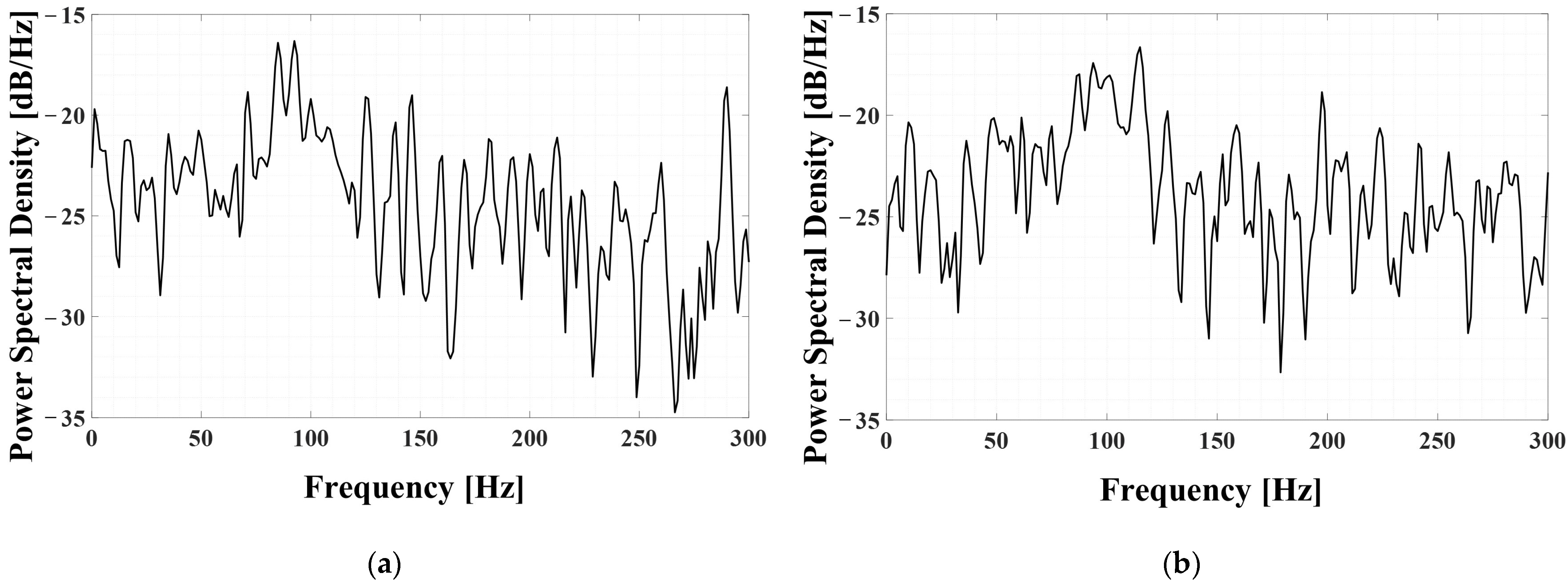
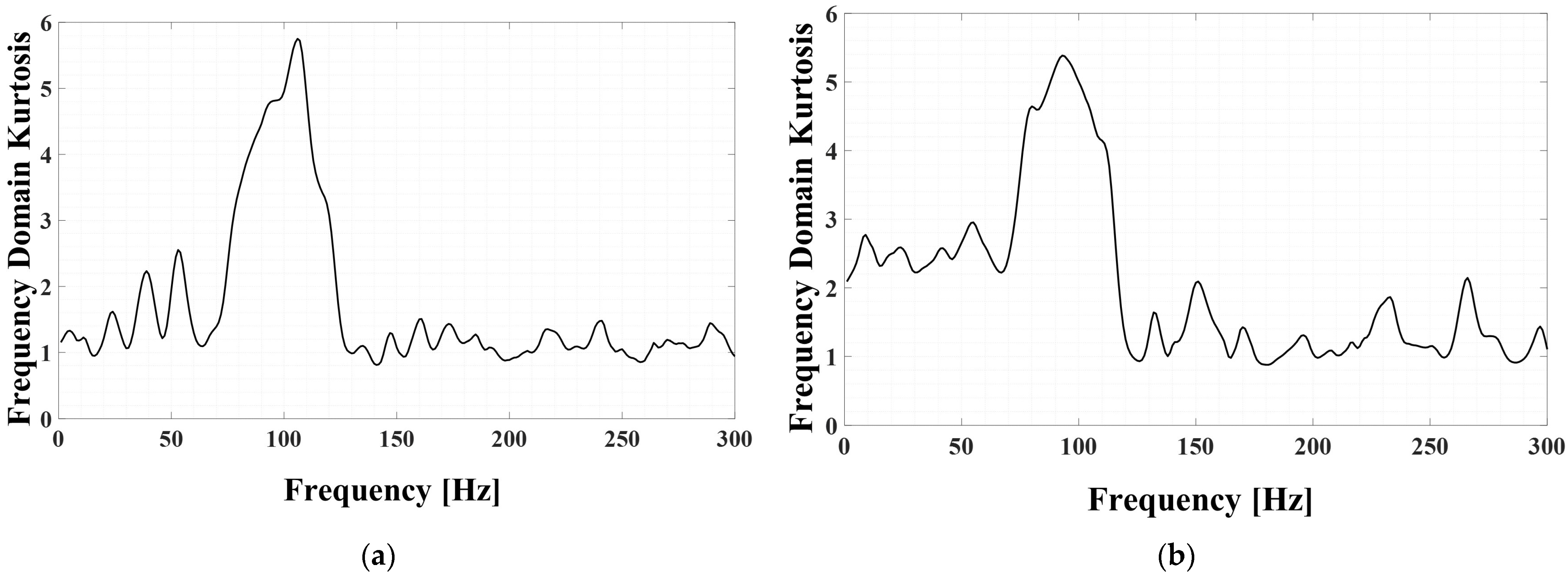
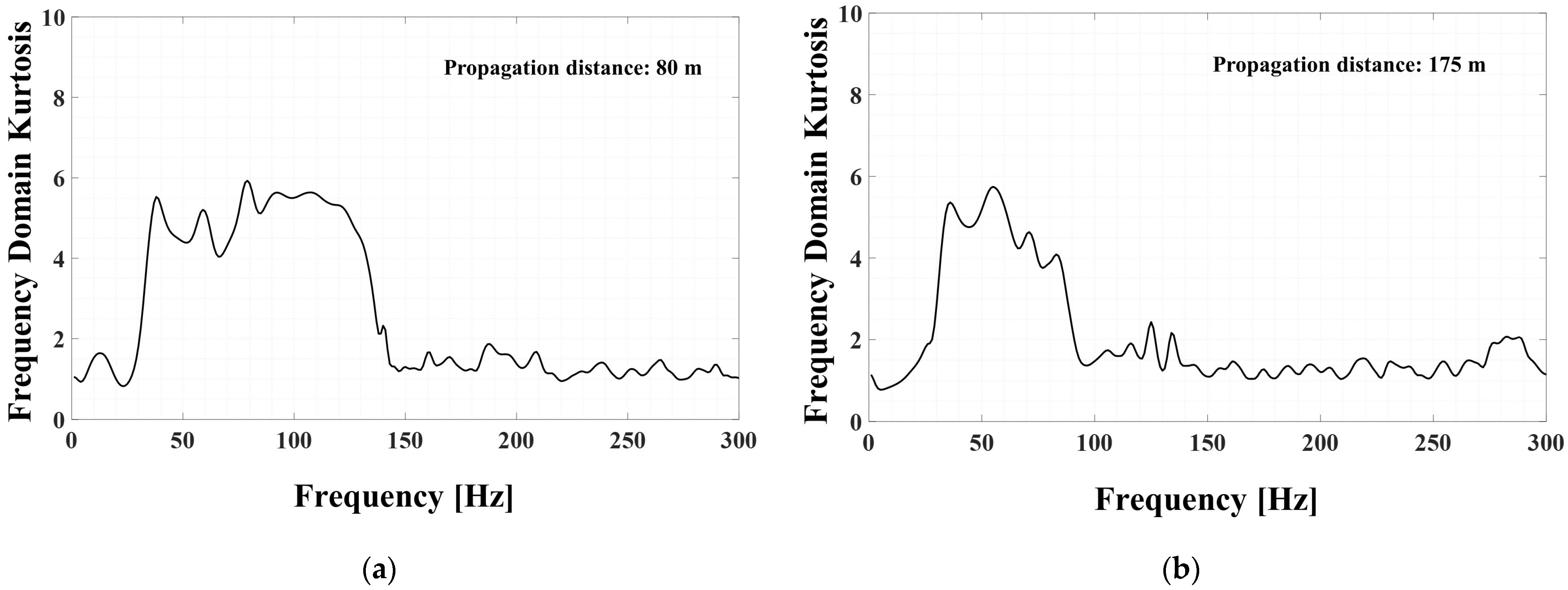
Figure 15a,b show the results of the FDK for the signals described earlier, serving as an indicator to find the dominant frequency band of the transient signal.
Figure 15a shows the FDK results of the impact signal that propagated from 80 m, and it can be observed that the dominant frequency range is approximately 30 to 120 Hz. The FDK of the signal transmitted to sensor 2, which is located 175 m away, shows that the dominant frequency range is 30–90 Hz. Therefore, it can be seen that some high-frequency bands were attenuated as the wave propagated over a long distance.
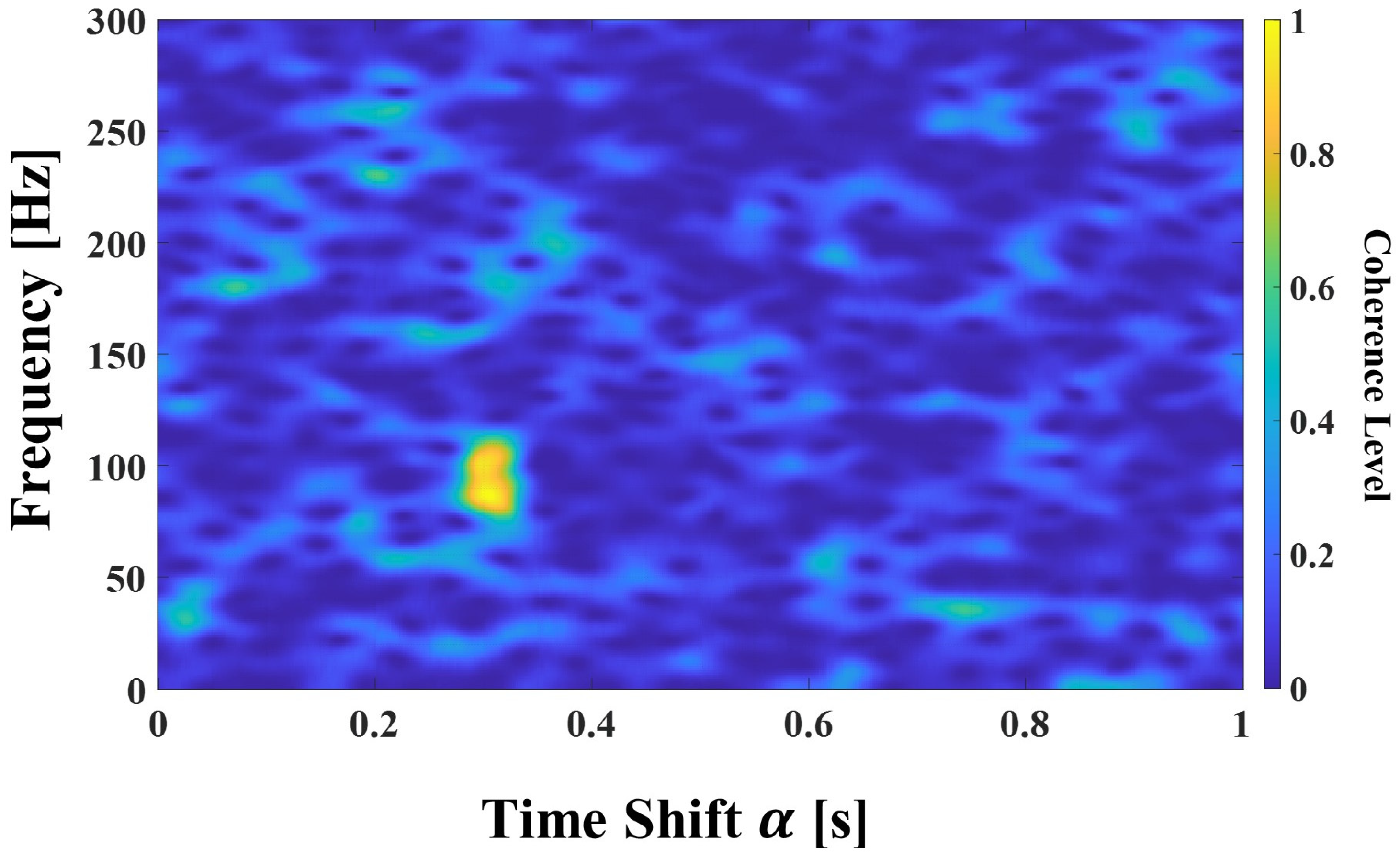
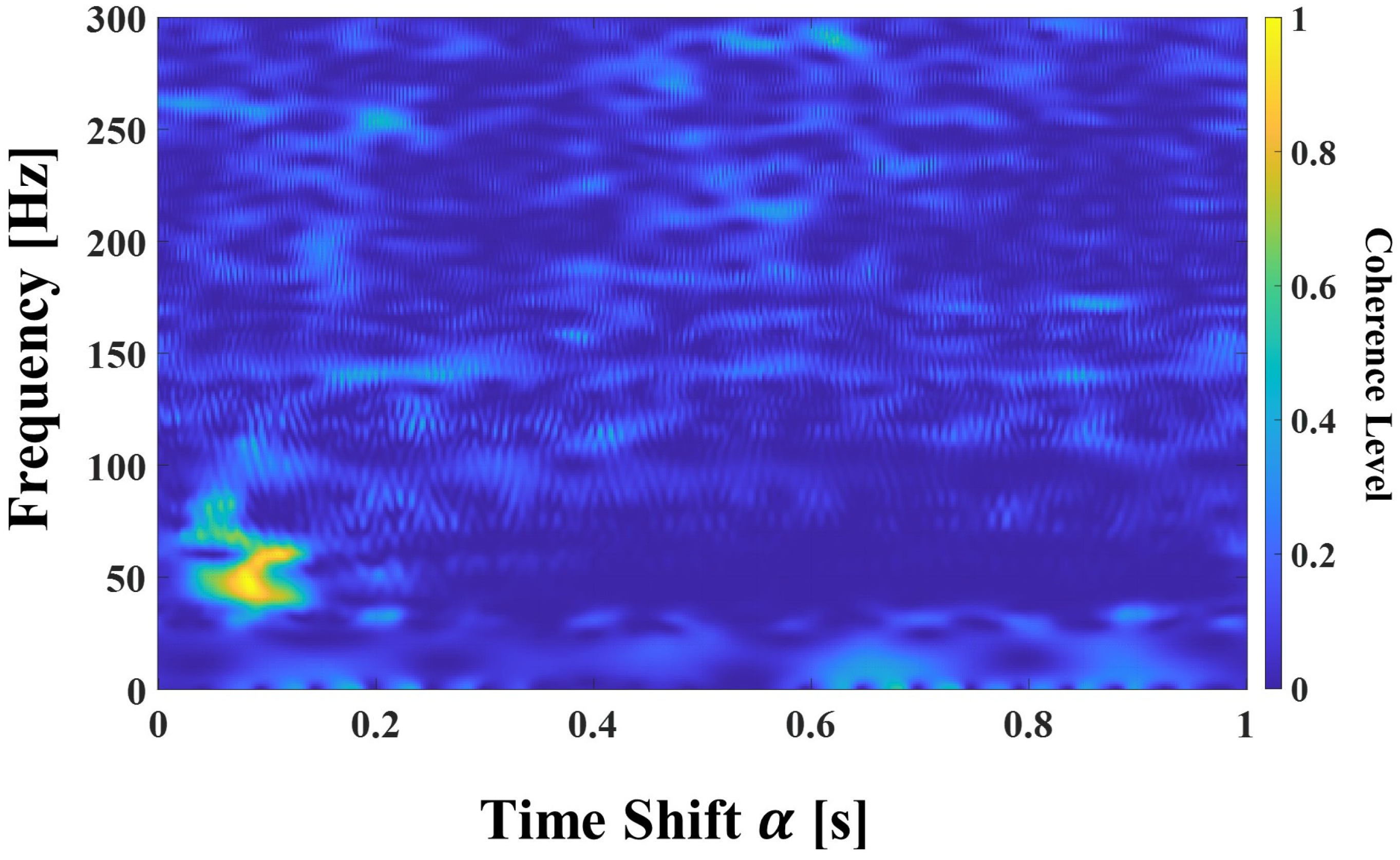
Figure 16 shows the results of the newly proposed
for a comparison of the similarities between the measured transient signals. The results of the proposed
, as shown in
Figure 16, indicate that the frequency band of 40–60 Hz, which is narrower than the 30–90 Hz frequency band that was determined as the optimal frequency band through the FDK observation, is the one with highest level of similarity.
As a result of these observations, the narrow frequency band of 40–60 Hz was selected as the optimal frequency band, rather than the wider 30–90 Hz frequency band that was initially considered as a candidate for the optimal frequency band based on the FDK observations.
Figure 17a,b show the two signals filtered using the optimal frequency band. The results indicate that the signal-to-noise ratios of both signals have improved. In particular, for the signal propagated at 175 m, it can be seen that most of the noise has been removed.
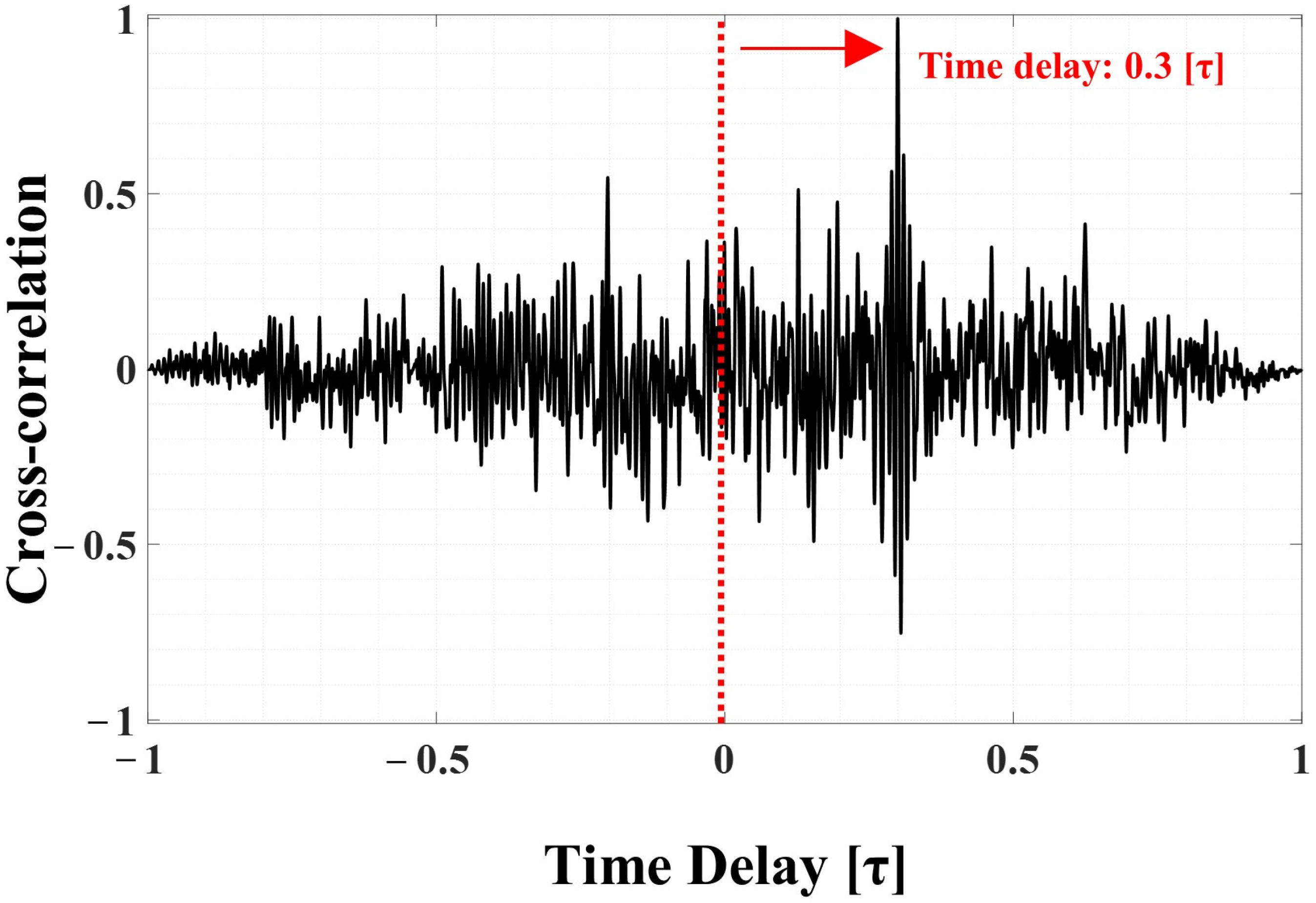
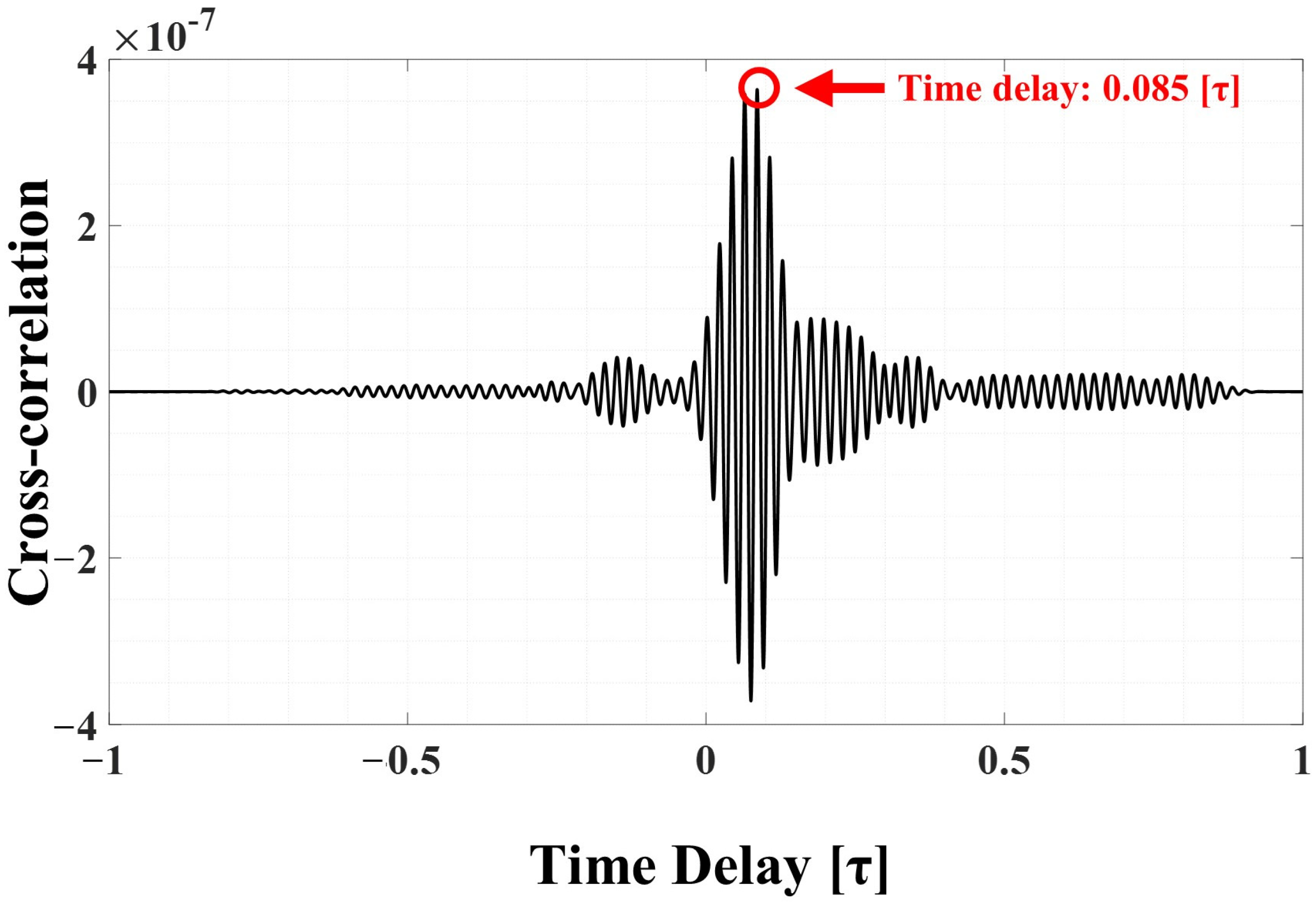
Figure 18 shows the calculation results of the cross-correlation using two signals with improved signal-to-noise ratios. As a result, it was confirmed that a time difference of approximately 0.085 s occurred between the two signals.
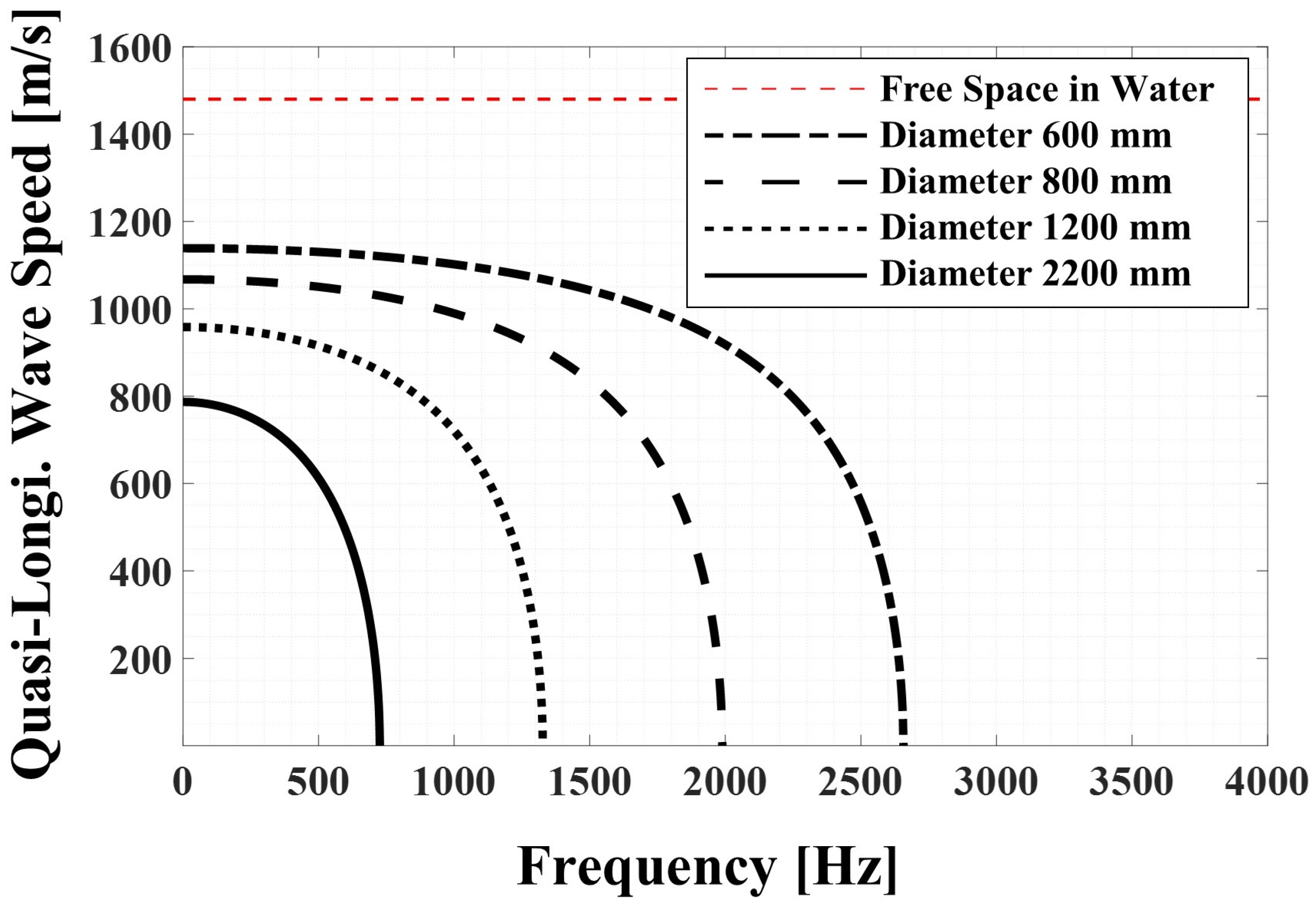
A characteristic of the speed of a quasi-longitudinal wave, which must be known when calculating the source location, is that it changes with the frequency, as depicted in
Figure 2. The theoretical propagation speed at 40~60 Hz, which was selected as the optimal frequency band, was approximately 820 m/s.
Therefore, by applying the arrival time difference (0.085 s), the propagation speed (820 m/s), and the total distance (255 m) to Equation (1) to express the source location, the damage location can be calculated as 92.65 m. This result shows that there is an error of approximately 12.65 m from actual TPI. The error was calculated using the time delay obtained by the cross-correlation of the two signals, as shown in
Figure 18. The error may be attributed to a variety of factors, but it is primarily thought to result from the use of theoretical speed values, as well as from the excavation activities being performed within a range of approximately 10 m from the designated location. This experimental result has demonstrated that the detection method proposed in this study can provide early warnings before the failure of buried pipelines occurs, and can be effectively utilized under actual field conditions, which suggests that the method is reasonably practical.
Additionally, when an impact is applied to the surface of the buried pipeline area, a ground-borne wave can also propagate [
27,
28], as shown in
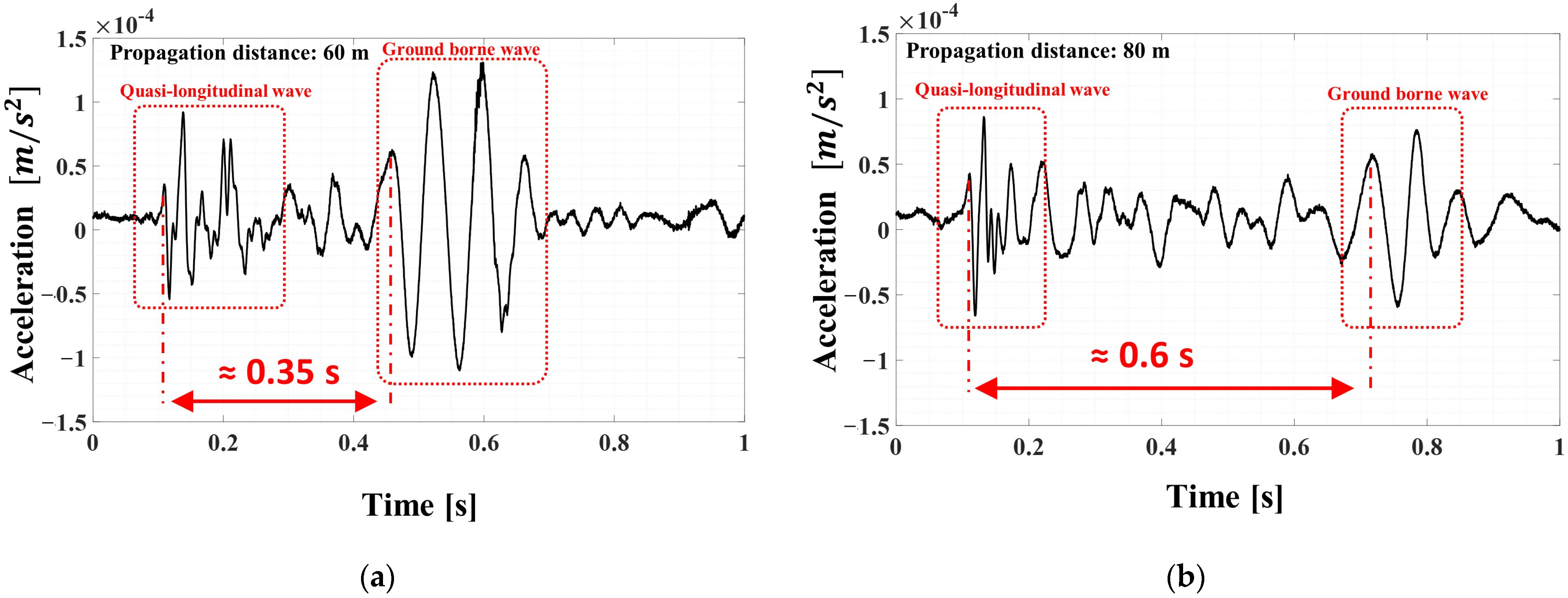
Figure 19a,b. The ground-borne wave refers to the wave that is generated when the impact energy is transmitted through the ground, and it is one of the noise sources that can cause errors in the source location. In particular, since the ground-borne wave is a type of transient signal that has a different propagation speed from the wave that propagates through the pipeline, it can introduce noise in the time-difference-of-arrival-based source location and needs to be filtered.
Figure 19a shows the measured signal from the sensor position 60 m from the excavation site on the ground. As previously mentioned, quasi-longitudinal waves propagate at a speed of approximately 820 m/s and the ground-borne wave arrives approximately 0.35 s later. Because the propagation distance is 60 m, it can be determined that the propagation speed of the ground-borne wave is approximately 141 m/s.
Figure 19b presents an excavation signal propagated 80 m, and it can be seen that the ground-borne wave arrives approximately 0.6 s later. Here, the time between the two wave groups was calculated based on the first peak, as shown in
Figure 19a,b. Therefore, it can be estimated that the propagation speed of the ground-borne wave is approximately 114 m/s in this case. The ground-borne waves in the area where this experiment was conducted are known to propagate at approximately 200 m/s or less [
29,
30]. These ground-borne waves propagate in a transient shape with lower propagation speed compared to quasi-longitudinal waves, and they are known to cause source location errors due to their contribution as noise. However, the approach proposed in this study includes a step to confirm the similarity between these two types of signals, meaning that even in the presence of various forms of noise, including ground-borne waves, high accuracy in detecting the source location is possible.
Figure 20a–f present signals obtained through excavation experiments conducted at various points. Here, the red dotted line indicates the location of the first peak of the quasi-longitudinal wave generated by TPI.
Figure 20a shows the results of an excavation test at approximately 60 m from the sensor 1 position. In this case, the signal that reaches sensor 2 propagated a distance of approximately 195 m. As previously described, it can be confirmed that at a relatively short distance of 60 m, the ground-borne wave propagated together with the quasi-longitudinal wave at a speed of approximately 140 m/s. However, this cannot be confirmed at sensor 2, as the ground-borne wave was fully attenuated.
Figure 20b through
Figure 20f present signals obtained from excavations at distances of 80 m, 100 m, 125 m, 150 m, and 180 m from the position of sensor 1, respectively. Especially when observing the excavation signal at a location approximately 75 m from sensor 2 in
Figure 20f, it can be observed that the ground-borne wave was measured concurrently, as shown in
Figure 20a. As described above, these results suggest that the proposed
method contributes significantly to the selection of the optimal frequency bands for the source location. Since the signals were aligned with reference to the sensor 1 signal in
Figure 20a–f, it can be observed that the time difference between the two signals gradually decreases. However, in
Figure 20e,f, it can be observed that the sensor 2 signal arrives earlier because the distance from the impact to sensor 2 is shorter than the distance to sensor 1.
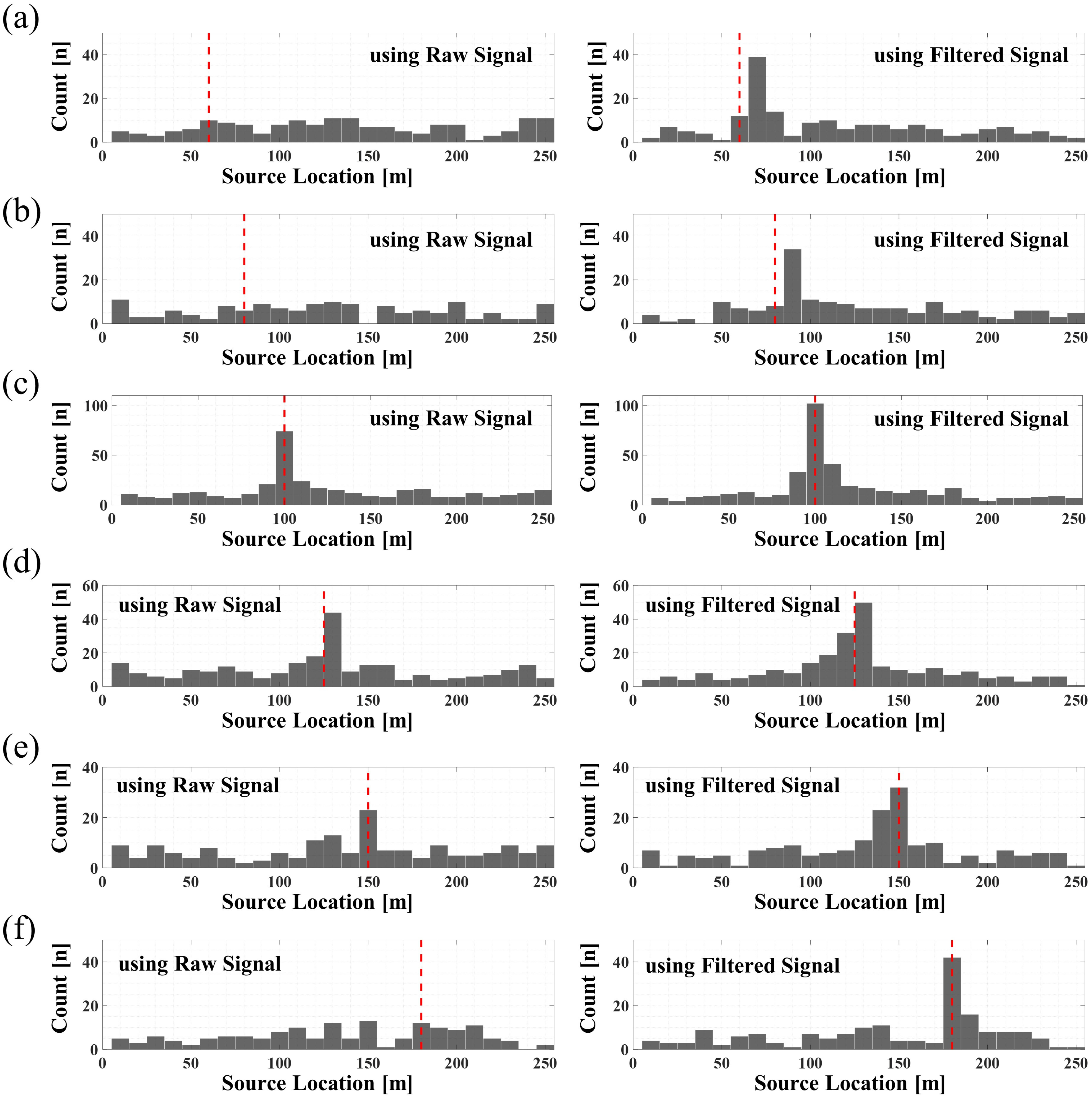
Figure 21a–f show the results after detecting excavation activity using raw and filtered signals. The actual excavation location is indicated by the red dashed line in all
Figure 21a–f, with excavation activity carried out for approximately 120 s at each position.
Figure 21a shows the source location results during excavation at a position of approximately 60 m. As a result, it was found that using the raw signal alone, it is not possible to detect excavation activity that can cause damage to the pipeline. However, by using the filtered signals obtained by the algorithm proposed in this study, excavation activity can be detected in the vicinity of 60 m. Similarly,
Figure 21b–f present the verification results of the excavation activities performed at the 80 m, 100 m, 125 m, 150 m, and 180 m positions, respectively, using the proposed algorithm. The detection results at all positions indicate that the algorithm proposed in this study makes it possible to detect excavation activity that can cause pipeline damage. In particular, even in the presence of ground-borne waves and background noise in actual field conditions, it is possible to effectively pinpoint excavation activity by selecting the optimal frequency band for the impact wave. Therefore, the results of this study demonstrate the validity of detecting TPI that can directly cause impacts to buried pipelines, and this has significant utility in preventing pipeline failure accidents.