Estimation of Aquifer Storativity Using 3D Geological Modeling and the Spatial Random Bagging Simulation Method: The Saskatchewan River Basin Case Study (Central Canada)
Abstract
:1. Introduction
2. Study Area and Database
2.1. Location, Physiography, and Climate
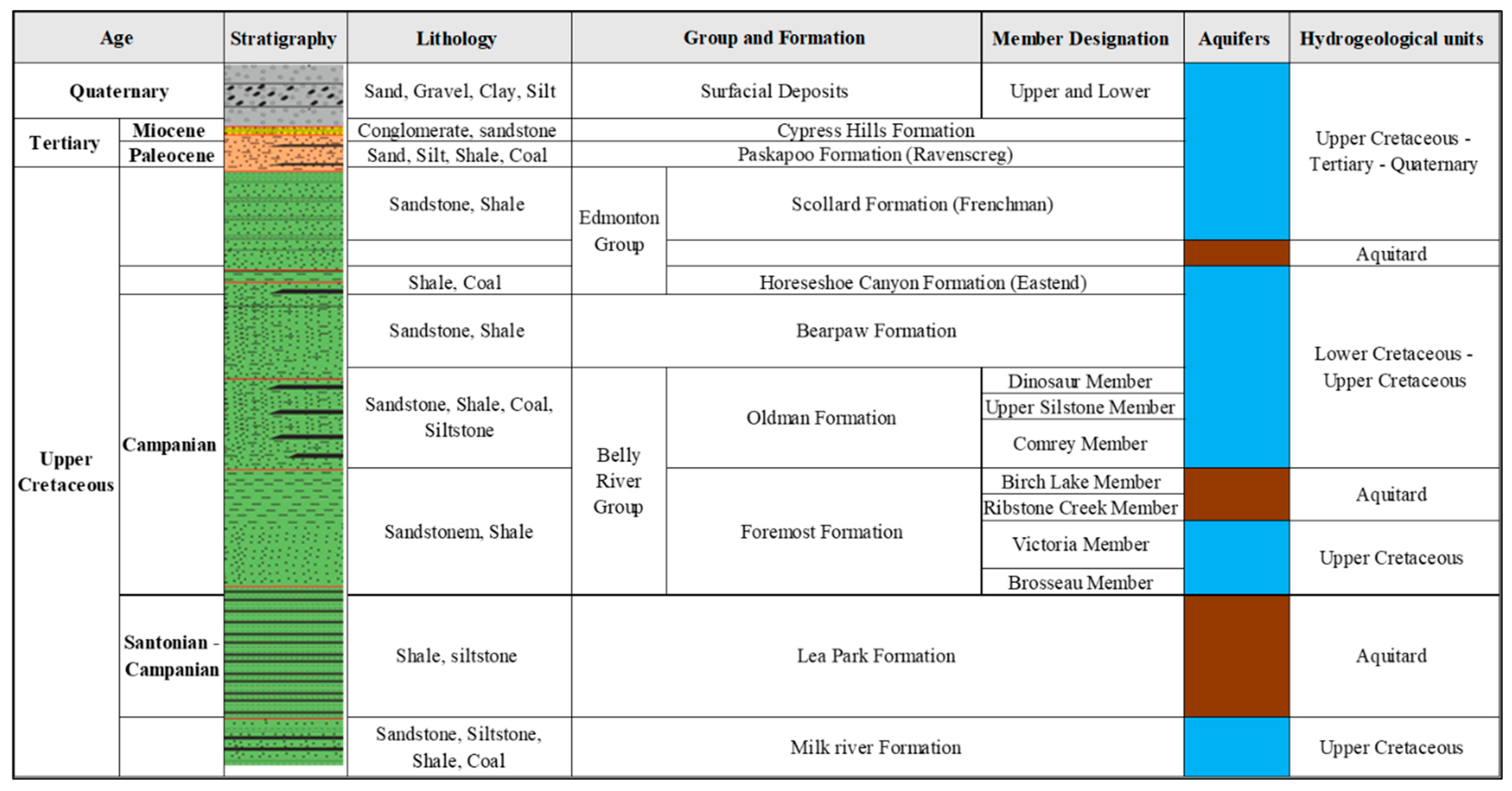
2.2. Geology and Hydrogeology
2.3. Geological, Hydrogeological, and Hydrodynamic Databases
3. Methods
3.1. Three-Dimensional Geological Modeling of the SRB Basin
3.2. Groundwater Storage Calculation
- -
- Calculation of geological reserves in an unconfined aquifer
- -
- Calculation of geological reserves in a confined aquifer
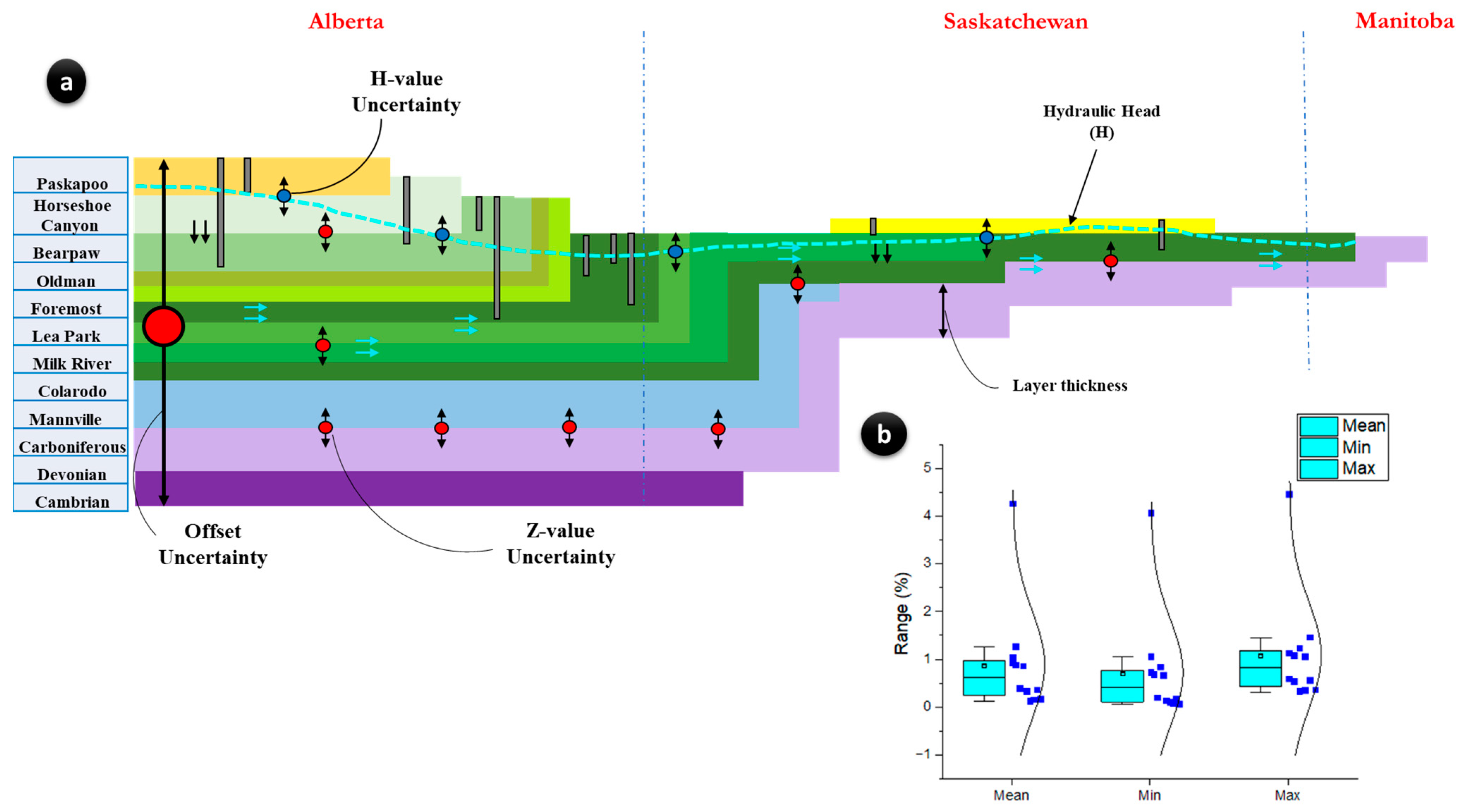
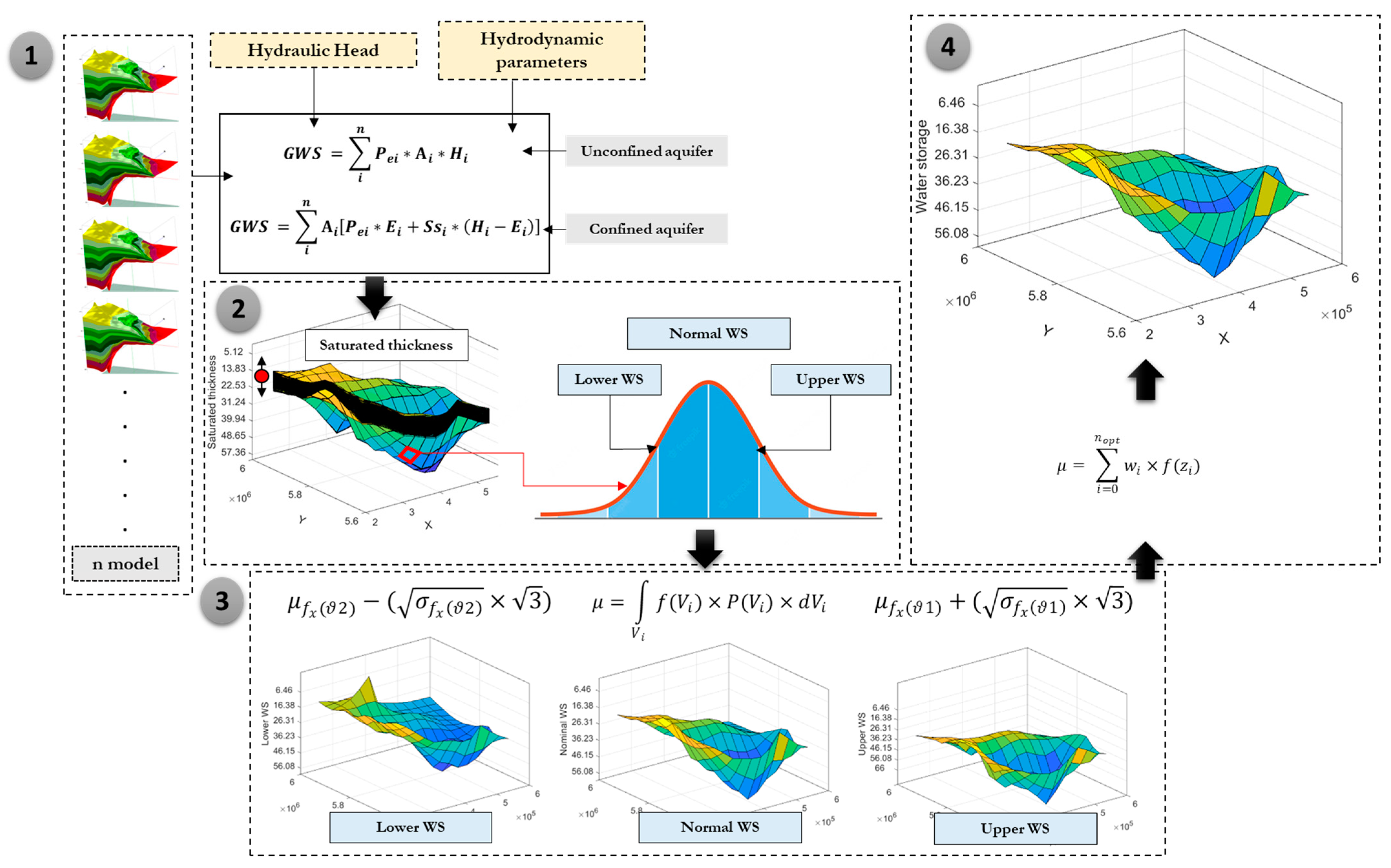
3.3. Uncertainty Assessment Using Spatial Random Bagging Simulation
3.3.1. Spatial Random Bagging Simulation (SRBS)
3.3.2. The Application of SRBS to Uncertainty Calculation and GWS Estimation
4. Results
4.1. Geostatistical Analysis
4.2. Regional 3D Geological Model of the Saskatchewan River Basin
- -
- Horizontal and vertical spatial extension of superficial aquifers and their hydrodynamics
- -
- Horizontal and vertical spatial extension of the deep aquifers and their hydrodynamics
- (i)
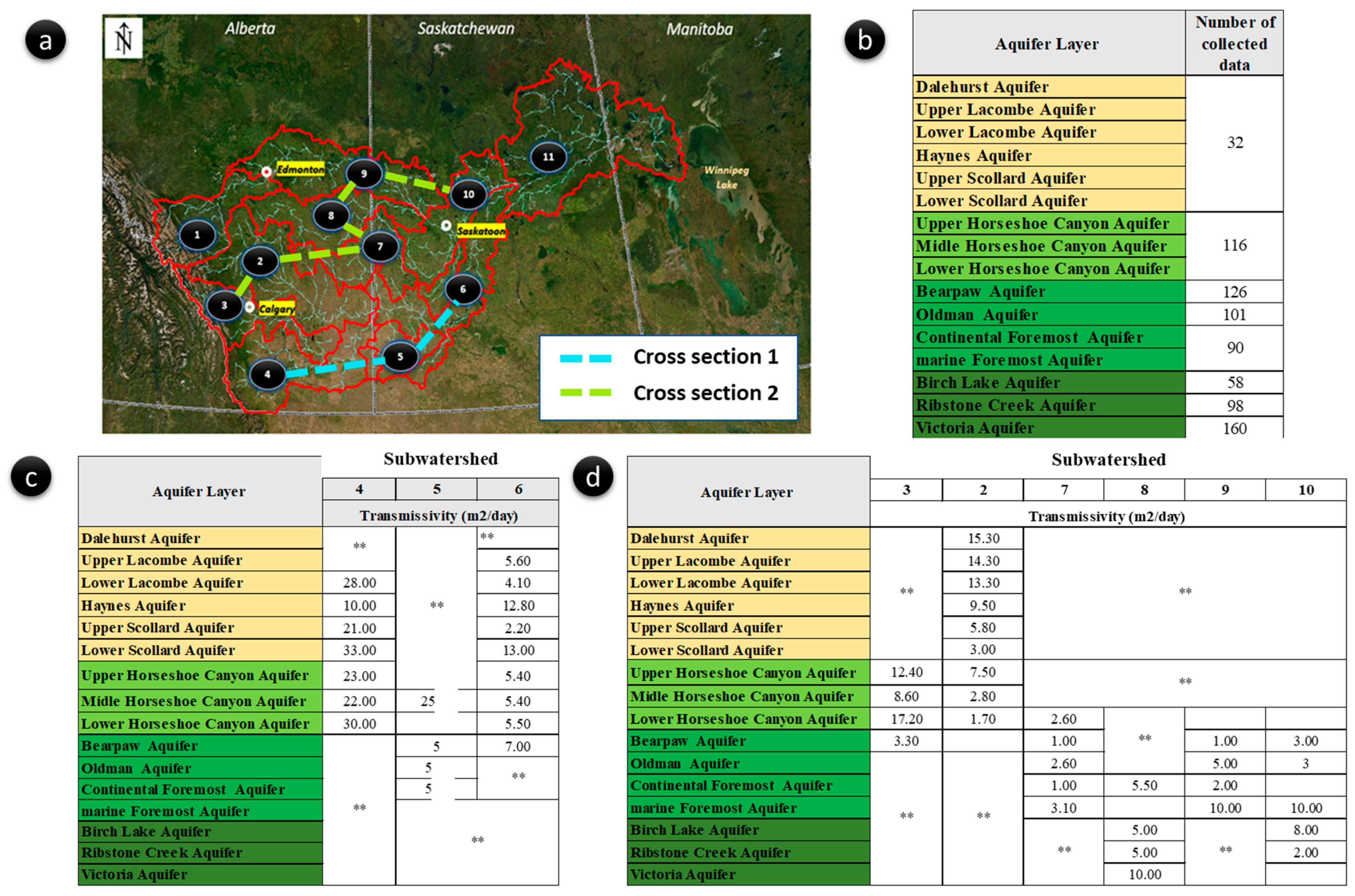
- Upper Horseshoe Canyon Aquifer: This aquifer ranges in thickness from 95 m to 180 m, while the ceiling depths range from 10 m to 700 m (Figure 9). The transmissivity (T) of this aquifer level varies from 5.4 to 25 m2/day. The variation in transmissivity is explained mainly by variation in its thickness, which is largely affected by erosion. The highest values of transmissivity were recorded in sub-catchments 2 and 5, on the order of 23 and 25 m2/day, respectively, given the sandy nature of the aquifer. However, the lowest transmissivities were recorded in sub-catchment 7 (T = 5.4 m2/day), in the northern part (T = 6 m2/day (Figure 5)) and center (T = 7.6 m2/day (Figure 5)). These low values are attributed to this aquifer level being enriched with sandy clay and bentonite at the level of these sub-catchments. In this area, the aquifers develop narrow and deep drawdown cones.
- (ii)
- Middle Horseshoe Canyon Aquifer: This aquifer level ranges in thickness from 50 m to 200 m (Figure 9). As was the case with the Upper Horseshoe Canyon Aquifer, the thickness of this aquifer is controlled by erosion, which explains the variability in its hydrodynamic behavior. The highest values of transmissivity were recorded in sub-catchment 2, averaging at 22 m2/day. This is due to the sandy nature of the aquifer. However, the lowest transmissivity values were recorded in the center of the basin (T = 2.8 to 5 m2/day (Figure 5)) and the southwestern part (T = 5.4 m2/day (Figure 5)), where it is enriched with discontinuous lenses of clay.
- (iii)
- Lower Horseshoe Canyon Aquifer: This aquifer level has a minimum thickness of ~60 m and a maximum thickness of about 170 m (Figure 9). The highest values of transmissivity were recorded at the level of sub-catchment 2, on the order of 30 m2/day. The lowest values were recorded at the level of sub-catchment 8 (T = 1.7 m2/day). This area is more exposed to drawdown and overexploitation of resources.
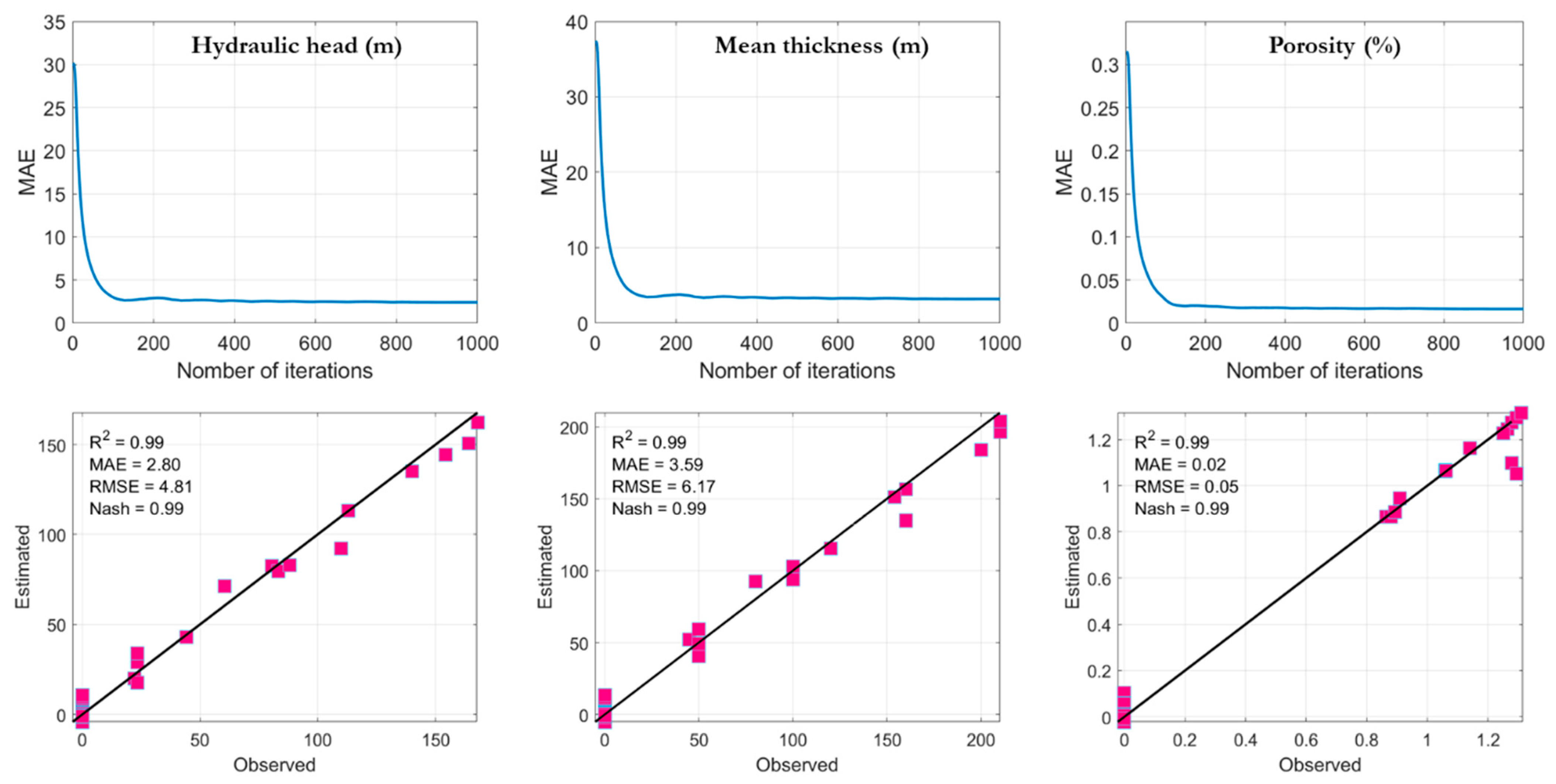
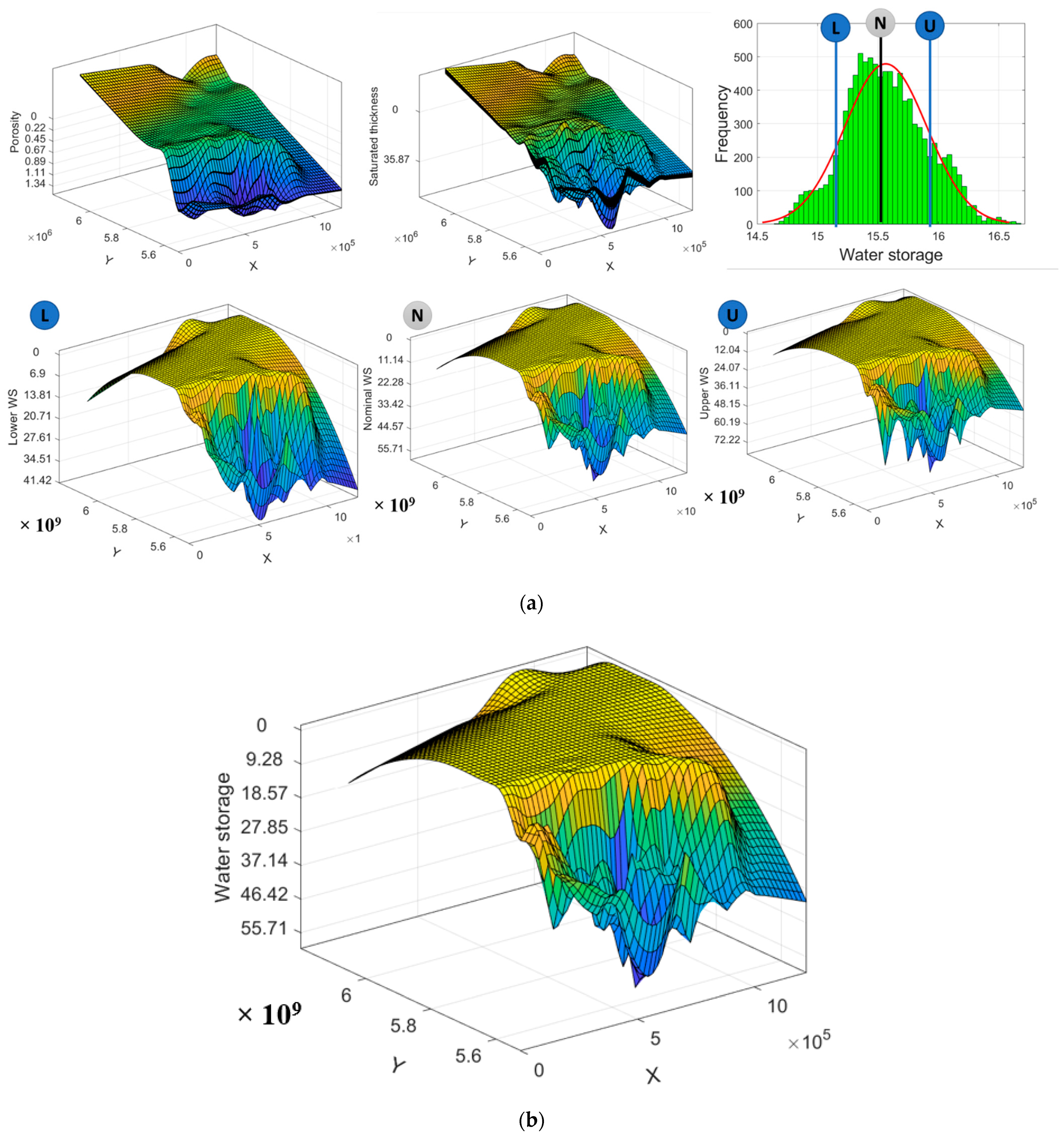
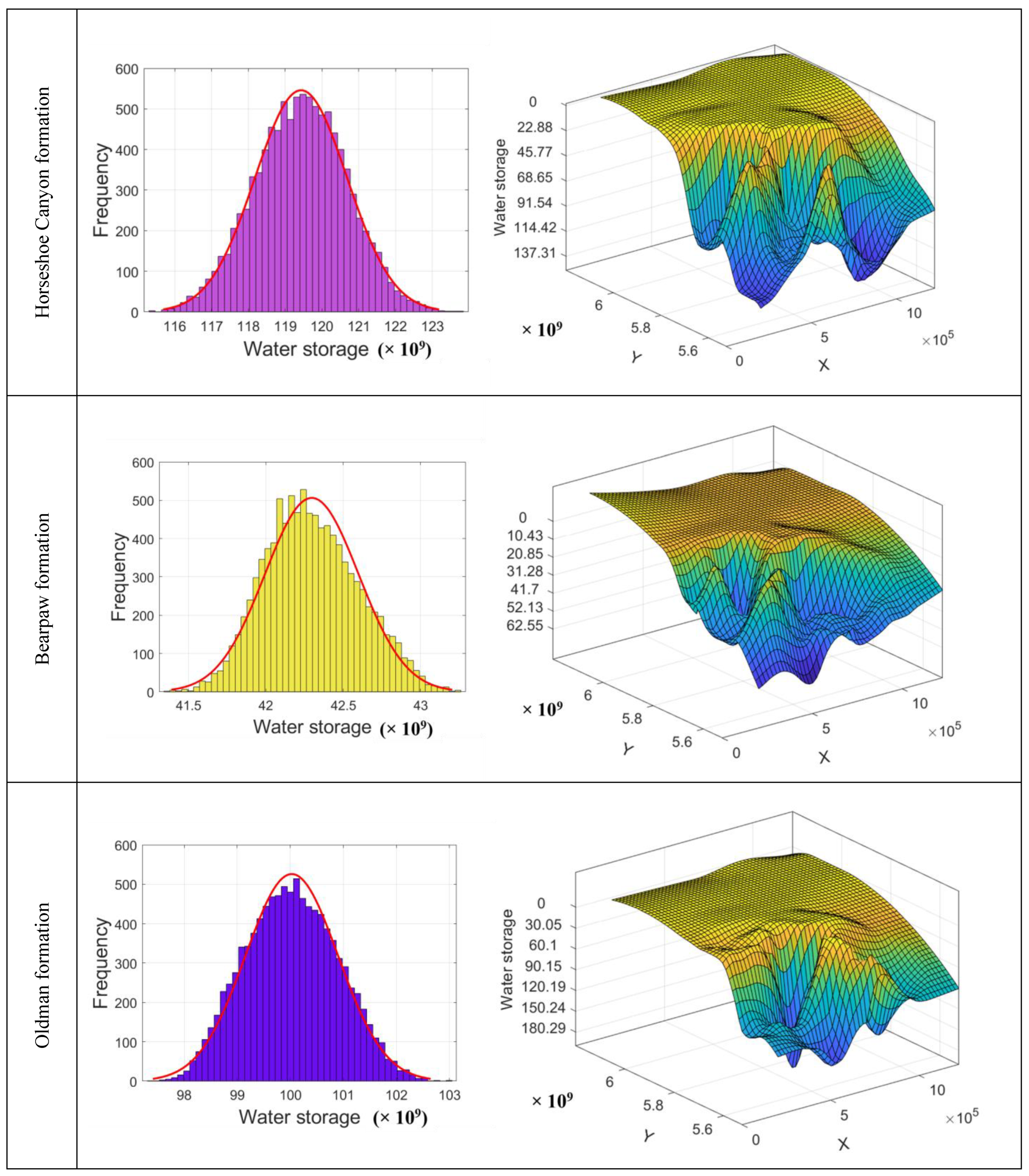
4.3. Uncertainty Assessment Using the New Spatial Random Bagging Simulation (SRBS) System and Groundwater Storage Calculation
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saha, G.C.; Li, J.; Thring, R.W.; Hirshfield, F.; Paul, S.S. Temporal Dynamics of Groundwater-Surface Water Interaction under the Effects of Climate Change: A Case Study in the Kiskatinaw River Watershed, Canada. J. Hydrol. 2017, 551, 440–452. [Google Scholar] [CrossRef]
- Jaxa-Rozen, M.; Kwakkel, J.H.; Bloemendal, M. A Coupled Simulation Architecture for Agent-Based/Geohydrological Modelling with NetLogo and MODFLOW. Environ. Model. Softw. 2019, 115, 19–37. [Google Scholar] [CrossRef]
- Xiang, W.; Cheng, B.; Biswas, A.; Li, Z. Geoderma Quantifying Dual Recharge Mechanisms in Deep Unsaturated Zone of Chinese Loess Plateau Using Stable Isotopes. Geoderma 2019, 337, 773–781. [Google Scholar] [CrossRef]
- Nong, X.; Shao, D.; Zhong, H.; Liang, J. Evaluation of Water Quality in the South-to-North Water Diversion Project of China Using the Water Quality Index (WQI) Method. Water Res. 2020, 178, 115781. [Google Scholar] [CrossRef] [PubMed]
- Zhu, R.; Croke, B.F.W.; Jakeman, A.J. Diffuse Groundwater Recharge Estimation Confronting Hydrological Modelling Uncertainty. J. Hydrol. 2020, 584, 124642. [Google Scholar] [CrossRef]
- Jiang, X.; Huang, J.G.; Cheng, J.; Dawson, A.; Stadt, K.J.; Comeau, P.G.; Chen, H.Y.H. Interspecific Variation in Growth Responses to Tree Size, Competition and Climate of Western Canadian Boreal Mixed Forests. Sci. Total Environ. 2018, 631–632, 1070–1078. [Google Scholar] [CrossRef]
- Saha, S.; Kundu, B.; Paul, G.C.; Mukherjee, K.; Pradhan, B.; Dikshit, A.; Abdul Maulud, K.N.; Alamri, A.M. Spatial Assessment of Drought Vulnerability Using Fuzzy-Analytical Hierarchical Process: A Case Study at the Indian State of Odisha. Geomat. Nat. Hazards Risk 2021, 12, 123–153. [Google Scholar] [CrossRef]
- Lian, X.; Piao, S.; Chen, A.; Huntingford, C.; Fu, B.; Li, L.Z.X.; Huang, J.; Sheffield, J.; Berg, A.M.; Keenan, T.F.; et al. Multifaceted Characteristics of Dryland Aridity Changes in a Warming World. Nat. Rev. Earth Environ. 2021, 2, 232–250. [Google Scholar] [CrossRef]
- La Pasta Cordeiro, M.; da Silva Junior, G.C.; Dereczynski, C.P.; Chrispim, Z.M.P.; Condesso de Melo, M.T. Analysis of Indicators of Climate Extremes and Projection of Groundwater Recharge in the Northern Part of the Rio de Janeiro State, Brazil. Environ. Dev. Sustain. 2021, 23, 18311–18336. [Google Scholar] [CrossRef]
- Pulido-Velazquez, M.; Peña-Haro, S.; García-Prats, A.; Mocholi-Almudever, A.F.; Henriquez-Dole, L.; Macian-Sorribes, H.; Lopez-Nicolas, A. Integrated Assessment of the Impact of Climate and Land Use Changes on Groundwater Quantity and Quality in the Mancha Oriental System (Spain). Hydrol. Earth Syst. Sci. 2015, 19, 1677–1693. [Google Scholar] [CrossRef] [Green Version]
- Webster, K.L.; Beall, F.D.; Creed, I.F.; Kreutzweiser, D.P. Impacts and Prognosis of Natural Resource Development on Water and Wetlands in Canada’s Boreal Zone. Environ. Rev. 2015, 23, 78–131. [Google Scholar] [CrossRef] [Green Version]
- Gleeson, T.; Befus, K.M.; Jasechko, S.; Luijendijk, E.; Cardenas, M.B. The Global Volume and Distribution of Modern Groundwater. Nat. Geosci. 2016, 9, 161–164. [Google Scholar] [CrossRef]
- Abdelmohsen, K.; Sultan, M.; Ahmed, M.; Save, H.; Elkaliouby, B.; Emil, M.; Yan, E.; Abotalib, A.Z.; Krishnamurthy, R.V.; Abdelmalik, K. Response of Deep Aquifers to Climate Variability. Sci. Total Environ. 2019, 677, 530–544. [Google Scholar] [CrossRef]
- Aliyari, F.; Bailey, R.T.; Tasdighi, A.; Dozier, A.; Arabi, M.; Zeiler, K. Coupled SWAT-MODFLOW Model for Large-Scale Mixed Agro-Urban River Basins. Environ. Model. Softw. 2019, 115, 200–210. [Google Scholar] [CrossRef]
- Hamdi, M.; Zagrarni, M.F.; Jerbi, H.; Tarhouni, J. Hydrogeochemical and Isotopic Investigation and Water Quality Assessment of Groundwater in the Sisseb El Alem Nadhour Saouaf Aquifer (SANS), Northeastern Tunisia. J. Afr. Earth Sci. 2018, 141, 148–163. [Google Scholar] [CrossRef]
- Yang, L.; Guan, Q.; Lin, J.; Tian, J.; Tan, Z.; Li, H. Evolution of NDVI Secular Trends and Responses to Climate Change: A Perspective from Nonlinearity and Nonstationarity Characteristics. Remote Sens. Environ. 2021, 254, 112247. [Google Scholar] [CrossRef]
- Kalbus, E.; Reinstorf, F.; Schirmer, M. Measuring Methods for Groundwater—Surface Water Interactions: A Review. Hydrol. Earth Syst. Sci. 2006, 10, 873–887. [Google Scholar] [CrossRef] [Green Version]
- Raiber, M.; Webb, J.A.; Cendón, D.I.; White, P.A.; Jacobsen, G.E. Environmental Isotopes Meet 3D Geological Modelling: Conceptualising Recharge and Structurally-Controlled Aquifer Connectivity in the Basalt Plains of South-Western Victoria, Australia. J. Hydrol. 2015, 527, 262–280. [Google Scholar] [CrossRef]
- Ligavha-Mbelengwa, L.; Gomo, M. Investigation of Factors Influencing Groundwater Quality in a Typical Karoo Aquifer in Beaufort West Town of South Africa. Environ. Earth Sci. 2020, 79, 196. [Google Scholar] [CrossRef]
- Tellam, J.H.; Barker, R.D. Towards Prediction of Saturated-Zone Pollutant Movement in Groundwaters in Fractured Permeable-Matrix Aquifers: The Case of the UK Permo-Triassic Sandstones. Geol. Soc. Spec. Publ. 2006, 263, 1–48. [Google Scholar] [CrossRef]
- Wang, T.Y.; Chang, C.L.; Zhou, N.Q. The Effects of Climate Change on Water Resources of Xiangjiang River Basin. J. Taiwan Agric. Eng. 2015, 61, 71–78. [Google Scholar] [CrossRef]
- Coffin, L.M.; Russell, H.A.J. 3D Surficial Geological Models in Canada: An Annotated Bibliography. Geol. Surv. Can. Open File 2017, 8186, 1–57. [Google Scholar] [CrossRef]
- Sun, A.Y.; Green, R.; Swenson, S.; Rodell, M. Toward Calibration of Regional Groundwater Models Using GRACE Data. J. Hydrol. 2012, 422–423, 1–9. [Google Scholar] [CrossRef]
- Rahmati, O.; Pourghasemi, H.R.; Melesse, A.M. Application of GIS-Based Data Driven Random Forest and Maximum Entropy Models for Groundwater Potential Mapping: A Case Study at Mehran Region, Iran. Catena 2016, 137, 360–372. [Google Scholar] [CrossRef]
- Khaki, M.; Hoteit, I.; Kuhn, M.; Forootan, E.; Awange, J. Assessing Data Assimilation Frameworks for Using Multi-Mission Satellite Products in a Hydrological Context. Sci. Total Environ. 2019, 647, 1031–1043. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, S.; Hyun, Y.; Lee, S.; Lee, M.-J. Groundwater Potential Mapping Using Remote Sensing and GIS-Based Machine Learning Techniques. Remote Sens. 2020, 12, 1200. [Google Scholar] [CrossRef] [Green Version]
- Moya, C.E.; Raiber, M.; Cox, M.E. Three-Dimensional Geological Modelling of the Galilee and Central Eromanga Basins, Australia: New Insights into Aquifer/Aquitard Geometry and Potential Influence of Faults on Inter-Connectivity. J. Hydrol. Reg. Stud. 2014, 2, 119–139. [Google Scholar] [CrossRef]
- Jørgensen, F.; Høyer, A.S.; Sandersen, P.B.E.; He, X.; Foged, N. Combining 3D Geological Modelling Techniques to Address Variations in Geology, Data Type and Density—An Example from Southern Denmark. Comput. Geosci. 2015, 81, 53–63. [Google Scholar] [CrossRef]
- Watson, C.; Richardson, J.; Wood, B.; Jackson, C.; Hughes, A. Improving Geological and Process Model Integration through TIN to 3D Grid Conversion. Comput. Geosci. 2015, 82, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Sandoval, J.A.; Tiburan, C.L. Identification of Potential Artificial Groundwater Recharge Sites in Mount Makiling Forest Reserve, Philippines Using GIS and Analytical Hierarchy Process. Appl. Geogr. 2019, 105, 73–85. [Google Scholar] [CrossRef]
- Hamdi, M.; Goïta, K.; Karaouli, F.; Zagrarni, M.F. Hydrodynamic Groundwater Modeling and Hydrochemical Conceptualization of the Mining Area of Moulares Redeyef (Southwestern of Tunisia): New Local Insights. Phys. Chem. Earth 2021, 121, 102974. [Google Scholar] [CrossRef]
- Tolche, A.D. Groundwater Potential Mapping Using Geospatial Techniques: A Case Study of Dhungeta-Ramis Sub-Basin, Ethiopia. Geol. Ecol. Landsc. 2021, 5, 65–80. [Google Scholar] [CrossRef]
- Russell, H.A.J.; Brodaric, B.; Keller, G.R.; Maccormack, K.E.; Snyder, D.B. A Perspective on a Three Dimensional Framework for Canadian Geology. AER AGS Spec. Rep. 2015, 101, 21–32. [Google Scholar]
- Di Salvo, C.; Mancini, M.; Cavinato, G.P.; Moscatelli, M.; Simionato, M.; Stigliano, F.; Rea, R.; Rodi, A. A 3d Geological Model as a Base for the Development of a Conceptual Groundwater Scheme in the Area of the Colosseum (Rome, Italy). Geosciences 2020, 10, 266. [Google Scholar] [CrossRef]
- Ehrendorfer, J.; National, S.; Erlmeier, K.; Formentin, G. 3D Geological Modelling of Fluvio-Glacial Aquifers to Improve Water Work Operations 3D Geological Modelling of Fluvio-Glacial Aquifers to Improve Water Work Operations. In Proceedings of the 24th EGU General Assembly, Vienna, Austria, 23–27 May 2022; pp. 3–4. [Google Scholar] [CrossRef]
- Statistics Canada Human Activity and the Environment: Freshwater Supply and Demand in Canada. 2010, 61. Available online: https://www150.statcan.gc.ca/n1/pub/16-201-x/16-201-x2017000-eng.pdf (accessed on 2 March 2023).
- Elshamy, M.; Pietroniro, A.; Wheater, H.S. Modelling the Hydrology and Streamflow of the Mackenzie River Basin. In Proceedings of the CGU & CSAFM Joint annual Scientific Meeting, Vancouver, BC, Canada, 28–31 May 2017. [Google Scholar]
- George, S.S. Streamflow in the Winnipeg River Basin, Canada: Trends, Extremes and Climate Linkages. J. Hydrol. 2007, 332, 396–411. [Google Scholar] [CrossRef]
- Hayashi, M.; van der Kamp, G.; Rosenberry, D.O. Hydrology of Prairie Wetlands: Understanding the Integrated Surface-Water and Groundwater Processes. Wetlands 2016, 36, 237–254. [Google Scholar] [CrossRef]
- Hendry, M.J. Hydrogeology of Clay Till in a Prairie Region of Canada. Groundwater 1988, 26, 607–614. [Google Scholar] [CrossRef]
- Eilers, R.G.; Eilers, E.D.; Fitzgerald, M.M. Eilers1997_Article_ASalinityRiskIndexForSoilsOfTh.Pdf. Hydrogeol. J. 1997, 5, 68–79. [Google Scholar] [CrossRef]
- Perez-Valdivia, C.; Sauchyn, D.; Vanstone, J. Groundwater Levels and Teleconnection Patterns in the Canadian Prairies. Water Resour. Res. 2012, 48, 1–13. [Google Scholar] [CrossRef]
- Berthold, S.; Bentley, L.R.; Hayashi, M. Integrated Hydrogeological and Geophysical Study of Depression-Focused Groundwater Recharge in the Canadian Prairies. Water Resour. Res. 2004, 40, 332–346. [Google Scholar] [CrossRef] [Green Version]
- Ireson, A.M.; van der Kamp, G.; Ferguson, G.; Nachshon, U.; Wheater, H.S. Hydrogeological Processes in Seasonally Frozen Northern Latitudes: Understanding, Gaps and Challenges. Hydrogeol. J. 2013, 21, 53–66. [Google Scholar] [CrossRef]
- Tóth, J. The Canadian School of Hydrogeology: History and Legacy. Ground Water 2005, 43, 640–644. [Google Scholar] [CrossRef]
- Cummings, D.I.; Russell, H.A.J.; Sharpe, D.R. Buried-Valley Aquifers in the Canadian Prairies: Geology, Hydrogeology, and Origin. Can. J. Earth Sci. 2012, 49, 987–1004. [Google Scholar] [CrossRef]
- Şener, E.; Varol, S.; Şener, Ş. Hydrochemistry and Geogenic Pollution Assessment of Groundwater in Akşehir (Konya/Turkey) Using GIS. In Computers in Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2022; pp. 477–490. [Google Scholar] [CrossRef]
- Li, Y.; Yan, D.; Peng, H.; Xiao, S. Evaluation of Precipitation in CMIP6 over the Yangtze River Basin. Atmos. Res. 2021, 253, 105406. [Google Scholar] [CrossRef]
- Dawson, F.M.; Evans, C.G.; Marsh, R. Uppermost Cretaceous and Tertiary Strat of the Western Canada Sedimentary Basin. J. Exp. Zool. 1997, 277, 345–352. [Google Scholar]
- Harrison, S.M.; Gentzis, T.; Payne, M. Hydraulic, Water Quality, and Isotopic Characterization of Late Cretaceous-Tertiary Ardley Coal Waters in a Key Test-Well, Pembina-Warburg Exploration Area, Alberta, Canada. Bull. Can. Pet. Geol. 2006, 54, 238–260. [Google Scholar] [CrossRef]
- Cheung, K.; Klassen, P.; Mayer, B.; Goodarzi, F.; Aravena, R. Major Ion and Isotope Geochemistry of Fluids and Gases from Coalbed Methane and Shallow Groundwater Wells in Alberta, Canada. Appl. Geochem. 2010, 25, 1307–1329. [Google Scholar] [CrossRef]
- (HCL) Hydrogeological Consultants Ltd. R Well Addendum; pp. 1–2.
- (HCL) Hydrogeological Consultants Ltd. County of Barrhead No. 11 Parts of the Pembina and Athabasca River Basins; W5M Regional Groundwater Assessment; Agriculture and Agri-Food Canada and the Prairie Farm Rehabilitation Administration: Ottawa, ON, Canada, 1999; Volume 1998.
- (HCL) Hydrogeological Consultants Ltd. County of Camrose No. 22; W5M Regional Groundwater Assessment; Agriculture and Agri-Food Canada and the Prairie Farm Rehabilitation Administration: Ottawa, ON, Canada, 2005.
- (HCL) Hydrogeological Consultants Ltd. Cardston County Part of the South Saskatchewan and Missouri River Basins PERMIT NUMBER P 385; W5M Regional Groundwater Assessment; Agriculture and Agri-Food Canada and the Prairie Farm Rehabilitation Administration: Ottawa, ON, Canada, 2003.
- (HCL) Hydrogeological Consultants Ltd. Clearwater County; W5M Regional Groundwater Assessment; Agriculture and Agri-Food Canada and the Prairie Farm Rehabilitation Administration: Ottawa, ON, Canada, 2004.
- (HCL) Hydrogeological Consultants Ltd. County of Minburn No. 27 Part of the North Saskatchewan River Basin PERMIT NUMBER: P 385; W5M Regional Groundwater Assessment; Agriculture and Agri-Food Canada and the Prairie Farm Rehabilitation Administration: Ottawa, ON, Canada, 1999.
- (HCL) Hydrogeological Consultants Ltd. Westlock County; W5M Regional Groundwater Assessment; Agriculture and Agri-Food Canada and the Prairie Farm Rehabilitation Administration: Ottawa, ON, Canada, 2000.
- (HCL) Hydrogeological Consultants Ltd. County of Wetaskiwin; W5M Regional Groundwater Assessment; Agriculture and Agri-Food Canada and the Prairie Farm Rehabilitation Administration: Ottawa, ON, Canada, 2008.
- (HCL) Hydrogeological Consultants Ltd. Wheatland County Part of the South Saskatchewan River Basin; W5M Regional Groundwater Assessment; Agriculture and Agri-Food Canada and the Prairie Farm Rehabilitation Administration: Ottawa, ON, Canada, 2003.
- (HCL) Hydrogeological Consultants Ltd. County of Vermilion River No. 24—Part of the North Saskatchewan and Battle River Basins—Regional Groundwater Assessment; W5M Regional Groundwater Assessment; Agriculture and Agri-Food Canada and the Prairie Farm Rehabilitation Administration: Ottawa, ON, Canada, 1999.
- (HCL) Hydrogeological Consultants Ltd. County of Two Hills No. 21 Part of the North Saskatchewan River Basin PERMIT NUMBER: P 385; W5M Regional Groundwater Assessment; Agriculture and Agri-Food Canada and the Prairie Farm Rehabilitation Administration: Ottawa, ON, Canada, 1999; ISBN 1800661797.
- (HCL) Hydrogeological Consultants Ltd. M.D. of Provost No. 52 Part of the Battle River Basin PERMIT NUMBER: P 385; W5M Regional Groundwater Assessment; Agriculture and Agri-Food Canada and the Prairie Farm Rehabilitation Administration: Ottawa, ON, Canada, 1999.
- (HCL) Hydrogeological Consultants Ltd. County of Forty Mile No. 8; W5M Regional Groundwater Assessment; Agriculture and Agri-Food Canada and the Prairie Farm Rehabilitation Administration: Ottawa, ON, Canada, 2004.
- (HCL) Hydrogeological Consultants Ltd. County of Athabasca No. 12 Part of the Athabasca River Basin PERMIT NUMBER P 385; W5M Regional Groundwater Assessment; Agriculture and Agri-Food Canada and the Prairie Farm Rehabilitation Administration: Ottawa, ON, Canada, 2000; ISBN 1800661797.
- (HCL) Hydrogeological Consultants Ltd. County of Stettler No. 6 Part of the Red Deer River and Battle River Basins PERMIT NUMBER: P 385; W5M Regional Groundwater Assessment; Agriculture and Agri-Food Canada and the Prairie Farm Rehabilitation Administration: Ottawa, ON, Canada, 1999.
- Van Everdingen, R.O. Influence of the South Saskatchewan Reservoir (Canada) on Piezometric Levels in Underlying Bedrock Aquifers. J. Hydrol. 1967, 5, 351–359. [Google Scholar] [CrossRef]
- Maathuis, H. Conceptual Aquifers Management Framework Study. In SRC Publication No. 12092-1C07; SRC: SK, Canada, 2007; p. 28. [Google Scholar]
- De La Varga, M.; Schaaf, A.; Wellmann, F. GemPy 1.0: Open-Source Stochastic Geological Modeling and Inversion. Geosci. Model Dev. 2019, 12, 1–32. [Google Scholar] [CrossRef] [Green Version]
- Schlosser, P.; Stute, M.; Sonntag, C.; Otto Münnich, K. Tritiogenic 3He in Shallow Groundwater. Earth Planet. Sci. Lett. 1989, 94, 245–256. [Google Scholar] [CrossRef]
- Struckmeier, W.F.; Margat, J. Hydrogeological Maps: A Guide and a Standard Legend. In International Contributions to Hydrogeology; Heise: Hannover, Germany, 1995; Volume 17, ISBN 3922705987. [Google Scholar]
- Tørvi, H.; Hertzberg, T. Estimation of Uncertainty in Dynamic Simulation Results. Comput. Chem. Eng. 1997, 21, 3–7. [Google Scholar] [CrossRef]
- Alkhatib, J.; Engelhardt, I.; Ribbe, L.; Sauter, M. An Integrated Approach for Choosing Suitable Pumping Strategies for a Semi-Arid Region in Jordan Using a Groundwater Model Coupled with Analytical Hierarchy Techniques. Hydrogeol. J. 2019, 27, 1143–1157. [Google Scholar] [CrossRef]
- Green, T.R.; Taniguchi, M.; Kooi, H. Potential Impacts of Climate Change and Human Activity on Subsurface Water Resources. Vadose Zone J. 2007, 6, 531. [Google Scholar] [CrossRef] [Green Version]
- D’Affonseca, F.M.; Finkel, M.; Cirpka, O.A. Combining Implicit Geological Modeling, Field Surveys, and Hydrogeological Modeling to Describe Groundwater Flow in a Karst Aquifer. Hydrogeol. J. 2020, 28, 2779–2802. [Google Scholar] [CrossRef]
- Hamdi, M.; Zagrarni, M.F.; Djamai, N.; Jerbi, H.; Goita, K.; Tarhouni, J. 3D Geological Modeling for Complex Aquifer System Conception and Groundwater Storage Assessment: Case of Sisseb El Alem Nadhour Saouaf Basin, Northeastern Tunisia. J. Afr. Earth Sci. 2018, 143, 178–186. [Google Scholar] [CrossRef]
- Purvis, K.; Kao, J.; Flanagan, K.; Henderson, J.; Duranti, D. Complex Reservoir Geometries in a Deep Water Clastic Sequence, Gryphon Field, UKCS: Injection Structures, Geological Modelling and Reservoir Simulation. Mar. Pet. Geol. 2002, 19, 161–179. [Google Scholar] [CrossRef]
- Sood, A.; Smakhtin, V. Revue Des Modèles Hydrologiques Globaux. Hydrol. Sci. J. 2015, 60, 549–565. [Google Scholar] [CrossRef]
- Harvey, J.; Gomez-Velez, J.; Schmadel, N.; Scott, D.; Boyer, E.; Alexander, R.; Eng, K.; Golden, H.; Kettner, A.; Konrad, C.; et al. How Hydrologic Connectivity Regulates Water Quality in River Corridors. J. Am. Water Resour. Assoc. 2019, 55, 369–381. [Google Scholar] [CrossRef]
- Massuel, S.; Riaux, J.; Molle, F.; Kuper, M.; Ogilvie, A.; Collard, A.L.; Leduc, C.; Barreteau, O. Inspiring a Broader Socio-Hydrological Negotiation Approach With Interdisciplinary Field-Based Experience. Water Resour. Res. 2018, 54, 2510–2522. [Google Scholar] [CrossRef] [Green Version]
- Sophocleous, M. Interactions between Groundwater and Surface Water: The State of the Science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Arabameri, A.; Saha, S.; Roy, J.; Tiefenbacher, J.P.; Cerda, A.; Biggs, T.; Pradhan, B.; Thi Ngo, P.T.; Collins, A.L. A Novel Ensemble Computational Intelligence Approach for the Spatial Prediction of Land Subsidence Susceptibility. Sci. Total Environ. 2020, 726, 138595. [Google Scholar] [CrossRef] [PubMed]
- Prasad, A.M.; Iverson, L.R.; Liaw, A. Newer Classification and Regression Tree Techniques: Bagging and Random Forests for Ecological Prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
- Chen, W.; Hong, H.; Li, S.; Shahabi, H.; Wang, Y.; Wang, X.; Ahmad, B. Bin Flood Susceptibility Modelling Using Novel Hybrid Approach of Reduced-Error Pruning Trees with Bagging and Random Subspace Ensembles. J. Hydrol. 2019, 575, 864–873. [Google Scholar] [CrossRef]





| Category | Data Type | Description |
|---|---|---|
| Climate | Precipitation | Daily measurements at 13 rainfall stations (1950–2020) Source: Government of Canada, historical climate data |
| Temperature | Minimum, maximum, and mean temperatures (1950–2020) Source: Government of Canada, historical climate data, https://climate.weather.gc.ca/historical_data/search_historic_data_e.html | |
| Evapotranspiration | A map of average annual potential evapotranspiration (PET) from soil and plant surfaces in areas of continuous ground cover and sufficient soil moisture for plant use Source: Government of Canada (Natural Resources Canada) | |
| Wind | Daily wind speed and direction from 1959 to the present Source: Government of Canada, historical climate data, https://climate.weather.gc.ca/historical_data/search_historic_data_e.html | |
| Relative humidity | Percentage values from 1959 to the present Source: Government of Canada, historical climate data, https://climate.weather.gc.ca/historical_data/search_historic_data_e.html | |
| Sunshine | Hours and duration of sunshine from 1950 to the present Source: Government of Canada, historical climate data, https://climate.weather.gc.ca/historical_data/search_historic_data_e.html | |
| Hydrogeology | Hydraulic wells | Structure, lithology, and hydrodynamic parameters Data (lithological sections and logs) and hydraulic soundings Pump tests conducted on public and private water wells Source 1 (Alberta): Alberta Water Well Information Database, https://www.alberta.ca/alberta-water-well-information-database.aspx Source 2 (Saskatchewan): Water Security Agency, Saskatchewan, https://www.wsask.ca/water-info/ground-water/observation-well-network/ Source 3 (Manitoba): The Groundwater Management Section, Manitoba https://www.gov.mb.ca/water/groundwater/wells_groundwater/index.html |
| Piezometric histories for several monitoring points Source 1 (Alberta): Groundwater Observation Well Network, Alberta, https://www.alberta.ca/lookup/groundwater-observation-well-network.aspx Source 2 (Saskatchewan): Water Security Agency, Saskatchewan, https://www.wsask.ca/water-info/ground-water/observation-well-network/ Source 3 (Manitoba): data are not available | ||
| Surface water | Gauging in control sections: water level and daily, monthly, and annual flow Their characteristics (conductance, topography, etc.) Common source for the three provinces: Explorateur de données d’Environnement et Changement Climatique Canada, base de données HYDAT, https://www.canada.ca/fr/environnement-changement-climatique/services/eau-apercu/volume/surveillance/releves/produits-donnees-services/archives-nationales-hydat.html Common source for the three provinces: Historical Hydrometric Data Search, https://wateroffice.ec.gc.ca/search/historical_e.html | |
| Geology | 1:250,000 geological maps that have been digitized and which include the following attributes: Geological units Formations Faults Outcrop lithology Coefficient of permeability Common source for the three provinces: GEOSCAN (Geological Survey of Canada (GSC)) Publications Database, https://geoscan.nrcan.gc.ca/starweb/geoscan/servlet.starweb?path=geoscan/geoscan_f.web | |
| Geophysical data | Results of geophysical campaigns in several sectors of the provinces Common source for the three provinces: Natural Resources Canada (NRC), http://gdr.agg.nrcan.gc.ca/gdrdap/dap/index-fra.php?db_project_no=429&db_project_part=1;2;3 | |
| Pedology | Soil unit (Soil type, rock, type of rock, saline load, texture, etc.) Common source for the three provinces: Canadian Soil Information Service (CanSIS), Government of Canada, https://sis.agr.gc.ca/siscan/nsdb/slc/index.html | |
| Gas and oil wells | Header Drill/Summary Geology of the well | Licensee, status, fluid (water or gas), type (exploitation or injection), depths, location Casing, types of cement, completion summary Stratigraphic log: depths and formation Common source for the three provinces: Petro Ninja Maps, https://petroninja.com/ |
| Archived data: scientific articles, internal reports, theses, dissertations | Scientific articles Internal reports | [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60] |
| Nodes (Opt) | ||
|---|---|---|
| 1 | 0 | 1 |
| 2 | −1, +1 | ½, ½ |
| 3 | 1/6, 2/3, 1/6 |
| Formation | Mathematical Variogram Model | Correlation Coefficient | Anisotropy Ratio | Nugget | Relative Sill | Major Axis Direction | Minor Axis Direction | Major Axis Range | Minor Axis Range |
|---|---|---|---|---|---|---|---|---|---|
| Paskapoo Formation | Gaussian without nugget | 0.91 | 0.84 | 0 | 4914 | 4.6 | 94.6 | 170,835 | 143,854 |
| Horseshoe Canyon Formation | Gaussian without nugget | 0.92 | 0.9 | 0 | 3787.9 | 176.1 | 86.1 | 172,975 | 156,145 |
| Bearpaw Formation | Gaussian without nugget | 0.94 | 0.95 | 0 | 2918 | 9.9 | 99.9 | 176,416 | 171,074 |
| Oldman Formation | Gaussian without nugget | 0.95 | 0.81 | 0 | 2490 | 177.1 | 87.1 | 188,086 | 153,192 |
| Foremost Formation | Exponential without nugget | 0.93 | 0.79 | 0 | 4027 | 1.1 | 91.1 | 182,141 | 143,957.2 |
| Lea Park Formation | Exponential without nugget | 0.89 | 0.55 | 0 | 16,977 | 2 | 92 | 189,186 | 103,874 |
| Milk River Formation | Exponential without nugget | 0.92 | 0.5 | 0 | 11,669 | 0.2 | 90.2 | 252,468 | 125,141 |
| Colorado Formation | Exponential without nugget | 0.93 | 0.79 | 0 | 4027 | 1.1 | 91.1 | 182,141 | 143,957 |
| Mannville Formation | Exponential with nugget | 0.89 | 0.44 | 0 | 6645 | 1.9 | 91.9 | 21,959 | 95,779 |
| Devonian Formation | Exponential without nugget | 0.86 | 0.52 | 237 | 6027 | 0.7 | 90.6 | 23,145 | 100,584 |
| Cambrian Formation | Exponential without nugget | 0.94 | 0.76 | 0 | 2910 | 0.1 | 90.1 | 183,626 | 140,234 |
| Precambrian Formation | Exponential without nugget | 0.92 | 0.5 | 0 | 11,669 | 0.2 | 90.2 | 252,468 | 125,141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamdi, M.; Goïta, K. Estimation of Aquifer Storativity Using 3D Geological Modeling and the Spatial Random Bagging Simulation Method: The Saskatchewan River Basin Case Study (Central Canada). Water 2023, 15, 1156. https://doi.org/10.3390/w15061156
Hamdi M, Goïta K. Estimation of Aquifer Storativity Using 3D Geological Modeling and the Spatial Random Bagging Simulation Method: The Saskatchewan River Basin Case Study (Central Canada). Water. 2023; 15(6):1156. https://doi.org/10.3390/w15061156
Chicago/Turabian StyleHamdi, Mohamed, and Kalifa Goïta. 2023. "Estimation of Aquifer Storativity Using 3D Geological Modeling and the Spatial Random Bagging Simulation Method: The Saskatchewan River Basin Case Study (Central Canada)" Water 15, no. 6: 1156. https://doi.org/10.3390/w15061156
APA StyleHamdi, M., & Goïta, K. (2023). Estimation of Aquifer Storativity Using 3D Geological Modeling and the Spatial Random Bagging Simulation Method: The Saskatchewan River Basin Case Study (Central Canada). Water, 15(6), 1156. https://doi.org/10.3390/w15061156







