Data-Driven Parameter Prediction of Water Pumping Station
Abstract
:1. Introduction
- (1)
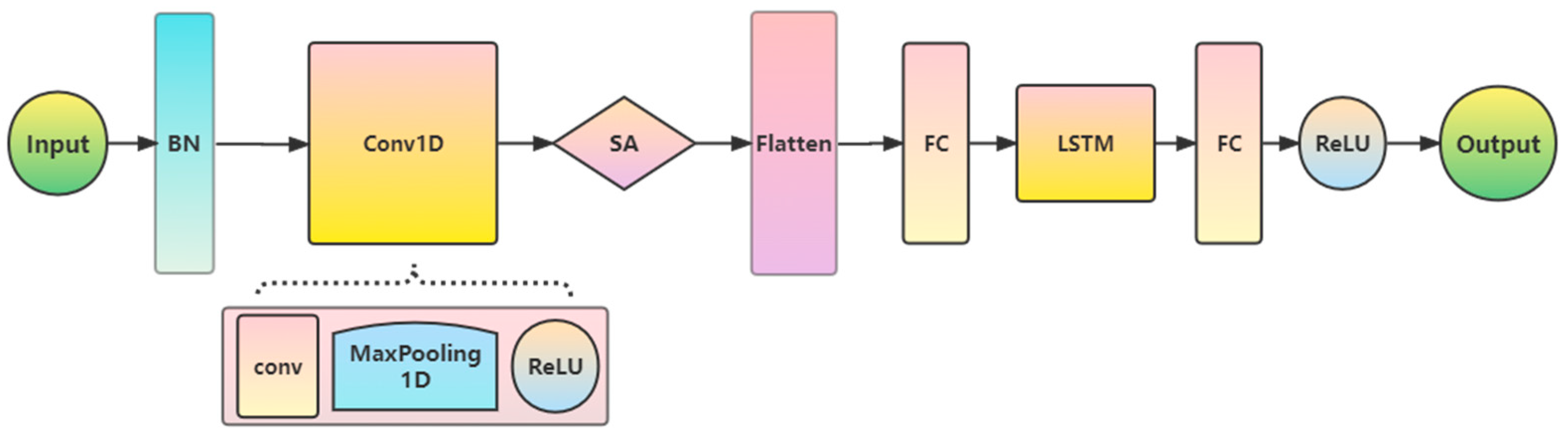
- A coupled CNN–LSTM deep neural network model is established for pumping station water level prediction, in which the CNN can extract the relationship between many features of the pumping station and an LSTM can also capture time series information with high prediction accuracy.
- (2)
- The self-attention mechanism (SA) is used to optimize the CNN, so that the model can better analyze the feature information contained in the vector, and further sort the feature importance. Finally, the bagging method is used to improve the accuracy and stability of the prediction results, making the model more robust.
- (3)
- Compare the model with the traditional machine learning algorithm support vector regression (SVR), a separate CNN, and a separate LSTM to prove its feasibility and superiority. Although the studies described above explored the ability of these methods to predict water level parameters, no studies compared their performance. Furthermore, to the best of the authors’ knowledge, this is the first time that a coupled CNN–LSTM model has been used to predict water level issues in pumping station projects.
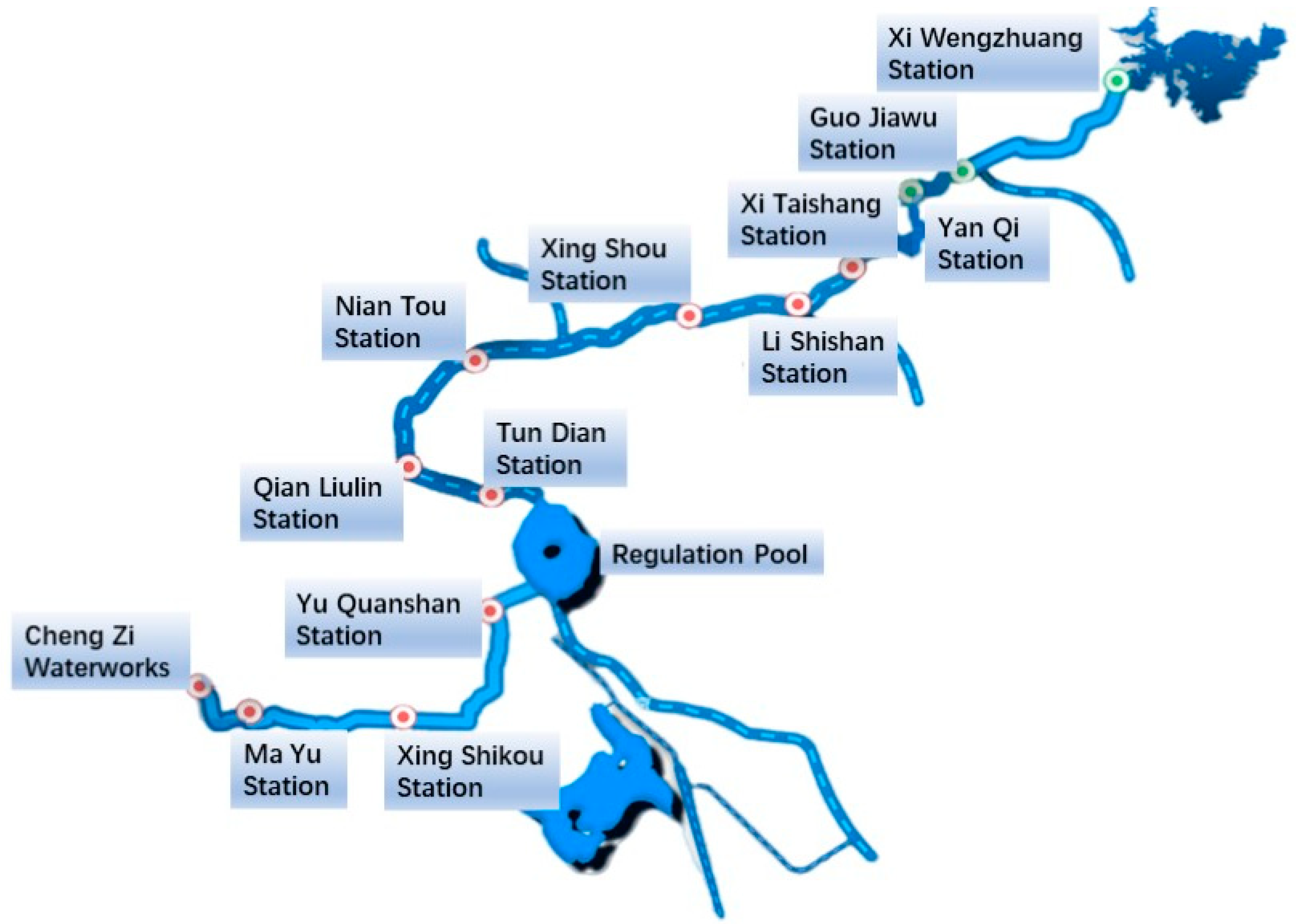
2. Data
3. Methodology
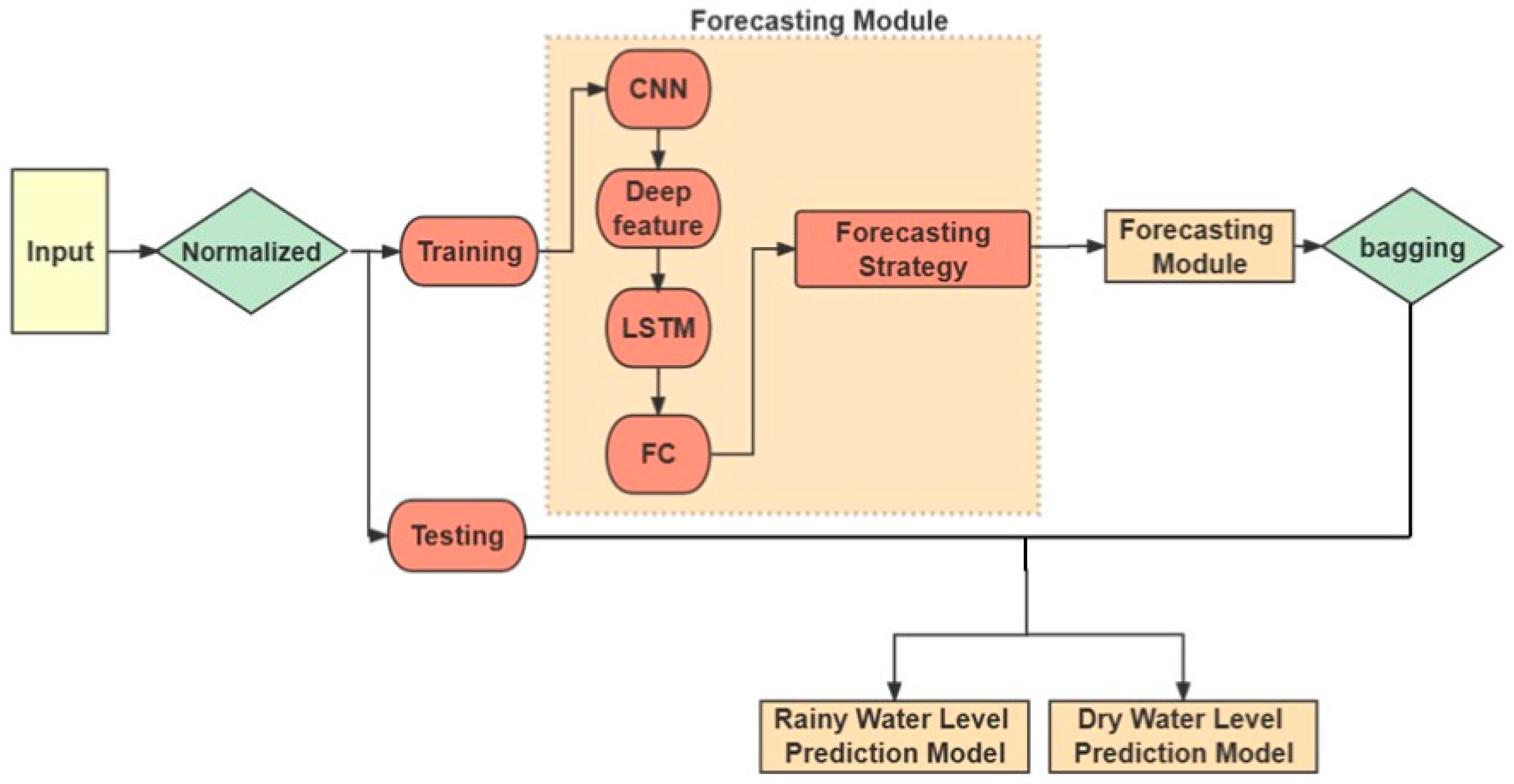
3.1. Forecasting Strategy
3.2. Convolutional Neural Network (CNN)
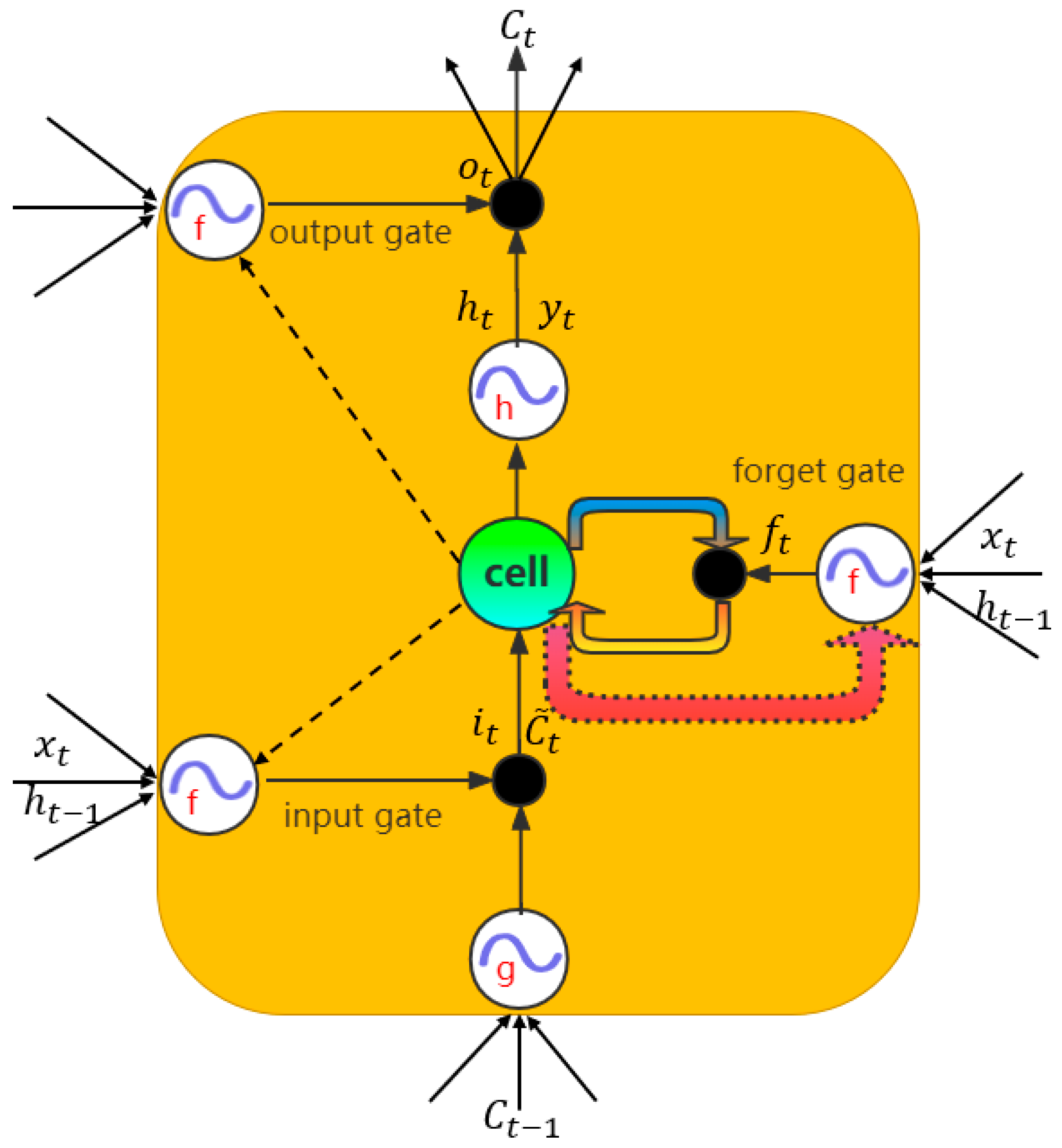
3.3. Long Short-Term Memory (LSTM)
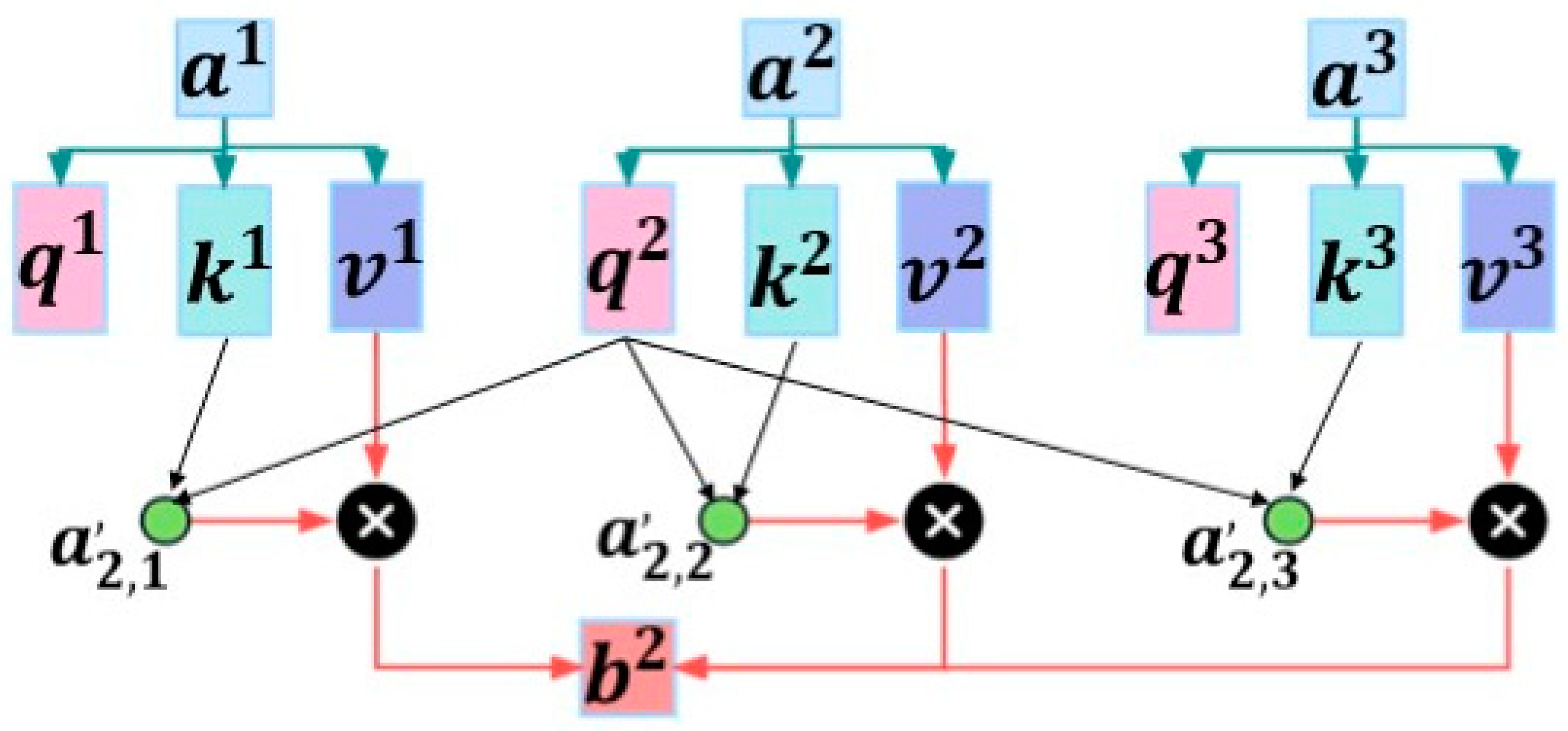
3.4. Self-Attention Mechanism
3.5. CNN–LSTM Principle Based on Self-Attention Mechanism
3.6. Bagging Strategy
4. Model Evaluations
5. Results
5.1. Hyperparameter Configuration
5.2. Feature Selection Results
5.3. Comparison of Model Prediction Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, L.B.; Tian, Y.; Lei, X.H.; Wang, H.; Qin, T.; Zhang, Z. Numerical analysis of the hydraulic transient process of the water delivery system of cascade pump stations. Water Sci. Technol. 2018, 18, 1635–1649. [Google Scholar] [CrossRef]
- Xu, W.; Chen, C. Optimization of Operation Strategies for an Interbasin Water Diversion System Using an Aggregation Model and Improved NSGA-II Algorithm. J. Irrig. Drain. Eng. 2020, 146, 04020006. [Google Scholar] [CrossRef]
- Lei, X.; Tian, Y.; Zhang, Z.; Wang, L.; Xiang, X.; Wang, H. Correction of pumping station parameters in a one-dimensional hydrodynamic model using the Ensemble Kalman filter. J. Hydrol. 2019, 568, 108–118. [Google Scholar] [CrossRef]
- Munar, A.M.C.J. Coupling large-scale hydrological and hydrodynamic modeling: Toward a better comprehension of watershed-shallow lake processes. J. Hydrol. 2018, 564, 424–441. [Google Scholar] [CrossRef]
- Siddique-E-Akbor, A.H.M.; Hossain, F.; Lee, H.; Shum, C.K. Inter-comparison study of water level estimates derived from hydrodynamic–hydrologic model and satellite altimetry for a complex deltaic environment. Remote Sens. Environ. 2011, 115, 1522–1531. [Google Scholar] [CrossRef]
- Timbadiya, P.V.; Krishnamraju, K.M. A 2D hydrodynamic model for river flood prediction in a coastal floodplain. Nat. Hazards 2022, 115, 1143–1165. [Google Scholar] [CrossRef]
- Yan, P.; Zhang, Z.; Hou, Q.; Lei, X.; Liu, Y.; Wang, H. A novel IBAS-ELM model for prediction of water levels in front of pumping stations. J. Hydrol. 2023, 616, 128810. [Google Scholar] [CrossRef]
- De Keyser, W.; Amerlinck, Y.; Urchegui, G.; Harding, T.; Maere, T.; Nopens, I. Detailed dynamic pumping energy models for optimization and control of wastewater applications. J. Water Clim. Chang. 2014, 5, 299–314. [Google Scholar] [CrossRef] [Green Version]
- Zhu, H.; Bo, G.; Zhou, Y.; Zhang, R.; Cheng, J. Performance prediction of pump and pumping system based on combination of numerical simulation and non-full passage model test. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Deng, B.; Lai, S.H.; Jiang, C.; Kumar, P.; El-Shafie, A.; Chin, R.J. Advanced water level prediction for a large-scale river–lake system using hybrid soft computing approach: A case study in Dongting Lake, China. Earth Sci. Inform. 2021, 14, 1987–2001. [Google Scholar] [CrossRef]
- Das, M.; Ghosh, S.K.; Chowdary, V.M.; Saikrishnaveni, A.; Sharma, R.K. A probabilistic nonlinear model for forecasting daily water level in reservoir. Water Resour. Manag. 2016, 30, 3107–3122. [Google Scholar] [CrossRef]
- Wei, C.; Hsu, N.; Huang, C. Two-stage pumping control model for flood mitigation in inundated urban drainage basins. Water Resour. Manag. 2014, 28, 425–444. [Google Scholar] [CrossRef]
- Liu, Z.; Cheng, L.; Lin, K.; Cai, H. A hybrid bayesian vine model for water level prediction. Environ. Model. Softw. 2021, 142, 105075. [Google Scholar] [CrossRef]
- Khan, M.S.; Coulibaly, P. Application of support vector machine in lake water level prediction. J. Hydrol. Eng. 2006, 11, 199–205. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, Z.; Li, F.; Chen, W. The prediction of water level based on support vector machine under construction condition of steel sheet pile cofferdam. Concurr. Comput. Pract. Exp. 2021, 33, e6003. [Google Scholar] [CrossRef]
- Tao, H.; Al-Bedyry, N.K.; Khedher, K.M.; Shahid, S.; Yaseen, Z.M. River Water Level Prediction in Coastal Catchment using hybridized relevance vector machine model with improved grasshopper optimization. J. Hydrol. 2021, 598, 126477. [Google Scholar] [CrossRef]
- Kaloop, M.R.; El-Diasty, M.; Hu, J.W. Real-time prediction of water level change using adaptive neuro-fuzzy inference system. Geomat. Nat. Hazards Risk 2017, 8, 1320–1332. [Google Scholar] [CrossRef] [Green Version]
- El-Diasty, M.; Al-Harbi, S.; Pagiatakis, S. Hybrid harmonic analysis and wavelet network model for sea water level prediction. Appl. Ocean. Res. 2018, 70, 14–21. [Google Scholar] [CrossRef]
- Luo, Y.; Dong, Z.; Liu, Y.; Wang, X.; Shi, Q.; Han, Y. Research on stage-divided water level prediction technology of rivers-connected lake based on machine learning: A case study of Hongze Lake, China. Stoch. Environ. Res. Risk Assess. 2021, 35, 2049–2065. [Google Scholar] [CrossRef]
- El-Diasty, M.; Al-Harbi, S. Development of wavelet network model for accurate water levels prediction with meteorological effects. Appl. Ocean Res. 2015, 53, 228–235. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Kartal, E. Performance comparison of continuous wavelet-fuzzy and discrete wavelet-fuzzy models for water level predictions at northern and southern boundary of Bosphorus. Ocean Eng. 2019, 186, 106097. [Google Scholar] [CrossRef]
- Altunkaynak, A. Predicting water level fluctuations in Lake Van using hybrid season-neuro approach. J. Hydrol. Eng. 2019, 24, 04019021. [Google Scholar] [CrossRef]
- Liu, W.C.; Chung, C.E. Enhancing the Predicting Accuracy of the Water Stage Using a Physical-Based Model and an Artificial Neural Network-Genetic Algorithm in a River System. Water 2014, 6, 1642–1661. [Google Scholar] [CrossRef] [Green Version]
- Hasan, A.N.; Twala, B. Mine’s pump station energy consumption and underground water dam levels monitoring system using machine learning classifiers and mutual information ensemble technique. Int. J. Innov. Comput. Inf. Control 2016, 12, 1777–1789. [Google Scholar]
- Bazartseren, B.; Hildebrandt, G.; Holz, K. Short-term water level prediction using neural networks and neuro-fuzzy approach. Neurocomputing 2003, 55, 439–450. [Google Scholar] [CrossRef]
- Chang, F.J.; Chen, P.A.; Lu, Y.R.; Huang, E.; Chang, K.Y. Real-time multi-step-ahead water level forecasting by recurrent neural networks for urban flood control. J. Hydrol. 2014, 517, 836–846. [Google Scholar] [CrossRef]
- Xiong, B.; Li, R.; Ren, D.; Liu, H.; Xu, T.; Huang, Y. Prediction of flooding in the downstream of the Three Gorges Reservoir based on a back propagation neural network optimized using the AdaBoost algorithm. Nat. Hazards 2021, 107, 1559–1575. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, H.; Yao, L.; Liu, Y.; Jiang, Z.; Feng, Z.; Ouyang, S.; Pei, S.; Zhou, J. Downstream water level prediction of reservoir based on convolutional neural network and long short-term memory network. J. Water Resour. Plan. Manag. 2021, 147, 04021060. [Google Scholar] [CrossRef]
- Ren, T.; Liu, X.; Niu, J.; Lei, X.; Zhang, Z. Real-time water level prediction of cascaded channels based on multilayer perception and recurrent neural network. J. Hydrol. 2020, 585, 124783. [Google Scholar] [CrossRef]
- Yuan, Z.; Liu, J.; Liu, Y.; Zhang, Q.; Li, Y.; Li, Z. A two-stage modelling method for multi-station daily water level prediction. Environ. Model. Softw. 2022, 156, 105468. [Google Scholar] [CrossRef]
- Han, H.; Morrison, R.R. Data-driven approaches for runoff prediction using distributed data. Stoch. Environ. Res. Risk Assess. 2021, 36, 2153–2171. [Google Scholar] [CrossRef]
- Wang, B.; Liu, S.; Wang, B.; Wu, W.; Wang, J.; Shen, D. Multi-step ahead short-term predictions of storm surge level using CNN and LSTM network. Acta Oceanol. Sin. 2021, 40, 104–118. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Short-term water quality variable prediction using a hybrid CNN–LSTM deep learning model. Stoch. Environ. Res. Risk Assess. 2020, 34, 415–433. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Z. A CNN-LSTM Model Based on a Meta-Learning Algorithm to Predict Groundwater Level in the Middle and Lower Reaches of the Heihe River, China. Water 2022, 14, 2377. [Google Scholar] [CrossRef]
- Zha, W.; Li, X.; Xing, Y.; He, L.; Li, D. Networks with gradient penalty. Adv. Geo-Energy Res. 2020, 4, 107–114. [Google Scholar] [CrossRef]
- Zha, W.; Gao, S.; Li, D.; Chen, K. Application of the ensemble Kalman filter for assisted layered history matching. Adv. Geo-Energy Res. 2018, 2, 450–456. [Google Scholar] [CrossRef] [Green Version]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent Advances in Convolutional Neural Networks. Pattern Recognit. 2015. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 2012, 25. [Google Scholar] [CrossRef] [Green Version]
- Yin, C.; Zhang, S.; Wang, J.; Xiong, N.N. Anomaly detection based on convolutional recurrent autoencoder for IoT time series. IEEE Trans. Syst. Man Cybern. Syst. 2020, 52, 112–122. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhang, S.; Zhang, W.; Peng, J.; Cai, Y. Multifactor spatio-temporal correlation model based on a combination of convolutional neural network and long short-term memory neural network for wind speed forecasting. Energy Convers. Manag. 2019, 185, 783–799. [Google Scholar] [CrossRef]







| Feature Name | Description | Unit |
|---|---|---|
| SAMP_TIME | Samping time | s |
| START_TIME | Startup time | s |
| VOLTAGE | Voltage | V |
| CURRENT | Current | A |
| IPB_ANGLE | Inlet pump blade angle | ° |
| PIPE_PRESS | Pipeline pressure | Mpa |
| PUMP_FERQ | Pump frequency | Hz |
| RUN_NUM | Number Of runs | 1 |
| RUN_TIME | This run time | 1 |
| CUM_RUN_TIME | Cumulative run time | 1 |
| CUM_FLOW | Cumulative flow | m3/s |
| RE_CUM_FLOW | Reverse cumulative flow | m3/s |
| ACT_POWER | Active power | kw |
| REACT_POWER | Reactive power | kw |
| UNIT_VIB | Unit vibration | μm |
| UNIT_SWING | Unit swing | mm |
| OUT_PRESS | Outlet pressure | Mpa |
| PUMP_SPEED | Pump speed | rpm |
| INLET_WL | Inlet water level | m |
| FORE_WL | Fore pool water level | m |
| REAR_WL | Rear pool water level | m |
| Model | Parameter | Details | Value |
|---|---|---|---|
| CNN, LSTM, CNN-LSTM | Minibatch | Batch size | 128 |
| Epoch | 1000 | ||
| L2 regularization | Penalty parameters | 0.01 | |
| Decayed learning rate | Initial learning rate | 0.01 | |
| Decay rate | 0.9 | ||
| Decay steps | 15 | ||
| Minimum learning rate | 1.00 × 10−4 | ||
| Dropout | Dropout rate | 0.001 | |
| SVR | Grid search | Kernel function | RBF |
| C | 1 | ||
| Gamma | 0.1 | ||
| Cross-validation | k-fold | 5 |
| Machine Learning Model | Neural Network Model | |||
|---|---|---|---|---|
| Indicator | SVR | CNN | LSTM | CNN-LSTM |
| MAE | 31.02 | 29.37 | 25.67 | 19.14 |
| R2 | 0.30 | 0.34 | 0.45 | 0.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Yu, Y.; Yan, J.; Chen, J. Data-Driven Parameter Prediction of Water Pumping Station. Water 2023, 15, 1128. https://doi.org/10.3390/w15061128
Zhang J, Yu Y, Yan J, Chen J. Data-Driven Parameter Prediction of Water Pumping Station. Water. 2023; 15(6):1128. https://doi.org/10.3390/w15061128
Chicago/Turabian StyleZhang, Jun, Yongchuan Yu, Jianzhuo Yan, and Jianhui Chen. 2023. "Data-Driven Parameter Prediction of Water Pumping Station" Water 15, no. 6: 1128. https://doi.org/10.3390/w15061128





