An Expanded Interpretive Structural Modeling Analysis of the Barriers to Integrated Flood Risk Management Adaptation in Metro Manila
Abstract
:1. Introduction
2. Materials and Methods
2.1. Barriers to IFRM Adaptation in Metro Manila
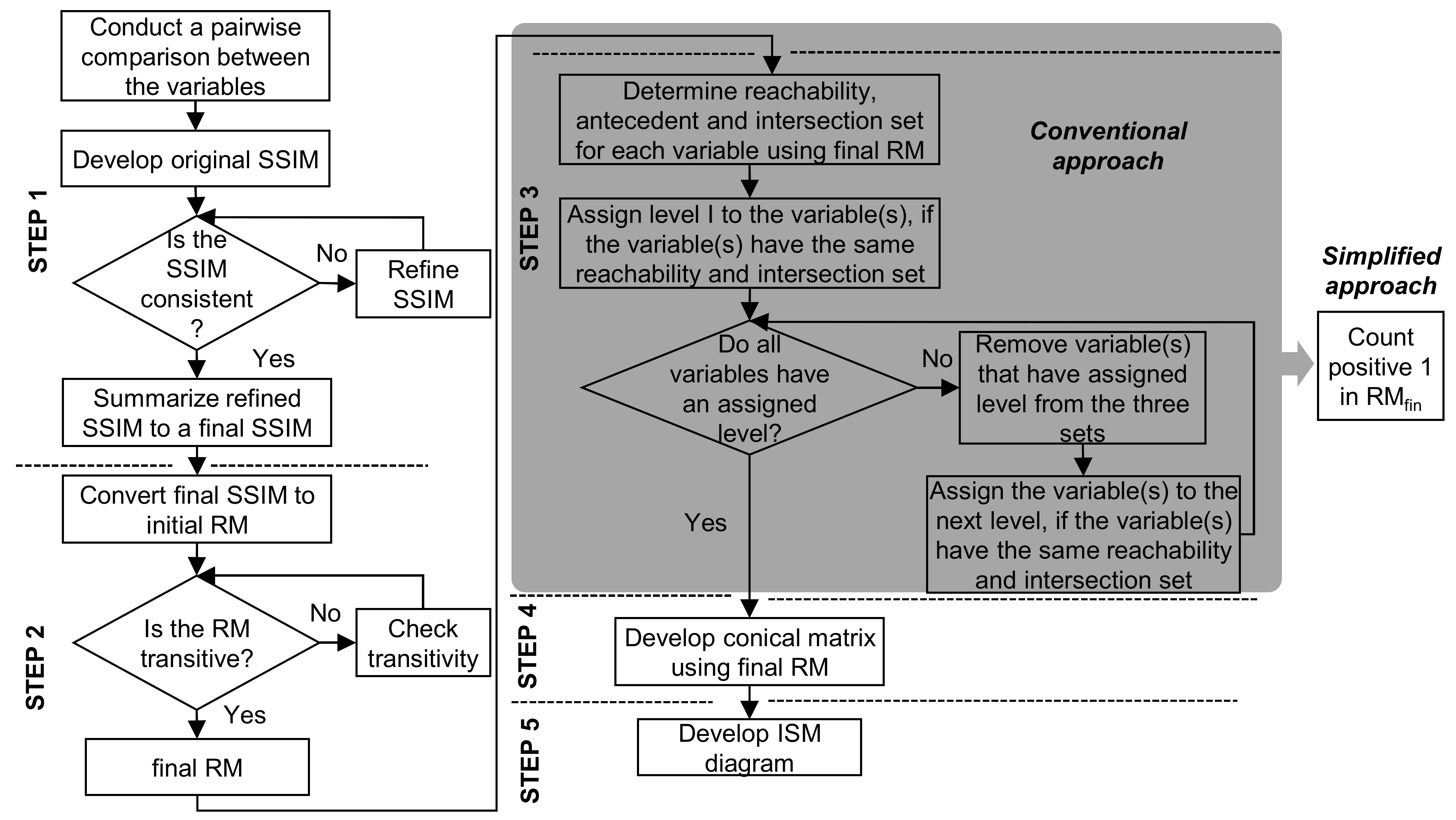
2.2. Expanded Interpretive Structural Modeling (Ex-ISM)
2.2.1. Step 1—Developing a Structural Self-Interaction Matrix (SSIM)
- The letter “V” is replaced with the symbol “+”, which denotes that variable i influences variable j and j does not influence i.
- The letter “A” is replaced with “-”, which denotes that variable i is influenced by variable j and j is not influenced by i.
- The letter “X” is replaced with the symbol “±” or “∓”, which means that variable i and variable j influence each other.
- The letter “O” is replaced with the symbol “0”, which means that variable i and variable j are independent of one another.
- To fill up the lower triangular half of the SSIM, the corresponding passive pairwise comparison SSIM(j, i) of the active SSIM(i, j) is filled with the corresponding passive symbolism, i.e., if SSIM(i, j) = + or −, then SSIM(j, i)= − or +.
2.2.2. Step 2—Developing a Reachability Matrix (RM)
- If SSIM(i, j) = V, then RMinit(i, j) = 1 and RMinit(j, i) = 0.
- If SSIM(i, j) = A, then RMinit(i, j) = 0 and RMinit(j, i) = 1.
- If SSIM(i, j) = X, then RMinit(i, j) = 1 and RMinit(j, i) = 1.
- If SSIM(i, j) = O, then RMinit(i, j) = 0 and RMinit(j, i) = 0.
- For the diagonal element SSIM(i, i), RMinit(i, i) = 1.
- If the SSIM(i, j) is “+”, then RMinit(i, j) is 1 and RMinit(j, i) is −1.
- If the SSIM(i, j) is “−”, then RMinit(i, j) is −1 and RMinit(j, i) is 1.
- If the SSIM(i, j) is “±” or “∓”, then RMinit(i, j) is ±1 or ∓1.
- If the SSIM(i, j) is “0”, then RMinit(i, j) is 0.
- For the blank diagonal element SSIM(i, i), RMinit(i, i) = ±1.
- If RMinit(i, j) has a positive sign, then +RMinit(i, j) = 1; otherwise +RMinit(i, j) = 0.
- If RMinit(i, j) has a negative sign, then −RMinit(i, j) = −1; otherwise −RMinit(i, j) = 0.
2.2.3. Step 3—Assigning Levels for Each Variable
2.2.4. Step 4—Developing a Conical Matrix (CM)
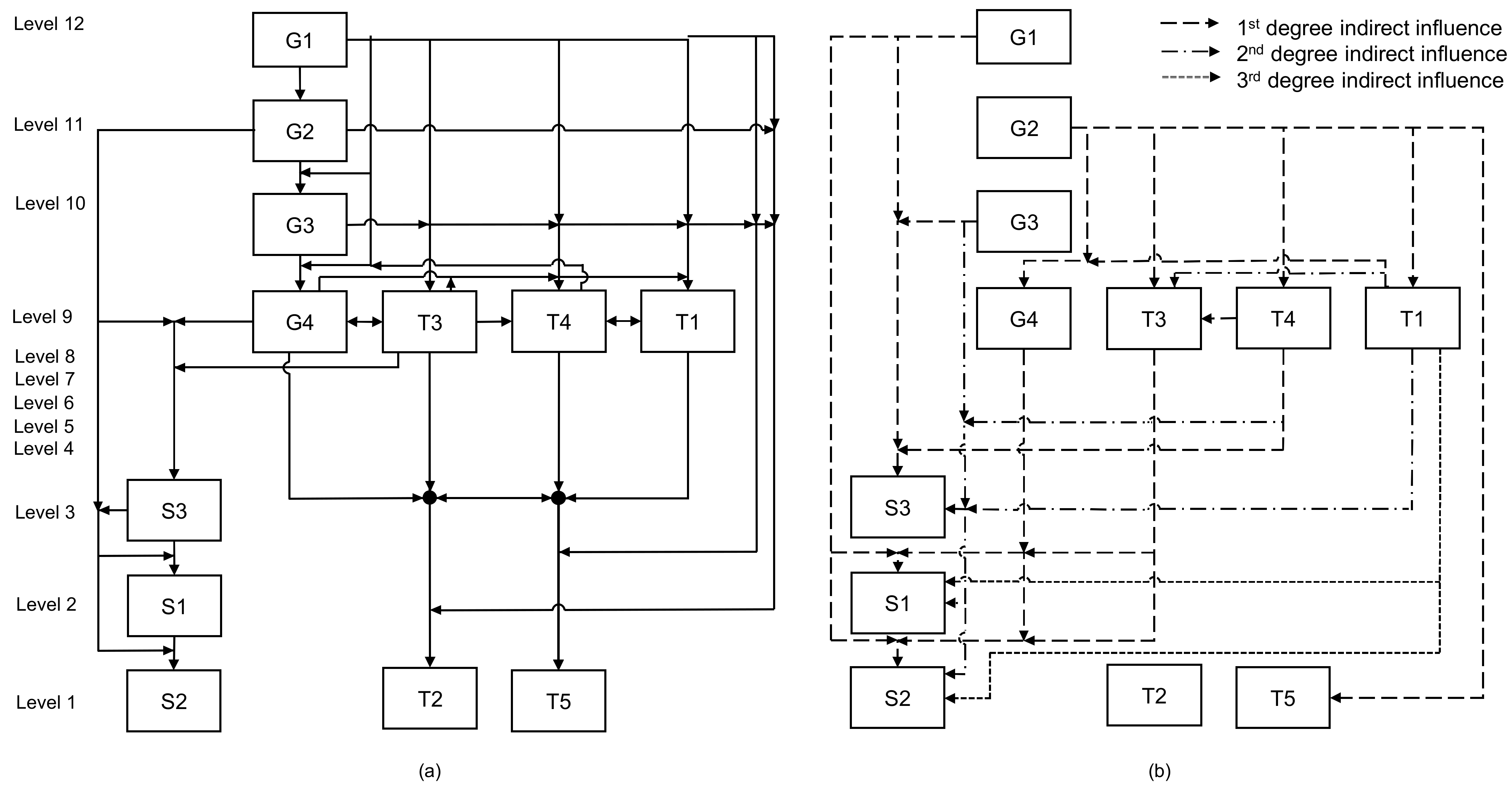
2.2.5. Step 5—Developing the ISM Diagram
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| i | j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Barrier | G1 | G2 | G3 | G4 | S1 | S2 | S3 | T1 | T2 | T3 | T4 | T5 | |
| 1 | G1 | V | V | V | O | O | O | V | V | V | V | V | |
| 2 | G2 | V | O | V | V | V | O | V | O | O | O | ||
| 3 | G3 | V | O | O | O | V | V | V | V | V | |||
| 4 | G4 | O | O | V | V | V | X | X | V | ||||
| 5 | S1 | V | A | O | O | O | O | O | |||||
| 6 | S2 | A | O | O | O | O | O | ||||||
| 7 | S3 | O | O | A | O | O | |||||||
| 8 | T1 | V | A | X | V | ||||||||
| 9 | T2 | A | A | O | |||||||||
| 10 | T3 | V | V | ||||||||||
| 11 | T4 | V | |||||||||||
| 12 | T5 |
| i | j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Barrier | G1 | G2 | G3 | G4 | S1 | S2 | S3 | T1 | T2 | T3 | T4 | T5 | |
| 1 | G1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 2 | G2 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 3 | G3 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 4 | G4 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 5 | S1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | S2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | S3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 8 | T1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 9 | T2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 10 | T3 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 11 | T4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 12 | T5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| i | j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Barrier | G1 | G2 | G3 | G4 | S1 | S2 | S3 | T1 | T2 | T3 | T4 | T5 | |
| 1 | G1 | 1 | 1 | 1 | 1 | 1 * | 1 * | 1 * | 1 | 1 | 1 | 1 | 1 |
| 2 | G2 | 0 | 1 | 1 | 1 * | 1 | 1 | 1 | 1 * | 1 | 1 * | 1 * | 1 * |
| 3 | G3 | 0 | 0 | 1 | 1 | 1 * | 1 * | 1 * | 1 | 1 | 1 | 1 | 1 |
| 4 | G4 | 0 | 0 | 0 | 1 | 1 * | 1 * | 1 | 1 | 1 | 1 | 1 | 1 |
| 5 | S1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | S2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | S3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 8 | T1 | 0 | 0 | 0 | 1 * | 1 * | 1 * | 1 * | 1 | 1 | 1 * | 1 | 1 |
| 9 | T2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 10 | T3 | 0 | 0 | 0 | 1 | 1 * | 1 * | 1 | 1 | 1 | 1 | 1 | 1 |
| 11 | T4 | 0 | 0 | 0 | 1 | 1 * | 1 * | 1 * | 1 | 1 | 1 * | 1 | 1 |
| 12 | T5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Barrier | Reachability Set | Antecedent Set | Intersection Set | Level |
|---|---|---|---|---|
| 1 | 1.2.3.4.5.6.7.8.9.10.11.12 | 1 | 1 | |
| 2 | 2.3.4.5.6.7.8.9.10.11.12 | 1.2 | 2 | |
| 3 | 3.4.5.6.7.8.9.10.11.12 | 1.2.3 | 3 | |
| 4 | 4.5.6.7.8.9.10.11.12 | 1.2.3.4.8.10.11 | 4.8.10.11 | |
| 5 | 5.6 | 1.2.3.4.5.7.8.10.11 | 5 | |
| 6 | 6 | 1.2.3.4.5.6.7.8.10.11 | 6 | I |
| 7 | 5.6.7 | 1.2.3.4.7.8.10.11 | 7 | |
| 8 | 4.5.6.7.8.9.10.11.12 | 1.2.3.4.8.10.11 | 4.8.10.11 | |
| 9 | 9 | 1.2.3.4.8.9.10.11 | 9 | I |
| 10 | 4.5.6.7.8.9.10.11.12 | 1.2.3.4.8.10.11 | 4.8.10.11 | |
| 11 | 4.5.6.7.8.9.10.11.12 | 1.2.3.4.8.10.11 | 4.8.10.11 | |
| 12 | 12 | 1.2.3.4.8.10.11.12 | 12 | I |
| Barrier | Reachability Set | Antecedent Set | Intersection Set | Level |
|---|---|---|---|---|
| 1 | 1.2.3.4.5.7.8.10.11 | 1 | 1 | |
| 2 | 2.3.4.5.7.8.10.11 | 1.2 | 2 | |
| 3 | 3.4.5.7.8.10.11 | 1.2.3 | 3 | |
| 4 | 4.5.7.8.10.11 | 1.2.3.4.8.10.11 | 4.8.10.11 | |
| 5 | 5 | 1.2.3.4.5.7.8.10.11 | 5 | II |
| 7 | 5.7 | 1.2.3.4.7.8.10.11 | 7 | |
| 8 | 4.5.7.8.10.11 | 1.2.3.4.8.10.11 | 4.8.10.11 | |
| 10 | 4.5.7.8.10.11 | 1.2.3.4.8.10.11 | 4.8.10.11 | |
| 11 | 4.5.7.8.10.11 | 1.2.3.4.8.10.11 | 4.8.10.11 |
| Barrier | Reachability Set | Antecedent Set | Intersection Set | Level |
|---|---|---|---|---|
| 1 | 1.2.3.4.7.8.10.11 | 1 | 1 | |
| 2 | 2.3.4.7.8.10.11 | 1.2 | 2 | |
| 3 | 3.4.7.8.10.11 | 1.2.3 | 3 | |
| 4 | 4.7.8.10.11 | 1.2.3.4.8.10.11 | 4.8.10.11 | |
| 7 | 7 | 1.2.3.4.7.8.10.11 | 7 | III |
| 8 | 4.7.8.10.11 | 1.2.3.4.8.10.11 | 4.8.10.11 | |
| 10 | 4.7.8.10.11 | 1.2.3.4.8.10.11 | 4.8.10.11 | |
| 11 | 4.7.8.10.11 | 1.2.3.4.8.10.11 | 4.8.10.11 |
| Barrier | Reachability Set | Antecedent Set | Intersection | Level |
|---|---|---|---|---|
| 1 | 1.2.3.4.8.10.11 | 1 | 1 | |
| 2 | 2.3.4.8.10.11 | 1.2 | 2 | |
| 3 | 3.4.8.10.11 | 1.2.3 | 3 | |
| 4 | 4.8.10.11 | 1.2.3.4.8.10.11 | 4.8.10.11 | IV |
| 8 | 4.8.10.11 | 1.2.3.4.8.10.11 | 4.8.10.11 | IV |
| 10 | 4.8.10.11 | 1.2.3.4.8.10.11 | 4.8.10.11 | IV |
| 11 | 4.8.10.11 | 1.2.3.4.8.10.11 | 4.8.10.11 | IV |
| Barrier | Reachability Set | Antecedent Set | Intersection Set | Level |
|---|---|---|---|---|
| 1 | 1.2.3. | 1 | 1 | VII |
| 2 | 2.3. | 1.2 | 2 | VI |
| 3 | 3. | 1.2.3 | 3 | V |
| Level | VII | VI | V | IV | IV | IV | IV | III | II | I | I | I | Level |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Barrier | G1 | G2 | G3 | G4 | T1 | T3 | T4 | S3 | S1 | S2 | T2 | T5 | |
| G1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 * | 1 * | 1 * | 1 | 1 | VII |
| G2 | 0 | 1 | 1 | 1 * | 1 * | 1 * | 1 * | 1 | 1 | 1 | 1 | 1 * | VI |
| G3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 * | 1 * | 1 * | 1 | 1 | V |
| G4 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 * | 1 * | 1 | 1 | IV |
| T1 | 0 | 0 | 0 | 1 * | 1 | 1 * | 1 | 1 * | 1 * | 1 * | 1 | 1 | IV |
| T3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 * | 1 * | 1 | 1 | IV |
| T4 | 0 | 0 | 0 | 1 | 1 | 1 * | 1 | 1 * | 1 * | 1 * | 1 | 1 | IV |
| S3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | III |
| S1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | II |
| S2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | I |
| T2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | I |
| T5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | I |
References
- Van Herk, S.; Rijke, J.; Zevenbergen, C.; Ashley, R. Understanding the Transition to Integrated Flood Risk Management in the Netherlands. Environ. Innov. Soc. Transit. 2015, 15, 84–100. [Google Scholar] [CrossRef]
- United Nations International Strategy for Disaster Reduction. UNISDR Terminology on Disaster Risk Reduction; United Nations: Geneva, Switzerland, 2009. [Google Scholar]
- Scott, M.; Kuhlicke, C.; Steinführer, A.; Sultana, P.; Thompson, P.; Minnery, J.; O’Neall, E.; Cooper, J.; Adamson, M.; Russell, E. Living with Flood Risk/The More We Know, the More We Know We Don’t Know: Reflections on a Decade of Planning, Flood Risk Management and False Precision/Searching for Resilience or Building Social Capacities for Flood Risks?/Participatory Floodplain Manage. Plan. Theory Pract. 2013, 14, 114–120. [Google Scholar] [CrossRef]
- Worldwide Fund for Nature, Mega-Stress for Megacities, A Climate Vulnerability Ranking of Major Coastal Cities in Asia. 2009. Available online: https://www.wwf.org.uk/sites/default/files/2009-13/mega_stress_cities_report.pdf (accessed on 15 January 2018).
- Mercado, J.M.R.; Kawamura, A.; Amaguchi, H. Interrelationships of the Barriers to Integrated Flood Risk Management Adaptation in Metro Manila, Philippines. Int. J. Disaster Risk Reduct. 2020, 49, 101683. [Google Scholar] [CrossRef]
- Vinke-de Kruijf, J.; Kuks, S.M.M.; Augustijn, D.C.M. Governance in Support of Integrated Flood Risk Management? The Case of Romania. Environ. Dev. 2015, 16, 104–118. [Google Scholar] [CrossRef]
- Mysiak, J.; Testella, F.; Bonaiuto, M.; Carrus, G.; De Dominicis, S.; Cancellieri, U.G.; Firus, K.; Grifoni, P. Flood Risk Management in Italy: Challenges and Opportunities for the Implementation of the EU Floods Directive (2007/60/EC). Nat. Hazards Earth Syst. Sci. 2013, 13, 2883–2890. [Google Scholar] [CrossRef]
- Samuels, P.; Klijn, F.; Dijkman, J. An Analysis of the Current Practice of Policies on River Flood Risk Management in Different Countries. Irrig. Drain. 2006, 55, S141–S150. [Google Scholar] [CrossRef]
- Xia, C.; Pahl-Wostl, C. Understanding the Development of Flood Management in the Middle Yangtze River. Environ. Innov. Soc. Transit. 2012, 5, 60–75. [Google Scholar] [CrossRef]
- Dieperink, C.; Hegger, D.L.T.; Bakker, M.H.N.; Kundzewicz, Z.W.; Green, C.; Driessen, P.P.J. Recurrent Governance Challenges in the Implementation and Alignment of Flood Risk Management Strategies: A Review. Water Resour. Manag. 2016, 30, 4467–4481. [Google Scholar] [CrossRef] [Green Version]
- Dos Muchangos, L.S.; Tokai, A.; Hanashima, A. Analyzing the Structure of Barriers to Municipal Solid Waste Management Policy Planning in Maputo City, Mozambique. Environ. Dev. 2015, 16, 76–89. [Google Scholar] [CrossRef]
- Barve, A.; Kanda, A.; Shankar, R. Analysis of Interaction among the Barriers of Third Party Logistics. Int. J. Agil. Syst. Manag. 2007, 2, 109–129. [Google Scholar] [CrossRef]
- Yadav, D.K.; Barve, A. International Journal of Disaster Risk Reduction Analysis of Critical Success Factors of Humanitarian Supply Chain: An Application of Interpretive Structural Modeling. Int. J. Disaster Risk Reduct. 2015, 12, 213–225. [Google Scholar] [CrossRef]
- Alora, A.; Barua, M.K. Barrier Analysis of Supply Chain Finance Adoption in Manufacturing Companies. Benchmarking 2019, 26, 2122–2145. [Google Scholar] [CrossRef]
- Bui, T.D.; Tsai, F.M.; Tseng, M.L.; Ali, M.D.H. Identifying Sustainable Solid Waste Management Barriers in Practice Using the Fuzzy Delphi Method. Resour. Conserv. Recycl. 2020, 154, 104625. [Google Scholar] [CrossRef]
- Ertas, A.; Smith, M.W.; Tate, D.; Lawson, W.D.; Baturalp, T.B. Complexity of System Maintainability Analysis Based on the Interpretive Structural Modeling Methodology: Transdisciplinary Approach. J. Syst. Sci. Syst. Eng. 2016, 25, 254–268. [Google Scholar] [CrossRef]
- Chandramowli, S.; Transue, M.; Felder, F.A. Analysis of Barriers to Development in Landfill Communities Using Interpretive Structural Modeling. Habitat Int. 2011, 35, 246–253. [Google Scholar] [CrossRef]
- Beikkhakhian, Y.; Javanmardi, M.; Karbasian, M.; Khayambashi, B. The Application of ISM Model in Evaluating Agile Suppliers Selection Criteria and Ranking Suppliers Using Fuzzy TOPSIS-AHP Methods. Expert Syst. Appl. 2015, 42, 6224–6236. [Google Scholar] [CrossRef]
- Thakkar, J.; Deshmukh, S.G.; Gupta, A.D.; Shankar, R. Selection of Third-Party Logistics (3PL): A Hybrid Approach Using Interpretive Structural Modeling (ISM) and Analytic Network Process (ANP). Supply Chain Forum Int. J. 2018, 6, 32–46. [Google Scholar] [CrossRef]
- Agi, M.A.N.; Nishant, R. Understanding Influential Factors on Implementing Green Supply Chain Management Practices: An Interpretive Structural Modelling Analysis. J. Environ. Manag. 2017, 188, 351–363. [Google Scholar] [CrossRef]
- Mudgal, R.K.; Shankar, R.; Talib, P.; Raj, T. Modelling the Barriers of Green Supply Chain Practices: An Indian Perspective. Int. J. Logist. Syst. Manag. 2010, 7, 81–107. [Google Scholar] [CrossRef]
- Singh, M.D.; Shankar, R.; Narain, R.; Agarwal, A. An Interpretive Structural Modeling of Knowledge Management in Engineering Industries. J. Adv. Manag. Res. 2003, 1, 28–40. [Google Scholar] [CrossRef]
- Sushil. Modified ISM/TISM Process with Simultaneous Transitivity Checks for Reducing Direct Pair Comparisons. Glob. J. Flex. Syst. Manag. 2017, 18, 331–351. [Google Scholar] [CrossRef]
- Sushil. Interpreting the Interpretive Structural Model. Glob. J. Flex. Syst. Manag. 2012, 13, 87–106. [Google Scholar] [CrossRef]
- Warfield, J.N. Binary Matrices in System Modeling. IEEE Trans. Syst. Man. Cybern. 1973, 5, 441–449. [Google Scholar] [CrossRef] [Green Version]
- Warfield, J.N. Societal Systems Planning, Policy, and Complexity. Cybern. Syst. 1978, 8, 113–115. [Google Scholar]
- Farris, D.R.; Sage, A.P. On the Use of Interpretive Structural Modeling for Worth Assessment. Comput. Electr. Eng. 1975, 2, 149–174. [Google Scholar] [CrossRef]
- Watson, R.H. Interpretive Structural Modeling—A Useful Tool for Technology Assessment? Technol. Forecast. Soc. Change 1978, 11, 165–185. [Google Scholar] [CrossRef]
- Attri, R.; Dev, N.; Sharma, V. Interpretive Structural Modelling (ISM) Approach: An Overview. Res. J. Manag. Sci. 2013, 2, 3–8. [Google Scholar] [CrossRef]
- Agarwal, A.; Shankar, R.; Tiwari, M.K. Modeling Agility of Supply Chain. Ind. Mark. Manag. 2007, 36, 443–457. [Google Scholar] [CrossRef]
- Huang, J.; Tzeng, G. Multidimensional Data in Multidimensional Scaling Using the Analytic Network Process. Pattern Recognit. Lett. 2005, 26, 755–767. [Google Scholar] [CrossRef]
- Saxena, J.P.; Sushil; Vrat, P. Impact of Indirect Relationships in Classification of Variables—A Micmac Analysis for Energy Conservation. Syst. Res. 1990, 7, 245–253. [Google Scholar] [CrossRef]
- Evers, M.; Jonoski, A.; Almoradie, A.; Lange, L. Collaborative Decision Making in Sustainable Flood Risk Management: A Socio-Technical Approach and Tools for Participatory Governance. Environ. Sci. Policy 2016, 55, 335–344. [Google Scholar] [CrossRef]
- Van Herk, S.; Zevenbergen, C.; Rijke, J.; Ashley, R.; Van Herk, S.; Zevenbergen, C.; Rijke, J.; Ashley, R. Collaborative Research to Support Transition towards Integrating Flood Risk Management in Urban Development. J. Flood Risk Manag. 2011, 4, 306–317. [Google Scholar] [CrossRef]
- Nye, M.; Tapsell, S.; Twigger-Ross, C. New Social Directions in UK Flood Risk Management: Moving towards Flood Risk Citizenship? J. Flood Risk Manag. 2011, 4, 288–297. [Google Scholar] [CrossRef]
- Faulkner, H.; Parker, D.; Green, C.; Beven, K. Developing a Translational Discourse to Communicate Uncertainty in Flood Risk between Science and the Practitioner. Ambio 2007, 36, 692–703. [Google Scholar] [CrossRef] [PubMed]
- Demeritt, D.; Nobert, S. Models of Best Practice in Flood Risk Communication and Management. Environ. Hazards 2014, 13, 313–328. [Google Scholar] [CrossRef] [Green Version]
- Rollason, E.; Bracken, L.J.; Hardy, R.J.; Large, A.R.G. Rethinking Flood Risk Communication. Nat. Hazards 2018, 92, 1665–1686. [Google Scholar] [CrossRef] [Green Version]
- Gilbuena, R.; Kawamura, A.; Medina, R.; Amaguchi, H.; Nakagawa, N. Gap Analysis of the Flood Management System in Metro Manila, Philippines: A Case Study of the Aftermath of Typhoon Ondoy. IAHS Publ. 2013, 357, 32–40. [Google Scholar]
- Hall, J.W.; Meadowcroft, I.C.; Sayers, P.B.; Bramley, M.E. Integrated Flood Risk Management in England and Wales. Nat. Hazards Rev. 2003, 4, 126–135. [Google Scholar] [CrossRef]
- Hall, J.W. Flood Risk Management: Decision Making under Uncertainty. In Applied Uncertainty Analysis for Flood Risk Management; Imperial College Press: London, UK, 2014; pp. 3–24. [Google Scholar] [CrossRef]
- Kekez, T.; Knezic, S.; Andricevic, R. Incorporating Uncertainty of the System Behavior in Flood Risk Assessment–Sava River Case Study. Water 2020, 12, 2676. [Google Scholar] [CrossRef]
- Mercado, J.M.R.; Kawamura, A.; Amaguchi, H.; Rubio, C.J.P. Fuzzy Based Multi-Criteria M&E of the Integrated Flood Risk Management Performance Using Priority Ranking Methodology: A Case Study in Metro Manila, Philippines. Int. J. Disaster Risk Reduct. 2021, 64, 102498. [Google Scholar] [CrossRef]
| Category | Barrier | Description | |
|---|---|---|---|
| Governance | G1 | Lack of a sole organizing body | Fragmented governance in flood management in Metro Manila because the current institutional framework does not have a clear demarcation of tasks among government agencies |
| G2 | Lack of communication | Weak inter-agency communication and the lack of information exchange and communication on the local level | |
| G3 | Lack of funding | Low funding for flood mitigation and control projects | |
| G4 | Lack of flood control measures | Inadequate existing flood control infrastructures | |
| Social | S1 | Informal settlers | Encroachment of marginalized communities in flood-prone areas where they can live cheaply |
| S2 | Poor solid waste management | Clogged waterways and drainages due to solid wastes | |
| S3 | Poor social planning | Services provided by the government of the Philippines are inadequate to address issues related to the community | |
| Technological Resources | T1 | Lack of technological capabilities | Absence of real-time flood forecasts, water level, and rainfall depth updates |
| T2 | Sparse data and limited access | Available hydro-meteorological information is thinly distributed, is not automated, and is measured on a large time interval only | |
| T3 | Lack of experts | Lack of experts from government agencies and local government units | |
| T4 | Lack of data processing systems | No data processing systems, which resulted in hydro-meteorological information just being stored and not used for analysis | |
| T5 | Deterioration of flood control structures | Deterioration of existing flood control structures (e.g., pumping stations, drainage systems, hydraulic control structures) due to poor maintenance and poor solid waste management |
| Multiplication | Addition | ||||||
|---|---|---|---|---|---|---|---|
| × | 0 | 1 | −1 | + | 0 | 1 | −1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | −1 |
| 1 | 0 | 1 | B | 1 | 1 | 1 | ±1/∓1 a |
| −1 | 0 | B | −1 | −1 | −1 | ±1/∓1 a | −1 |
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i | Category | Governance | Social | Technological Resources | ||||||||||
| Barrier | G1 | G2 | G3 | G4 | S1 | S2 | S3 | T1 | T2 | T3 | T4 | T5 | ||
| 1 | Governance | G1 | +++ +- | +++ ++ | +++ +0 | +00 00 | ++0 00 | ++0 00 | +++ 00 | +++ ++ | +++ +0 | +++ +± | +++ +± | |
| 2 | G2 | - - - -∓ | +++ +± | ++0 00 | +++ +0 | ++0 0+ | +++ 0± | +00 0± | +++ ±± | -00 00 | -00 00 | +00 00 | ||
| 3 | G3 | - - - - - | --- -∓ | +++ -± | -00 0± | 000 ±± | +00 0± | +++ -± | +++ 0± | +++ 0± | +++ ± ± | +++ ±± | ||
| 4 | G4 | - - - -0 | --0 00 | --- +∓ | +00 0± | +00 00 | +++ 00 | +++ +± | +++ +± | ++± ±± | +0± ±± | +++ ++ | ||
| 5 | Social | S1 | -00 00 | --- -0 | +00 0∓ | -00 0∓ | +++ +± | +-- -± | 000 00 | 000 00 | 000 00 | 000 00 | 000 0± | |
| 6 | S2 | --0 00 | --0 0- | 000 ∓∓ | -00 00 | --- -∓ | --- 00 | -00 00 | 000 00 | -00 00 | 000 00 | 000 0± | ||
| 7 | S3 | --0 00 | --- 0∓ | -00 0∓ | --- 00 | -++ +∓ | +++ 00 | -00 00 | -00 0± | --- 00 | 000 ±± | 000 0± | ||
| 8 | Technological Resources | T1 | --- 00 | -00 0∓ | --- +∓ | --- -∓ | 000 00 | +00 00 | +00 00 | +++ +± | ++- -- | +±± ±± | +++ 0± | |
| 9 | T2 | --- -- | --- ∓∓ | --- 0∓ | --- -∓ | 000 00 | 000 00 | +00 0∓ | --- -∓ | +-- -- | +-- -± | +00 0± | ||
| 10 | T3 | --- -0 | +00 00 | --- 0∓ | --∓ ∓∓ | 000 00 | +00 00 | +++ 00 | --+ ++ | -++ ++ | +++ 00 | +++ 00 | ||
| 11 | T4 | --- -∓ | +00 00 | --- ∓∓ | -0∓ ∓∓ | 000 00 | 000 00 | 000 ∓∓ | -∓∓ ∓∓ | -++ +∓ | --- 00 | 0+0 ++ | ||
| 12 | T5 | --- -∓ | -00 00 | --- ∓∓ | --- -- | 000 0∓ | 000 0∓ | 000 0∓ | --- 0∓ | -00 0∓ | --- ∓∓ | 0-0 -- | ||
| i | j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Barrier | G1 | G2 | G3 | G4 | S1 | S2 | S3 | T1 | T2 | T3 | T4 | T5 | |
| 1 | G1 | + | + | + | 0 | 0 | 0 | + | + | + | + | + | |
| 2 | G2 | − | + | 0 | + | + | + | 0 | + | 0 | 0 | 0 | |
| 3 | G3 | − | − | + | 0 | 0 | 0 | + | + | + | + | + | |
| 4 | G4 | − | 0 | − | 0 | 0 | + | + | + | ± | ± | + | |
| 5 | S1 | 0 | − | 0 | 0 | + | − | 0 | 0 | 0 | 0 | 0 | |
| 6 | S2 | 0 | − | 0 | 0 | − | − | 0 | 0 | 0 | 0 | 0 | |
| 7 | S3 | 0 | − | 0 | − | + | + | 0 | 0 | - | 0 | 0 | |
| 8 | T1 | − | 0 | − | − | 0 | 0 | 0 | + | − | ± | + | |
| 9 | T2 | − | − | − | − | 0 | 0 | 0 | − | − | − | 0 | |
| 10 | T3 | − | 0 | − | ∓ | 0 | 0 | + | + | + | + | + | |
| 11 | T4 | − | 0 | − | ∓ | 0 | 0 | 0 | ∓ | + | − | + | |
| 12 | T5 | − | 0 | − | - | 0 | 0 | 0 | − | 0 | − | − |
| i | j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Barrier | G1 | G2 | G3 | G4 | S1 | S2 | S3 | T1 | T2 | T3 | T4 | T5 | |
| 1 | G1 | ±1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 2 | G2 | −1 | ±1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 3 | G3 | −1 | −1 | ±1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 4 | G4 | −1 | 0 | −1 | ±1 | 0 | 0 | 1 | 1 | 1 | ±1 | ±1 | 1 |
| 5 | S1 | 0 | −1 | 0 | 0 | ±1 | 1 | −1 | 0 | 0 | 0 | 0 | 0 |
| 6 | S2 | 0 | −1 | 0 | 0 | −1 | ±1 | −1 | 0 | 0 | 0 | 0 | 0 |
| 7 | S3 | 0 | −1 | 0 | −1 | 1 | 1 | ±1 | 0 | 0 | −1 | 0 | 0 |
| 8 | T1 | −1 | 0 | −1 | −1 | 0 | 0 | 0 | ±1 | 1 | −1 | ±1 | 1 |
| 9 | T2 | −1 | −1 | −1 | −1 | 0 | 0 | 0 | −1 | ±1 | −1 | −1 | 0 |
| 10 | T3 | −1 | 0 | −1 | ∓1 | 0 | 0 | 1 | 1 | 1 | ±1 | 1 | 1 |
| 11 | T4 | −1 | 0 | −1 | ∓1 | 0 | 0 | 0 | ∓1 | 1 | −1 | ±1 | 1 |
| 12 | T5 | −1 | 0 | −1 | −1 | 0 | 0 | 0 | −1 | 0 | −1 | −1 | ±1 |
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i | Barrier | G1 | G2 | G3 | G4 | S1 | S2 | S3 | T1 | T2 | T3 | T4 | T5 |
| 1 | G1 | 1 | 1 | 1 | 1 | 1 * | 1 * | 1 * | 1 | 1 | 1 | 1 | 1 |
| 2 | G2 | 0 | 1 | 1 | 1 * | 1 | 1 | 1 | 1 * | 1 | 1 * | 1 * | 1 * |
| 3 | G3 | 0 | 0 | 1 | 1 | 1 ** | 1 ** | 1 * | 1 | 1 | 1 | 1 | 1 |
| 4 | G4 | 0 | 0 | 0 | 1 | 1 * | 1 * | 1 | 1 | 1 | 1 | 1 | 1 |
| 5 | S1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | S2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | S3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 8 | T1 | 0 | 0 | 0 | 1 * | 1 *** | 1 *** | 1 ** | 1 | 1 | 1 ** | 1 | 1 |
| 9 | T2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 10 | T3 | 0 | 0 | 0 | 1 | 1 * | 1 * | 1 | 1 | 1 | 1 | 1 | 1 |
| 11 | T4 | 0 | 0 | 0 | 1 | 1 ** | 1 ** | 1 * | 1 | 1 | 1 * | 1 | 1 |
| 12 | T5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i | Barrier | G1 | G2 | G3 | G4 | S1 | S2 | S3 | T1 | T2 | T3 | T4 | T5 |
| 1 | G1 | −1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | G2 | −1 | −1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | G3 | −1 | −1 | −1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | G4 | −1 | −1 * | −1 | −1 | 0 | 0 | 0 | −1 * | 0 | −1 | −1 | 0 |
| 5 | S1 | −1 * | −1 | −1 ** | −1 * | −1 | 0 | −1 | −1 *** | 0 | −1 * | −1 ** | 0 |
| 6 | S2 | −1 * | −1 | −1 ** | −1 * | −1 | −1 | −1 | −1 *** | 0 | −1 * | −1 ** | 0 |
| 7 | S3 | −1 * | −1 | −1 * | −1 | 0 | 0 | −1 | −1 ** | 0 | −1 | −1 * | 0 |
| 8 | T1 | −1 | −1 * | −1 | −1 | 0 | 0 | 0 | −1 | 0 | −1 | −1 | 0 |
| 9 | T2 | −1 | −1 | −1 | −1 | 0 | 0 | 0 | −1 | −1 | −1 | −1 | 0 |
| 10 | T3 | −1 | −1 * | −1 | −1 | 0 | 0 | 0 | −1 ** | 0 | −1 | −1 * | 0 |
| 11 | T4 | −1 | −1 * | −1 | −1 | 0 | 0 | 0 | −1 | 0 | −1 | −1 | 0 |
| 12 | T5 | −1 | −1 * | −1 | −1 | 0 | 0 | 0 | −1 | 0 | −1 | −1 | −1 |
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | Level | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i | Barrier | G1 | G2 | G3 | G4 | S1 | S2 | S3 | T1 | T2 | T3 | T4 | T5 | |
| 1 | G1 | ±1 | 1 | 1 | 1 | 1 * | 1 * | 1 * | 1 | 1 | 1 | 1 | 1 | 12 |
| 2 | G2 | −1 | ±1 | 1 | 1 * | 1 | 1 | 1 | 1 * | 1 | 1 * | 1 * | 1 * | 11 |
| 3 | G3 | −1 | −1 | ±1 | 1 | 1 ** | 1 ** | 1 * | 1 | 1 | 1 | 1 | 1 | 10 |
| 4 | G4 | −1 | −1 * | −1 | ±1 | 1 * | 1 * | 1 | ±1 * | 1 | ±1 | ±1 | 1 | 9 |
| 5 | S1 | −1 * | −1 | −1 ** | −1 * | ±1 | 1 | −1 | −1 *** | 0 | −1 * | −1 ** | 0 | 2 |
| 6 | S2 | −1 * | −1 | −1 ** | −1 * | −1 | ±1 | −1 | −1 *** | 0 | −1 * | −1 ** | 0 | 1 |
| 7 | S3 | −1 * | −1 | −1 * | −1 | 1 | 1 | ±1 | −1 ** | 0 | −1 | −1 * | 0 | 3 |
| 8 | T1 | −1 | −1 * | −1 | ∓1 * | 1 *** | 1 *** | 1 ** | ±1 | 1 | ∓1 ** | ±1 | 1 | 9 |
| 9 | T2 | −1 | −1 | −1 | −1 | 0 | 0 | 0 | −1 | ±1 | −1 | −1 | 0 | 1 |
| 10 | T3 | −1 | −1 * | −1 | ∓1 | 1 * | 1 * | 1 | ±1 ** | 1 | ±1 | ±1 * | 1 | 9 |
| 11 | T4 | −1 | −1 * | −1 | ∓1 | 1 ** | 1 ** | 1 * | ∓1 | 1 | ∓1 * | ±1 | 1 | 9 |
| 12 | T5 | −1 | −1 * | −1 | −1 | 0 | 0 | 0 | −1 | 0 | −1 | −1 | ±1 | 1 |
| Level | 12 | 11 | 10 | 9 | 9 | 9 | 9 | 3 | 2 | 1 | 1 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Barrier | G1 | G2 | G3 | G4 | T1 | T3 | T4 | S3 | S1 | S2 | T2 | T5 | |
| 12 | G1 | ±1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 * | 1 * | 1 * | 1 | 1 |
| 11 | G2 | −1 | ±1 | 1 | 1 * | 1 * | 1 * | 1 * | 1 | 1 | 1 | 1 | 1 * |
| 10 | G3 | −1 | −1 | ±1 | 1 | 1 | 1 | 1 | 1 * | 1 ** | 1 ** | 1 | 1 |
| 9 | G4 | −1 | −1 * | −1 | ±1 | ±1 * | ±1 | ±1 | 1 | 1 * | 1 * | 1 | 1 |
| 9 | T1 | −1 | −1 * | −1 | ∓1 * | ±1 | ∓1 ** | ±1 | 1 ** | 1 *** | 1 *** | 1 | 1 |
| 9 | T3 | −1 | −1 * | −1 | ∓1 | ±1 | ±1 | ±1 | 1 | 1 * | 1 * | 1 | 1 |
| 9 | T4 | −1 | −1 * | −1 | ∓1 | ∓1 | ∓1 * | ±1 | 1 * | 1 ** | 1 ** | 1 | 1 |
| 3 | S3 | −1 * | −1 | −1 * | −1 | −1 ** | −1 | −1 * | ±1 | 1 | 1 | 0 | 0 |
| 2 | S1 | −1 * | −1 | −1 ** | −1 * | −1 *** | −1 * | −1 ** | −1 | ±1 | 1 | 0 | 0 |
| 1 | S2 | −1 * | −1 | −1 ** | −1 * | −1 *** | −1 * | −1 ** | −1 | −1 | ±1 | 0 | 0 |
| 1 | T2 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 0 | 0 | 0 | ±1 | 0 |
| 1 | T5 | −1 | −1 * | −1 | −1 | −1 | −1 | −1 | 0 | 0 | 0 | 0 | ±1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mercado, J.M.; Kawamura, A.; Medina, R. An Expanded Interpretive Structural Modeling Analysis of the Barriers to Integrated Flood Risk Management Adaptation in Metro Manila. Water 2023, 15, 1029. https://doi.org/10.3390/w15061029
Mercado JM, Kawamura A, Medina R. An Expanded Interpretive Structural Modeling Analysis of the Barriers to Integrated Flood Risk Management Adaptation in Metro Manila. Water. 2023; 15(6):1029. https://doi.org/10.3390/w15061029
Chicago/Turabian StyleMercado, Jean Margaret, Akira Kawamura, and Reynaldo Medina. 2023. "An Expanded Interpretive Structural Modeling Analysis of the Barriers to Integrated Flood Risk Management Adaptation in Metro Manila" Water 15, no. 6: 1029. https://doi.org/10.3390/w15061029




